Projeto de Controladores
Aula de 28/04/2025. Iniciando nova seção de trabalho (recuperando arquivo dados.mat):
xxxxxxxxxx>> diary aula_2804025.txt>> % Recuperando dados da aula anterior:>> what % lembrar/veriricar arquivos de dadosMATLAB Code files in the current folder /Volumes/DADOS/Users/fpassold/Documents/UPF/Controle_3/2025_1find_polo_zero_d MAT-files in the current folder /Volumes/DADOS/Users/fpassold/Documents/UPF/Controle_3/2025_1ControlSystemDesignerSession-PI3 ControlSystemDesignerSession_PI1a dados >> load dados % carregando dados da aula passada>> close all % fechhando qualquer janela gráfica abertaProjeto de ControladoresProjeto Controladores Ação DerivativaProjeto de PD 1Projeto de PD 2: opção (c)Projeto de PD 3: Opção (d)
Projeto Controladores Ação Derivativa
Teoria sobre Ação Derivativa? Rever:
- Teoria inicial sobre Ação Derivativa + Filtros;
- Resumo Controladores PD & Lead (arquivo PDF; Aula de 21/05/2020);
Projeto de PD 1
Nosso controlador segue a eq. genérica:
Como se trata de um PD já sabemos onde estará localizado o pólo deste controlador (; na origem do plano-z). Nossa única incógnita está associada com saber onde posicionar o zero deste controlar, mas sabemos que (não pode estar localizado sobre o círculo unitário). Mas pode-se especultar 3 posições diferentes para o zero deste controlador quando associado com planta que desejamos controlar:
xxxxxxxxxx>> zpk(BoG) % lembrando da nossa plantaans = 0.00012224 (z+2.747) (z+0.1903) -------------------------------- (z-0.9048) (z-0.8187) (z-0.3679) Sample time: 0.1 secondsDiscrete-time zero/pole/gain model.Analisando 3 opções para o zero do PD (recomenda-se ver antes: Projeto de Controlador PD (Aula de 28/05/2020)):
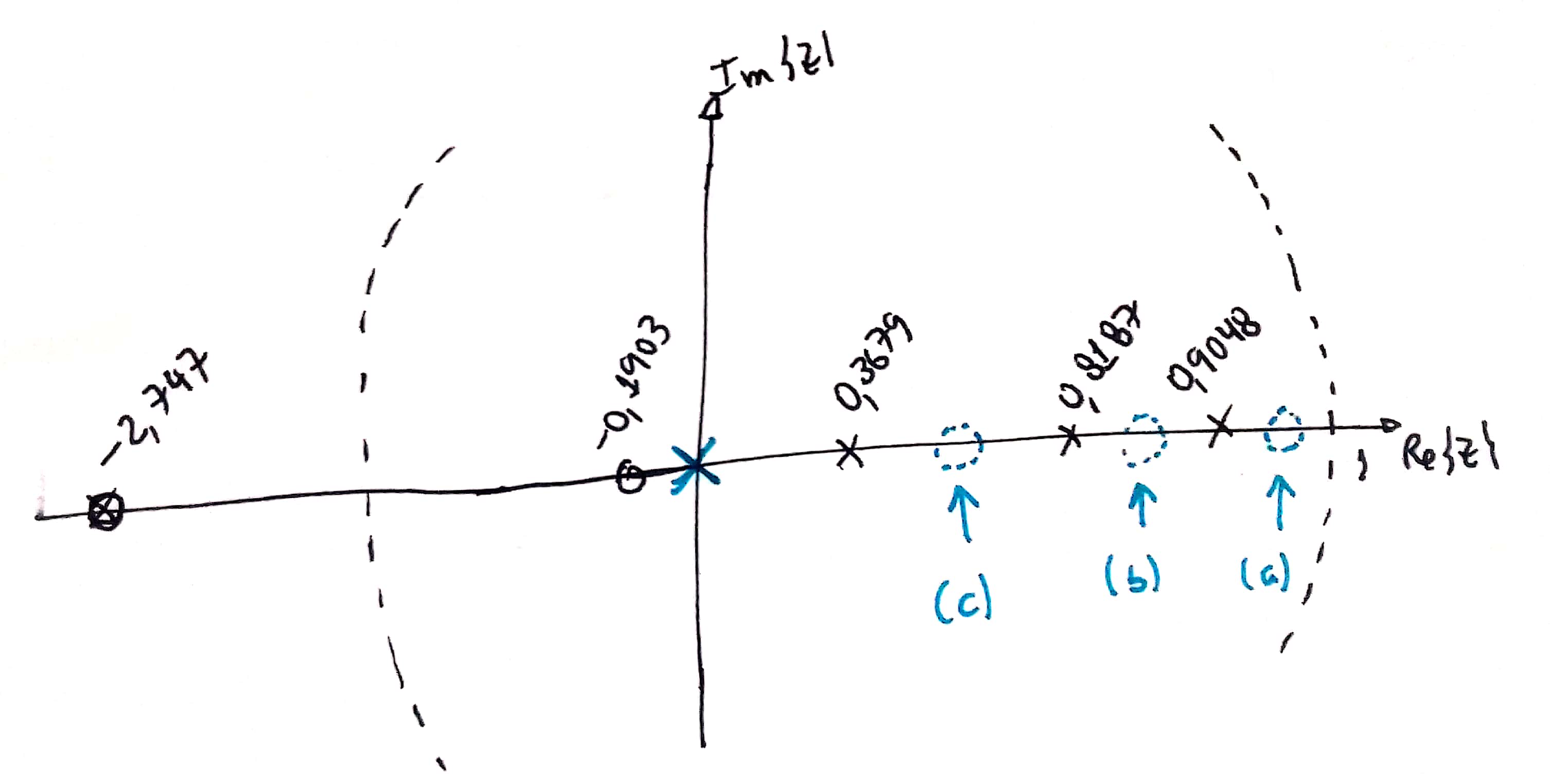
Casos sendo analisados:
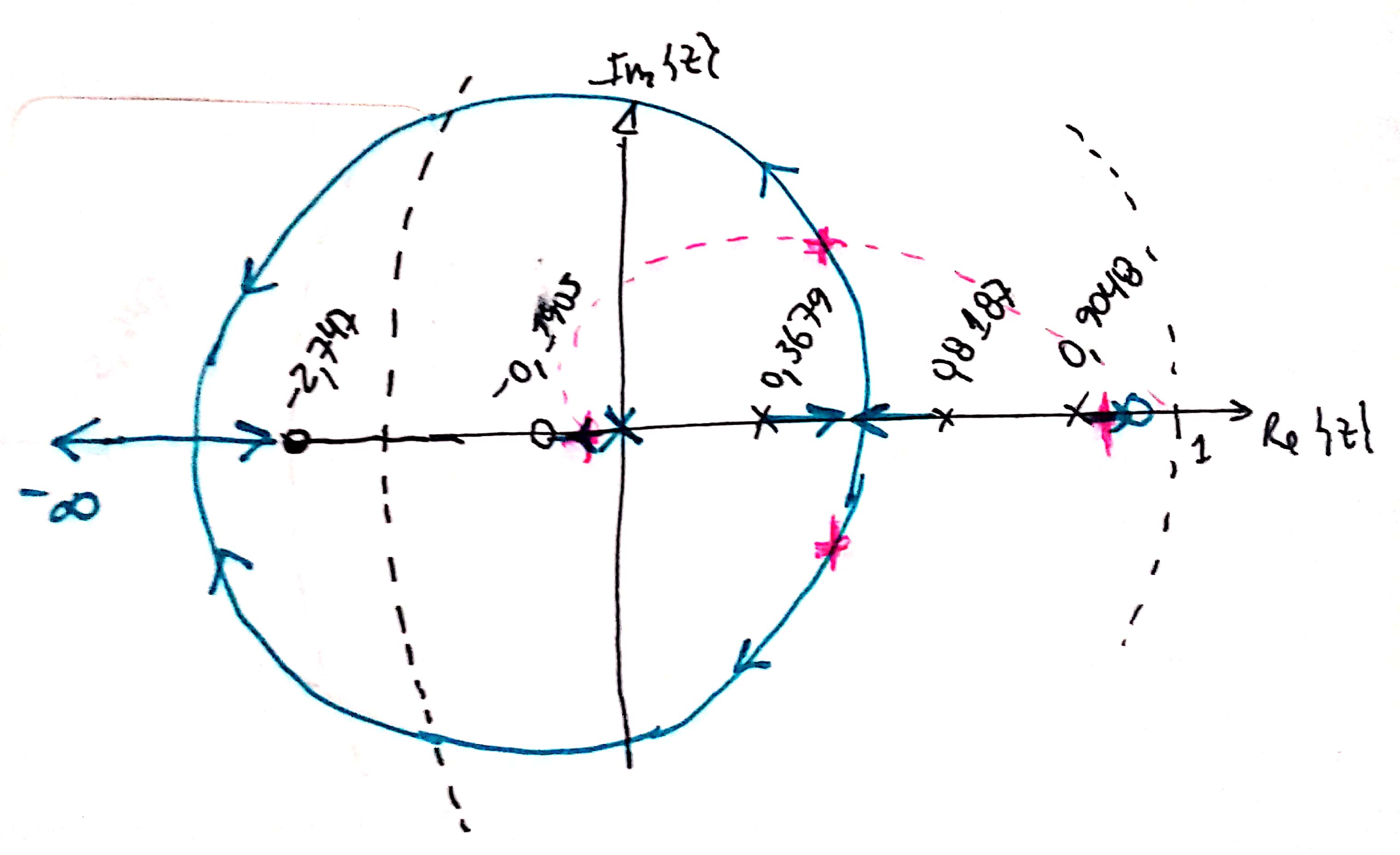
- a) : o esboço do RL revela:
- b) : o esboço deste RL revela:
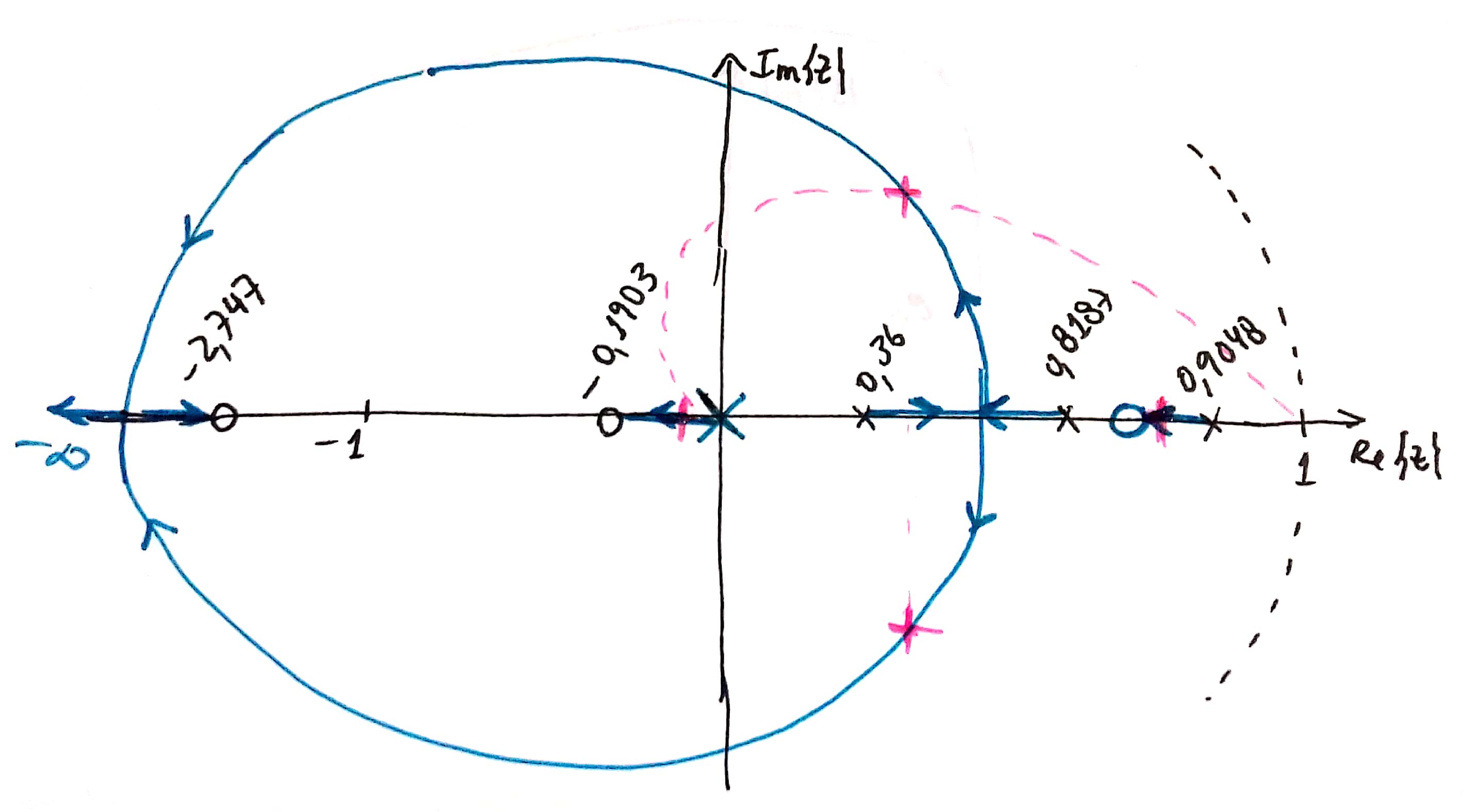 Comparando (a) e (b), percebemos que esta opção (b) é melhor que a opção (a).
Comparando (a) e (b), percebemos que esta opção (b) é melhor que a opção (a). - c) : este RL revela:
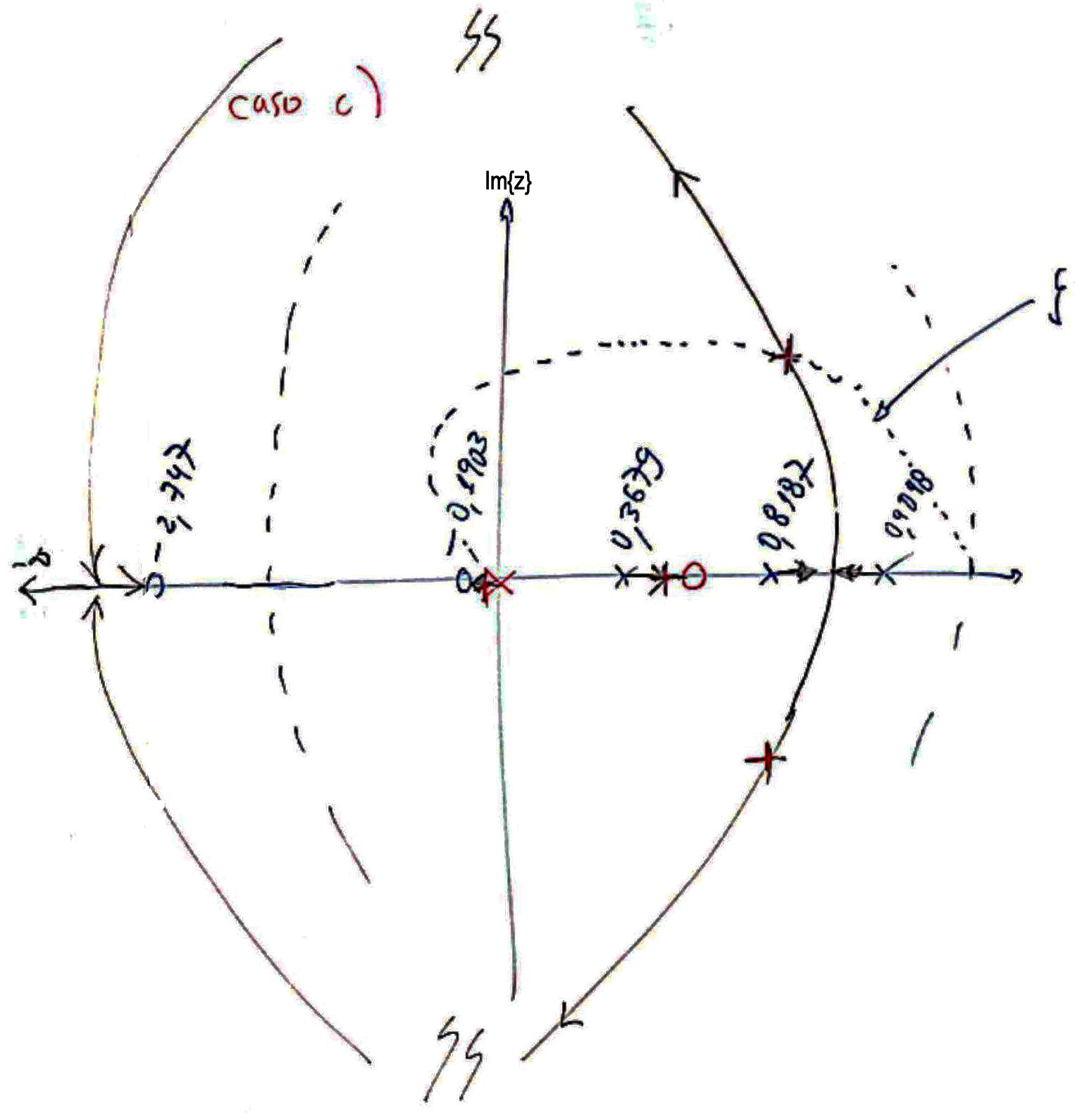 A opção (c) parece tão boa quanto a opção (b).
A opção (c) parece tão boa quanto a opção (b).
Iniciando pelo controlador do caso (b):
xxxxxxxxxx>> C_PDb = tf([1 -0.85], [1 0], T) % definindo tf deste controladorC_PDb = z - 0.85 -------- z Sample time: 0.1 secondsDiscrete-time transfer function.Completando projeto usando App Control System Designer:
Segue 1a-versão do PDb:
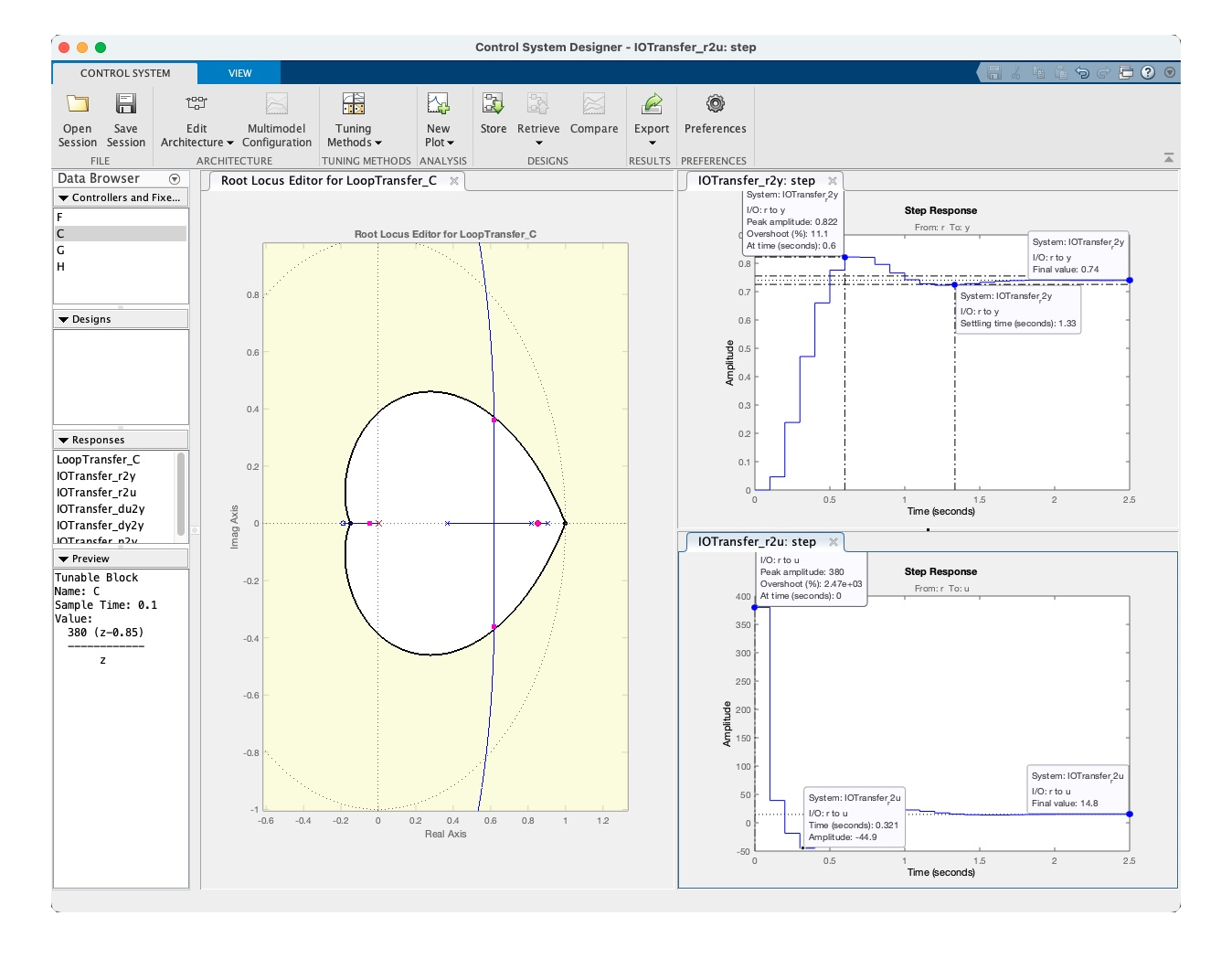
Notamos que O tempo de assentamento deste PD em comparação ao Controlador Proporcianal é quase 4 vezes menor. Os projetos anteriores de controladores Proporcinais (aula 31/03/2025) permitiram: (segundos).
Melhorando esta versão: aumentando o ganho para ():
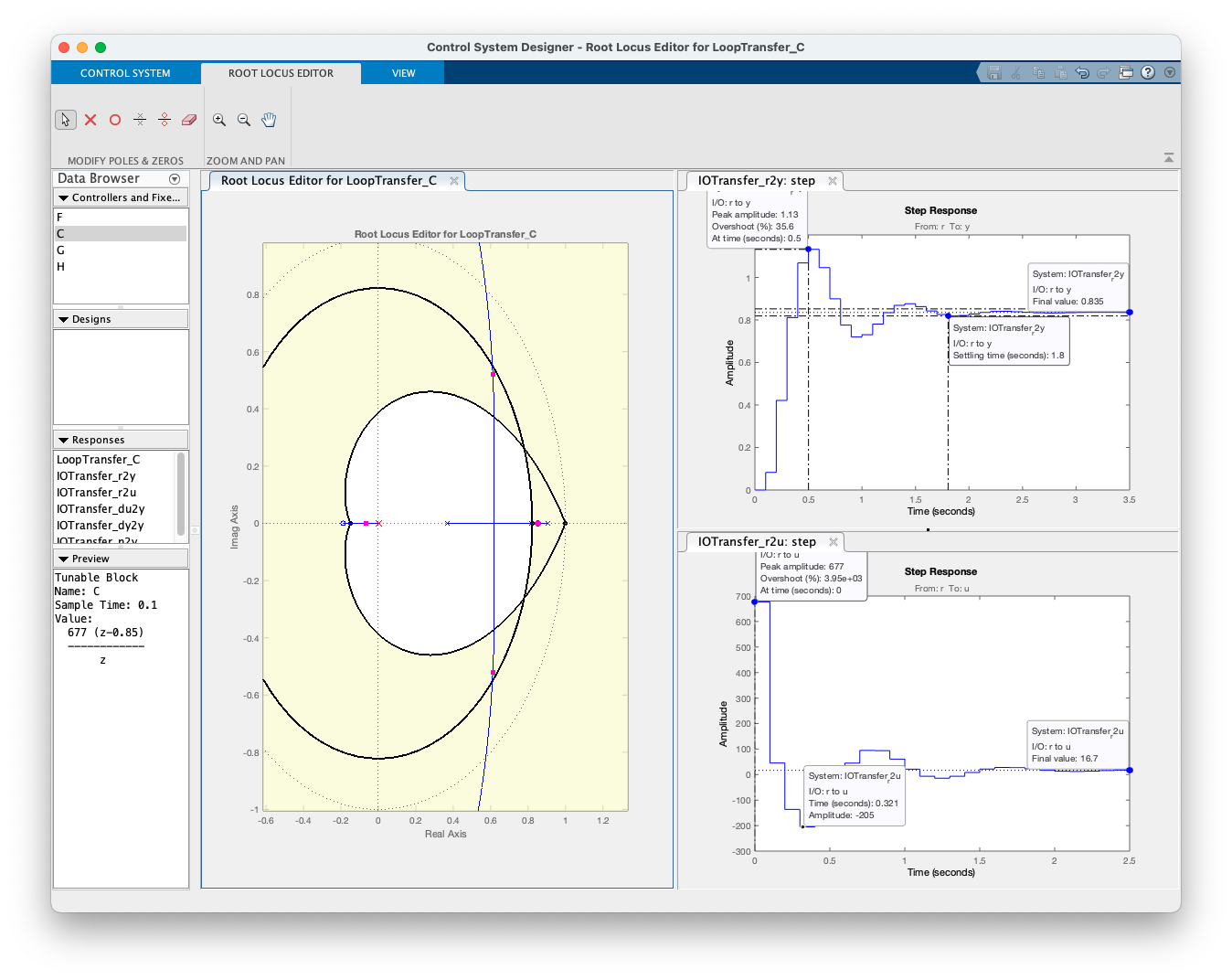
Supondo que a "meta" seja projetar um controlador duas vez mais rápido que um Controlador Proporcional, teremos um requisito como: (segundos).
Obs.: Lembrar de exportar tf deste controlador para uma variável no workspace, neste caso: PDb:
xxxxxxxxxx>> zpk(PDb)ans = 677 (z-0.85) ------------ z Name: CSample time: 0.1 secondsDiscrete-time zero/pole/gain model.>> Falta testar: Opção (c) e opção (d) (o zero do PD cancela o 2o-pólo mais lento da planta).
Projeto de PD 2: opção (c)
A idéia deste PD é alocar o zero do PD entre os 2 pólos mais "internos" da planta: :
xxxxxxxxxx>> zero_PDc=(0.8187+0.3679)/2zero_PDc = 0.5933Completando o projeto no App Control System Designer
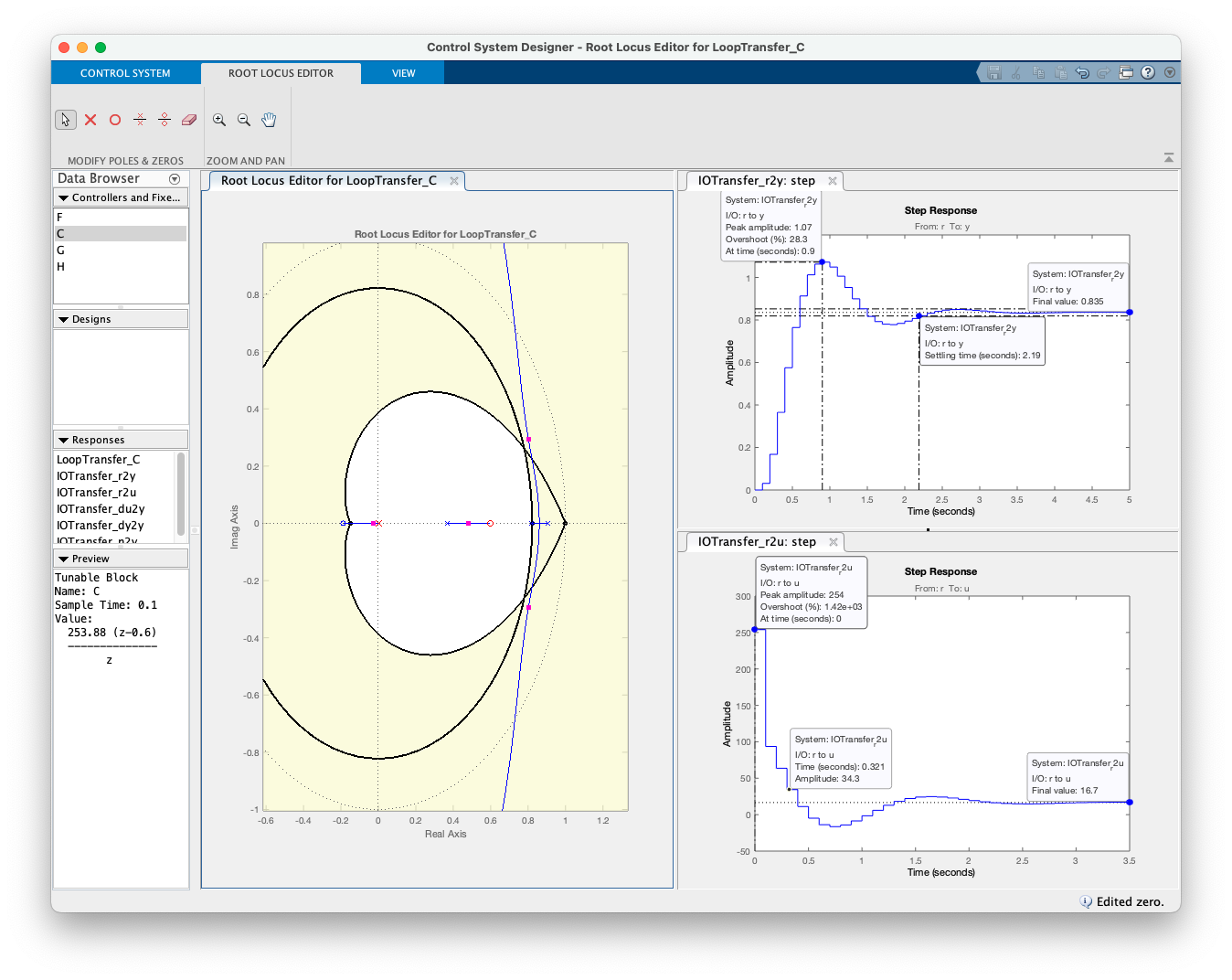
Arrastando zero do controlador para mais próximo do pólo em :
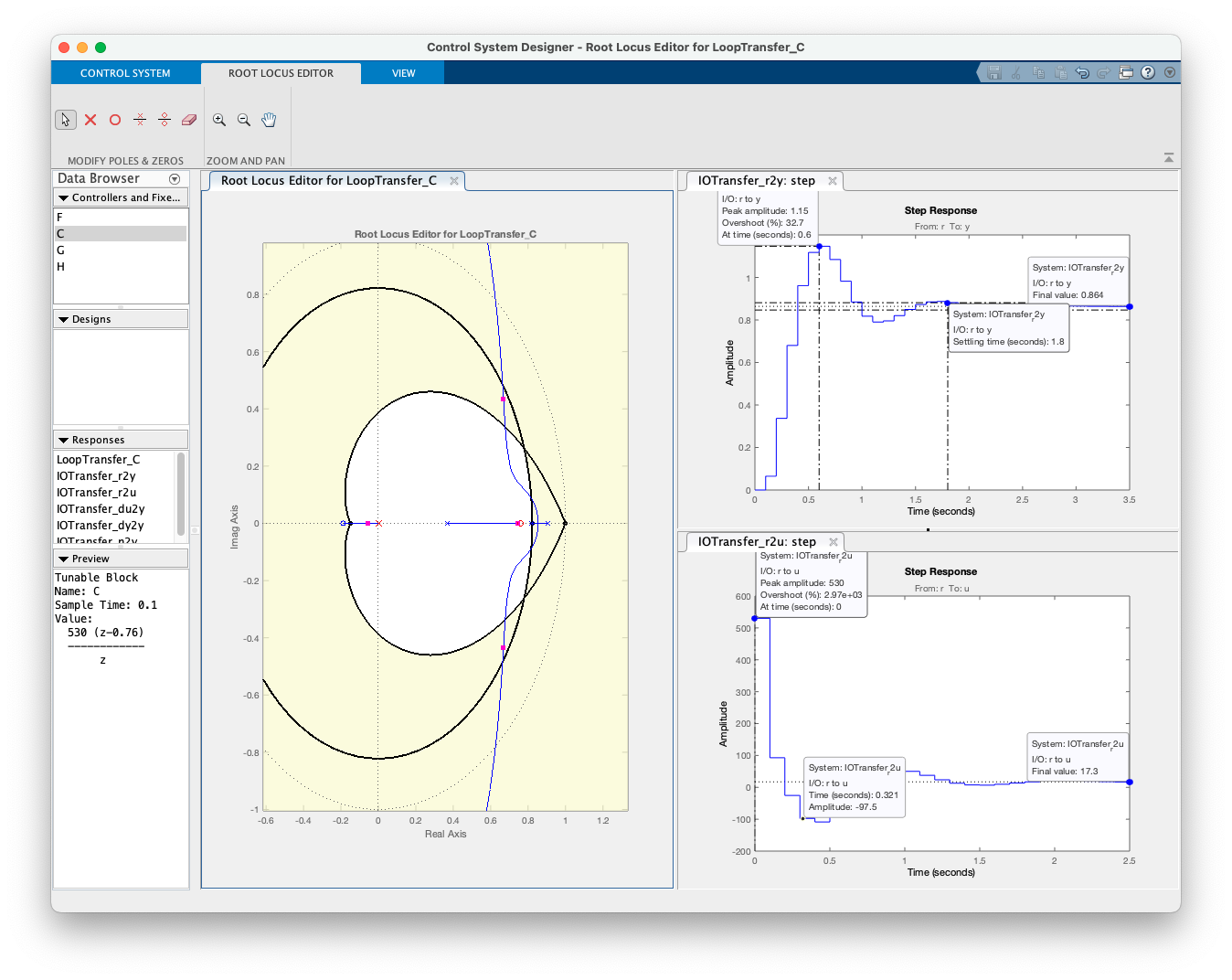
Exportado a tf deste controlador na variável PDc:
xxxxxxxxxx>> zpk(PDc)ans = 530 (z-0.76) ------------ z Name: CSample time: 0.1 secondsDiscrete-time zero/pole/gain model.>> Comparando este PD com o anterior:
| Parâmentros | PD (b) | PD (c) |
|---|---|---|
| 1,8 | 1,8 | |
| 1,13 | 1,15 | |
| 0,835 | 0,864 | |
| 16,5% | 13,6% | |
| 677 | 530 | |
Este PD é similar em desempenho ao PD anterior, e este PD (c), gera uma "pressão de controle" (amplitudes máximas do sinal de controle, ) mais baixa que o PD (b), por este motivo, é preferível inmplementar o PD (c), além de resultar num erro de regime permanente ligeiramente menor.
Resta testar um PD que cancela o 2o-pólo mais lento da planta.
Projeto de PD 3: Opção (d)
Desta vez, vamos alocar o zero do PD exatamente sobre o 2o-pólo mais lento da planta em
xxxxxxxxxxzpk(BoG)ans = 0.00012224 (z+2.747) (z+0.1903) -------------------------------- (z-0.9048) (z-0.8187) (z-0.3679) Sample time: 0.1 secondsDiscrete-time zero/pole/gain model.Controlador PD (d) sintonizado:
xxxxxxxxxx>> zpk(PDd)ans = 630 (z-0.8187) -------------- z Name: CSample time: 0.1 secondsDiscrete-time zero/pole/gain model.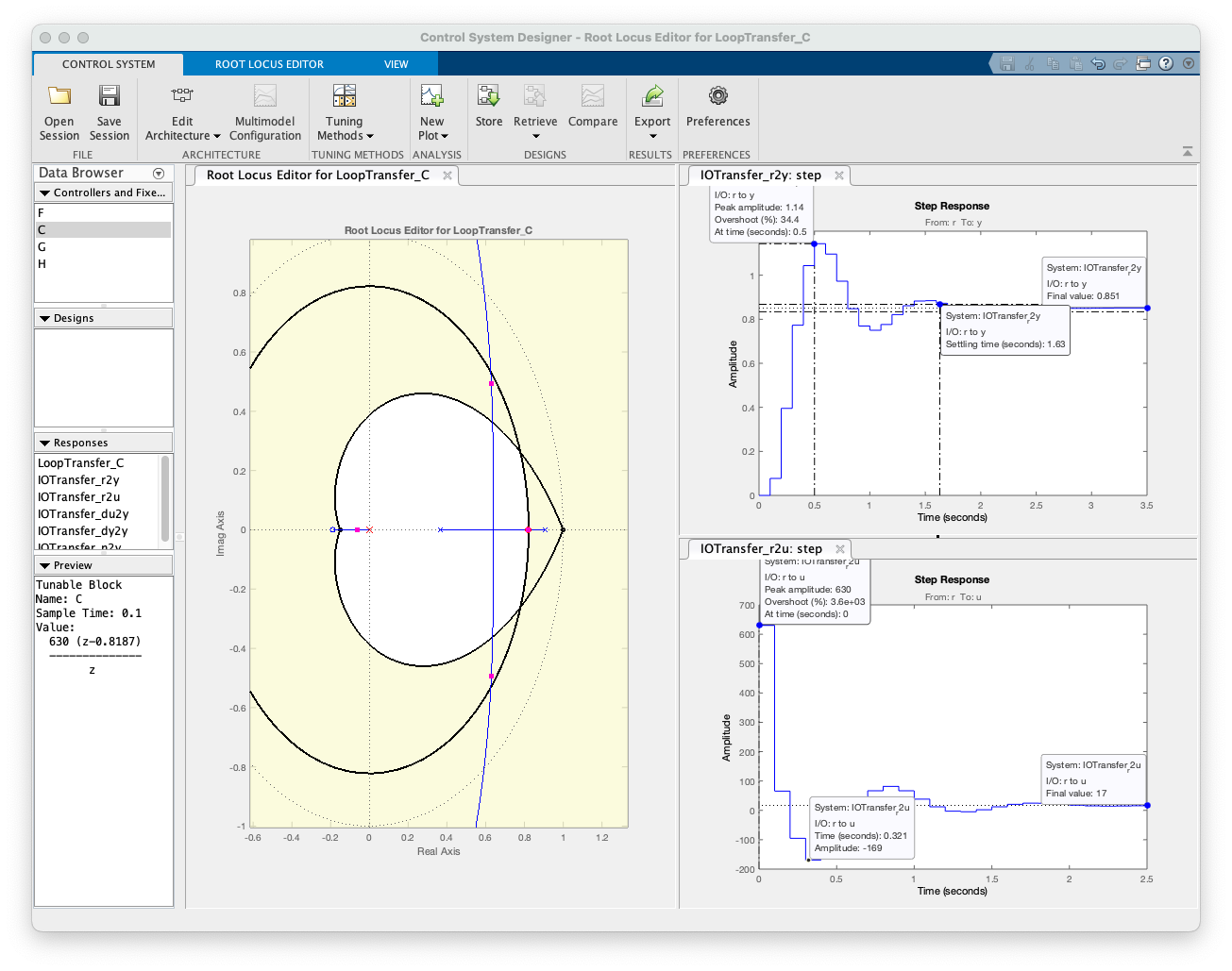
Note:
- com o cancelamento do 2o-pólo mais lento da planta, reduzimos a complexidade do sistema em MF (de 4a-ordem passou para 3a-ordem, em MF);
- Este é o PD mais rápido possível para esta planta.
Última tabela comparativa:
| Parâmentros | PD (b) | PD (c) | PD (d) |
|---|---|---|---|
| 1,8 | 1,8 | 1,63 | |
| 1,13 | 1,15 | 1,14 | |
| 0,835 | 0,864 | 0,851 | |
| 16,5% | 13,6% | 14,9% | |
| 677 | 530 | 630 | |
Se quisermos comparar respostas à entrada degrau destes controladores:
xxxxxxxxxx>> ftma_PDb=PDb*BoG;>> ftma_PDc=PDc*BoG;>> ftma_PDd=PDd*BoG;>> ftmf_PDb=feedback(ftma_PDb,1);>> ftmf_PDc=feedback(ftma_PDc,1);>> ftmf_PDd=feedback(ftma_PDd,1);>> figure; step(ftmf_PDb, ftmf_PDc, ftmf_PDd, ftmf_K)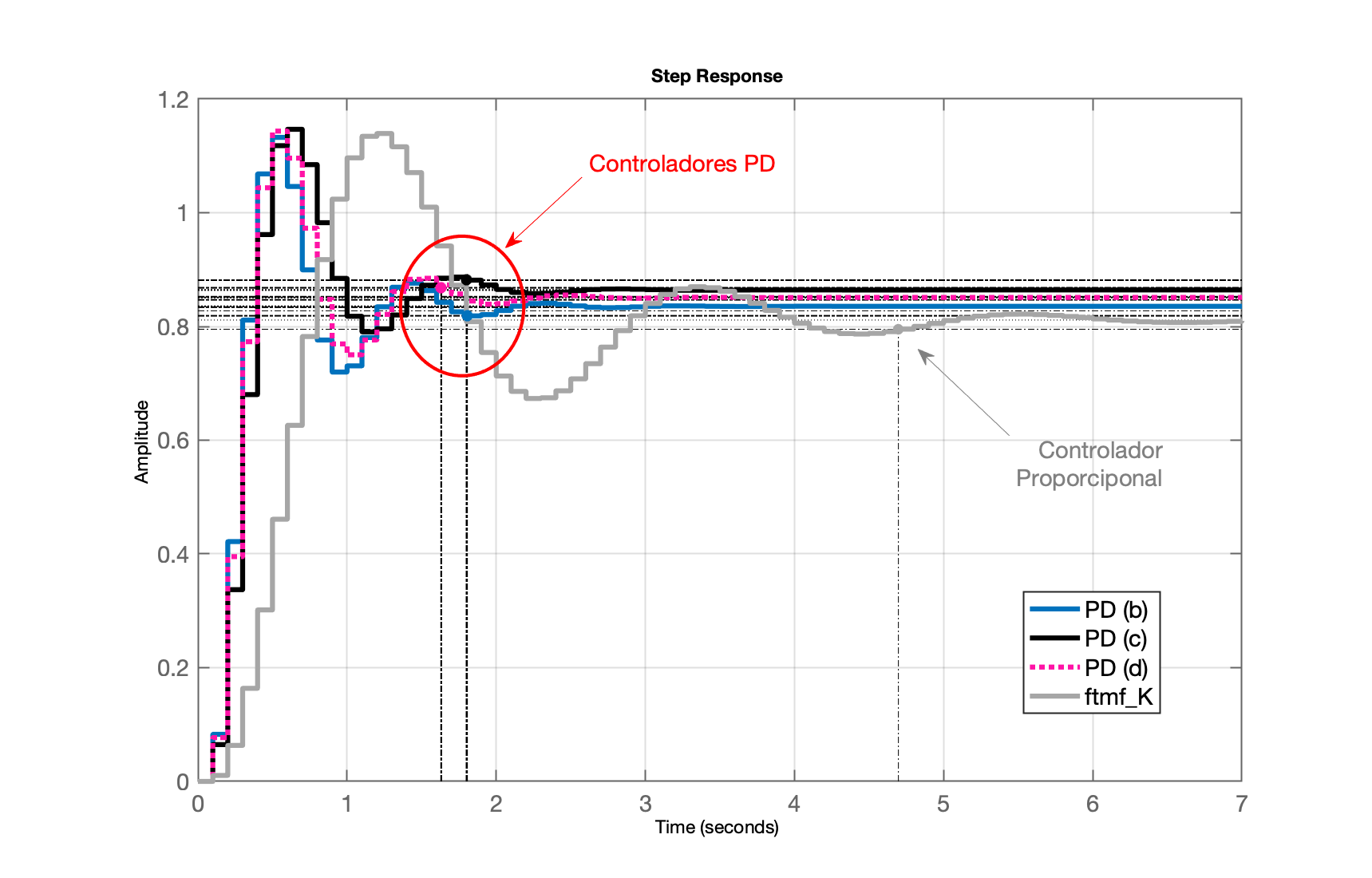
Obs.: ftmf_K corresponde ao controlador Proporcional com .
Encerrando atividades desta aula:
xxxxxxxxxx>> save dados>> diary off>> quitFernando Passold, em 28/04/2025
