Projeto de Controladores Digitais usando RL

Ingressando Planta

Obs.: dorvanente neste curso, vamos usar sempre a mesma placa, um modelo de 3a-ordem para realizar diferentes projetos de controladores.

Ingressando com a planta (mundo contínuo):

​x
>> G=tf(1, poly([-1 -2 -10]))
​
G =
 
             1
  ------------------------
  s^3 + 13 s^2 + 32 s + 20
 
Continuous-time transfer function.
​
>> zpk(G) % para perceber pólos e zeros
ans =
 
          1
  ------------------
  (s+10) (s+2) (s+1)
 
Continuous-time zero/pole/gain model.
​
>> T=0.1; % periodo de amostragem
>> BoG= c2d(G, T)  % incluindo sustentador de ordem zero, cálculo de BoG(z)
​
BoG =
 
  0.0001222 z^2 + 0.0003591 z + 6.391e-05
  ---------------------------------------
    z^3 - 2.091 z^2 + 1.375 z - 0.2725
 
Sample time: 0.1 seconds
Discrete-time transfer function.
​
>> zpk(BoG)
ans =
 
  0.00012224 (z+2.747) (z+0.1903)
  --------------------------------
  (z-0.9048) (z-0.8187) (z-0.3679)
 
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.

Controlador Proporcional

Iniciando com controlador mais simples possível. Ganho proporcional. E usando valor unitário. Verificando o que acontece com o sistema em MF.

xxxxxxxxxx
>> K=1;
>> ftmf=feedback(K*BoG, 1)
ftmf =
 
  0.0001222 z^2 + 0.0003591 z + 6.391e-05
  ---------------------------------------
    z^3 - 2.091 z^2 + 1.375 z - 0.2725
 
Sample time: 0.1 seconds
Discrete-time transfer function.
​
>> step(ftmf)   % resposta à referência (degrau unitário)

A resposta deste sistema para referência sendo um degrau unitário é mostrado na próxima figura:

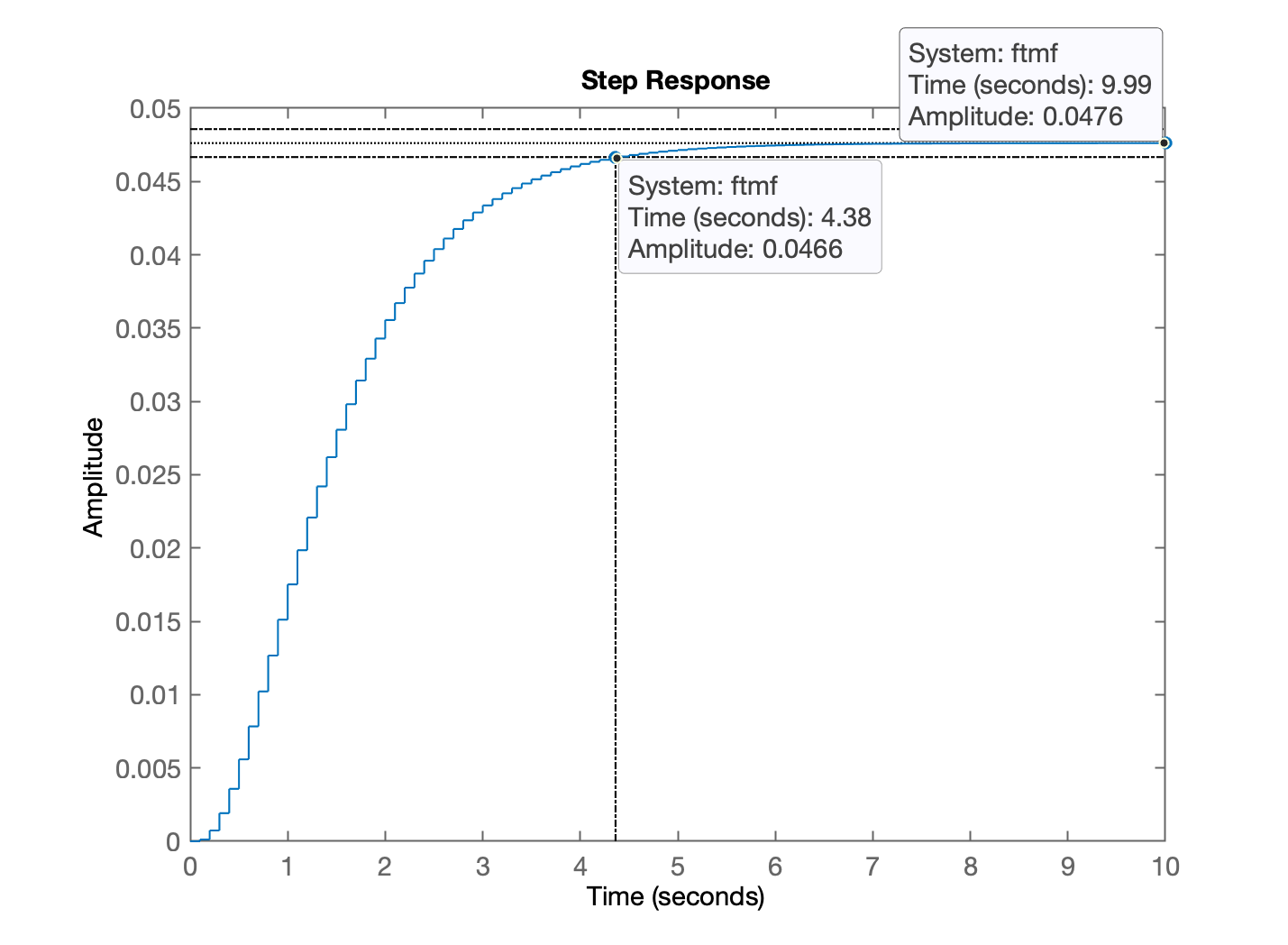
Percebe-se que obviamente fechar a malha com um simples controlador proporcional com ganho unitário "não resolve" o sistema em MF (erro elevadíssimo, a saída do sistema em MF, deveria alcançar a mesma amplitude da referência adotada, o degrau unitário, e no caso: $y[\infty] < 0,05$).

Para começar a compreender este sitema começamos levantando o RL (Root Locus) do sistema:

xxxxxxxxxx
>> rlocus(BoG)
>> xlim([-8 2]) % concentrando o RL numa certa região

Assim, para esta planta ($BoG(z)$), obtemos o seguinte diagrama do lugar geométrico das raízes:

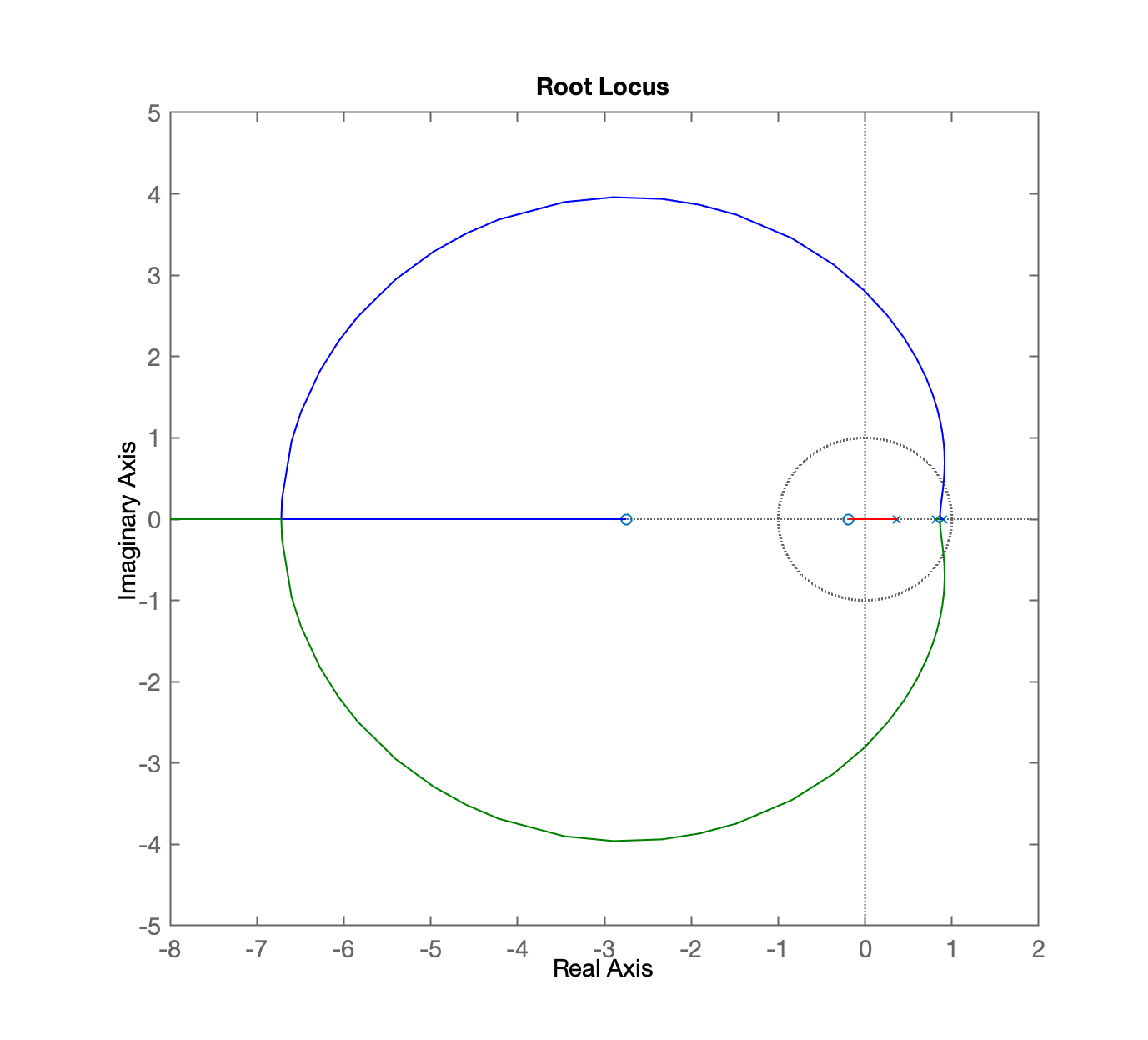
Interpretando o RL...

xxxxxxxxxx
>> zpk(BoG) % lembrando da eq. de BoG(z)
ans =
 
  0.00012224 (z+2.747) (z+0.1903)
  --------------------------------
  (z-0.9048) (z-0.8187) (z-0.3679)
 
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.
​
>> % Realizando zoom na região de interesse
>> axis([0.5 1.1 -0.6 0.6])

Aproveitmos que estamos com um "zoom" sobre a região de interesse do RL e acrescentamos a linha guia correspondendo à certo fator de amortecimento, $\zeta$, que depende do overshoot tolerado para mesmo, neste caso, estipulamos $\%OS=15\%$:

xxxxxxxxxx
>> OS=15;
>> zeta=(-log(OS/100))/(sqrt(pi^2+(log(OS/100)^2)))
zeta =
    0.5169
>> hold on; zgrid(zeta,0)

Agora temos um RL na região de interesse com informações relevantes sobre faixas de ganho possíveis:

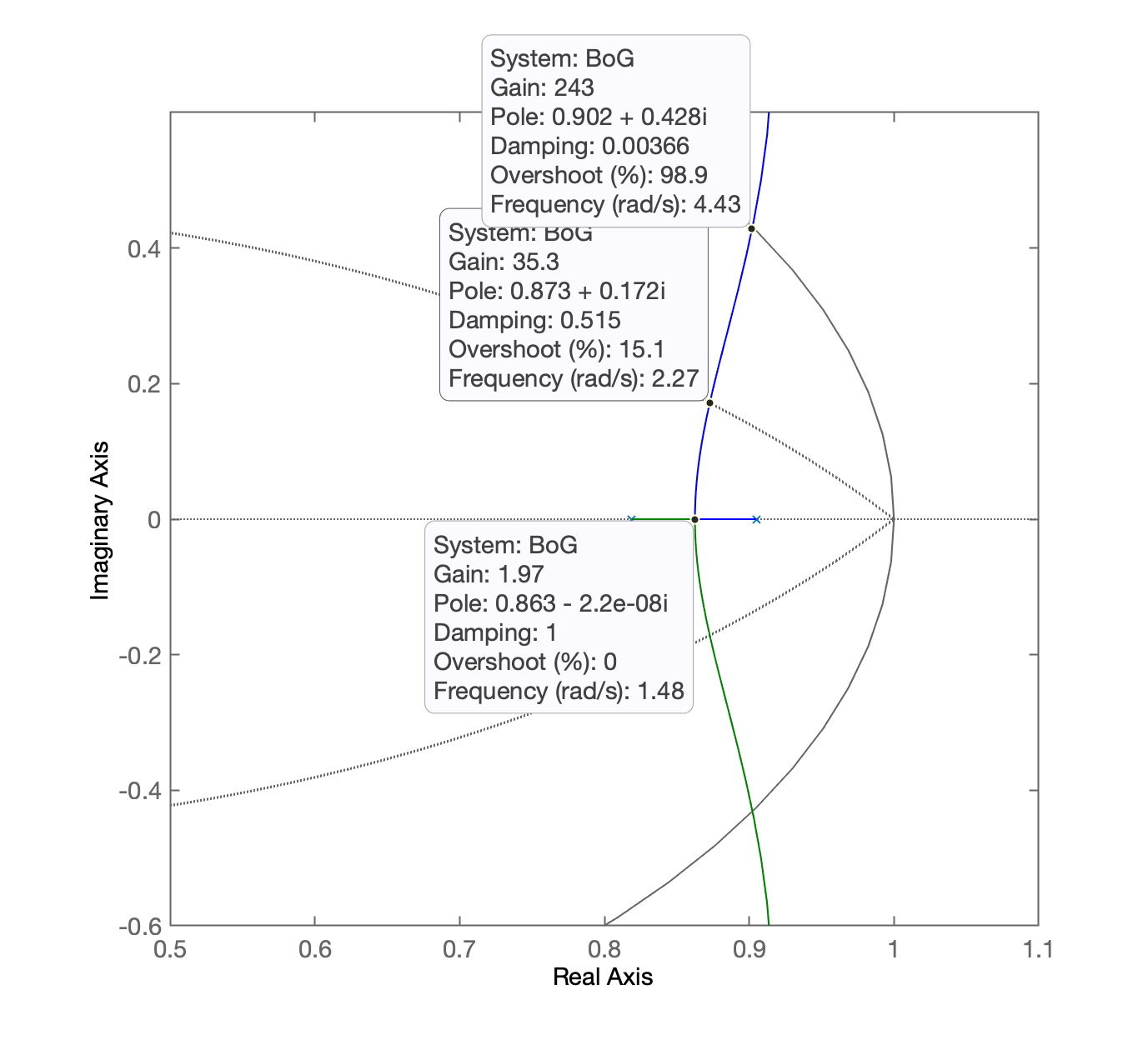
Comentários:

• Se for adotado $K \cong 2$, teremos 2 pólos de MF dominantes ainda com parte imaginária nula, o que significa resposta super-amortecida (sem overshoot);
• Se for adotado $K \cong 35$, teremos 2 pólos de MF dominantes com parte imaginária não nula, isto implica em resposta sub-amortecida (com oveshoot), no caso, com $\%OS \cong 15\%$.
• O ganho máximo, $K_u \cong 245$, o que significa que se $K > 245$, teremos um sistema instável em MF.

Aprimorando nossos projetos de controladores proporcionais...

Controle Proporcional com resposta super-amortecida

Como podemos notar pelo RL anterior, com $K \cong 2$, ainda temos pólos de MF dominantes com apenas partes reais (parte imaginária nula). Verificando:

xxxxxxxxxx
>> K=2;
>> ftmf=feedback(K*BoG, 1)
ftmf =
 
  0.0002445 z^2 + 0.0007181 z + 0.0001278
  ---------------------------------------
    z^3 - 2.091 z^2 + 1.376 z - 0.2724
 
Sample time: 0.1 seconds
Discrete-time transfer function.
​
>> pole(ftmf)
ans =
   0.8625 + 0.0050i
   0.8625 - 0.0050i
   0.3661 + 0.0000i
>> figure; step(ftmf)
>> title('Controlador Proporcional (sem overshoot)')

Via comando pole() anterior, notamos que com $K=2$, o sistema em MF já possui pólos dominantes de MF com parte imaginária não nula (pólos de MF em $z= 0,8625 \pm j0,005$), com valores reduzidos, mas não nulos, o que implica num reduzido e eventualmente imperceptível overshoot:

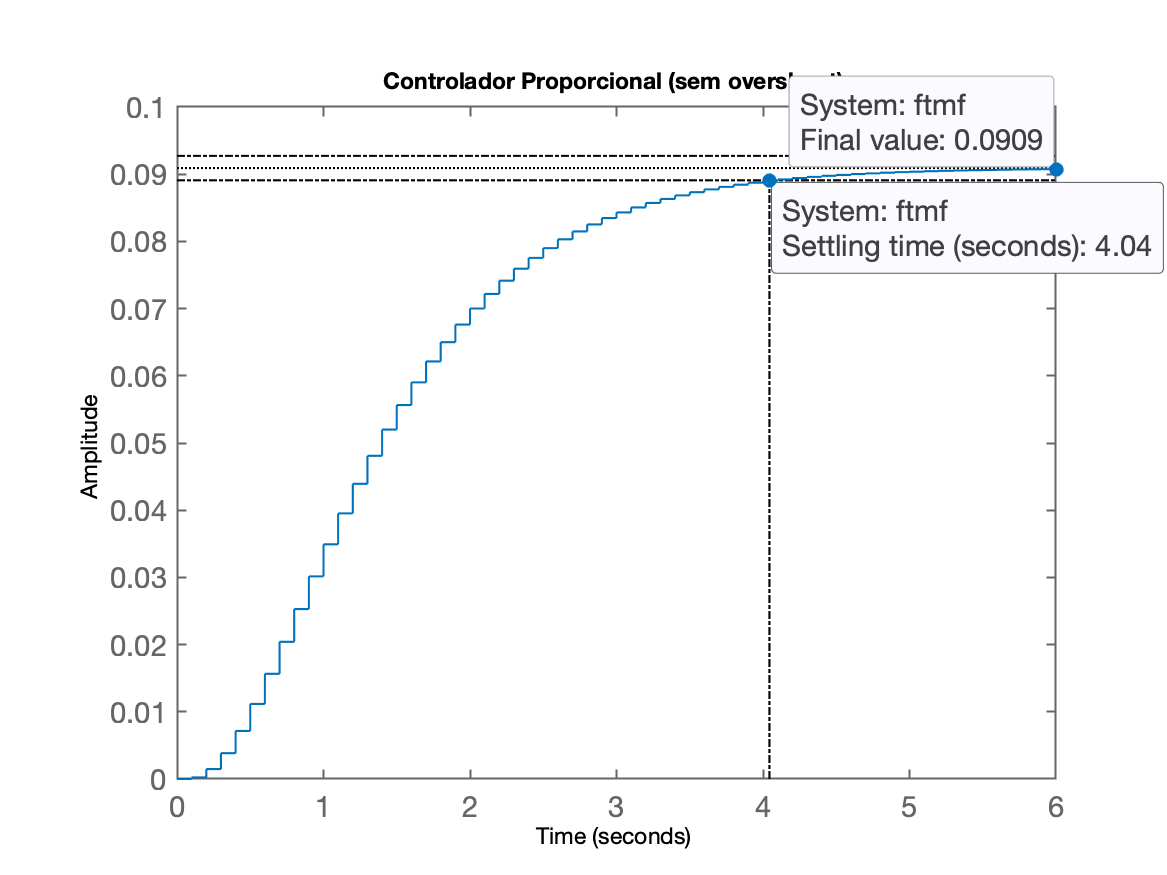
Note ainda que o valor em regime permanente da resposta do sistema está muito abaixo da referência desejada (valor unitário == degrau unitário). Isto se deve ao baixo ganho estático (DC) do sistema em MF:

xxxxxxxxxx
>> dcgain(ftmf)
ans =
    0.0909

Este valor de ganho implica num erro ainda muito elevado:

xxxxxxxxxx
>> erro=((1-dcgain(ftmf))/1)*100
erro =
   90.9091

Notar que o ganho DC da planta é baixo:

xxxxxxxxxx
>> dcgain(BoG)
ans =
    0.0500

Isto significa que em malha-aberta, aplicar um degrau unitário na planta, fará a mesma atingir no máximo o valor: $y[\infty]=0,05$.

No caso do sistema em MF, o ganho do mesmo em MF continua sendo baixo. Neste caso, quer dizer que se queremos que o sistema em MF alcance $y[\infty]=1,0$, temos que injetar uma referência com valor:

xxxxxxxxxx
> 1/0.0909
ans =
   11.0011
>> 

Ou aumentar bastante o ganho proporcional. Aumentar o ganho vai reduzir o erro (rever Teoria do erro para sistemas tipo 0). Mas com certeza teremos pólos de MF complexos, isto é, uma resposta oscilatória (com overshoot, oscilações).

Controlador Proporcional para %OS = 15%

Pelo RL levantado anteriormente, podemos aumentar o ganho tentando restringir o sobresinal à 15%, ajustando o ganho em $K \cong 35$:

xxxxxxxxxx
>> K=35;
>> ftmf=feedback(K*BoG, 1);
>> figure(2); title('Controlador Proporcional (sem overshoot)')
figure;
step(ftmf)
title('Controlador Proporcional (%OS=15%)')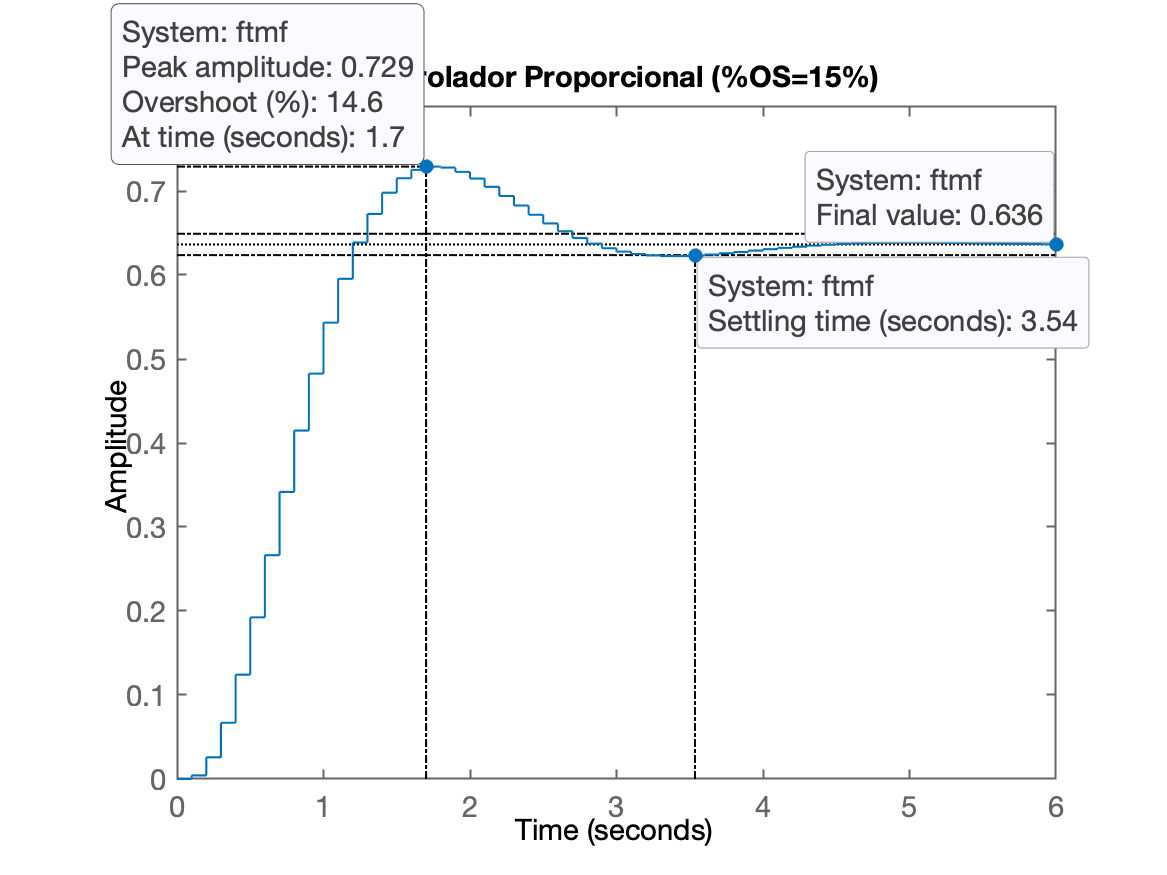

Percebemos que erro diminuiu:

xxxxxxxxxx
erro=((1-dcgain(ftmf))/1)*100
erro =
   36.3636

Questão: - Este erro é aceitável?

xxxxxxxxxx
>> stepinfo(ftmf)
​
        RiseTime: 0.8000
    SettlingTime: 3.6000
     SettlingMin: 0.5955
     SettlingMax: 0.7290    % <-- Note o valor máximo de y[kT]!
       Overshoot: 14.5639
      Undershoot: 0
            Peak: 0.7290
        PeakTime: 1.7000

Repare que o $\%OS=15\%$ é em relação à $y[\infty]$ e não em relação à $r[\infty]=1,0$ (degrau unitário).

Isto quer dizer que podemos aumentar o ganho para forçar $Max{y[\infty]} \cong 1,15$, o que corresponde à 15% de overshoot em relação à entrada degrau.

Fica mais fácil encontrar este valor usando o App Control System Designer:

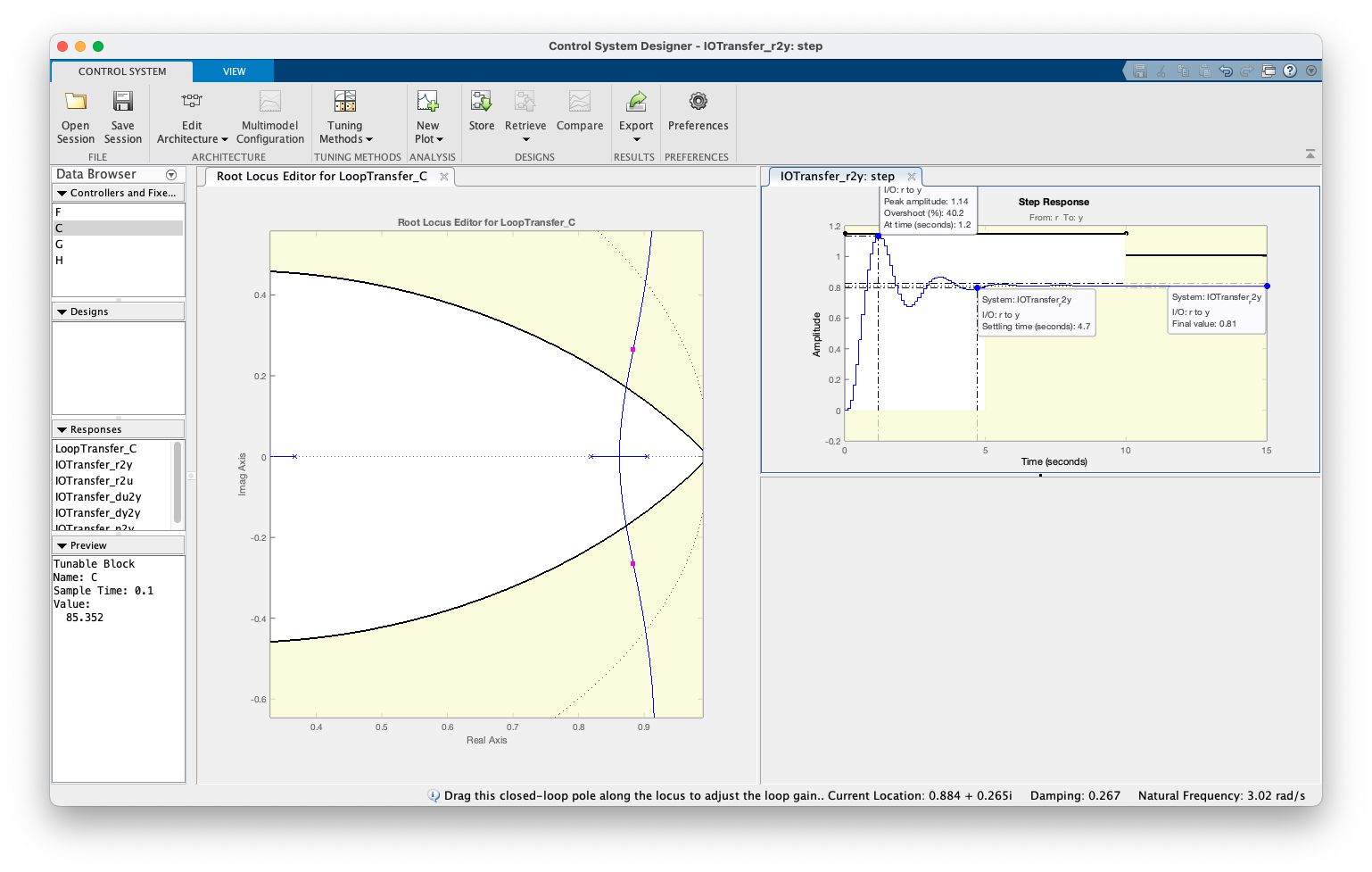
xxxxxxxxxx
>> K=86;   % valor de ganho descoberto com auxílio do App Control System Designer
>> ftmf=feedback(K*BoG, 1);
>> figure; step(ftmf)
>> title('Controlador Proporcional (%OS=15% para r[\infty])')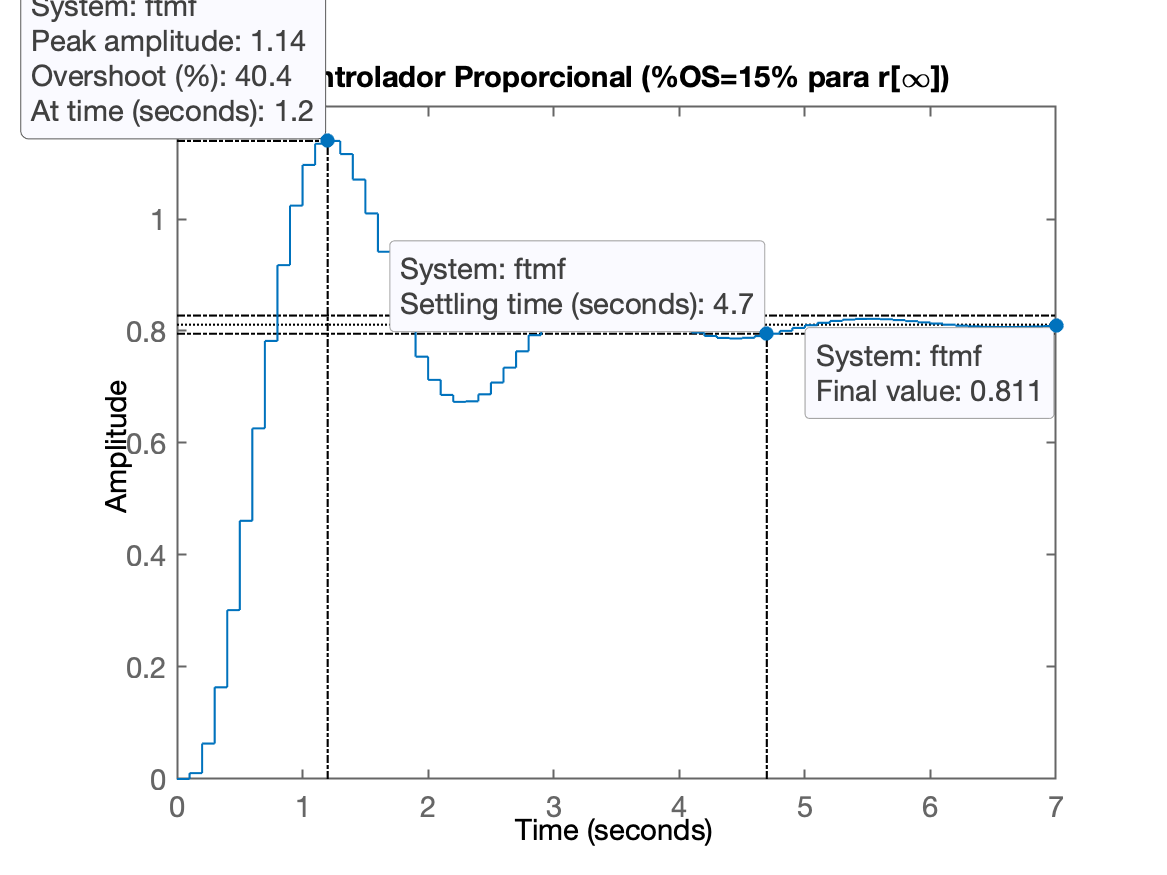

O erro agora fica:

xxxxxxxxxx
>> erro=((1-dcgain(ftmf))/1)*100
erro =
   18.8679

Questão: - E se o requisito de controle fosse manter erro de regime permanente abaixo de 10%?

Com auxílio do App Control System Designer descobrimos que neste caso, necessitamos aumentar $K$ até o valor aproximado de 170, o que leva a resposta:

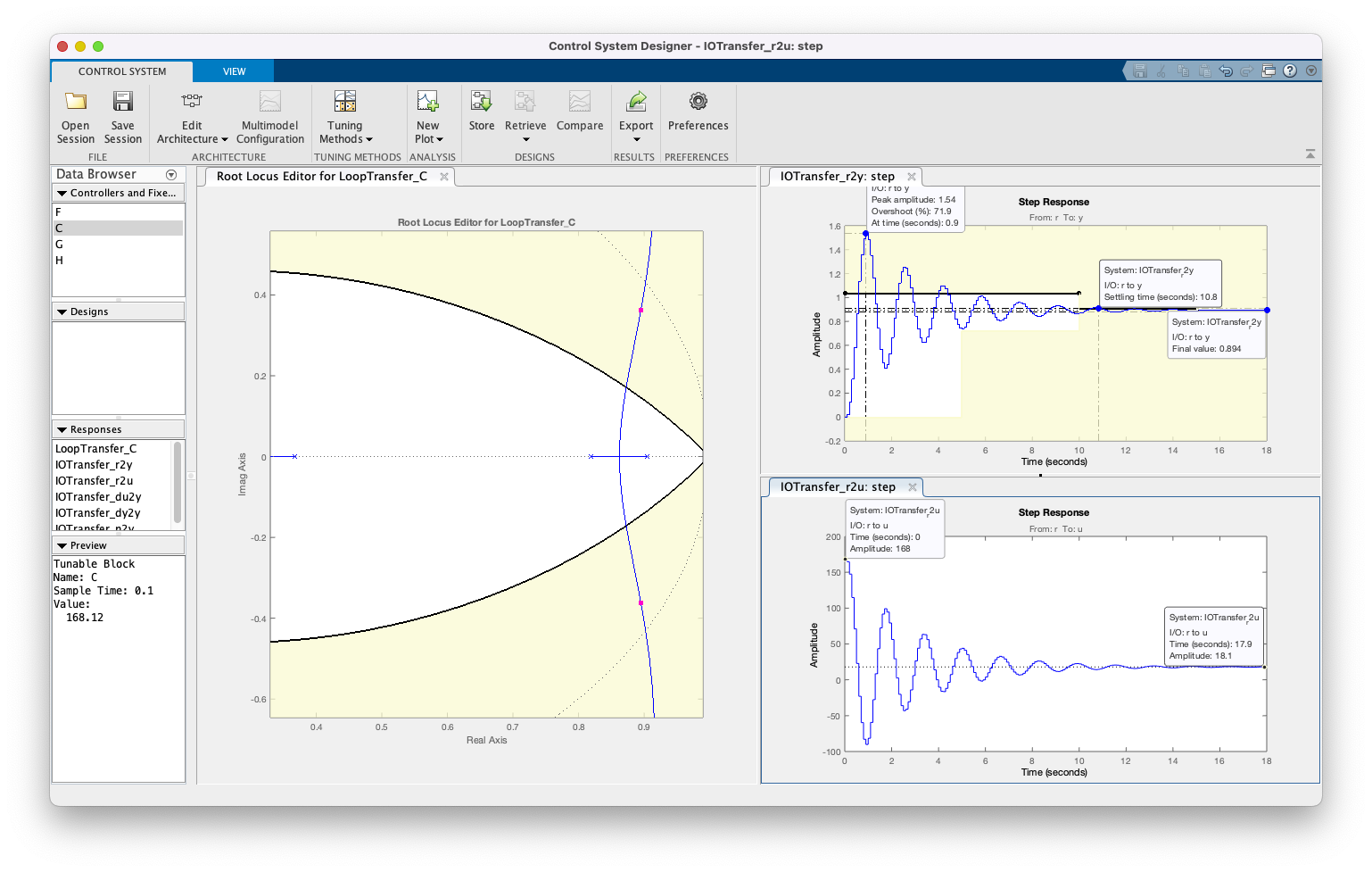
Obs.: Na figura anterior, é possível se estabelecer uma linha guia para $y[\infty]=0,9$ (erro de 10%), clicando com o botão direito do mouse sobre a região "branca" da janela 'Step Response', e selecionando-se: "Design Requirements > Edit" e definindo Final value em 0,9:

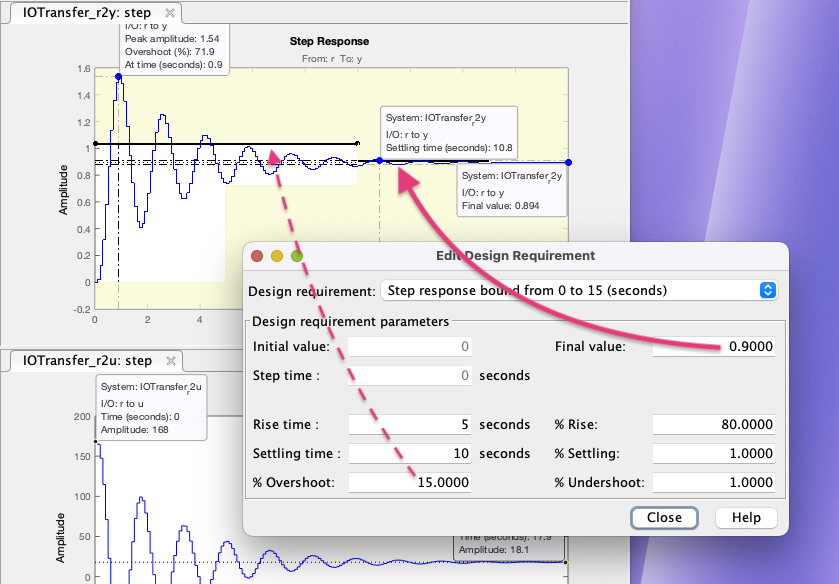
Próxima aula: usar Teoria do Erro para descobrir que valor deveria ser adotado para $K$ de forma a fazer $e[\infty] \le 10\%$.

Finalizando a seção de trabalho atual:

xxxxxxxxxx
>> save dados
>> diary off

Fernando Passold, em 31/03/2025]