Projeto Controladores Ação Derivativa
Aula de 01/10/2019; Diretório de trabalho:
\6_Controle_Digital, arquivo:projeto_PD_lead_2020.md, figuras gravadas em:\6_Controle_Digital\figuras_acao_der.
Embasamento teórico
Ver arquivos:
- acao_derivativa_4a_parte.html.pdf;
- pd_plus_filtro.pdf
Resumo
| Controlador Derivativo Puro | Controlador PD (P+D) | Controlador PD+FPB (Lead) |
|---|---|---|
| Pólo na origem do plano-z e zero em z=1. | O pólo continua na origem do plano-z e p zero agora foi ligeiramente deslocado para dentro do plano-z (não está mais em z=1). | (agora está em ); e pólo em , mais especificamente, em ; ( = coef. filtro) |
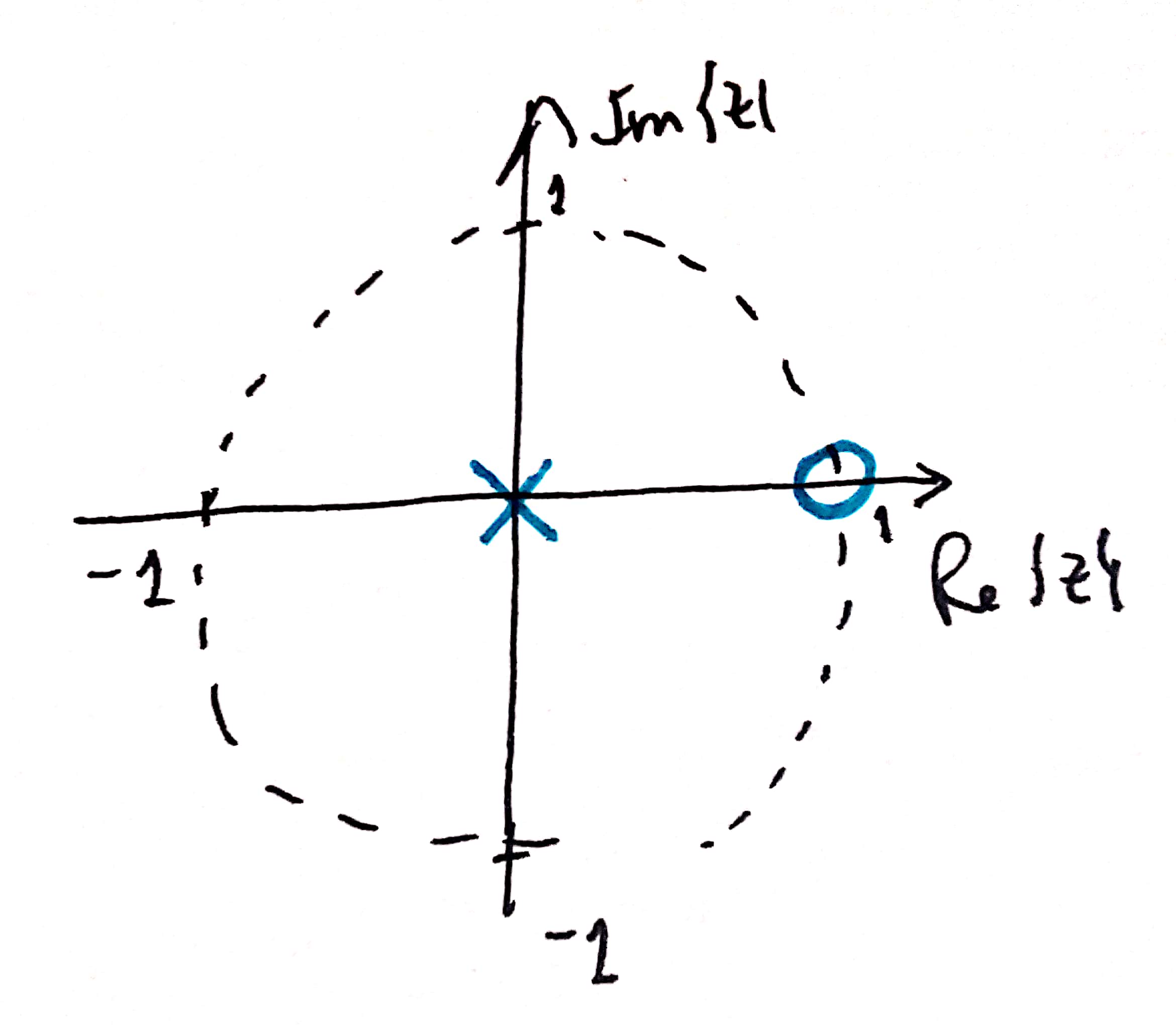 | 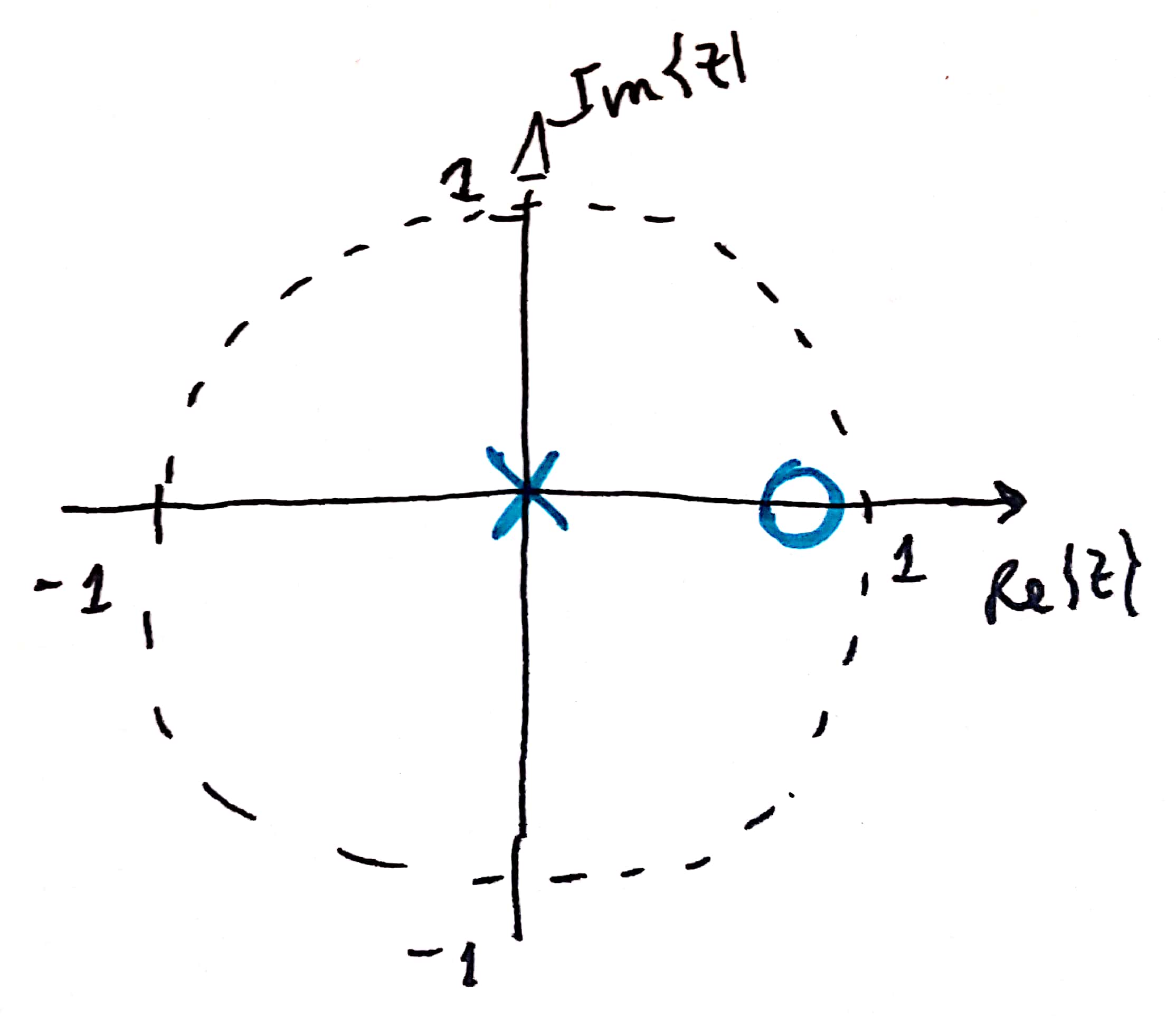 | 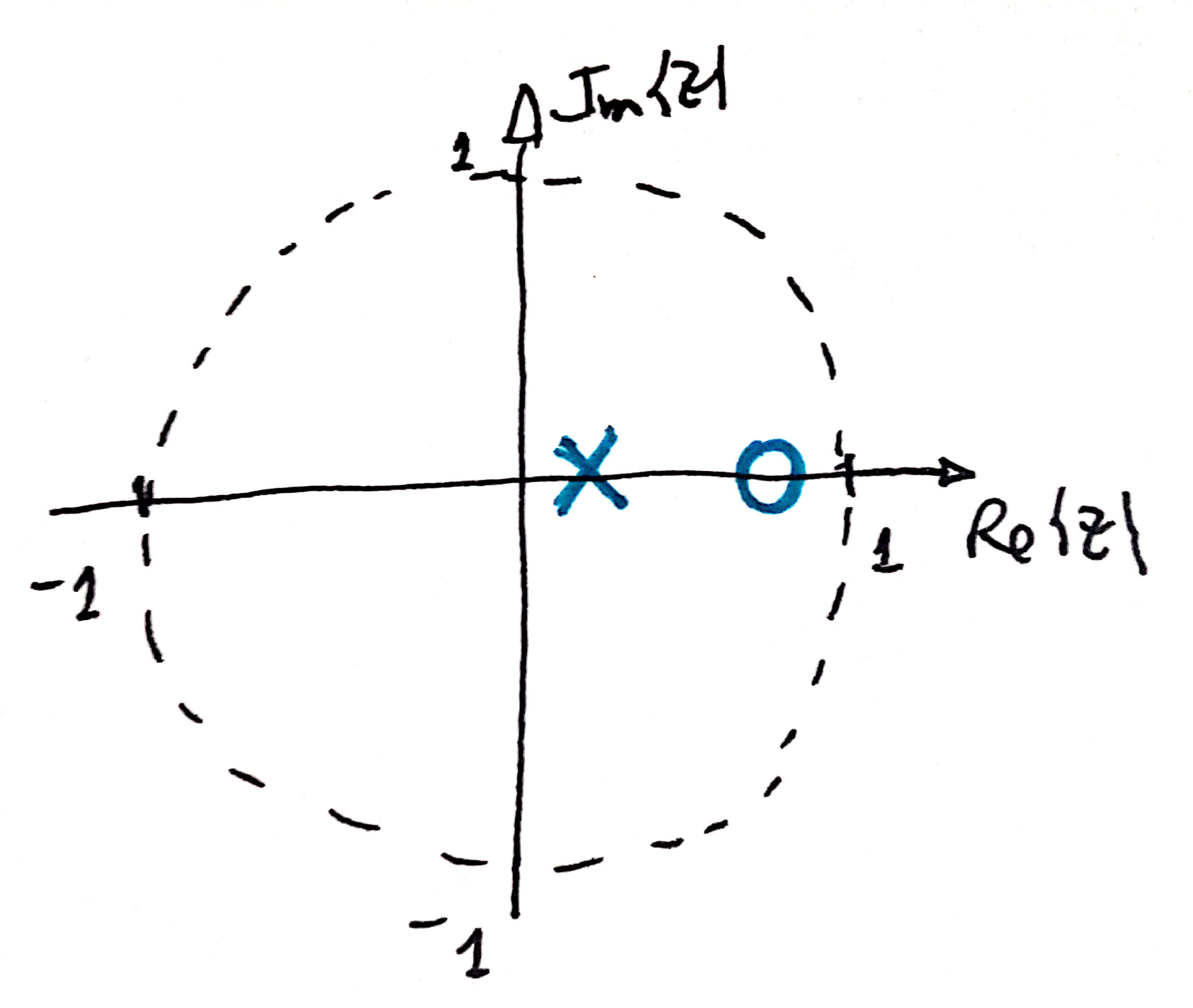 |
Projeto de PD para Planta do Estudo de Caso
xxxxxxxxxx>> load planta % carregandando dados de aulas passadas>> zpk(BoG) % verificando localização dos pólos e zeros da plantaans = 0.00012224 (z+2.747) (z+0.1903) -------------------------------- (z-0.9048) (z-0.8187) (z-0.3679) Sample time: 0.1 secondsDiscrete-time zero/pole/gain model.>>Avaliando opções para localização do zero do PD. Note que já temos certeza de que o pólo fica localizado em , apenas necessitamos esclarescer um local adequado para o zero deste controlador.
Avaliando 3 opções, conforme mostra a próxima figura:
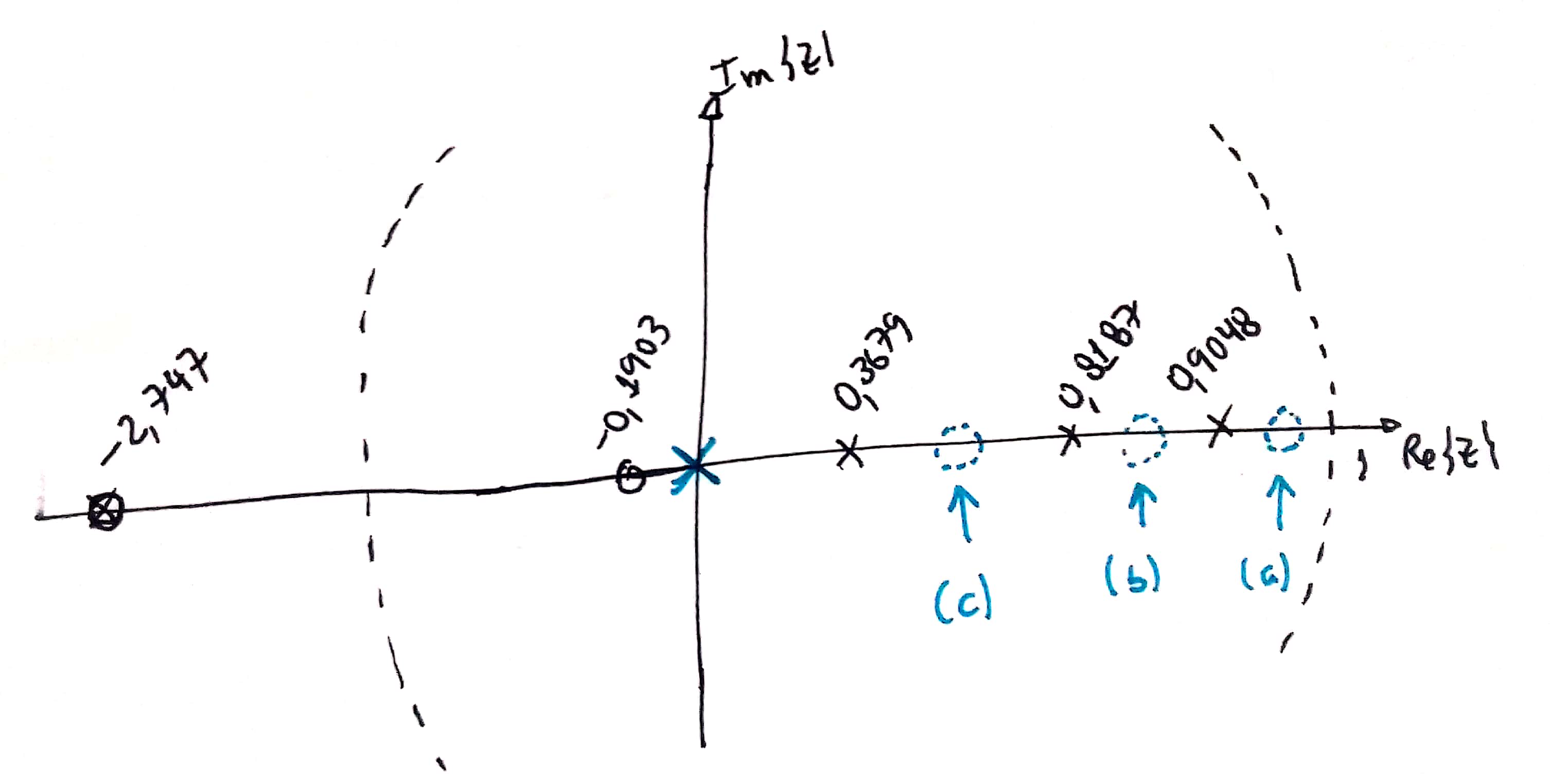
Opção (a): Zero em (zero entre o pólo mais lento da planta e o círculo unitário). Esta opção nos leva ao seguinte RL:
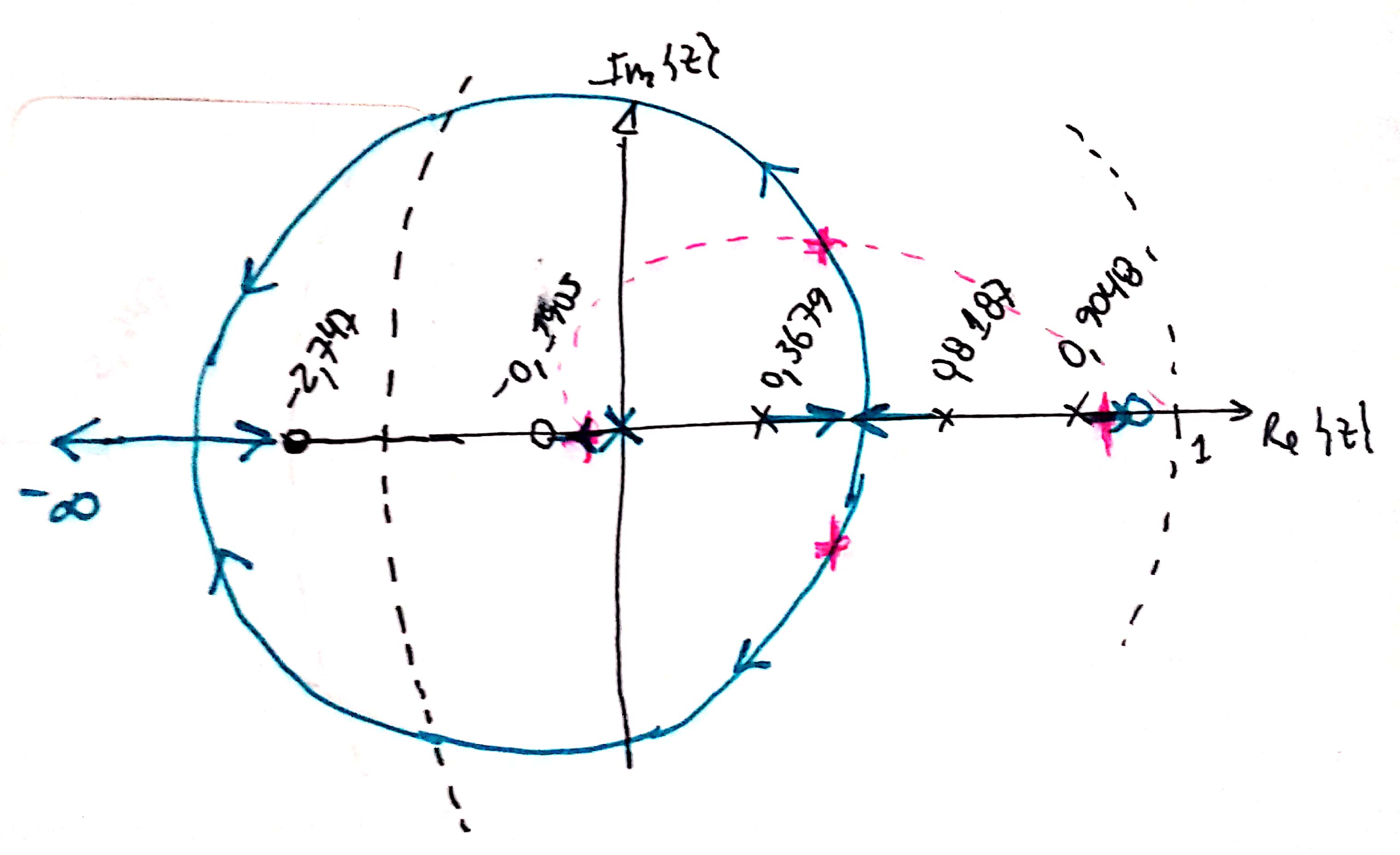
Comentário: Nesta opção o RL resultante fará surgir um pólo de MF real entre o zero do controlador e o pólo mais lento da planta, com um efeito indesejável, este pólo será atraído pelo zero do controlador localizado muito próximo da borda, o que implica um alto tempo de resposta -- provavelmente .
Opção (b): Zero em (zero entre os 2 pólos mais lentos da planta). Esta opção nos leva a outro RL:
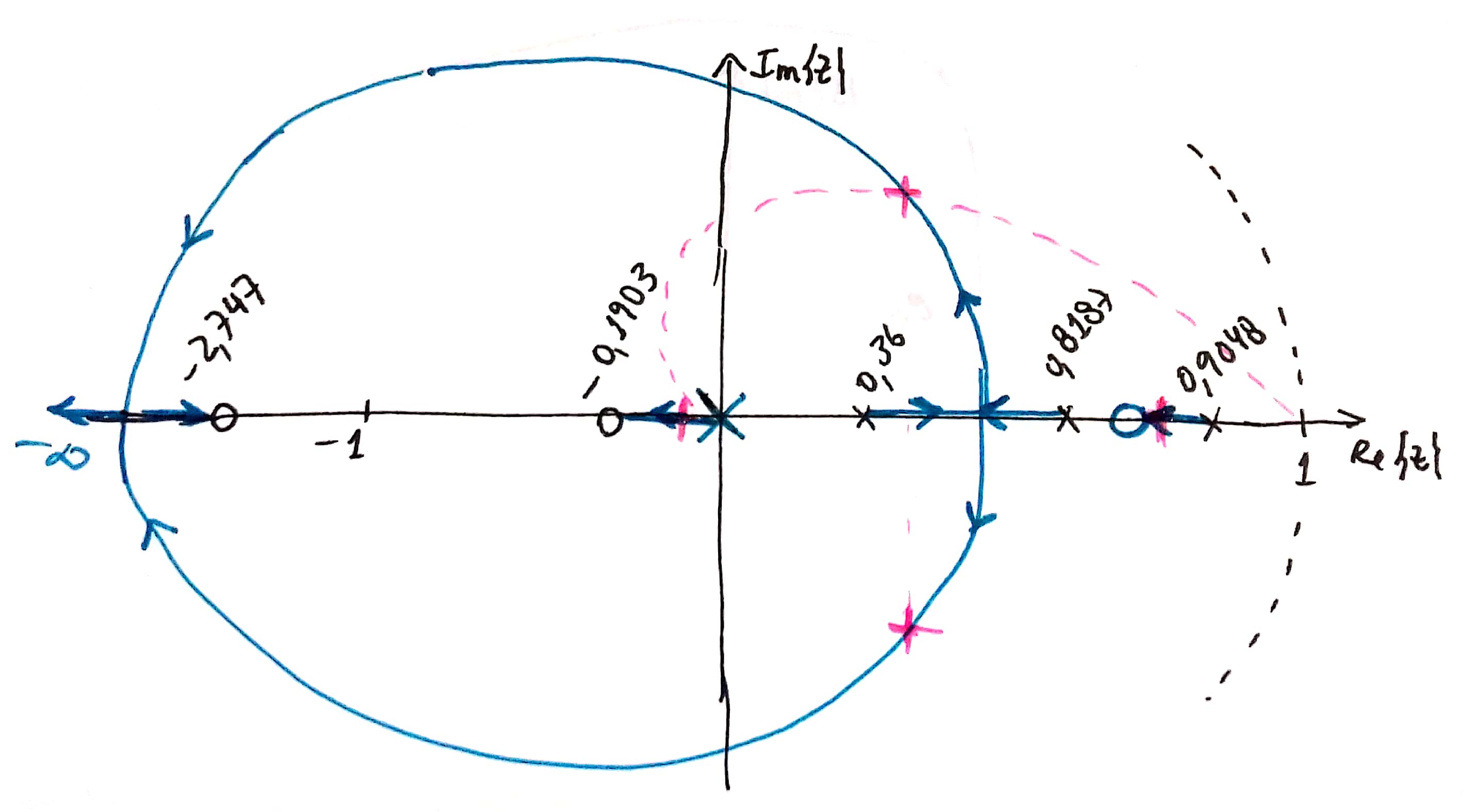
Comentário: Neste caso, resulta um RL semelhante à opção (a), mas o pólo real mais lento estará "caminhando" do pólo mais lento da planta, em , para a direção do zero do controlador (em ), o que resulta num .
Opção (c ): Zero em (zero menor que o segundo pólo mais lento da planta). Esta opção leva a outro RL.
Testando a opção (b):
Opção (b):
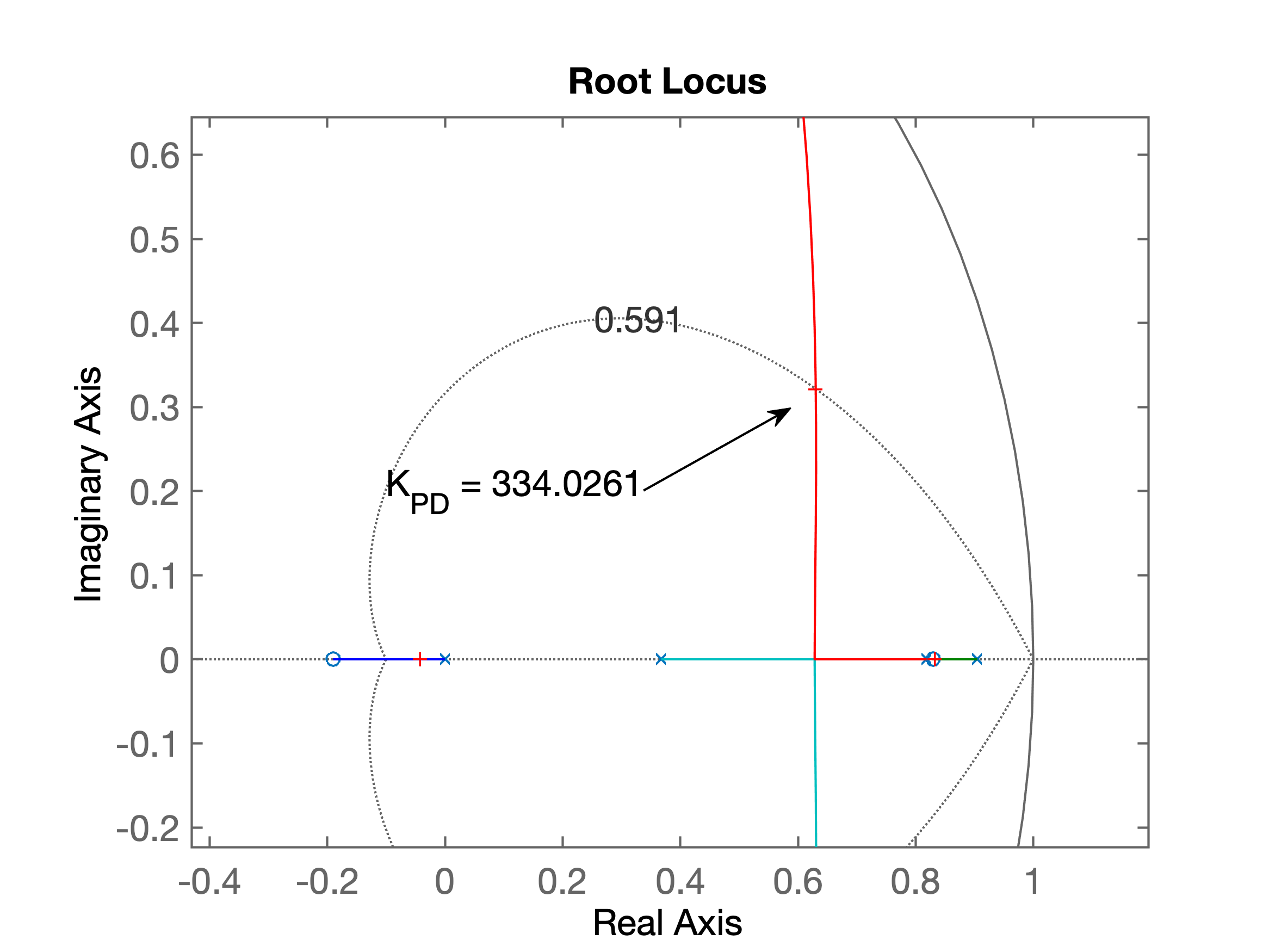
xxxxxxxxxx>> C_PD=tf( [1 -0.83], [1 0], T) % Entrando com eq. do controladorC_PD = z - 0.83 -------- z Sample time: 0.1 secondsDiscrete-time transfer function.>> ftma_PD=C_PD*BoG; % determinando a FTMA c/este controlador>> figure; rlocus(ftma_PD) % avaliando o RL obtido>> hold on;>> zgrid(zeta,0)>> [K_PD,polosMF_PD]=rlocfind(ftma_PD)Select a point in the graphics windowselected_point = 0.6321 + 0.3212iK_PD = 334.0261polosMF_PD = 0.8326 + 0.0000i 0.6303 + 0.3212i 0.6303 - 0.3212i -0.0425 + 0.0000i>>O RL obtido, já mostrando o ganho adotado é mostrado na próxima figura:
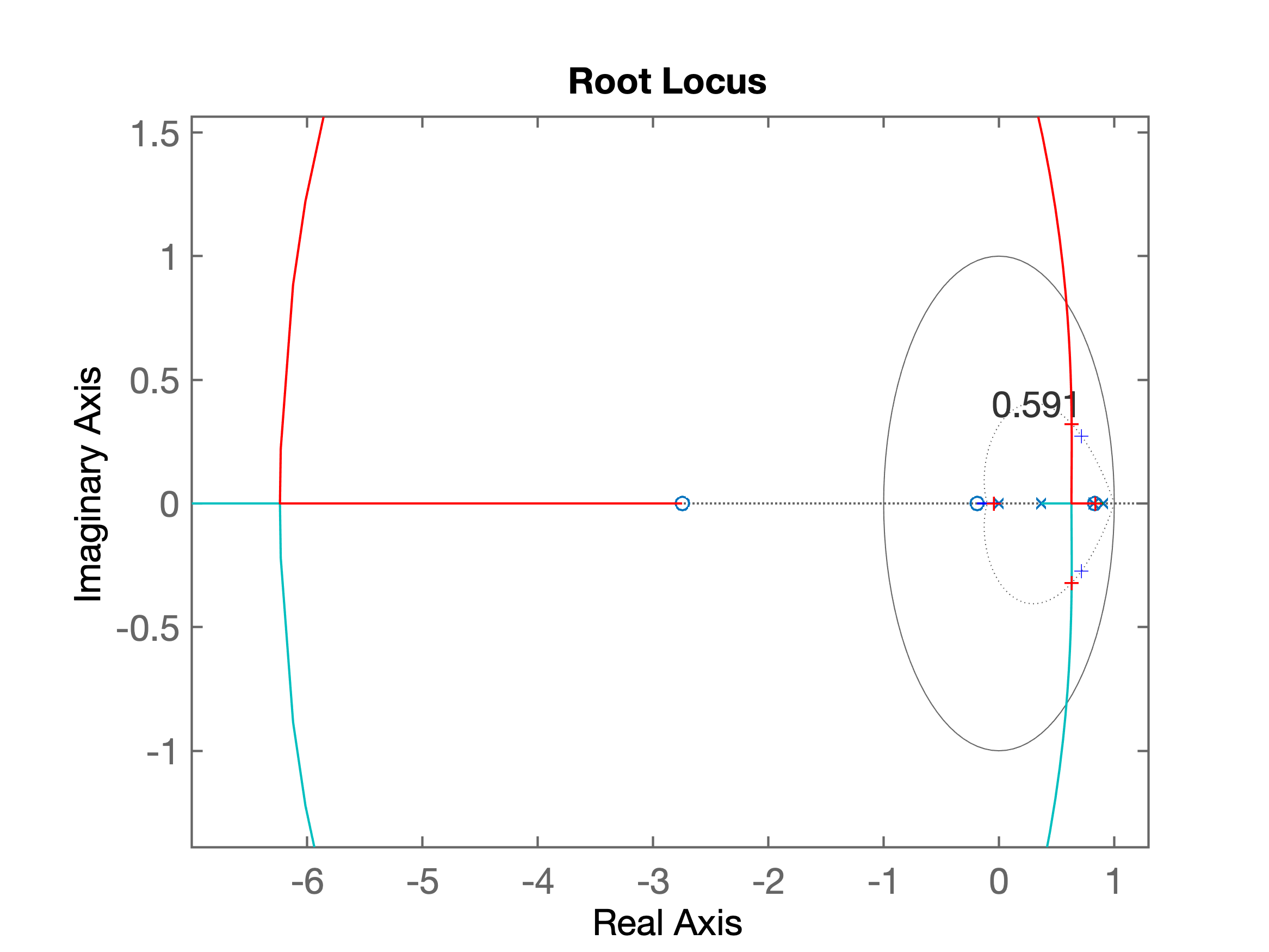
A próxima figura motra a zona de interesse do RL ("zoom na parte de interesse") já com o ganho ajustado:
Fechando a malha:
xxxxxxxxxx>> ftmf_PD=feedback(K_PD*ftma_PD, 1);>> figure; step(ftmf, ftmf_PI, ftmf_PD) % comparando a resposta de 3 controladores>> % resposta salva em comparativo_PD.png>> % gráfico do RL salvo como: RL_PD.pngA próxima figura mostra a saída obtida para o sistema em MF para 3 controladores:
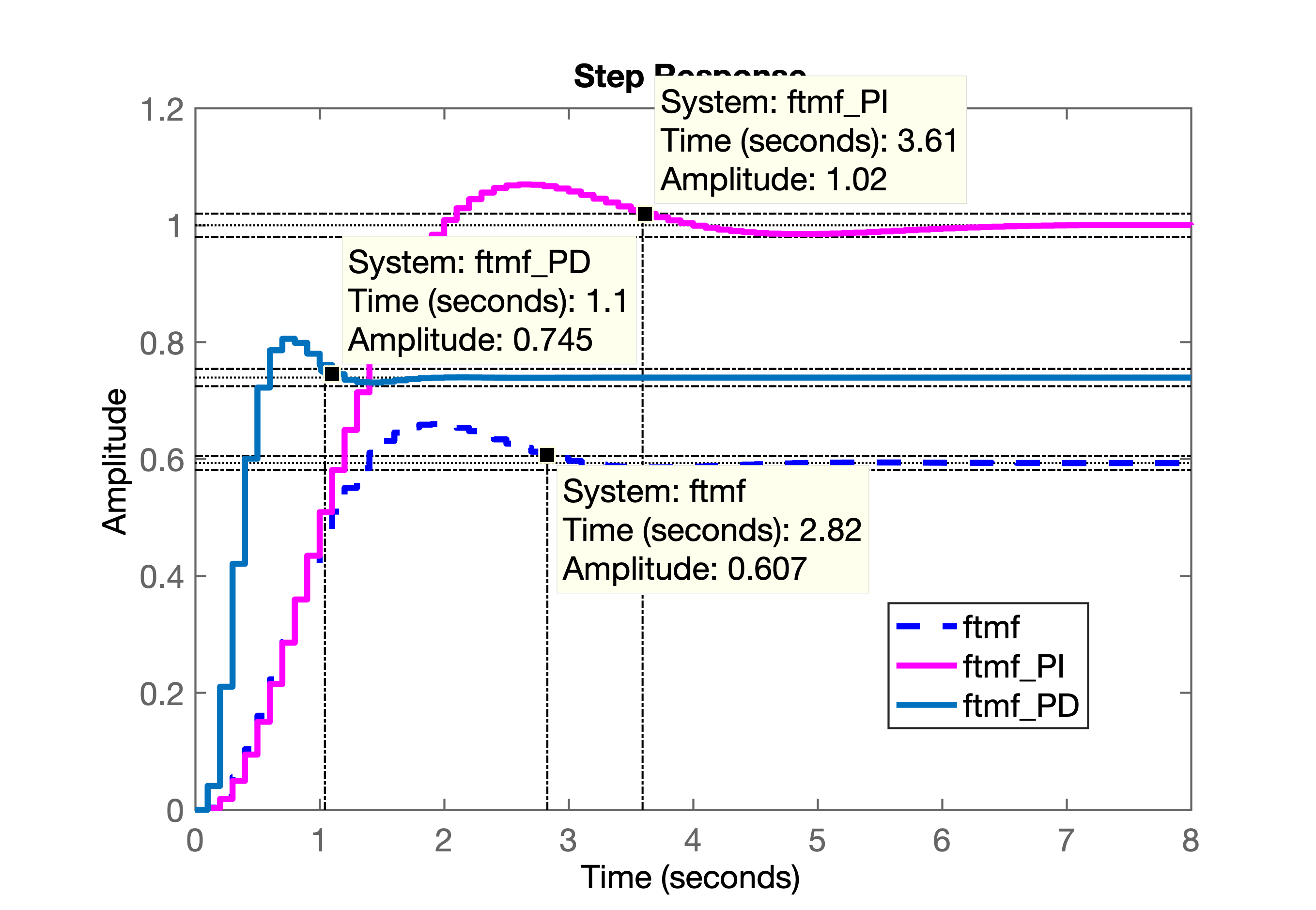
Note que o controlador PI, conforme esperado, anula o erro em regime permanente, mas é o que possui o maior tempo de assentamento.
Já o controlador Proporcional, apesar do tempo de assentamento menor que o do controlador PI, sofre com o erro em regime permanente em torno dos 40%.
E o PD, conforme esperado, foi o que o que mais acelerou a resposta da planta (menor ), mas note que este tipo de controlador não serve para zerar o erro de regimente que continua algo elevado (), mas menor do que o do controlador Proporcional.
Mas... existe um "preço" à pagar para acelerar a plnta desta forma. Controladores do tipo PD ou Lead geram amplitutes bastante elevados para os valores da ação de controle. Verificando as amplitudes geradas pelas ações de controle dos 3 controladores comparados na figura anterior...
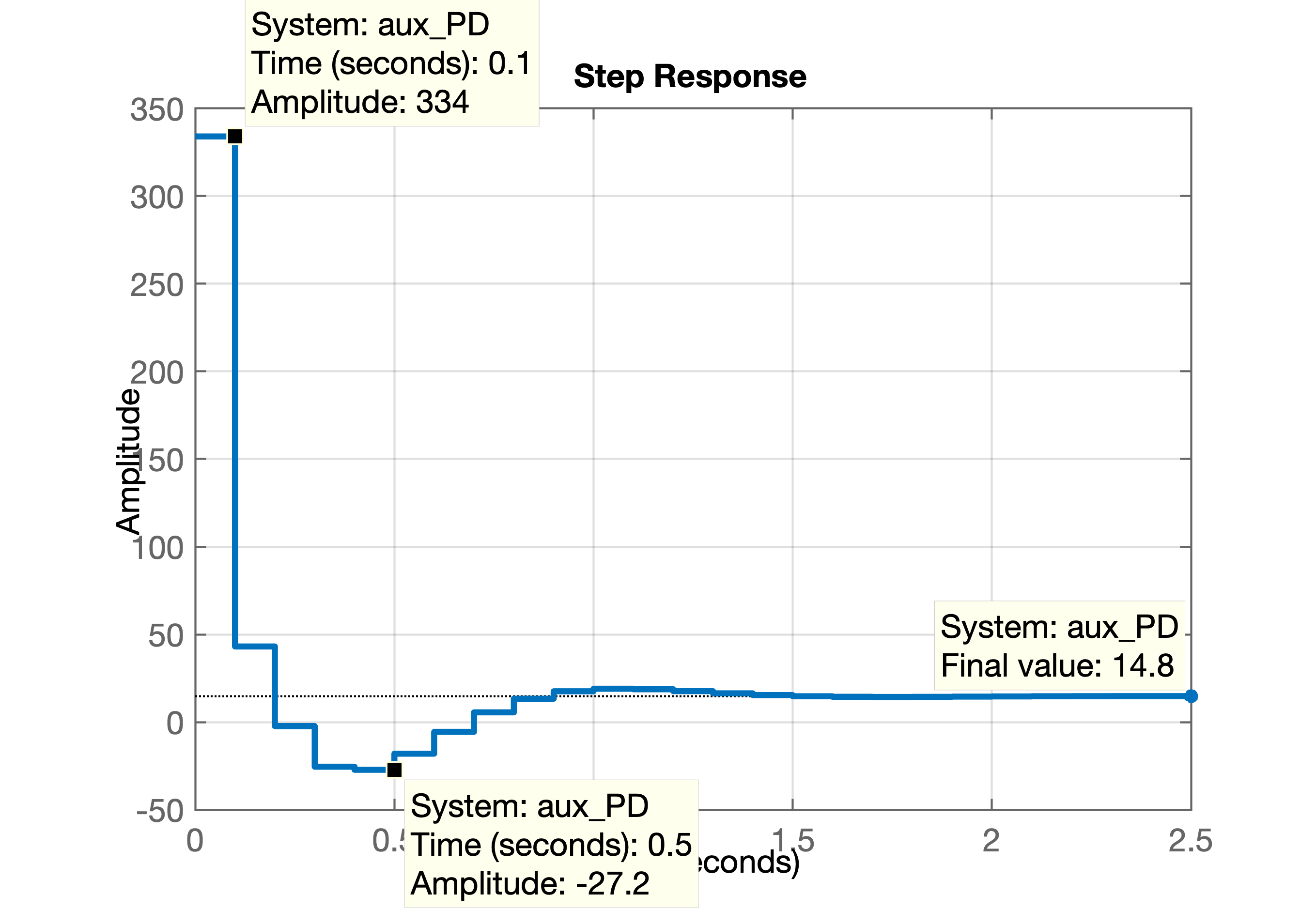
xxxxxxxxxx>> aux_PD=K_PD*C_PD/(1+K_PD*ftma_PD);>> zpk(aux_PD)ans = 334.03 z (z-0.9048) (z-0.83) (z-0.8187) (z-0.3679) -------------------------------------------------- z (z-0.8326) (z+0.04252) (z^2 - 1.261z + 0.5004) Sample time: 0.1 secondsDiscrete-time zero/pole/gain model.>> figure; step(aux_PD)>> % grafico acao controle salvo em acao_controle_PD.pngA próxima figura mostra as elevadas amplitudes iniciais geradas pelo nosso controlador PD no período transitório:
Comparando a ação de controle com os outros controladores:
xxxxxxxxxx>> save planta>> aux_Kp=K/(1+K*BoG);>> aux_PI=K_PI/(1+K_PI*ftma_PI);>> figure;>> step(aux_Kp, aux_PI, aux_PD)>> % Gráfico salvo como acoes_controle.png>> save plantaA próxima figura permite comparar as amplitudes geradas por cada ação de controle:
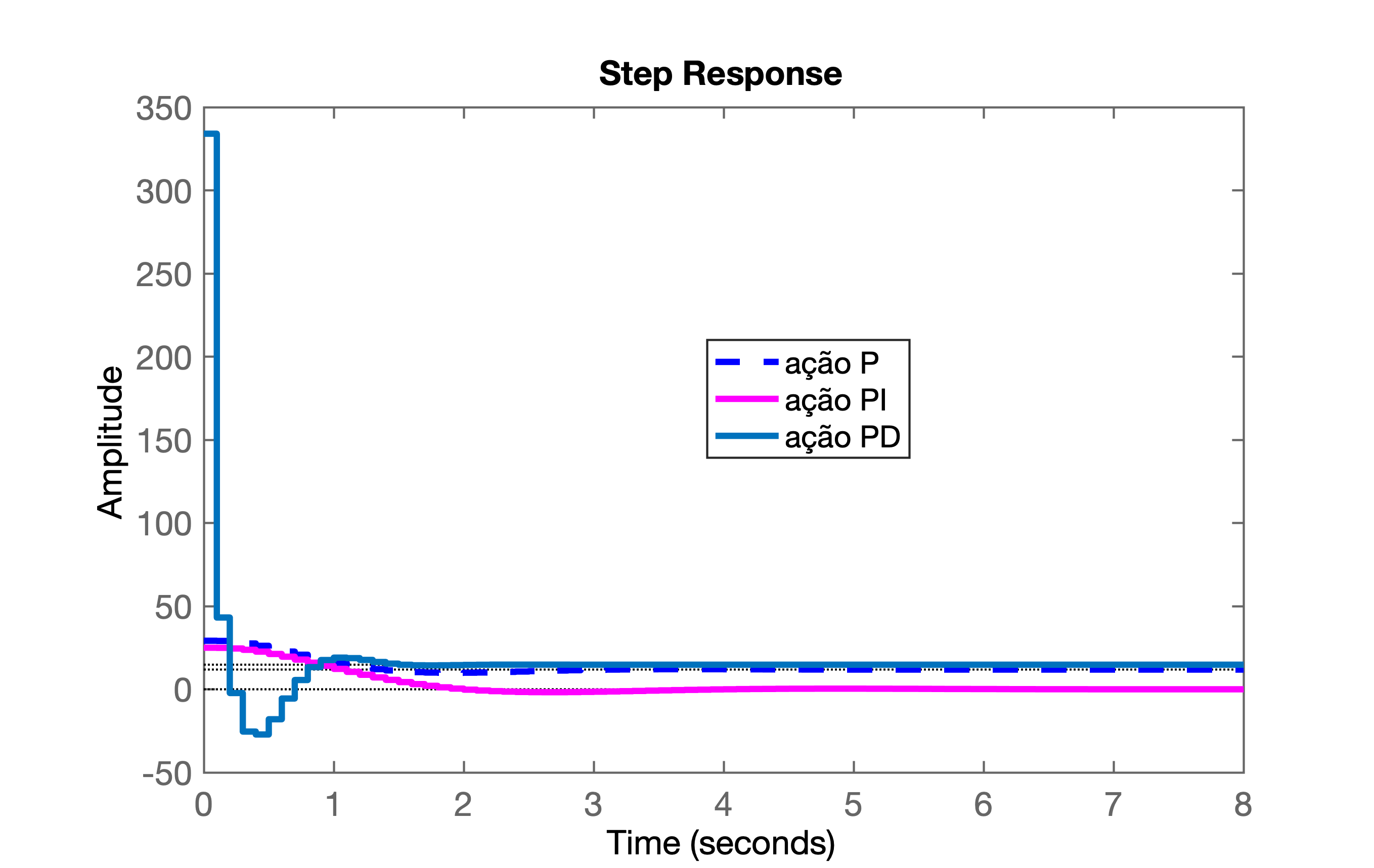
Questão: -- Existe outro método mais determinístico para projetar um controlador PD ou Lead (ou outro qualquer)?
Resposta: Pode-se usar o método da contribuição angular, que permite definir com precisão a posição de um pólo ou zero do controlador.
Projeto de Controlador Lead (por Avanço de Fase) via Contribuição angular
Para este caso, foi desenvolvido um script (no Matlab) para determinação precisa do zero, usando contribuição angular. O usuário apenas necessita arbitrar a posição inicial do pólo deste controlador e repassar outras informações importantes para que este script consiga determinar o ponto desejado para o par de pólos complexos conjugados de MF para o sistema.
Neste caso, executar na CLI do Matlab, o script: angulos2.m (Obs.: este script necessita a função arc.m (este script necessita a função arc.m que deve estar previamente instalada no mesmo diretório do script anterior):
xxxxxxxxxx>> angulos2Lead Controller DesignIn this version you should arbitrate the initial position of the pole of C(z)Plant (in s-plan) informed, G(s):ans = 1 ------------------ (s+10) (s+2) (s+1) Continuous-time zero/pole/gain model.Sampling time informed: T=0.1Plant in discrete form, BoG(z):ans = 0.00012224 (z+2.747) (z+0.1903) -------------------------------- (z-0.9048) (z-0.8187) (z-0.3679) Sample time: 0.1 secondsDiscrete-time zero/pole/gain model.Maximum overshoot desired (%OS), in %: ? 10zeta (damping factor) should be: 0.5912Enter desired settling time, t_s: ? 1.5It results in the natural oscillation frequency, wn = 4.5109 (rad/s)The MF poles (in the s-plane) should be located in:2.6667 +/- j3.6383Localization of MF poles in the z-plane should be:z = 0.7158 +/- j0.2726Enter the position of the controller pole (z-plane): ? 0Working with the temporary FTMA(z)...Open poles = 0Open poles = 0.904837Open poles = 0.818731Open poles = 0.367879Open zeros = -2.74711Open zeros = -0.190308Angular contribution of each pole in the z-plane: p1 = 0.0000 --> 20.85^o p2 = 0.9048 --> 124.74^o p3 = 0.8187 --> 110.69^o p4 = 0.3679 --> 38.08^oSum of angular contribution of poles: 294.36^oCheck the figure window -> Paused (enter to continue)...Angular contribution of each zero in the z-plane: z1 = -2.7471 --> 4.50^o z2 = -0.1903 --> 16.74^oSum of angular contribution of zeros: 21.24^oFinal angle for the zero of C(z): 93.1152^oOk, determining the position for zero of C (z)...Final position for the Lead zero: z_c=0.7306Updating final RL graph...The Lead controller final result is (variable C):ans = (z-0.7306) ---------- z Sample time: 0.1 secondsDiscrete-time zero/pole/gain model.>> Resultado dos cálculos de contribuição angular:
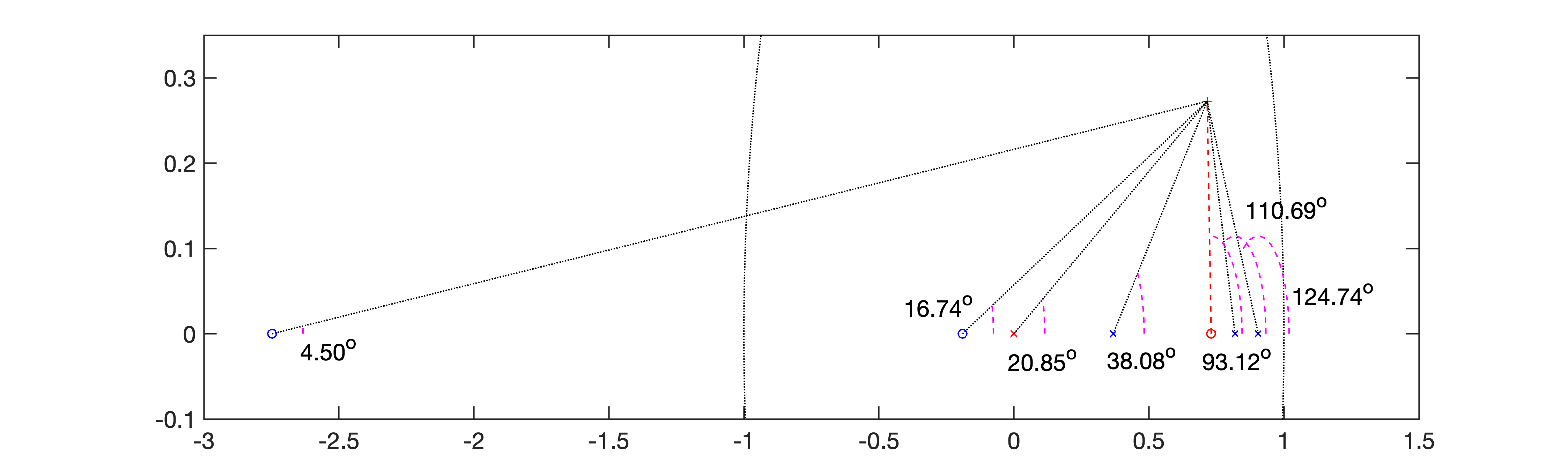
Note que o resultado da contribuição angular para o ângulo deo zero resultou em , ou:
O somatório dos ângulos dos pólos resultou: . Pela regra de um ponto pertencente ao RL teremos:
Resultado do RL obtido:
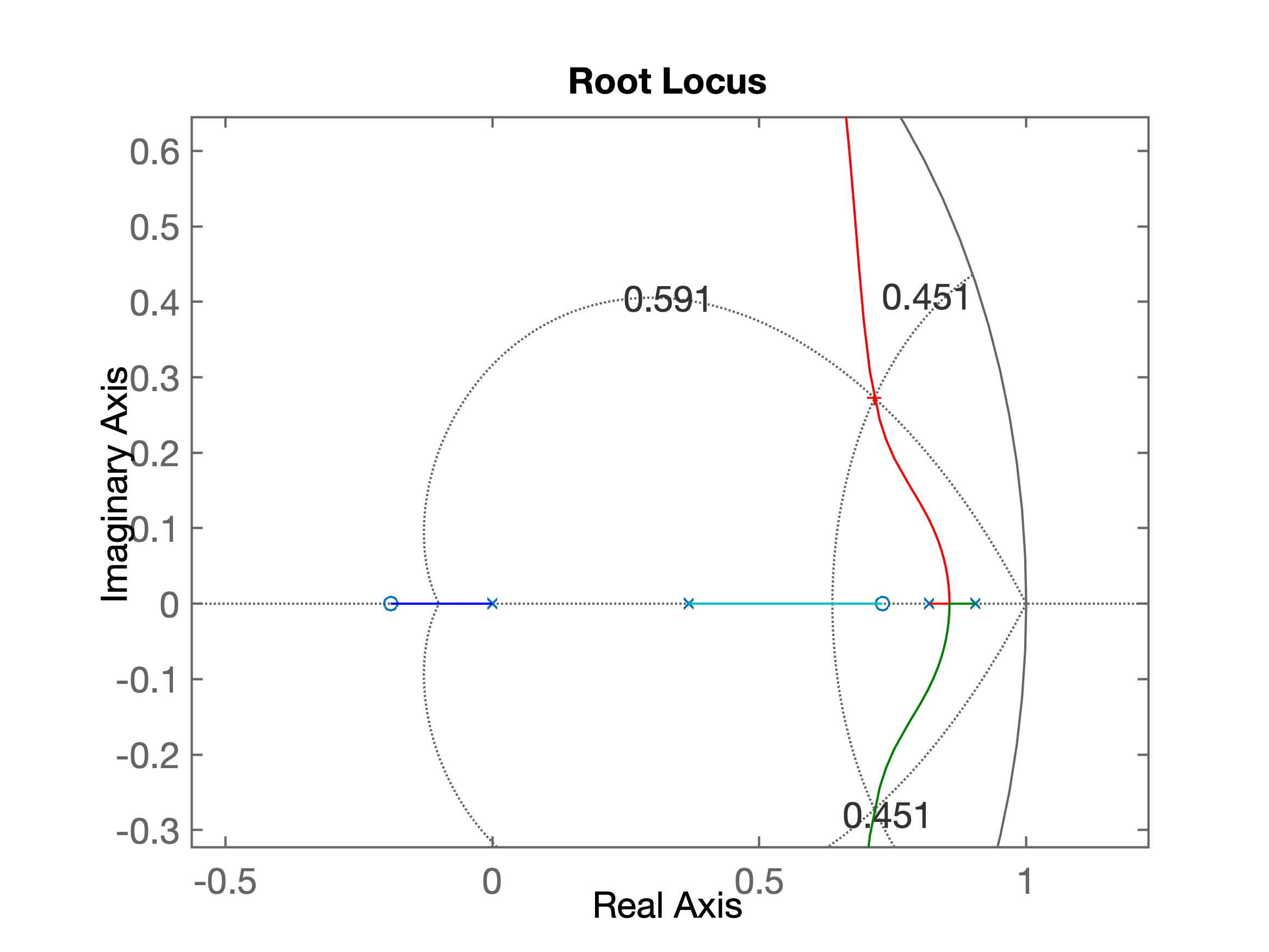
Resultado final para equação do PD:
Este PD garante (segundos).
Parte final: mostrar resultado para entrada degrau unitário, calcular erro e comparar controladores.
(c) Fernando Passold, em 28/05/2020
