Controle com Ação Derivativa

> Arquivo fonte: /Volumes/Macintosh_HD/Users/fernandopassold/Documents/UPF/Controle\_Auto\_3/Derivador/Controle\_Acao\_Derivativa.md (24/04/2018) >

Controle com Ação Derivativa

Derivador "Puro"

Seja: $y(t)=\dfrac{du(t)}{dt}$ , sua aproximação numérica pode ser realizada simplesmente como:

$y(t)=\dfrac{du(t)}{dt} \cong \dfrac{u[k]-u[k-1]}{\Delta t}$

no nosso caso, $\Delta t=T$ (período de amostragem).

A equação acima leva à:

$Y(z)=\dfrac{U(z)-z^{-1} \cdot U(z)}{T} \cdot \dfrac{z^1}{z^1} = \dfrac{U(z)(\cdot z -1)}{T \cdot z}$

ou:

$\dfrac{Y(z)}{U(z)} = \dfrac{1}{T} \cdot \dfrac{(z-1)}{z}$

que rende: zero em $z=1$ (e um pólo na origem em $z=0$ ).

No plano-z este controlador pode ser visualizado como:

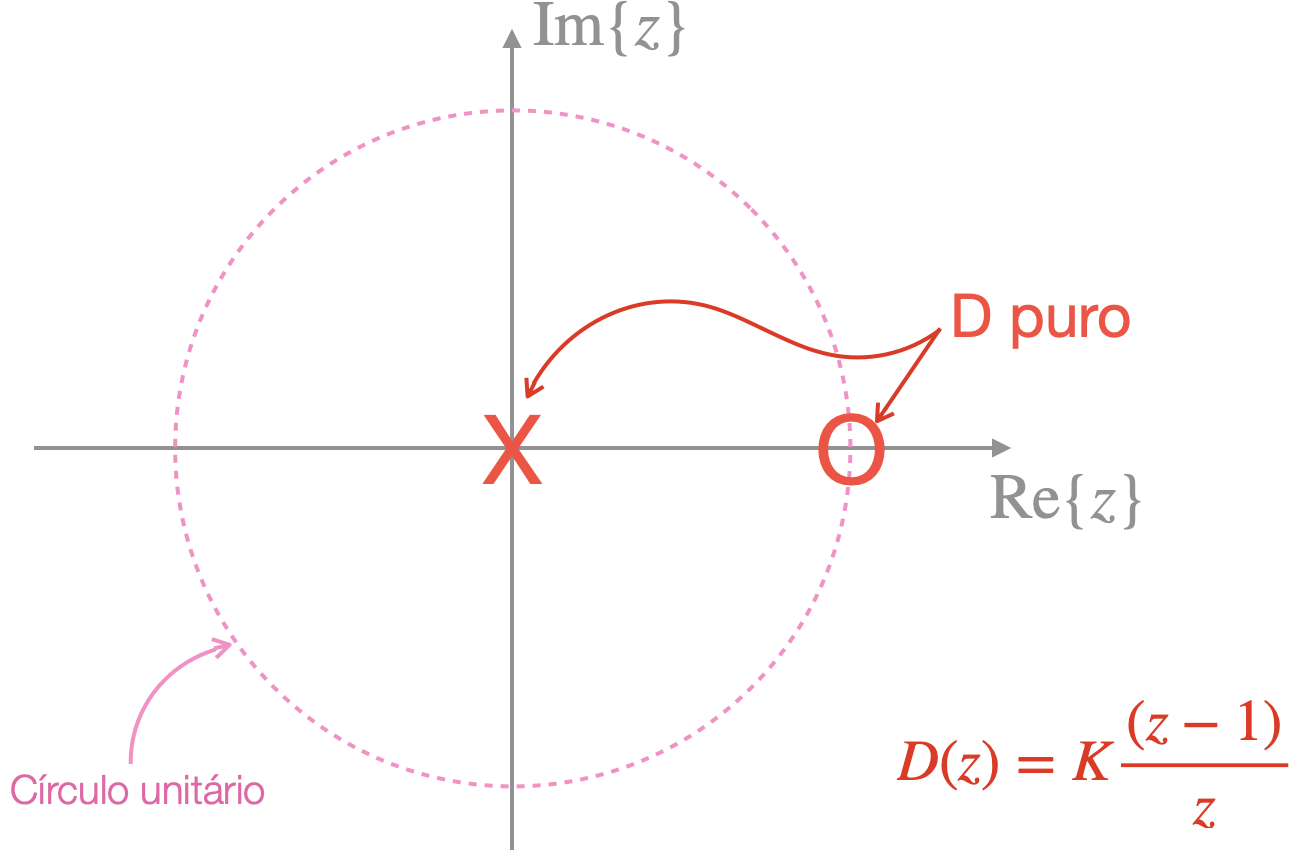
O problema é que um ação derivativa pura leva à:

$D(s)=s$

que resulta no seguinte diagrama de Bode:

>> bode([1 0], 1)

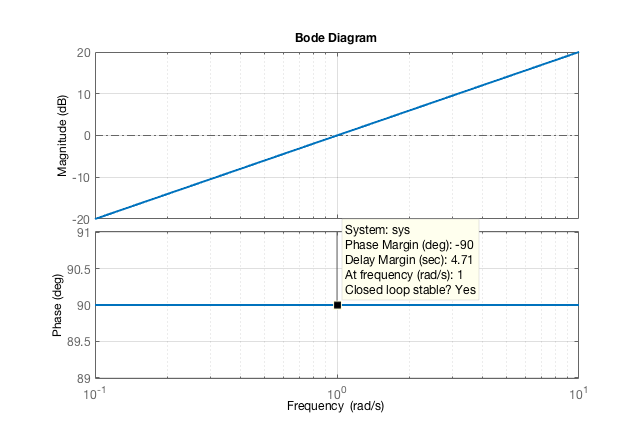
Ou seja, repare que o ganho só aumenta (e tende à $\infty$ ) à medidade que a frequência aumenta (ou seja, onde está o ruído). Note também que esta última função transferência é irealizável.

Amplificador Derivador

Na prática, um circuito derivador puro se poderia tentar realizar através do seguinte circuito usando amplificador operacional:

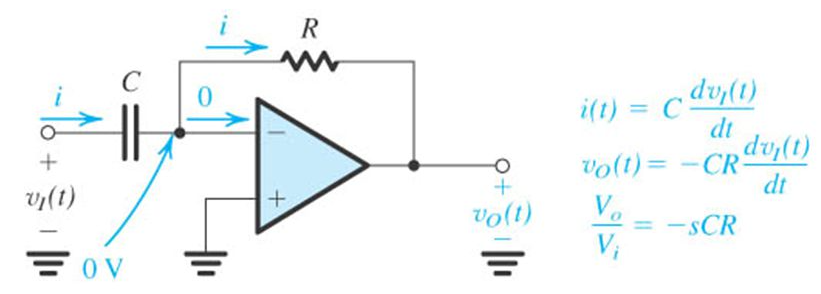
Fonte: The op-amp Differentiator - ppt video online download, Operational amplifier applications - WikiVisually

Em frequencias baixas a impedância do capacitor é praticametne $\infty$ e então o ganho é mínimo ( $-\infty$ ). Mas à medida que a frequencia aumenta, $X_c \approx 0$ e então o ganho tende à $+\infty$ e neste caso o amp.op. não funciona mais porque atura e entra em oscilação.

Já um circuito realizável seria algo como:

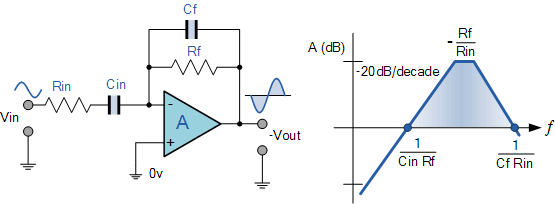
Ref.: Differentiator Amplifier - The Op-amp Differentiator

Efeito de Derivada sobre Sinal Ruidoso

Suponha que o seguinte sinal está sendo amostrado:

$x(t) = \underbrace{1 \cdot \sin (2 \pi \; 1 \; t)}_{\text{Sinal esperado (1 Hz)}} + \underbrace{ \frac{1}{100} \cdot \sin (2 \pi \; 60 \; t) }_{ \text{Ruído sobreposto} }$

Note na eq. anteriror que o ruído ocorre na frequência da rede elétrica e corresponde à apenas 1% da amplitude do sinal esperado -- o que significa que a princípio ele é praticamente negligenciável (imperceptível) -- veja gráfico à seguir:

>> ezplot( 'sin(2*pi*t)+(1/100)*sin(2*pi*100*t)',[0 2] ) % 2 ciclos do sinal esperado
>> grid

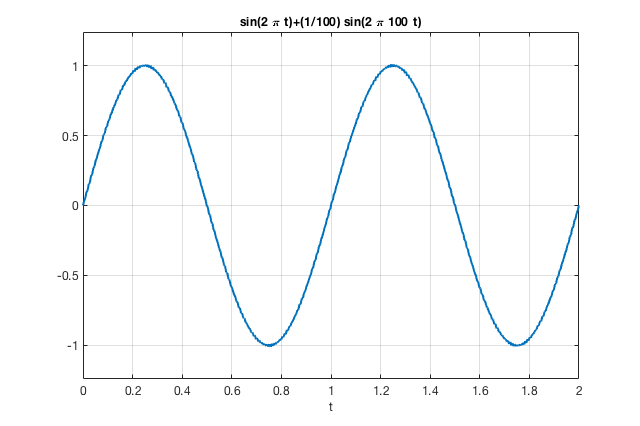
Um "zoom" sobre o sinal anterior permite visualizar o erro:

>> ezplot( 'sin(2*pi*t)+(1/100)*sin(2*pi*100*t)',[0.2 0.4] ) % zoom sobre o sinal anterior
>> grid

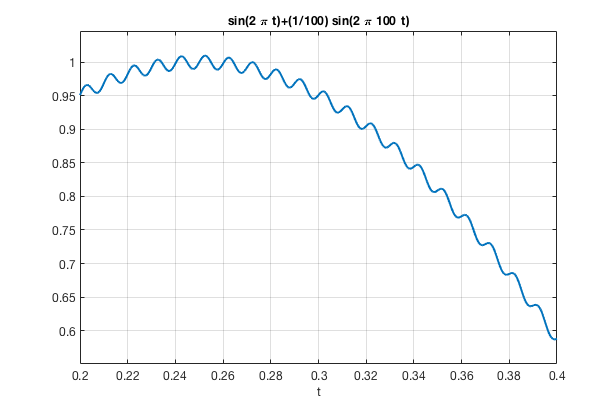
Note porém que derivada deste sinal rende:

$y(t)=\dfrac{\text{d}x(t)}{\text{d}t} = \cos(2\pi \;t) + \underbrace{ \dfrac{1}{100} \cdot 60 \cdot \cos (2\pi \; 60 \; t) }_{\text{Derivada do Ruído}}$

Note agora que a amplitude do sinal derivado, amplificou (ressaltou) o ruído presente no sinal. A amplitudade do ruído que antes estava na faixa de 0,01 Vp agora passou para 0,6 Vp (ou seja, aumentou $60 \times$ ).

Um gráfico do sinal deraivado $y(t)$ rende:

>> ezplot( 'cos(2*pi*t)+(60/100)*cos(2*pi*100*t)',[0 2] )
>> grid

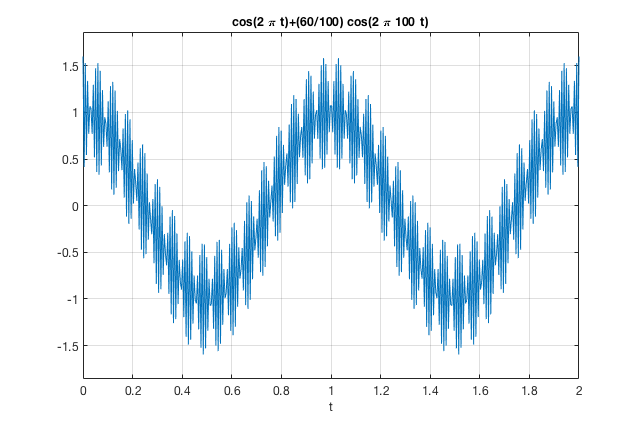
Um "zoom" sobre a figura anterior permite "contemplar" melhor o efeito da derivada sobre um sinal ruidoso:

>> t=0.4:0.001:0.6; % zoom sobre a parte interessada
>> x=sin(2*pi.*t)+(1/100)*sin(2*pi*100.*t); % sinal + ruido
>> y=cos(2*pi.*t)+(60/100)*cos(2*pi*100.*t);  % derivada do sinal com ruido 
>> y2=cos(2*pi.*t); % derivada apenas do sinal esperado
>> figure;
>> plot(t,y,'b-', t,y2,'m--')
>> legend('d\dt Sinal com ruído', 'd/dt Sinal sem ruído')

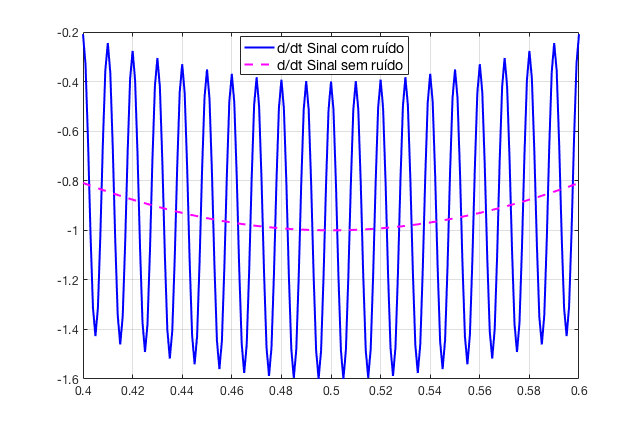
Conforme esperado, o próprio diagrama de Bode um um derivador puro indica que a amplitude de sinais de alta frequência será elevada proporcionalmente à sua frequência.

Derivador Puro Numérico

Mesmo usando um algoritmo digital para implementar a derivada, resulta em:

$y[k] \approx K_d \cdot \dfrac{x[k]-x[k-1]}{T}$

onde $K_d$ corresponderia ao ganho derivativo.

Simulando sobre o sinal anterior, resulta em:

T=8E-4; % período de amostragem - Note que 1/(20*60) = 0.0008333
t=0:T:1; % zoom sobre a parte interessada
x=sin(2*pi.*t)+(1/100)*sin(2*pi*100.*t); % sinal + ruido
y=cos(2*pi.*t)+(60/100)*cos(2*pi*100.*t);  % derivada do sinal com ruido 
y2=cos(2*pi.*t); % derivada apenas do sinal esperado
% Simulando uma derivada numerica no vetor y3
u=length(t);    % retorna qtdade de pontos do vetor t (amostras)
y3=zeros(1,u);  % inicializando vetor da derivada numerica
for i = 2:u
    y3(i) = ( x(i) - x(i-1) ) / T;
end
figure;
plot(t,y,'b-', t,y2,'m--', t,y3,'go-')
legend('d\dt Sinal com ruído', 'd/dt Sinal sem ruído',...
    'Derivada Numerica')

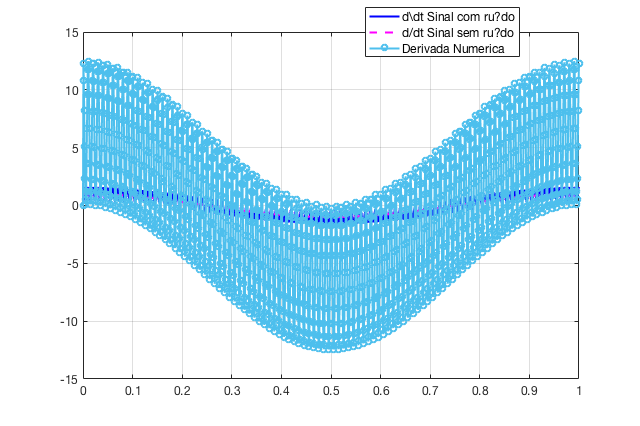
Um "zoom" sobre a figura anterior rende:

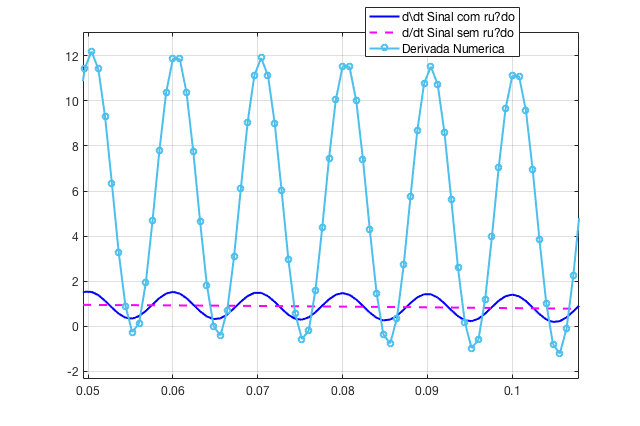
O resultado está londe do esperado. E piora se considerarmos que sobre o resutlado do gráfico falta aplicar o ganho Derivativo $\mathbf{K_d}$ .Note a baixa precisão nesta aproximação numérica para uma derivada.

Solução: ?

Uso de Filtro Passa Baixas

Notamos que não é interessante derivar a parte de frequencias elevadas (ruído) de um sinal. Então a solução é aplicar um Filtro Passa Baixas, antes de derivar o sinal desejado.

A equação diferencial de um filtro passa-baixas (FPB) de 1a-ordem é dada por:

$\tau_F \cdot \dfrac{\text{d}y(t)}{\text{d}t} + y(t) = x(t)$

onde $\tau_F$ corresponde à constante de tempo do filtro. Então:

$f_c = \dfrac{1}{2\pi \; \tau_F} \quad \text{(Hz)}$

Para $\tau_F < 3$ segundos, o filtro pode ser passivo, constituído por um simples circuito RC.

Na prática sugere-se $\tau_F < 0,1 \cdot \tau_{\text{máx}}$ (ou seja, com frequencia de corte uma década abaixo); $\tau_\text{máx}$ corresponde à constante de tempo dominante (maior) do sistema.

Note que o emprego de FPB numa malha de controle, inevitavelmente implica na introdução de um significativo atraso dinâmico (no tempo).

A função transferência do filtro seria:

$G(j\omega) = \dfrac{1}{\tau_F \; j \omega + 1}$

ou como $s=j\omega$ :

$G(s)=\dfrac{1}{\tau_F \; s + 1}$

A amplitude fica caracterizada por:

$|G(j\omega)|=\sqrt{ \left( \frac{1}{\omega^2 \; \tau_F^2 +1} \right)^2 + \left( \frac{-\omega \; \tau_F}{\omega^2 \; \tau_F^2+1}\right)^2}$

$|G(j\omega)|=\sqrt{ \frac{( 1+\omega^2\; \tau_F^2)}{(\omega^2 \; \tau_F^2+1 )} }$

$|G(j\omega)|=\dfrac{1}{ \sqrt{\omega^2 \; \tau_F^2 + 1} }$

e a fase é caracterizada por:

$\phi=\angle{G(j\omega)}=\tan^{-1}{(-\omega \; \tau_F)} = - \tan^{-1}{(\omega \; \tau_F)}$

Se $\tau_F=1,0$ (segundo), então: $\omega_F = 1 / \tau_F = 1,0$ (rad/s). A função transferência deste filtro ficaria como:

$G(s)=\dfrac{1}{s+1}$

O que rende os seguintes diagramas de Bode:

>> figure; bode(1, [1 1]); grid

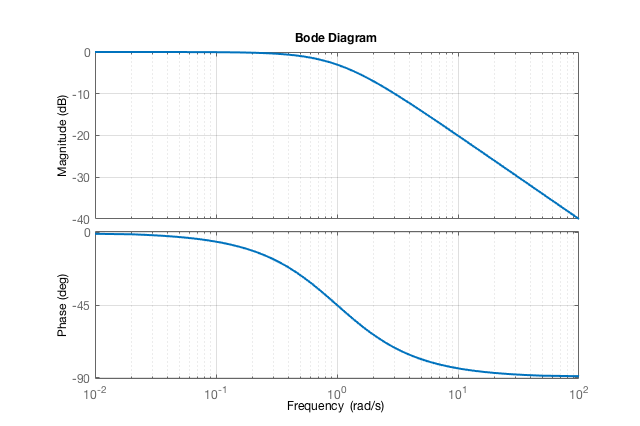
Por exemplo:

>> 20*log10(0.1)
ans =
   -20
>>

Filtro Passa-Baixas RC

Um simples filtro passa-baixas RC é mostrado na próxima figura:

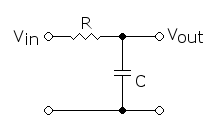
Para este circuito:

$f_c = \dfrac{1}{2\pi \; R \; C}$

A frequência do filtro deveria esta na faixa: $\omega_{\text{máx}} < \omega_F < \omega_N$ ; onde: $\omega_F=1 / \tau_F$ , $\omega_{\text{máx}}=1/\tau_{\text{máx}}$ e onde $\tau_{\text{máx}}$ corresponde a mair constante de tempo (a dominante) do processo e $\omega_N$ corresponde à frequência do ruído (rad/s). É esperado que $\omega_F < \omega_N$ .

Filtro Exponencial Digital

Seja um filtro do tipo:

Uma derivada numérica simples se consegue através de:

$\dfrac{\text{d}y(t)}{\text{d}t} \approx \dfrac{y[n]-y[n-1]}{\Delta t}$

Note que se aproxima da equação do filtro analógico de 1a-ordem:

$\tau_F \cdot \dfrac{\text{d}y(t)}{\text{d}t} + y(t) = x(t)$

que resultaria neste caso em:

$\tau_F \cdot \dfrac{(y[n]-y[n-1])}{\Delta t} + y[n] = x[n]$

trabalhando a equação anterior à fim de isolar $y[n]$ (FPB sobre o sinal $x[k]$ ), teremos:

$\begin{array}{rcl} \dfrac{\tau_F \; y[n]}{\Delta t} - \dfrac{\tau_F \; y[n-1]}{\Delta t} + y[n] & = & x[n] \\ & & \\ y[n] \left( 1+\dfrac{\tau_F}{\Delta t} \right) &=& x[n] + \dfrac{\tau_F \; y[n-1]}{\Delta t} \\ & & \\ y[n] & = & \dfrac{ \dfrac{x[n]}{1} }{ 1 + \dfrac{\tau_f}{\Delta t} } + \dfrac{ \dfrac{\tau_F \; y[n-1]}{\Delta t} }{ 1 + \dfrac{\tau_F}{\Delta t} }\\ & & \\ y[n] & = & \dfrac{ \dfrac{x[n]}{1} }{ 1 + \dfrac{\Delta t + \tau_F}{\Delta t} } + \dfrac{ \dfrac{\tau_F \; y[n-1]}{\Delta t} }{ \dfrac{\Delta t + \tau_F}{\Delta t}} \\ & & \\ y[n] & = & \left( \dfrac{\Delta t}{\tau_F + \Delta t} \right) \cdot x[n] + \left( \dfrac{\tau_F}{\tau_F + \Delta t} \right) \cdot y[n-1] \\ \end{array}$

Podemos criar a variável $\alpha$ tal que:

$\alpha = \dfrac{1}{ \dfrac{\tau_F}{\Delta t} + 1}$

e então:

$(1-\alpha) = 1 - \dfrac{1}{ \dfrac{\tau_F}{\Delta t} + 1 } = \dfrac{\tau_F}{\tau_F + \Delta t}$

e assim chegamos a um formato mais simples de equação para o filtro digital exponencial de 1a-ordem:

$y[n] = \alpha \; x[n] + (1 - \alpha) \; y[n-1]$

onde: $0 < \alpha < 1$ . Tipicamente é empregado o valor $\alpha = 0,1$ .

Note que:
Se $\alpha = 1$	$\rightarrow$ não existe filtragem	$\rightarrow \quad y[n] = x[n]$ .
Se $\alpha = 0$	$\rightarrow$ Sinal original é ignorado	$\rightarrow \quad y[n] = 0$ .

Filtro exponencial duplo (ou de 2a-ordem)

Pode ser formado pelo cascateamento de 2 filtros de 1a-ordem:

Derivando as equações, teremos:

$\begin{array}{rcl} \bar{y}[n] & = & \gamma \; y[n] + (1 - \gamma) \; \bar{y}[n-1] \\ & & \\ \bar{y}[n] & = & \gamma \; \alpha \; x[n] + \gamma (1 - \alpha) y[n-1] + (1 - \gamma) \; \bar{y}[n-1] \\ & & \\ \bar{y}[n-1] & = & \gamma \; y[n-1] + (1 - \gamma) \; y[n-2] \\ & & \\ y[n-1] & = & \dfrac{1}{\gamma} \; \bar{y}[n-1] - \dfrac{(1 - \gamma)}{\gamma} \; \bar{y}[n-2]\\ & & \\ \bar{y}[n] & = & \gamma \; \alpha \; x[n] + (2 - \gamma - \alpha) \; \bar{y}[n-1] - (1-\alpha)(1-\gamma)\; \bar{y}[n-2] \end{array}$

Se $\gamma = \alpha$ , este filtro resulta em:

$\bar{y}[n] = \alpha^2 \; x[n] + 2(1-\alpha)\; \bar{y}[n-1] - (1-\alpha)^2 \; \bar{y}[n-2]$

Note que existe uma vantagem deste filtro sobre o anterior de 1a-ordem: este filtro atenua mais fortemente ruídos de alta frequencia, especialmetne se $\gamma = \alpha$ .

Este filtro resulta em algo semelhante à:

$G(s) = \dfrac{1}{(s+1)^2}$

Cujo diagrama de Bode resulta:

>> figure; bode(1, conv( [1 1], [1 1] ) ); grid

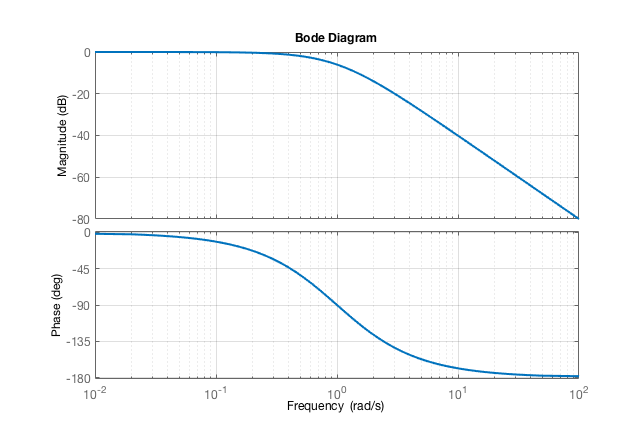
Note: corte de 40 db/déc!

>> 20*log10(0.01/1)
ans =
   -40

Filtro de Média Móvel

Neste caso se aplica simplesmente a equação:

$y[n] = \dfrac{1}{J} \; \sum_{i=n-J+1}^{n}{x[i]}$

que representa a média dos últimos $J$ pontos soobre o sinal de entrada $x[n]$

Esta equação pode ser reescrita como:

$y[n-1] = \dfrac{1}{J} \; \sum_{i=n-J}^{n-1}{}x[i]$

mesclando as 2 últimas equações obtemos:

$y[n] = y[n-1] + \dfrac{1}{J} \; \left( x[n] - x[n-J] \right)$ que resulta num comportamento semelhante à um filtro passa-baixas, servindo também para eliminar componentes (ruídos) de alto frequência.

Problema Sugerido

Os 3 filtros anteriores poderiam ser aplicados sobre este tipo de sinal:

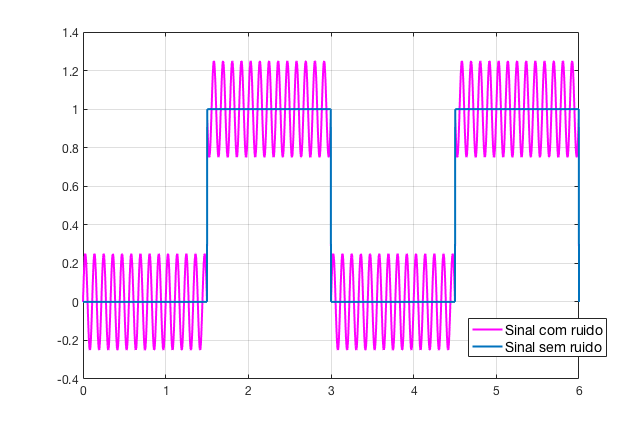
uma onda quadrada (sinal esperado) oscilando entre 0,0 e 1,0 Volts à frequência de $f=1/3$ , acompanhado de um ruído (senoide) oscilando na frequência de 9 Hz com amplitude de 0,25 Vp. Simular alguns casos:

Filtro analógico de 1a-ordem com $\tau_F = 0,1$ minutos;
Filtro analógico de 1a-ordem com $\tau_F = 0,4$ minutos;
Filtro digital exponencial de 1a-ordem com $\tau_F = 0,1$ minutos; e usando período de amostragem $T = 0,05$ minutos;
Filtro digital exponencial de 1a-ordem com $\tau_F = 0,1$ minutos; e usando período de amostragem $T = 0,1$ minutos;
Filtro de média móvel com $J=3$ (ainda se deve perceber ruído);
Filtro de média móvel com $J=7$ (o ruído praticamente some).

Alguns resultados que poderiam ser obtidos:

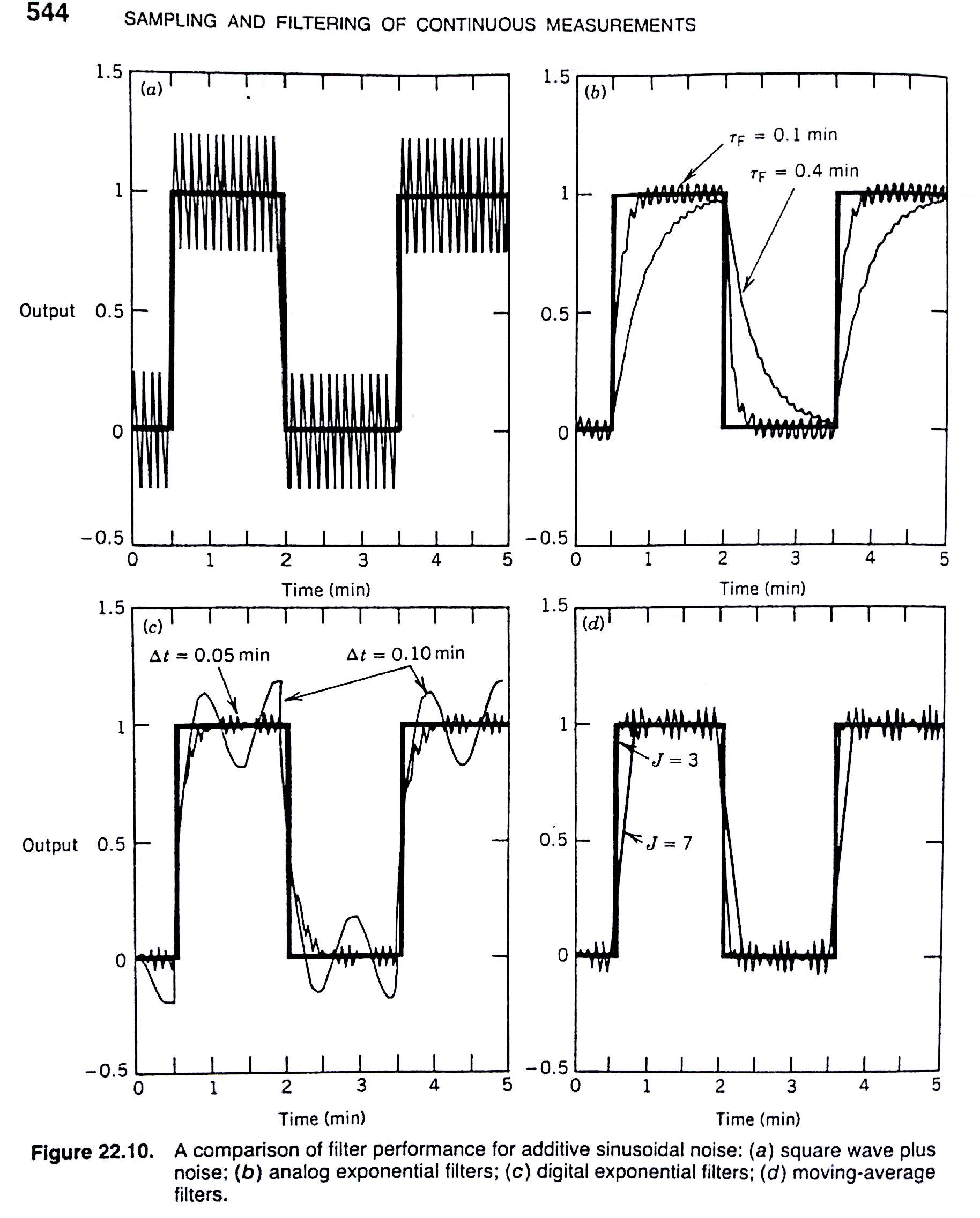
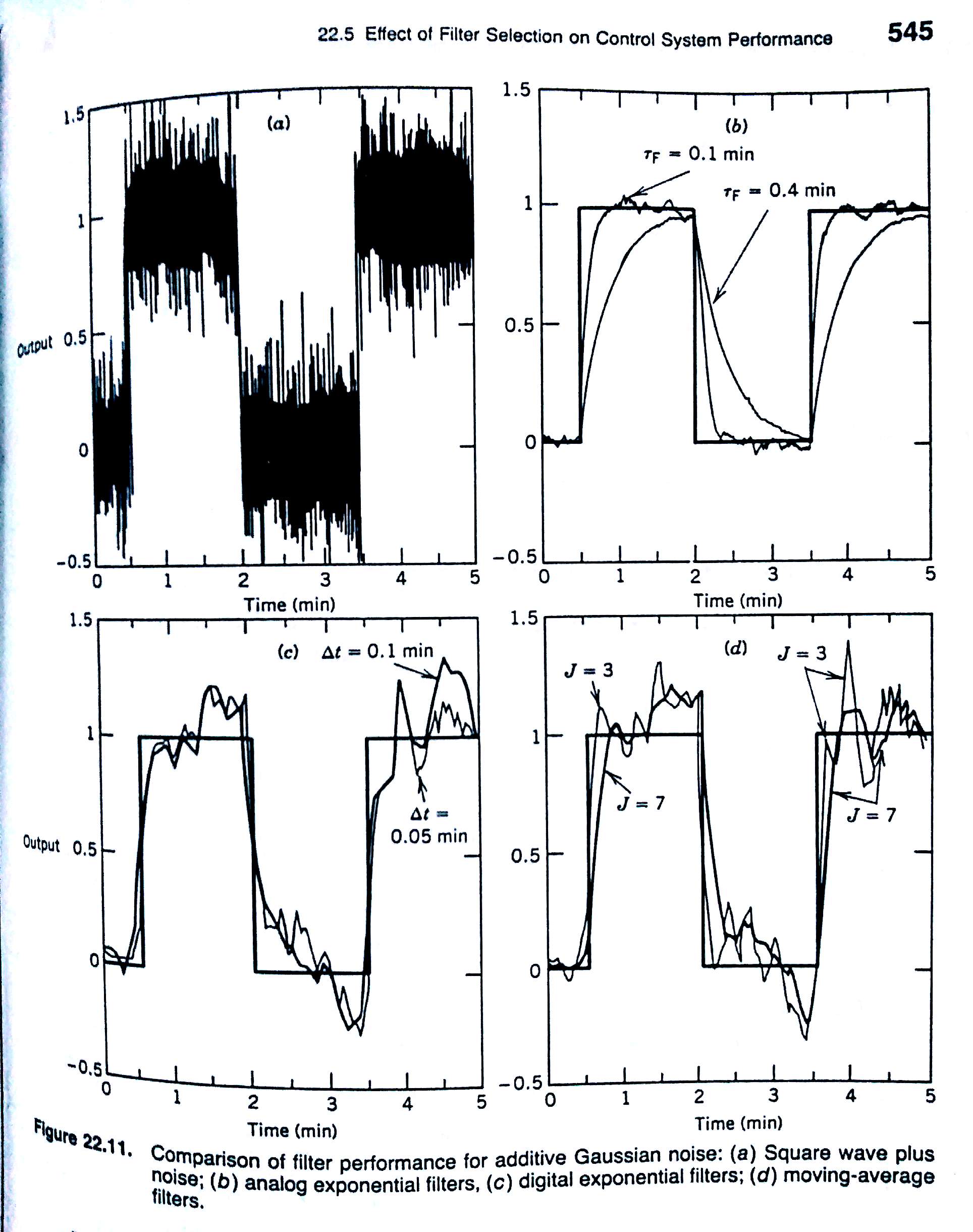
Ref.: Process Dynamics and Control 4th Edição, por Dale E. Seborg (Author), Thomas F. Edgar (Author), Duncan A. Mellichamp (Author), Francis J. Doyle III (Author), Wiley; 4ª edição (13 setembro 2016), 512 páginas, ISBN-10: 1119285917, ISBN-13 : 978-1119285915.

Segue script adotado no MATLAB que gerou figura com ruido:

% Problema sugerido - controladores ação derivativa
% Fernando Passold, 24/04/2018
T1=1/(0.05*60) % 1o-periodo de amostragem
T2=1/(0.1*60)   % 2o-periodo de amostragem
% Simulando os primeiros 2 ciclos de uma onda
% quadrada, f = 1/3 (Hz)
% amostrar este sinal 20 x f
disp('Onda quadrada oscilando à:')
f = 1/3
fs = 20*20;
T_square = 1/f;
T = 1/fs;
k=0:T:2*T_square;
u=length(k); % qtadade de amostras geradas
square=zeros(1, u);
for i=1:u
    t = k( i );    % calculando tempo real em segundos
    if ( t > T_square/2 )&&( t < T_square)
        square(1, i) = 1;
    end
    if ( t > (T_square + T_square/2) )&&( t < 2*T_square)
        square(1, i) = 1;
    end
end
% Sobrepondo a senoide (ruido) de 0,25 Vp, freq = 9 Hz
f_N = 9;
T_N = 1/f_N;
for i=1:u
    t = k( i );
    noise( i ) = 0.25*sin(2*pi*f_N*t);
    signal( i ) = square( i ) + noise( i );
end
plot(k, signal,'m-', k, square)
legend('Sinal com ruido','Sinal sem ruido')
grid

> Arquivo fonte: /Volumes/Macintosh_HD/Users/fernandopassold/Documents/UPF/Controle\_Auto\_3/Derivador/Controle\_Acao\_Derivativa.md (Abril/2018)

Fernando Passold, Abril/2018