Projeto de Controladores Digitais

Recuperando dados da aula passada (de 07/04/2025 ), arquivo: [dados.mat]:

xxxxxxxxxx
>> diary aula_140402025.txt
>> load dados % recuperar dados da aula passada

Continuando da aula passada. Faltou integrador por "Atraso de Fase", ou simplemente "Lag". Sugere-se ver antes: Projeto de Lag (com teoria) (PDF).

Projeto do Lag

Para este tipo de controlador, seu pólo "sai" do círculo unitário ($p_{Lag} < 1$). Considerar que quanto maior o afastamento, menor sua ação algo integradora (aumenta o erro de regime permanente), passando a atuar mais como um simples filtro passa-baixa. O zero deste controlador obviamente deve estar localizado no plano-z antes do pólo, mas muito provavelmente antes do pólo mais lento da planta à ser controlada (maior dominânica na resposta). Um esboço rápido no plano-z revela algo como:

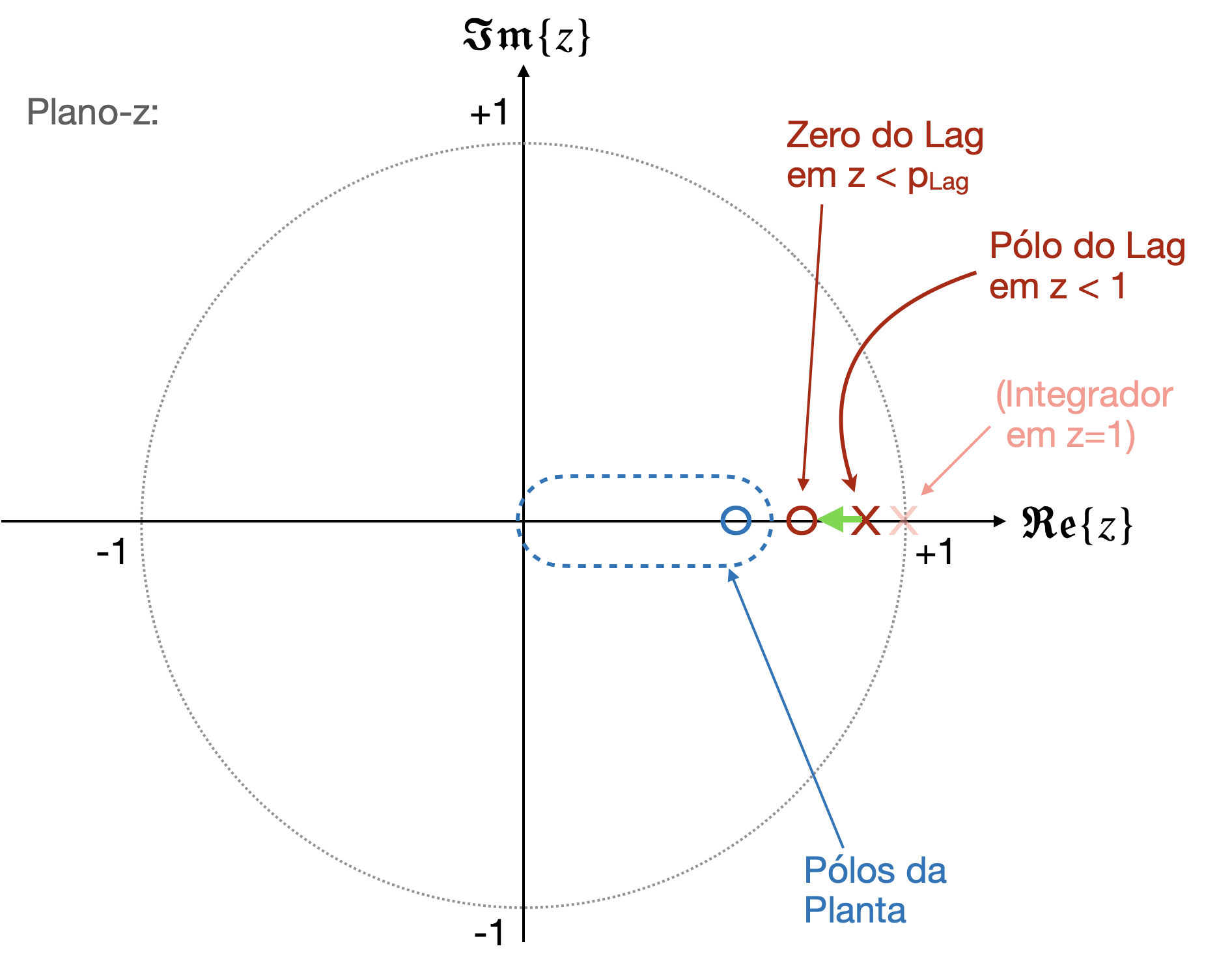
Lembrando da eq. da planta, $BoG(z)$ para alocar pólos e zeros para o controlador Lag:

xxxxxxxxxx
>> zpk(BoG)
​
ans =
 
  0.00012224 (z+2.747) (z+0.1903)
  --------------------------------
  (z-0.9048) (z-0.8187) (z-0.3679)
 
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.
​
>> p_Lag=(1+0.9048)/2
p_Lag =
       0.9524

Localizando o zero do Lag no mesmo local do zero do PI1a realizado na aula anterior:

$C_{PI1a}=\dfrac{13.5 (z-0.91)}{(z-1)}$

xxxxxxxxxx
>> C_Lag1=tf( [1 -0.92], [1 -0.95], T )
​
C_Lag1 =
 
  z - 0.92
  --------
  z - 0.95
 
Sample time: 0.1 seconds
Discrete-time transfer function.
​
>> ftma_Lag1=C_Lag1*BoG;
>> rlocus(ftma_Lag1)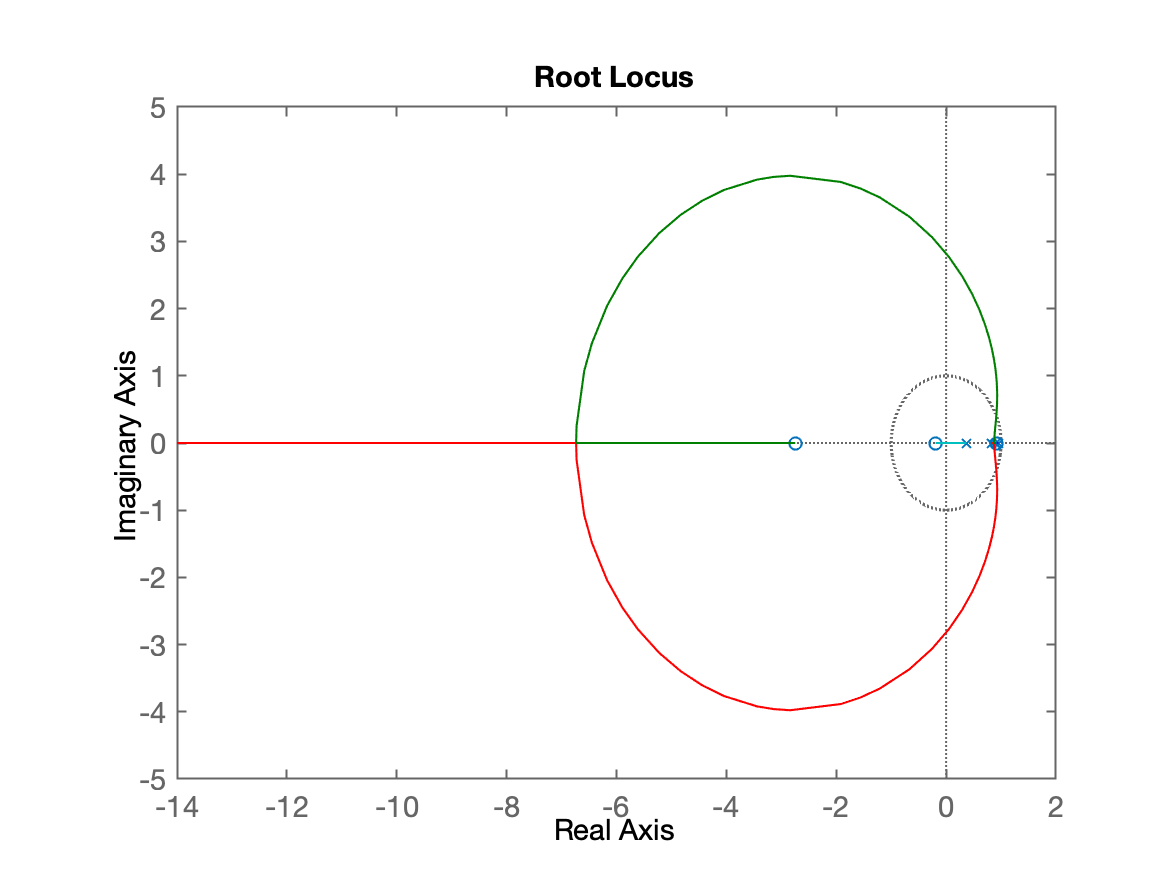

Realizando o zoom na região de interesse:

xxxxxxxxxx
>> axis([0.6 1.1 -0.6 0.6])
>> hold on; zgrid(zeta,0) % acrescentnado linha guia do zeta para OS=15%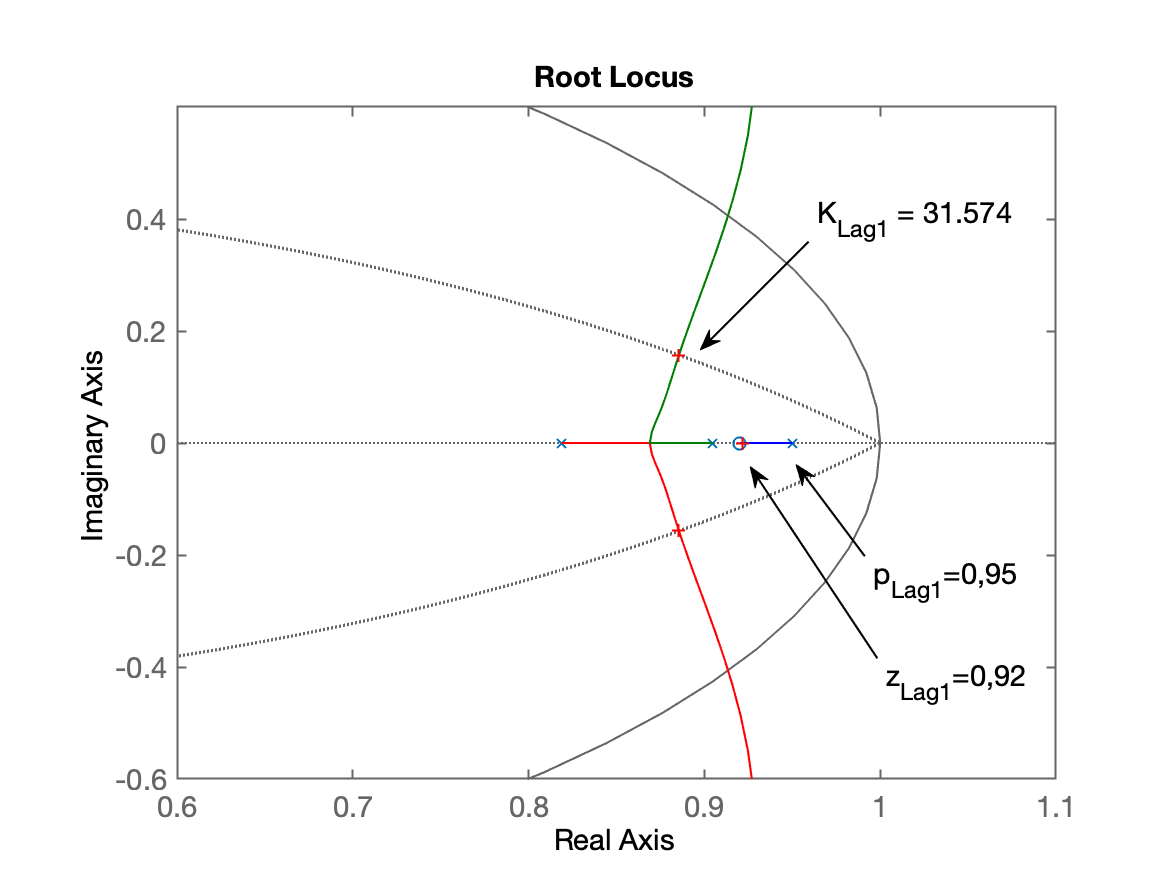

Terminando projeto:

xxxxxxxxxx
>> [K_Lag1,polosMF]=rlocfind(ftma_Lag1)
Select a point in the graphics window
selected_point =
      0.88614 +    0.15604i
K_Lag1 =
       31.574
polosMF =
      0.92173 +          0i
      0.88544 +    0.15611i
      0.88544 -    0.15611i
      0.34499 +          0i
>> ftmf_Lag1=feedback(K_Lag1*ftma_Lag1, 1);
>> figure; step(ftmf_PI1a, ftmf_Lag1)
>> legend('PI1a', 'Lag1') % já comparando resposta com PI1a feito antes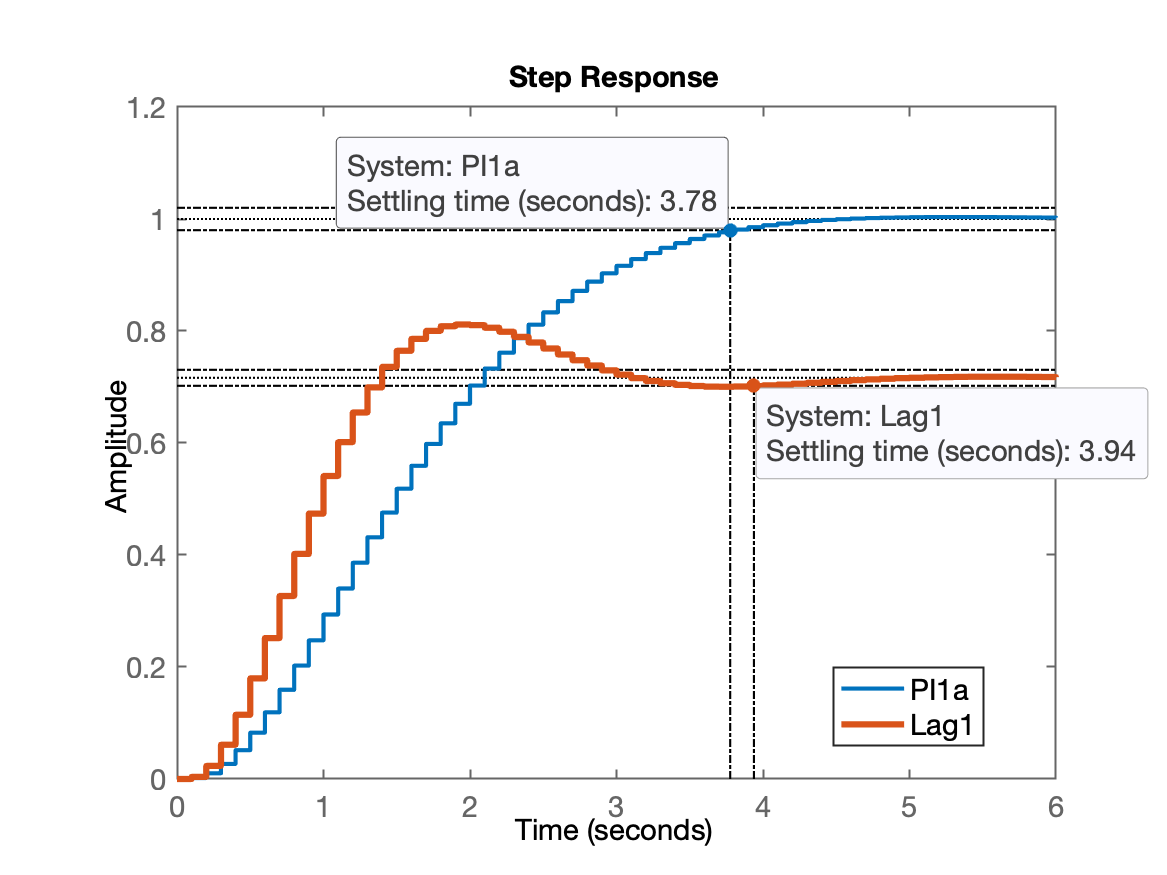

Calculando erro:

xxxxxxxxxx
>> erro_Lag1=((1-dcgain(ftmf_Lag1))/1)*100
erro_Lag1 =
       28.362

Realizando o projeto melhorado do "Lag2", usando o App Control System Designer.

Projeto do Lag2

Repare que antes poderiámos ter ampliado o ganho do Lag1 para forçar $\%OS \cong 15\%$ (em relação à referência: entrada degrau unitário):

xxxxxxxxxx
>> zpk(C_Lag1b)
​
ans =
 
  68 (z-0.92)
  -----------
   (z-0.95)
 
Name: C
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.

Projeto do controlador até este ponto:

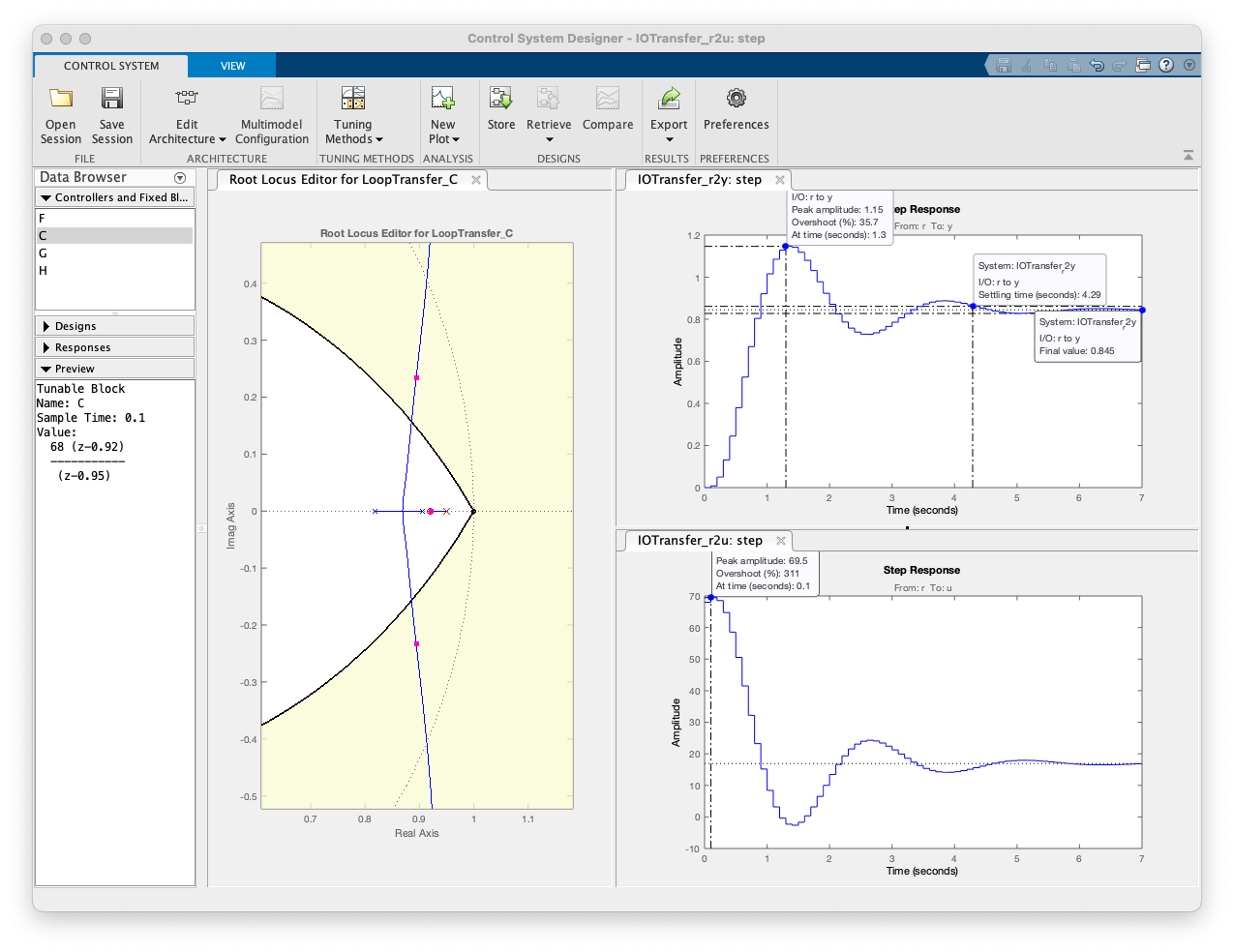
Melhorando este controlador...

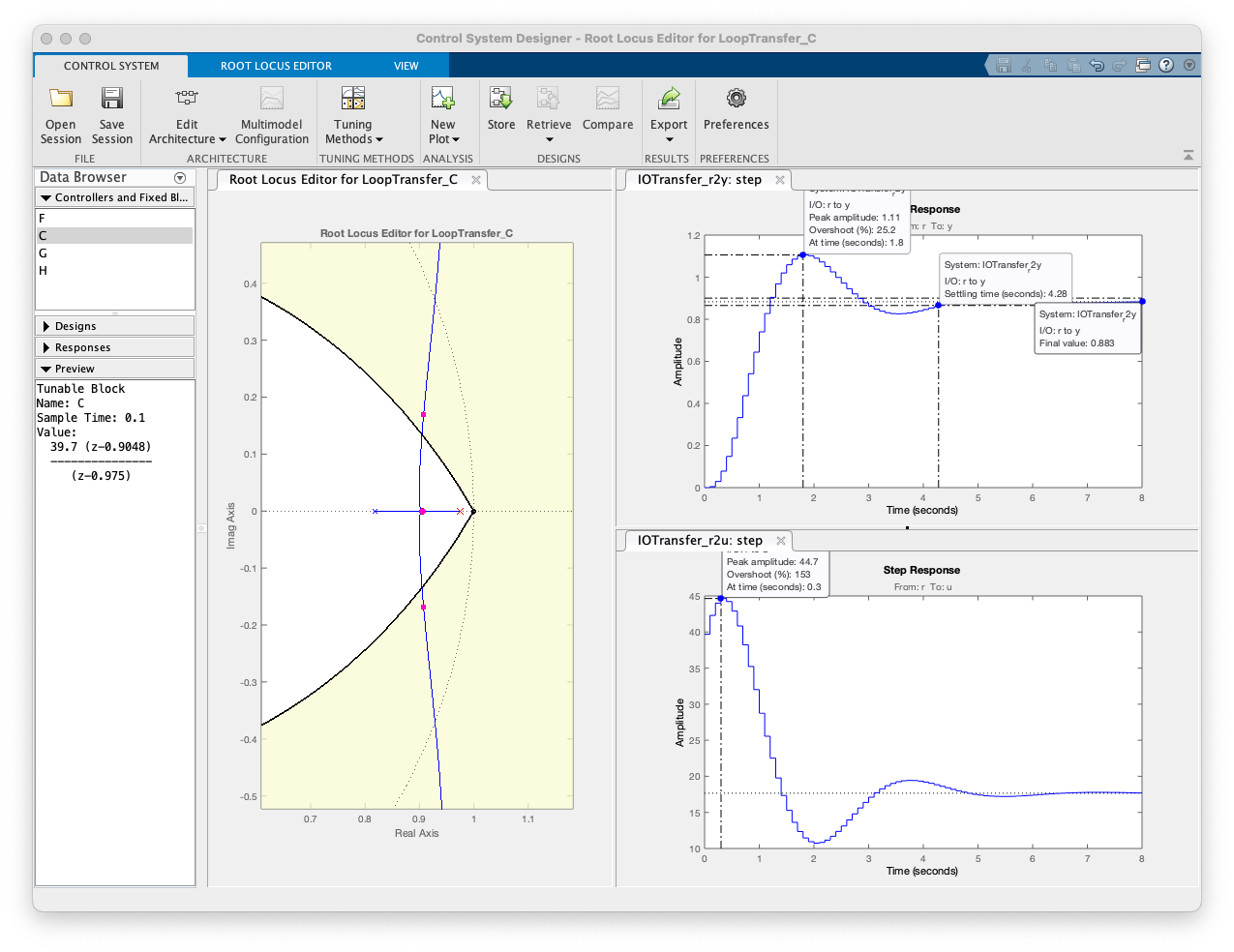
Equação do Lag2:

xxxxxxxxxx
zpk(C_Lag2)
​
ans =
 
  39.7 (z-0.9048)
  ---------------
     (z-0.975)
 
Name: C
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.

Se o ganho deste controlador for reduzido para $K\cong22,442$, reduzimos o $t_s$ para 3,79 segundos, mas o erro em regime permanente aumenta para quase 20% ($y[\infty]=0,81$).

Tentando outro Lag: o "Lag3", mas note que $t_s$ aumenta às custas de erro mais baixo:

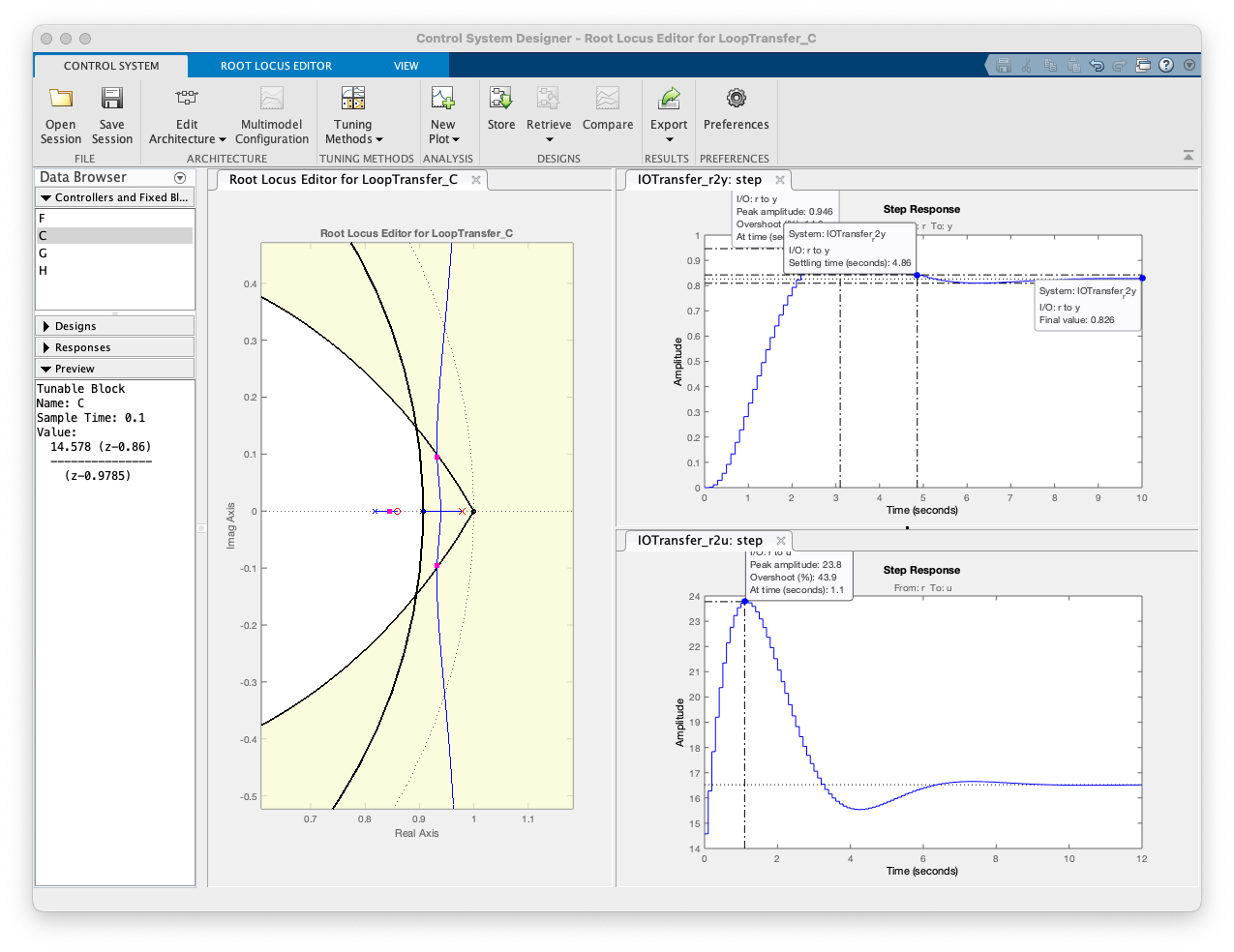
Lag Usando Contribuição Angular

O script find_polo_zero_d.m permite definir um controlador usando contribuição angular para terminar de definir o pólo ou zero que falta num controlador.

xxxxxxxxxx
>> help find_polo_zero_d
  find_polo_zero_d.m
  
  Rotina de contribuicao angular para descobrir onde
  localizar polo ou zero dependendo do local desejado para
  os polos de MF - no plano-z (controle digital)
 
  Uso:
     Esta rotina ja' espera uma tf de nome "ftma_aux"
  onde: ftma_aux(z)=C(z)*BoG(z);
  e onde: C(z) esta' parcialmente fornecido, ou ja' contendo
  zero(s) ou ja' contendo polo(s)
  
  A rotina pergunta durante a execucao se a ideia e'
  determinar o local de um zero ou de um polo do controlador.
 
  Fernando Passold, em 14/10/2020, 20/10/2020
​
>> 

Neste caso, primeiro devemos "montar" uma função transferência auxiliar para definir o controlador, no caso um "Lag" onde inicialmente arbitramos o local do seu pólo em $z=0,95$, criando a variável C_aux e depois calculamos a variável ftma_aux:

xxxxxxxxxx
>> C_aux=tf( 1, [1 -0.95], T ) % não esquecer o terceiro parâmetro T = período de amostragem
>> ftma_aux=C_aux*BoG;
>> zpk(ftma_aux)    % verificando se está tudo correto
​
ans =
 
       0.00012224 (z+2.747) (z+0.1903)
  -----------------------------------------
  (z-0.95) (z-0.9048) (z-0.8187) (z-0.3679)
 
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.
​
>> 

Finalmente executando o script find_polo_zero_d.m, ocorre:

xxxxxxxxxx
>> find_polo_zero_d
Overshoot desejado (em %): ? 15
ts_d (settling time desejado): ? 4
Polos (desejados) de MF em:
  $z = 0.892459 \pm j0.149155$ (ou $0.90 \angle \pm 9.49^o$)
Calculando angulos dos polos:
  Polo 1 em $z= 0.95$ --> angulo: $111.10^o$
  Polo 2 em $z= 0.904837$ --> angulo: $94.74^o$
  Polo 3 em $z= 0.818731$ --> angulo: $63.70^o$
  Polo 4 em $z= 0.367879$ --> angulo: $15.87^o$
Soma angular dos polos: $285.41^o$
​
Calculando angulos dos zeros:
  Zero 1 em $z=-2.74711$  --> angulo: $2.35^o$
  Zero 2 em $z=-0.190308$  --> angulo: $7.84^o$
Soma angular dos zeros: $10.19^o$
​
Determinar: [p]=polo ou [z]=zero do controlador: ? z
​
Angulo requerido para zero do controlador: $95.22^o$
O zero do controlador deve estar em:
`zero_c` em $z = 0.906081$
​
Eq. da ftma(z) com controlador --> `ftma`:
ans =
 
  0.00012224 (z+2.747) (z-0.9061) (z+0.1903)
  ------------------------------------------
  (z-0.95) (z-0.9048) (z-0.8187) (z-0.3679)
 
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.
​
>> 

Note que o script find_polo_zero_d.m acaba gerando além das informa~çaoes numéricas, uma primeira janela gráfica mostrando a contribuição angular e uma segunda janela gráfica mostrando o RL final considerando a $FTMA(z)$ do sistema com o controlador recém projetado.

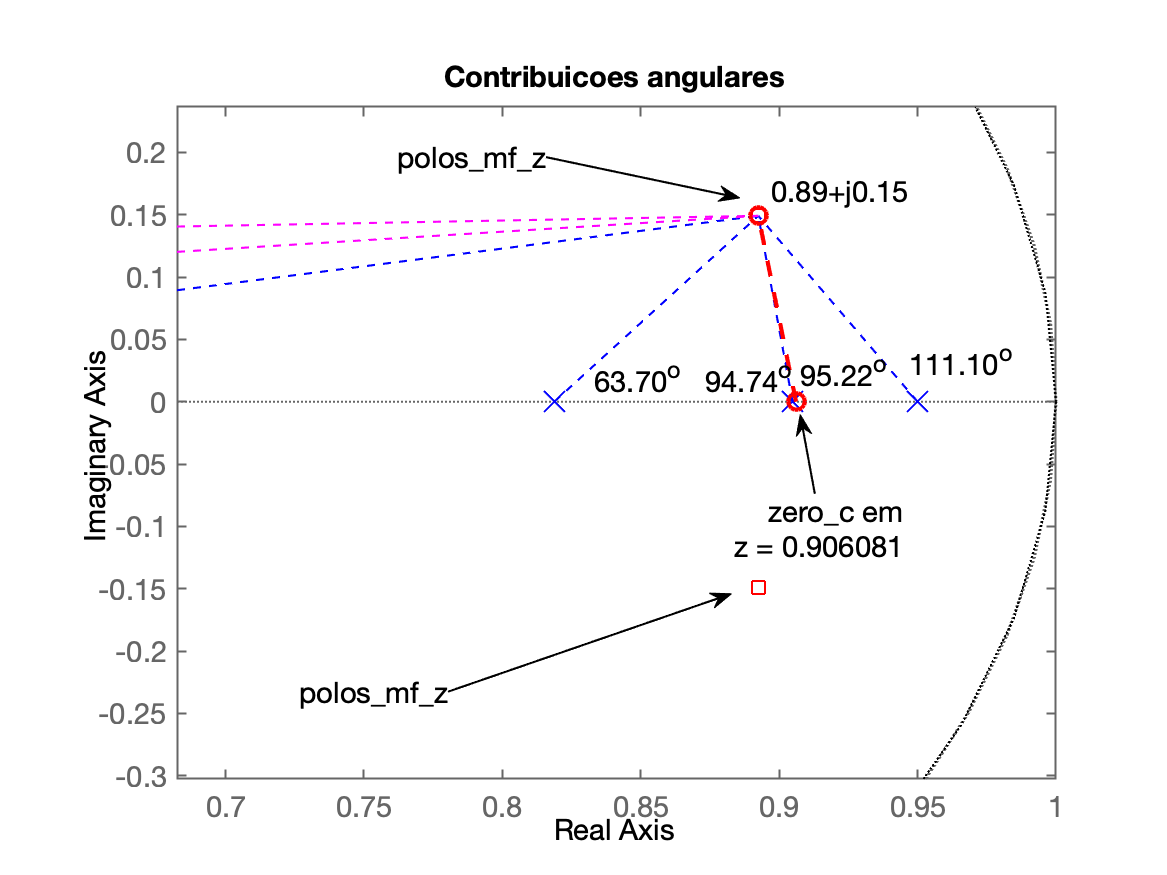
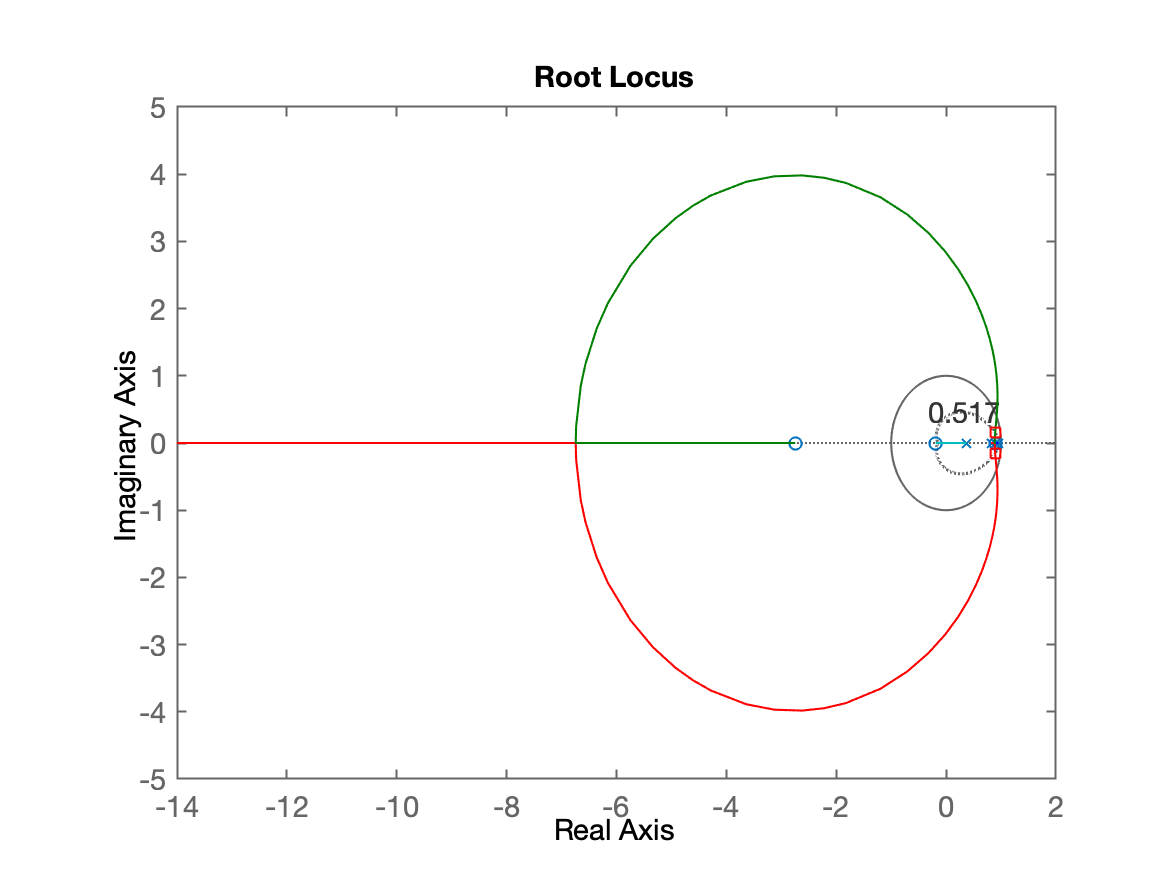
Um zoom no RL anterior permite visualizar:

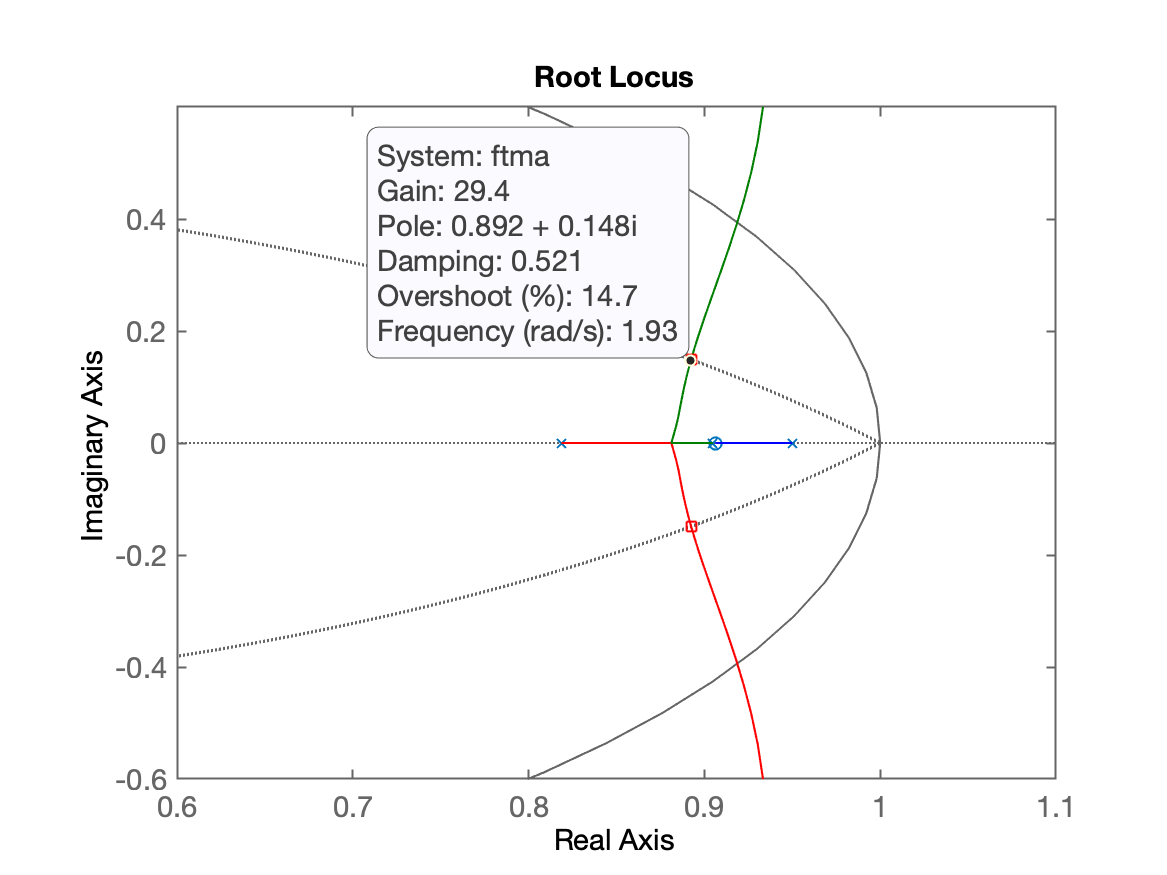
O zero ou pólo que este script ajudou a encontrar se encontra na variável polo_c ou zero_c, respectivamente para o caso do pólo ou zero que faltou definir.

No caso acima:

xxxxxxxxxx
>> zero_c
zero_c =
      0.90608

Neste caso, a eq. final deste controlador Lag resultou:

$C_{Lag}(z)=\dfrac{29,4 \, (z-0,9061)}{(z - 0,95)}$

Terminando de fechar a malha e verificando como fica a resposta para entrada degrau:

xxxxxxxxxx
>> ftma_Lag4=ftma;
>> ftmf_Lag4=feedback(29.4*ftma_Lag4, 1);
>> figure; step(ftmf_Lag4)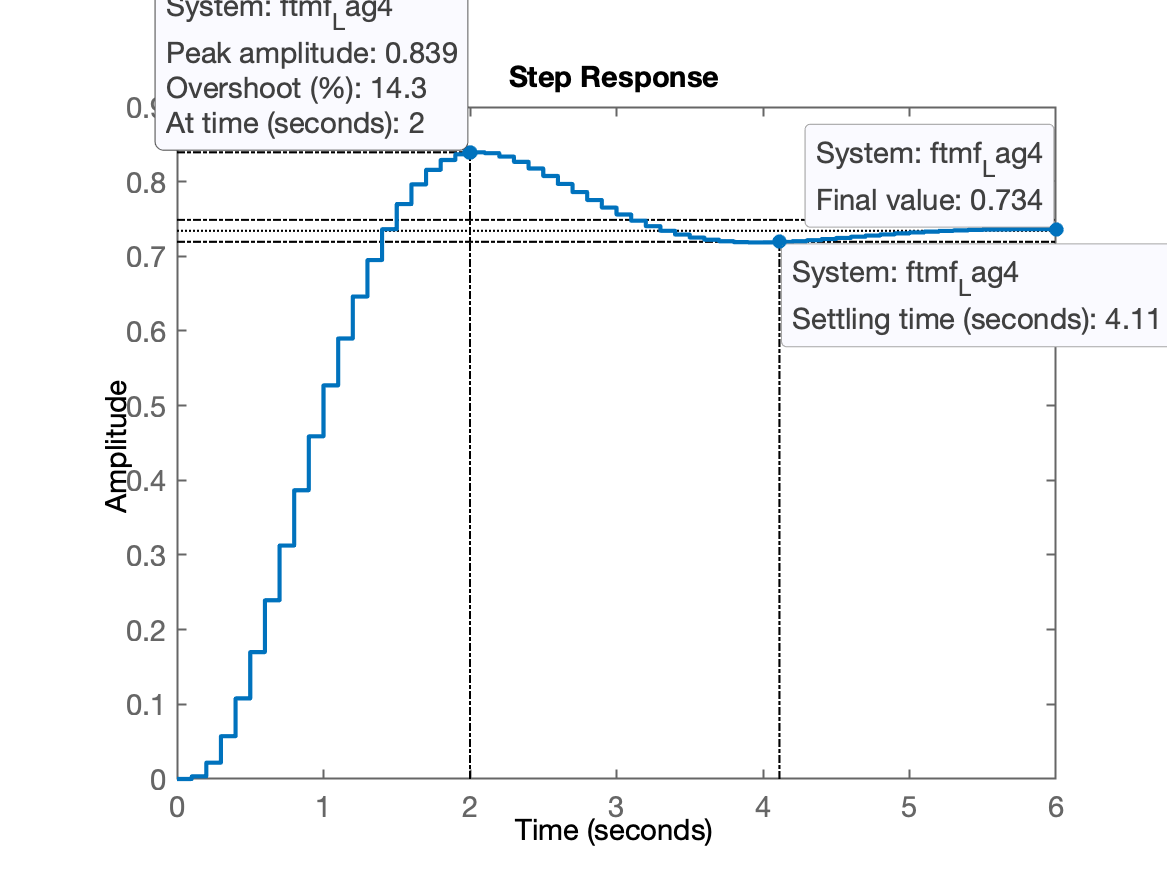

Encerrando atividades usando MATLAB nesta aula:

xxxxxxxxxx
>> save dados
>> diary off
>> quit

Continuando com teoria de controladores com Ação Derivativa, tópicos:

• Teoria inicial sobre Ação Derivativa + Filtros;
• Resumo Controladores PD & Lead (arquivo PDF; Aula de 21/05/2020);

Outros tópicos:

• Conteúdo das aulas anteriores (Semestre 2025/1);
• Conteúdo completo da disciplina.

Fernando Passold, em 14/04/2025