Projeto Controladores Digitais

Aula de 07/04/2025.

Recuperando dados da aula passada (arquivo dados.mat):

​x
>> diary aula_07042025.txt   % registra informações em arquivo texto
>> load dados
>> who
​
Your variables are:
​
BoG   G     K     OS    T     ans   erro  ftmf  zeta  
​
>> zpk(G)  % Recordando eq. da plata
 
          1
  ------------------
  (s+10) (s+2) (s+1)
 
Continuous-time zero/pole/gain model.

Controlador Proporcional limitando e[∞]

A idéia no início desta aula é projetar um Controlador Proporcional e ajustar seu ganho de forma à limitar o erro em regime permanente (em malha-fechada).

Sugere-se uma revisão da Teoria do erro aplicado no projeto de Controladores Proporcionais (aula de 23/09/2021).

Suponha que queira definir o ganho do controlar para limitar erro em 15%.

A planta é um sistema tipo 0:

xxxxxxxxxx
>> zpk(BoG)
 
  0.00012224 (z+2.747) (z+0.1903)
  --------------------------------
  (z-0.9048) (z-0.8187) (z-0.3679)
 
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.

Calculando o ganho de posição, $K_p$:

$K_p = \displaystyle\lim_{z \to 1} FTMA(z)$

neste caso:

$K_p = \displaystyle\lim_{z \to 1} K \cdot BoG(z)$

$K_p = K \cdot \displaystyle\lim_{z \to 1} BoG(z)$

Calculando apenas o termo $\displaystyle\lim_{z \to 1} BoG(z) = K_{aux}$:

$K_{aux} = \displaystyle\lim_{z \to 1} \dfrac{0.00012224 (z+2.747) (z+0.1903)}{(z-0.9048) (z-0.8187) (z-0.3679)}$

$K_{aux} = \dfrac{0.00012224 (1+2.747) (1+0.1903)}{(1-0.9048) (1-0.8187) (1-0.3679)}$

$K_{aux} = 0,05$

xxxxxxxxxx
>> K_aux = (0.00012224*(1+2.747)*(1+0.1903))/((1-0.9048)*(1-0.8187)*(1-0.3679))
K_aux =
     0.049973
​
>> % Ou usando função dcgain do MATLAB
>> dcgain(BoG)
         0.05
​
>> % Valor de y[∞] em regime permanente para e[∞]=15% (entrada degrau)
>> 1-15/100
         0.85

Equação do erro:

$e[\infty]=\dfrac{1}{1+K_p}$

considerando os valores neste caso:

$0,15 = \dfrac{1}{1+K_p}$

$K_{p_{necessario}}=\dfrac{1-0.15}{0.15}$

xxxxxxxxxx
>> Kp_d = (1-0.15)/0.15
Kp_d =
       5.6667

Este é valor necessário (desejado) para o ganho estático de posição.

Mas $K_p$ é definido como:

$K_p = \displaystyle\lim_{z \to 1} FTMA(z)$

Neste caso:

$K_p = \displaystyle\lim_{z \to 1} K \cdot BoG(z) = K \cdot dcgain(BoG) = K \cdot 0,05$

Substituindo valor de $K_p$ encontrado antes na equação acima, temos:

$5,6667 = K \cdot 0,05$

$K=5,6667/0,05$

Usando MATLAB:

xxxxxxxxxx
>> K = Kp_d/dcgain(BoG)
K =
       113.33

Comparando com $K_u \cong 243$ (ganho máximo permitido para o Controlador Proporcional), notamos que o valor encontrado ainda resulta num sistema estável em MF.

Fechando a malha e terminando com simulação para entrada degrau:

xxxxxxxxxx
>> ftmf_K = feedback(K*BoG, 1);
>> step(ftmf_K)
>> stepinfo(ftmf_K)
​
        RiseTime: 0.3
    SettlingTime: 6.1
     SettlingMin: 0.60898
     SettlingMax: 1.289
       Overshoot: 51.648
      Undershoot: 0
            Peak: 1.289
        PeakTime: 1
​
>> % Valor de y[∞]:
>> dcgain(ftmf_K)
         0.85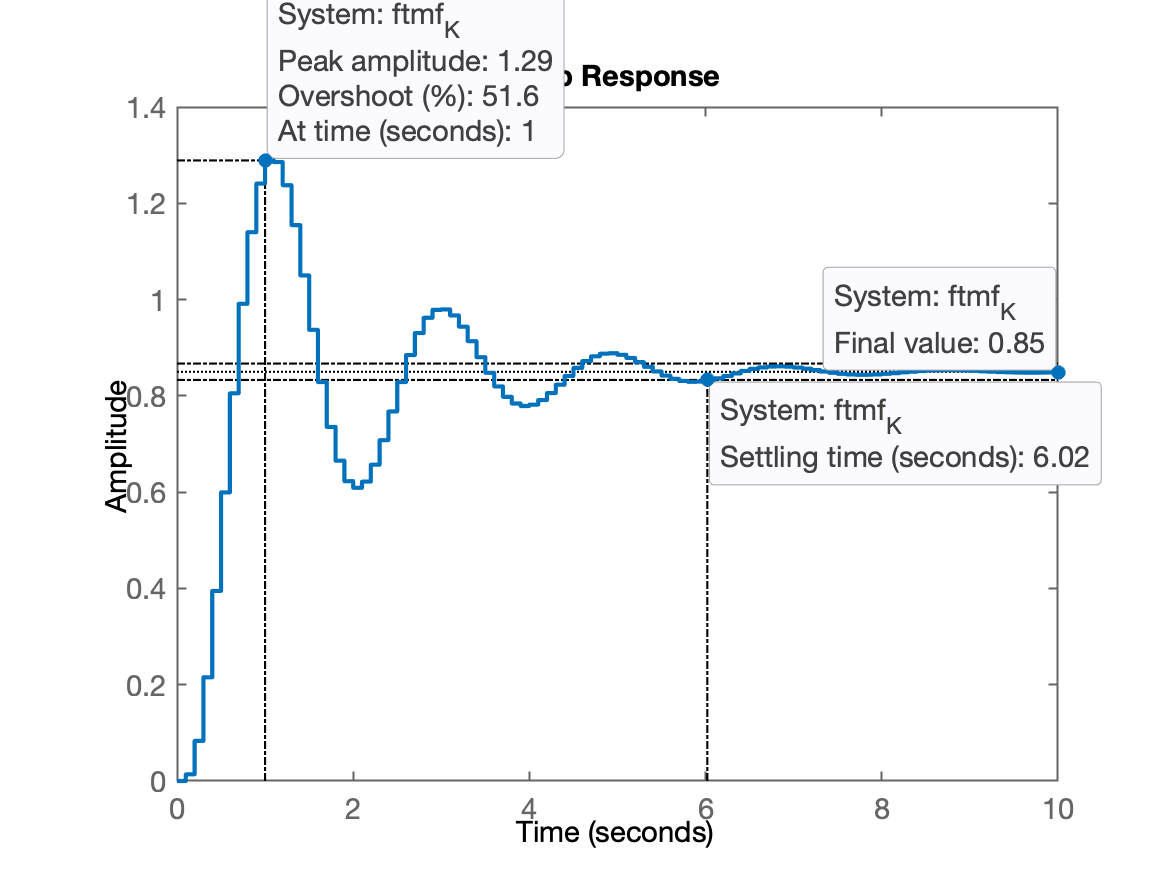

O overshoot em relação ao degrau (unitário) foi de 29% ($y[\infty]=1,29$).

Próximo passo: zerar erro de regime permanente.

Acrescentando Ação Integral

Equação da Ação Integral Pura:

$C_I(z)=\dfrac{K_I}{(z-1)}$

onde a ação integral é caracterizada pelo pólo em $z=1$.

Usando MATLAB:

xxxxxxxxxx
>> C_I = tf(1, [1 -1])
​
C_I =
 
    1
  -----
  s - 1
 
Continuous-time transfer function.
​
>> % Ops, como esquecemos de informat o T, MATLAB montou tf no plano-s e não no plano-z
>> C_I = tf(1, [1 -1], T)
​
C_I =
 
    1
  -----
  z - 1
 
Sample time: 0.1 seconds
Discrete-time transfer function.
​
>> ftma_I = C_I*BoG;
>> zpk(ftma_I)
​
     0.00012224 (z+2.747) (z+0.1903)
  --------------------------------------
  (z-1) (z-0.9048) (z-0.8187) (z-0.3679)
 
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.
​
>> figure; rlocus(ftma_I)
>> axis equal % melhora aparência no plano-z (círculo unitário)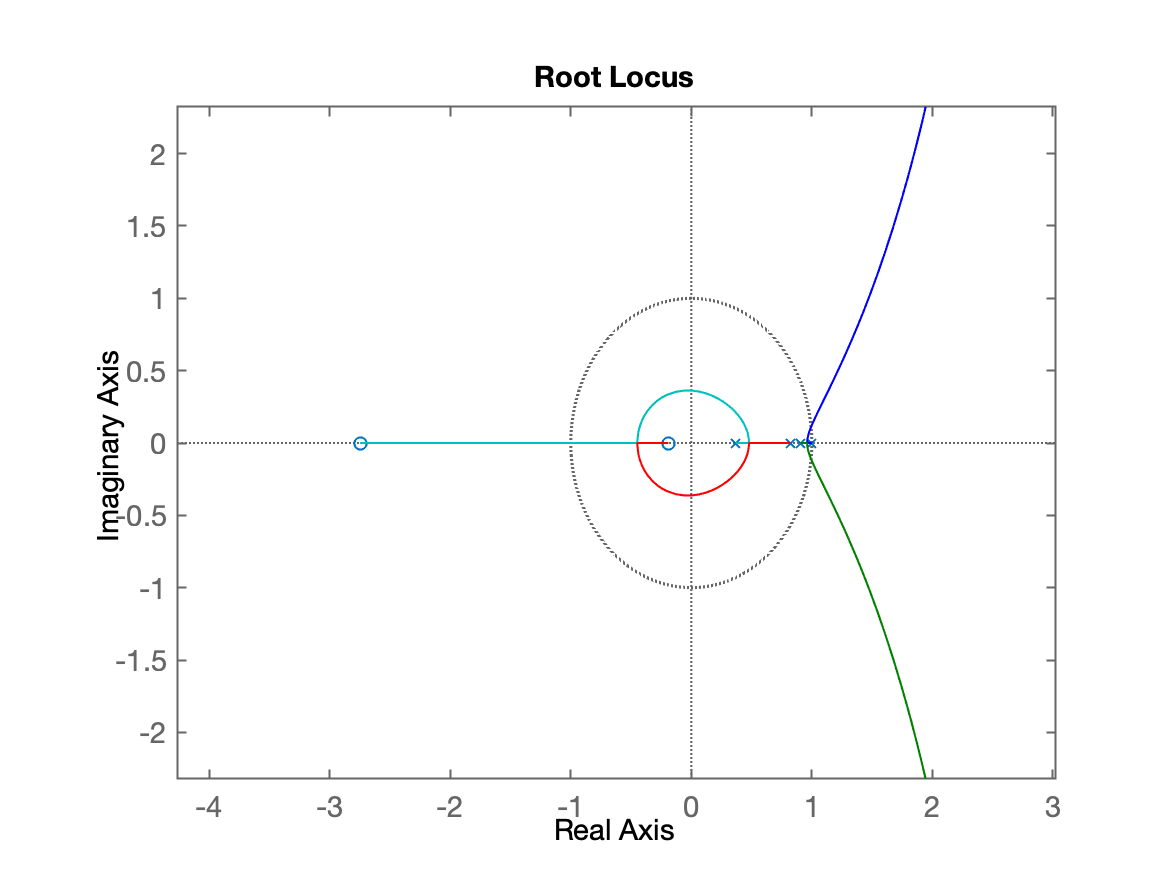

Fazendo "zoom" na região de interesse:

xxxxxxxxxx
>> axis([0.7 1.1 -0.25 0.25])
>> hold on
>> zgrid(zeta,0) % acrescentando linha guia para o zeta correspondento à %OS=15%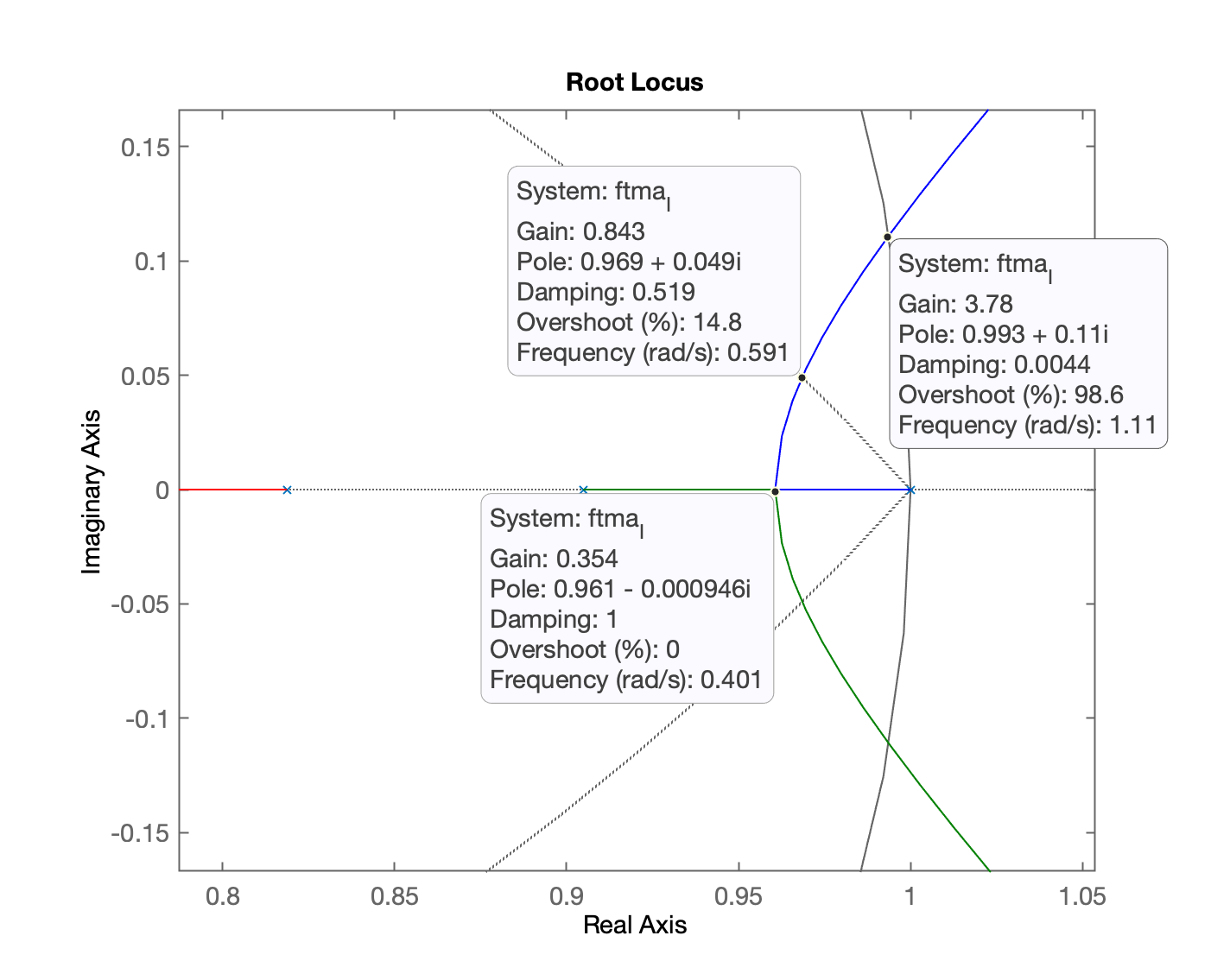

xxxxxxxxxx
>> % "Sintonizando" controlador
>> [K_I,polosMF]=rlocfind(ftma_I)
Select a point in the graphics window
​
selected_point =
      0.96845 +   0.049356i
​
K_I =
      0.85046
​
polosMF =
      0.96854 +   0.049328i
      0.96854 -   0.049328i
      0.78529 +          0i
      0.36907 +          0i
​
>> ftmf_I = feedback(K_I*ftma_I, 1); % fechando a malha
>> figure; step(ftmf_I, ftmf_K)
>> legend('Integrador Puro (%OS=15%)', 'Proporcional (e[\infty]=15%)')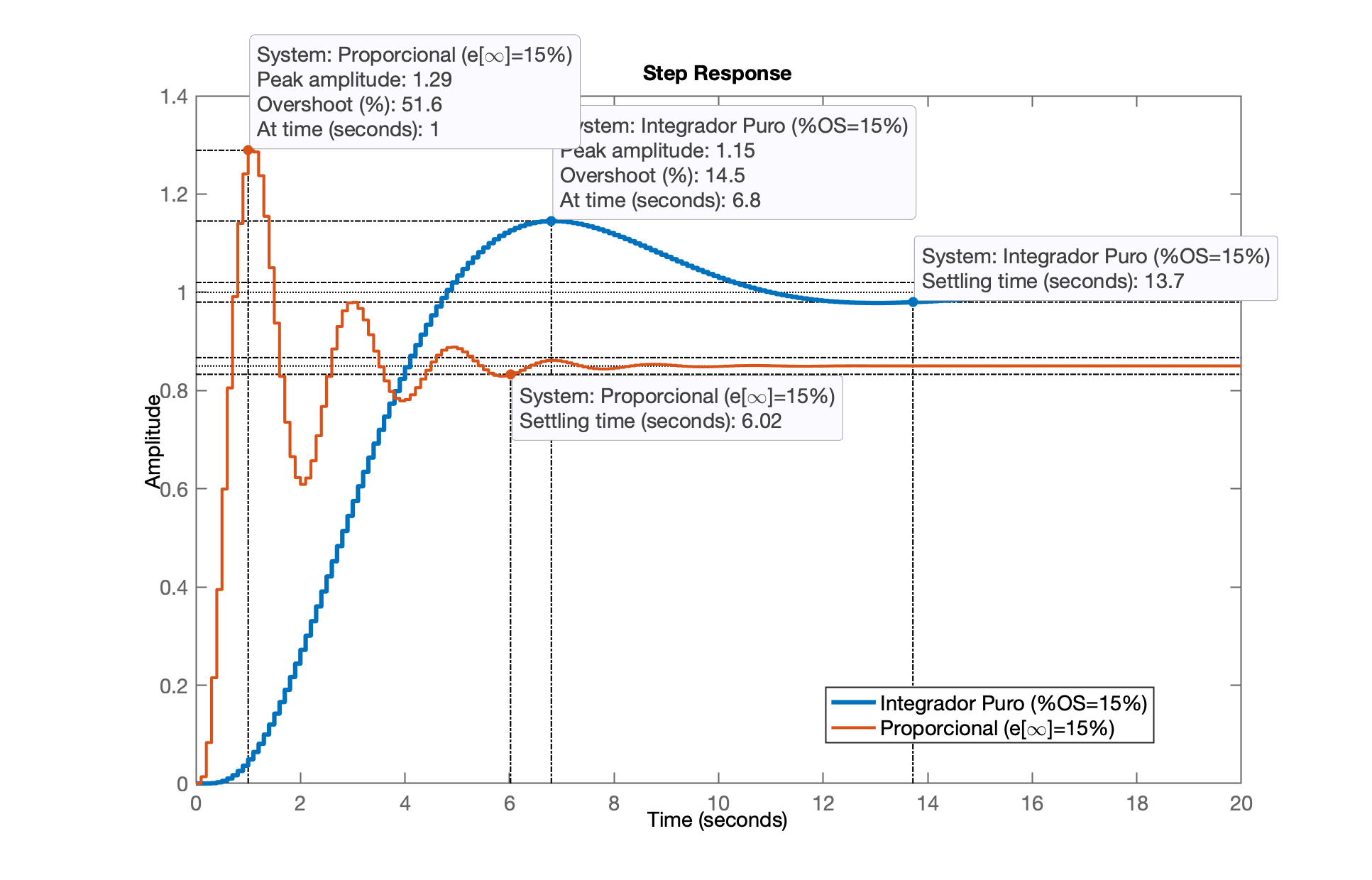

O erro de regime permanente foi anulado, $e[\infty]=0$, mas $t_s = 13,7$ segundos é muito elevado.

Para "consertar" este efeito, temos que acrescentar ação de controle Proporcional à (pura) ação Integral.

Controlador PI

O diagrama de blocos do controlador PI aparece abaixo:

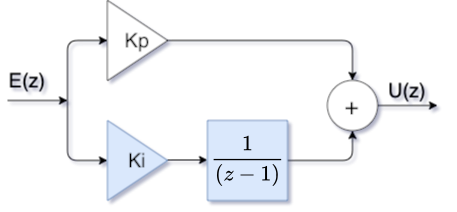
Dedução da eq. do PI, ver Controlador PI (aula de 14/05/2020)

Equação genérica do PI fica:

$C_{PI}(z)=\dfrac{K(z-z_{PI})}{(z-1)}$

Surge uma incógnica extra que é: - onde posicionar o zero do PI ($z_{PI}$)?

Alguma discussão aparece na Aula de 05/05/2021.

Testando 2 opções para $z_{PI}$:

• Opção 1: $z_{PI} = 0,91$;
• Opção 2: $z_{PI} = 0,83$.

Controlador PI (Opção 1)

xxxxxxxxxx
>> C_PI1=tf([1 -0.91],[1 -1],T)
​
C_PI1 =
 
  z - 0.91
  --------
   z - 1
 
Sample time: 0.1 seconds
Discrete-time transfer function.
​
>> ftma_PI1=C_PI1*BoG;
>> zpk(ftma_PI1)
​
  0.00012224 (z+2.747) (z-0.91) (z+0.1903)
  ----------------------------------------
   (z-1) (z-0.9048) (z-0.8187) (z-0.3679)
 
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.
​
>> figure; rlocus(ftma_PI1)
>> hold on; zgrid(zeta,0)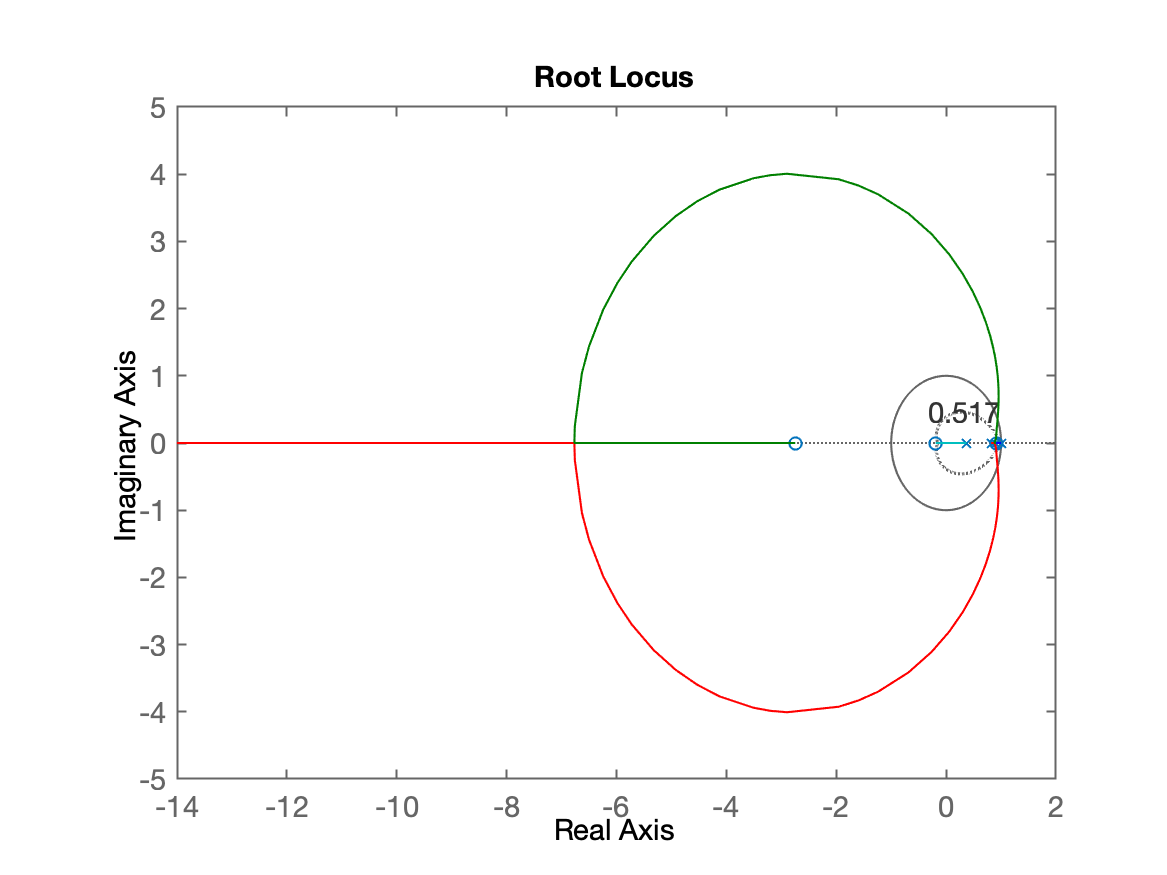

xxxxxxxxxx
>> % Fazendo zooom na região de interesse:
>> axis([0.2 1.1 -0.5 0.5])
>> axis([0.7 1.1 -0.5 0.5])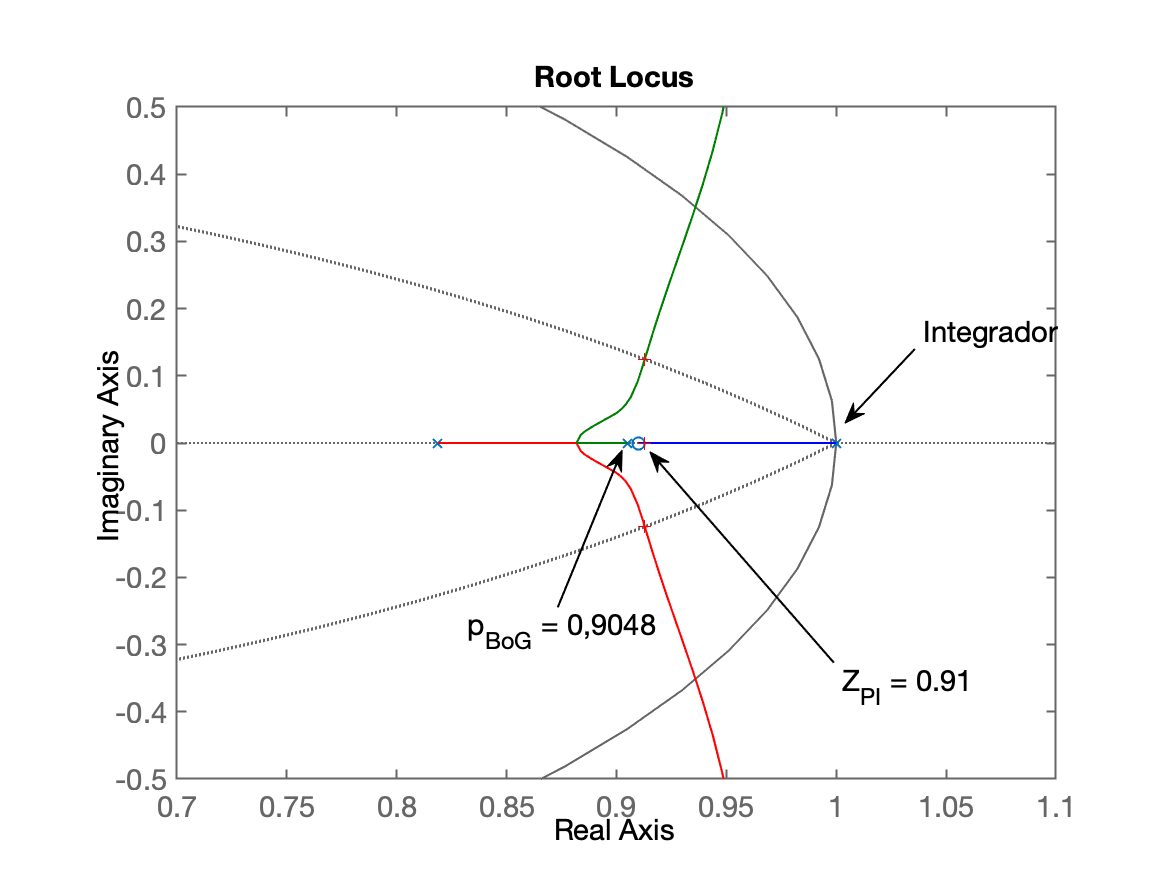

xxxxxxxxxx
>> % Sintonizando este controlador
>> [K_PI1,polosMF]=rlocfind(ftma_PI1)
Select a point in the graphics window
​
selected_point =
       0.9128 +    0.12384i
​
K_PI1 =
       26.538
​
polosMF =
      0.91281 +    0.12384i
      0.91281 -    0.12384i
      0.91268 +          0i
      0.34991 +          0i
​
>> ftmf_PI1=feedback(K_PI1*ftma_PI1, 1); % fechando a malha
>> figure; step(ftmf_PI1)
>> stepinfo(ftmf_PI1)
​
        RiseTime: 1.2
    SettlingTime: 5
     SettlingMin: 0.9502
     SettlingMax: 1.1345
       Overshoot: 13.447
      Undershoot: 0
            Peak: 1.1345
        PeakTime: 2.5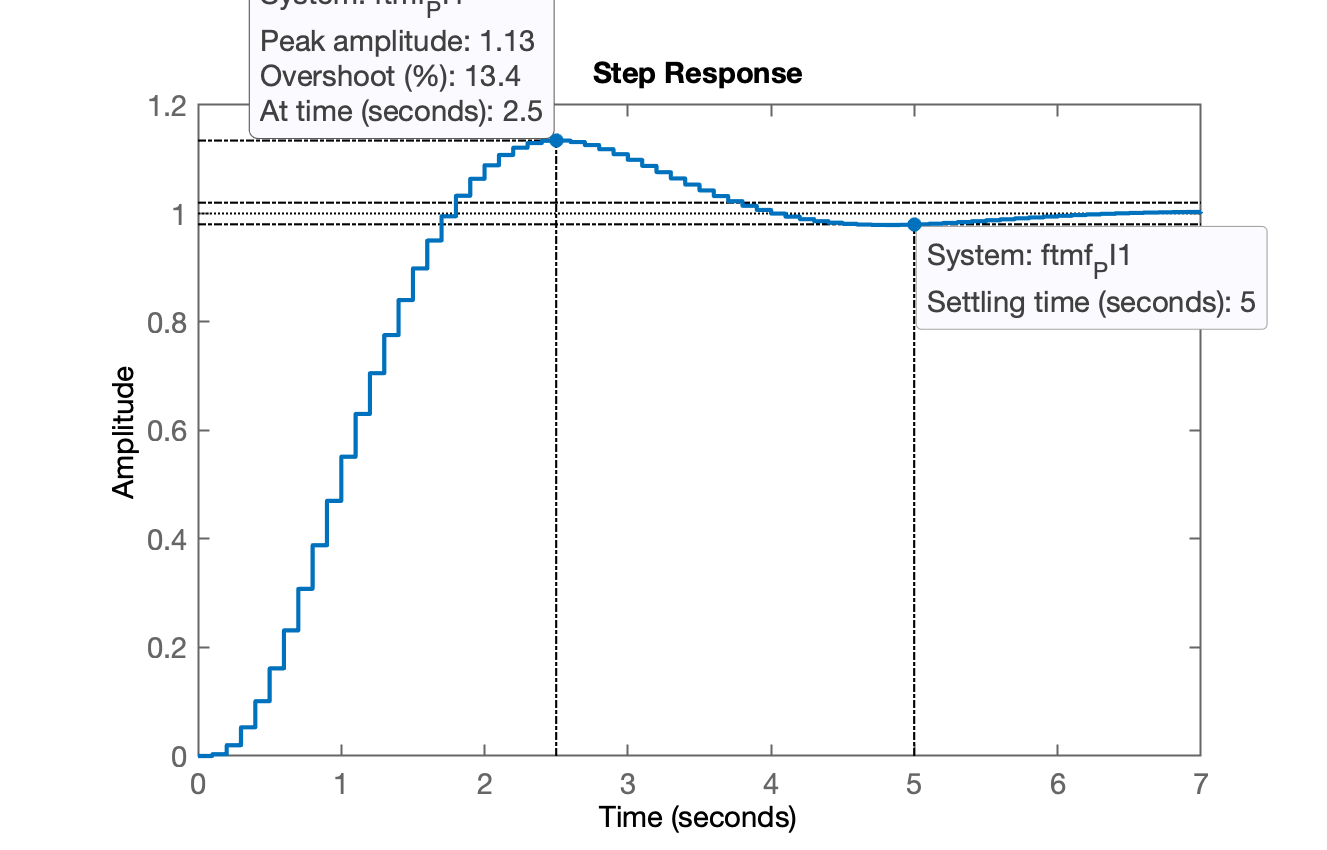

Obs.: Notamos que $t_s$ diminuiu consideravelmente em relação à ação integral pura.

Projeto do PI (Opção 2)

xxxxxxxxxx
>> C_PI2=tf([1 -0.83],[1 -1],T)
​
C_PI2 =
 
  z - 0.83
  --------
   z - 1
 
Sample time: 0.1 seconds
Discrete-time transfer function.
​
>> ftma_PI2=C_PI2*BoG;
>> zpk(ftma_PI2)
​
  0.00012224 (z+2.747) (z-0.83) (z+0.1903)
  ----------------------------------------
   (z-1) (z-0.9048) (z-0.8187) (z-0.3679)
 
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.
​
>> figure; rlocus(ftma_PI2)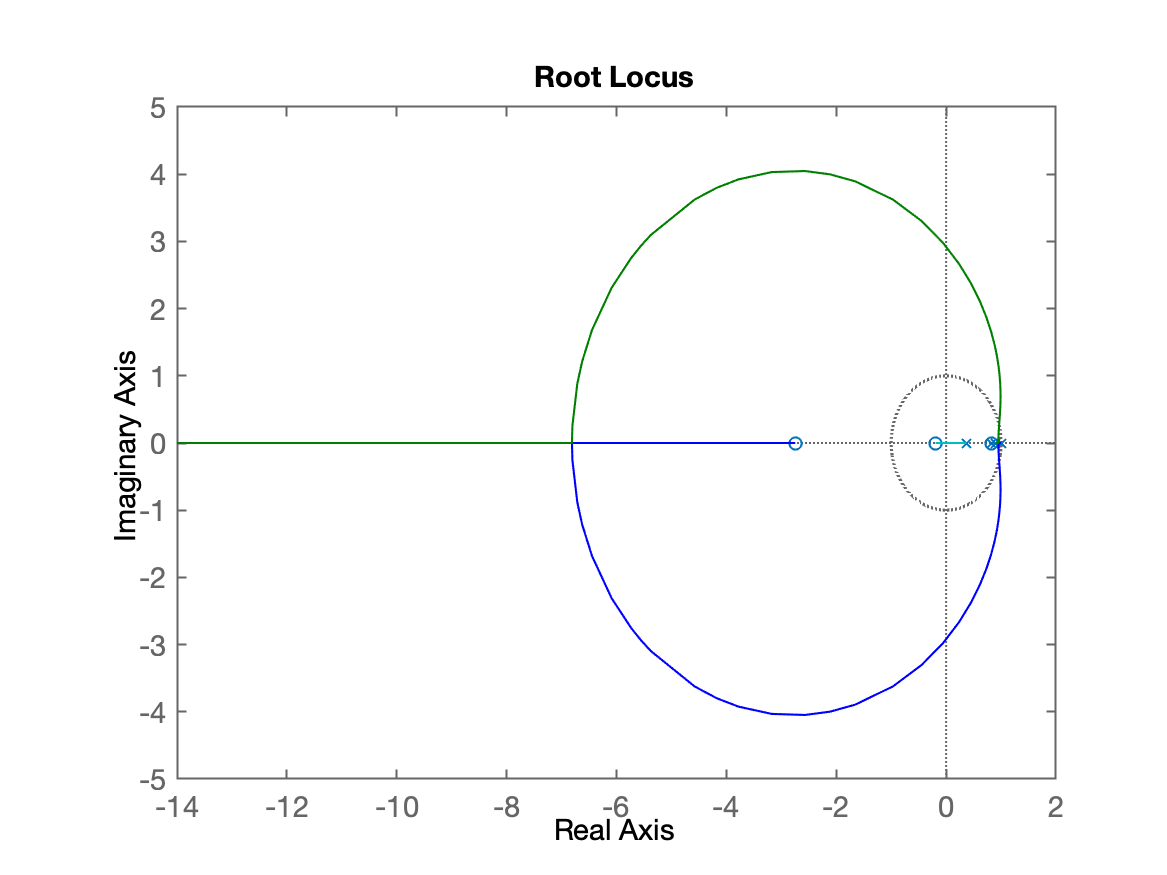

xxxxxxxxxx
>> % Fazendo zoom na região de interesse
>> axis([0.7 1.1 -0.5 0.5])
>> hold on; zgrid(zeta,0)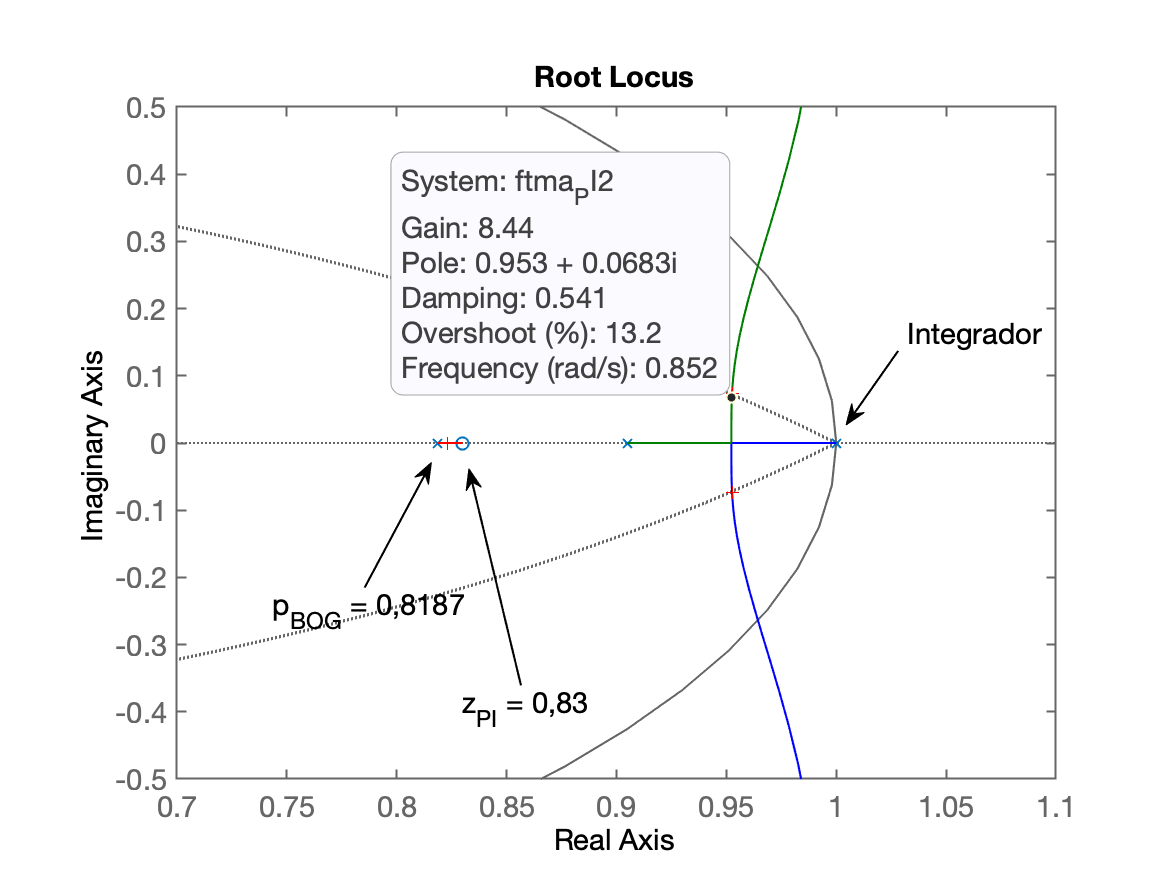

xxxxxxxxxx
>> [K_PI2,polosMF]=rlocfind(ftma_PI2) % encontrado ganho do controlador
Select a point in the graphics window
​
selected_point =
      0.95355 -   0.074303i
​
K_PI2 =
       9.4628
​
polosMF =
      0.95259 +   0.074322i
      0.95259 -   0.074322i
      0.82311 +          0i
        0.362 +          0i
​
>> ftmf_PI2=feedback(K_PI2*ftma_PI2, 1);
>> figure; step(ftmf_PI1, ftmf_PI2)
>> legend('PI_1', 'PI_2') % já comparando com PI1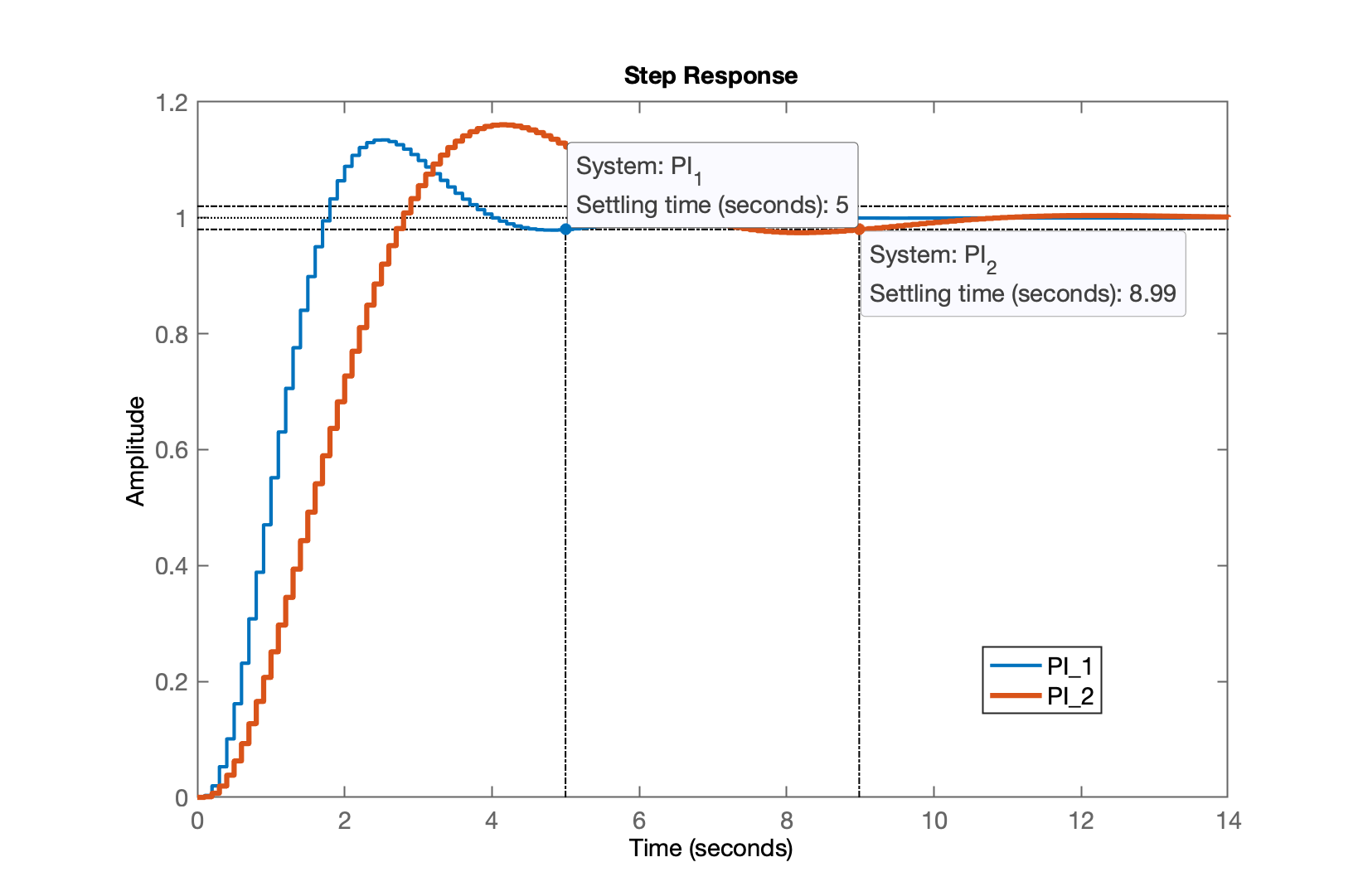

Conclusão final: O PI1 se saiu melhor que o PI2 ($t_s$ é menor para PI1).

Outros PIs

Podemos projetar PI fazendo:

• Cancelando o pólo mais lento da planta fazendo o $z_{PI}$ recair sobre ele (cancelamento pólo-zero - improvável no mundo real);
• Podemos definir a posição do $z_{PI}$ usando Contribuição Angular, mas neste caso, necessitamos de algum requisito de controle temporal ($t_s$, $t_r$ ou $t_p$)
• Posso usar o App Control System Designer.

PI usando Contribuição Angular

Neste caso, temos que definir algum critério temporal.

Antes fizemos o projeto de um Controlador Proporcional com $t_s = 3,54$ segundos mas com $e[\infty]=36,36%$. Será que é possível realizar um PI (erro nulo para entrada degrau), responder em até 4 segundos ($t_s \le 4$ segundos)?

Usando App Control System Designer...

Seguem telas capturadas do App:

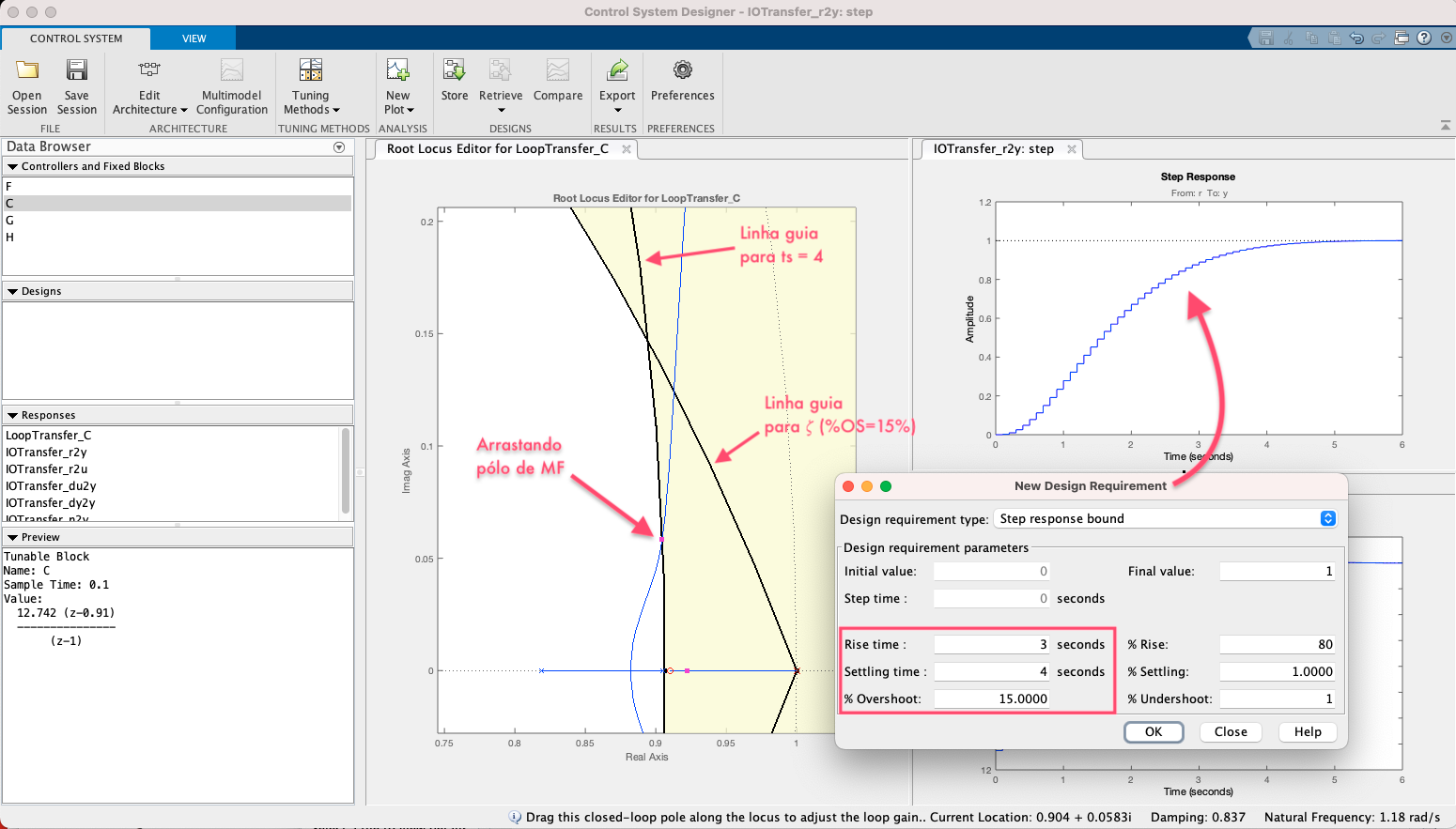
E então temos:

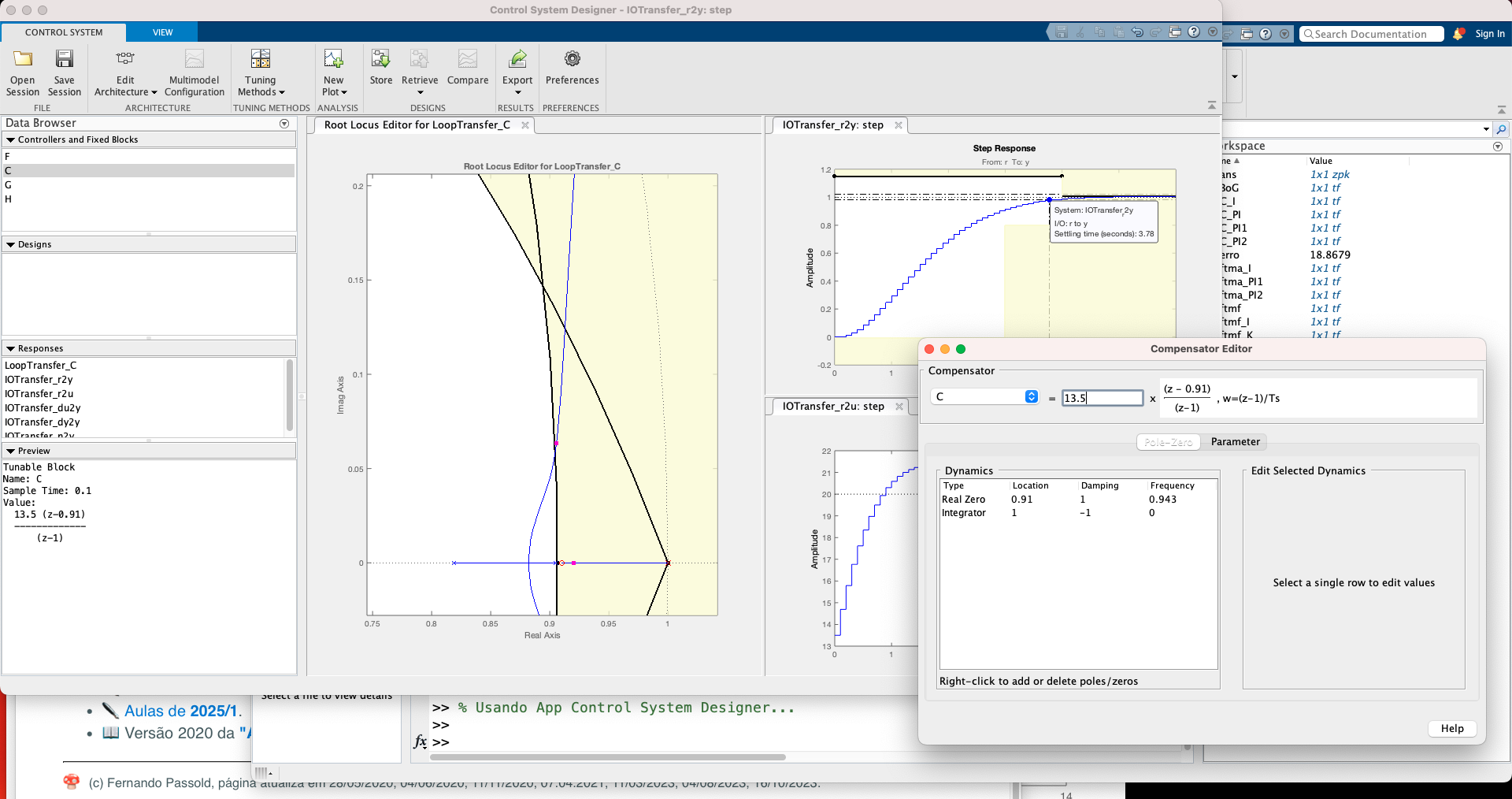
Equação encontrada para o controlador (usando opção Exportar "C"):

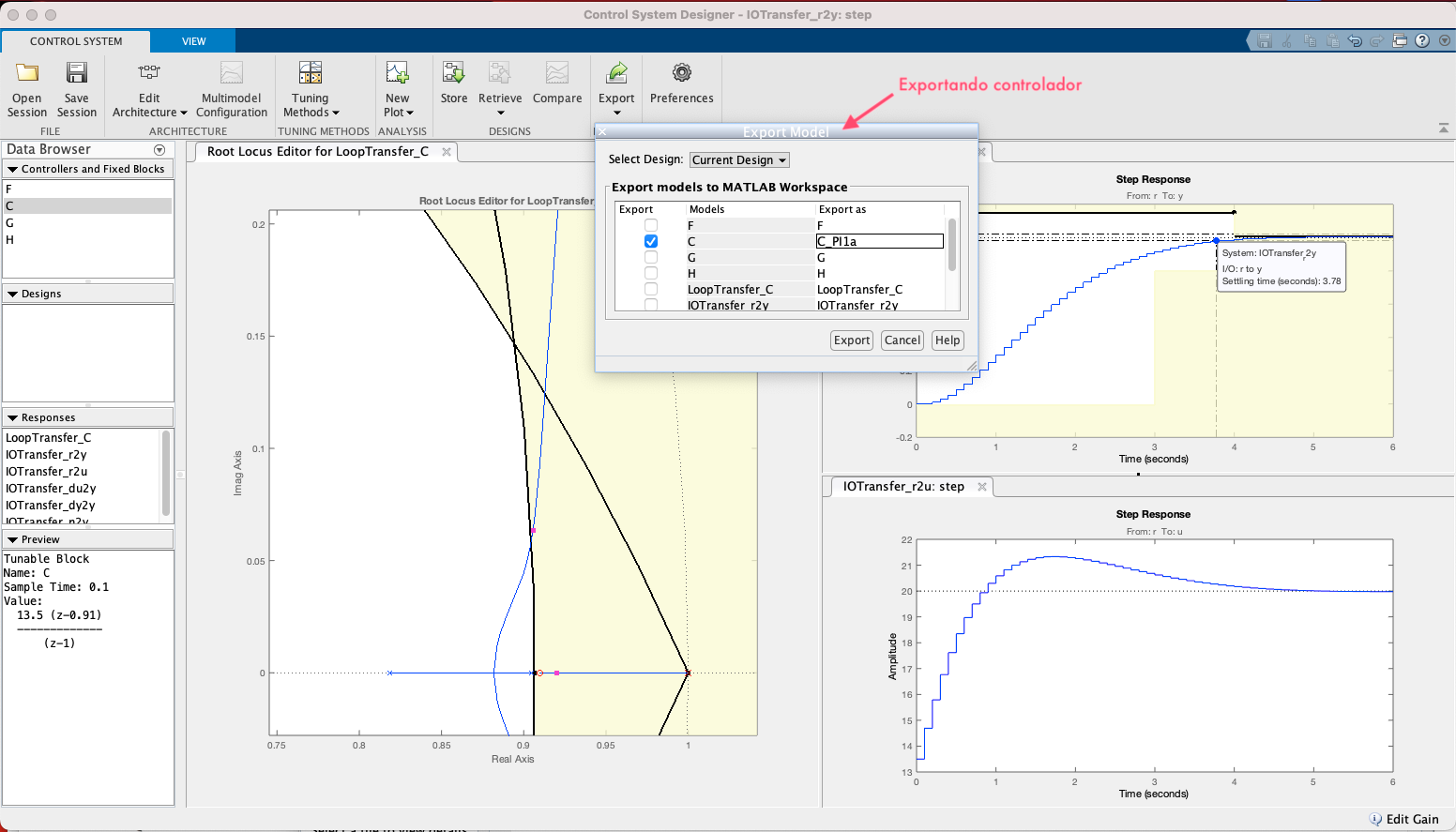
xxxxxxxxxx
>> zpk(C_PI1a)
​
  13.5 (z-0.91)
  -------------
      (z-1)
 
Name: C
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.
​
>> ftma_PI1a=C_PI1a*BoG;
>> ftmf_PI1a=feedback(ftma_PI1a, 1);
>> figure; step(ftmf_PI1a)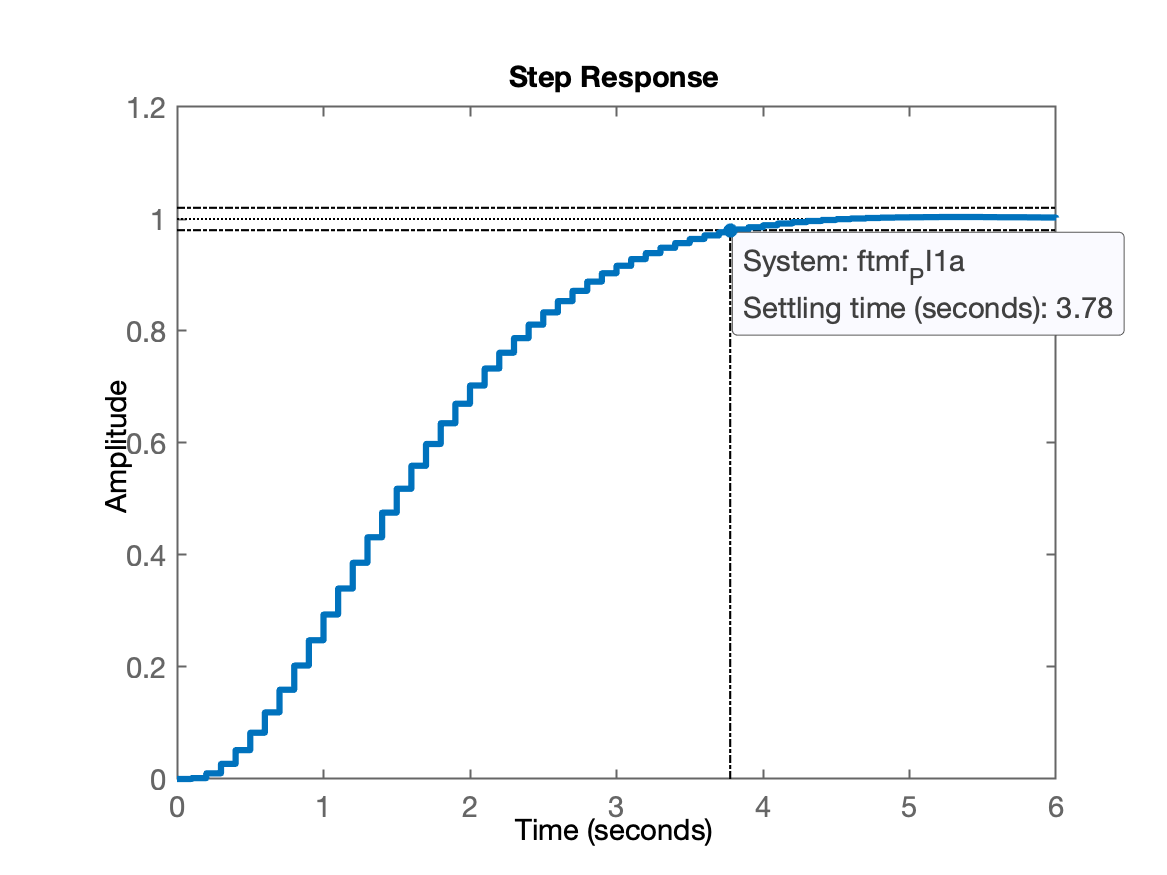

Faltou testar cancelamento pólo-zero do pólo dominante da planta.

PI mais rápido!?

xxxxxxxxxx
>> zpk(BoG)
​
  0.00012224 (z+2.747) (z+0.1903)
  --------------------------------
  (z-0.9048) (z-0.8187) (z-0.3679)
 
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.

Seguem telas usando o App...

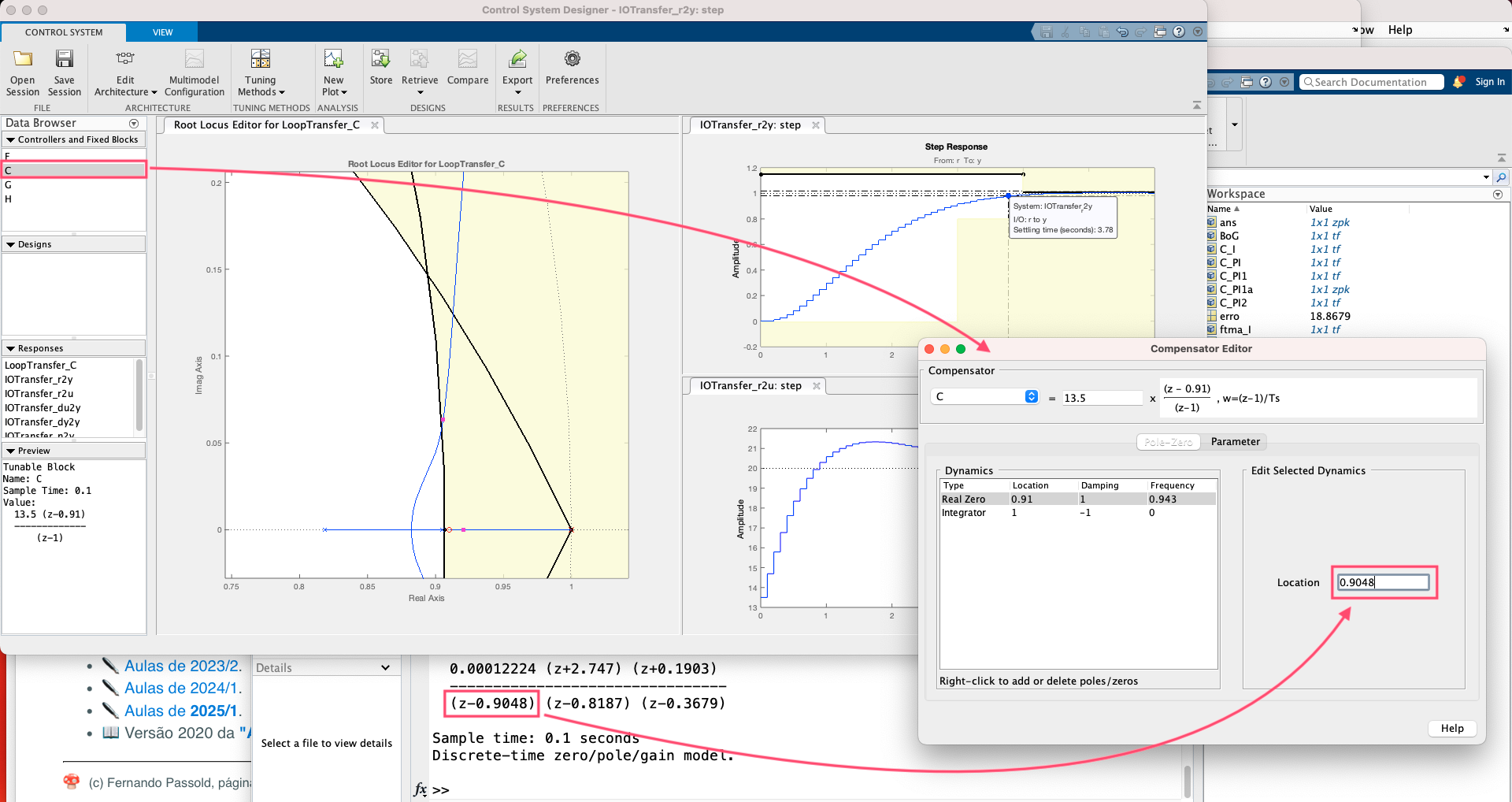
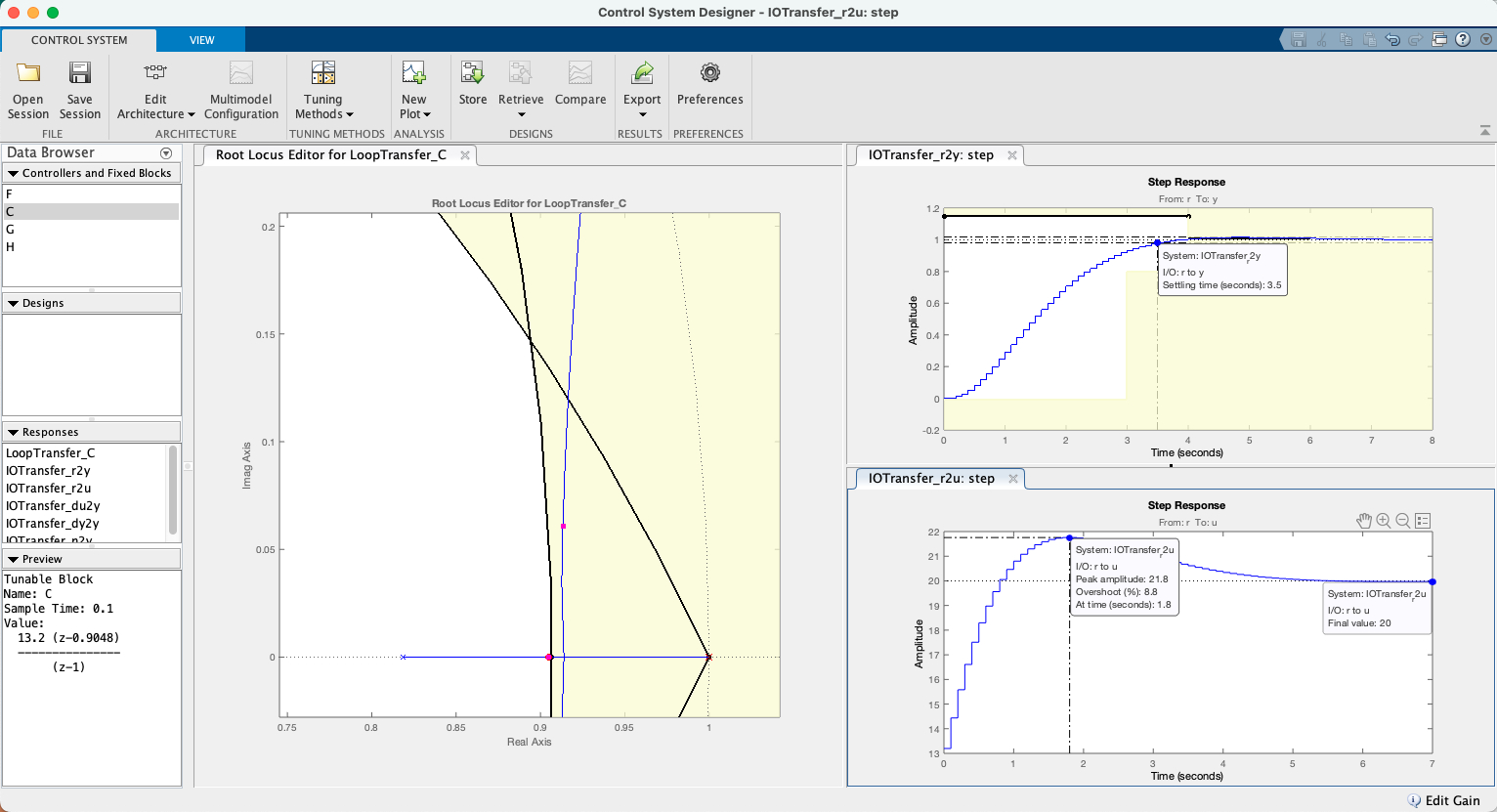
Equação encontrada para o controlador:

xxxxxxxxxx
>> zpk(C_PI3)
​
  13.2 (z-0.9048)
  ---------------
       (z-1)
 
Name: C
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.
​
>> ftma_PI3=C_PI3*BoG;
>> ftmf_PI3=feedback(ftma_PI3, 1);
>> figure; step(ftmf_PI3)
>> stepinfo(ftmf_PI3)
​
        RiseTime: 2.2
    SettlingTime: 3.5
     SettlingMin: 0.901
     SettlingMax: 1.0151
       Overshoot: 1.5137
      Undershoot: 0
            Peak: 1.0151
        PeakTime: 4.8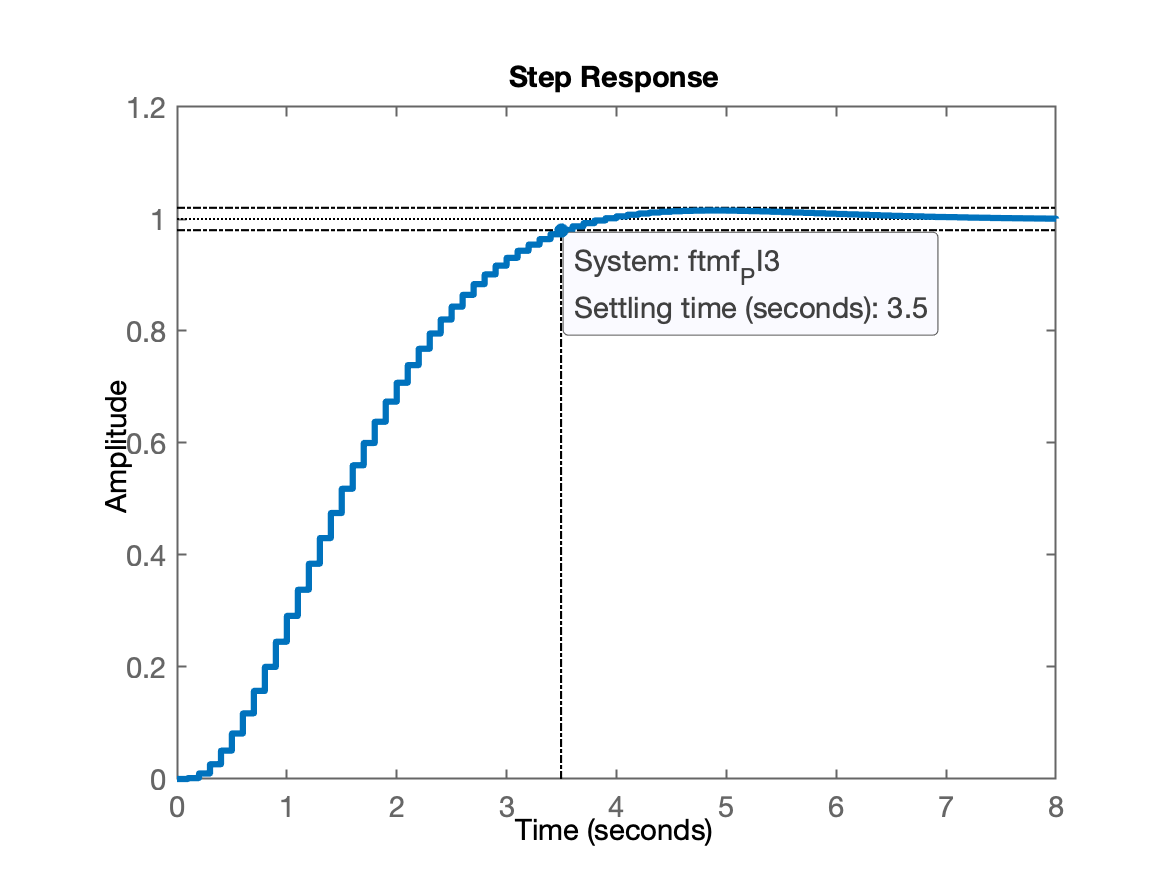

Obs.: Este é provavelmente um dos menores $t_s$ passíveis de serem obtidos para um controlador do tipo PI para esta planta.

Encerrando atividades nesta aula:

xxxxxxxxxx
>> save dados
>> diary off

Fernando Passold, em 07/04/2025