Projeto Controladores

Ingressando planta

Amostrando à $T=0,1$$T=0,1$ Segundos:

>> G=tf(1,poly([-1 -2 -10]));
>> zpk(G)
 
          1
  ------------------
  (s+10) (s+2) (s+1)
 
Continuous-time zero/pole/gain model.

>> T=0.1;
>> BoG=c2d(G, T);
>> zpk(BoG)
 
  0.00012224 (z+2.747) (z+0.1903)
  --------------------------------
  (z-0.9048) (z-0.8187) (z-0.3679)
 
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.

>> save planta
>> rlocus(BoG)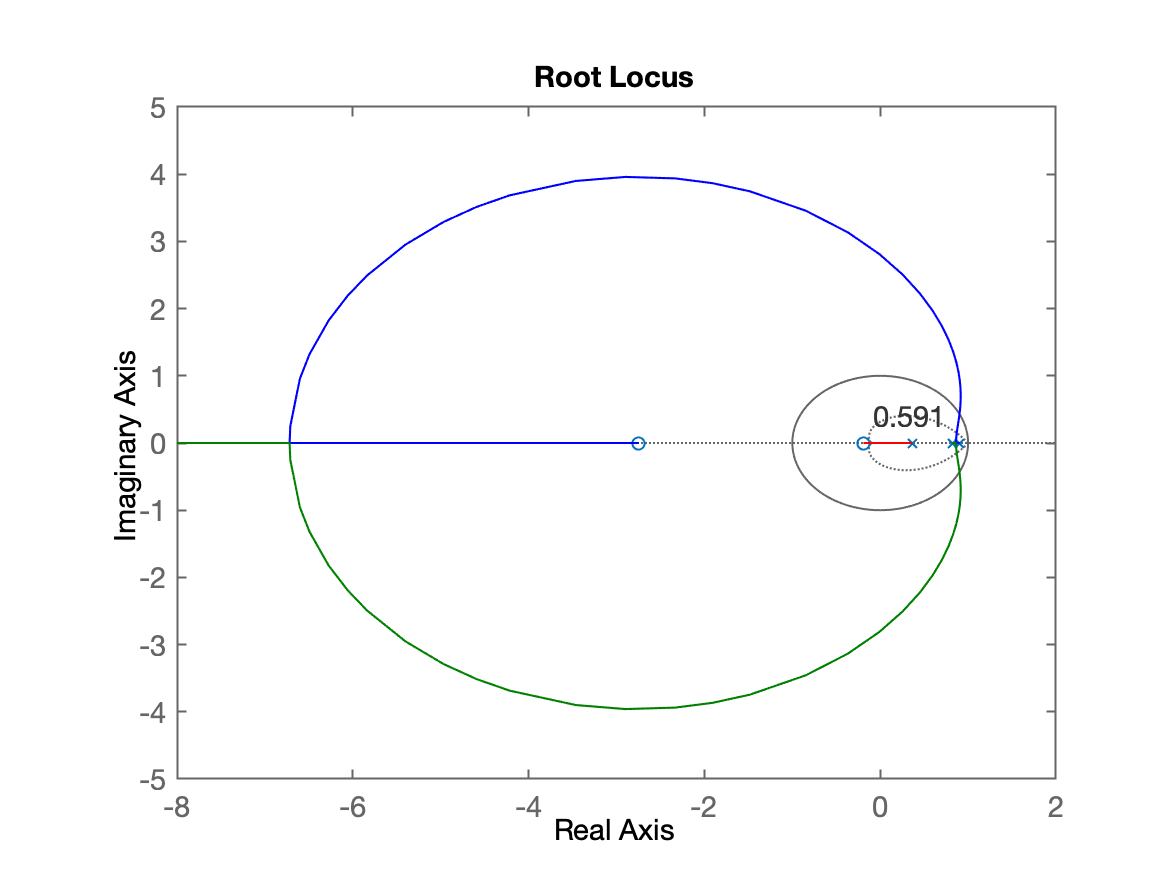

1. Controlador Proporcional

Requisito de controle: $\mathrm{\%}OS\le 10\mathrm{\%}$$\%OS \le 10\%$.

>> OS=10;
>> zeta=(-log(OS/100))/(sqrt(pi^2+(log(OS/100)^2)))
zeta =
      0.59116
>> 

RL com zoom na região de interesse:

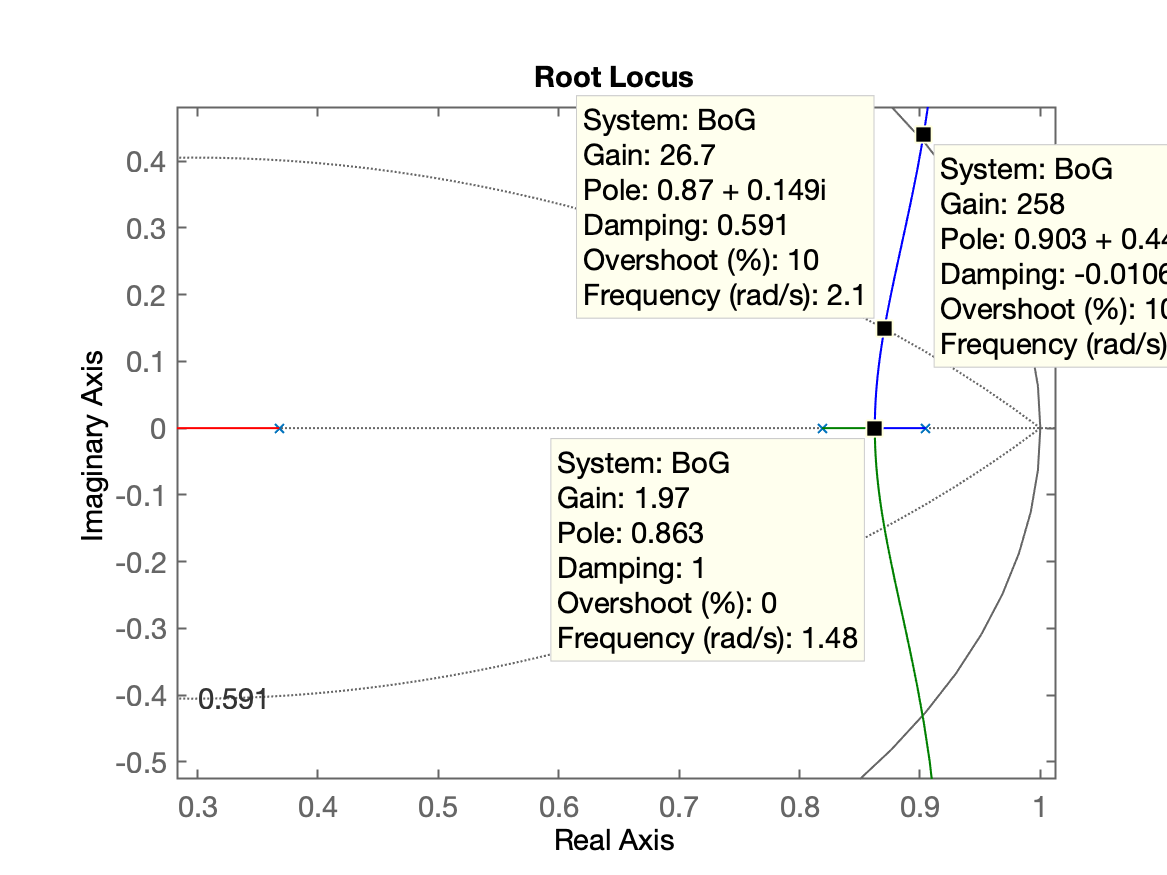
Continuando com projeto:

>> axis([-8 2 -5 5])
>> hold on;
>> zgrid(zeta, 0)
>> K=26;
>> ftmf = feedback(K*BoG, 1);
>> figure; step(ftmf)

Resposta ao degrau:

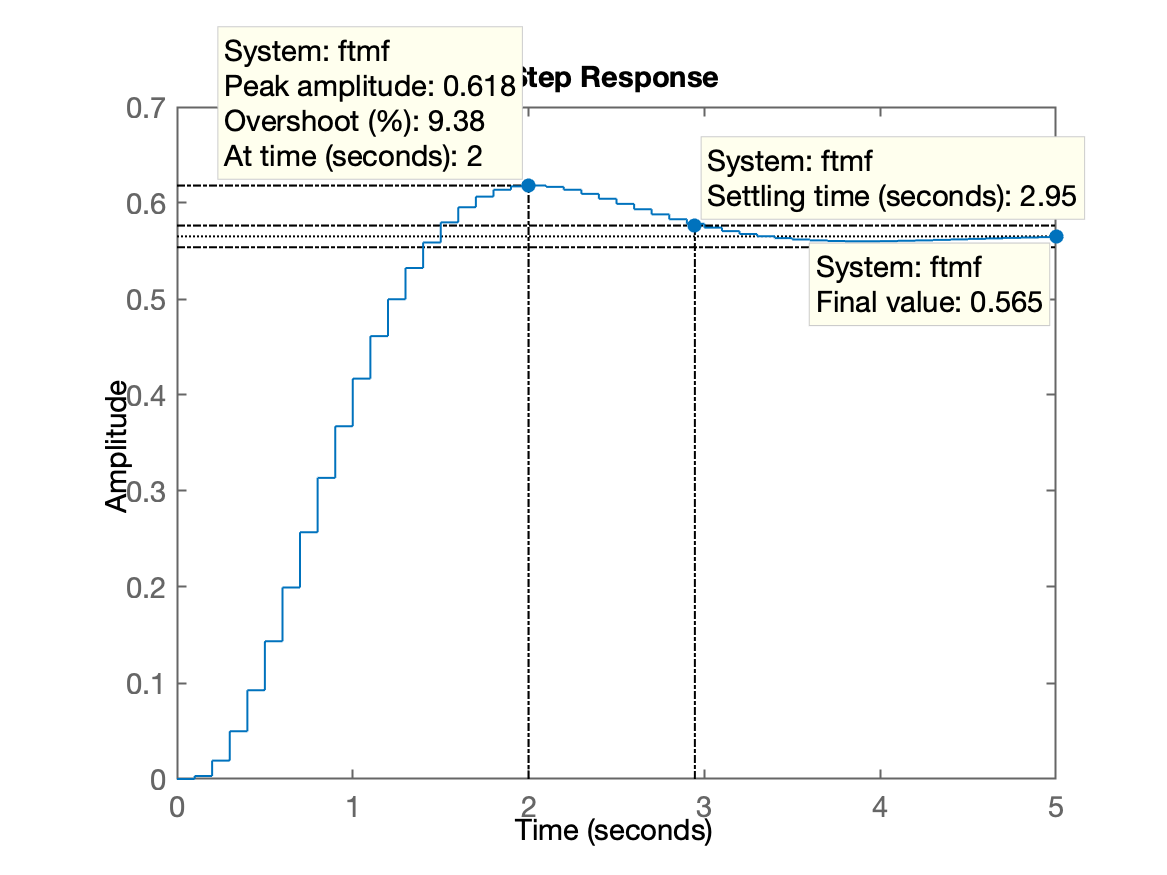
Repare no elevado erro de regime permanente:

>> dcgain(ftmf)
ans =
      0.56522
>> erro_Kp=((1-dcgain(ftmf))/1)*100
erro_Kp =
       43.478
>>       

E se o requisito de controle fosse: $e(\mathrm{\infty })\le 10\mathrm{\%}$$e(\infty) \le 10 \%$ ?

Lembrando da teoria de erro --> Erro para entrada degrau:

Calcular o $Kp$$Kp$ (ganho de posição):

$e[\mathrm{\infty }]={\displaystyle \frac{1}{1+Kp}}$$e[\infty]=\dfrac{1}{1+Kp}$

$e(\mathrm{\infty })=10\mathrm{\%}\therefore y(\mathrm{\infty })=0.9\therefore e(\mathrm{\infty })=0,1$$e(\infty)=10\% \quad \therefore \quad y(\infty)=0.9 \quad \therefore \quad e(\infty)=0,1$

$0,1={\displaystyle \frac{1}{1+Kp}}$$0,1=\dfrac{1}{1+Kp}$

$0,1(1+Kp)=1$$0,1(1+Kp)=1$

$Kp={\displaystyle \frac{1-0,1}{0,1}}$$Kp=\dfrac{1-0,1}{0,1}$

>> Kp=(1-0.1)/0.1
Kp =
      9

$Kp=\underset{z\to 1}{lim}FTMA(z)=\underset{z\to 1}{lim}{\displaystyle \frac{K\cdot 0.00012224(z+2.747)(z+0.1903)}{(z-0.9048)(z-0.8187)(z-0.3679)}}$$Kp=\lim_{z \to 1} FTMA(z)=\lim_{z \to 1} \dfrac{K \cdot 0.00012224 (z+2.747) (z+0.1903)}{(z-0.9048) (z-0.8187) (z-0.3679)}$

>> dcgain(BoG)
ans =
         0.05
>> % Note:
>> num = 0.00012224*(1+2.747)*(1+0.1903)
num =
    0.0005452
>> den=(1-0.9048)*(1-0.8187)*(1-0.3679)
den =
      0.01091
>> num/den
ans =
     0.049973

$Kp=K\cdot 0,05$$Kp=K \cdot 0,05$

$9=0,05\cdot K\therefore K={\displaystyle \frac{9}{0,05}}$$9=0,05\cdot K \quad \therefore \quad K = \dfrac{9}{0,05}$

>> Knesc=Kp/dcgain(BoG)
Knesc =
       180

Aplicando este ganho:

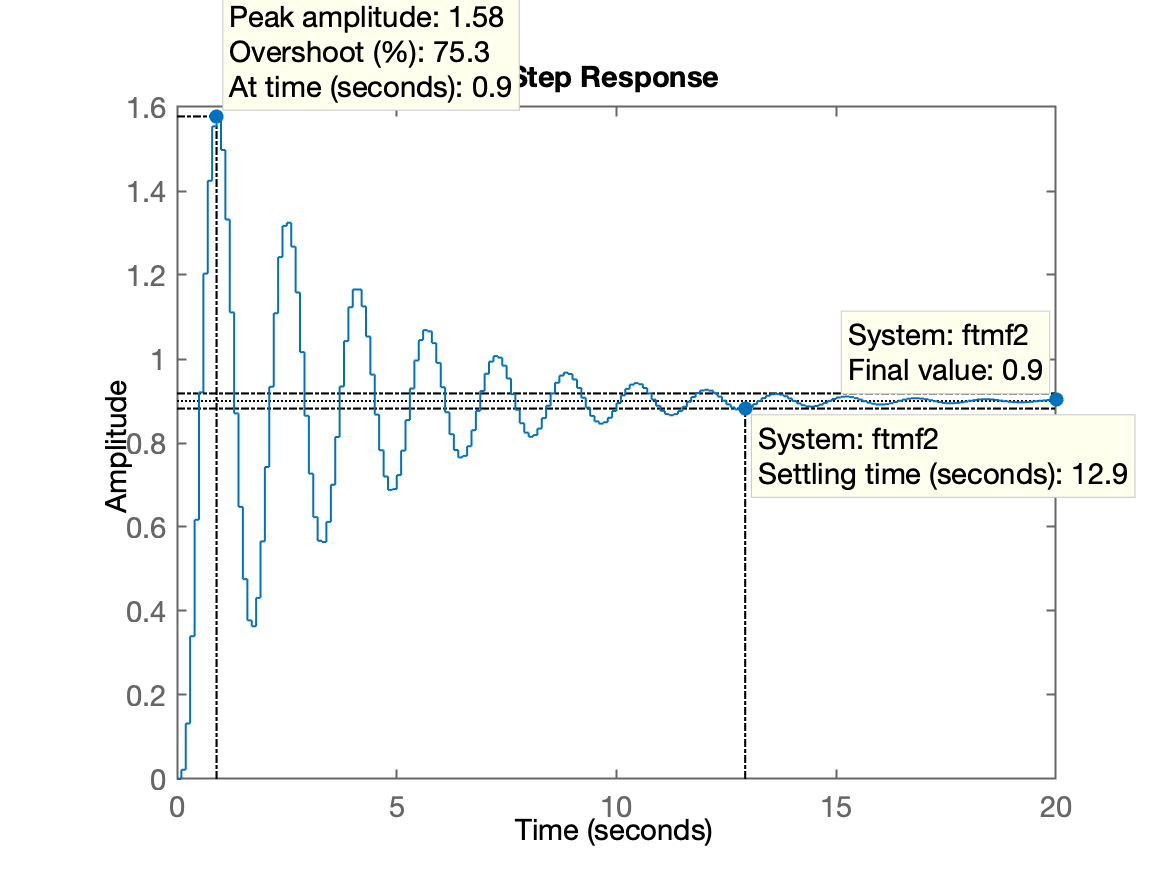
Provavelmente as especificações de controle aqui seriam:

• $e[\mathrm{\infty }]\le 10\mathrm{\%}$$e[\infty] \le 10\%$;
• $\mathrm{\%}OS\le 10\mathrm{\%}$$\%OS \le 10\%$.

Novas especificações de controle:

• $e[\mathrm{\infty }]=0$$e[\infty]=0$
• $\mathrm{\%}OS\le 10\mathrm{\%}$$\%OS \le 10\%$

Solução: Acrescentar ação integral (para zerar o erro em regime permanente).

Integrador Puro (I)

Equação do Controlador com ação integral pura:

Deduzindo a $FTMA(z)$$FTMA(z)$:

>> C_I=tf(1, [1 -1], T)

C_I =
 
    1
  -----
  z - 1
 
Sample time: 0.1 seconds
Discrete-time transfer function.

>> ftma_I = C_I*BoG;
>> zpk(ftma_I)

ans =
 
     0.00012224 (z+2.747) (z+0.1903)
  --------------------------------------
  (z-1) (z-0.9048) (z-0.8187) (z-0.3679)
 
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.

>> figure; rlocus(ftma_I)
>> axis equal

RL gerado:

RL sem zoom	RL com zoom

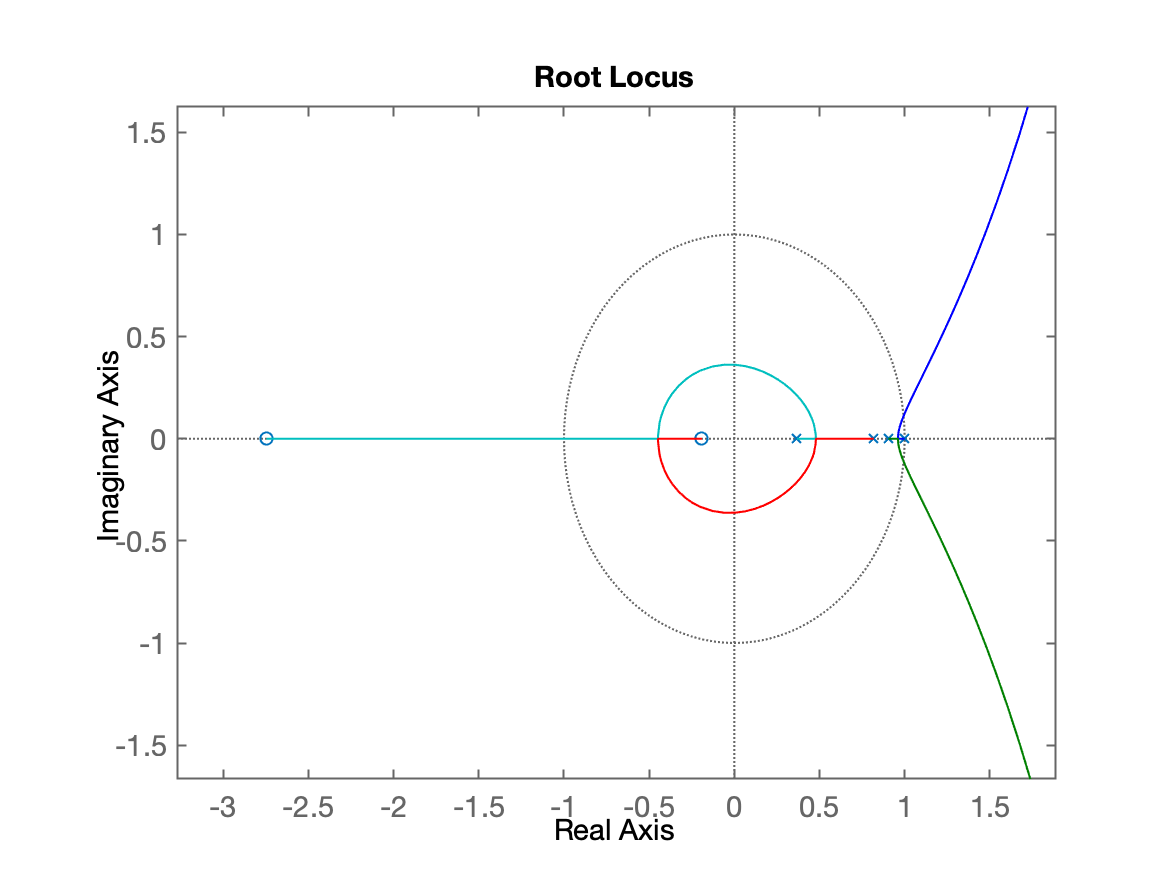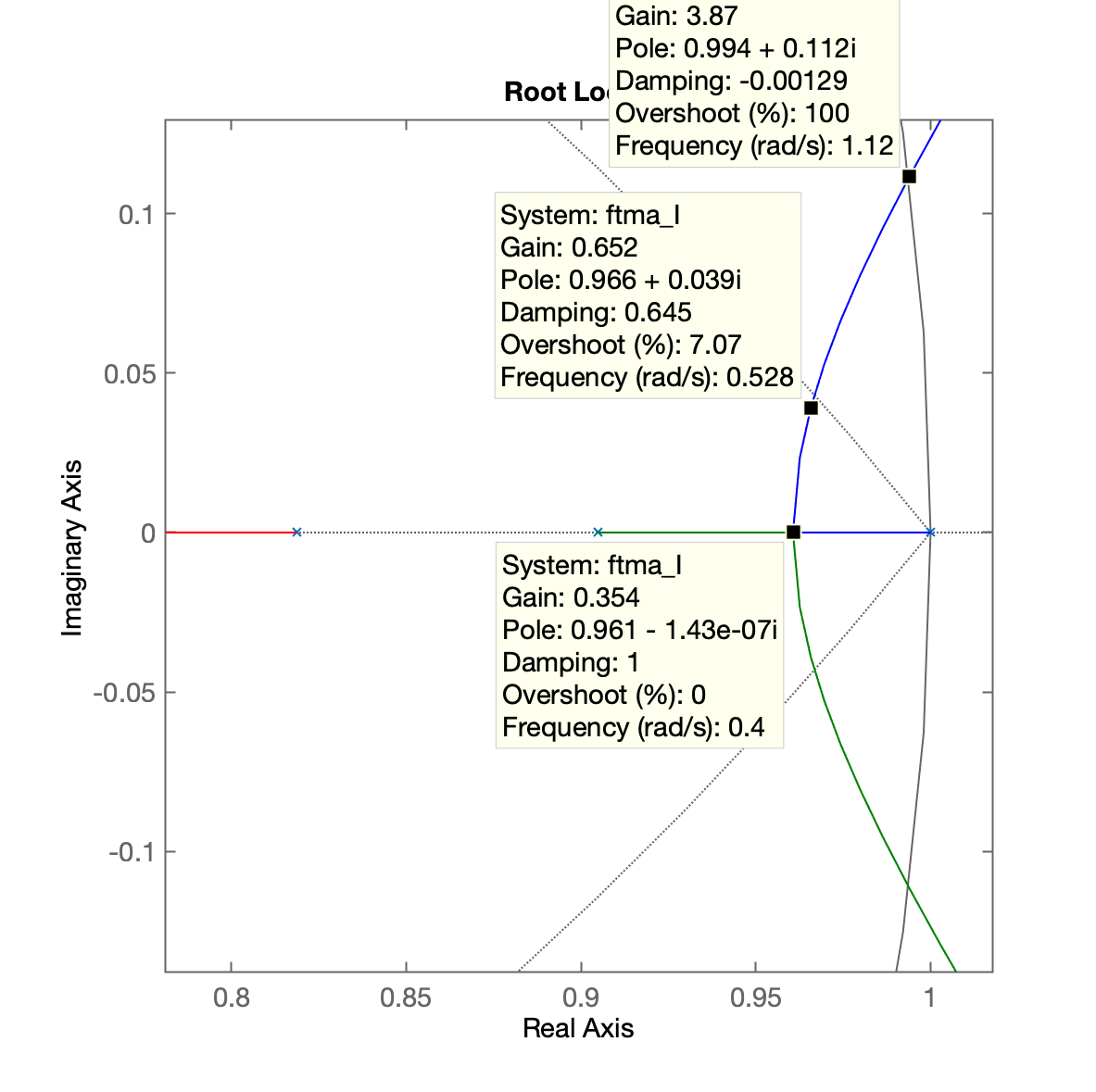Vamos adotar $K_i=0,652$$K_i=0,652$:

>> hold on;
>> zgrid(zeta, 0)
>> K_I=0.652;
>> ftmf_I = feedback(K_I*ftma_I, 1);
>> figure; step(ftmf_I)

Resposta ao degrau:

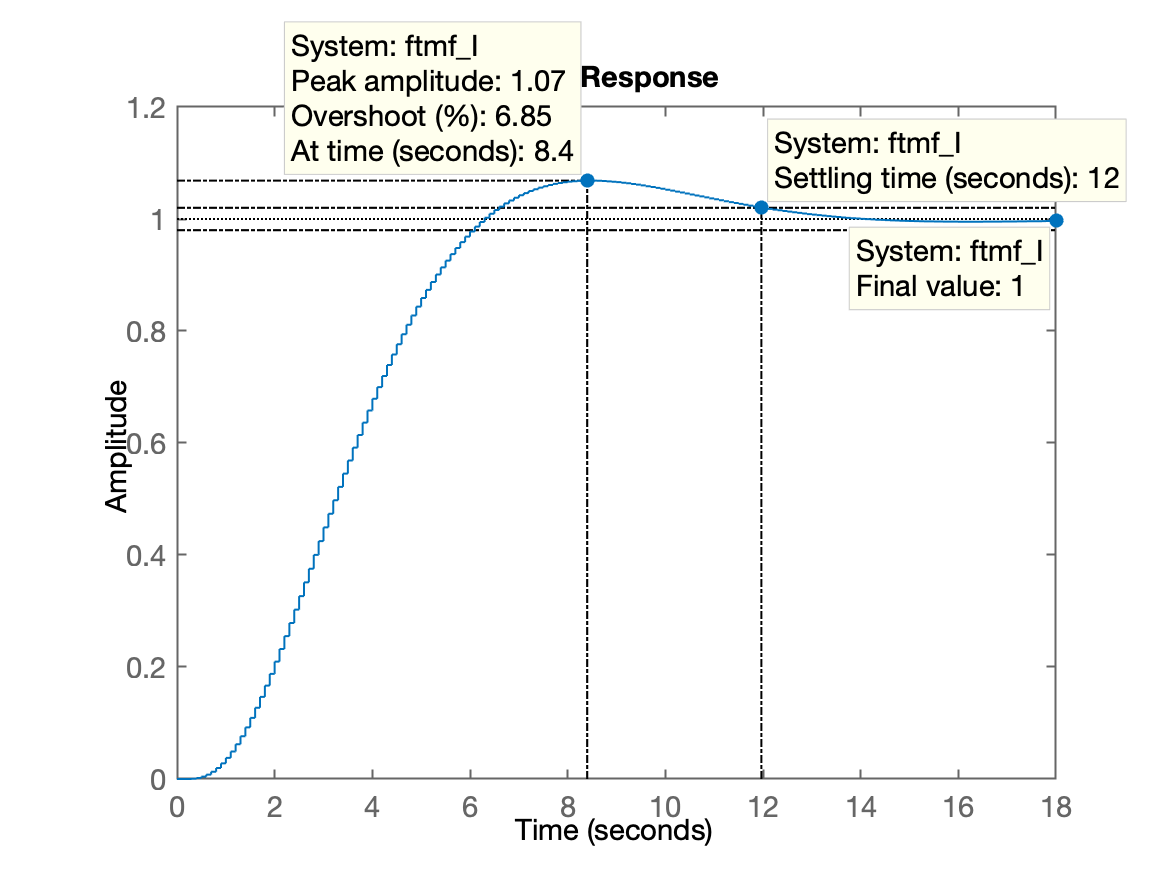
Note:

• $\mathrm{\%}OS=6,85\mathrm{\%}✓$$\%OS = 6,85\% \quad \checkmark$;
• $e[\mathrm{\infty }]=0✓$$e[\infty]=0 \quad \checkmark$.

Mas...

• repare no $t_s=12$$t_s = 12$ Segundos ! (Comparando com $t_s\approx 3$$t_s \approx 3$ segundos do controlador proporcional).

Solução para reduzir o $t_s$$t_s$ é usar 2 ações de controle: P + I = PI.

Controlador PI (P + I)

Note que um PI é um controlador onde 2 ações de controle são executadas paralelamente (ao mesmo tempo): a ação Proporcional + a ação Integral.

Resolvendo algebricamente o resultado destas ações paralelas, chegamos a equação:

onde $z_a=(1-{\displaystyle \frac{K_i}{K_p}})$$z_a=\left( 1- \dfrac{K_i}{K_p}\right)$ e $K=K_p$$K=K_p$.

poderíamos tentar definir o zero do PI usando os valores encontrados anteriormente para $K_p$$K_p$ e $K_i$$K_i$, mas o melhor é estudar como o RL é afetado pelo acréscimo do zero do PI. E neste caso, resta avaliar algumas opções diferentes para o RL que variam em função da posição escolhida para o zero do PI:

a) zero em: $0,8187<z_a<0,9048$$0,8187 < z_a < 0,9048$ :	b) zero em: $0,9048<z_a<1$$0,9048 < z_a < 1$ :
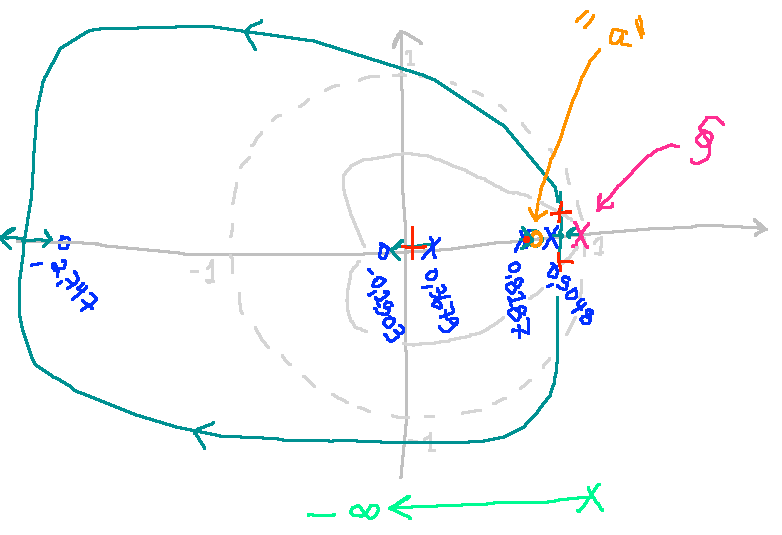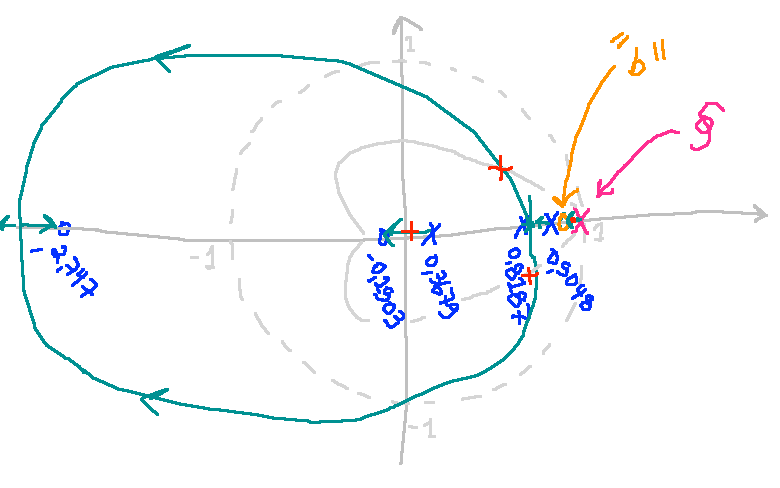c) zero em: $0,3679<z_a<0,8187$$0,3679 < z_a < 0,8187$ :	d) zero exatamente sobre $z_a=0,9048$$z_a=0,9048$ :

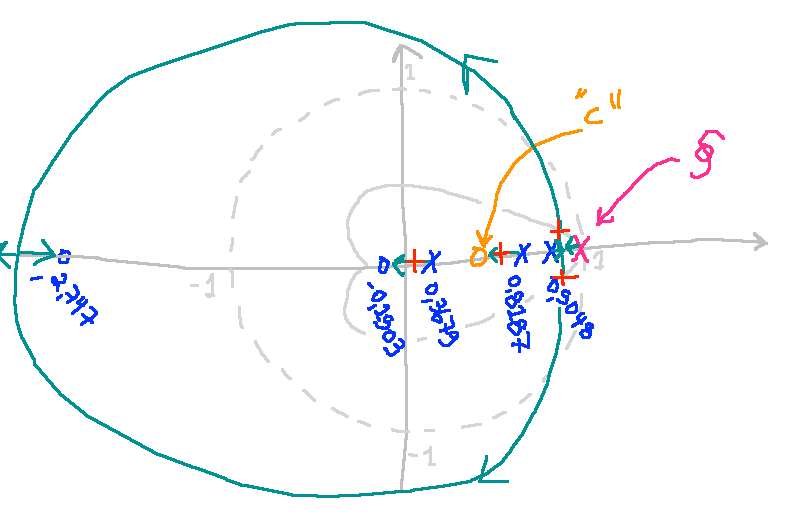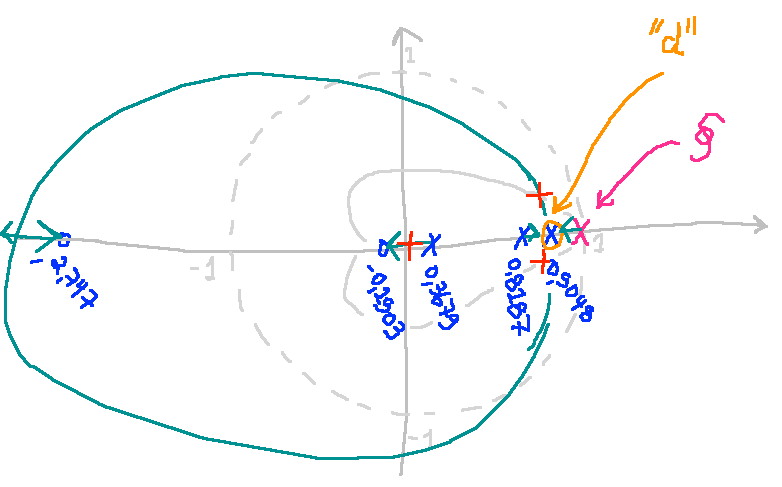Analisando os RL's anteriores, temos que:

• A opção a) parece ser a pior. Teremos pólos complexos (de MF) partindo muito próximos do círculo unitário (lentos), além do pólo real lento (de MF) localizado entre o pólo mais lento da planta ($z=0,9048$$z=0,9048$) e seu segundo pólo mais lento (em $z=0,8187$$z=0,8187$); ou seja, temos 3 pólos lentos, sendo que os pólos complexos estão muito próximos do círculo unitário.
• A opção b) é mais interessante que a opção (a), os pólos complexos de MF partirão mais afastados do círculo unitário, mas não devemos ignorar que ainda há um pólo real lento (de MF) localizado entre o integrador (em $z=1$$z=1$) e o pólo mais lento da planta ($z=0,9048$$z=0,9048$);
• Opção c) "avançando" o zero na direção da origem do plano-z, pode-se pensar em localizar o zero entre o pólo mais rápido da planta (em $z=0,3679$$z=0,3679$) e o segundo pólo mais lento da planta (em $z=0,8187$$z=0,8187$); porém pólos complexos de MF partirão tão próximo do círculo unitário quanto a opção (a), com a única diferença sendo que o terceiro pólo (real) mais lento vai estar localizado à direira do pólo em $z=0,8187$$z=0,8187$ e não à esquerda como ocorre na opção (a), o que implica provável $t_s$$t_s$ menor que o obtido com a opção (a).
• Opção d) Por que não colocar o zero deliberadamente sobre o pólo mais lenta da planta (em $z=0,9048$$z=0,9048$)? Observe algumas vantagens: 1) a complexidade do sistema é reduzida (em MF, obtemos um sistema de 3a-ordem ao invés de um de 4a-ordem); 2) os pólos complexos partirão mais afastados do círculo unitário, próximo do pólo mais lento da planta que foi cancelado e o terceito pólo real mais "lento" entará entre o pólo mais rápido da planta (em $z=0,3679$$z=0,3679$) e o zero mais rápido da planta (em $z=0,1903$$z=0,1903$), com sorte próximo da origem do plano-z e ainda na parte real positiva. Provavelmente a melhor opção para o zero do PI no caso desta planta.

Resta realizar simulações no Matlab para comprovar os raciocínios anteriores.

Avaliando as opções "b" e "c" e considerando a opção "d" como um caso especial já que envolve cancelamento de par pólo-zero.

Até aqui na aula de 23/09/2021

Opção b) zero em: $0,9048<z_a<1$$0,9048 < z_a < 1$ :

Colocando o zero mais afastando do círculo unitário em $z=0,92$$z=0,92$, vamos obter o seguinte RL:

>> C_PIb=tf([1 -0.92], [1 -1], T)

C_PIb =
 
  z - 0.92
  --------
   z - 1
 
Sample time: 0.1 seconds
Discrete-time transfer function.

>> ftma_PIb=C_PIb*BoG;
>> figure; rlocus(ftma_PIb)
>> hold on; zgrid(zeta,0)

Vamos obter o seguinte RL:

RL sem zoom	RL com zoom

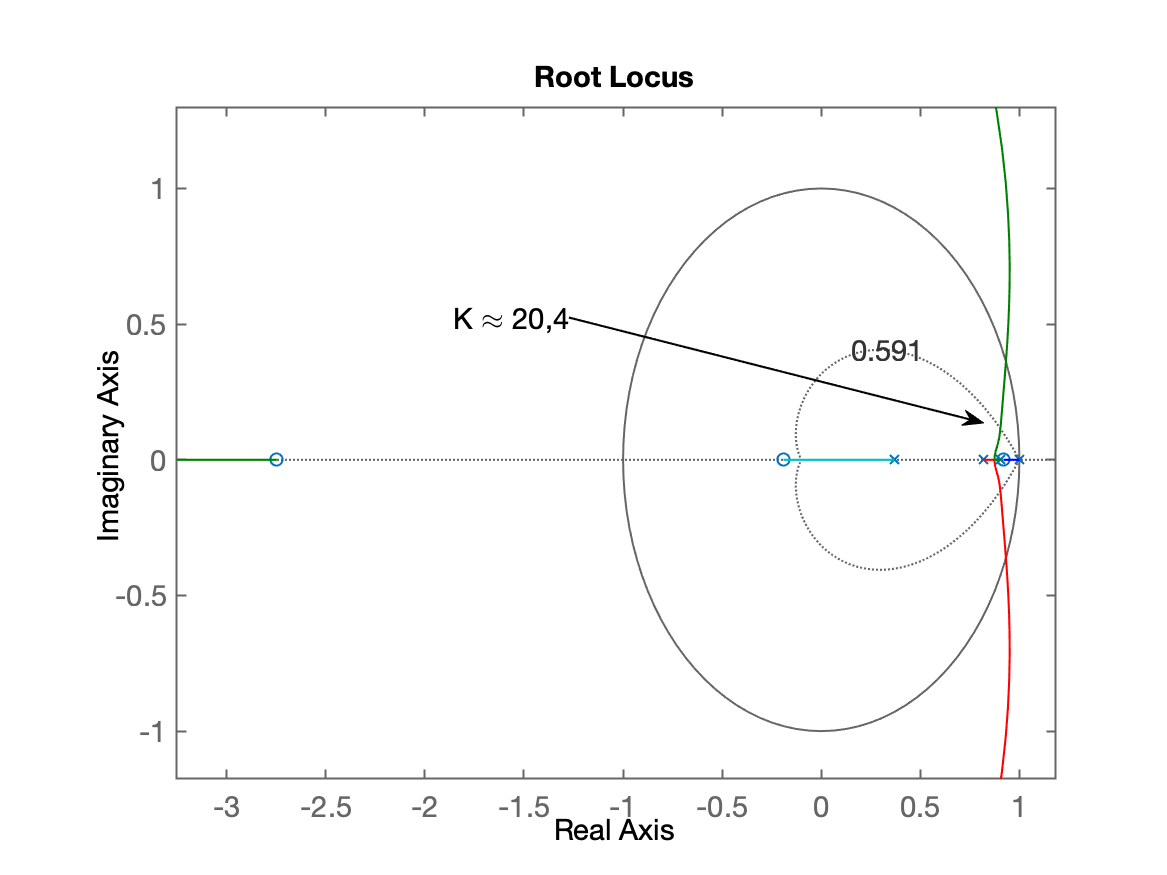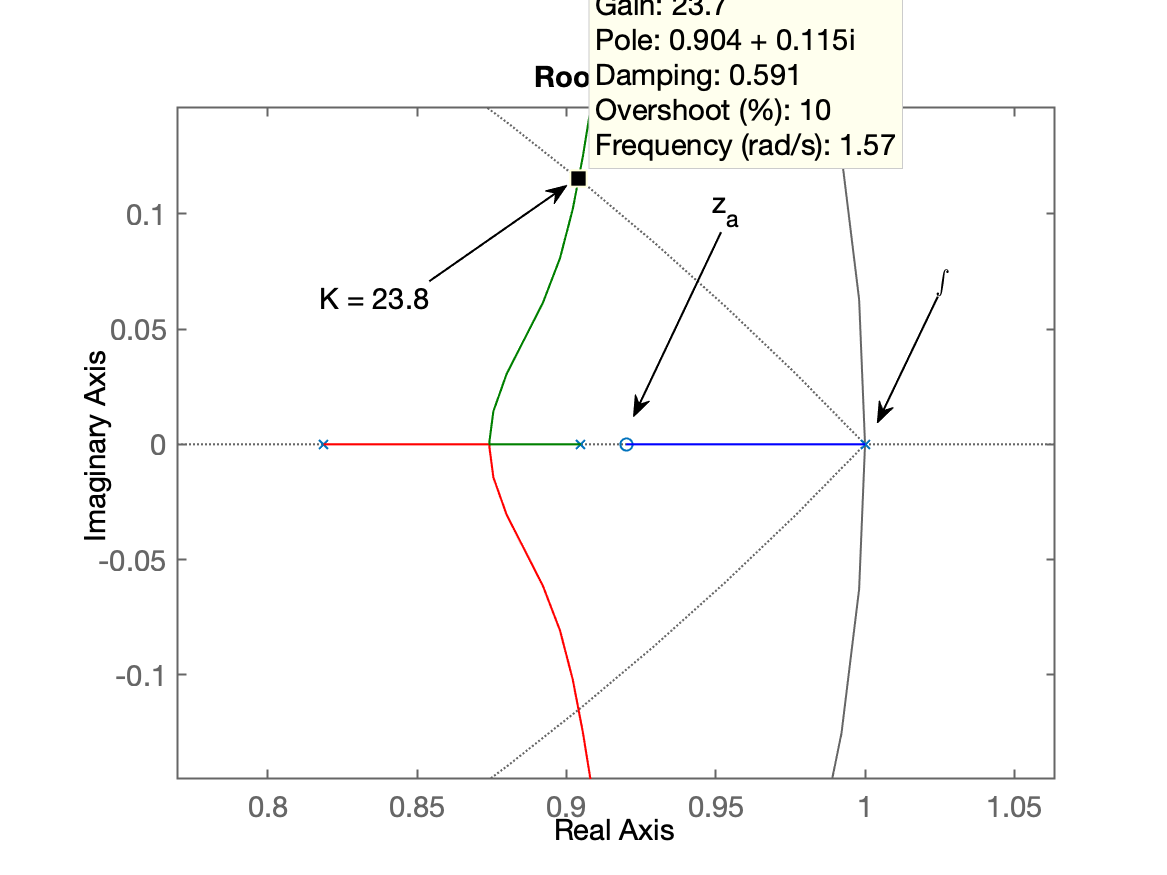Teria que ser adotado o ganho de $K=23,8$$K=23,8$; o que renderia a seguinte resposta:

>> K_PIb=23.8;
>> ftmf_PIb=feedback(K_PIb*ftma_PIb, 1);
>> figure; step(ftmf_PIb)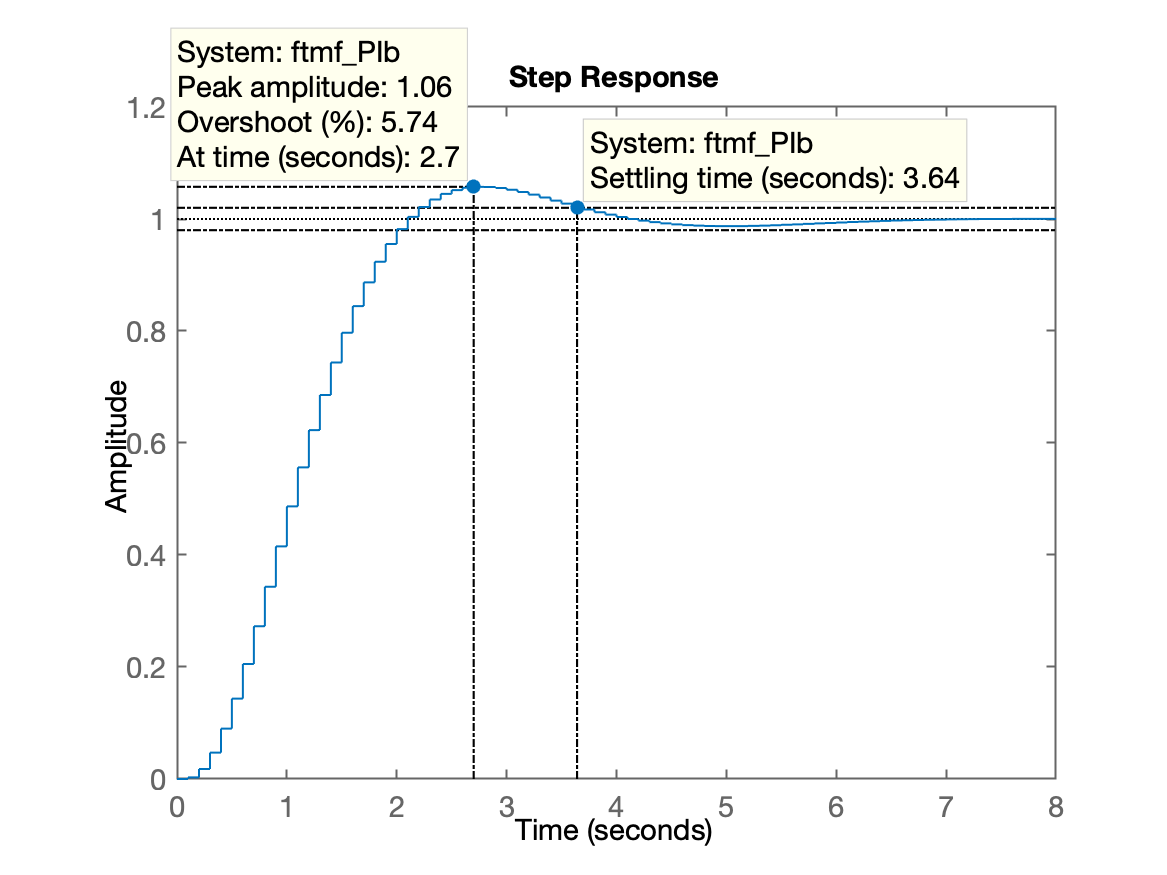

Note que o tempo de assentamento baixou consideravelmente em relação ao Controlador Integrador Puro, mas é maior que o controlador Proporcional limitado à $\mathrm{\%}OS\le 10\mathrm{\%}$$\%OS \le 10\%$.

Opção c) zero em: $0,3679<z_a<0,8187$$0,3679 < z_a < 0,8187$ :

Colocando o zero do PI no centro geométrico dos pólos mais internos da planta:

>> za=(0.3679+0.8187)/2
za =
       0.5933
>> C_PIc=tf([1 -0.6], [1 -1], T)

C_PIc =
 
  z - 0.6
  -------
   z - 1
 
Sample time: 0.1 seconds
Discrete-time transfer function.

>> ftma_PIc=C_PIc*BoG;
>> figure; rlocus(ftma_PIc)
>> hold on; zgrid(zeta,0)

O que gera o seguinte RL:

RL antes do zoom:	RL com zoom:

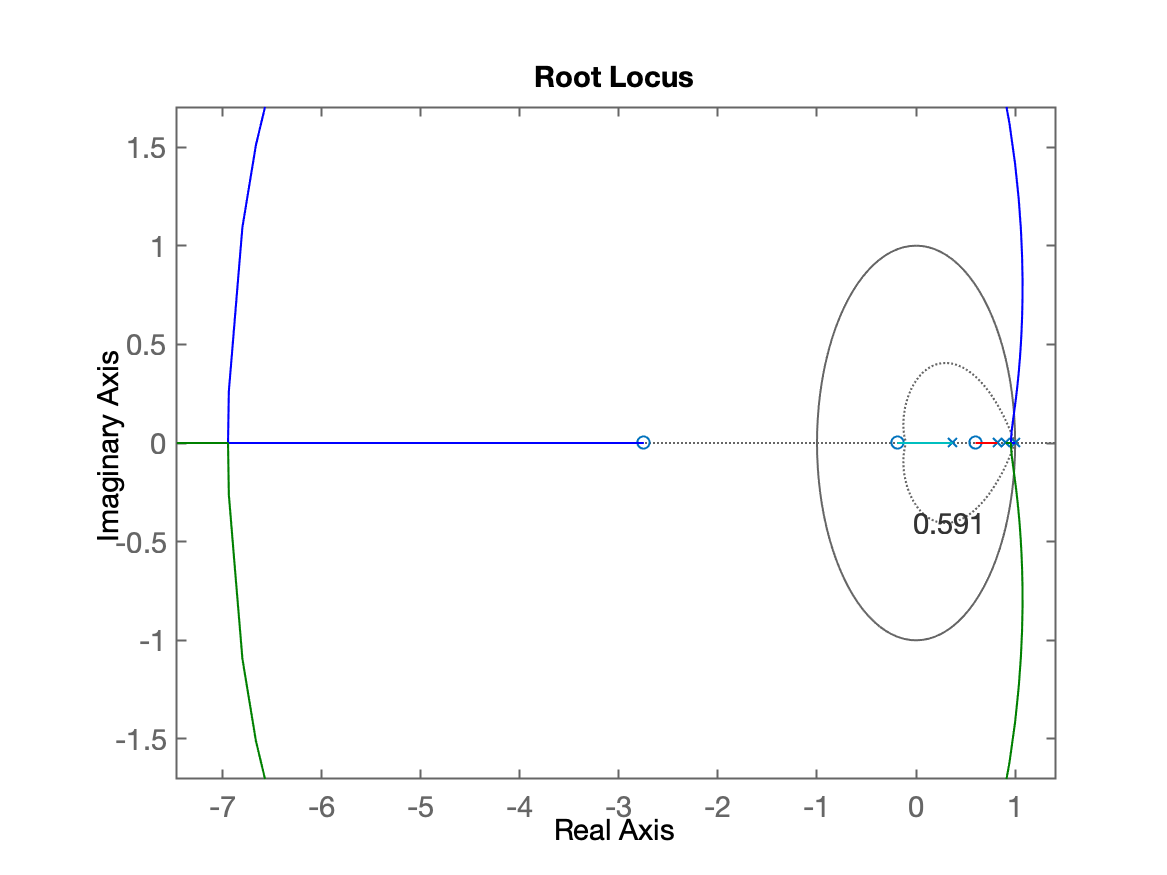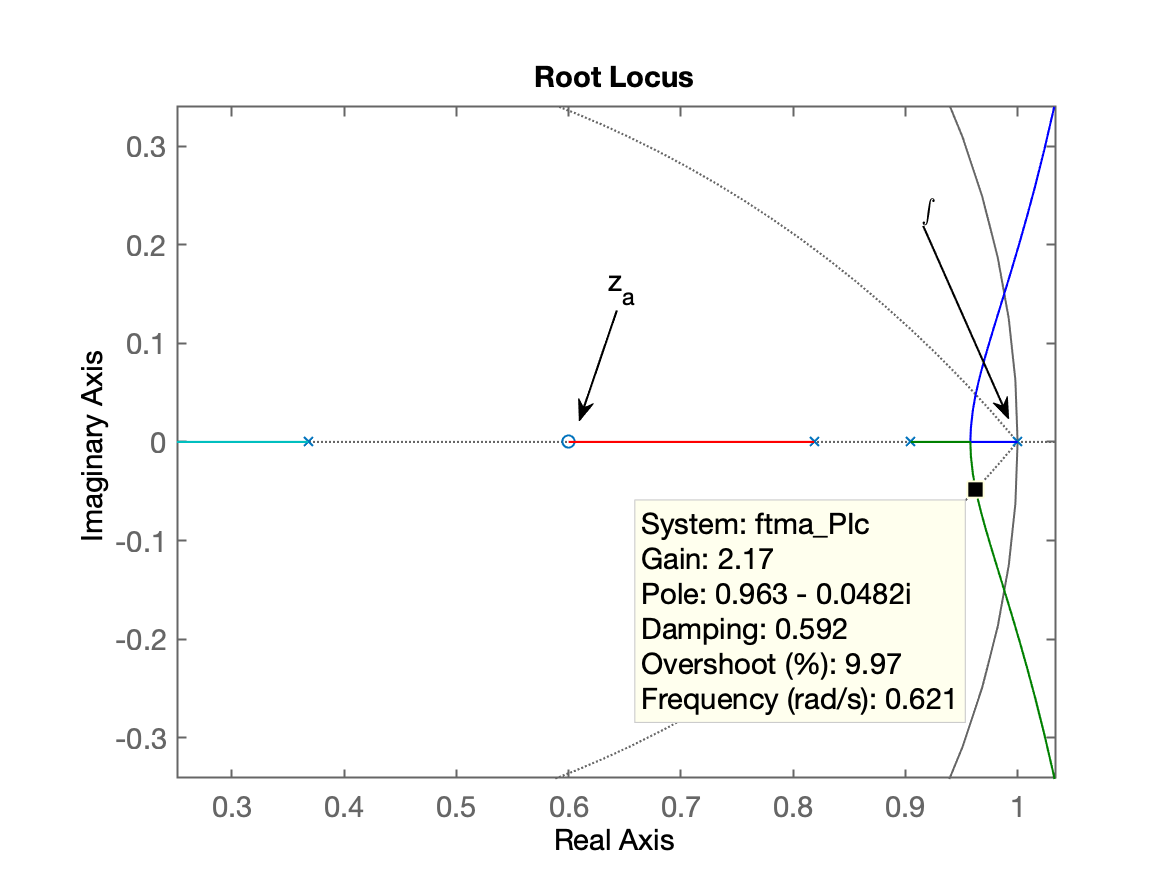Adotando o ganho de $K=2,17$$K=2,17$; teremos como resultado:

>> K_PIc=2.17;
>> ftmf_PIc=feedback(K_PIc*ftma_PIc, 1);
>> figure; step(ftmf_PIc)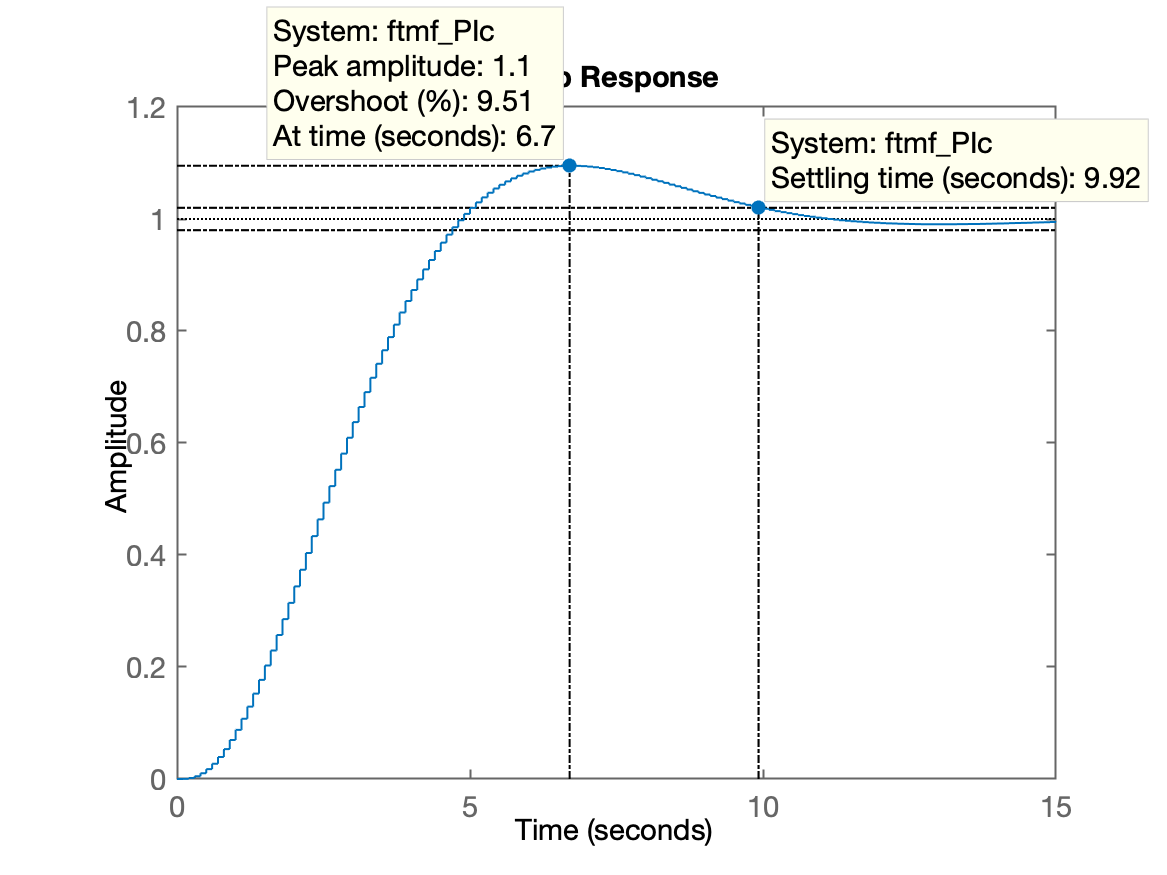

Percebe-se que o $t_s$$t_s$ aumentou consideravelmente em relação à opção (b). Esta opção (c), ainda gera um resultado um pouco melhor que a opção (a), mas não é uma opção tão rápida quanto a opção (b).

Note a distância dos pólos de MF da origem para o círculo unitário nas 2 opções:

Comparando opções (b) e (c)

Note que estes resultados já poderiam ter sido previstos, considerando-se a distância dos pólos de MF até o centro do plano-z:

Opção (b):	Opção (c):
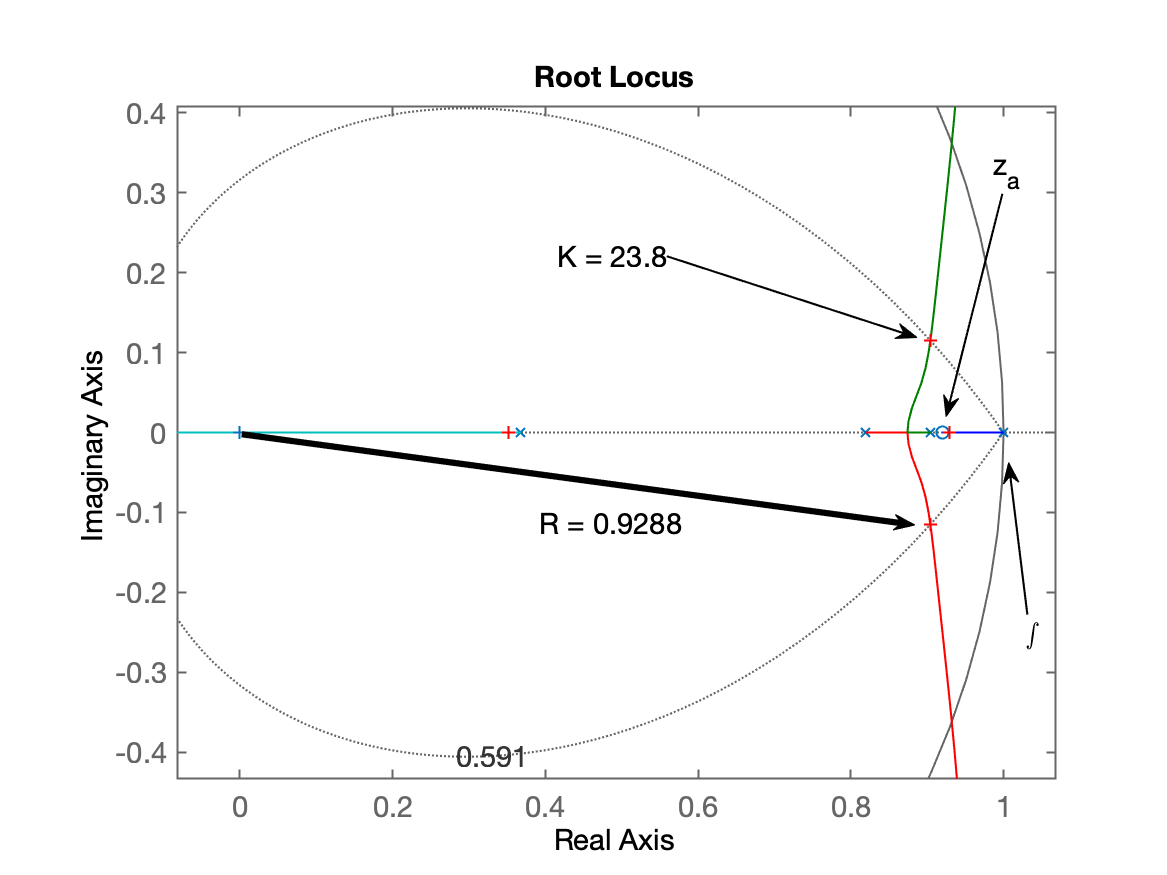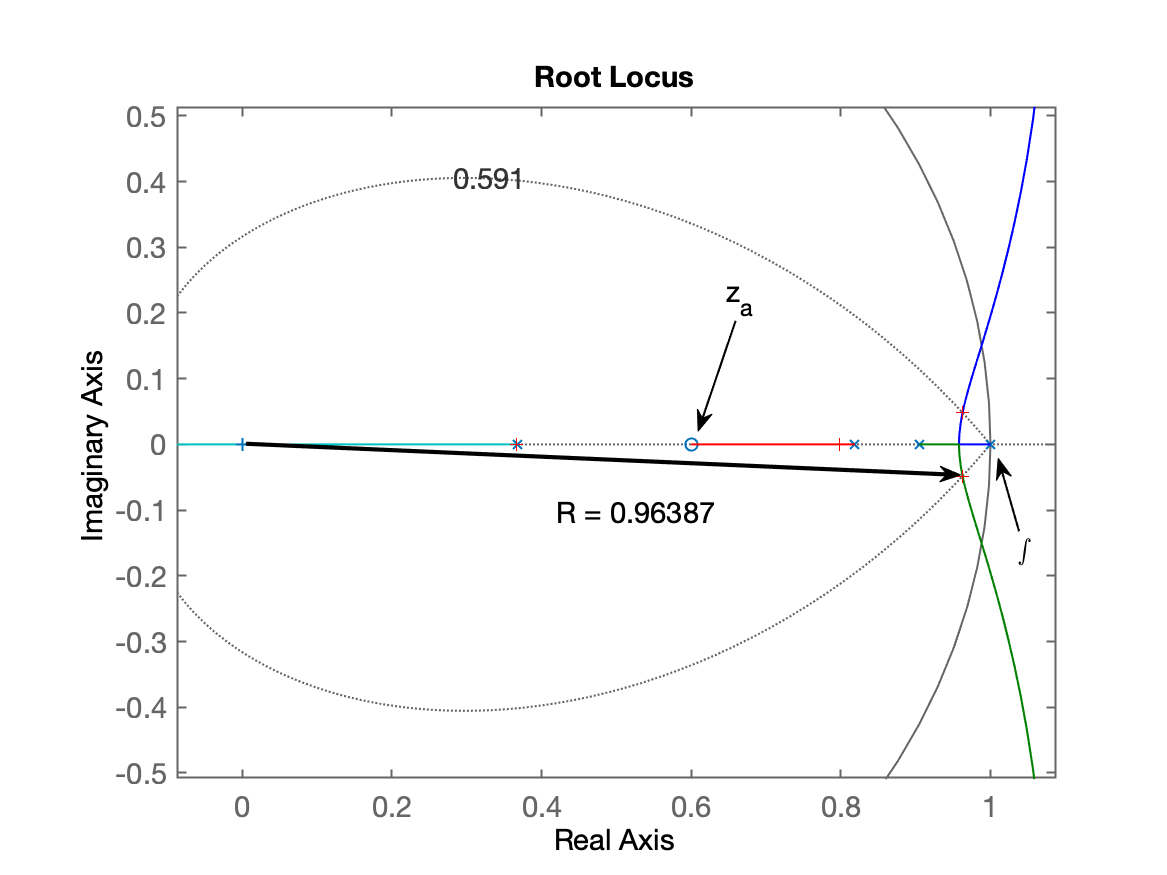>> polesMF_PIb=pole(ftmf_PIb) polesMF_PIb = 0.9288 + 0i 0.9042 + 0.11532i 0.9042 - 0.11532i 0.35133 + 0i >> R = abs(polesMF_PIb(1)) R = 0.9288 >> plot(polesMF_PIb,'r+')	>> polesMF_PIc=pole(ftmf_PIc) polesMF_PIc = 0.96267 + 0.048173i 0.96267 - 0.048173i 0.79866 + 0i 0.36718 + 0i >> R = abs(polesMF_PIc(1)) R = 0.96387 >> plot(polesMF_PIc,'r+')
R = 0,9288	R = 0,96387

Note que na opção (b), a distância ($R$$R$ nas figuras) do centro do plano-z até os pólos complexos é maior na opção (c). A diferença, numérica, parece pequena, mas note o impacto causado na resposta do sistema.

Falta considerar (numa próxima aula), a opção "d"...

Não esquecendo de salvar os dados para continuação na próxima aula:

>> save planta

Arquivo: planta.mat

:🚀🚀🚀🚀🚀

Fernando Passold, em 23/09/2021