Chase Clark, Unsplash
Projeto de Controladores com Ação Integral
Recuperando dados da aula passada:
xxxxxxxxxx>> load plantaProjeto do Controlador com Ação Integral Pura
Este controlador deve seguir o formato:
Ingressando este controlador no Matlab:
xxxxxxxxxx>> C = tf ( 1 , poly(1) , T )C = 1 ----- z - 1Sample time: 0.1 secondsDiscrete-time transfer function.>> % Calculando a FTMA(z):>> ftma_I = C*BoG;Comparando o que muda quando se acrecenta um controlador com pólo na de um sistema:
xxxxxxxxxx>> zpk(BoG) 0.00012224 (z+2.747) (z+0.1903) -------------------------------- (z-0.9048) (z-0.8187) (z-0.3679)Sample time: 0.1 secondsDiscrete-time zero/pole/gain model.>> zpk(ftma_I) 0.00012224 (z+2.747) (z+0.1903)-------------------------------------- (z-1) (z-0.9048) (z-0.8187) (z-0.3679)Sample time: 0.1 secondsDiscrete-time zero/pole/gain model.Levantando o Root Locus da com este controlador:
xxxxxxxxxx>> rlocus(ftma_I)>> axis equal % transforma o círculo unitário num círculo na tela>> % axis([xmim xmax ymin ymax]) <-- uso da função axis()>> axis ([-3 3 -3 3])Gráfico do RL (sem zoom ainda):
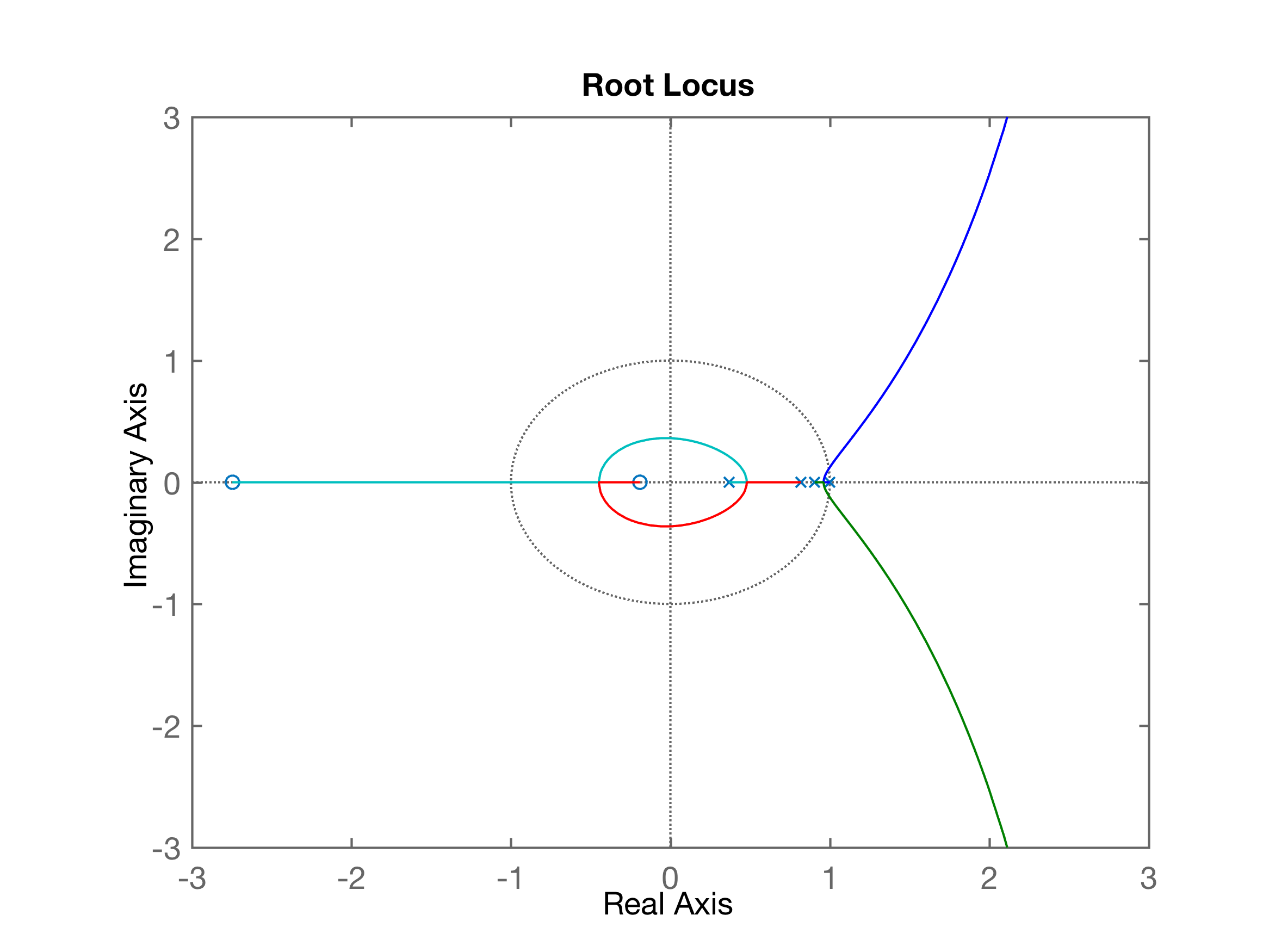
Realizando um zoom no gráfico do RL anterior:
xxxxxxxxxx>> figure; rlocus(ftma_I); axis equal>> axis([ 0.5 1.5 -0.5 0.5])>> axis([ 0.7 1.2 -0.2 0.2])>> hold on;>> OS % lembrando o %OS sendo adotadoOS = 5>> zeta % fator de amortecimento correspondentezeta = 0.6901>> zgrid(zeta, 0) % sobrepondo o traçado do \zeta no RL anteriorGráfico do Root Locus com Zoom:
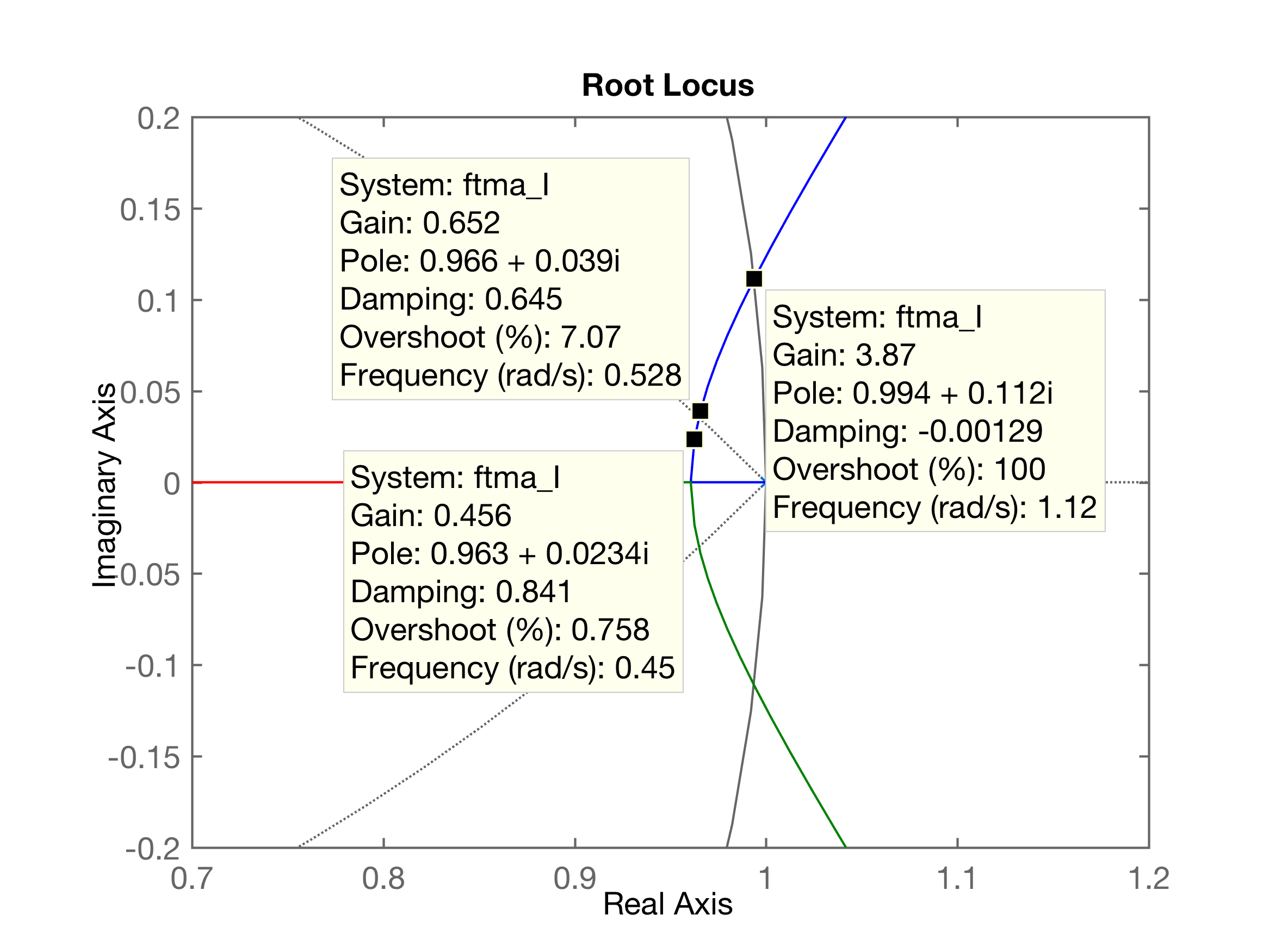
Fechando a malha com :
xxxxxxxxxx>> K_I=0.55;>> ftmf_I=feedback( K_I*ftma_I, 1);Observando resposta à entrada degrau (unitário):
xxxxxxxxxx>> figure; step(ftmf_I)Gráfico da resposta ao degrau:
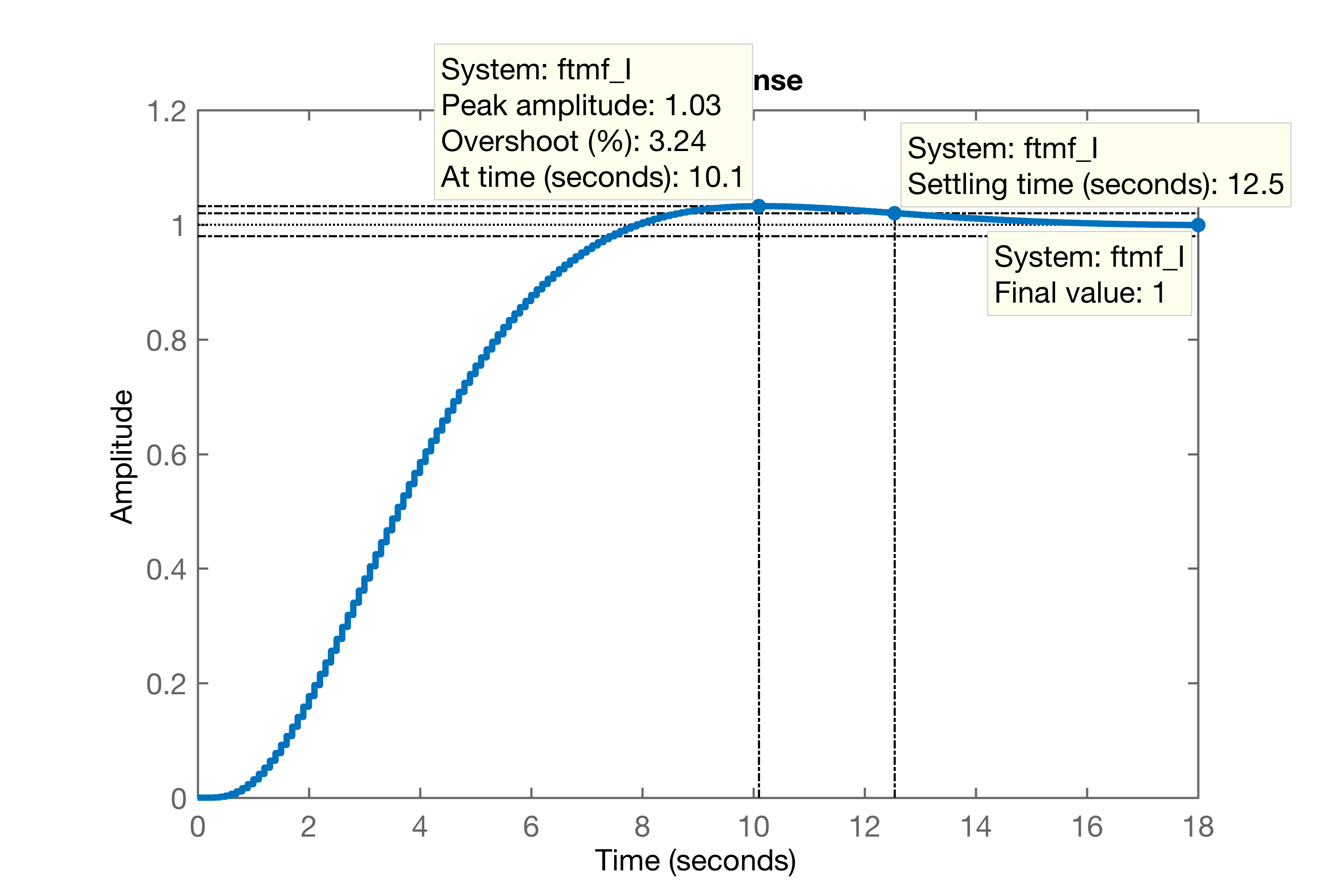
Comentários:
- Se manteve o e o erro nulo em regime permanente como seria esperado para uma com ação interal (sistema tipo 1) -- ver Teoria do Erro.
- Mas o tempo de assentamento, aumentou consideravelmente.
Comparando respostas do Controlador Proporcional com o de Ação Integral Pura:
xxxxxxxxxx>> figure; step(ftmf, ftmf_I)>> grid>> legend('Cont. Proporcional', 'Ação Integral Pura')Segue gráfico comparativo da resposta entre Controlador Proporcional e o de Ação Integral Pura:
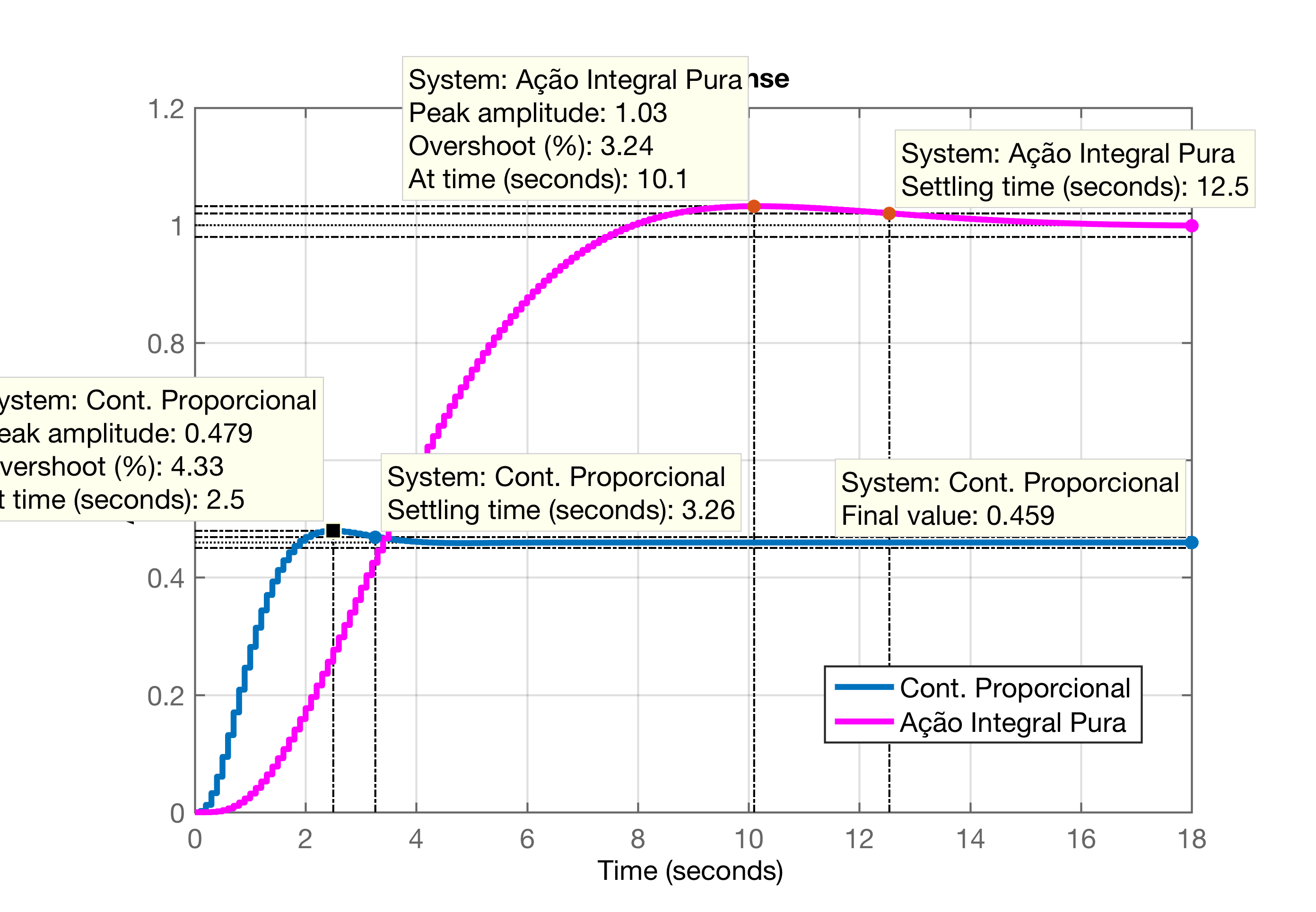
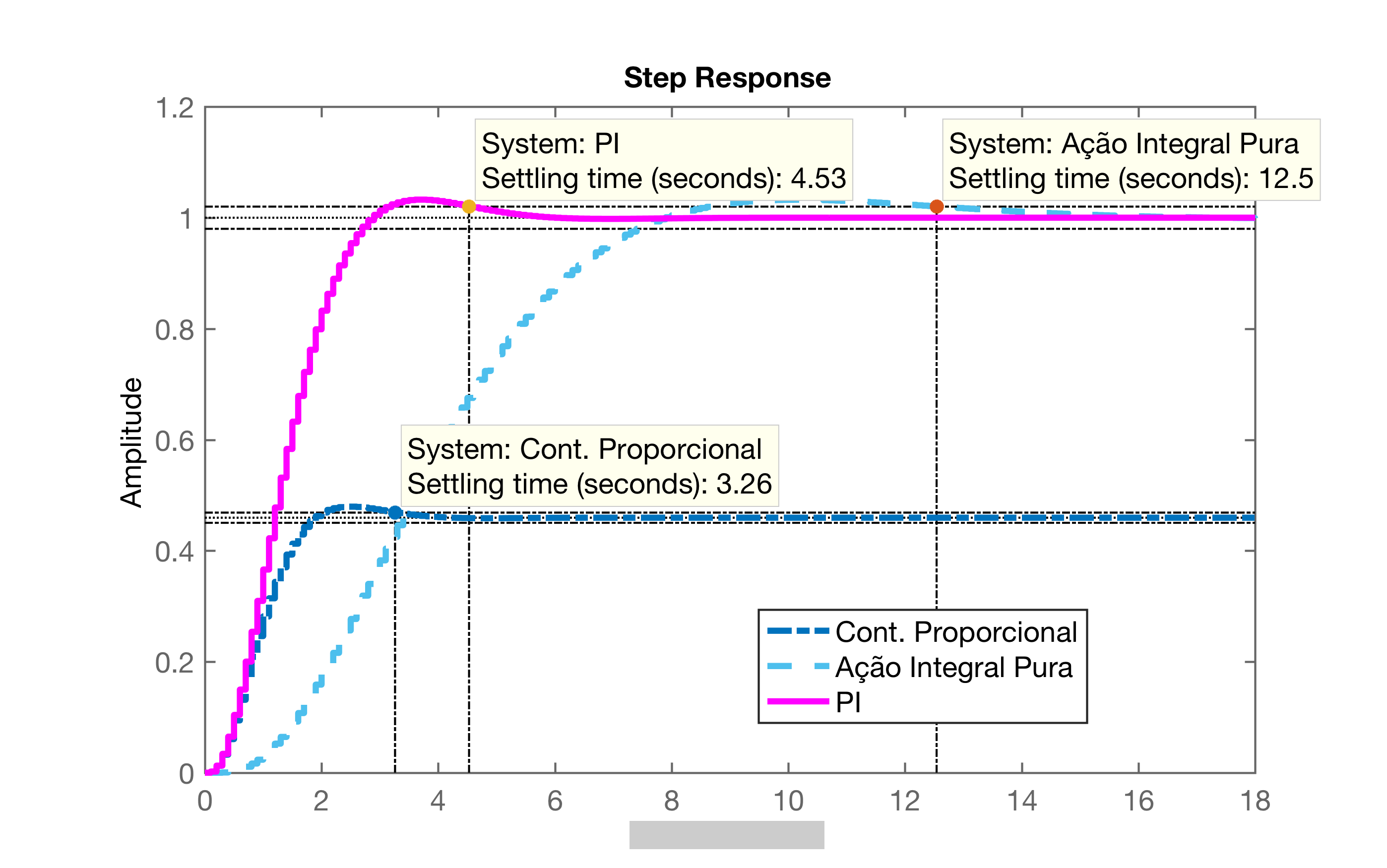
Conclusões: A ação integral permitiu zerar o erro em regime permanente mas, o tempo de assentamento aumentou quase 4 vezes ().
Projeto do PI (Proporcional + Integral)
Antes foi realizado um integrador puro que cunmpriu com o objetivo inicial pretendido: zerar o erro de regime permanente, mas neste caso, às custas de um atraso grande na resposta do sistema.
Note porém que um Controlador PI é formado pela soma de duas ações de controle: a ação Proporcional + a ação Integral, ou na forma de um diagrama de blocos:
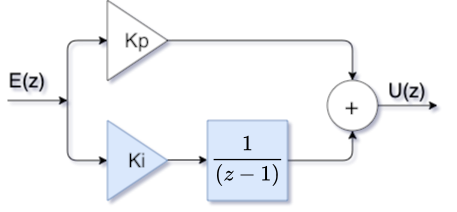
Obs.: usado o aplicativo online da Google: draw.io para gerar a figura anterior. Note que este aplicativo permite inserir equações matemáticas no formato LaTeX (mathematical typesetting), colocando a expressão dentro de um par de $$, tal qual se faz em arquivos Markdown.
Deduzindo a equação deste controlador:
Note então que este controlador segue a equação genérica:
A questão agora é: -- Onde posicionar o zero deste controlador?
Lembrando da equação de :
Notamos algumas opções para posicionamento do zero do PI:
- Opção 1) .
- Opção 2) Colocar o (entre os 2 pólos mais lentos da planta).
Comprovando os RL's para cada uma das opções:
xxxxxxxxxx>> C_PI1=tf([1 -0.95], [1 -1], T) % opção 1) pólo mais lento da planta < zero < pólo integradorC_PI1 = z - 0.95 -------- z - 1>> % Opção 2) Colocar o 0,8187 < zero_PI < 0,9048 (entre os 2 pólos mais lentos da planta)>> C_PI2=tf( [1 -0.85] , [1 -1], T)C_PI2 = z - 0.85 -------- z - 1>> % Calculando as correspondentes FTMA(z)'s:>> ftma_PI1=C_PI1*BoG;>> ftma_PI2=C_PI2*BoG;>> % Traçando os RL's >> figure; rlocus(ftma_PI1)>> hold on; zgrid(zeta, 0)>> figure; rlocus(ftma_PI2)>> hold on; zgrid(zeta, 0)Comparando os RL para estas 2 opções de PI's:
| Opção 1: | Opção 2: |
|---|---|
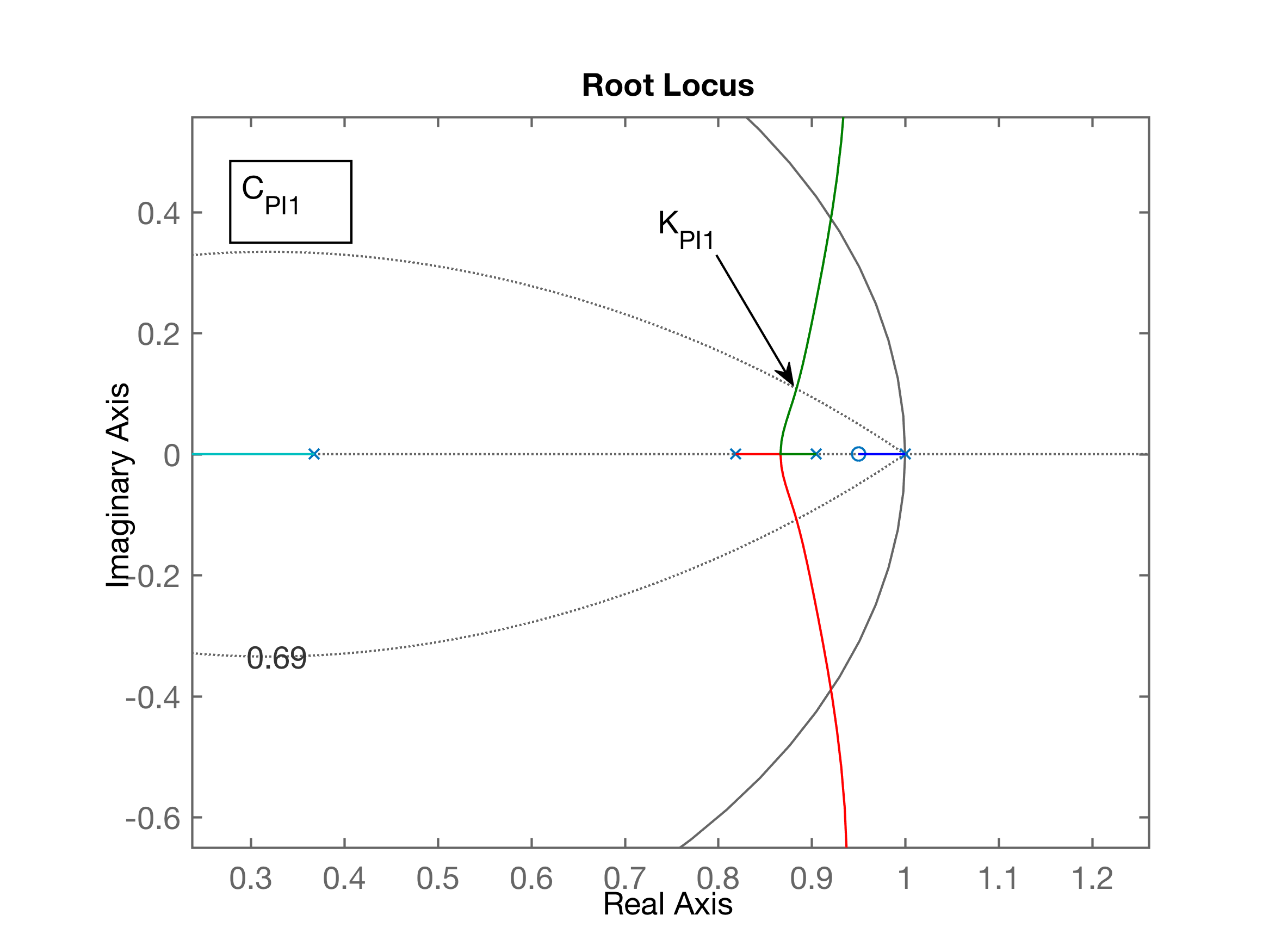 | 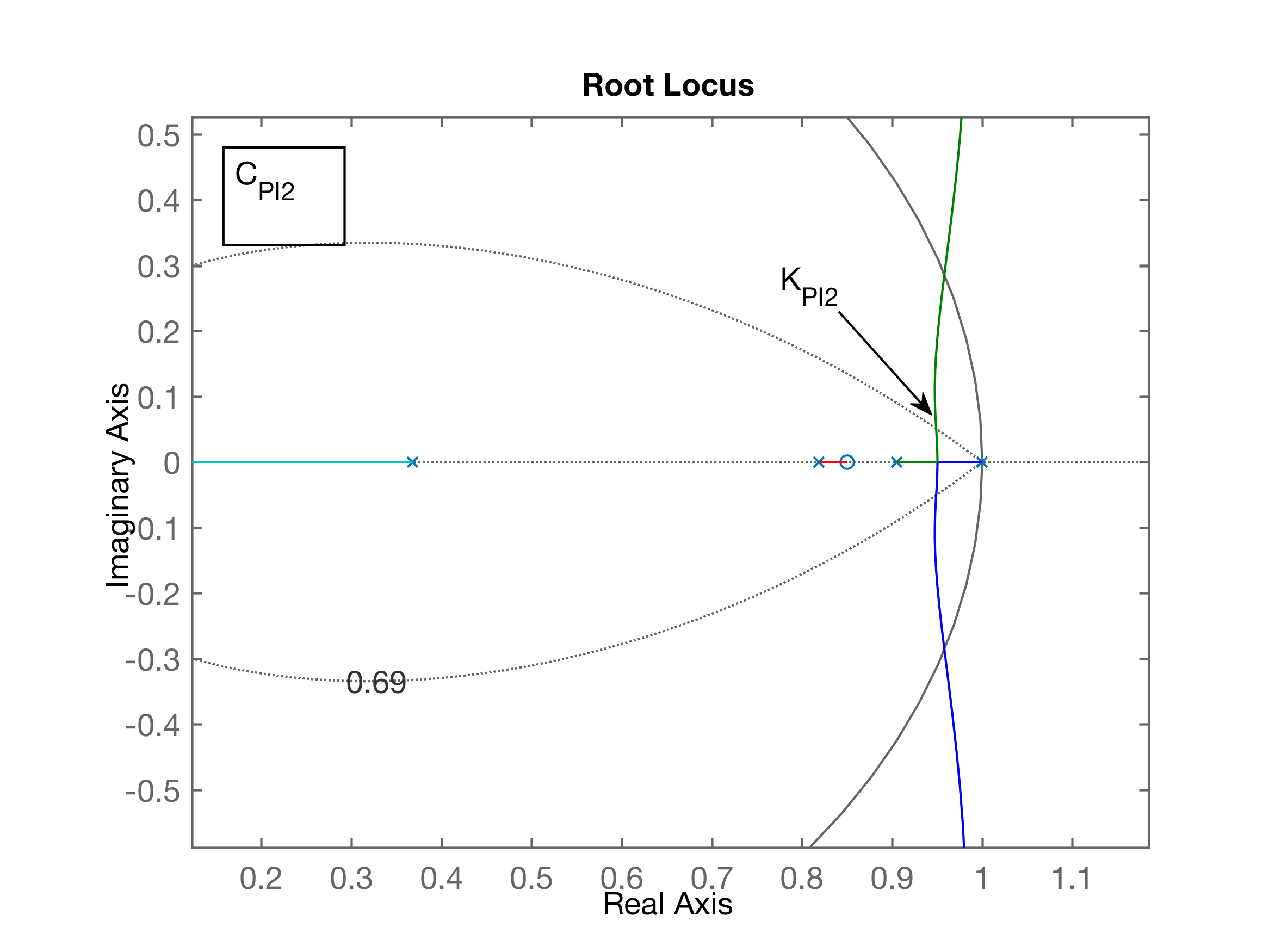 |
Comparando os 2 RL's se perecebe que os pólos dominantes complexos do RL para PI1 (opção 1) estão mais afastados do círculo unitário, portanto resultarão num tempo de assentamento menor (resposta mais rápida) que o PI2.
Continuando com o projeto do PI:
Se percebe que provavelmetne quanto mais próximo do zero do PI estiver do pólo mais lento da planta, mais rápida deve ser a resposta do sistema em malha-fechada.
Lembrando da equação de :
Colocando o zero do PI em , o ponto mais próximo possível do pólo dominante da planta (em ):
xxxxxxxxxx>> C_PI=tf( [1 -0.91] , [1 -1] , T)C_PI = z - 0.91 -------- z - 1>> ftma_PI=C_PI*BoG; % Calculando a FTMA(z)>> figure; rlocus(ftma_PI) % Levantando este RL>> hold on; zgrid(zeta, 0);>> axis([0.6 1.2 -0.4 0.4]) % "zoom" na área de interesse>> % Encontrando o ponto desejado no RL>> [K_PI, polos_MF]=rlocfind(ftma_PI)Select a point in the graphics windowselected_point = 0.9092 + 0.0842iK_PI = 17.0320polos_MF = 0.9158 + 0.0000i 0.9088 + 0.0843i 0.9088 - 0.0843i 0.3559 + 0.0000iSegue gráfico do RL, mostrando ponto de ganho selecionado no RL:
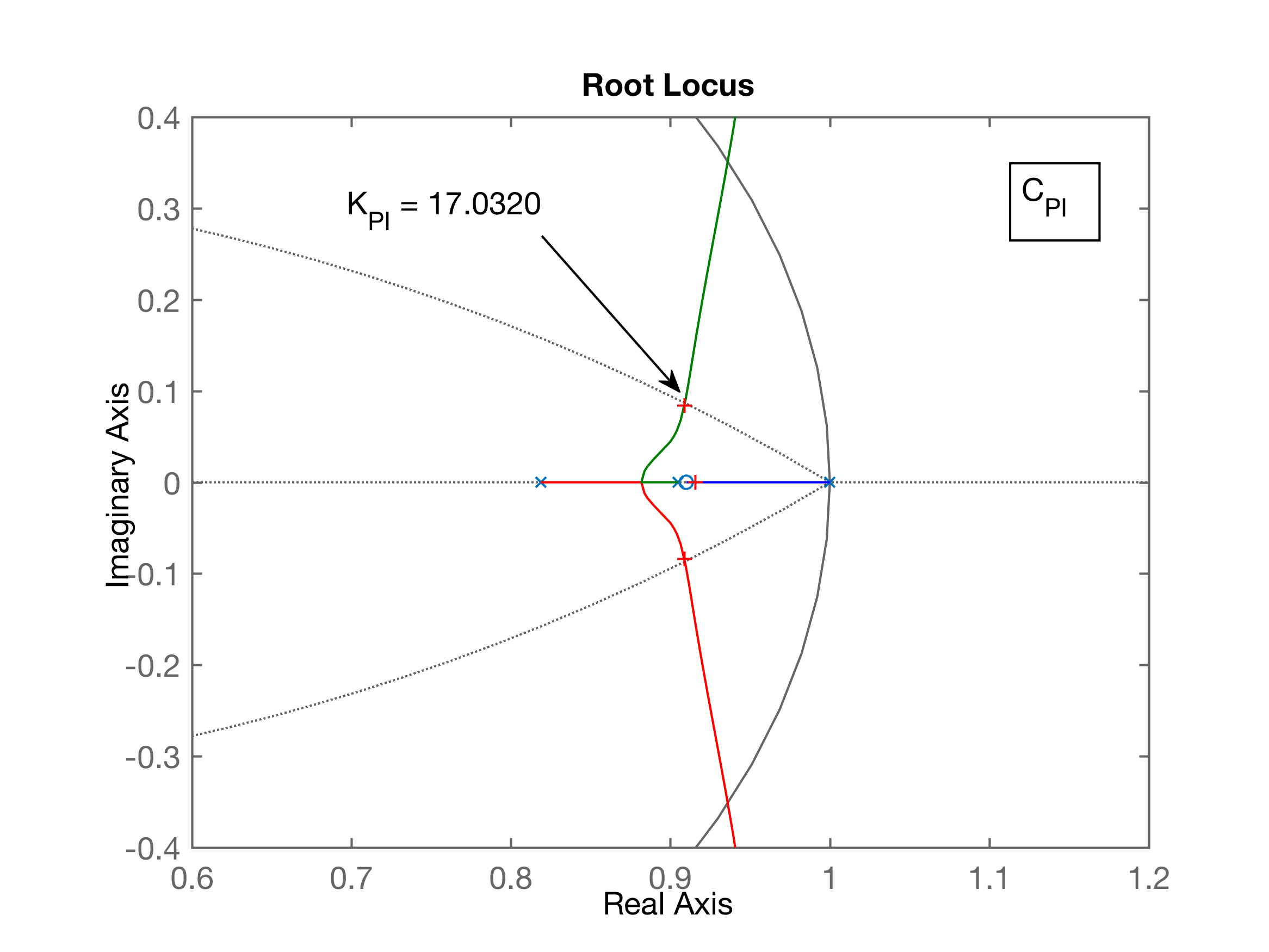
Fechando a malha...
xxxxxxxxxx>> ftmf_PI=feedback(K_PI*ftma_PI, 1);>> figure; step(ftmf_PI)Segue gráfico da resposta ao degrau unitário para este PI:
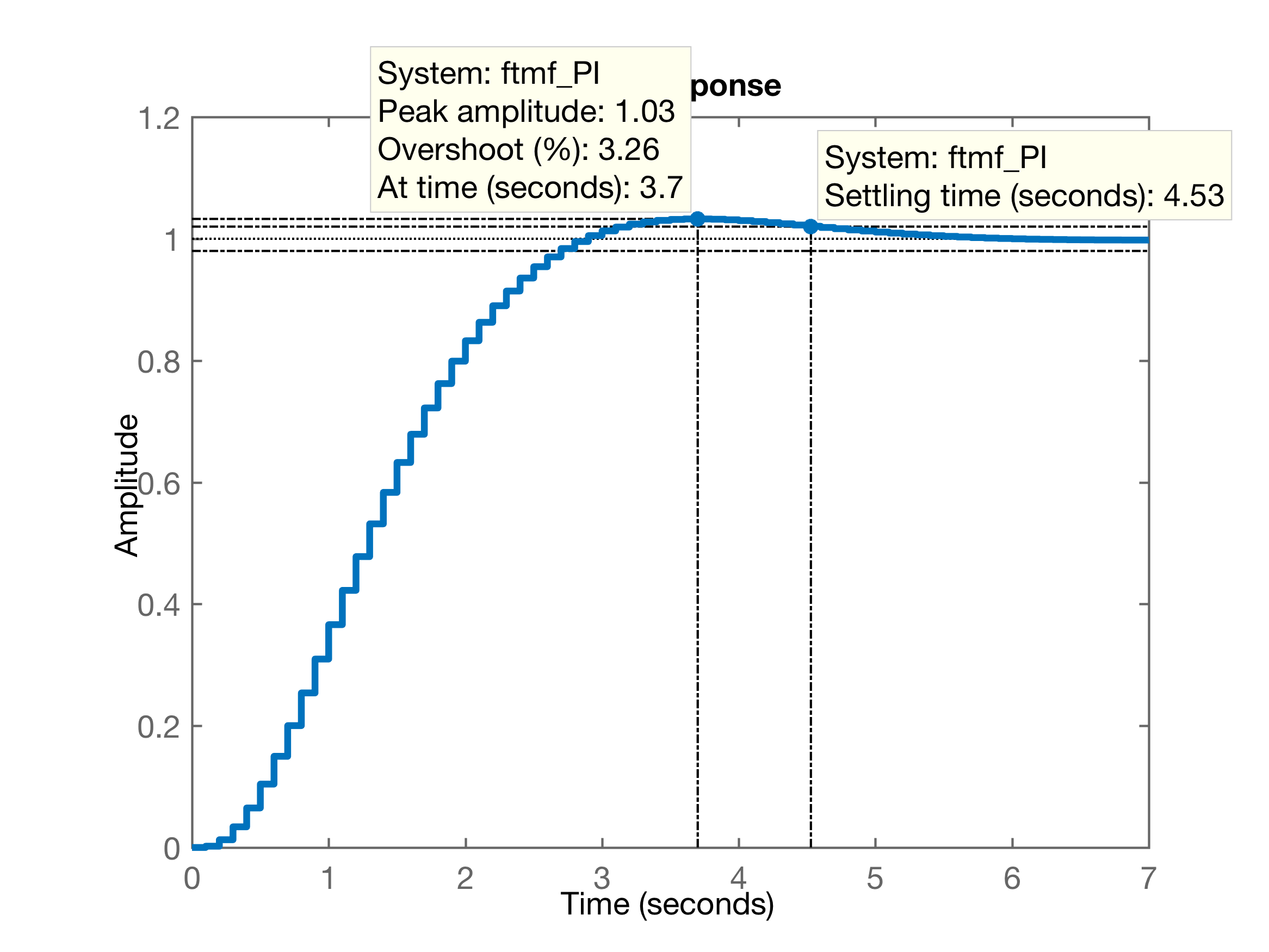
Comparando os 3 controladores já projetados até o momento:
- Proporcional;
- de Acão Integral Pura;
- PI (P+I)
xxxxxxxxxx>> figure; step(ftmf, ftmf_I, ftmf_PI);>> legend('Cont. Proporcional', 'Ação Integral Pura', 'PI')Gráfico resultante:
Finalizando esta seção de trabalho no Matlab:
xxxxxxxxxx>> save planta>> diary off>> quitFim.
🎶 Fernando Passold, em 05.05.2021
