Impacto dos pólos e zeros na magnitude da resposta em frequência.

• Impacto dos pólos e zeros na magnitude da resposta em frequência.

  • Intro

  • Exemplo 1

  • Diagrama de Bode no mundo discreto

    • Uso da função freqz()

  • Notas sobre pólos e zeros localizados na origem

    • Por que acrescentar pólos e zeros na origem do plano-z?

  • Exemplo 2

Intro

Como os pólos e zeros afetam a magnitude da resposta em frequência de um sistema?

Anteriormente (no tópico: [Funções Trasferência]) foi mostrado como a localização dos pólos e zeros afeta os contornos da superfície $H(z)$ de um sistema:

• Os pólos ficam associados a "cones positivos" no gráfico de superfície de $H(z)$ $\Longrightarrow$ resulta em ganhos no sinal de entrada.
• Os zeros ficam associados a "cones negativos" no gráfico de superfície de $H(z)$ $\Longrightarrow$ resulta em atenuações no sinal de entrada.

Neste documento, será mostrado como os pólos e zeros afetam a resposta de frequência de um sistema usando vários exemplos. Você pode achar que o primeiro exemplo não é muito claro, mas se você relacionar cada um dos exemplos entre si, isso pode ajudar na sua compreensão.

Exemplo 1

Para o primeiro exemplo, será usado o sistema fornecido pelo diagrama de fluxo de sinal mostrado abaixo. Também são fornecidas a equação de diferenças de sistemas e a função de transferência.

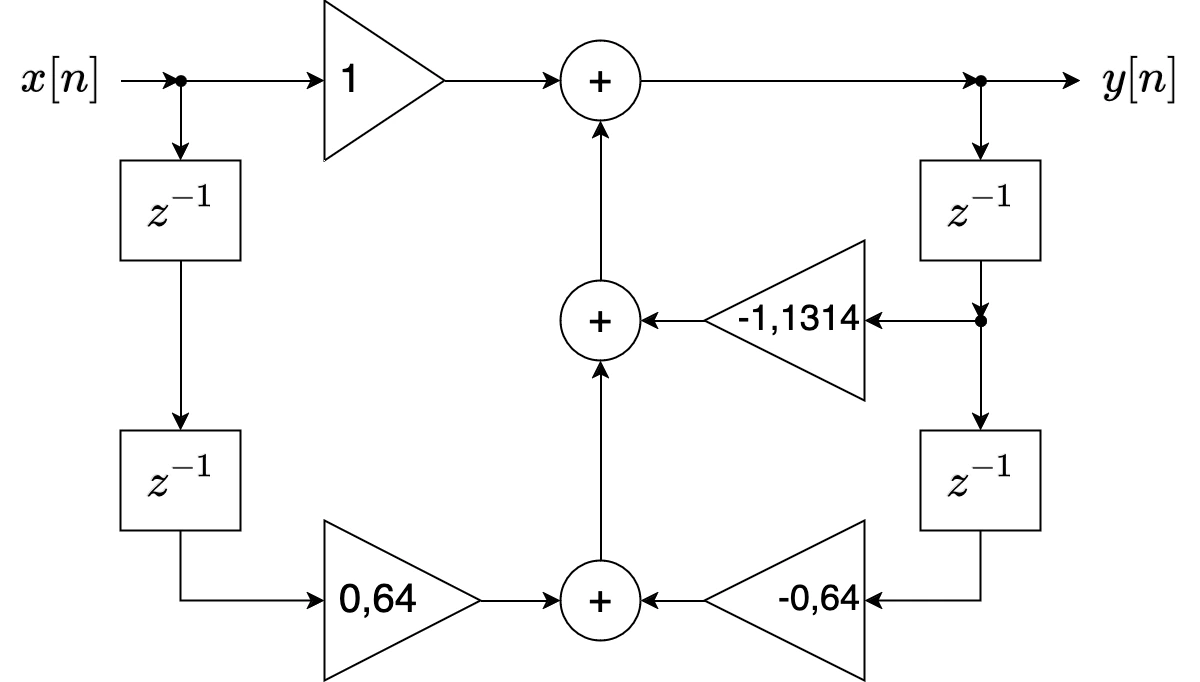
A eq. de diferenças do sistema ilustrado acima fica:

$y[n]=x[n]+0,64x[n-2]-1,1314y[n-1]-0,64y[n-2]$

Trabalhando esta expressão algebricamente:

$y[n]+1,1314y[n-1]+0,64y[n-2]=x[n]+0,64x[n-2]$

$Y(z)+1,1314z^{-1}Y(z)+0,64z^{-2}Y(z)=X(z)+0,64z^{-2}X(z)$

$Y(z)\left( 1+1,1324z^{-1}+0,64z^{-2}\right)=X(z)\left( 1+0,64z^{-2}\right)$

Que rende a seguinte função transferência:

$H(z)=\dfrac{Y(z)}{X(z)}=\dfrac{1+0,64z^{-2}}{1+1,1314z^{-1}+0,64z^{-2}} \cdot \dfrac{z^{+2}}{z^{+2}}$

eue rende a seguinte função transferência

$H(z)=\dfrac{z^2+0,64}{z^2+1,1314z+0,64}$

Neste função percebemos 2 zeros (raízes do numerador), localizados em $z=\pm \sqrt{-0,64}=\pm j\,0,8=0,8 \angle{(\pm 1,5708 \text{ (rad)})}= 0,8 \angle \pm{90^o}$.

Adicionalmente temos pólos em $z=-0.5657 \pm j\,0.56567=0,8 \angle{(\pm 2,3562 \text{ (rad)})}=0,8 \angle{(\pm 135^o)}$.

Os pólos correspondem às raízes do denominador de $H(z)$.

Um diagrama pólo-zero deste sistema rende:

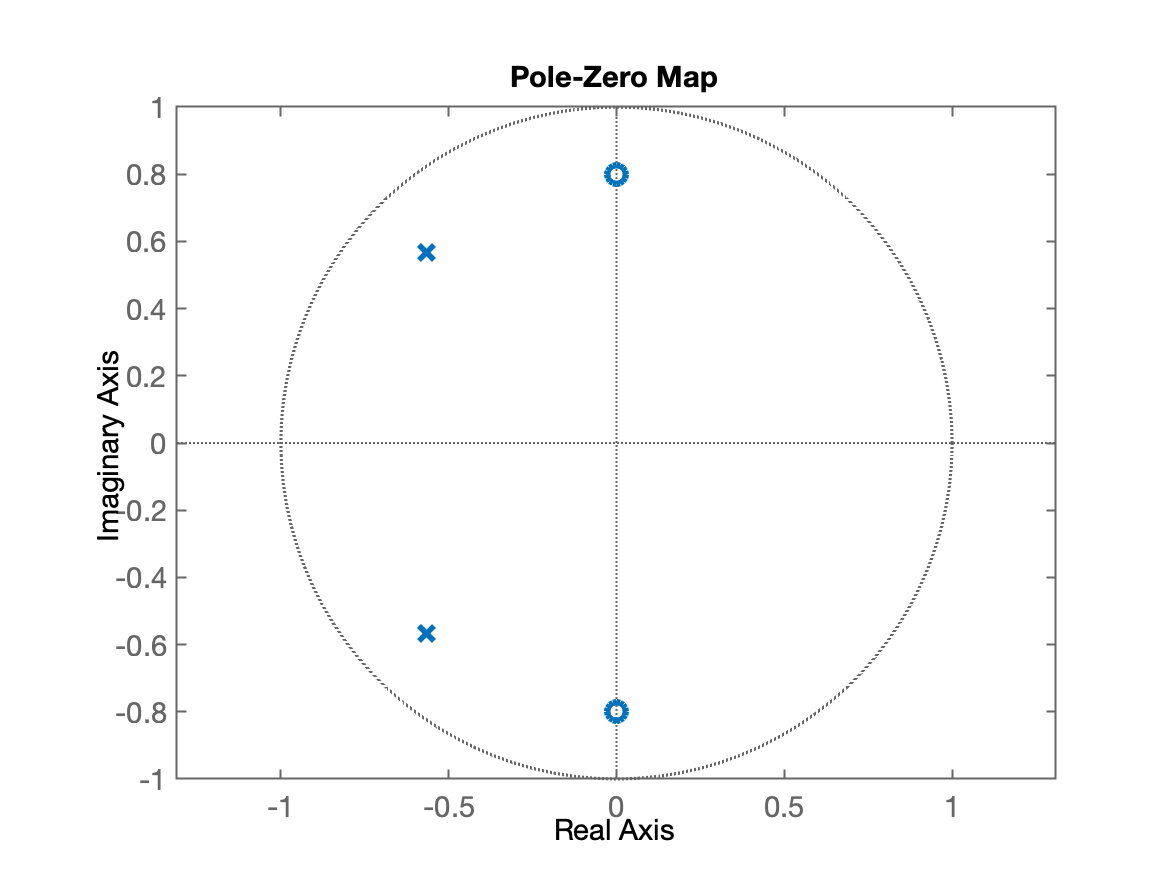
Usando a função bode() do Matlab para sistemas discretos (no plano-z), rende algo como:

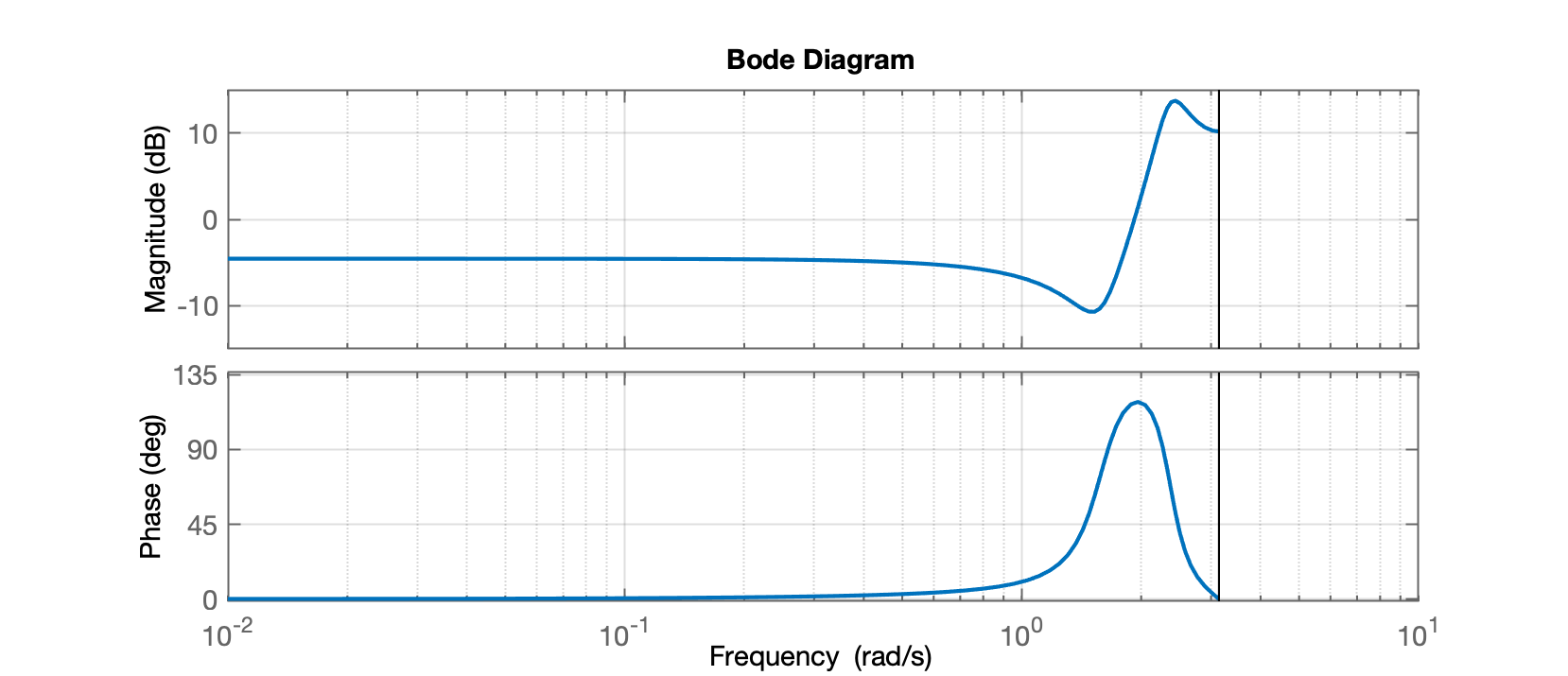
Note que o próprio Matlab alerta para a forma como calcula este diagrama:

Para modelos de tempo discreto com tempo de amostragem $T_s$, bode() usa a transformação $z = \exp(j \cdot \omega \cdot T_s)$ para mapear o círculo unitário para o eixo real de frequência. A resposta de frequência é plotada apenas para frequências menores que a frequência de Nyquist $\pi/T_s$ (rad) ou $180^o/T_s$ (graus), e o valor padrão 1, para unidade de tempo (= 1 segundo), é assumido quando $Ts$ não é especificado.

O gráfico anterior foi feito usando os comandos:

​x
>> H=tf([1 0 0.64],[1 1.1314 0.64],1)
​
H =
 
       z^2 + 0.64
  --------------------
  z^2 + 1.131 z + 0.64
 
Sample time: 1 seconds
Discrete-time transfer function.
​
>> bode(H)

Podemos usar a função bodeplot() que agrega mais opções para melhorar o gráfico anterior:

xxxxxxxxxx
>> handler=bodeplot(H);
>> setoptions(handler,'FreqUnits','Hz','PhaseVisible','off');
>> xlim([1/(2*10) 1/2])

E então temos o gráfico:

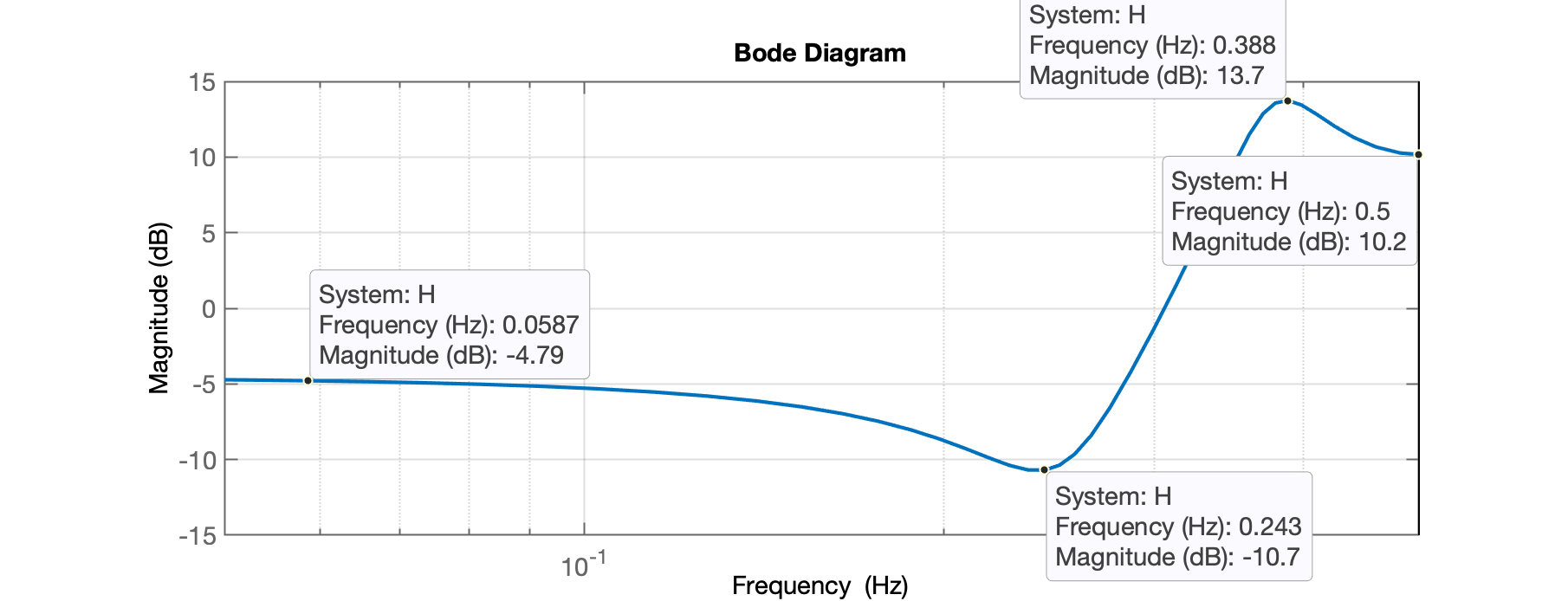
Note que o "eixo $x$" (das frequências), ainda está na escala logarítmica ($\log(\omega)$).

Modificando para variação linear do eixo $x$ (frequências) obtemos um gráfico mais útil:

xxxxxxxxxx
>> setoptions(handler,'FreqScale','linear');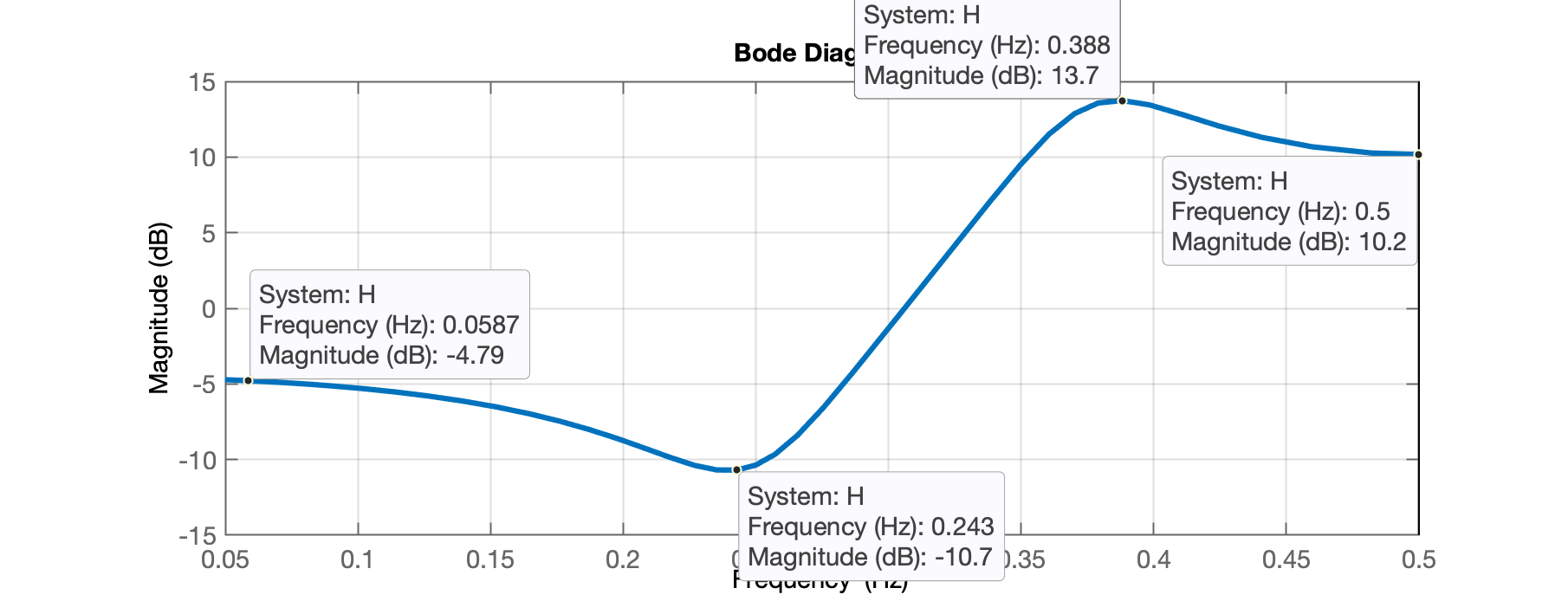

Note que o Matlab vai variar a frequência deste "Diagrama de Bode" até a metade da frequência de Nyquist. Neste caso: $f_s=1/T=1$ Hz, então, o diagrama só avança até $f_{max}=$ 0,5 Hz.

Este gráfico indica um pico de atenuação do sinal de entrada na frequência aproximada de 0,243 Hz ou, se considerarmos um gráfico genérico, temos que considerar que $180^o=\pi$ corresponde à $f_s/2$.

No caso anterrior, quando ingressamos a transfer function no Matlab, somos "obrigados" à especificar um período de amostragem, e neste caso foi adotado $T=1$ segundo, o que corresponde à $f_s=1$ Hz. Mas o sistema será implementado usando $T=1$ segundos !?

Se este sistema for amostrado à $f_s=100$ Hz, o pico de atenuação de sinal ($-10,7$ dB) terá ocorrido em $0,243*100=24,3$ Hz. Ou:

xxxxxxxxxx
>> H=tf([1 0 0.64],[1 1.1314 0.64], 1/100)
​
H =
 
       z^2 + 0.64
  --------------------
  z^2 + 1.131 z + 0.64
 
Sample time: 0.01 seconds
Discrete-time transfer function.
​
>> % Note que H(z) não mudou (em relação à fs = 1 Hz)
>> % Mas o "diagrama de Bode" vai mudar
>> handler=bodeplot(H);
>> setoptions(handler,'FreqUnits','Hz','FreqScale','linear','PhaseVisible','off');
>> xlim([100/(2*10) 100/2]) % iniciando uma década abaixo de fs/2 até fs/2
>> grid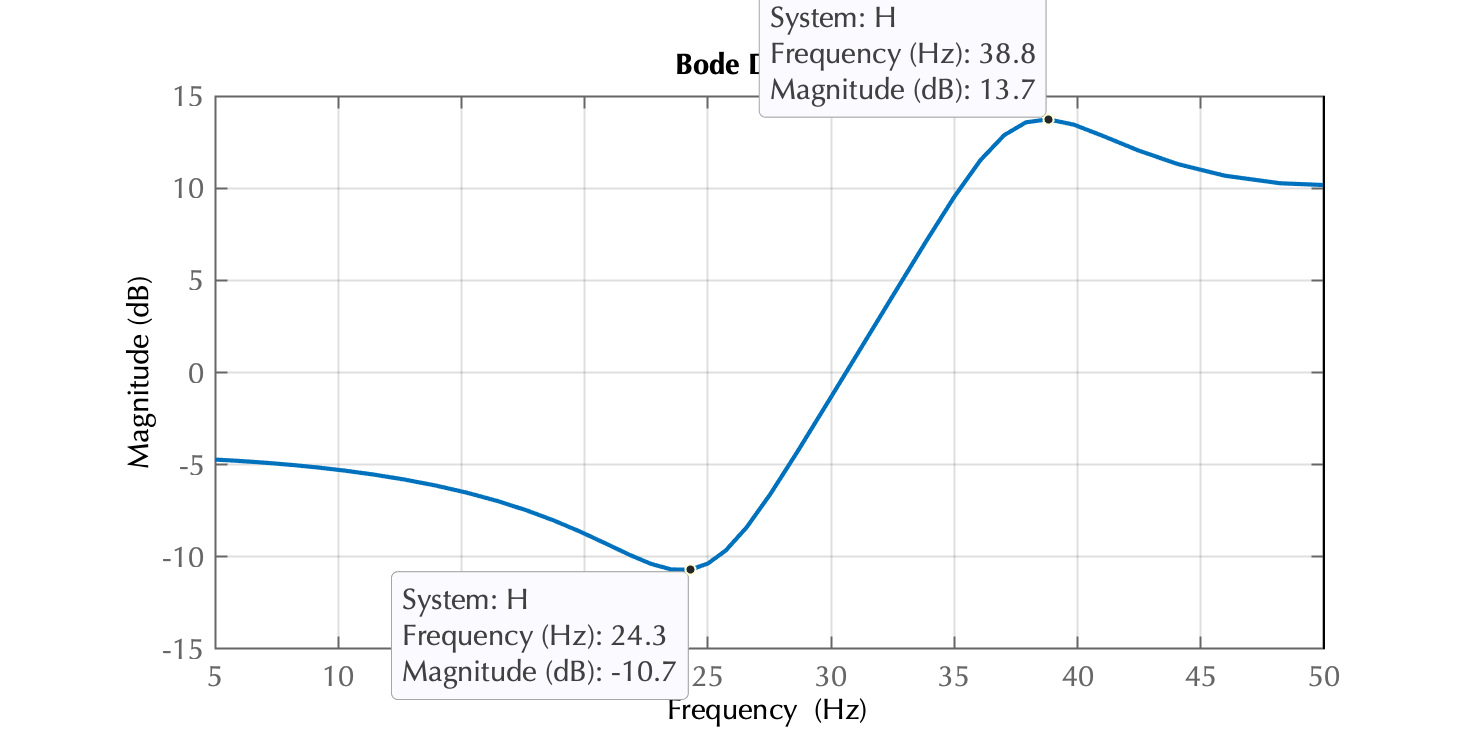

Voltando ao primeiro gráfico usando $f_s=1$ Hz, seu diagrama completo (amplitudes e fase $\times$ frequência) rende:

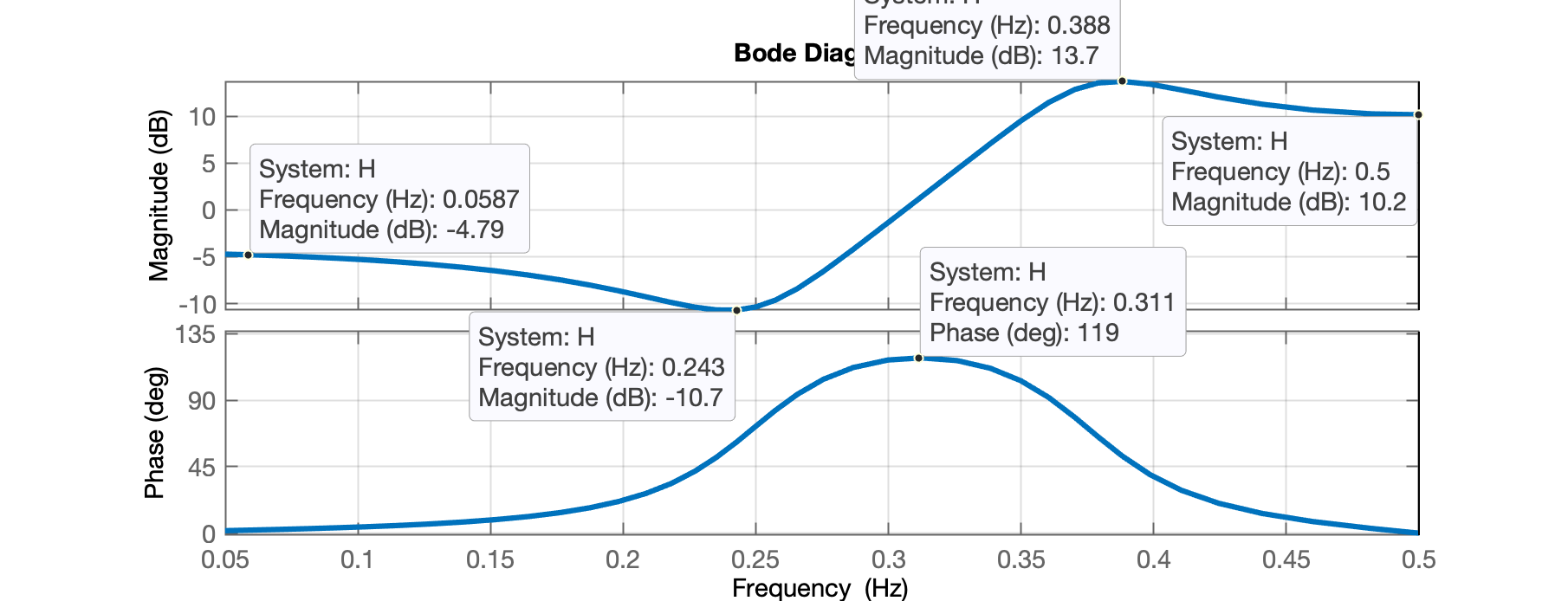
Note que o gráfico anterior corresponde à vista superior de um gráfico de superfície da função $H(z)$:

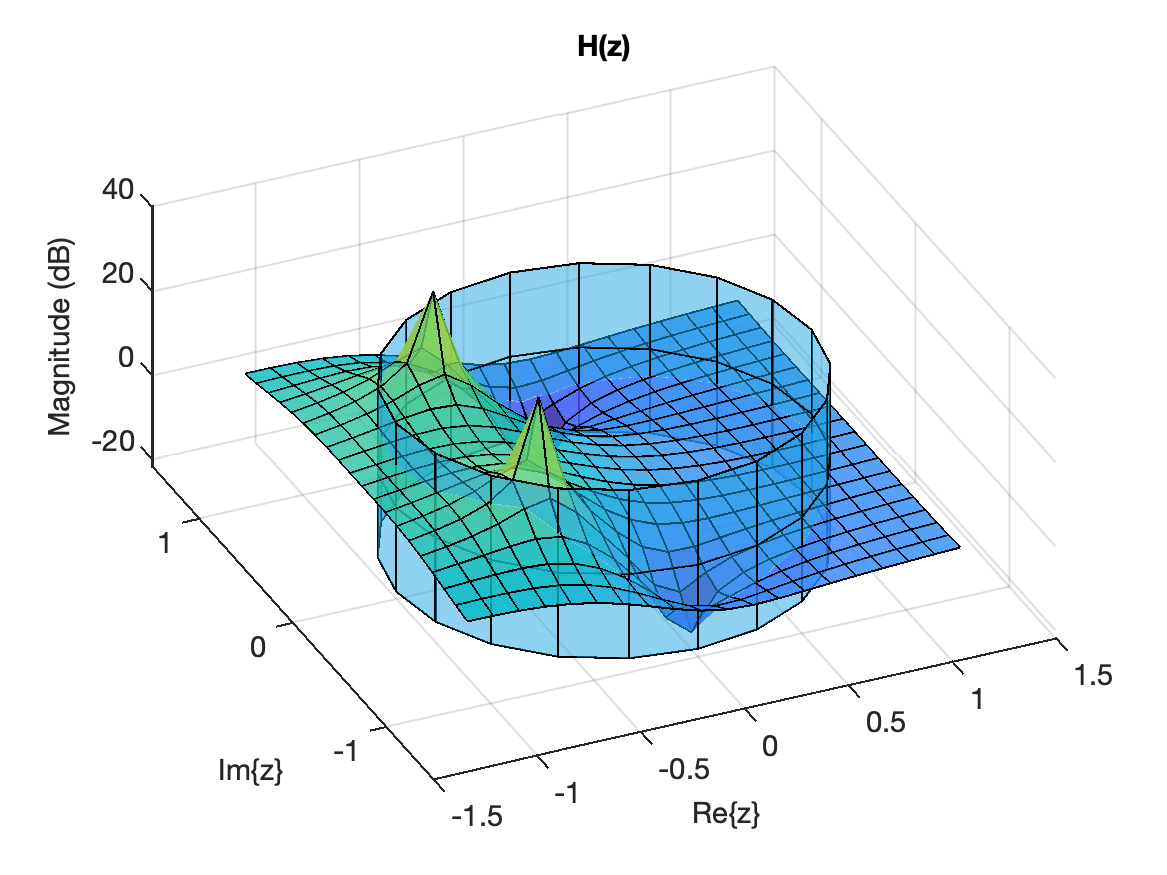
Pode-se perceber os picos positivos associados com os zeros de $H(z)$ e os picos negativos associados com os pólos de $H(z)$. Uma "vista superior" rende:

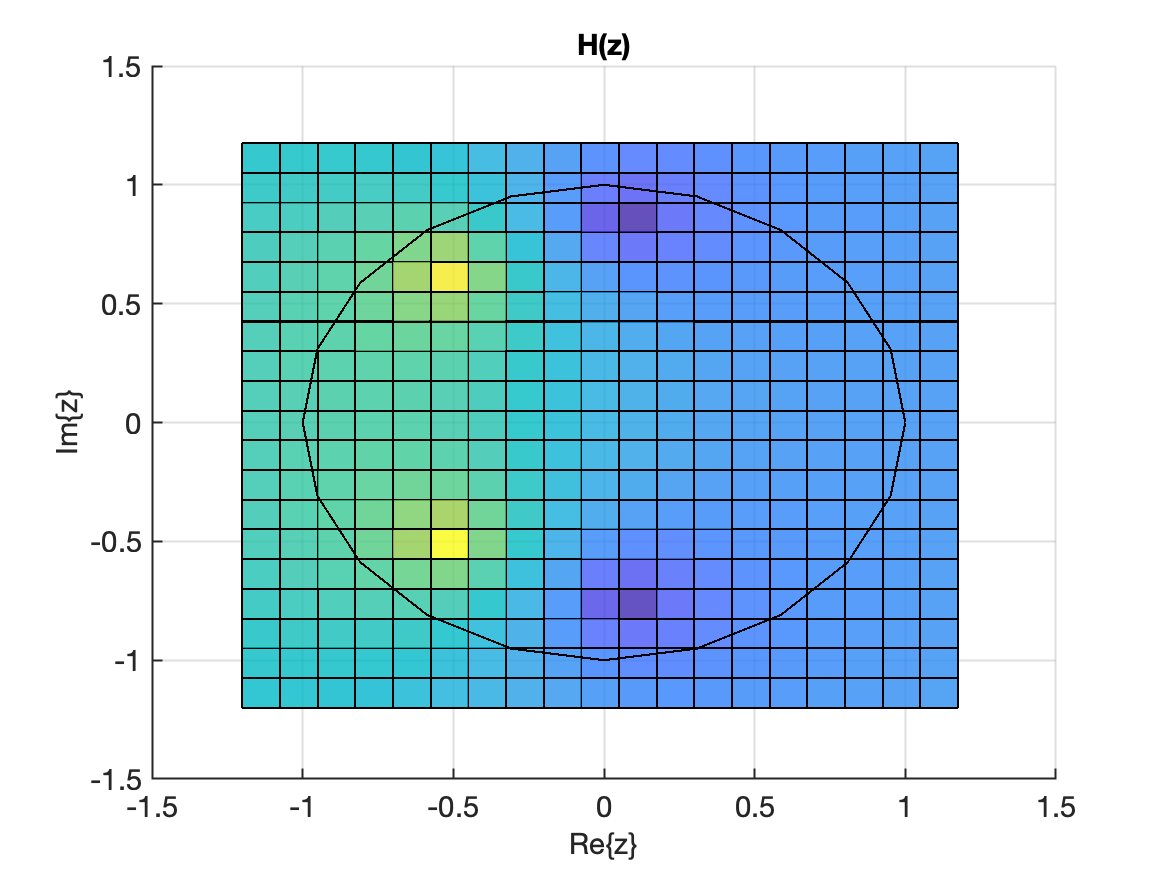
Gráficos gerados usando script:

xxxxxxxxxx
z_real_vals = [-1.2:0.125:1.2]; % z_real_vals = [-1.2:0.02:1.2];
z_imag_vals = [-1.2:0.125:1.2];
for m = 1: length(z_real_vals)
 for n = 1: length(z_imag_vals)
     z = z_real_vals(m)+z_imag_vals(n)*j;
     H_z(n,m) = (z*z+0.64)/(z*z+1.1314*z+0.64);
 end
end
figure
[X,Y,Z]=cylinder(1);    % cria cilindro "3D", raio=1
Z1=Z*20;                % alturas -20 e +20 para anéis circulares cilindro
Z2=Z*(-20);
u=length(Z);
h1=surf (X, Y, Z1);
h1.FaceAlpha = 0.5;
hold on
h2=surf (X, Y, Z2);
h2.FaceAlpha = 0.5;
​
% gráfico de superfície de H(z)
h3=surf(z_real_vals, z_imag_vals, 20*log10(abs(H_z)));
h3.FaceAlpha = 0.8;
​
xlabel('Re\{z\}')
ylabel('Im\{z\}')
zlabel('Magnitude (dB)')
title('H(z)')

Perceba mais alguns detalhes comparando o gráfico anterior com o diagrama de pólos e zeros:

Gráfico de superfície de $H(z)$	Diagrama pólo-zero

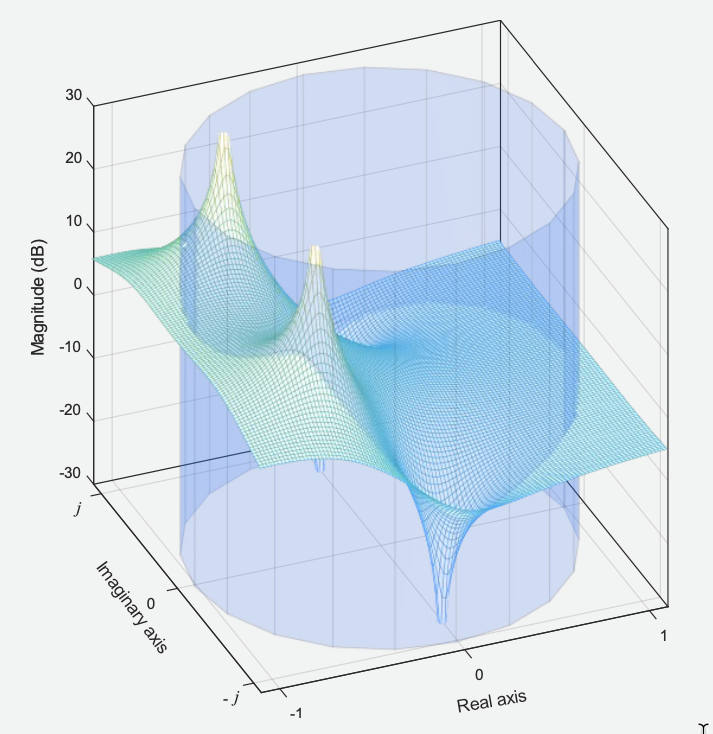Perceba a intersecção entre o círculo unitário e a superfície formada por $H(z)$. A figura abaixo mostra os pontos de intersecção que o cilindro faria com o superfície de $H(z)$, mostrada como linhas de cores diferentes (azul, verde, vermelho e amarelo):

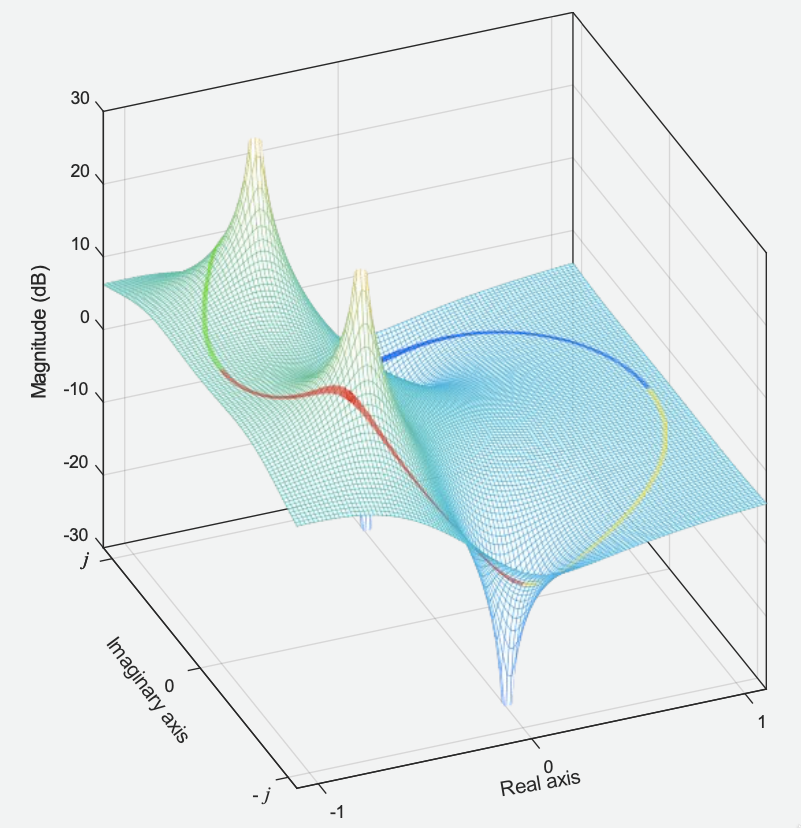
Uma vista superior plana (com um diagrama de pólo zero sobreposto) mostra que a linha azul está associada ao intervalo de ângulos de $0$ a $\frac{\pi}{2}=0,5\pi$ (rad) (0 à $90^o$) e a linha verde está associada aos ângulos de $0,5\pi$ à $\pi$ radianos ($90^o$ à $180^o$). Você também deve observar que os contornos das linhas azuis e amarelas serão “espelhados” no eixo real. Da mesma forma, as linhas de contorno verdes e vermelhas serão “espelhadas” ao longo do eixo real:

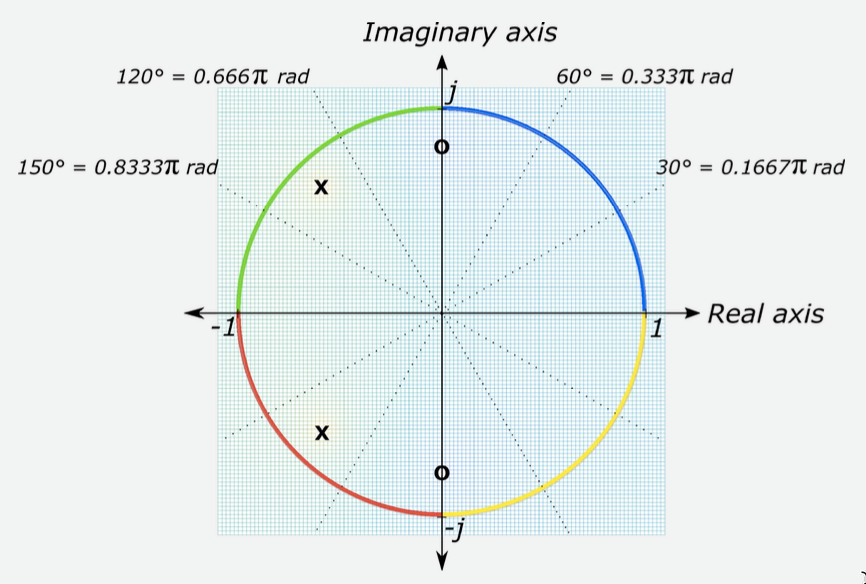
Se você traçasse a magnitude dos pontos de intersecção em relação ao ângulo feito com o eixo real, na faixa de ângulos de $-\pi$ a $\pi$ radianos ($-180^o$ à $+180^o$), (ou seja, plotasse a amplitude das linhas coloridas de interseção em relação ao ângulo), você obteria o gráfico mostrado abaixo:

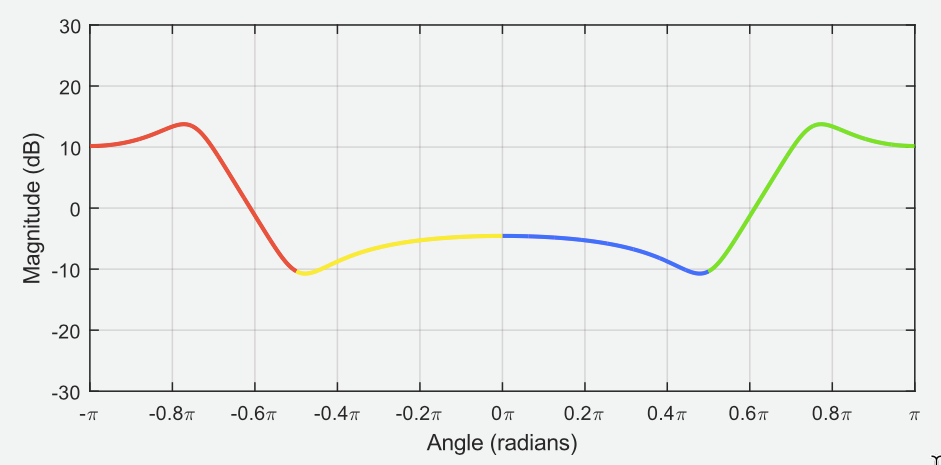
Você notará que o lado esquerdo do gráfico acima "espelha” o lado direito. Traçar o lado direito, de 0 a $\pi$ radianos (ou de 0 até $180^o$), por si só resulta no gráfico a seguir:

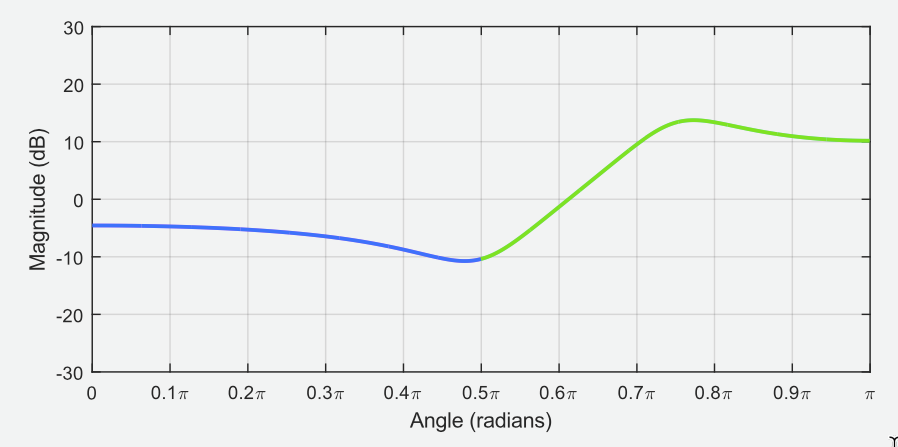
Note que o aumento da magnitude no ângulo de $0,5\pi$ é causado pelo "contorno do cone" associado ao pólo localizado em $-0,5657+j0,5657$. Observe também que a redução na magnitude em um ângulo de $0,5\pi$ é causada pelo "contorno do cone invertido" associado ao zero localizado em $0+j0,8$.

Diagrama de Bode no mundo discreto

Acontece que se o eixo do ângulo horizontal for interpretado como frequência com unidades de radianos por amostra, então o gráfico acima é a magnitude da resposta em frequência do sistema, conforme mostrado na figura abaixo:

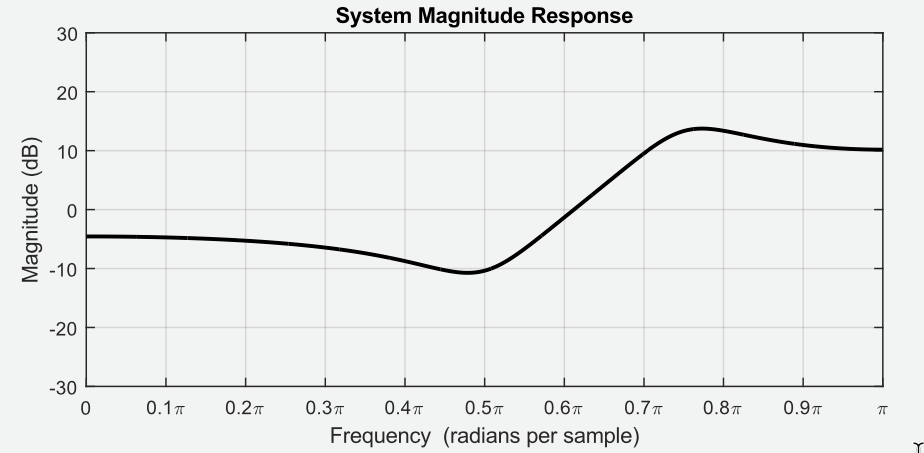
Observe que se você quisesse interpretar a resposta de frequência em Hertz (em vez de radianos por amostra), então você precisaria saber a taxa de amostragem associada ao sinal que estava passando pelo sistema. Para converter o eixo horizontal para Hertz, substitua $\pi$ por "metade da taxa de amostragem". Por exemplo, se a taxa de amostragem fosse de 100 Hz, então o ponto médio de $0,5\pi$ radianos por amostra no gráfico acima equivaleria a 25 Hz ($0,5*100/2=25$):

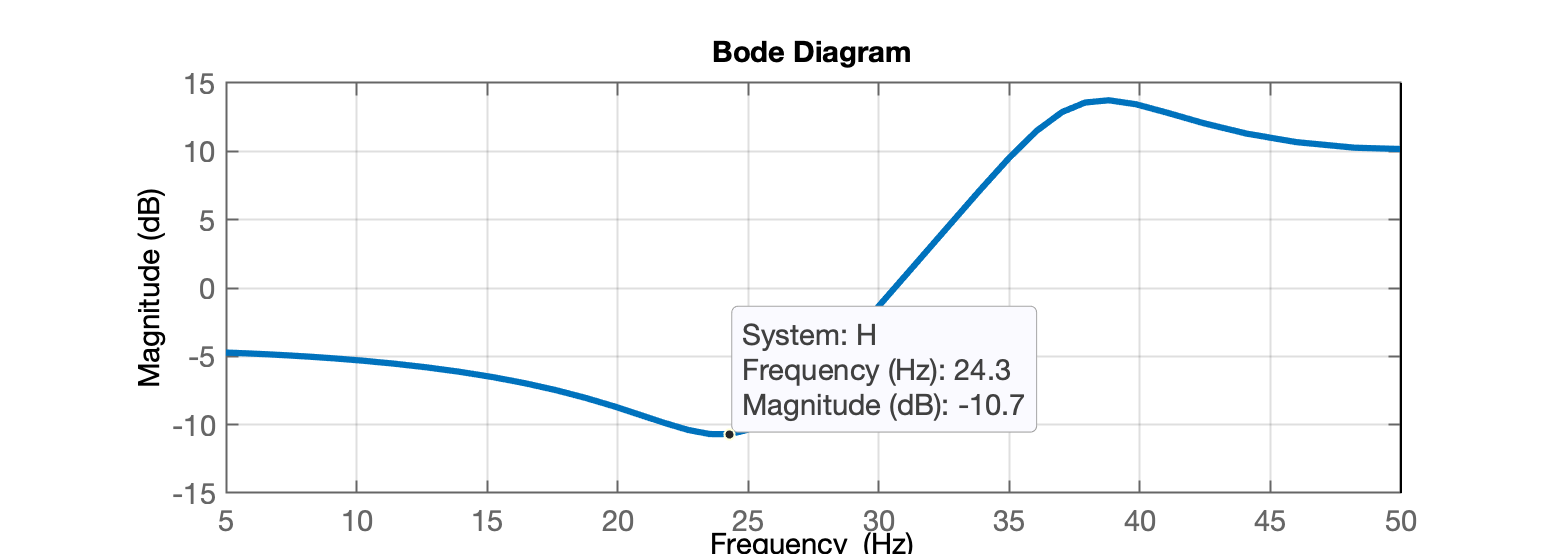
Note que o gráfico só avança até a frequência de Nyquist ($=f_s/2$).

Uso da função freqz()

O Matlab pode facilitar as coisas ao disponibilizar a função:

[h, w] = freqz(b, a, n, fs)

Esta função retorna o diagrama de resposta frequêncial (magnitude e fase) e o vetor $f$ que corresponderá a frequência física real (em Hz), de $n-$pontos da função transferência do filtro fornecida com base nos seus coeficientes $b$ e $a$. $n=[\; ]$ se o usuário não quiser especificar o número desejado de pontos.

Note:

$H(z)=\dfrac{Num(z)}{Den(z)} = \dfrac{b_0z^{n_b}+b_1z^{n_b-1}+\ldots+b_{n_b}z^0}{a_0z^{n_a}+a_1z^{n_a-1}+\ldots+a_{n_a}z^0}=\dfrac{Y(z)}{X(s)}$

Onde: $n_b=$ grau do numerador, $Num(z)$ (ou $n_b=$ número de zeros de $H(z)$); $n_a=$ grau do denominador, $Den(z)$ (ou $n_a=$ número de pólos de $H(z)$).

$H(z)=\dfrac{b_0z^0 + b_1z^{-1}+b_2z^{-2}+\ldots+b_{n_b}z^{-n_b}}{ a_0z^0 + a_1z^{-1}+a_2z^{-2}+\ldots+a_{n_a}z^{-n_a} } = \dfrac{Y(z)}{X(z)}$

$Y(z)\left(a_0 + a_1z^{-1} + a_2z^{-2} + \ldots + a_{n_a}z^{-n_a} \right) = X(z)\left( b_0 + b_1z^{-1} + b_2z^{-2} + \ldots + b_{n_b}z^{-n_b} \right)$

$\begin{array}{rcll} a_0\,y[n] &=& b_0\,x[n] &+& b_1\,x[n-1] + b_2\,x[n-2] + \ldots + b_{n_b}\,x[n-n_b] +\\ & & &-& a_1\,y[n-1] - a_2\,x[n-2] - \ldots - a_{n_a}\,y[n-n_a] \end{array}$

Lembre-se eventualmente da função filter().

A função freqz() aplicada no caso anterior, resultaria em:

xxxxxxxxxx
>> figure;
>> zpk(H)
​
ans =
 
      (z^2 + 0.64)
  ---------------------
  (z^2 + 1.131z + 0.64)
 
Sample time: 0.01 seconds
Discrete-time zero/pole/gain model.
​
>> [numd, dend]=tfdata(H,'v')
numd =
            1            0         0.64
dend =
            1       1.1314         0.64
>> freqz(numd, dend, [], 100)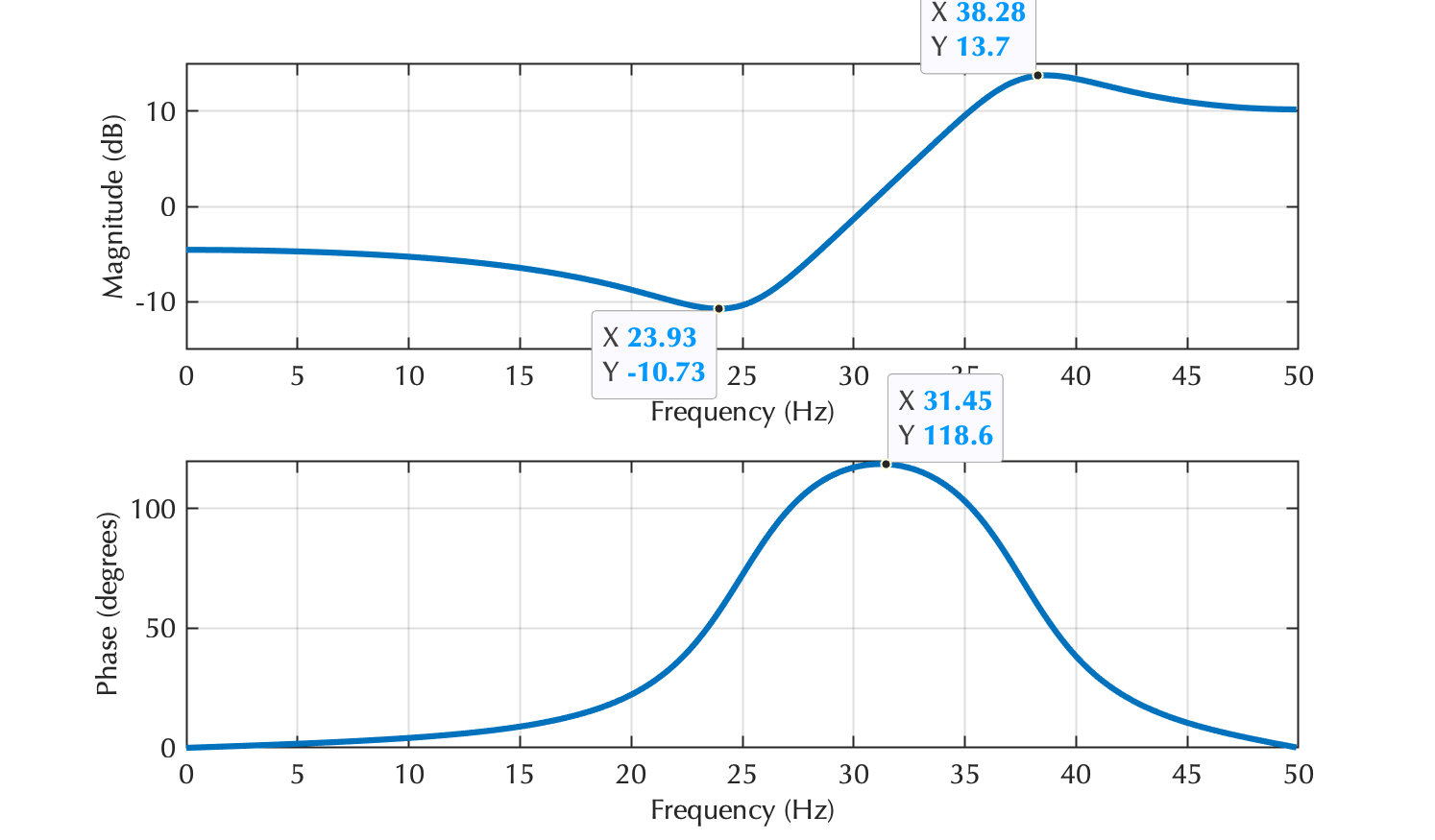

Notas sobre pólos e zeros localizados na origem

⚠️ Detalhes: você verá que um pólo ou zero localizado na origem ($0 + 0𝑗$) não afeta a resposta em frequência de um sistema.

Considere a função transferência abaixo:

$H(z)=\dfrac{1}{z}$

Este sistema possui um pólo localizado em $z=0=0j$, isto é, na origem do plano-z.

Num sistema com um único pólo na origem, a intersecção da superfície $H(z)$ com o cilindro unitário seria tal que a amplitude dos pontos de interseção seria igual, conforme mostrado nas ilustrações abaixo. Na verdade, você descobrirá que a amplitude dos pontos de interseção seria de 0 dB.

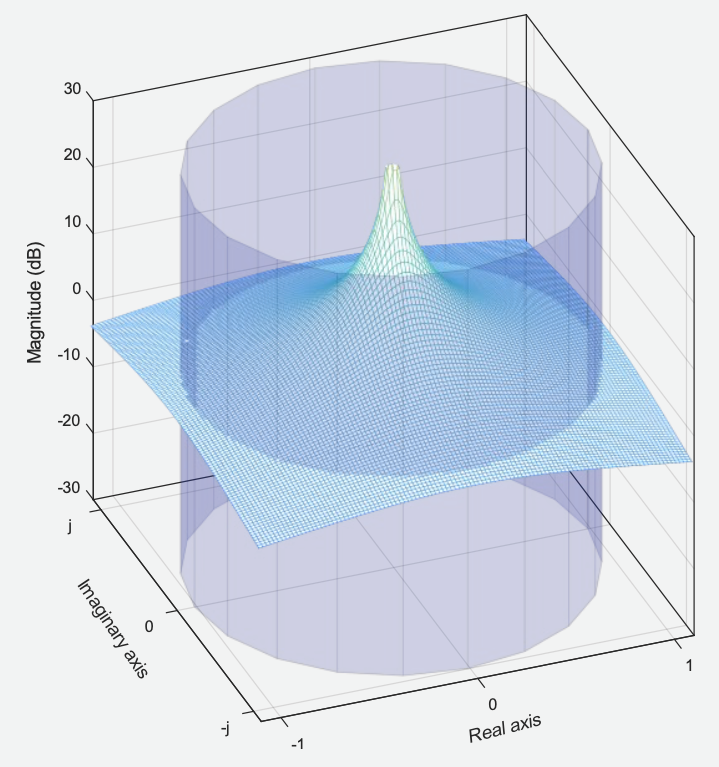
Outra interpretação pode ser feita de um ponto de vista matemático. Recorde que a superfície de $H(z)$ mostra a magnitude de $𝐻(𝑧)$ na escala de decibéis (ou seja, $20\log_{10}(\vert H(z) \vert)$) para um intervalo de valores de $z$ e $z$ é um número complexo. Na imagem anterior, para gerar a superfície $H(z)$, foram calculados pontos para vários valores de $z$, com a parte real variando no intervalo: $[-1.1, 1.1]$ e a parte imaginária variando no intervalo: $[-1.1j, 1.1j]$.

As interseções ocorrem quando a magnitude de $z$ é igual à 1, ou $|z|=1$. Alguns pontos de interseção são fáceis de serem identificados, por exemplo quando $z$ é igual à: $-1$, $1$, $j$ e $-j$, os quais possuem magnitude de 1.

Para encontrar todos os pontos de intersecção será necessário avaliar a expressão $20\log_{10}(|H(z|)$ para todos os casos de magnitude de $z$ igual à 1. Uma vez que $H(z)=1/z$, então $|H(z)|=1/|z|$, assim, a magnitude de $H(z)$ será igual à 1 quando $|z|=1$:

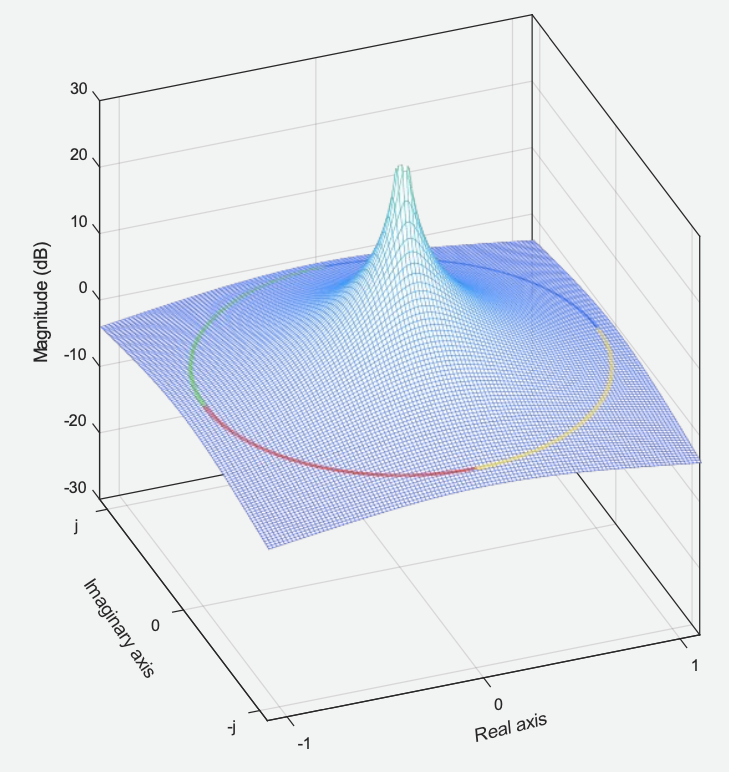
Ou do ponto de vista "superior":

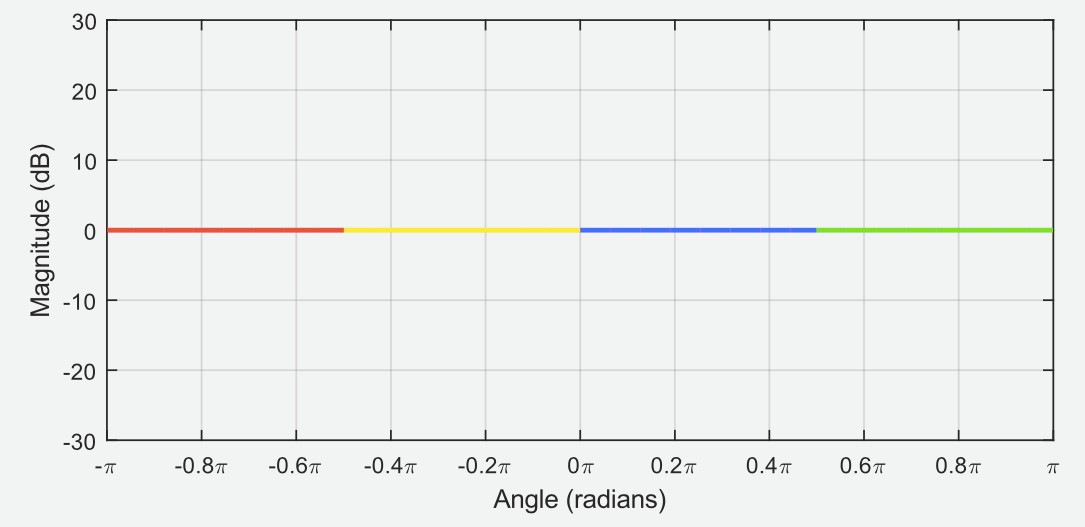
Uma situação muito semelhante surgiria se existisse um único zero na superfície $H(z)$. Desta vez você descobriria que a interseção da superfície $H(z)$ com o cilindro unitário seria tal que a amplitude dos pontos de interseção seria igual a 0 dB ($=|z|=1$).

Atenção:

👋 O que isso mostra é que: pólos ou zeros colocados na origem não afetarão a magnitude da resposta em frequência de um sistema.

Por que acrescentar pólos e zeros na origem do plano-z?

Isto levanta a questão:

− Por que então é que existem pólos e zeros na origem se eles não afectam o comportamento de “magnitude” do sistema?

A resposta é que, embora não afetem a resposta de magnitude, afetam os atrasos no sistema (que está associado ao diagrama de fase (ou defasagens) na resposta frequêncial de um sistema).

Em geral, você descobrirá que um sistema normalmente possui um número igual de pólos e zeros. Sistemas que não possuem um número igual de pólos e zeros terão atrasos “desnecessários” introduzidos no sistema.

Voltando ao sistema anterior (com pólo na origem do plano-z):

$H(z)=\dfrac{1}{z}$

Se multiplicarmos o numerador e denominador por $z^{-1}$, a função transferência fica:

$H(z)=\left(\dfrac{1}{z}\right) \cdot \left( \dfrac{z^{-1}}{z^{-1}}\right)= \dfrac{z^{-1}}{1} = \dfrac{1z^{-1}+0z^0}{1z^0}$

Adaptando esta expressão para o formato usualmente adotado para filtros, podemos determinar os componentes $b$ a $a$. Neste caso, $b_1=1$, $b_0=0$ e $a_0=1$. A equação de diferenças fica:

$H(z)=\dfrac{Y(z)}{X(z)}=\dfrac{z^{-1}}{1}$

$Y(z)=z^{-1}X(z)$

$y[n]=x[n-1]$

Na forma de um diagrama de fluxo de sinais teríamos algo como:

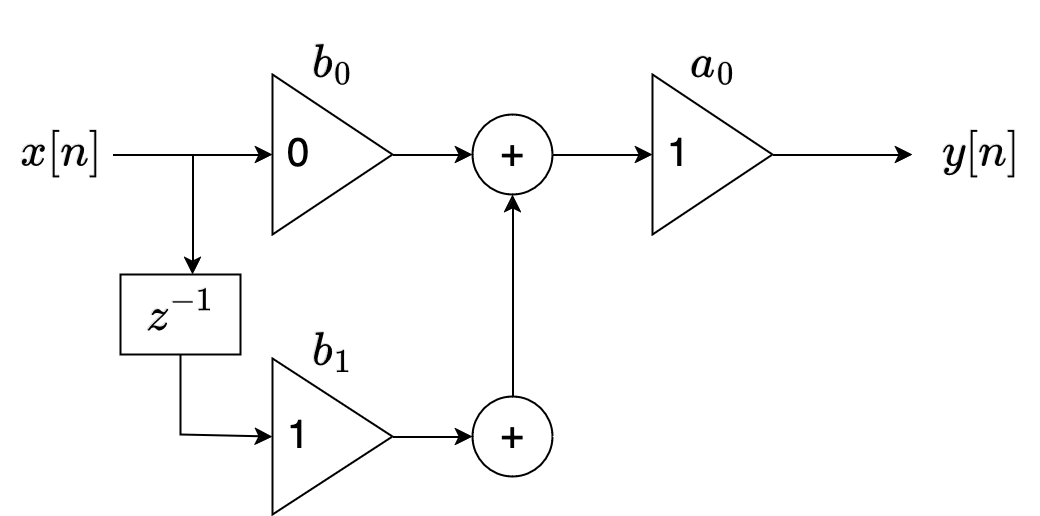
Que rende uma estrutura simplificada como:

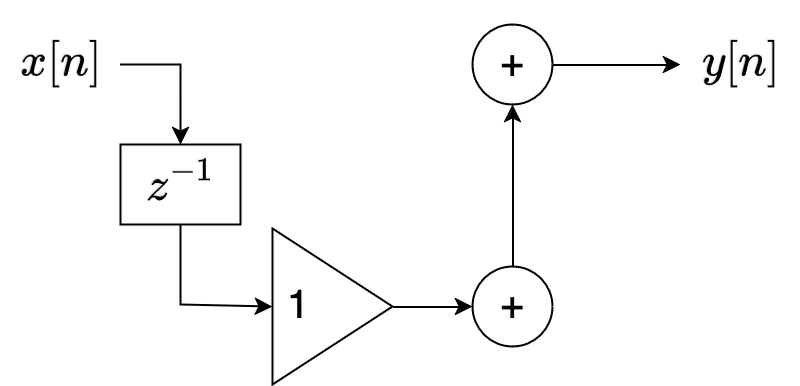
O que você deve perceber é que este sistema simplesmente atrasa a entrada em uma amostra e nada mais. Embora possa haver razões práticas para querer atrasar um sinal por uma amostra, em muitos casos, como na filtragem de sinais, o atraso pode não ser desejável e serve simplesmente para desacelerar um processo em uma amostra.

Na maioria dos casos, você descobrirá que os sistemas terão o mesmo número de pólos e zeros; caso contrário, atrasos desnecessários poderão ser introduzidos no sistema, como demonstrado no exemplo anterior.

Exemplo 2

Neste segundo exemplo, como no primeiro exemplo, há também um par de pólos e um par de zeros. No entanto, os pólos e zeros estão em locais diferentes. Observe que os pólos estão mais próximos do círculo unitário e em um ângulo diferente, quando comparados ao primeiro exemplo. Os zeros estão à mesma distância do círculo unitário, mas estão localizados em um ângulo de 45 graus ($\pi/4=0,25\pi$ radianos). Esta mudança na localização dos pólos e zeros resulta em contornos diferentes na superfície H(z) e, portanto, as interseções do ‘cilindro unitário’ com a superfície H(z) também serão diferentes.

A expressão para $H(z)$ neste caso é:

$H(z)=\dfrac{z^2-1,1314z+0,64}{z^2+0,95z+0,9025}$

Trabalhando esta expressão no Matlab/Ocatve, descobrimos que:

xxxxxxxxxx
>> T=1; % definindo uma taxa de amostragam arbitrária de 1 Hz
>> H=tf([1 -1.1314 0.64], [1 0.95 0.9025], T)
​
H =
 
  z^2 - 1.131 z + 0.64
  ---------------------
  z^2 + 0.95 z + 0.9025
 
Sample time: 1 seconds
Discrete-time transfer function.
​
>> pole(H)
ans =
       -0.475 +    0.82272i
       -0.475 -    0.82272i
>> zero(H)
ans =
       0.5657 +    0.56567i
       0.5657 -    0.56567i
>> pzmap(H)
>> axis equal
>> % isolando magnitude e fase de um dos zeros:
>> angle([0.5657 +    0.56567i])
ans =
      0.78537
>> ans*180/pi   % resposta em graus
ans =
       44.998
>> abs(0.5657 +    0.56567i)
ans =
          0.8
>> % calculando magnitude e fase de um dos pólos:
>> angle([-0.475 +    0.82272i])
ans =
       2.0944
>> ans*180/pi
ans =
          120
>> abs([-0.475 +    0.82272i])
ans =
         0.95
>> % observando os resultados no gráfico do plano-z...

Percebemos a seguinte disposição no plano-z:

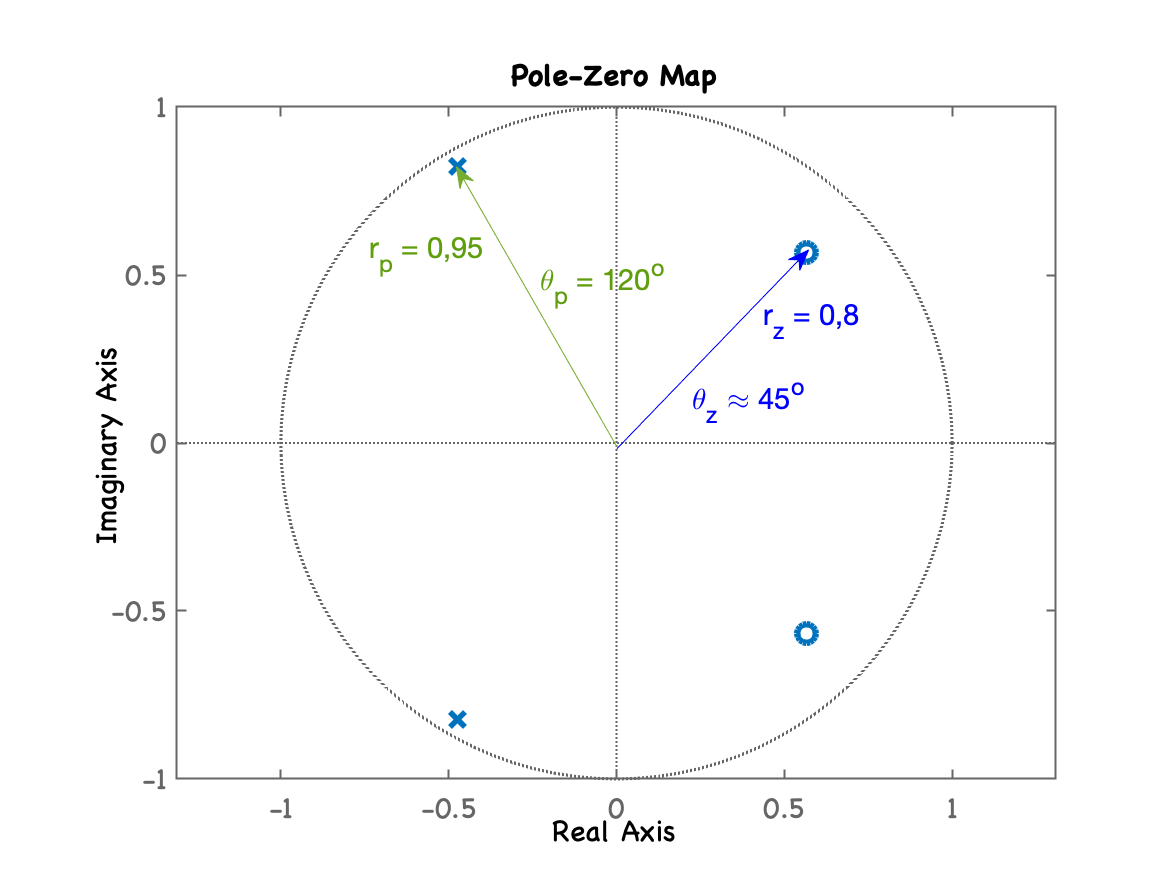
Um gráfico de superfície de $H(z)$ gera:

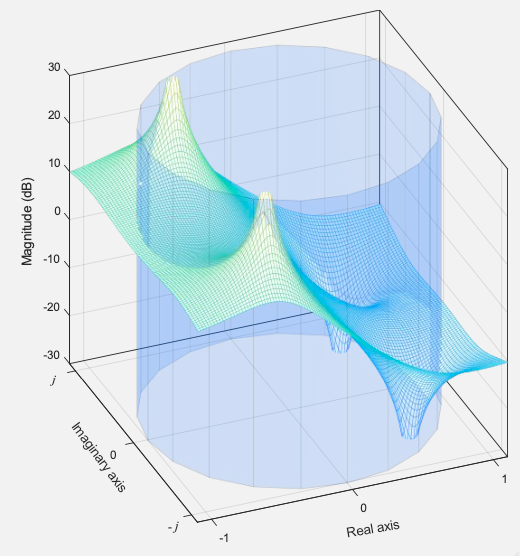
Destacando a intersecção com o círculo unitário temos:

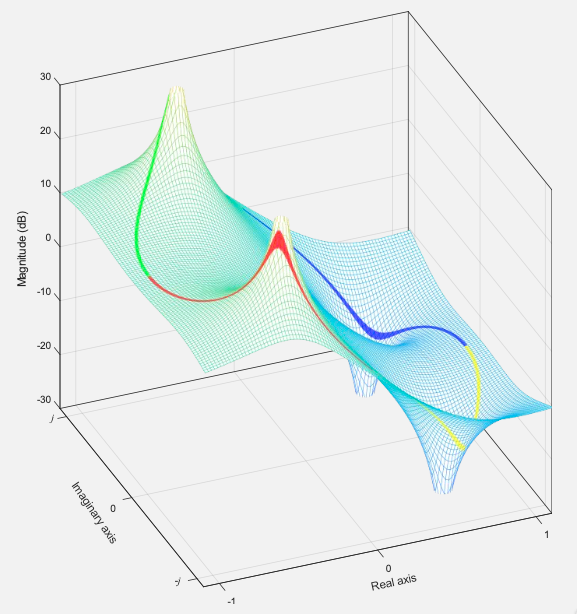
O gráfico à seguir mostra a amplitude dos pontos de intersecção em relação ao ângulo feito com o eixo real, na faixa de ângulos de $-180^o$ a $180^o$ para este segundo exemplo.

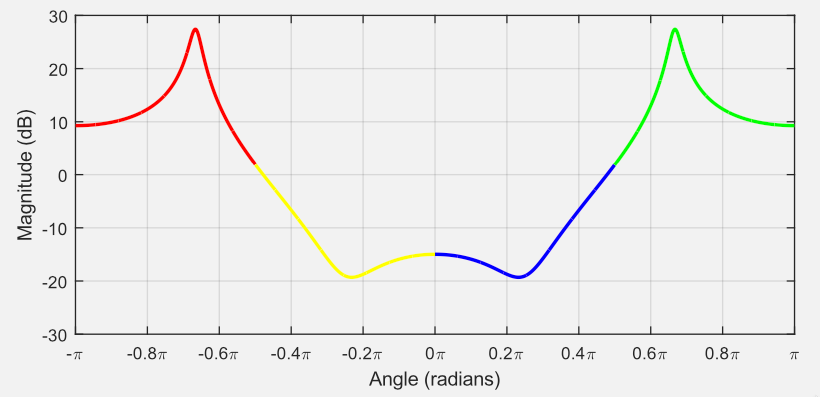
Você deve comparar isso com o primeiro exemplo e notar a amplificação significativa em $0,66\pi$ e $-0,66\pi$ radianos ($0,66\pi = 118,8^o$), causada pelos pólos estarem mais próximos do círculo unitário e posicionados na linha de ângulo radial 0,66π radianos e -0,66π radianos. Note, que a antenução (cones negativos) está concentrada próxima dos $45^o= \pi/4=0,25 \pi$ (onde estão localizados os zeros de $H(z)$).

Mais uma vez, os lados esquerdo e direito são versões espelhadas um do outro e vamos nos concentrar no lado direito de 0 a $\pi$ radianos (ou de 0 à $180^o$) (que corresponde à freq. de Nyquist, ou $f_s/2$):

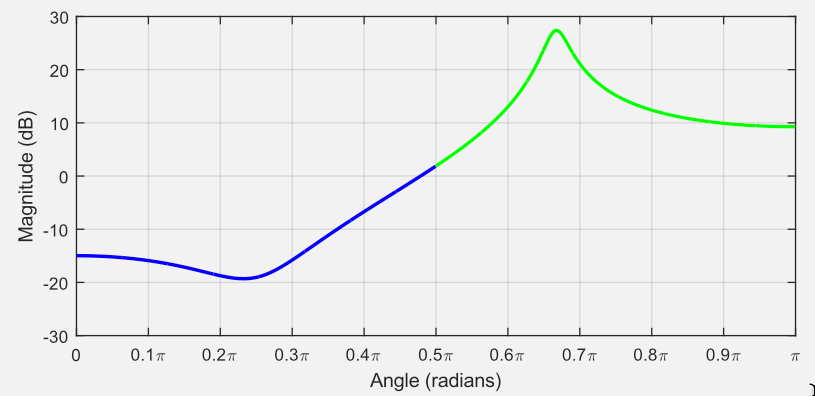
Gráfico similar pode ser obtido no Matlab fazendo-se:

xxxxxxxxxx
>> figure; handler=bodeplot(H);
>> setoptions(handler,'FreqUnits','Hz','PhaseVisible','off');
>> xlim([1/(2*10) 1/2])
>> setoptions(handler,'FreqScale','linear');
>> grid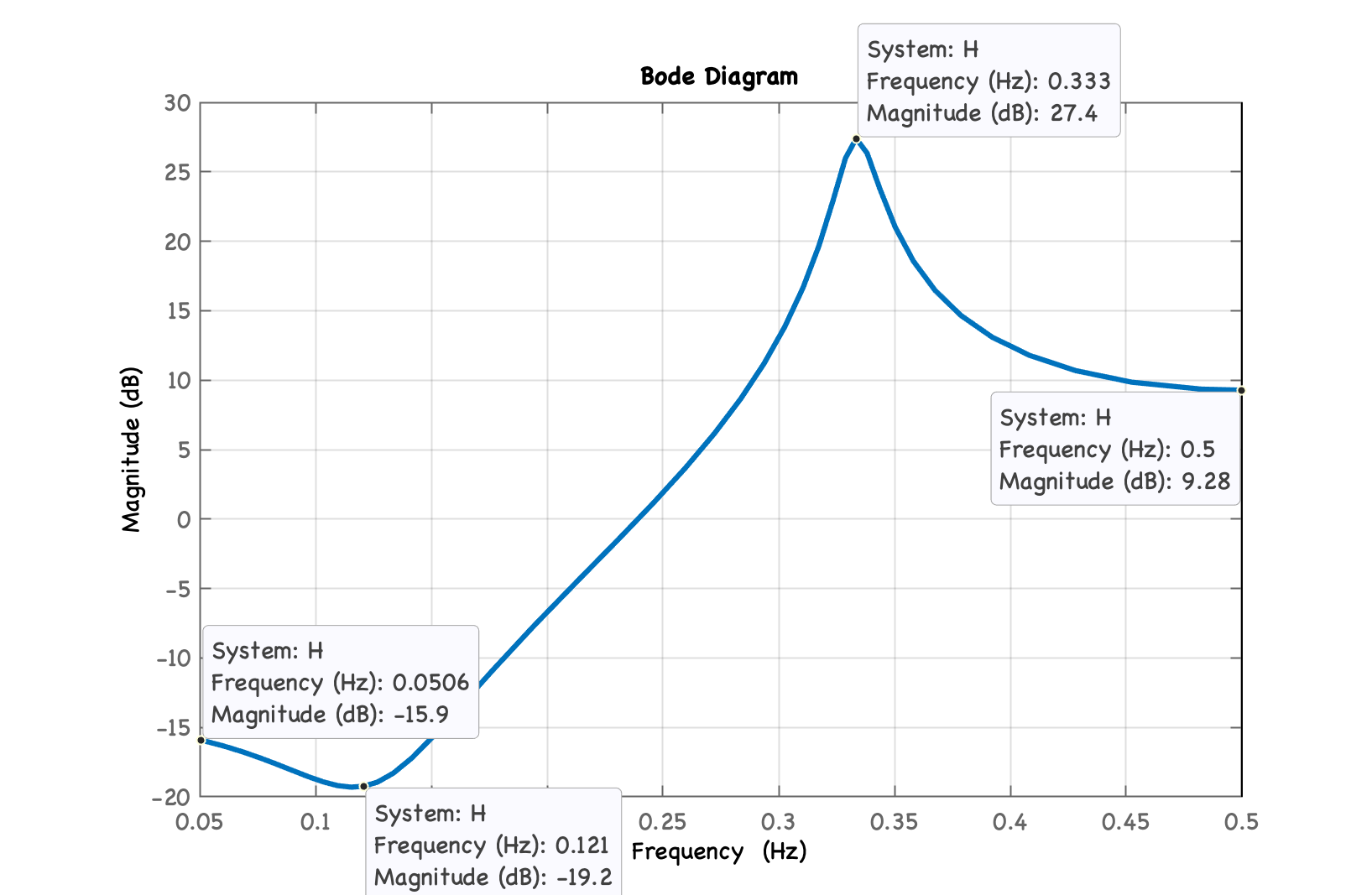

Opcional:

• O site do Matemática/Wolfrang traz um aplicativo Java capaz de gerar os gráficos acima para filtros de 1a-ordem:

  First-Order Digital Filter Design (acessado em 13/05/2024);

   

⏩ Próximo tópico sugerido: projeto de sistema usando alocação pólo-zero.

Theme: Fluent.