Flamingos no Parque Bicentenário, bairro de Vitacura, Santiago, Chile.

Projeto usando Alocação Pólo-Zero

• Projeto usando Alocação Pólo-Zero

  • Intro

    • Exemplo 1: Filtro Notch - Parte 1/2
    • Exemplo 2: Filtro Notch - Parte 2/2 (sem atrasos desnecessários)

  • Filtro Notch Melhorado

Intro

No tópico anterior (Papel dos pólos e zeros na magnitude da resposta em frequência), você deve ter percebido que:

• pólos próximos ao círculo unitário tenderão a amplificar o sinal em certas frequências, enquanto que;
• zeros próximos ao círculo unitário tenderão a atenuar certas frequências.

Depois de ter entendido como a posição dos pólos e zeros afeta a resposta de frequência (no tópico anterior), você pode então projetar um sistema para ter uma resposta de frequência específica alocando pólos e zeros em locais apropriados e derivando a função de transferência do sistema usando esses locais, como mostrado nos exemplos abaixo. Depois de ter a função de transferência, e os coeficientes $b$ e $a$ da equação de diferenças do sistema pode ser determinada e o filtro implementado na prática.

Exemplo 1: Filtro Notch - Parte 1/2

O exemplo a seguir descreve o processo para projetar um filtro Notch, que remove uma faixa muito pequena de componentes de frequência de um sinal, usando alocação de pólos e zeros.

Isto pode ser usado para remover o ruído de “zumbido da rede elétrica” (na faixa de 50 Hz para o caso dos dados usados para fins de simulação). Esta frequência á ser removida depende da frequência da fonte de alimentação elétrica local (no caso do Brasil, provavelmente seria na frequênica de 60 Hz)

Neste exemplo, vamos considerar uma situação em que um sinal de ECG (uma medida da atividade elétrica do coração), foi amostrado na frequência de 120 Hz, e foi corrompido com ruído de rede de 50 Hz. O sinal original bruto do ECG pode ser baixado em: noisy_ecg.txt.

Projetando o filtro

Sabe-se que no círculo unitário: $\pi$ (rad) $= 180^o$ corresponde à frequència de Nyquist. Então, neste caso: $\pi$ (rad) $=180^p=\omega_s/2=2\pi f_s/2$, ou:

$\begin{array}{rcl}0 \text{ (rad)} & \longleftrightarrow & 0 \text{ (Hz)}\\ \pi=180^o & \longleftrightarrow & f_s/2=120/2=60 \text{ (Hz)}\\ \Omega & \longleftrightarrow & 50 \text{ (Hz)} \end{array}$

Nesta frequência de amostragem, os 50 Hz equivalem à $50/60\pi$ radianos por amostra (isto é, $0,83333\pi$ (rad) $=150^o$):

$\Omega=\dfrac{50}{60}\pi \text{ (rad)} = 0,83333\pi \text{ (rad)}$, ou:

$\Omega=\dfrac{50\cdot 180^o}{60} = 150^o$.

ou generalizando:

$\Omega= \dfrac{f_c \vert_{\text{Hz}} \cdot 2 \pi}{f_s \vert_{\text{Hz}}}$ ou $\Omega= \dfrac{f_c \vert_{\text{Hz}} \cdot 2 \cdot 180^o}{f_s \vert_{\text{Hz}}}$

Para reduzir o ruído em 50 Hz do sinal de ECG, podemos então posicionar um par de zeros na localização:

$\mathcal{Re}\{ \text{zero} \}=1 \cdot \cos(150^o)$

$\mathcal{Im\{ \text{zero} \}}=1 \cdot \sin(150^o)$

No Matlab:

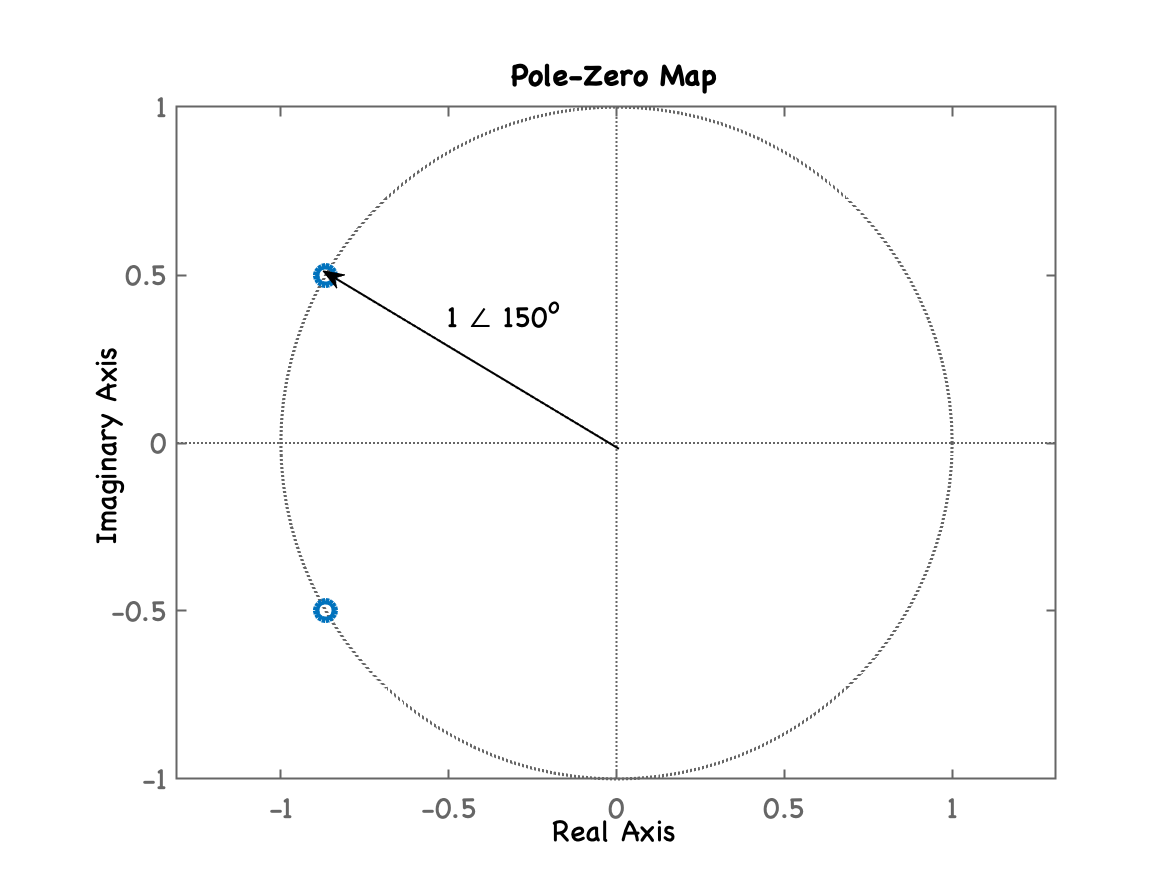
​x
>> Re=1*cos(150*pi/180)     % não esquecer de passar graus para radianos
Re =
     -0.86603
>> Im=1*sin(150*pi/180)
Im =
          0.5
>>
>> % ou poderíamos ter usado a função deg2rad:
>> help deg2rad
  deg2rad Convert angles from degrees to radians.
    deg2rad(X) converts angle units from degrees to radians for each
    element of X.
 
    See also rad2deg.
​
>> Re=1*cos(deg2rad(150))
Re =
     -0.86603
>> Im=1*sin(deg2rad(150))
Im =
          0.5
>> 
>> % Poderíamos ainda ter usado a função: pol2cart:
>> help pol2cart
 pol2cart Transform polar to Cartesian coordinates.
    [X,Y] = pol2cart(TH,R) transforms corresponding elements of data
    stored in polar coordinates (angle TH, radius R) to Cartesian
    coordinates X,Y.  The arrays TH and R must the same size (or
    either can be scalar).  TH must be in radians.
​
>> [Re, Im]=pol2cart(deg2rad(150), 1)
Re =
     -0.86603
Im =
          0.5

ou seja:

$1 \, \angle \pm 150^o= 1 \; \angle \pm 0,8333\pi = -0.86603 \pm j0,5$.

Num diagrama pólo-zero (ou ROC) fica:

Montando a função transferência do filtro e testando:

xxxxxxxxxx
>> ze = [Re+i*Im   Re-i*Im]     % cria vetor/polinômio contendo os 2 zeros conjungados
ze =
     -0.86603 +        0.5i     -0.86603 -        0.5i
>> size(ze)     % conferindo dimensões deste vetor
ans =
     1     2
>> % Montando H(z):
>> H=tf(poly(ze), 1, 1/120)
​
H =
 
  z^2 + 1.732 z + 1
 
Sample time: 0.0083333 seconds
Discrete-time transfer function.

Note que a eq. de diferenças associada com esta função transferência rende:

$H(z)=(z+0,86603+j0,5)(z+0,86603-j0,5) = z^2 + 1.732 z + 1$

Note porém que esta função transferência não possui denominador, e que o grau no numerador é superior ao grau do denominador (zero), o que leva a um sistema com atrasos na resposta ou um sistema antecipativo 👀 -- observe o desenvolvimento à seguir:

A eq. de diferenças desta $H(z)$ é:

$H(z)=\dfrac{Y(z)}{X(z)}=\left( z^2 + 1,732 z + 1 \right) \cdot \dfrac{z^{-2}}{z^{-2}}$

$\dfrac{Y(z)}{X(z)}=\dfrac{1+1,732z^{-1}+1z^{-2}}{z^{-2}}$

$z^{-2}Y(z)=\left( 1+1,732z^{-1}+1z^{-2} \right)X(z)$

$y[n-2]=x[n]+1,732x[n-1]+x[n-2]$ (eq. (1))

Note que não existem os termos $y[n]$ ou $y[n-1]$.

Apenas temos $y[n-2]$, isto significa que este filtro só passará a emitir um sinal de saída depois da 2a-amostragem realizada sobre o sinal de entrada (ver simulação mais aditante).

Lembrando que a função filter() tabalha com eq. do tipo:

$y[n]=\displaystyle\sum_{i=0}^{b_n} b_i \cdot x[n-i] - \displaystyle\sum_{j=1}^{n_a} a_j \cdot y[n-j]$

Então:

$b_0=1$, $b_1=1,732$, $b_2=1$, $a_0=0$, $a_1=0$ e $a_2=1$.

⚠️ O detalhe é que a funçao filter() não aceita $a_0=0$, então a forma de compensar isto, é "atrasando" o sistema em 2 períodos de amostragem (ou 2 amostras):

$z^{-2}Y(z) \cdot z^{2}=\left( 1+1,732z^{-1}+1z^{-2} \right)X(z) \cdot z^{2}$

$Y(z)=(z^2+1,732z^1+1)X(z)$

Ou:

$y[n]=x[n+2]+1,732x[n+1]+x[n]$

O problema é que $x[n+2]$ representa uma amostra do sinal $x(t)^*$ adiantado no tempo em 2 amostras e $x[n+1]$ uma amostra do sinal $x(t)^*$ adiantado no tempo em 2 amostras. Valores impossíveis de serem computados. Este sistema desta forma seria o que chamamos de um "sistema antecipativo" 👀.

Mas podemos voltar a eq. (1) para tentar computar/simular os termos de $y[n]$ usando um Diagrama de Fluxo de sinal e o Simulink (filtro_ECG0.slx):

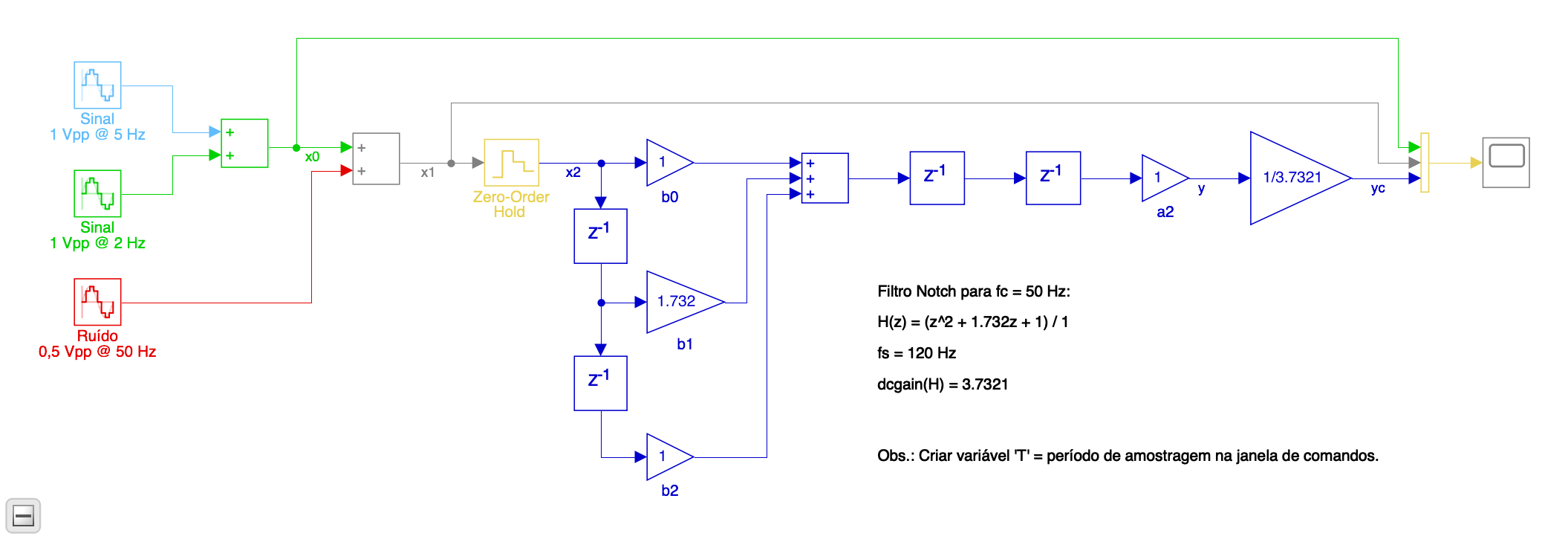
Note que o último bloco de ganho trabalha com um ganho com valor $1/3.7321$ para compensar o "ganho DC" de $H(z)$:

xxxxxxxxxx
>> dcgain(H)
ans =
       3.7321

A simulação rende:

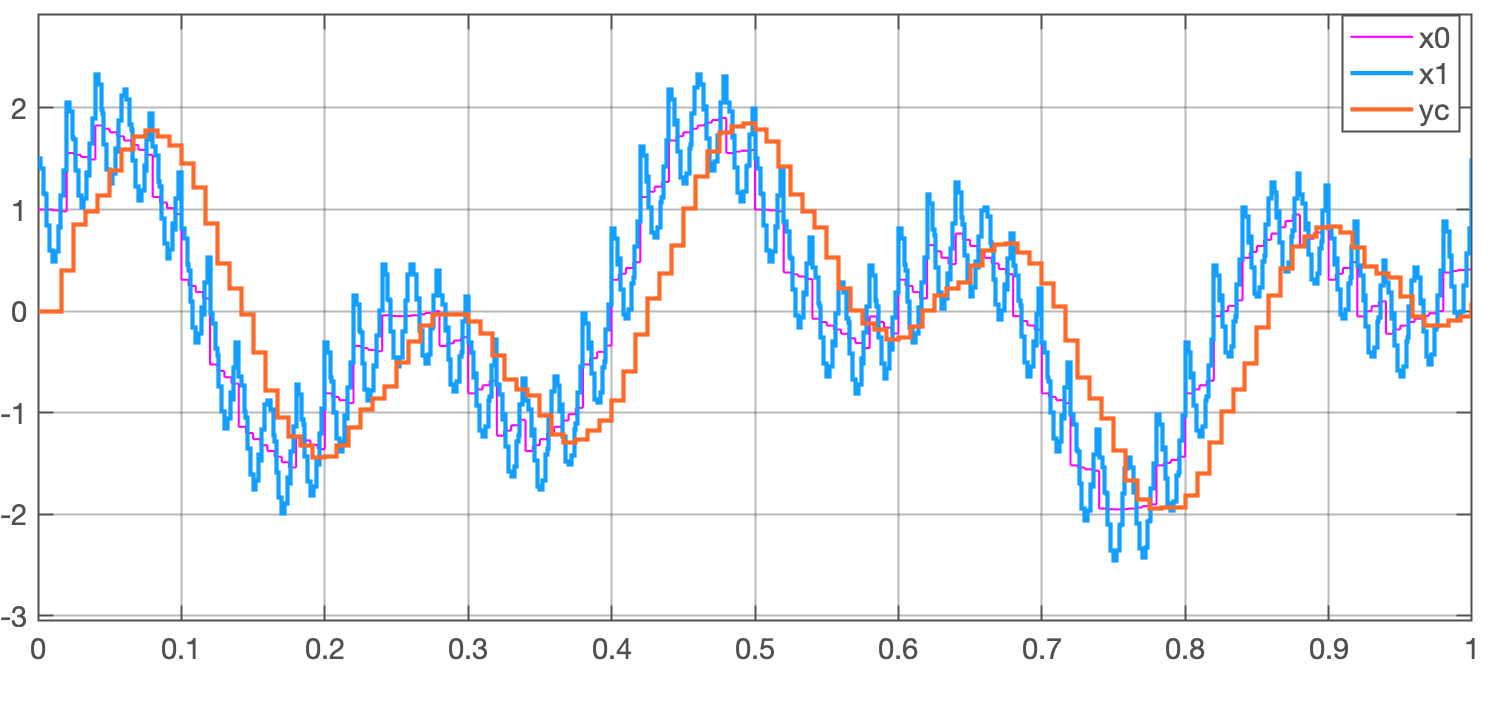
Note na figura anterior, que $x0=$ sinal composto pela soma das 2 senóides (uma oscilando à 2 Hz e outra oscilando à 5 Hz) e que $x1=$ sinal entregue ao filtro, "contaminado" pelo ruído de 50 Hz.

Perceba que a saída do filtro $yc$, corresponde ao sinal amostrado $x0$, mas atrasado de 2 períodos de amostragem (neste caso: 0,0167 segundos).

Exemplo 2: Filtro Notch - Parte 2/2 (sem atrasos desnecessários)

Ocorre que, se não quisermos atrasos desnecessários num sistema (caso do exemplo 1 anterior), devemos acrescentar um par de pólos na origem, para garantir que não sejam introduzidos atrasos desnecessários no sistema.

Note que esses pólos não afetarão a resposta de frequência do sistema (consulte o tópico anterior: Papel dos pólos e zeros na magnitude da resposta em frequência.

Por acaso, o gráfico de superfície de $H(z)$ associado a este sistema é mostrado à seguir:

xxxxxxxxxx
>> fs=120;  % freq de amostragem em Hz
>> T=1/fs   % taxa de amostragem em segundos
T =
    0.0083333
>> ang=50/60
ang =
      0.83333
>> x=1*cos(ang*pi)
x =
     -0.86603
>> y=1*sin(ang*pi)
y =
          0.5
>> (ang*pi)*180/pi  % valor em graus
ans =
          150
>> ze=[x+i*y x-i*y] % zeros de H(z)
ze =
     -0.86603 +        0.5i     -0.86603 -        0.5i
>> % Note: antes:
>> % H=tf(poly(ze),1,T)
>> % Agora:
>> % Acrescentando os 2 pólos na origem e considerando fs=120 Hz:
>> H=tf(poly(ze),[1 0 0],T)
​
H =
 
  z^2 + 1.732 z + 1
  -----------------
         z^2
 
Sample time: 0.0083333 seconds
Discrete-time transfer function.
​
>> pzmap(H)

O diagrama pólo-zero (ou ROC) deste $H(z)$ fica:

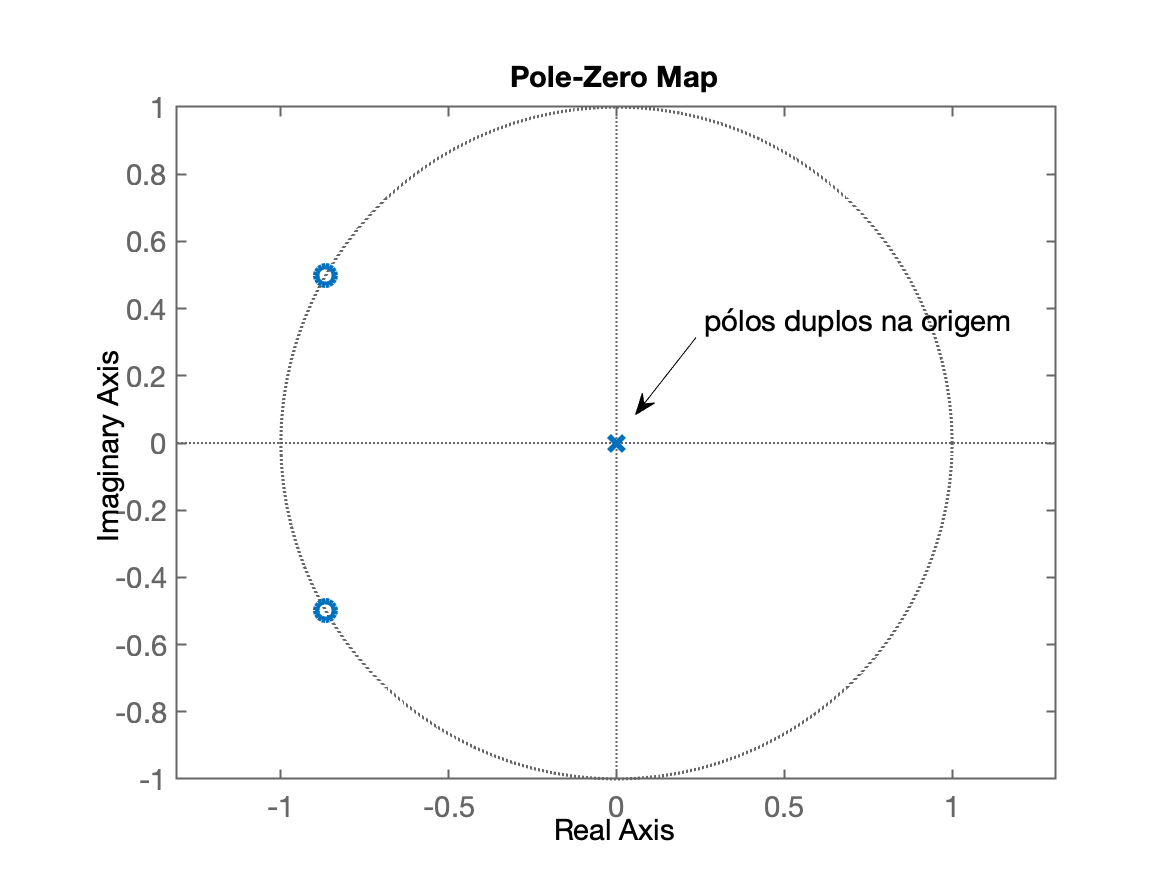
O gráfico de superfíce deste $H(z)$ rende:

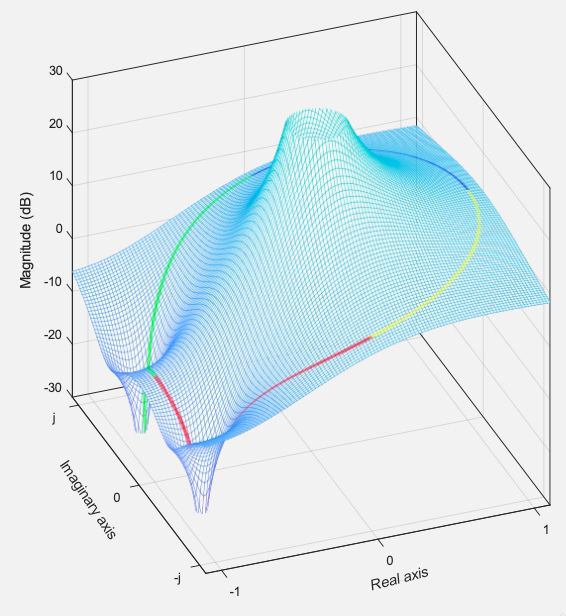
Observe como o efeito dos dois pólos se acumula na origem. Eles não afetam a superfície $H(z)$ nos pontos correspondentes ao círculo unitário, ou seja, se os pólos foram removidos, a amplitude da superfície $H(z)$ nos pontos correspondentes ao círculo unitário ficaria inalterado.

A amplitude da superfície $H(z)$ nos pontos correspondentes ao círculo unitário é mostrada abaixo e plotada em relação ao ângulo feito com o eixo real:

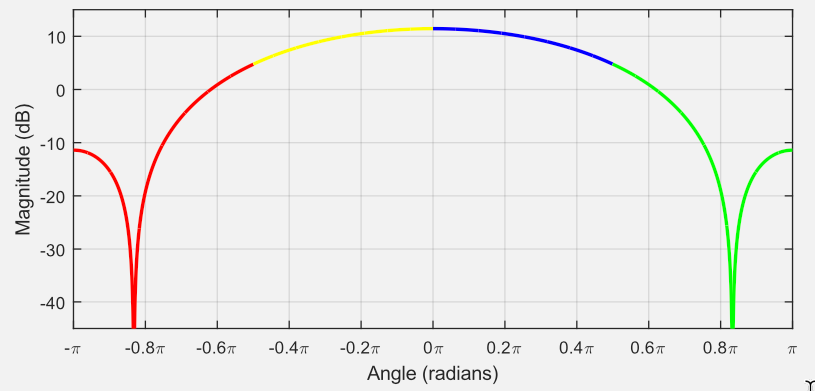
O gráfico à seguir é igual ao gráfico acima, exceto que apenas os pontos de amplitude da superfície $H(z)$ de 0 a $\pi$ radianos são mostrados, uma vez que esses pontos refletem os pontos entre $-\pi$ e 0 radianos.

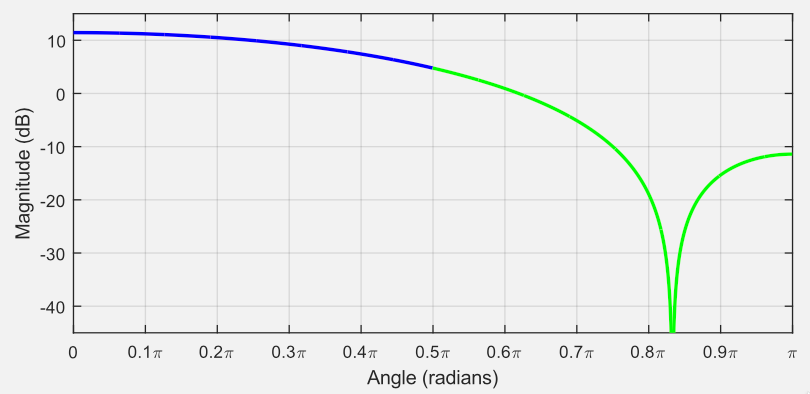
Neste tipo de gráfico (como antes), a resposta de frequência associada a este sistema pode ser obtida substituindo as unidades do gráfico acima por unidades de frequência de radianos por amostra.

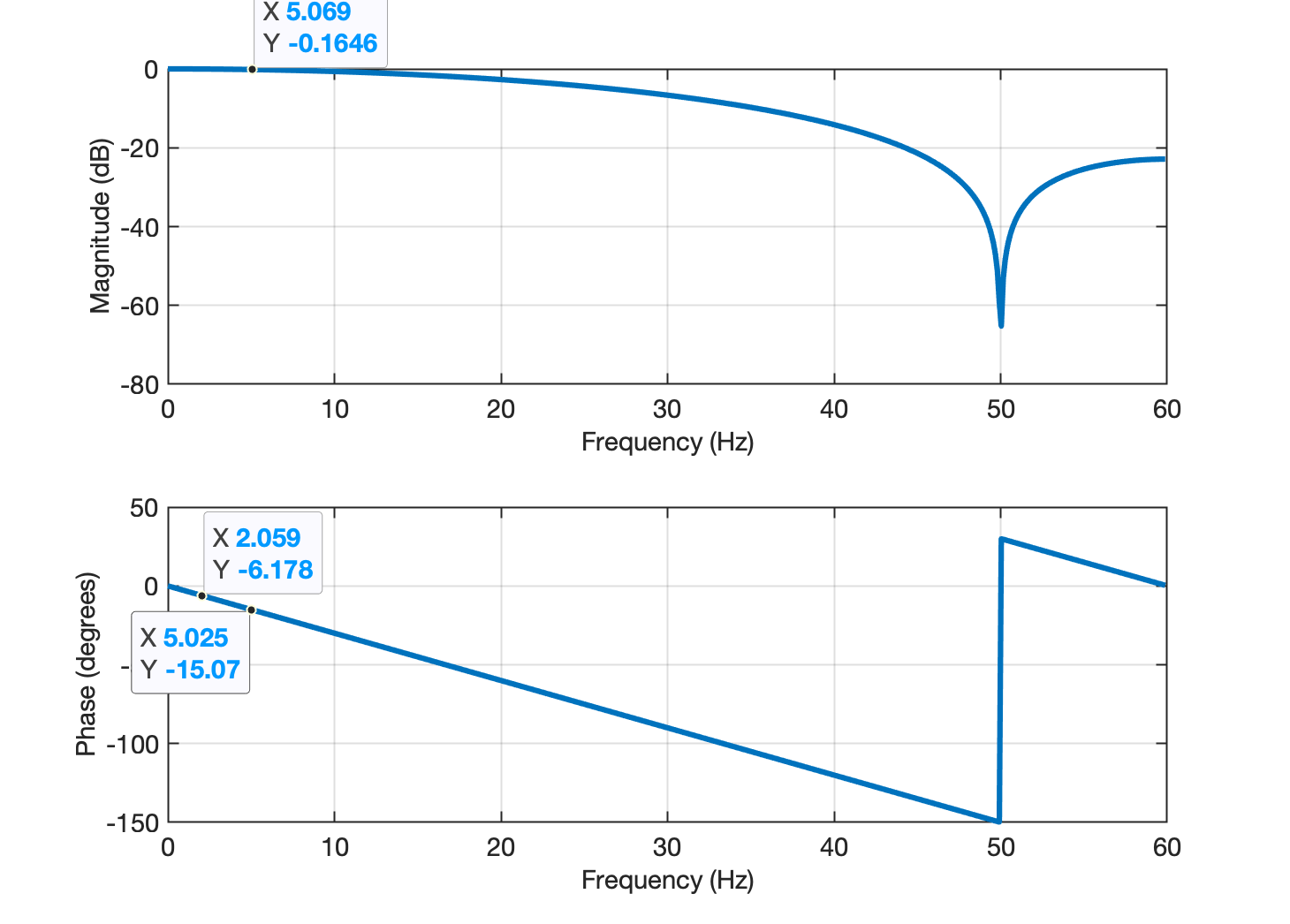
O diagrama equivalente de Bode equivalente, usando Matlab, resultaria:

xxxxxxxxxx
>> figure; handler=bodeplot(H);
>> setoptions(handler,'FreqUnits','Hz','FreqScale','linear');)
>> xlim([fs/(2*10) fs/2])
>> grid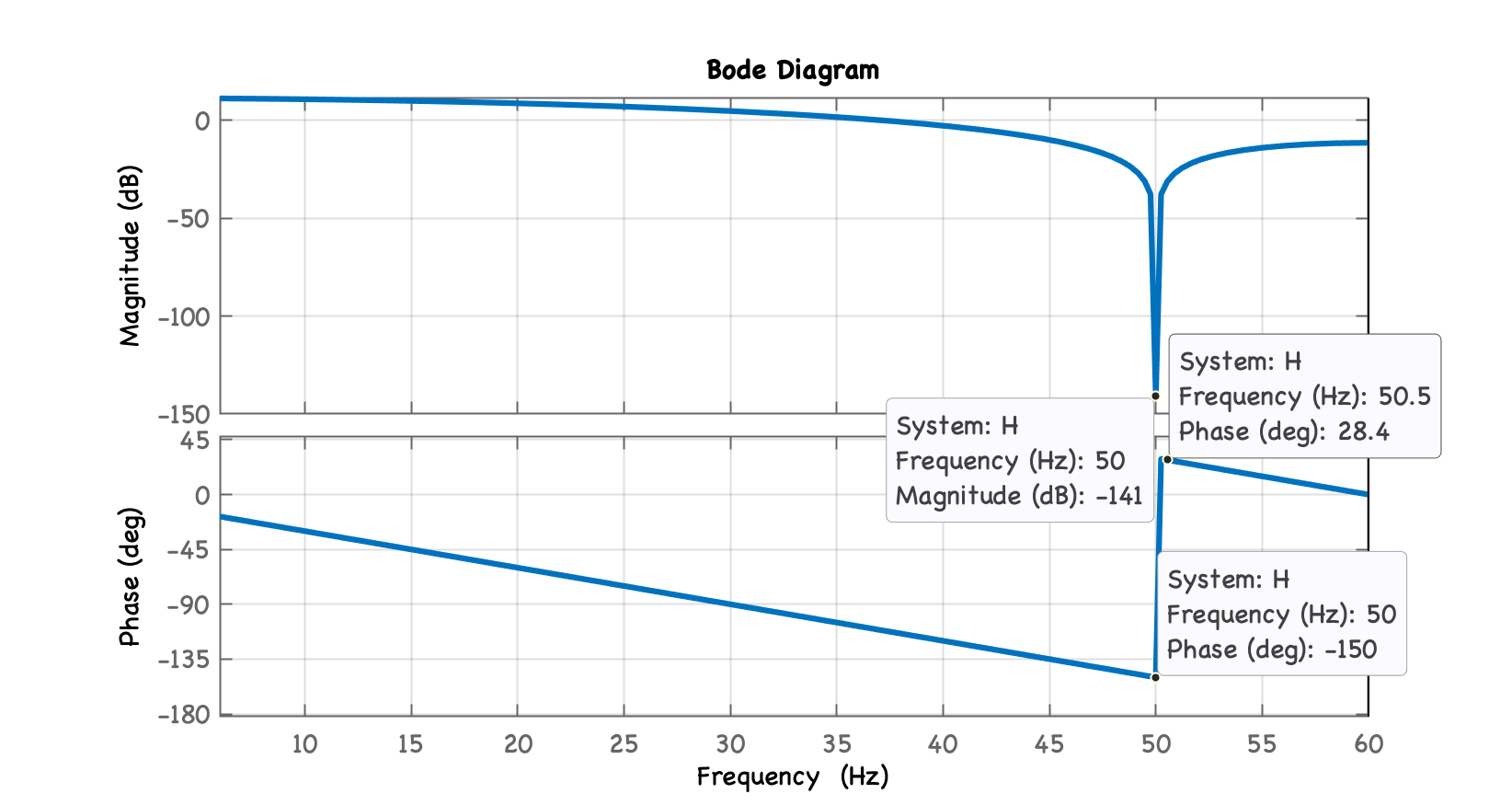

Pode-se ver que um sistema associado ao diagrama pólo-zero acima atenuaria significativamente o ruído de 50 Hz (lembre-se que 50 Hz equivale a $0,833\pi$ radianos por amostra) (Note: $-141$ dB $= 8,9125 \times 10^{-8}=0,000000089125$). No entanto, você deve apreciar que uma ampla faixa de frequências fora de 50 Hz também seria alterado, ver distorção em fase causado por esta $H(z)$, o que não é o ideal, uma vez que a forma do sinal de ECG pode ser significativamente alterada (atrasos introduzidos em harmônicas elevadas), talvez dificultando a interpretação do profissional de saúde. Uma melhoria neste projeto será fornecida posteriormente, mas por enquanto vamos determinar os coeficientes $b$ e $a$ associados ao sistema, para que possamos implementar o filtro.

A função transferência associada com este filtro fica:

$H(z)=\dfrac{(z +0.86603 + j0.5)(z +0.86603 - j0.5)}{z^2}=\dfrac{z^2 + 1.732 z + 1}{z^2}$

Multiplicando numerador e denominador por $z^{-1}$, obtemos:

$H(z)=\dfrac{1 + 1.732 z^{-1} + z^{-2}}{1}$

Sendo assim:

$H(z)=\dfrac{Y(z)}{X(z)}=\dfrac{1 + 1.732 z^{-1} + z^{-2}}{1}$

Resulta na seguinte equação de diferenças:

$y[n]=x[n]+1,732x[n-1]+x[n-2]$

e assim teremos: $a_0=1$, $b_0=1$, $b_2=1,732$ e $b_2=1$.

Obs: Note que os coeficientes de $a$ correspondem ao denominador da transfer function $H(z)$ e que os coeficientes de $b$ correspondem ao numerador da transfer function $H(z)$, mas considerando a notação de $H(z)$ expressa como expoentes negativos em $z$ ($z^{-n}$) 👀

Simulando este filtro usando o diagrama de fluxo de sinais atualizado para esta $H(z)$ -- arquivo: filtro_ECG1.slx:

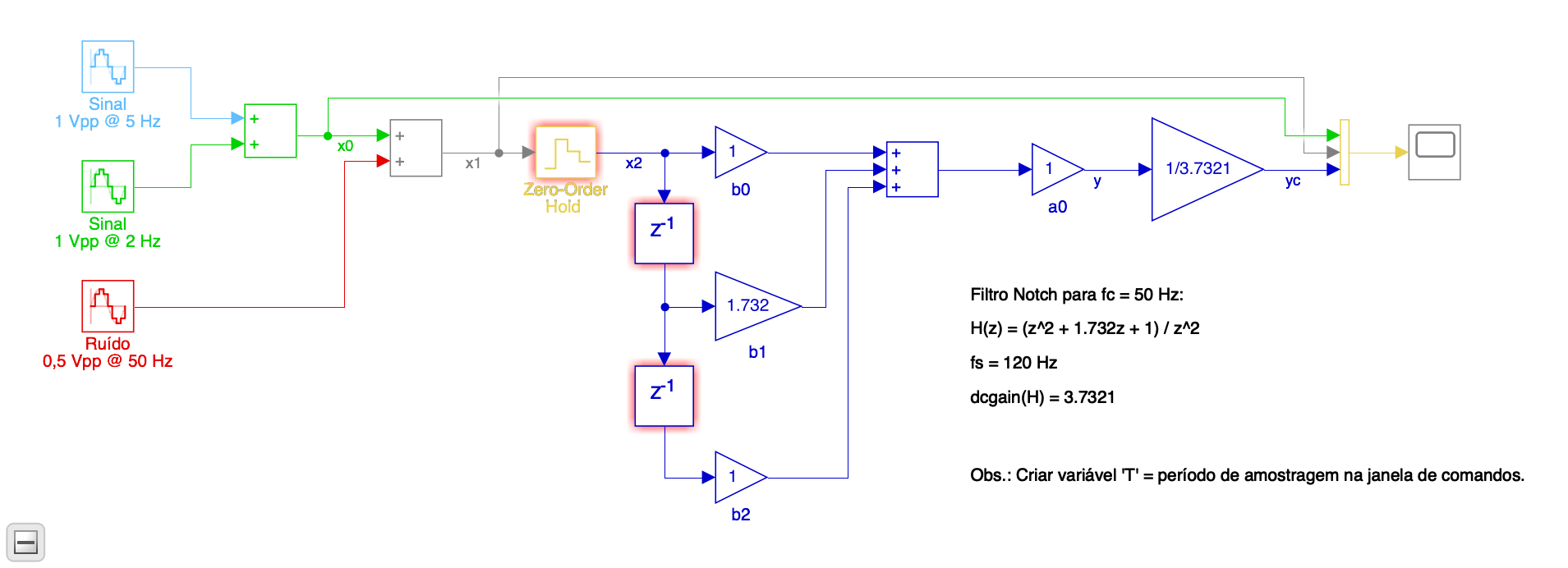
E neste caso, a simulação rende:

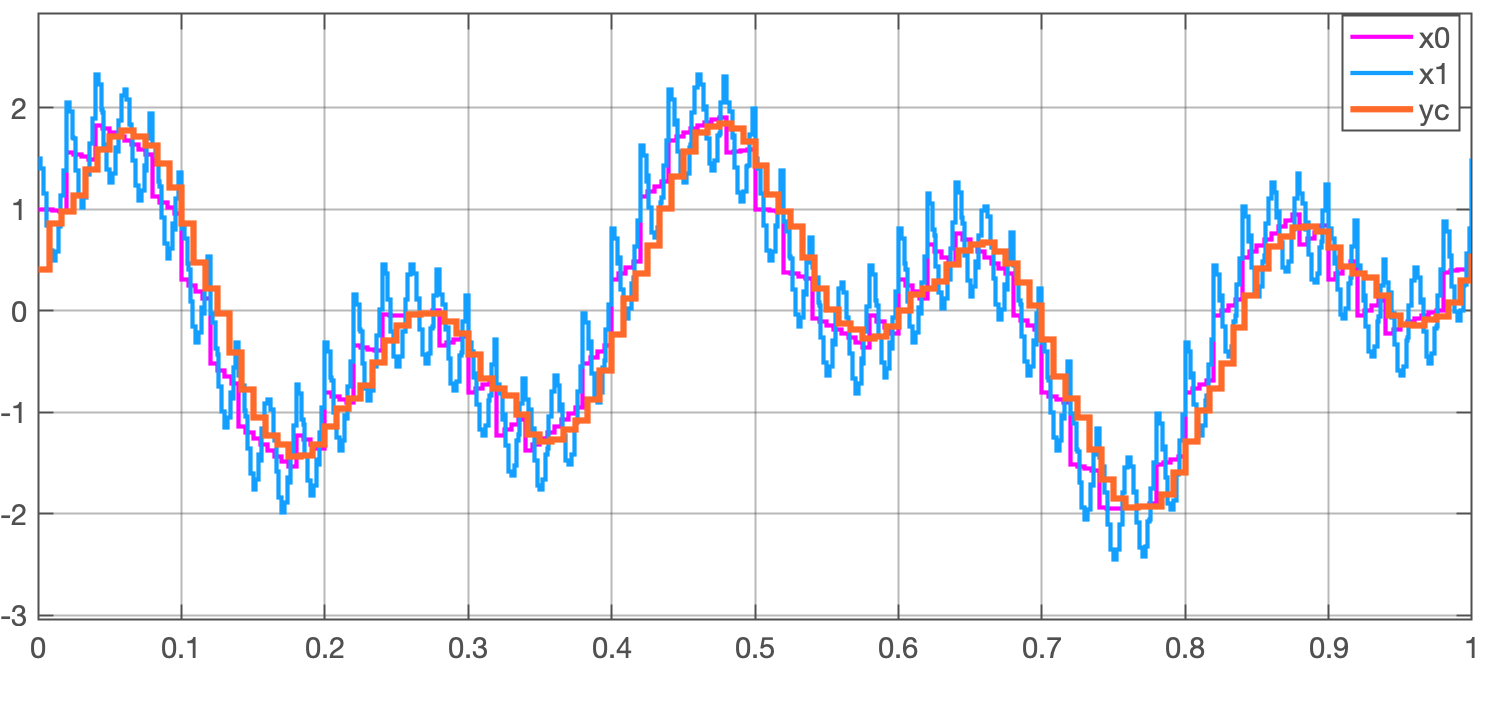
O atraso de 2 períodos de amostragem sobre o sinal de entrada foi eliminado, entretanto, perceba um ligeiro atraso no sinal de saída que aumenta conforme aumenta a frequência do sinal de entrada.

Calculando as distorções (atrasos) incorporados nos sinais de entrada:

Frequência (Hz)	Fase ($^o$)	Atraso (ms)
2	$-6,178^o$	8,5806 ms
5	$-15,07^o$	8,3722 ms

Lembrando que $2\pi = 360^o$ corresponde a um período do sinal de entrada:

$\begin{array}{rcl} 360^o & \longleftrightarrow & 1/2 \text{ (componente de 2 Hz)}\\ 6,179^o & \longleftrightarrow & \Delta t \end{array}$ $\Delta t = 0.0085806$

$\begin{array}{rcl} 360^o & \longleftrightarrow & 1/5 \text{ (componente de 5 Hz)}\\ 15,07^o & \longleftrightarrow & \Delta t \end{array}$ $\Delta t = 0.0083722$

E lembrando que $T=8,3333$ ms, percebemos que estes atrasos, apesar de parecerem pequenos, equivalem aproximadamente à um período de amostragem.

Podemos usar o Matlab/Octave para comprovar o funcionamento deste filtro sobre o sinal de ECG ( noisy_ecg.txt ):

xxxxxxxxxx
>> [num,den]=tfdata(H,'v')
num =
            1       1.7321            1
den =
     1     0     0
>> a=den;
>> b=num;
>> dir *.txt    % verificando presença do arquivo
noisy_ecg.txt           
​
>> x=load('noisy_ecg.txt');
>> y=filter(b,a,x);
>> subplot(2,1,1);
>> plot(x);title('Sinal de ECG com ruído'); xlim([0 1000])
>> xlabel('Amostras'); ylabel('Atividade Elétrica');
>> subplot(2,1,2)
>> plot(y); title('Sinal ECG filtrado'); xlim([0 1000])
>> xlabel('Amostras'); ylabel('Atividade Elétrica');

E então temos o resultado:

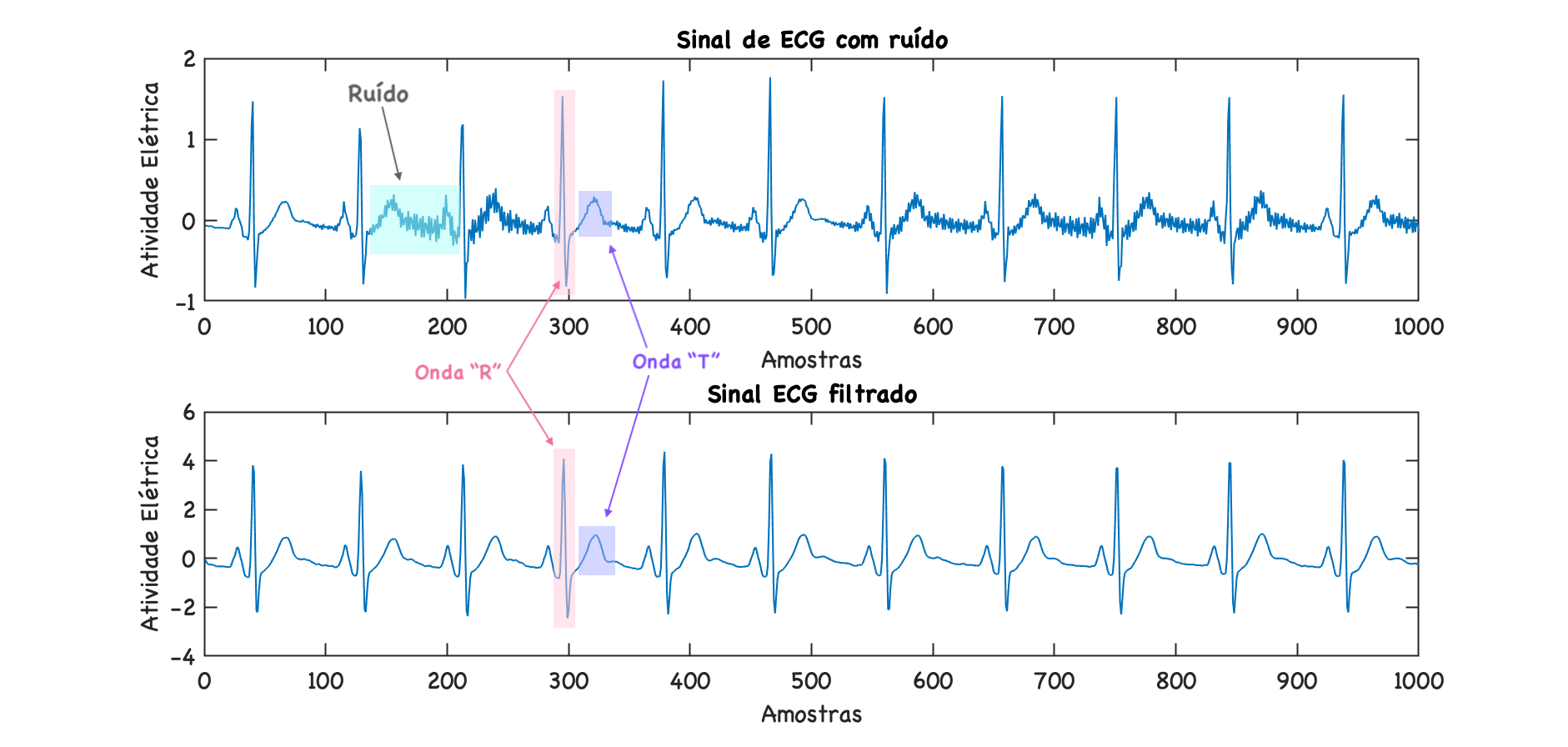
Você pode ver nos gráficos no domínio do tempo do ECG e nos sinais de ECG filtrados acima que o “ruído” foi reduzido. Mas..., a amplitude do sinal também foi alterada. A relação entre a amplitude do pico dominante da "onda R" e da "onda T" vizinha também foi ligeiramente alterada.

Filtro Notch Melhorado

Um filtro notch melhorado pode ser obtido posicionando um par de pólos “muito próximo” dos zeros. Adicionar os pólos desta forma tem o efeito de “compensar” a contribuição de zero para a forma da superfície H(z) para a maior parte do plano z, exceto nas regiões muito próximas dos zeros.

Isso pode ser melhor compreendido considerando o que aconteceria se um pólo fosse posicionado exatamente no local do zero; você deve perceber que o pólo cancelaria completamente a contribuição do zero e a superfície $H(z)$ seria plana para todo o plano z.

Quando os pólos e os zeros são colocados próximos uns dos outros, eles tendem a se anular na maioria das regiões do plano z, exceto nas regiões que estão muito próximas do pólo ou do zero.

A título de exemplo, vamos posicionar pólos no mesmo ângulo dos zeros, mas distantes 0,9 da origem, como ilustrado adiante. Estes pólos seriam localizados em: $z=0,9\;\angle\,\pm150^o = -0,77942 \pm j0,45$; ver cálculos à seguir:

xxxxxxxxxx
>> % Os zeros estão em:
>> [Re Im]=pol2cart(deg2rad(150), 1)
Re =
     -0.86603
Im =
          0.5
>> ze = [Re+i*Im   Re-i*Im]
ze =
     -0.86603 +        0.5i     -0.86603 -        0.5i
>> % Localizando os pólos em raio = 0,9 teremos:
>> [Re_p Im_p]=pol2cart(deg2rad(150), 0.9)
Re_p =
     -0.77942
Im_p =
         0.45
>> po = [Re_p+i*Im_p   Re_p-i*Im_p]
po =
     -0.77942 +       0.45i     -0.77942 -       0.45i
>> % Montando a nova função transferência:
>> fs=120;
>> H2=tf(poly(ze), poly(po), 1/fs)
​
H2 =
 
   z^2 + 1.732 z + 1
  --------------------
  z^2 + 1.559 z + 0.81
 
Sample time: 0.0083333 seconds
Discrete-time transfer function.

Ou seja, terminamos por obter a seguinte função transferência:

$H(z)=\dfrac{(z+0,86603+j0.5)(z+0,86603+j0.5)}{(z+0.77942+j0.45)(z+0.77942-j0.45)}=\dfrac{z^2 + 1.732 z + 1}{z^2 + 1.559 z + 0.81}$

Verificando como ficou o ROC e resposta espectral:

xxxxxxxxxx
>> % Diagrama ROC
>> figure;
>> pzmap(H2)
>> th=0:2*pi/360:2*pi;
>> x=0.9*sin(th);
>> y=0.9*cos(th);
>> axis equal
>> hold on;
>> plot(x,y,'LineStyle','--', 'color',[0.7 0.7 0.7])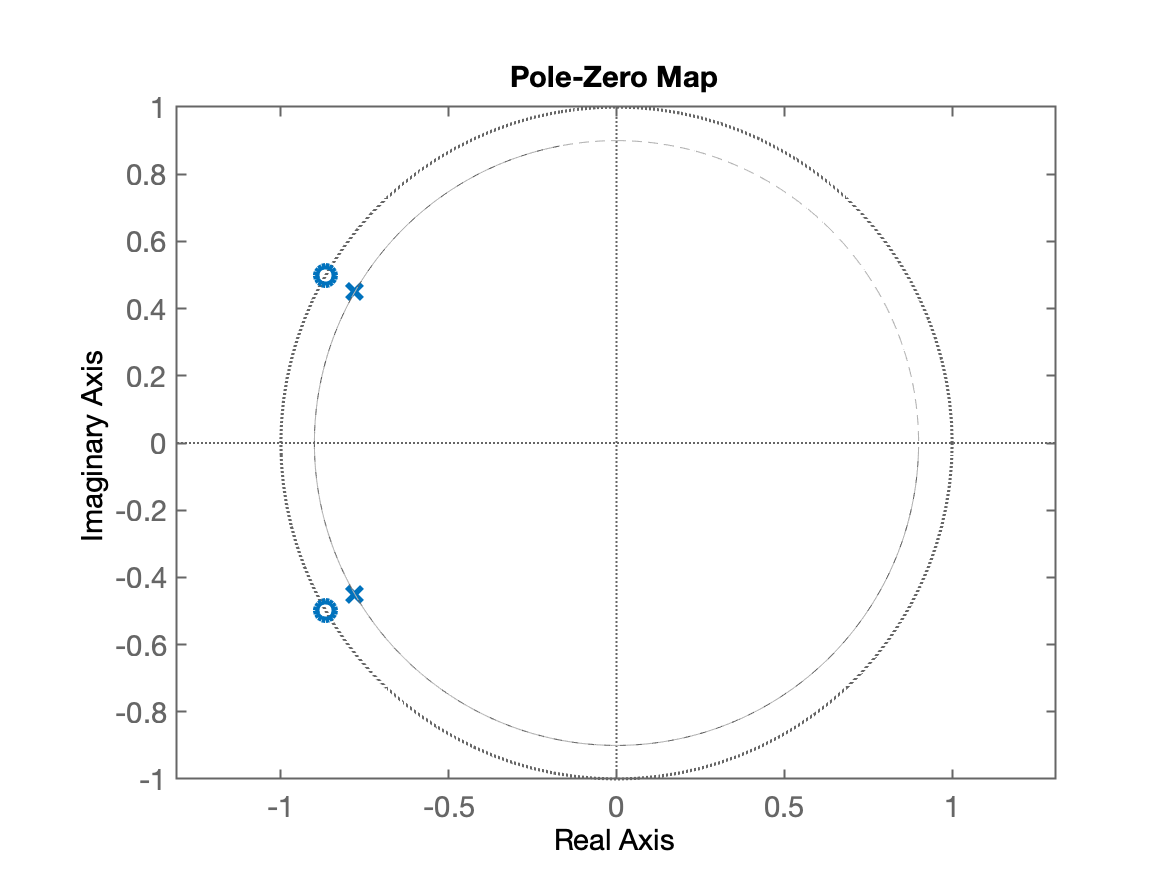

xxxxxxxxxx
>> figure;
>> h=bodeplot(H, H2);
>> setoptions(h,'FreqUnits','Hz','FreqScale','linear')
>> xlim([30 fs/2])
>> grid
>> legend('H(z)', 'H2(z)')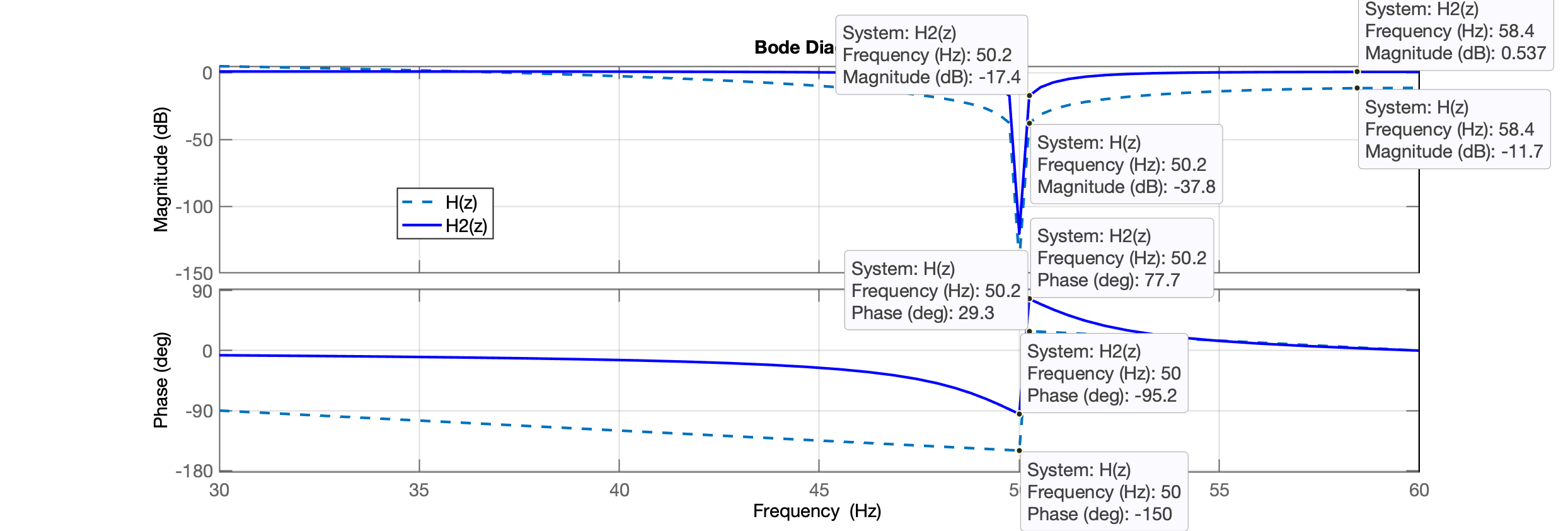

Pode-se perceber as diferenças, principalmente no diagrama de Fase. Desta vez, maiores defasagens no sinal serão acrescentadas nas frequências próximas da frequência de corte deste filtro (50 Hz).

Aplicando-se sobre o sinal de ECG resulta:

xxxxxxxxxx
>> [num2, den2]=tfdata(H2,'v')
num2 =
            1       1.7321            1
den2 =
            1       1.5588         0.81
>> a2=den2;
>> b2=num2;
>> x=load('noisy_ecg.txt');
>> y2=filter(b2,a2,x);
>> figure;
>> subplot(311);
>> plot(x); title('Sinal de ECG ruidoso'); xlim([0 1000])
>> xlabel('Amostras'); ylabel('Amplitude');
>> subplot(312);
>> plot(y); title('Sinal de ECG filtrado (Notch #1)'); xlim([0 1000])
>> xlabel('Amostras'); ylabel('Amplitude');
>> subplot(313);
>> plot(y2); title('Sinal de ECG filtrado (Notch #2)'); xlim([0 1000])
>> xlabel('Amostras'); ylabel('Amplitude');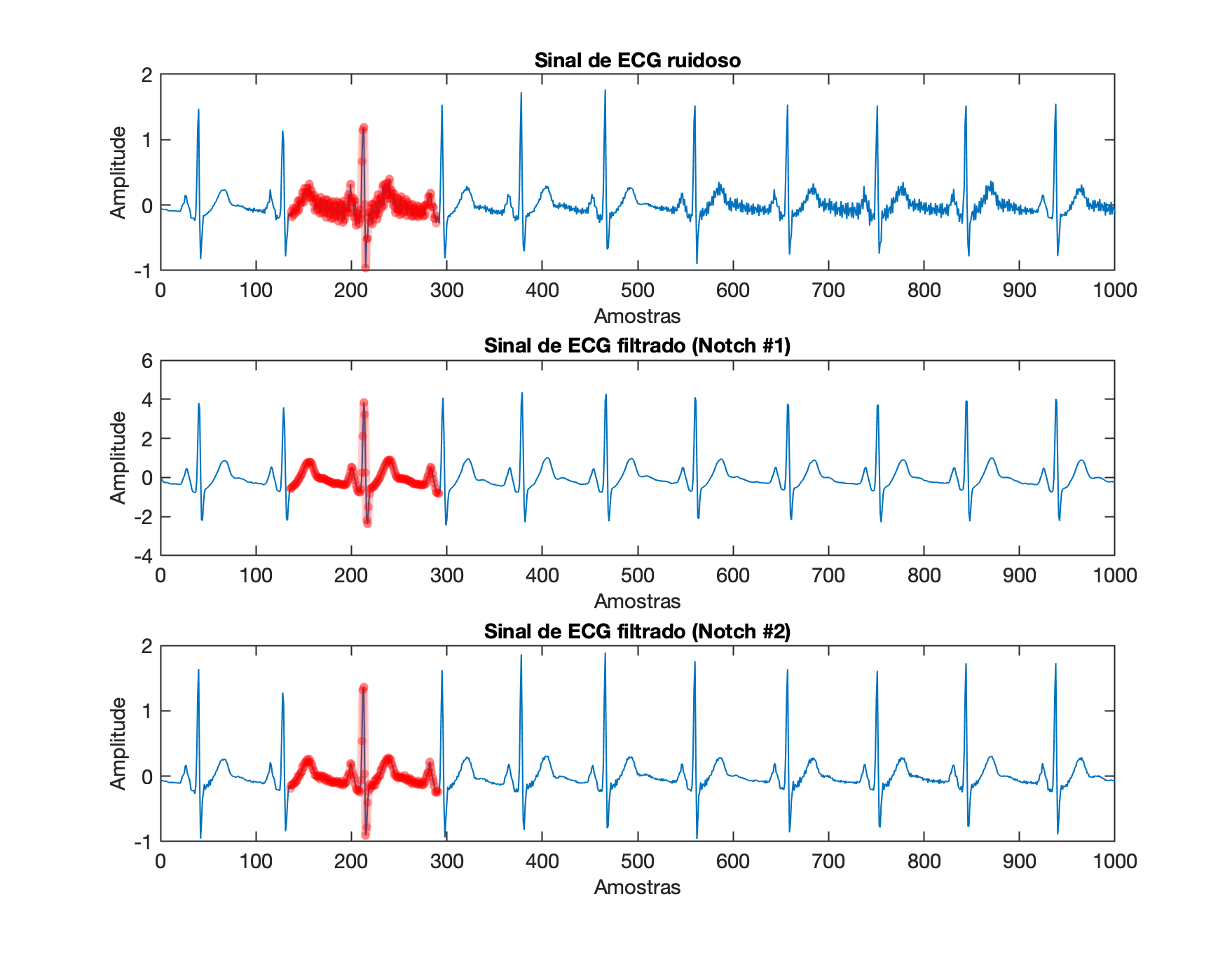

Note que desta vez, o filtro Notch melhorado além de reduzir atrasos em certos componentes frequenciais próximos de 50 Hz, também não distorceu tanto as amplitudes originais do sinal.

Fim.