cool-macbook-beach

A função filter() do Matlab/Octave

A função filter() do Matlab pode ser útil para determinar resposta temporal (no domínio tempo discreto) da saída de um filtro discreto/digital.

Sintaxe de uso:


>> Y = filter(B, A, X);

$X=$ $Y=$ $A$ $B$ são os coeficientes do filtro e estão associados com a implementação da equação de diferenças relacionada com a forma "Direta II Transposta", no Matlab:

$\begin{array}{rcll} a(1)*y(n) &=& b(1)*x(n) &+& b(2)*x(n-1) + ... + b(nb+1)*x(n-nb) +\\ & & &-& a(2)*y(n-1) - ... - a(na+1)*y(n-na) \end{array}$ (eq. (1))

o que dá no mesmo algébricamente (eq. de diferenças) que:

$\begin{array}{rcll} a_0\,y[n] &=& b_0\,x[n] &+& b_1\,x[n-1] + b_2\,x[n-2] + \ldots + b_{n_b}\,x[n-n_b] +\\ & & &-& a_1\,y[n-1] - a_2\,x[n-2] - \ldots - a_{n_a}\,y[n-n_a] \end{array}$ (eq. (2))

Note que no Matlab, os índices dos vetores/matrizes iniciam em 1 e não em zero como em outras linguagens de programação como C, C++..

$a_0=1$ (como normalmente acontece), então podemos generalizar a eq. (2) para:

$y[n]=\displaystyle\sum_{i=0}^{b_n} b_i \cdot x[n-i] - \displaystyle\sum_{j=1}^{n_a} a_j \cdot y[n-j]$ (eq. (3))

Podemos realizar a transformada Z sobre a eq. (2) e obter:

$\begin{array}{rcll} a_0\,Y(z) &=& b_0\,X(z) &+& b_1\,z^{-1}X(z) + b_1\,z^{-2}X(z) + \ldots + b_{n_b}\,z^{-n_b}X(z) +\\ & & &-& a_1\,z^{-1}Y(z) - a_2\,z^{-2}Y(z) - \ldots - a_{n_a}\,z^{-n_a}Y(z) \end{array}$ (eq. (4))

$n_b$ $X(z)$ $n_a$ $Y(z)$ .

Trabalhando um pouco mais com a eq. (4), podemos rescreve-la na forma:

$\begin{array}{l} Y(z) \left( a_0 + a_1 z^{-1} + a_2 z^{-2} + \ldots + a_{n_a} z^{-n_a} \right)= \\ \qquad = X(z) \left( b_0 + b_1\,z^{-1} + b_2\,z^{-2} + \ldots + b_{n_b}\,z^{-n_b} \right) \end{array}$

$H(z)=\dfrac{Y(z)}{X(z)}=\dfrac{b_0\,z^{0} + b_1\,z^{-1} + b_2\,z^{-2} + \ldots + b_{n_b}\,z^{-n_b}}{a_0\,z^{0} + a_1\,z^{-1} + a_2\,z^{-2} + \ldots + a_{n_a}\, z^{-n_a}}$ (eq. (5))

$H(z)=\dfrac{Y(z)}{X(z)}=\dfrac{b_0\,z^{n_b} + b_1\,z^{n_b-1} + b_2\,z^{n_b-2} + \ldots + b_{n_b}\,z^{0}}{a_0\,z^{n_a} + a_1\,z^{n_a-1} + a_2\,z^{n_a-2} + \ldots + a_{n_a}\,z^{0}}$ (eq. (6))

Note que as equações (5) e (6) representam a função transferência de um filtro digital, no plano-z.

$b_i$ $a_i$ do filtro, correspondem à polinômios e seus valores são ingressados simplesmente fazendo algo como:


xxxxxxxxxx
>> H = tf(B, A, T);

$T$ $T$ $A$ $B$ $T$ ).

$B=[b_0 \quad b_1 \quad b_2 \quad \ldots \quad b_{n_b}]=$ $A=[a_0 \quad a_1 \quad a_2 \quad \ldots \quad a_{n_b}]=$ vetor (polinômio) do denomindador da função transferência do filtro.

$a_0$ $b_0$ $z$ -- eq. (6)).

$a_{n_a}=$ $y[n]$ , ou seja:

$(a_{n_a}) \, z^{-n_a} \, Y(z) \quad \rightleftharpoons \quad (a_{n_a}) \, y[n-n_a]$ .

$a_0=$ $y[n]$ (sem atraso).

A eq. (3), para um filtro digital de 2a-ordem pode ser visualizada num diagrama de fluxo de sinais como:

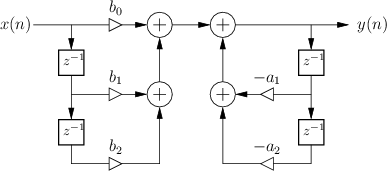
forma_direta_1

Obs.: Este diagrama está no formato conhecido como Forma Direta I.

Uso da função `filter()`

$b$ $a$ .

$b$ $a$ , você será capaz de implementar e analisar rapidamente sistemas discretos usando funções Matlab/Octave integradas.

$b$ $a$ $b$ $a$ no lado direito da tabela.

Ex.	Eq. de diferença	$a$ $b$
Ex1	$y[n]=3x[n]+2x[n-1]$	$a=[ 1 ]$ $b=[ 3 \quad 2 ]$
Ex2	$y[n] = 0,5x[n]-x[n-1]+2x[n-2]$	$a=[ 1 ]$ $b=[0.5 \quad -1 \quad 2]$
Ex3	$y[n]=-x[n]+x[n-3]$	$a=[ 1 ]$ $b=[ -1 \quad 0 \quad 0 \quad 1 ]$
Ex4	$y[n]=2x[n]+0,3y[n-1]$	$a=[ 1 \quad -0,3]$ $b=[ 2 ]$
Ex5	$y[n]=0,1x[n]+x[n-2]-0,2y[n-2]$	$a=[ 1 \quad 0 \quad 0,2]$ $b=[ 0,1 \quad 0 \quad 1 ]$

$b$ $a$ $a$ $y$ $b$ $x$ .

$y[n]$ $y[n-1]$ $y[n-2]$ ; etc.

$b$ $x[n]$ $x[n-1]$ $x[n-2]$ ; etc.

Implementando exemplos

$b$ $a$ de um sistema, a implementação é uma tarefa trivial usando funções Matlab/Octave integradas. Esta seção aborda os exemplos mostrados antes (amplificador, média móvel e modelo de sistema) que você mesmo deve experimentar. Se você não possui Matlab ou Octave instalado em seu computador, você pode usar uma versão online http://octave-online.net.

Exemplo_1: Amplificador Um sistema amplificador que amplifica por um fator de 2 é descrito pela seguinte equação de diferenças:

$y[n] = 2\,x[n]$

$b$ $a$ $a = [1]$ $b = [2]$ .

$x[n]$ $x[n]=[2 \quad 1,1 \quad 3,2 \quad 0,31 \quad 0]$


xxxxxxxxxx
>> x = [2 1.1 3.2 0.31 0]; 
>> b = 2;
>> a = 1;
>> y = filter(b, a, x)

Exemplo_2: filtro de média móvel de 4 pontos Seja um filtro de média móvel de 4 amostras, cuja equação de diferenças é dada abaixo:

$y[n]=0,25x[n]+0,25x[n-1]+0,25x[n-2]+0,25x[n-3]$

$b$ $a$ $a=[1]$ $b=[0,25 \quad 0,25 \quad 0,25 \quad 0,25]$ .

Use o código abaixo para determinar e traçar a saída após passar o rio seguinte sinal de nível através do sistema:

$[.375 \quad .35 \quad .425 \quad .475 \quad .4 \quad .375 \quad .525 \quad .425 \quad .475 \quad .425 \quad .5 \quad .45 \quad .575 \quad .525 \quad .6 \quad .675 \quad .575 \quad .7 \quad .725 \quad .6]$


xxxxxxxxxx
>> x = [.375 .35 .425 .475 .4 .375 .525 .425 .475 .425 .5 .45 .575 .525 .6 .675 .575 .7 .725 .6]; b = [0.25 0.25 0.25 0.25];
>> a = 1;
>> y = filter(b, a, x)
>> plot(y)

Exemplo_3: Modelo térmico Um modelo da mudança de temperatura de um copo de água colocado em uma geladeira é dado pela equação abaixo:

$y[n]=-0,0099x[n]+0,9901y[n-1]$

A constante de resfriamento é 0,01 e o modelo opera com dados amostrados a 1 Hz.

$x[n]$ $y[n]$ representa a mudança na temperatura da água em relação à temperatura inicial.

$x[n]$ estará constantemente à 11 °C.

Use o código a seguir para modelar esta configuração por 1.000 segundos:


xxxxxxxxxx
>> x = ones(1, 1000)*11; %1000 seconds 
>> b = [ -0.0099 ];
>> a = [ 1 -0.9901];
>> y = filter(b, a , x);
>> n=0:1000-1;
>> plot(n,y)
>> xlabel('Tempo (segundos)') 
>> ylabel('\Delta Temp (^oC)')
>> title('Variação da Temperatura') 
>> figure
>> plot(n,y+15)
>> xlabel('Tempo (segundos)')
>> ylabel('Temp (^oC)')
>> title('Temperatura da água')

Fim.

A função filter() do Matlab/Octave

Uso da função filter()

Implementando exemplos

Uso da função `filter()`