Funções Transferência, $H(z)$

Gráfico de Superfície de $H(z)$

Os engenheiros normalmente aplicam a transformada $\mathbb{Z}$ à resposta ao impulso de um sistema discreto, então vamos passar por esse processo com um sistema básico, como o do filtro da média móvel.

A resposta ao impulso é a saída do sistema quando a entrada é a seguinte sequência de números:

$x[n]=$ {1, 0, 0, 0, 0, 0, ... ...,0}

para este sistema de exemplo (filtro de média móvel de 2 passos), a resposta ao impulso é a sequência:

$y[n]=$ {0,5, 0,5, 0, 0, 0, 0, 0, 0, ..., 0}.

Lembrando da eq. de diferenças do filtro de média móvel de 2 passos:

$y[n] = 0,5 \, x[n] +0,5 \, x[n-1]$ (eq. (1))

Calculando:

$k=0,$ $x[0]=1$, a saída do filtro fica: $y[0]=0,5 \, x[0]+0,5\, x[-1]= 0,5(1) + 0,5(0) = 0,5$.

$k=1$, $x[1]=0$, a saída do filtro fica: $y[1]=0,5 \, x[1]+0,5\, x[0]= 0,5(0) + 0,5(1) = 0,5$.

$k=2$, $x[2]=0$, a saída do filtro fica: $y[2]=0,5 \, x[2]+0,5\, x[1]= 0,5(0) + 0,5(0) = 0$.

assim, para $k \ge 2$, a saída do filtro fica $y[k]=0$.

Lembrando então da definição da transformada $\mathbb{Z}$:

$H(z)=\displaystyle\sum_{n=0}^{\infty} h[n]\,z^{-n}$

e aplicando sobre a eq. (1), podemos determinar a função transferência deste filtro:

$y[n] = 0,5 \, x[n] +0,5 \, x[n-1]$ (eq. (1))

$\downarrow \mathbb{Z}$

$Y(z)=0,5 \, X(z) + 0,5 z^{-1}X(z)$

$Y(z)=\left( 0,5 + 0,5z^{-1}\right) \, X(z)$

$H(z)=\dfrac{Y(z)}{X(z)}= 0,5 + 0,5\,z^{-1}$

ou:

$H(z)=\dfrac{Y(z)}{X(z)}= \left( 0,5 + 0,5\,z^{-1} \right) \cdot \dfrac{z^1}{z^1}$

$H(z)=\dfrac{0,5\,z + 0,5}{z}$

Note que $𝑧$ é um número complexo.

Se pode obter uma perspectiva muito útil de um sistema visualizando o gráfico de magnitude de 𝐻(𝑧) usando uma escala de decibéis (ou seja, $20\, 𝑙og_{10}(|𝐻(𝑧)|$), quando avaliado para diferentes valores de $𝑧$, ao longo dos eixos real e imaginário, conforme mostrado abaixo.

O código Matlab/Octave para reproduzir o que é chamado superfície $H(z)$ segue abaixo:

grafico_superficie_media_movel.m :

z_real_vals = [-2:0.02:2];
z_imag_vals = [-2:0.02:2];
for m = 1: length(z_real_vals)
    for n = 1: length(z_imag_vals)
        z = z_real_vals(m)+z_imag_vals(n)*j;
        H_z(n,m) = (0.5*z + 0.5)/z;
    end
end
mesh (z_real_vals, z_imag_vals, 20*log10(abs(H_z)))
xlabel('Re\{z\}')
ylabel('Im\{z\}')
zlabel('|H(z)|')

O código anterior gera o seguinte gráfico:

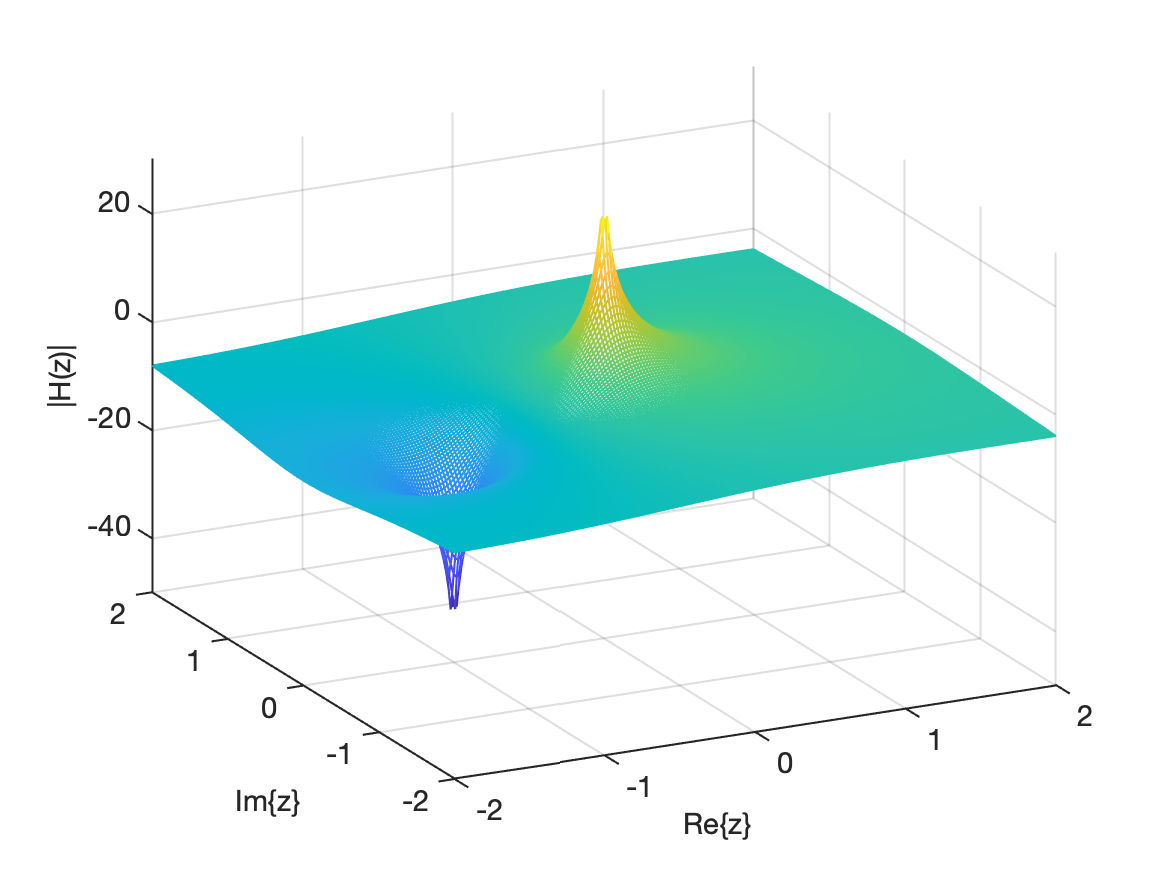
Note que o "cone" amarelo (superior), está associado com o pólo de $H(z)$ e o "cone invettido" azul está associado com o zero da função $H(z)$.

O que é importante compreender é que estes “cones” afetam os contornos de toda a superfície H(z). Na verdade, a superfície H(z) de todos os sistemas discretos é essencialmente apenas uma combinação destes “cones” e “cones invertidos” interagindo uns com os outros. A quantidade e a posição desses 'cones crescentes' e 'cones invertidos' serão diferentes para cada sistema, de modo que os contornos da superfície H(z) serão únicos para cada sistema discreto que possui uma equação de diferença única.

Melhor que visualizar 3D é trabalhar com um gráfico "2D" de $H(z)$, ou trabalhar com diagramas de pólo-zero.

Diagramas de pólo-zero

Podemos "girar" o gráfico anterior e obter uma figura como:

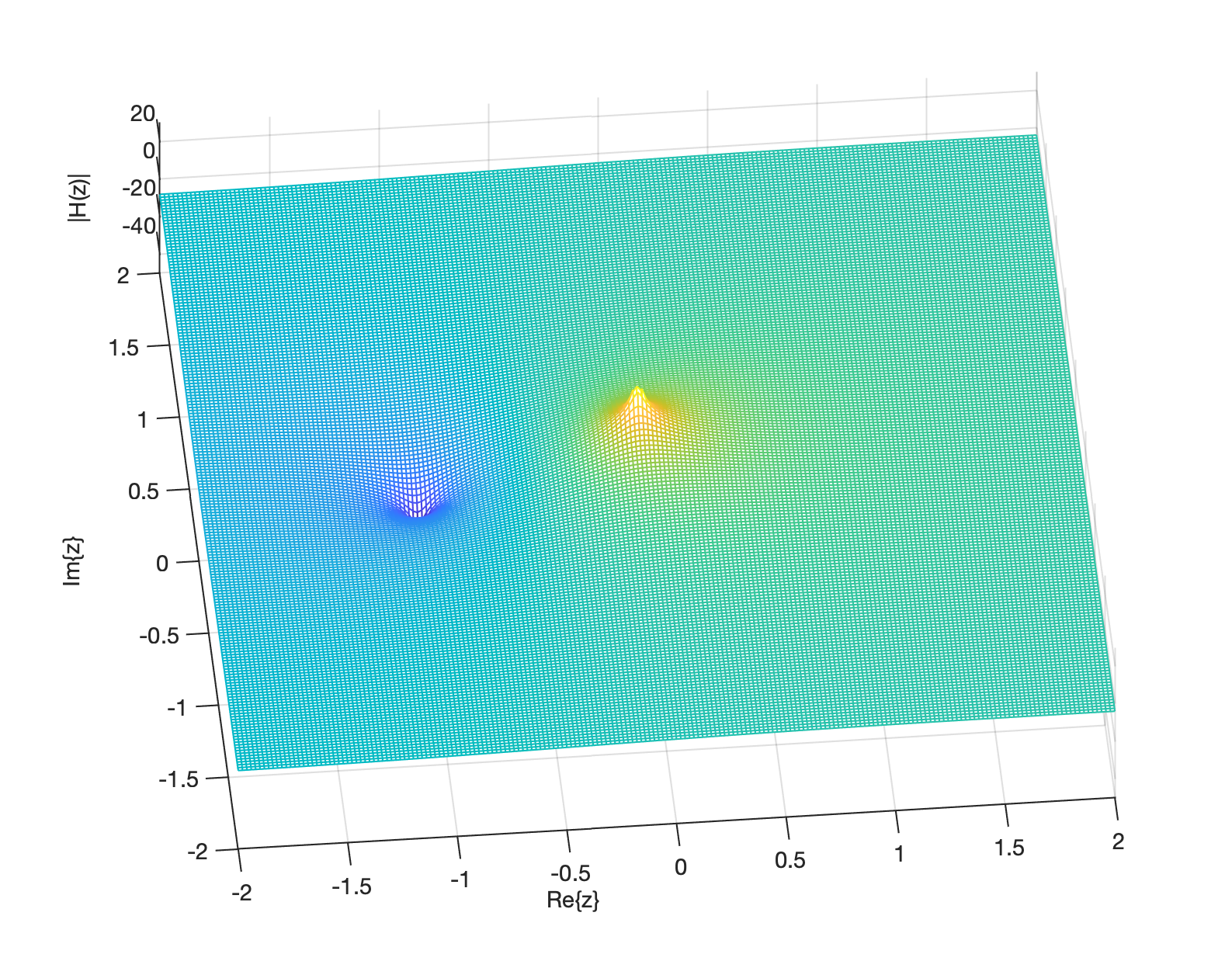
ou podemos nos concentrar apenas nas partes real e imaginária do plano-z e obter algo do tipo:

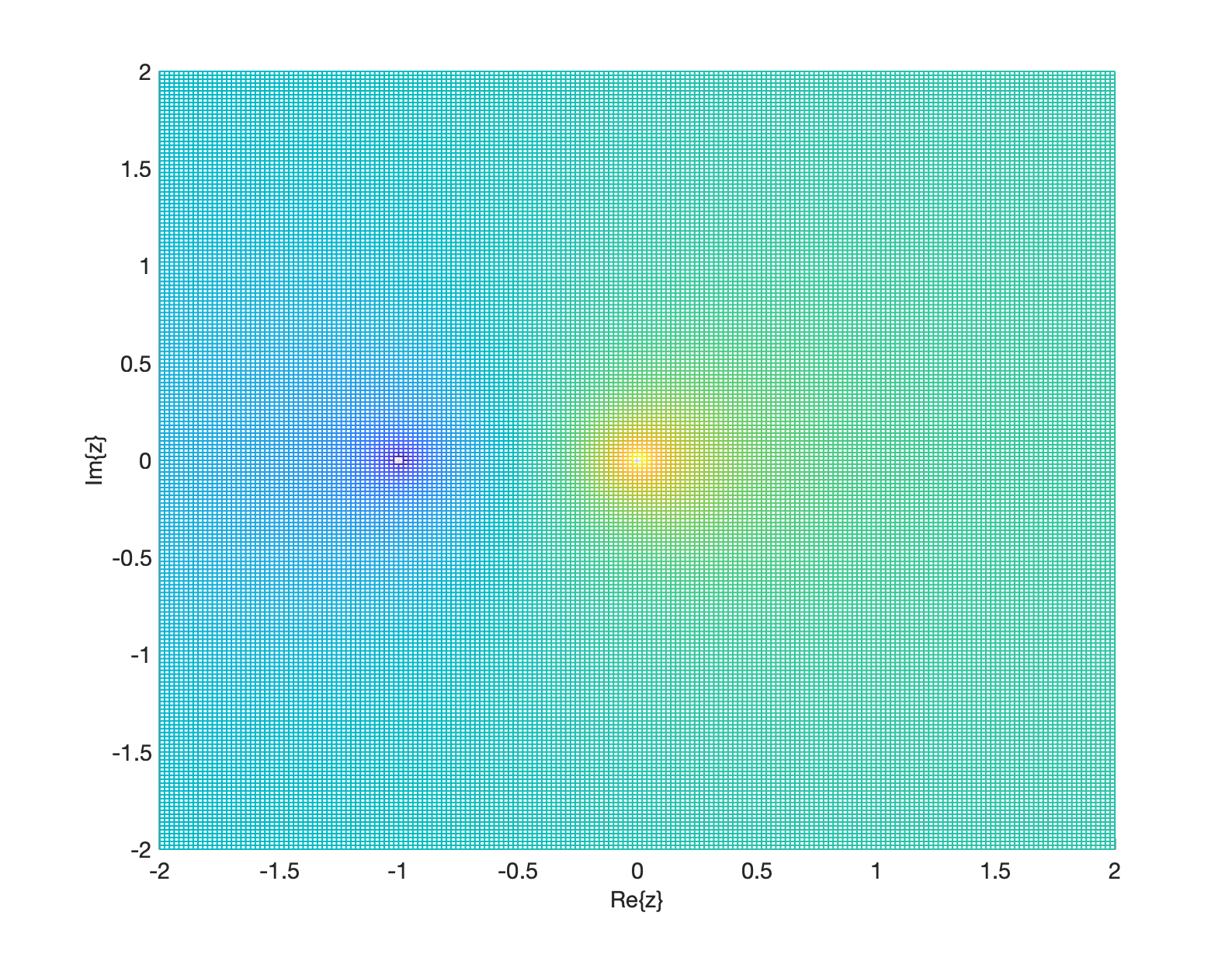
Um diagrama pólo-zero, é similar a esta "vista superior" da superfície 3D gerada antes, mas é ainda acrescentado um círculo unitário de raio igual à um (1,0) que passa pelos pontos $1+0j$, $0+j$, $-1+0j$ e $0-j$.

Este outro diagrama é mais fácil de ser obtidpo usando a função pzmap():

​x
>> H=tf([0.5 0.5], [1 0], 1)
​
H =
 
  0.5 z + 0.5
  -----------
       z
 
Sample time: 1 seconds
Discrete-time transfer function.
​
>> figure; pzmap(H)
>> axis([-1.5 1.5 -1.5 1.5])
>> axis equal

Segue figura gerada pelo pzmap() para esta função $H(z)$:

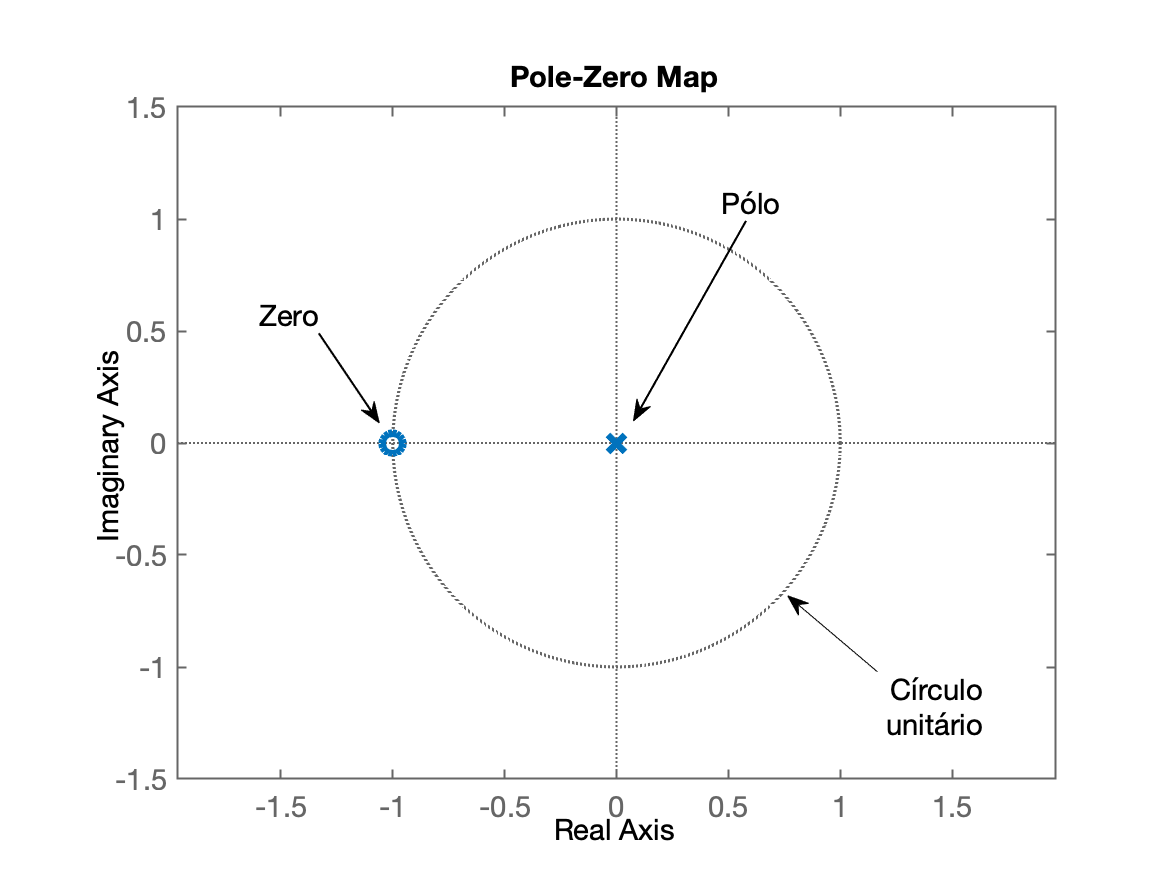
Note que desenhar um gráfico 3D da superfície H(z) à mão livre pode ser um desafio. Portanto, muitas vezes usam-se em diagramas de pólo-zero, que indicam as posições dos pólos (centros dos 'cones') e zeros (centros dos 'cones invertidos').

Nesta figura e lembrando da função transferência deste filtro, temos um zero em $z=-1$ e um pólo em $z=0$ (na origem do plano-z):

$H(z)=\dfrac{0,5\,z + 0,5}{z}=\dfrac{1}{2} \left( \dfrac{z+1}{z} \right)$

O zero se refere à raiz do numerador de $H(z)$ e o pólo se refere à raíz do denominador de $H(z)$. Note que uma função transferência pode conter mais que 1 zero (ou nenhum) e mais que um pólo. Os zeros são sempre representados com o símbolo "o" e os pólos sempre representados com o símbolo "x".

Este tipo de diagrama é útil para inferir a estabilidade de um sistema e sua resposta frequencial.

Note ainda que como $z$ é um número complexo:

Com um pequeno treinamento, engenheiros e cientistas podem visualizar a superfície $H(z)$ associada a um diagrama de pólo zero específico para ajudá-los a analisar o comportamento de um sistema. Reserve um momento para combinar o diagrama do pólo zero com a superfície $H(z)$ correspondente nas imagens mostradas na figura da próxima página para verificar sua compreensão. Esperamos que você possa perceber que o gráfico do pólo zero na parte superior corresponde ao gráfico da superfície $H (z)$ no topo, o gráfico do pólo zero do meio corresponde ao gráfico da superfície $H (z)$ inferior; e o gráfico do pólo zero inferior corresponde ao gráfico da superfície $H (z)$ intermediária.

Observe que o diagrama pólo-zero mostra as localizações dos pólos e zeros associados a um sistema no que é chamado de plano$-z$ (mais geralmente chamado de plano complexo ou diagrama de Argand). Muitas vezes há muita confusão sobre os termos plano z, plano complexo e diagrama de Argand. Eles se referem essencialmente à mesma coisa (todos fornecem uma maneira de representar visualmente números complexos), mas no contexto da análise do domínio z o termo plano z parece ser o mais comumente usado. Além disso, observe que um diagrama de pólo zero também geralmente inclui um círculo unitário sobreposto ao plano z, para facilitar a identificação de sistemas instáveis.

Função Transferência & Equação de Diferenças

A função de transferência de um sistema é determinada aplicando a transformada$-\mathbb{Z}$ à resposta ao impulso do sistema.

No caso do filtro da média móvel de 2 passos, $H(z)$ fica:

$H(z)=\dfrac{0,5\,z + 0,5}{z}=\dfrac{1}{2} \left( \dfrac{z+1}{z} \right)$

As localizações dos "zeros" para qualquer sistema podem ser encontradas determinando quais valores de $z$ fazem com que o numerador da função de transferência, $𝐻(𝑧)$, sejam iguais à zero. Em outras palavras, o "zero" é um valor de $𝑧$ que faz com que o numerador de $𝐻(𝑧)$ seja igual a zero, ou seja, as raízes do numerador.

Para o caso do filtro de média móvel de dois passos quando $z=-1$, $H(z)=0$, assim se diz que zero existe no ponteo $z=-1+0j$ no plano-z.

As localizações dos "pólos" para qualquer sistema podem ser encontradas determinando quais valores de $𝑧$ fazem com que o denominador da função de transferência, $𝐻(𝑧)$, seja igual a zero, ou seja, as raízes do denominador.

Para a média móvel de dois toques, o denominador de $𝐻(𝑧)$ é $0$ quando $z=0$, então diz-se que existe um pólo na localização $z=0+0j$ no plano z (ponto que também é conhecido como origem do plano z).

Mas... você deve estar ciente de que qualquer sistema discreto pode ser descrito usando a equação de diferenças, onde os coeficientes $b$ e $a$ mudarão de sistema para sistema:

$\begin{array}{rcl}a_0\,y[n] &=& b_0\,x[n]+b_1\,x[n-1]+b_2\,x[n-2]+ \ldots + b_f\,x[n-f] +\\ & & -a_1\,y[n-1] -a_2\,y[n-2]-a_3\,y[n-3]- \ldots -a_g\,y[n-g] \end{array}$

Esta pode ser reescrita da seguinte forma, se os termos de $y$ forem trazidos para o lado esquerdo da equação:

$\begin{array}{rcl}a_0\,y[n] +a_1\,y[n-1] +a_2\,y[n-2]+a_3\,y[n-3]+ \ldots +a_g\,y[n-g] =\\ = b_0\,x[n]+b_1\,x[n-1]+b_2\,x[n-2]+ \ldots + b_f\,x[n-f] \end{array}$

Esta equação de diferenças tem um conjunto de coeficientes $b$ (na frente dos termos $x$) e coeficientes $a$ (na frente dos termos $y$). Para cada sistema único, os coeficientes $b$ e $a$ serão diferentes e o sistema pode ser descrito apenas usando os valores dos coeficientes.

Por exemplo, para o filtro da média móvel de dois passos, representada pela equação de diferença:

$y[n] = 0,5 \, x[n] +0,5 \, x[n-1]$,

os coeficientes $b_0$ e $b_1$ são ambos $0,5$ e todos os outros coeficientes $b$ são zero . Além disso, o coeficiente $a_0$ é $1$, enquanto todos os outros coeficientes $a$ sõa nulos.

Para qualquer sistema descrito usando a fórmula da equação de diferenças, a função de transferência será dada pela seguinte equação:

$H(z)=\dfrac{Y(z)}{X(z)}=\dfrac{b_0\,z^0 + b_1\,z^{-1} + b_2\,z^{-2} + \ldots + b_f\,z^{-f}}{a_0\,z^0+a_1\,z^{-1}+a_2\,z^{-2}+\ldots+a_g\,z^{-g}}$

Para o sistema de média móvel de dois passos, como $b_0$, $b_1$ e $a_0$ são os únicos coeficientes diferentes de zero, a fórmula da função de transferência torna-se:

$H(z)=\dfrac{Y(z)}{X(z)}=\dfrac{b_0\,z^0 + b_1\,z^{-1}}{a_0\,z^0}$

no caso:

$H(z)=\dfrac{0,5\,z^0+0,5\,z^{-1}}{1\,z^0}=0,5 + 0,5\,z^{-1}$

ou:

$H(z)=\left( 0,5 + 0,5\,z^{-1} \right) \cdot \dfrac{z^1}{z^1}$

$H(z)=\dfrac{0,5\,z + 0,5}{z}$

Observe que a transformada$-\mathbb{Z}$ para a função de transferência acima é a mesma determinada anteriormente, quando a transformada$-\mathbb{Z}$ foi aplicada diretamente à resposta ao impulso do sistema de média móvel de dois passos. Este segundo método (usando os coeficientes $b$ e $a$) para determinar a função de transferência de um sistema é muitas vezes muito mais fácil de usar e é frequentemente utilizado na prática de filtros digitais.

Exemplos de Diagramas Pólo-Zero

Aqui estão mais três exemplos de como determinar a função de transferência de um sistema e o diagrama de pólo zero para três sistemas diferentes. Você deve revisar esses exemplos para garantir que entendeu o processo antes de prosseguir. O terceiro exemplo mostra como usar o Octave/Matlab para determinar convenientemente os pólos e zeros do sistema.

Exemplo 1

Considere o sistema dado pela seguinte equação de diferença:

$y[n]=2x[n]+3x[-1]+0,5y[n-1]$

Normalmente, uma equação de diferenças de sistemas é escrita com a saída $y[𝑛]$ à esquerda da equação e todos os outros termos à direita, uma vez que geralmente estamos interessados em determinar a saída do sistema. No entanto, para determinar os coeficientes $b$ e $a$ do sistema, pode ser mais conveniente trazer todos os termos $𝑦$ para a esquerda da equação e todos os termos $𝑥$ para a direita, como mostrado abaixo:

$y[n]+0,5y[n-1]=2x[n]+3x[n-1]$

Os coeficientes $b$ estão associados aos termos $𝑥$ e neste caso: $b_0=2$ e $b_1=3$. Todos os outros coeficientes $b$ são zero. Os coeficientes $a$ estão associados ao termos $y$ e neste caso: $a_0=1$ e $a_1=0,5$. Todos os outros coeficientes de $a$ são nulos.

Neste caso, a função transferência fica como:

$H(z) = \dfrac{Y(z)}{X(z)} = \dfrac{b_0\,z^0 + b_1\,z^{-1}}{a_0\,z^0 + a_1\,z{-1}}$

e substituindo os valores para $b$ a $a$ teríamos:

$H(z)=\dfrac{2z^0+3z^{-1}}{1z^0+0,5z^{-1}}$

Ou:

$H(z)=\dfrac{2z+3}{z+0,5}$

Para encontrar os zeros deste sistema, necessitamos encontrar as raízes do numerador:

$2z+3=0$

$2z=-3$

$z=-\dfrac{3}{2}=-1,5$

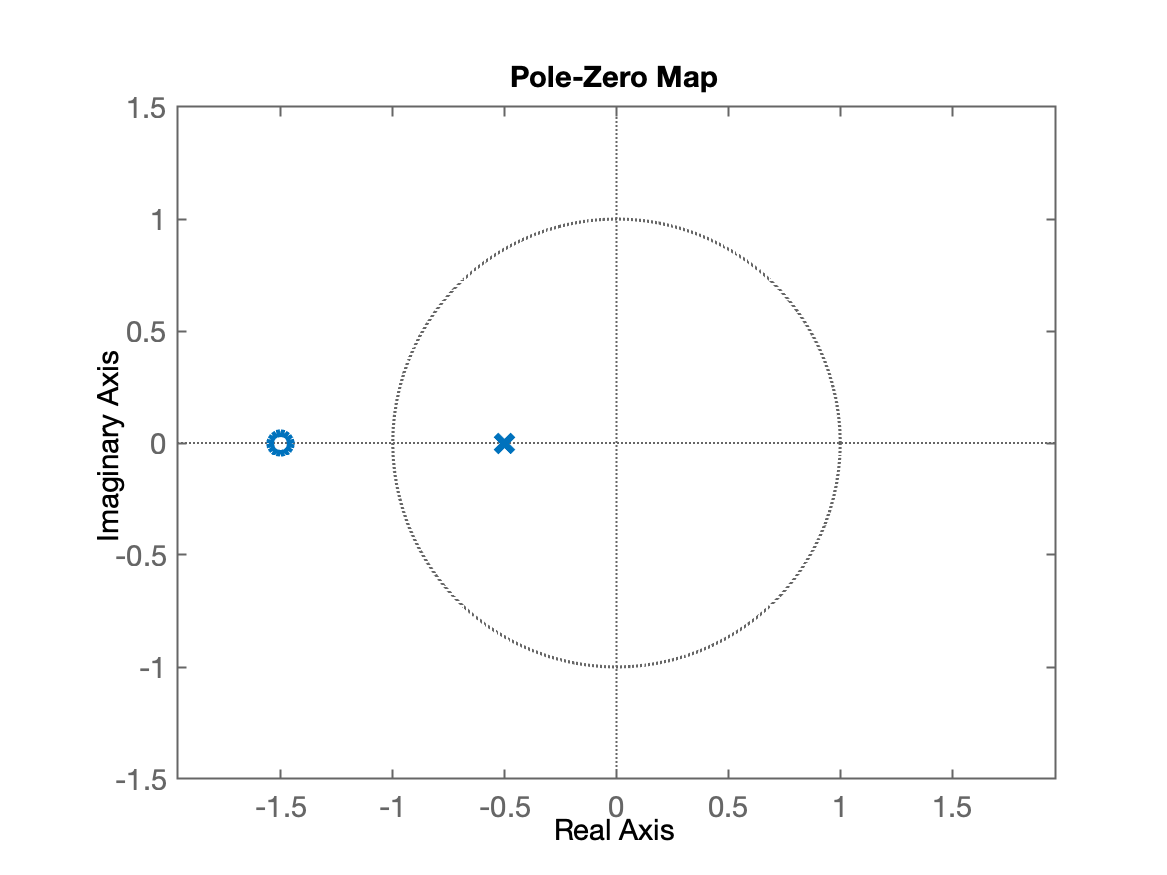
Neste caso, temos um zero localizado em $z=-1,5$.

E para encontrar os pólos deste sistemas, temos que encontrar as raízes do denominador:

$z+0,5=0$

$z=-0,5$

O que significa que neste caso, temos um pólo localizado em $z=-0,5$.

Ou na forma de um gráfico:

Exemplo 2

Para este próximo exemplo consideraremos o sistema dado por esta equação de diferenças:

$y[n]=0,5x[n]-0,6x[n-1]+0,5y[n-1]-0,25y[n-2]$

Esta equação pode ser reescrita como:

$y[n]-0,5y[n-1]+0,25y[n-2]=0,5x[n]-0,6x[n-1]$

Os coeficientes $b$ e $a$ resultam:

$\begin{array}{l} b_0=0,5\\ b_1=-0,6\\ a_0=1\\ a_1=-0,5\\ a_2=0,25\end{array}$

E a função transferência ficaria como:

$H(z) = \dfrac{Y(z)}{X(z)} = \dfrac{b_0z^0+b_1z^{-1}}{a_0z^0+a_1z^{-1}+a_2z~{-2}}$

neste caso:

$H(z)=\dfrac{0,5z^0-0,6z^{-1}}{1z^0-0,5z^{-1}+0,25z^{-2}}=\dfrac{0,5-0,6z^{-1}}{1-0,5z^{-1}+0,25z^{-2}}$

Ou:

$H(z)=\dfrac{0,5-0,6z^{-1}}{1-0,5z^{-1}+0,25z^{-2}} \cdot \dfrac{z^2}{z^2}$

$H(z)=\dfrac{0,5z^2-0,6z}{z^2-0,5z+0,25}$

Encontrando os zeros:

$0,5z^2-0,6z=0$

$z(0,5z-0,6)=0$

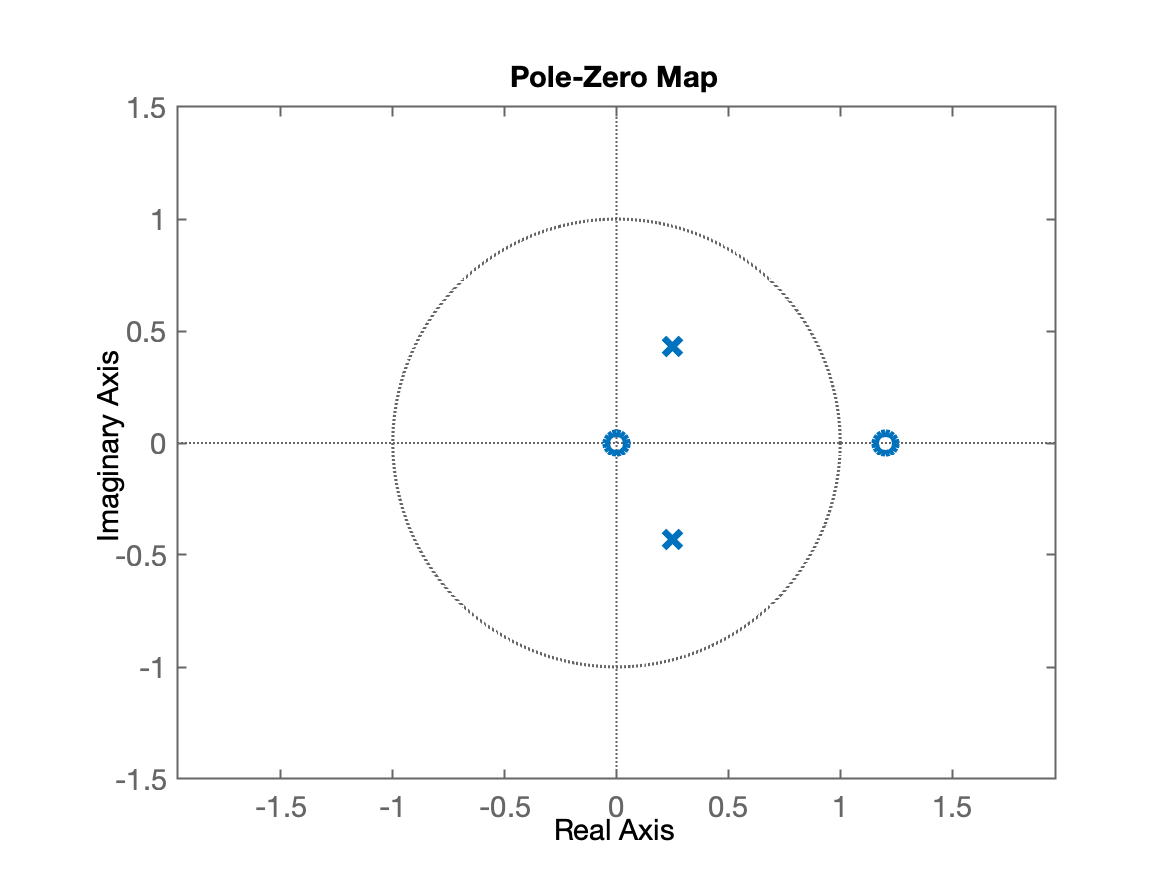
então percebemos um zero em $z=0$ e outro zero em:

$0,5z-0,6=0$

$0,5z=0,6$

$z=\frac{0,6}{0,5}=1,2$

E teremos pólos localizados em:

$z^2-0,5z+0,25=0$

$z=\dfrac{0,5 \pm \sqrt{(-0,5)^2-4(0,25)}}{2}$

$z=\dfrac{0,5 \pm \sqrt{0,25-1}}{2} = \dfrac{0,5 \pm \sqrt{-0,75}}{2} = \dfrac{0,5 \pm j0,8667}{2}$

$z=0,25 \pm j0,433$

Então neste caso, teremos um par de pólos complexos conjugados localizados em $z=0,25 \pm j0,433$.

Na forma de um gráfico:

Exemplo 3

Neste caso:

$\begin{array}{rcl}y[n] &=& 5,342\,x[n]+6,23\,x[n-1]+0,97\,x[n-2]+ 0,7\,x[n-3] + 0,237\,y[n-1] + \\ & & -0,89\,y[n-2]-0,47\,y[n-3]- 0,2\,y[n-4] \end{array}$

Comparando com:

$\begin{array}{rcl}a_0\,y[n] &=& b_0\,x[n]+b_1\,x[n-1]+b_2\,x[n-2]+ \ldots + b_f\,x[n-f] +\\ & & -a_1\,y[n-1] -a_2\,y[n-2]-a_3\,y[n-3]- \ldots -a_g\,y[n-g] \end{array}$

teríamos então:

$H(z)=\dfrac{Y(z)}{X(z)} = \dfrac{5,342z^4+6,23z^3+0,97z^2+0,7z}{z^4-0,237z^3+0,89z^2-0,47z-0,2}$

Podemos encontrar os zeros fazendo:

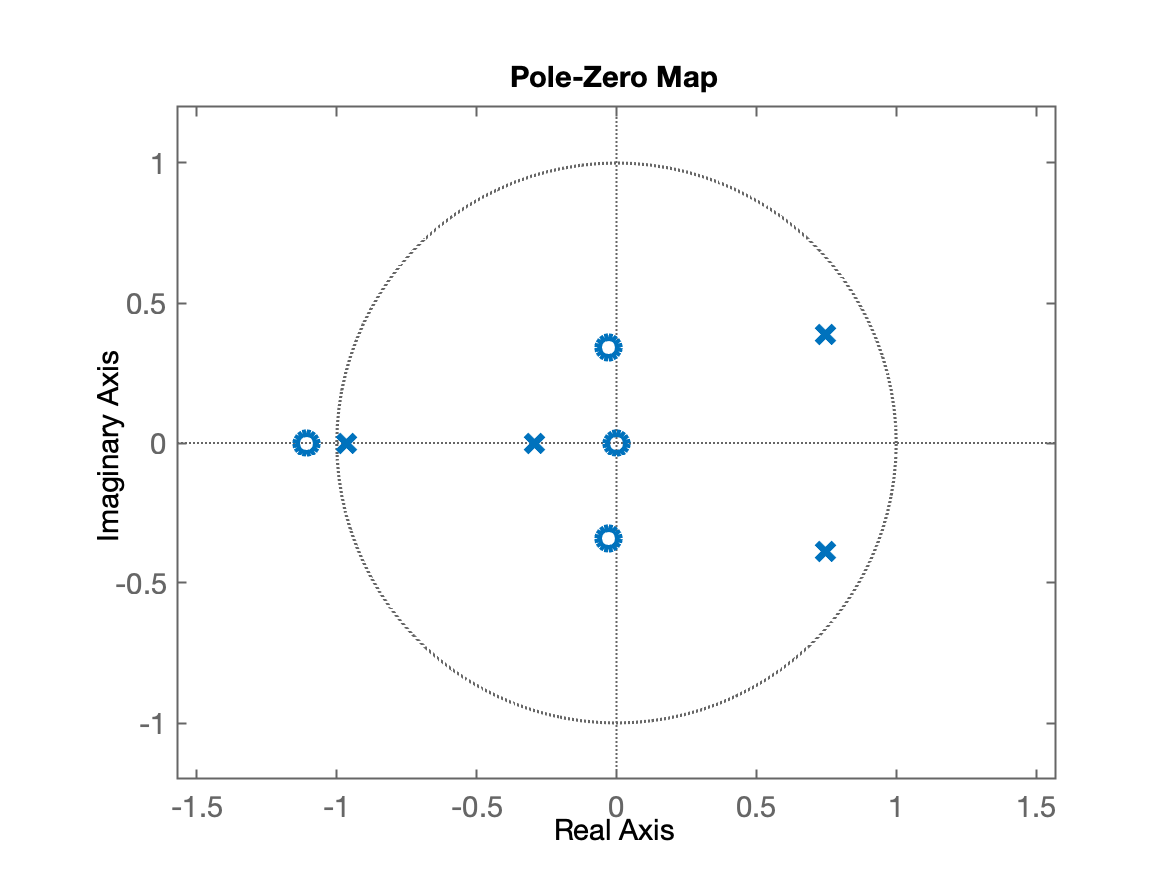
xxxxxxxxxx
>> b=[5.342 6.23 0.97 0.7 0];
>> zeros=roots(b)
zeros =
            0 +          0i
       -1.109 +          0i
    -0.028595 +    0.34254i
    -0.028595 -    0.34254i

ou podemos estabelever os zeros na notação $\text{modulo } \angle{\text{graus}}$:

xxxxxxxxxx
>> [abs(zeros) angle(zeros)*180/pi]
ans =
            0            0
        1.109          180
      0.34373       94.772
      0.34373      -94.772

E assim podemos proceder para a determinação dos pólos deste sistema:

xxxxxxxxxx
>> a = [1 -0.237 -0.89 0.47 0.2];
>> polos=roots(a)
polos =
      0.74755 +    0.38734i
      0.74755 -    0.38734i
     -0.96605 +          0i
     -0.29205 +          0i
>> [abs(polos) angle(polos)*180/pi]
ans =
      0.84194        27.39
      0.84194       -27.39
      0.96605          180
      0.29205          180

O que num diagrama pólo-zero resulta em:

Fim.

Próximo item >> Estabilidade de um sistema (discreto).