Projeto Controladores

Controlador DeadBeat

Aula de 19/05/2025.

Terminando projeto da aula de 12/05/2025:

​x
>> diary aula_19052025.txt % inciando novo regsitro
>> load dados   % carregando dados antigos (das aulas passadas)
>> zpk(BoG)     % lembrando da tf da planta
 
  0.00012224 (z+2.747) (z+0.1903)
  --------------------------------
  (z-0.9048) (z-0.8187) (z-0.3679)
 
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.
​
>> polos_BoG    % Os pólos de BoG(z) já haviam sido "isolados" na aula passada
polos_BoG =
      0.90484
      0.81873
      0.36788
>> zeros_BoG    % Os zeros de BoG(z) já haviam sido "isolados" na aula passada
zeros_BoG =
      -2.7471
     -0.19031

Montando eq. d controlador, lembrando que não posemor incluir pólos ou zeros fora do círculo unitário:

xxxxxxxxxx
>> C_dead1=tf(poly(polos_BoG), poly([zeros_BoG(2)  1]), T);   % montando C(z)
>> zpk(C_dead1)
​
 
  (z-0.9048) (z-0.8187) (z-0.3679)
  --------------------------------
          (z-1) (z+0.1903)
 
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.

Esta função transferência possui grau do numerador maior que o grau do denominador, implicando num sistema antecipativo ﹣ impraticável (seria exigido conhecer o valor de $e[k+1]$).

Falta então acrescentar um pólo à eq. anterior. Arbitramos este pólo "extra" em $z=-0,5$ porque queremos o ponto de partida do RL deste sistema tenha ponto de partida próxiumo da origem do plano-z. Queremos que acontece algo do tipo:

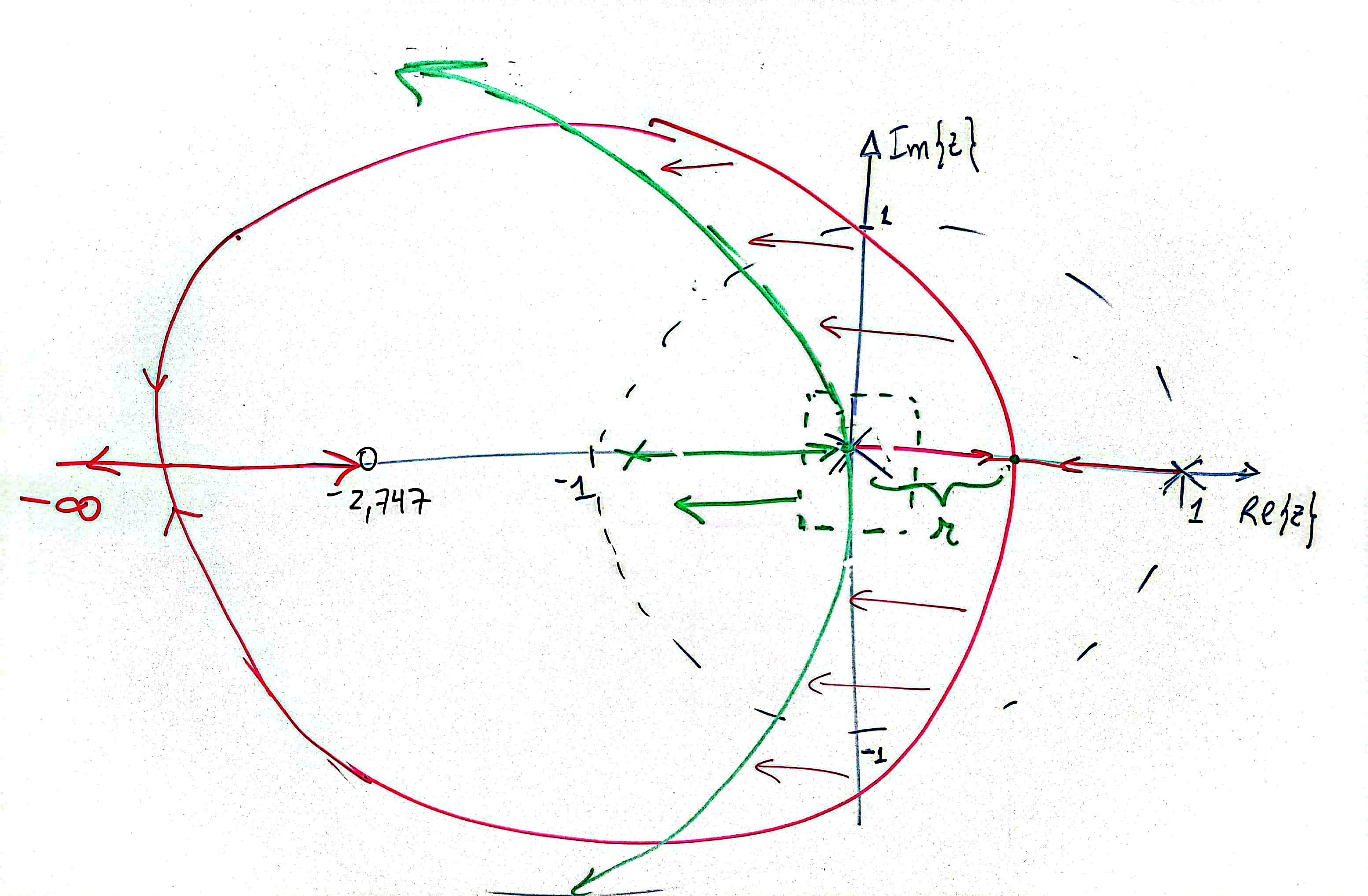
Lembrar que pólos de MF reais rendem respostas super-amortecidas (sem overshoot) e que se queremos uma resposta a mais rápida possível, então eles devem estar localizados próximos da origem do plano-z (ver [gráficos aqui]).

xxxxxxxxxx
>> C_dead2=tf(poly(polos_BoG), poly([zeros_BoG(2)  1  -0.5]), T);   % montando C(z)
>> zpk(C_dead2)
 
  (z-0.9048) (z-0.8187) (z-0.3679)
  --------------------------------
      (z-1) (z+0.5) (z+0.1903)
 
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.
​
>> C_dead2=tf(poly(polos_BoG), poly([zeros_BoG(2)  1  -0.5]), T);
>> ftma_dead2=C_dead2*BoG;
>> zpk(ftma_dead2)
 
  0.00012224 (z+2.747) (z-0.9048) (z-0.8187) (z-0.3679) (z+0.1903)
  ----------------------------------------------------------------
     (z-1) (z-0.9048) (z-0.8187) (z-0.3679) (z+0.5) (z+0.1903)
 
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.
​
>> zpk(minreal(ftma_dead2)) % com termos comuns simplificados
 
  0.00012224 (z+2.747)
  --------------------
     (z-1) (z+0.5)
 
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.
​
>> figure; rlocus(ftma_dead2)

Notamos um RL próximo do desejado:

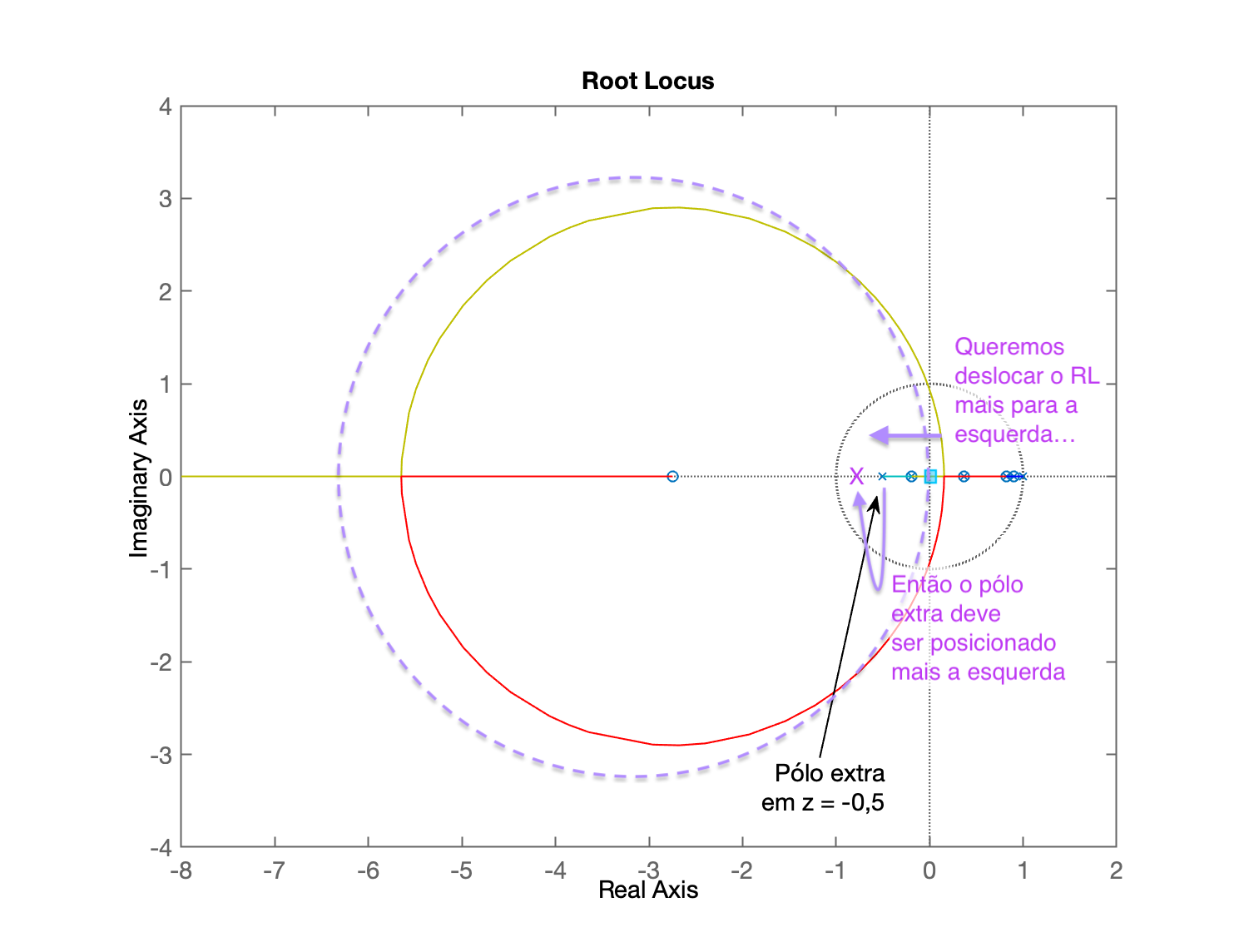
Modificando uma terceita vez a eq. do controlador, deslocando o pólo "extra" ainda mais a esquerda, mas desta vez com o auxílio do App Control System Designer:

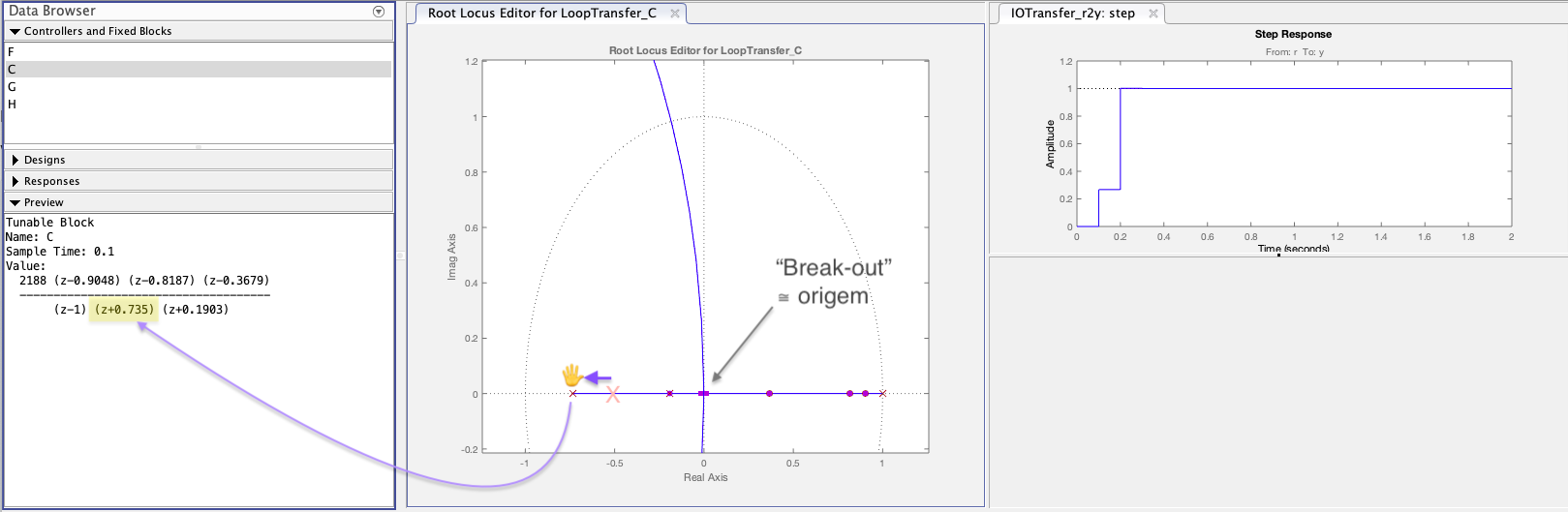
Resultado obtido (depois de exportar controlador C como Cdead3):

xxxxxxxxxx
>> zpk(Cdead3)
 
  2188 (z-0.9048) (z-0.8187) (z-0.3679)
  -------------------------------------
       (z-1) (z+0.735) (z+0.1903)
 
Name: C
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.

Projeto salvo como: ControlSystemDesigner_Cdead3.mat.

Fechando a mallha, levantando o RL, verificando a resposta ao defrau e estas coisas...😑

xxxxxxxxxx
>> ftma_dead3=Cdead3*BoG;
>> ftmf_dead3=feedback(Cdead3*BoG,1);
>> pole(ftmf_dead3)     % pólos finais em MF:
ans =
     -0.19031
      0.90484
      0.81873
    -0.017698
     0.015242
      0.36788
>> % Algo "sobrecarregado", dicícil perceber os pólos de MF que interessam...
>> zpk(ftma_dead3)  % função complenta
 
  0.26746 (z-0.9048) (z-0.8187) (z-0.3679) (z+0.1903) (z+2.747)
  -------------------------------------------------------------
   (z-1) (z-0.9048) (z-0.8187) (z-0.3679) (z+0.735) (z+0.1903)
 
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.
​
>> minreal(ftma_dead3)  % função com simplificações
 
  0.26746 (z+2.747)
  -----------------
   (z-1) (z+0.735)
 
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.
​
>> ftma_dead3r=minreal(ftma_dead3); % criando uma variável "r"eduzida (com as simplificações)
>> ftmf_dead3r=feedback(ftma_dead3r,1);
>> pole(ftmf_dead3r) % mostrando os pólos de MF que realmente interessam
ans =
    -0.017698
     0.015242
>> % Notamos 2 pólos reais quase concentrados na origem do plano-z
>> % Poderiamos ter aumentado um pouco mais o ganho (sutilmente)
>> figure; step(ftmf_dead3r)    % observando resposta ao degrau em MF
>> grid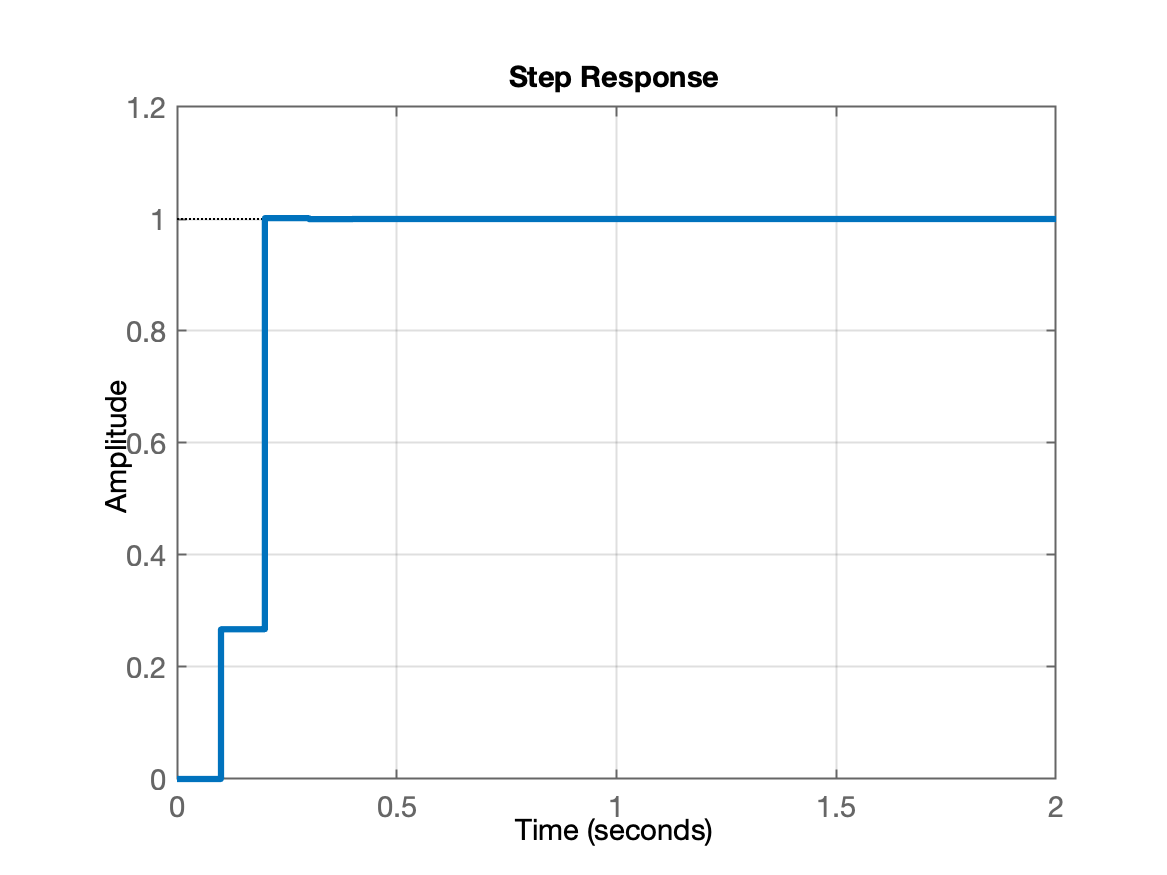

Nota-se um quase imperceptível overshoot.

Mas com certeza com expressivas amplitudes para ação de controle:

xxxxxxxxxx
>> % Deduzindo tf auxiliar para mostrar gráfico de u[kT]:
>> % aux(z) = C(z)/(1+C(z)*BoG(z))
>> % u[kT]=step(aux(z))
>> aux=Cdead3/(1+ftma_dead3);
>> figure; step(aux)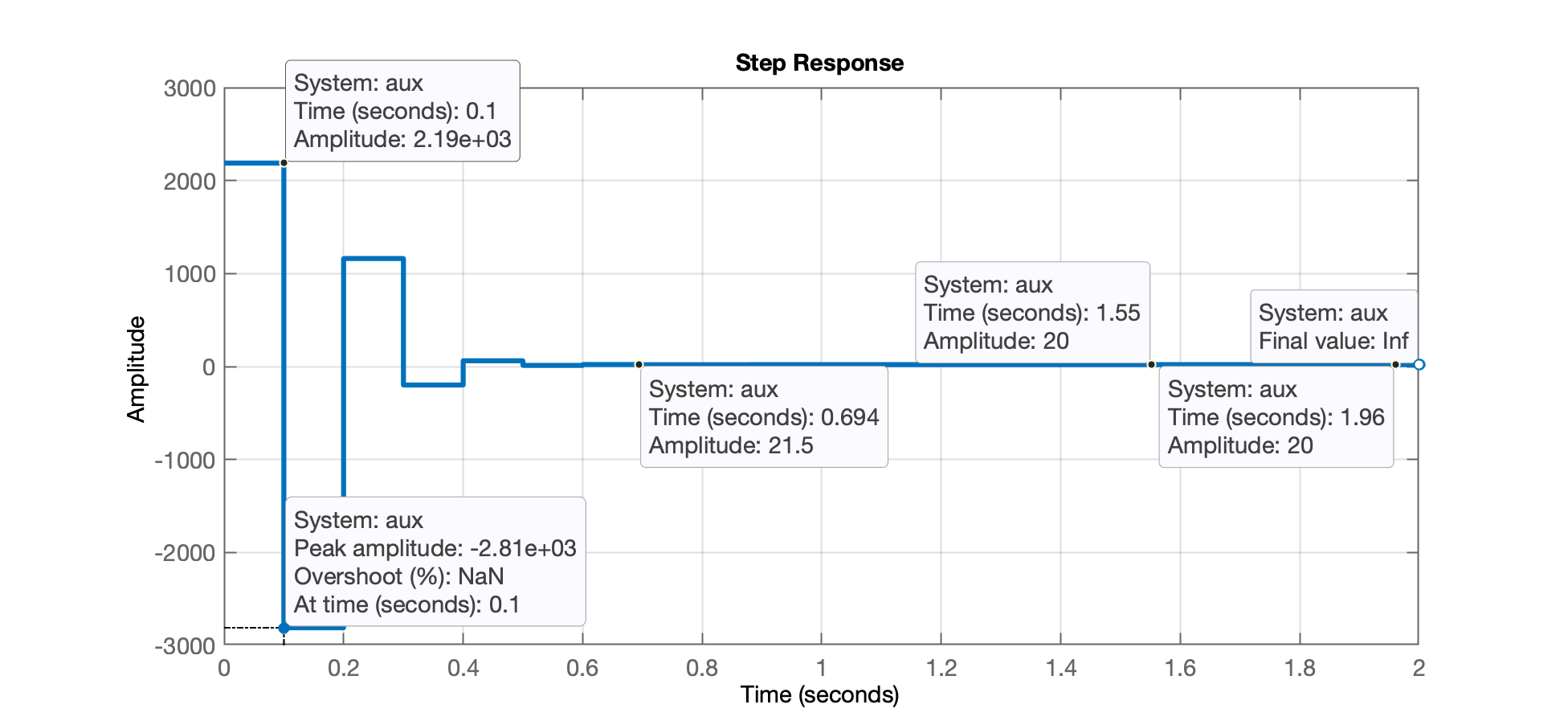

Note ações de controle iniciais entre $+2190$ e $-2810$ convergindo depois de 0,7 segundos para $u[kT] \approx 20$.

Ou seja, este tipo de controlador "cobra seu preço" para fazer o sistema convergir tão rápido ao valor desejado de regime permanente: gera sinais de controle iniciais mais de 140 vezes maior que o valor à ser adotado em regime permanente. Algo provavelmente improvável de ser realizado na prática.

Terminando esta seção de trabalho...

xxxxxxxxxx
>> save dados
>> diary off
>> quit()

💾 dados.mat.

Fernando Passold, em 19/05/2025