Controlador Deadbeat

Conhecido também como controlador do tempo mínimo.

Ideia

O objetivo por trás deste tipo de controlador é fazer o sistema entrar em regime permanente o mais rápido possível, por isto é conhecido também como controlador de tempo mínimo.

Suponha qque se consiga acrescentar um controlador digital à um sistema em malha-fechada de tal forma que a $FTMF(z)$ resulte:

$FTMF(z)=\dfrac{FTMA(z)}{1+FTMA(z)}=\dfrac{1}{z}=z^{-1}$

Isto significa que quando este sistema for exposto à uma entrada degrau unitário, $U(z)=\dfrac{z}{z-1}$, sua resposta em malha-fechada resulta em:

$Y(z) = R(z) \cdot FTMF(z) = \dfrac{ \cancel{z}} {(z-1)} \cdot \dfrac{1}{ \cancel{z} }=z^{-1}+z^{-2}+z^{-3}+\ldots$

ou:

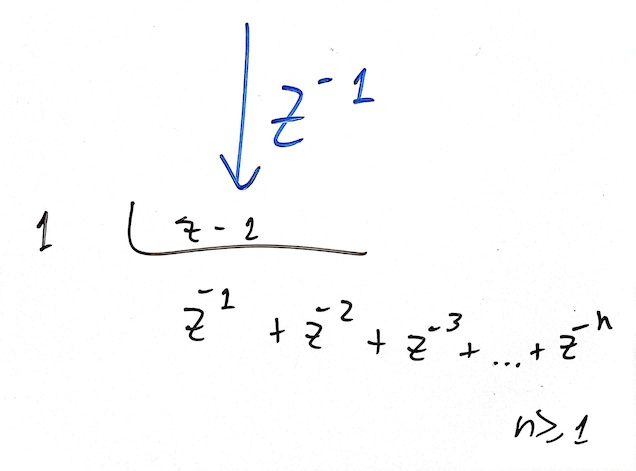
ou seja, a mesmo sinal que um degrau unitário atrasado de um período de amostragem:

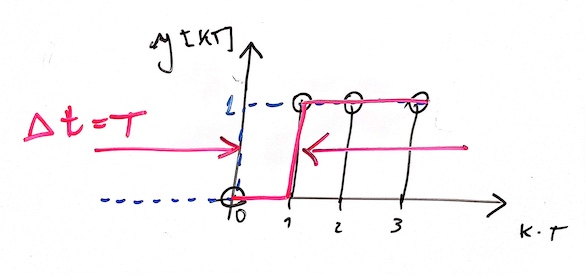
Isto pode ser mais fácil de se obter do que se imagina. Uma opção é que a $FTMA(z)$ final contenha apenas um pólo, em $z=1$, um integrador, o que ainda garantiria erro nulo em regime permanente para sistemas do tipo 0 frente à uma entrada degrau. Isto renderia um RL semelhante ao mostrado abaixo:

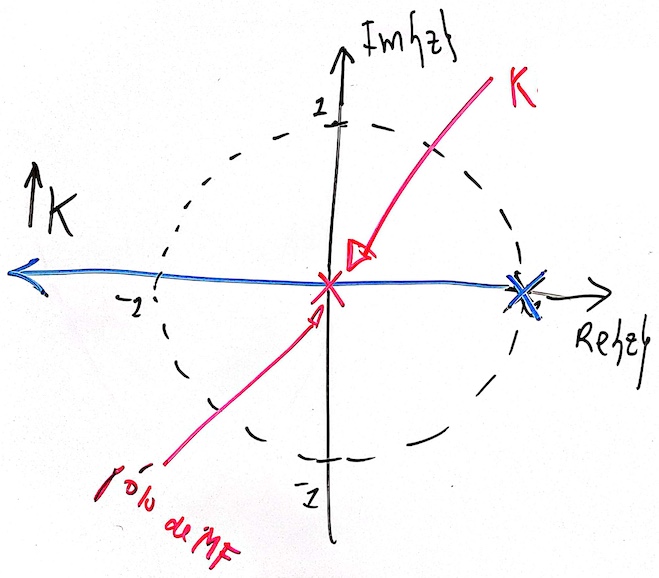
Neste caso, a $FTMA(z)$ assumiria um polinômio do tipo:

$FTMA(z)=\dfrac{1}{z-1}$

Esta $FTMA(z)$ resulta na seguinte $FTMF(z)$ (supondo realimentação unitária):

$\begin{array}{rcl} % FTMF(z) &=& \dfrac{FTMA(z)}{1+FTMA(z)} = \dfrac{ \dfrac{1}{z-1} }{ 1 + \dfrac{1}{z-1} } = \dfrac{ \dfrac{1}{z-1} }{ \dfrac{(z-1)+1}{z-1} } = \dfrac{ \dfrac{1}{ \cancel{(z-1)} } }{ \dfrac{z}{ \cancel{(z-1)} } }\\ % \dfrac{FTMA(z)}{1+FTMA(z)}= \dfrac{ a }{ b }\\ % &=& \dfrac{ \dfrac{1}{z-1} }{ 1 + \dfrac{1}{z-1} }\\ % &=& \dfrac{ \dfrac{1}{z-1} }{ \dfrac{(z-1)+1}{z-1} }\\ % &=& \dfrac{ \dfrac{1}{ \cancel{(z-1)} } }{ \dfrac{z}{ \cancel{(z-1)} } }\\ FTMF(z) &=& \dfrac{1}{z} = z^{-1} \end{array}$

Então o objetivo no momento de propor o controlador digital para que isto ocorra é fazer com que o mesmo anule todos os zeros e pólos "estáveis" (dentro do círculo unitário) de $BoG(z)$ (planta), acrescentando ainda um pólo em $z=1$ (integrador), já que isto ainda garantiria erro nulo para entrada degrau.

Exemplo de Deadbeat

Testando um caso simples, mas antes "limpando" oworkspace do MATLAB:

xxxxxxxxxx
>> clear all % limpando dados da seção de trabalho anterior
>> close all % fechando todas as janelas gráficas da seção de trabalho anterior

Testando um caso simples, seja a planta, $G(s)$:

$G(s)=\dfrac{10}{(s+1)(s+10)}$

amostrada à $T=0,1$ segundos.

xxxxxxxxxx
>> G=tf(10,poly([-1 -10])); % planta
>> T=0.1;
>> BoG=c2d(G, T); % versão "digitalizada" da planta
>> zpk(BoG)
​
ans =
 
   0.035501 (z+0.6945)
  ---------------------
  (z-0.9048) (z-0.3679)
 
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.

Temos que "montar" o controlador que praticamente é uma função transferência inversa da planta, sem incoporar pólos ou zeros instáveis.

xxxxxxxxxx
>> zeros_BoG=zero(BoG)
zeros_BoG =
     -0.69446
>> polos_BoG=pole(BoG)
polos_BoG =
      0.90484
      0.36788
>> C_dead=tf(poly(polos_BoG), poly(zeros_BoG), T)
​
C_dead =
 
  z^2 - 1.273 z + 0.3329
  ----------------------
        z + 0.6945
 
Sample time: 0.1 seconds
Discrete-time transfer function.
​
>> zpk(C_dead)
​
ans =
 
  (z-0.9048) (z-0.3679)
  ---------------------
       (z+0.6945)
 
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.

Até este ponto $c(z)$ seria a tf inversa de $BoG(z)$, mas note que o grau do numerador é maior que o grau do denominador o que levaria a um controlador antecipativo, que neste caso, exigiria uma amostra futura do sinal de erro ($e[k+1]$)!.

Falta igualar o grau do numerador com o grau do numerador, normalmente incorporando um integrador, o que, para o caso desta planta (sistema tipo 0), ainda vai garantir erro nulo para regime permanente (rever Teoria do Erro se for o caso).

xxxxxxxxxx
>> C_dead=tf(poly(polos_BoG), poly([zeros_BoG  1]), T) % acrescentamos o pólo em z=1 (integrador) na tf do C(z)
​
C_dead =
 
  z^2 - 1.273 z + 0.3329
  -----------------------
  z^2 - 0.3055 z - 0.6945
 
Sample time: 0.1 seconds
Discrete-time transfer function.
​
zpk(C_dead)
​
ans =
 
  (z-0.9048) (z-0.3679)
  ---------------------
    (z-1) (z+0.6945)
 
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.

Continuando o projeto:

xxxxxxxxxx
>> ftma_dead=C_dead*BoG;
>> zpk(ftma_dead)
​
ans =
 
  0.035501 (z+0.6945) (z-0.9048) (z-0.3679)
  -----------------------------------------
   (z+0.6945) (z-0.9048) (z-1) (z-0.3679)
 
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.

Note o cancelamento de termos:

$FTMA_{Dead}(z) = \dfrac{0.035501 \cdot K_{Dead} \cdot \cancel{(z+0.6945)} \bcancel{(z-0.9048)} \cancel{(z-0.3679)} }{ \cancel{(z+0.6945)} \bcancel{(z-0.9048)} (z-1) \cancel{(z-0.3679)} }$

e assim resta apenas:

$FTMA_{Dead}(z) = \dfrac{0.035501 \cdot K_{Dead}} { (z-1)}$

ou seja, teríamos um RL com apenas 1 pólo de MF, iniciando da posição $z=1$ (integrador).

No MATLAB é possivel realizar estes cancelamentos de termos comuns entre numerador e denominador usando a função minreal():

xxxxxxxxxx
>> ftma_dead_r = minreal(ftma_dead)
​
ftma_dead_r =
 
  0.0355
  ------
  z - 1
 
Sample time: 0.1 seconds
Discrete-time transfer function.

Então por fim, teremos o RL esperado:

xxxxxxxxxx
>> rlocus(ftma_dead)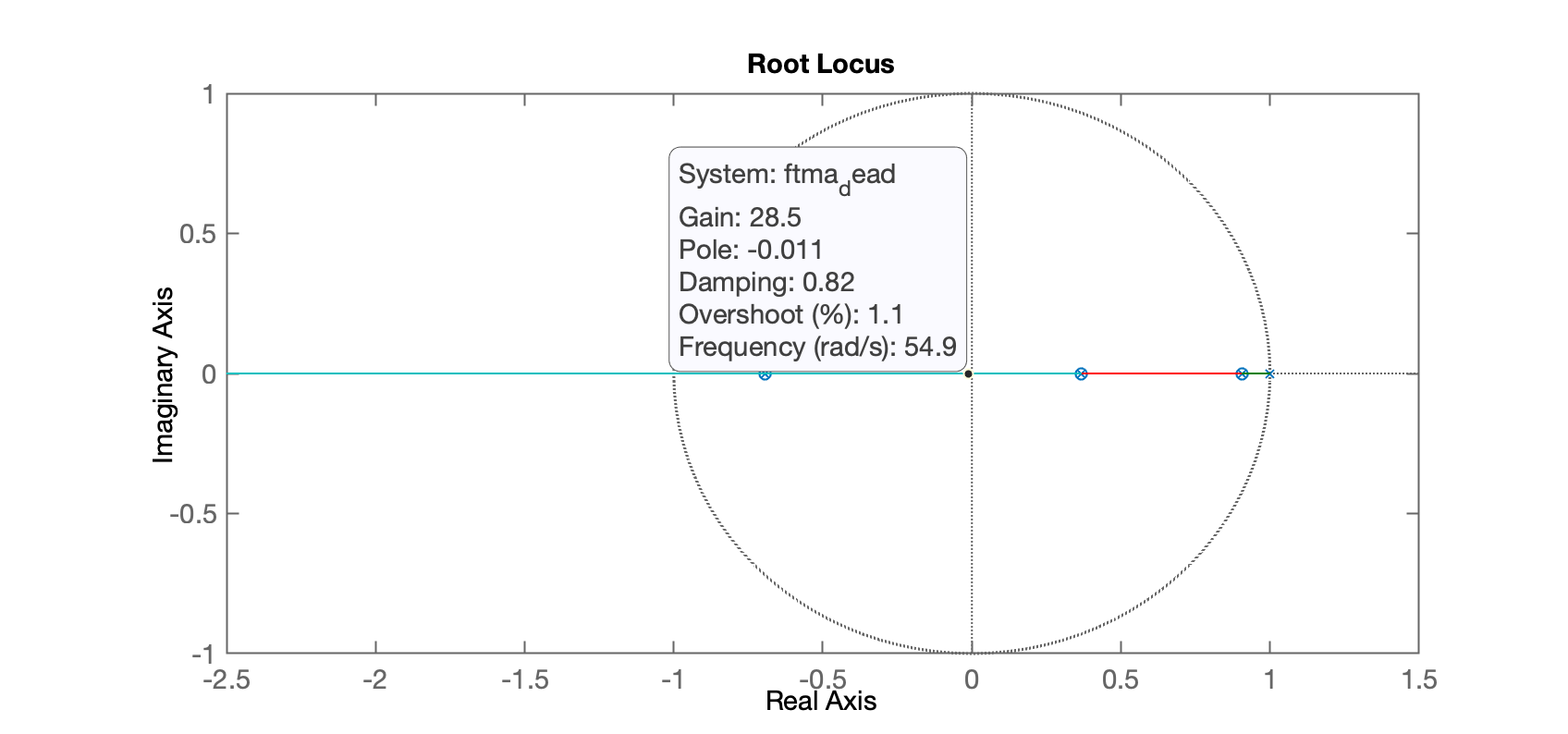

Falta apenas definir o ganho do controlador. Note que o objetivo seria obter:

$FTMA_{Dead}(z) = \dfrac{1}{z-1}$ (um simples integrador)

o que levaria à $FTMF(z)$:

$FTMF(z)= \dfrac{FTMA(z)}{1+FTMA(z)} = \dfrac{ \dfrac{1}{(z-1)} }{1 + \dfrac{1}{(z-1)} } = \dfrac{ \dfrac{1}{ \cancel{(z-1)} } }{ \dfrac{z -1 +1}{ \cancel{(z-1)} } } = \dfrac{1}{z} = z^{-1}$

ou seja, quando $R(z)=\dfrac{1}{(z-1)}$ (degrau), o sistema irá responder como:

$Y(s) = R(z) \cdot FTMF(z)$

$Y(z) = \dfrac{1}{(z-1)} \cdot z^{-1}$

ou seja, $y[k] = r[k-1]$, isto é, $y[k]=$ degrau atrasado de um período de amostragem (ou apenas pelo período de tempo $T$). Ou seja, obtemos o controlador de tempo mínimo ou deadbeat.

Note que:

• $FTMF(z)=z^{-1}= \frac{1}{z}$, equivale a posicionar o pólo de MF na origem do plano-z.
• O RL inicia no pólo em MA localizado em $z=1$ (integrador). O traçado do Rl inicia neste ponto, em $z=1$ e segue na direção de $z \to -\infty$ à medida que o ganho do controlador aumenta.
• A idéia é ajustar o ganho do controlador de tal forma que o RL passe pela origem do plano-z, o que implica na resposta ao degrau atrasado em apenas 1 período de amostragem, ou graficamente:

Respostas ao degrau, pólo real simples, no plano-z:

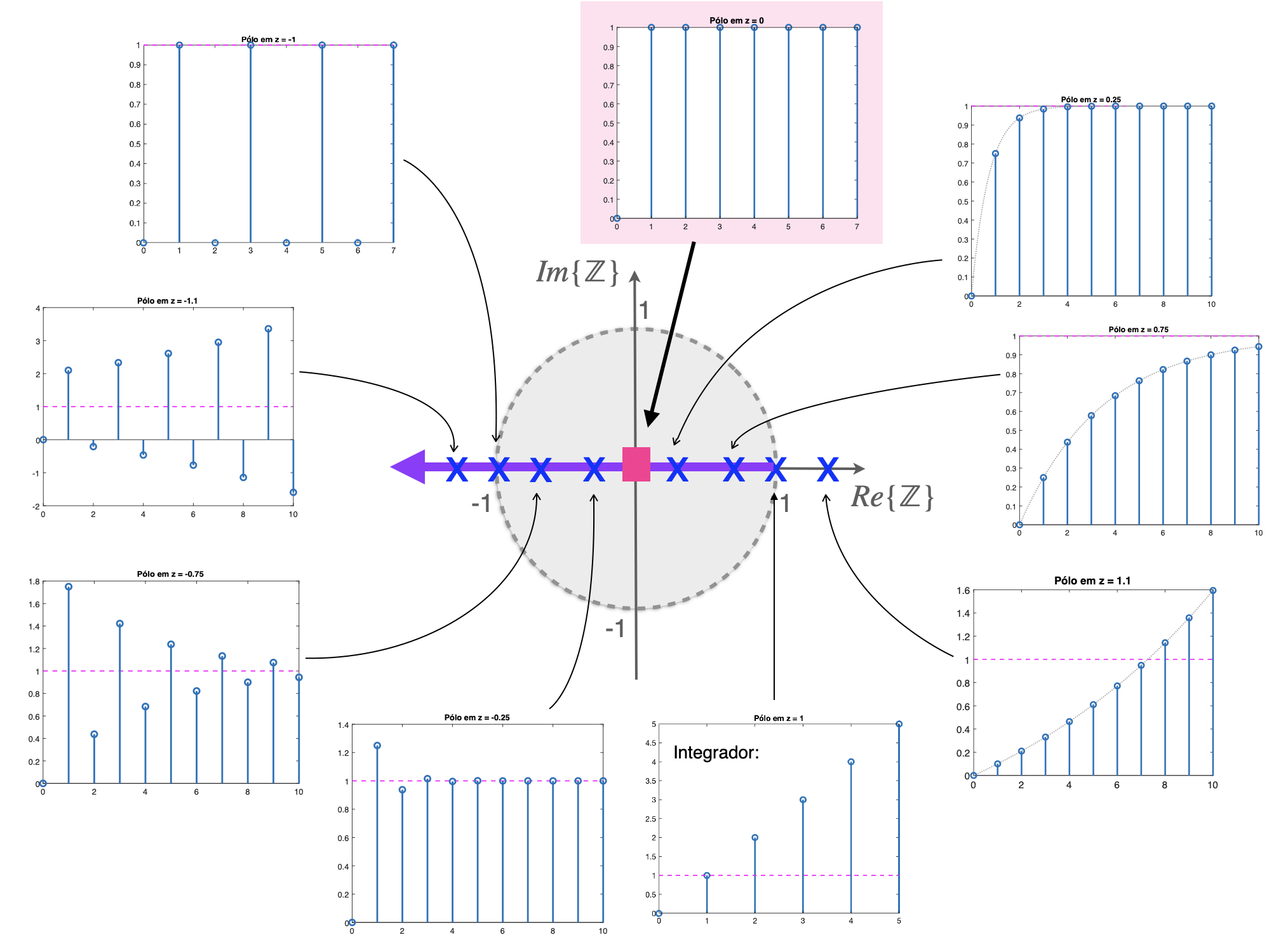Voltando ao caso do nosso exemplo, significa definir o valor de ganho do controlador, de tal forma que o pólo de MF seja posicionado em $z=0$ (na origem), ou: $FTMF(z)=1 \cdot z^{-1}$. Assim sendo:

xxxxxxxxxx
>> ftma_dead_r
​
ftma_dead_r =
 
  0.0355
  ------
  z - 1
 
Sample time: 0.1 seconds
Discrete-time transfer function.
​
>> K_dead=1/0.035501
K_dead =
       28.168
>> ftmf_dead=feedback(K_dead*ftma_dead, 1)
​
ftmf_dead =
 
          z^3 - 0.5783 z^2 - 0.551 z + 0.2312
  ---------------------------------------------------
  z^4 - 0.5783 z^3 - 0.551 z^2 + 0.2312 z - 2.705e-06
 
Sample time: 0.1 seconds
Discrete-time transfer function.
​
>> zpk(ftmf_dead)
​
ans =
 
        (z+0.6945) (z-0.9048) (z-0.3679)
  ---------------------------------------------
  (z+0.6945) (z-0.9048) (z-0.3679) (z-1.17e-05)
 
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.

Ou seja, note como terminou a $FTMF(z)$:

$FTMF(z)=\dfrac{ \cancel{(z+0.6945)} \bcancel{(z-0.9048)} \cancel{(z-0.3679)} }{ \cancel{(z+0.6945)} \bcancel{(z-0.9048)} \cancel{(z-0.3679)} (z-\underbrace{1.17 \times 10^{-5}}_{\cong 0})} = \dfrac{1}{z} = z^{-1}$

Comprovando que a resposta será um degrau atrasado de um período de amostragem:

xxxxxxxxxx
>> figure; step(ftmf_dead)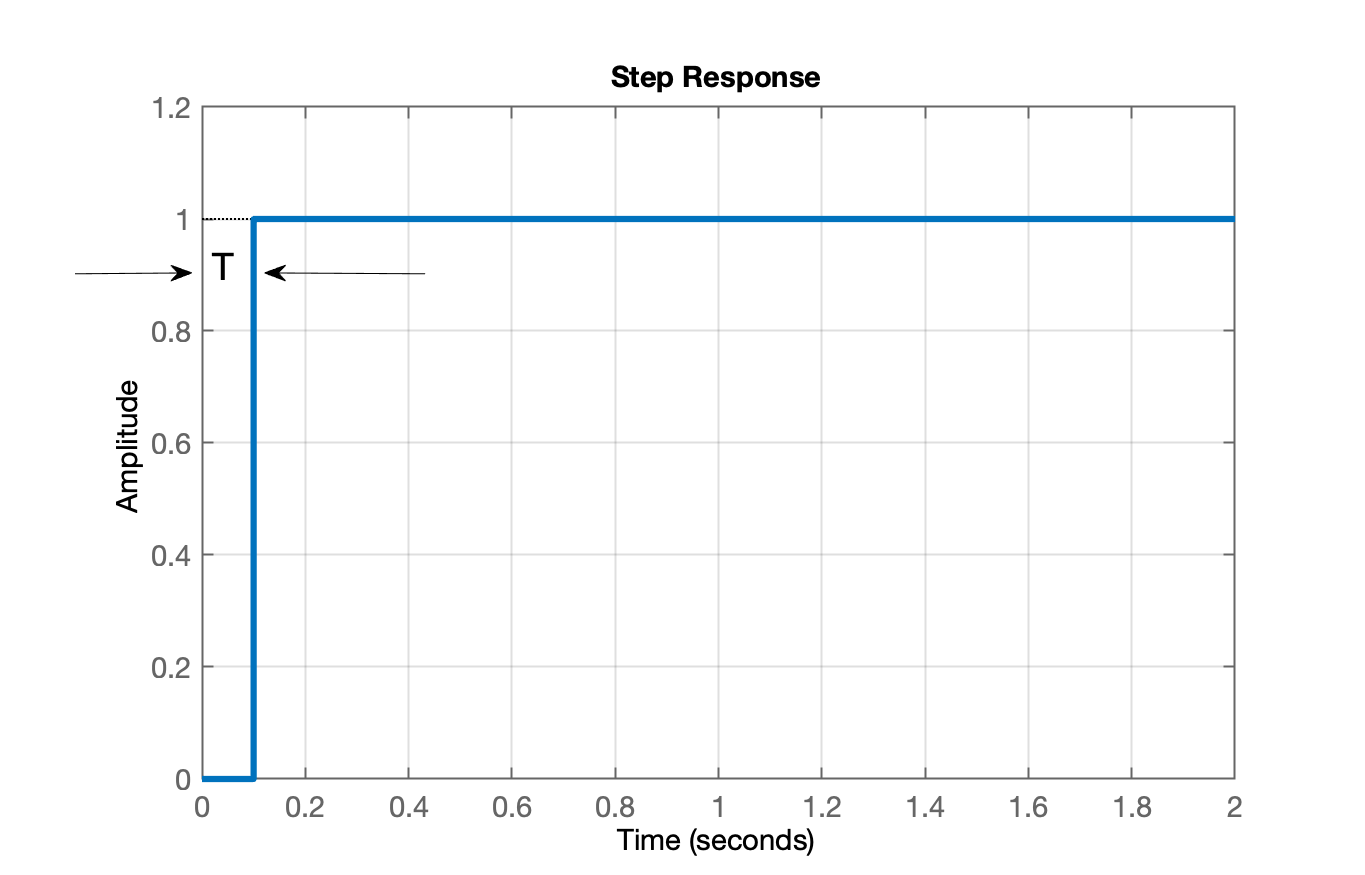

Amplitudes do sinal atuador

Mas... existe um porém, fique atento para as amplitudes desenvolvidas para o sinal de controle.

Calculando agora as amplitudes desenvolvidas pelo sinal de controle, $u[kT]$ (ou tendo uma idéia do "esforço de controle"). Para saber mais sobre como na janela de comanddos do MATLAB obter os gráficos de $u[k]$ ou $e[k]$, ver: Como obter gráficos de u[k] e e[k] na linha de comandos do Matlab.

xxxxxxxxxx
>> % Calculando a tf associada com cálculo de u[k]
>> u_aux = (K_dead*C_dead)/(1+K_dead*ftma_dead);
>> zpk(u_aux)   % a título de curiosidade (apenas para inspeção)
​
ans =
 
    28.168 (z+0.6945) (z-0.9048)^2 (z-1) (z-0.3679)^2
  -----------------------------------------------------
  (z+0.6945)^2 (z-0.9048) (z-1) (z-0.3679) (z-1.17e-05)
 
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.
​
>> figure; step(u_aux)

E agora podemos observar de que maneira este controlar força a planta à reagir no tempo mínimo:

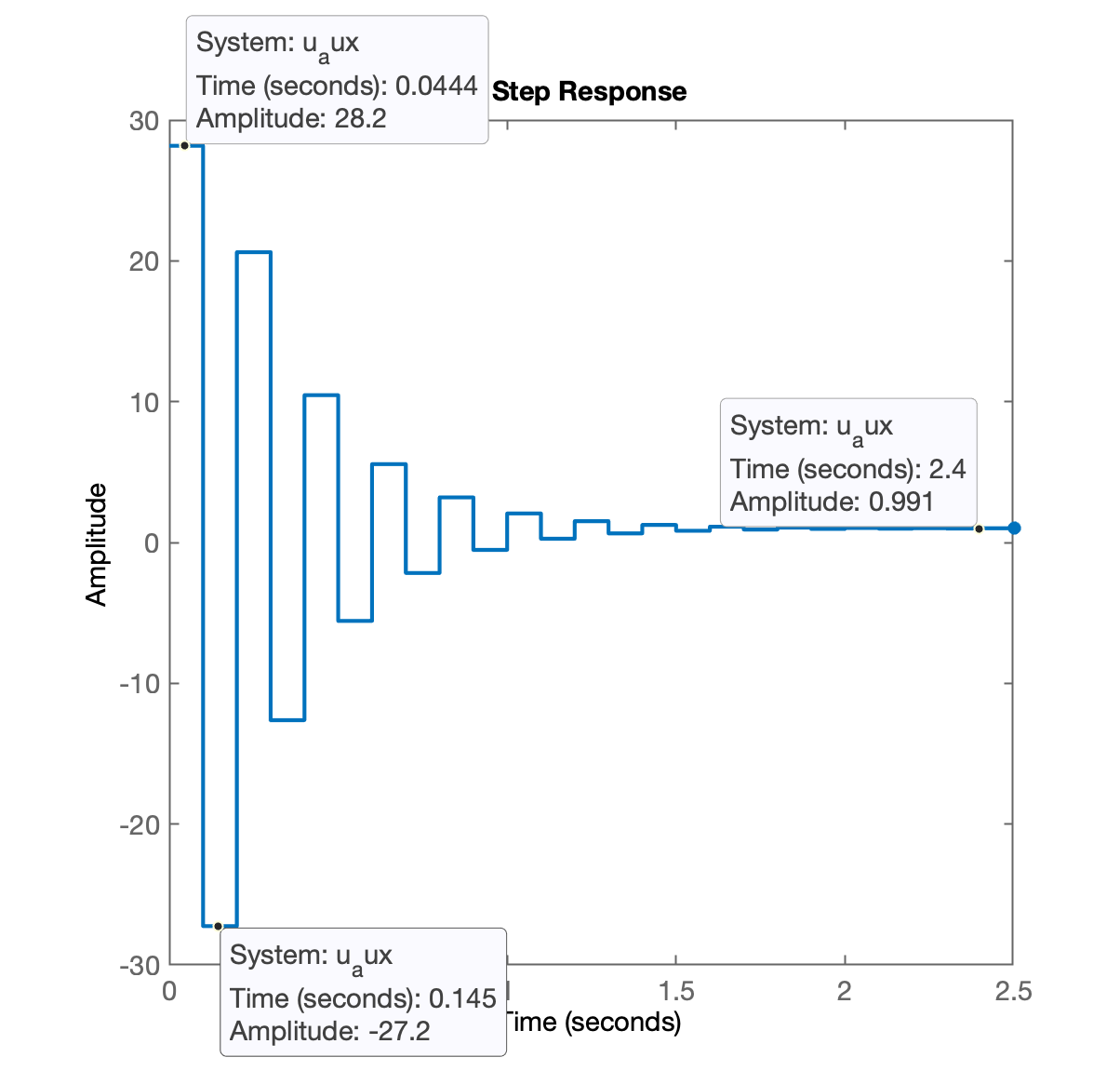
Note as amplitudes bastantes elevadas (tanto positivas, quanto negativas) desenvolvidas pelo sinal de controle na fase inicial transitória. Perceba que são gerados valores quase 30 vezes maiores que o valor em regime permanente de $u[k]$ ($28,2/0,991 = 28,4561049445$).

Outras respostas (resposta "programada")

Outro tipo de resposta ainda pode ser "programada". Por exemplo, para uma referência (entrada) degrau, se espera uma resposta do tipo:

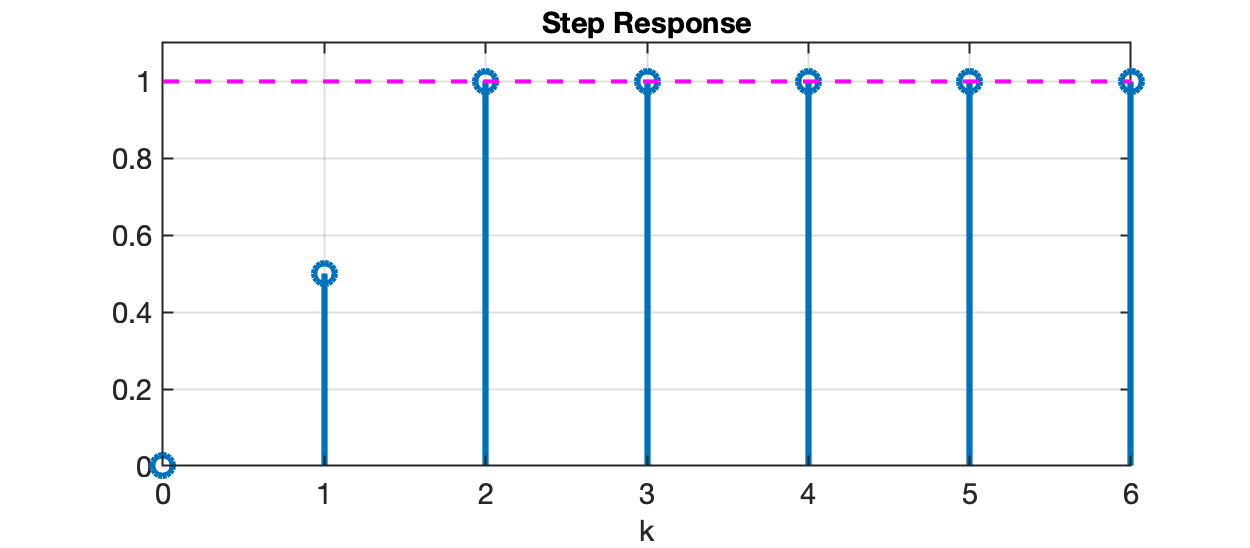
ou seja:

$Y(z)=0 \cdot z^{0} + 0,5 \cdot z^{-1} + 1 \cdot z^{-2} + 1 \cdot z^{-3} + 1 \cdot z^{-4} + \ldots$

o que implica num sinal de erro como:

$E(z)=1 \cdot z^{0} + 0,5 \cdot z^{-1} + 0 \cdot z^{-2} + 0 \cdot z^{-3} + \ldots$

$E(z)=1+0,5z^{-1}$

$E(z)=\big( 1+0,5z^{-1} \big) \cdot \dfrac{z^{1}}{z^{1}}$

$E(z)=\dfrac{z+0,5}{z}$

Mas note que podemos definir a eq. do controlador, $C(z)$ em função do erro, $E(z)$ e de $BoG(z)$.

Note que:

$FTMF(z) = \dfrac{C(z) \cdot BoG(z)}{1 + C(z) \cdot BoG(z)}$

$FTMF(z) \big[ 1 + C(z) BoG(z) \big] = C(z) BoG(z)$

$FTMF(z) + FTMF(z) C(z) BoG(z) = C(z) BoG(Z)$

$C(z) BoG(z) FTMF(z) = C(z) BoG(z) - FTMF(z)$

$C(z) BoG(z) - FTMF(z) = C(z) BoG(z) FTMF(z)$

$C(z) \Big[ BoG(z) - BoG(z) FTMF(z) \Big] = FTMF(z)$

$C(z) = \dfrac{ FTMF(z) }{ BoG(z) \Big[ 1 - FTMF(z) \Big] }$

Se conhecemos a $FTMF(z)$ desejada e conhecemos $BoG(z)$, temos como projetar C(z).

Antes, a $FTMF(z)$ desejada era do tipo: $FTMF(z)= \dfrac{1}{z}$, o que resultava em:

$C(z)= \dfrac{ \dfrac{1}{z} }{ BoG(z) \left( 1 - \dfrac{1}{z} \right) } = \dfrac{ \dfrac{1}{z} }{ BoG(z) \dfrac{\left( z-1 \right)}{z} } = \dfrac{1}{ BoG(z)(z - 1)}$

ou seja, a eq. de $C(z)$ era o inverso de $BoG(z)$ acrescido de um pólo em $z=1$.

Agora para obter este sinal de erro, a $FTMF(z)$ deve ser do tipo:

$E(z) = R(z) - Y(z)$

$Y(z) = R(z) - R(z) \cdot FTMF(z)$

$E(z) = R(z) - R(z) FTMF(z)$

$E(z) = R(z) \left[ 1 - FTMF(z) \right]$

$E(z) = R(z) - R(z) FTMF(z)$

$R(z) FTMF(z) = R(z) - E(z)$

$FTMF(z) = \dfrac{R(z) - E(z)}{R(z)}$

Se $R(z)$ é uma entrada degrau, então: $R(z)=\dfrac{z}{z-1}$, e:

$E(z)=\dfrac{z+0,5}{z}$, teremos:

$FTMF(z) = \dfrac{ \left(\dfrac{z}{z-1}\right) - \left(\dfrac{z+0,5}{z}\right) }{ \dfrac{z}{z-1} }$

$FTMF(z) = \dfrac{ \dfrac{z^2 - (z^2 -0,5z -0,5)}{z(z-1)} }{ \dfrac{z}{z-1} }$

$FTMF(z) = \dfrac{ \dfrac{0,5(z+1)}{z(z-1)} }{ \dfrac{z}{z-1} }$

$FTMF(z) = \dfrac{ 0,5(z+1)}{z^2}$

Note:

xxxxxxxxxx
>> ftmf_d=tf(0.5*poly(-1), [1 0 0], T);
>> figure; step(ftmf_d)

Rende:

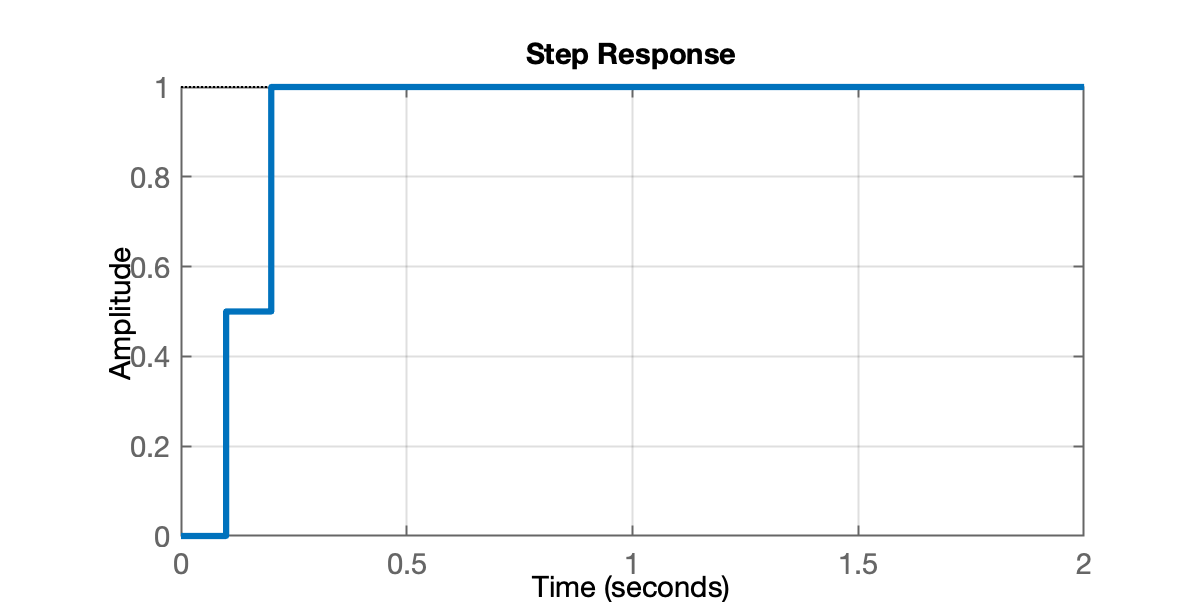
Continuando, $C(z)$ deve ficar:

$C(z) = \dfrac{ FTMF(z) }{ BoG(z) \left[ 1 - FTMF(z) \right] } = \dfrac{ \dfrac{0,5(z+1)}{z^2} }{ BoG(z) \left[ 1 - \dfrac{0,5(z+1)}{z^2} \right] }$

$C(z) = \dfrac{ \dfrac{0,5(z+1)}{z^2} }{ BOG(z) \left[ \dfrac{z^2-0,5z-0,5}{z^2} \right] } = \dfrac{ 0,5(z+1)}{ BoG(z) \left( z^2 -0,5z -0,5\right) }$

$C(z) = \dfrac{ 0,5(z+1) }{ BoG(z) \left[ (z-1)(z+0,5) \right]}$

Como: $BoG(z)= \dfrac{0.035501 (z+0.6945)}{(z-0.9048) (z-0.3679)}$, então finalmente:

$C(z) = \dfrac{ 0,5(z+1) (z-0.9048) (z-0.3679)}{ 0.035501 (z+0.6945) (z-1)(z+0,5) }$

Testando:

xxxxxxxxxx
>> C2=ftmf_d/(BoG*(1-ftmf_d)); % deixando o MATLAB compor a `tf`
>> zpk(C2)
​
ans =
 
  14.084 z^2 (z+1) (z-0.9048) (z-0.3679)
  --------------------------------------
       z^2 (z-1) (z+0.6945) (z+0.5)
 
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.
​
>> C2r=minreal(C2,1e-4); % cancelando termos comuns
>> zpk(C2r)
​
ans =
 
  14.084 (z+1) (z-0.9048) (z-0.3679)
  ----------------------------------
       (z-1) (z+0.6945) (z+0.5)
 
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.
​
>> ftma2=C2*BoG;
>> ftma2r=minreal(ftma2,1e-4); % cancelando termos comuns
>> zpk(ftma2r)
​
ans =
 
    0.5 (z+1)
  -------------
  (z-1) (z+0.5)
 
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.
​
>> ftmf2=feedback(ftma2r,1);
>> zpk(ftmf2)
​
ans =
 
      0.5 (z+1)
  -----------------
  (z^2 + 2.165e-15)
 
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.
​
>> figure; step(ftmf2)

E temos o resultado:

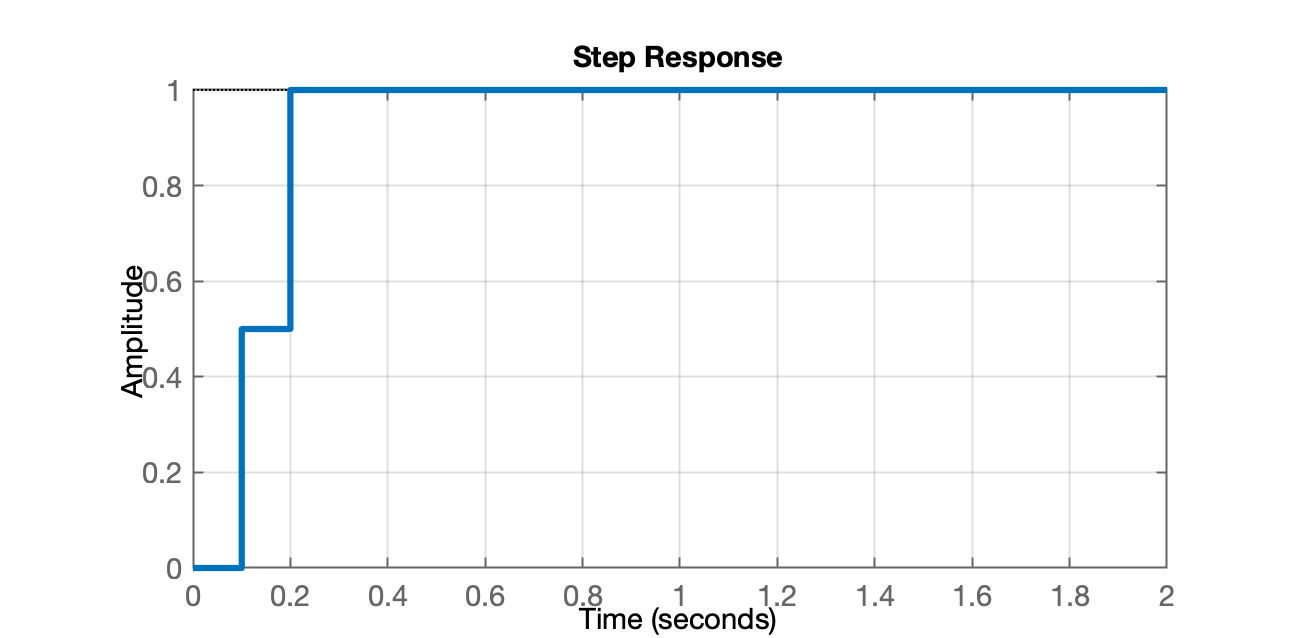
Por curiosidade, podemos tentar levantar o RL para este sistema:

xxxxxxxxxx
>> zpk(C2)
​
ans =
 
  14.084 z^2 (z+1) (z-0.9048) (z-0.3679)
  --------------------------------------
       z^2 (z-1) (z+0.6945) (z+0.5)
 
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.
​
>> C2_aux=C2/14.084;
>> zpk(C2_aux)
​
ans =
 
  z^2 (z+1) (z-0.9048) (z-0.3679)
  -------------------------------
   z^2 (z-1) (z+0.6945) (z+0.5)
 
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.
​
>> ftma_aux=C2_aux*BoG;
>> figure; rlocus(ftma_aux)
>> hold on
>> pole(ftmf2)
ans =
   -2.498e-15 + 4.6529e-08i
   -2.498e-15 - 4.6529e-08i
>> plot(real(pole(ftmf2)), imag(pole(ftmf2)), 'r+')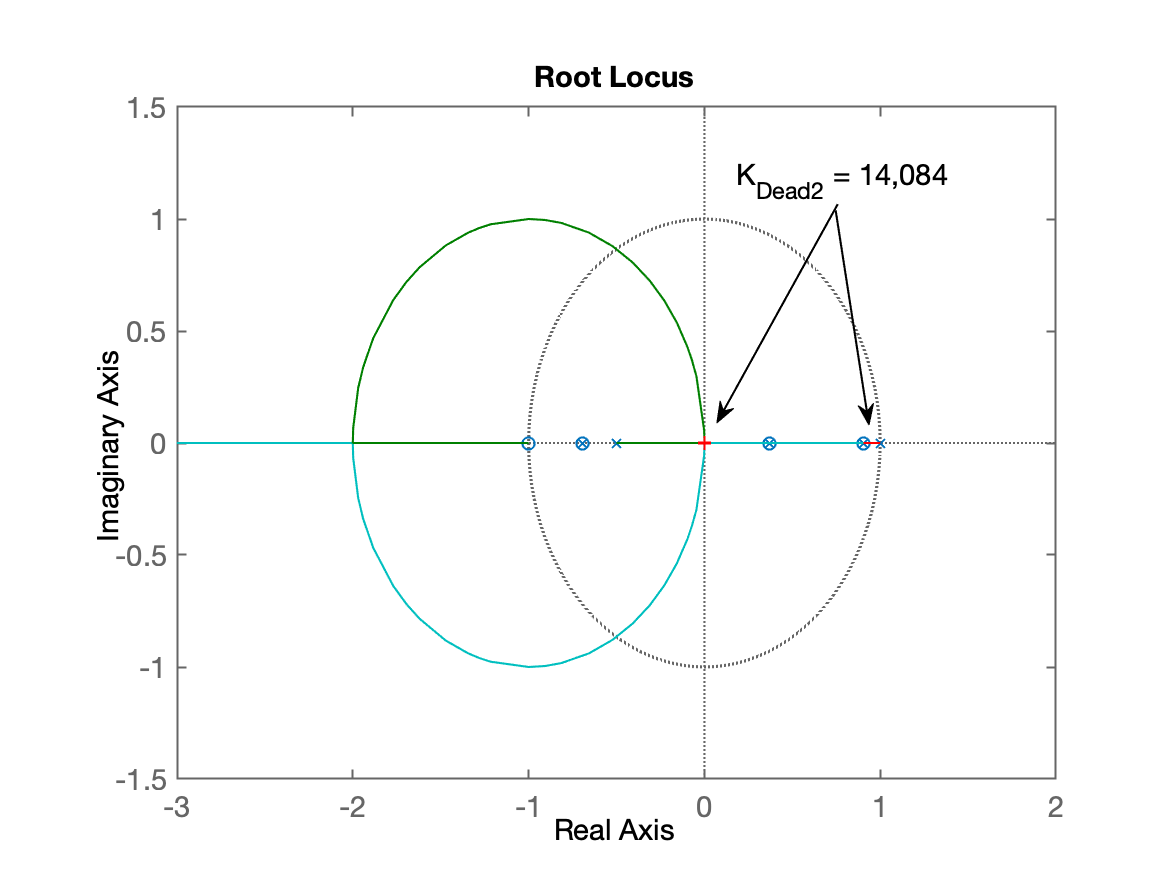

No gráfico acima pode ficar um pouco complicado para entender o que aconteceu, então vamos "simplificar" um pouco:

xxxxxxxxxx
>> zpk(ftma_aux)
​
ans =
 
  0.035501 z^2 (z+1) (z+0.6945) (z-0.9048) (z-0.3679)
  ---------------------------------------------------
  z^2 (z+0.6945) (z+0.5) (z-0.9048) (z-1) (z-0.3679)
 
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.
​
>> ftma_aux_r=minreal(ftma_aux,1e-4);
>> zpk(ftma_aux_r)
​
ans =
 
  0.035501 (z+1)
  --------------
  (z-1) (z+0.5)
 
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.
​
>> ftma_aux_r2=ftma_aux_r/0.035501;
>> figure; rlocus(ftma_aux_r2)
>> hold on
>> plot(real(pole(ftmf2)), imag(pole(ftmf2)), 'r+')
>> xlim([-3 2])
>> ylim([-1.5 1.5])

E temos um RL mais simplicado, onde os cancelamentos de pólos e zeros "estáveis" de $BoG(z)$ não aparecem:

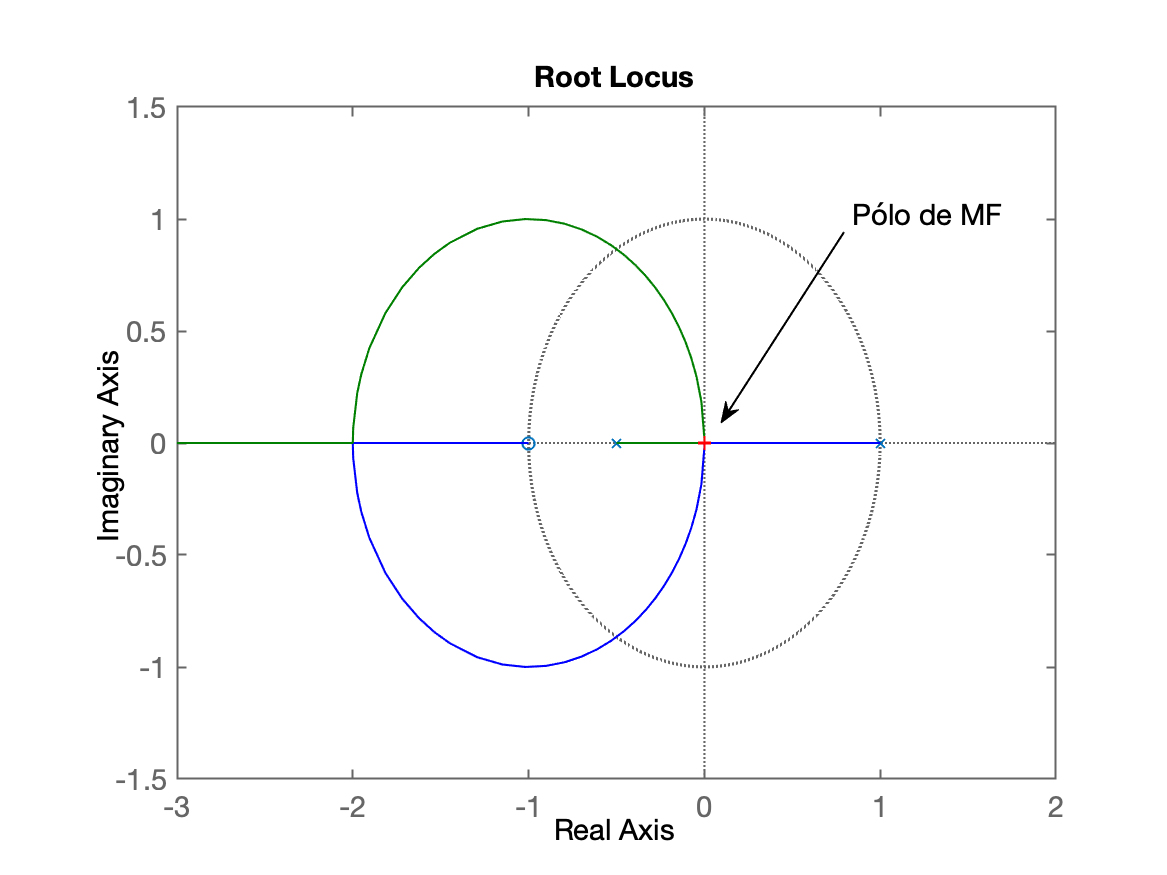
O dados usados para este exemplo estão disponíveis em dead.mat.

Referências sobre Controladores Deadbeat

• J. Hetthéssy, A. Barta, R. Bars: Dead beat controller design, Publicado em Nov/2004 (acessado em 06/05/2025);
• NPTEL (National Programme on Technology Enhanced Learning - Phase II), Dept. of Electronics and Electrical Eng., Indian Institute of Technology Guwahati, Assam, India: Digital Control System - Web course, Module No. 6: Deadbeat response design, Lecture 1: Design of digital control systems with deadbeat response, Lecture 2: Practical issues with deadbeat response design, Lecture 3: Sampled data control systems with deadbeat response. Publicado em 27/06/2012, (acessado em 06/05/2025).

Outras opções para tempo mínimo

Observe que se $FTMF(z)$ resulta algo como $FTMF(z)=z^{-5}$, podemos tentar fazer o sistema reagir com atraso de $n$ amostras de período de amostragem.

$\begin{array}{rcl} % FTMF(z) &=& z^{-5}\\ % &=& \dfrac{1}{z^5}\end{array}$

Resolvendo o restante no MATLAB:

Fernando Passold, em 06/05/2025