Entendendo Root Locus & Respostas Temporais

Objetivo: A idéia aqui é usar comandos simples do Matlab para entender como o root locus é formado e qual a relação entre os pólos de malha-fechada e respostas temporais de um processo em malha-fechada submetido à uma entrada degrau.

Se sugere fortemente uma eventual revisão do material Respostas Transitórias de Sistemas Lineares.

Neste documento, vamos explorar um root locus formado quando se fecha uma realimentação para uma planta como:

$G(s)=\dfrac{1}{s (s+10)}$

ou na forma de um diagrama de blocos:

Esta é a mesma planta que aparece no slide No. 9 de Lugar Geométrico das Raízes (ou root-locus).

Iniciando o Matlab 🎧:

📝 Assim que você entrar no Matlab recomendo que crie um "log" da seção da trabalho. Para tanto, ative a função: diary <arquivo.txt>:

xxxxxxxxxx
>> diary aula_26042024.txt      % recomendo acrescentar extensão .txt

Ingressando uma função transferência $G(s)$ no Matlab usando a função tf (num, den), onde num e den se referem aos polinômios (em s) referentes ao numerado e denominador da função transferência:

xxxxxxxxxx
>> % G = tf(num,den)
>>
>> num=1;
>> den=[1 10 0];
>> G = tf(num,den)
​
G =
 
      1
  ----------
  s^2 + 10 s
 
Continuous-time transfer function.
​
>> % A expressão acima não permite reconhecer prontamente os
>> % pólos, zeros e o "ganho". Usamos a função: zpk(<tf-object>)
>>zpk(G)
 
     1
  --------
  s (s+10)
 
Continuous-time zero/pole/gain model.

A idéia agora é compravar as raízes do denominador, que seriam os pólos do sistema. Usaremos a função: roots(<vetor-polinômio>).

xxxxxxxxxx
>> roots(den)
ans =
     0
   -10

Neste caso, obtermos resposta esperada, uma planta com pólos em $s=0$ e $s=-10$.

Mas poderíamos ter isolado diretamente os pólos à partir de uma transfer-function, usando a função pole():

xxxxxxxxxx
>> pole(G)
ans =
     0
   -10

Vamos fechar a malha, através de uma simples realimentação unitária. Usaremos a função: feedback():

xxxxxxxxxx
>> % ftmf=feedback(K*G, H, -1) 

A próxima figura exemplifica à que correspondem os atributos de entrada $G$ e $H$:

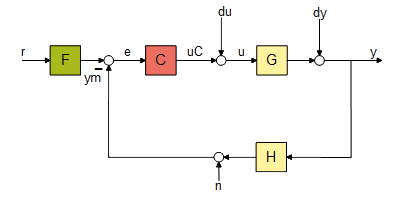
Neste caso, $H(s)=1$ (não há funrção transferência associada com um sensor retratando limitações de banda passante do mesmo). A função transferência $H(s)$ seria similar a um filtro passa-baixas, com certa freq. de corte (ou largura de banda do sensor). Normalmente, o sensor responde mais rápido que a planta (salvo casos de "retrições orçamentárias").

O terceiro parâmetro de entrada da função feedback, confirma o sinal da realimentação, "$-1$" corresponde a uma tradiconal realimentação negativa. Se este terceiro parâmetro não for informado o Matlab subentende que trata-se de realimentação negativa. Se por acaso for "$+1$", corresponderia à uma realimentação positiva (menos usual).

Neste caso, $H(s)=1$, então vamos acabar estabelecendo uma realimentação unitária.

Note ainda que apesar de não estarmos indicando explicitamente nenhum ganho nno comando abaixo, fica implícito (matematicamente) que estaríamos fechando a malha, com ganho unitário:

$K*G(s)$, se $K=1$, implica em: $1 \cdot G(s)=G(s)$

xxxxxxxxxx
>> ftmf=feedback(G, 1)
​
ftmf =
​
        1
--------------
  s^2 + 10 s + 1
​
Continuous-time transfer function.
​

Note que a equação acima corresponde ao que teria ocorrido se tivéssemos fechado a malha de modo analítico (algébrico):

$FTMF(s) = \dfrac{K \, G(s)}{1+K\,G(s)} = \dfrac{ \frac{K}{s(s+10)} }{ 1 + \frac{K}{s(s+10)} } = \dfrac{K}{ s(s+10)+K}$

$FTMF(s)=\dfrac{K}{s^2+10s+K}$

Se $K=1$, teremos:

$FTMF(s)=\dfrac{1}{s^2+10s+1}$

Comprovando o local dos pólos de MF, mesmo para K=1 (ganho unitário):

xxxxxxxxxx
>> pole(ftmf)
ans =
       -9.899
     -0.10102

Podemos comprovar que um root-locus inicia à partir dos pólos de MA do sistema adotando explicitamente um ganho muito baixo (no caso, $K = 0,01$):

xxxxxxxxxx
>> ftmf=feedback(0.01*G, 1);
pole(ftmf)
ans =
       -9.999
   -0.0010001

Note que estes pólos de MF para um valor tão baixo de ganho, praticamente coincidem com a posição dos pólos de MA do sistema repassado para o root-locus.

Vamos aumentar o ganho gradualmente para perceber como os pólos de MF "caminham" no plano$-s$:

xxxxxxxxxx
>> ftmf=feedback(5*G, 1);   % Fechando malha com ganho, K=5
>> pole(ftmf)
ans =
      -9.4721
     -0.52786

Podemos verificar a nova posição assumida para os pólos de MF se aumentamos mais o ganho:

xxxxxxxxxx
>> ftmf=feedback(15*G, 1);
>> pole(ftmf)
ans =
      -8.1623
      -1.8377

Aumentando um pouco mais o ganho:

xxxxxxxxxx
>> ftmf=feedback(25*G, 1);
>> pole(ftmf)
ans =
    -5
    -5

Note os pólos "caminhando", um em direção ao outro (para este caso de sistema).

Mas... Seria mais interessante "graficar" a trajetória dos pólos de MF. Então vamos "plotar" os pólos de MF no plano-z.

Voltando aos pólos de MF, com $K=15$:

xxxxxxxxxx
>> ftmf=feedback(15*G, 1);
>> pzmap(G)             % mostra no plano-s os pólos e zeros da transfer-function
>> hold on              % "segura as pontas", isto é, os próximos comandos gráficos serão
>>                      % sobrepostos no gráfico anterior
>> pzmap(pole(ftmf))    % a idéia é plotar os pólos de MF
Error using pzmap
Wrong number of input arguments.
>>
>> % Ok, houve um erro. Simplesmente nos esquecemos que pzmap() não aceita como
>> % argumento de entrada, variável que não seja transfer-function
>> % Então vamos usar a função: plot(x,y)
>> % E para isto, necessitamos primeiramente "guardar" as posições destes pólos de MF:
>> polesMF = pole(ftmf)
polesMF =
      -8.1623
      -1.8377
>> % Ok, Não podemos fazer: plot(polesMF) porque o Matlab vai interpretar que cada
>> % um dos pólos de MF calculado anteriormente será transformado numa "altura",
>> % coordenada no eixo Y (a coordenada no eixo X corresponderá à ordem do polo: 1 ou 2)
>> % E então nos lembramos que o plano-s é um plano cartesiano complexo, onde o 
>> % eixo X corresponde à parte real de pólos ou zeros, e o eixo Y corresponde à
>> % para imaginária dos pólos ou zeros.
>> % Felizmente o Matlab consegue "separar" as partes reais e imaginárias de um
>> % número complexo:
>> real(polesMF)
ans =
      -8.1623
      -1.8377
>> imag(polesMF)
ans =
     0
     0
>> % Então agora basta plotar (acrescentar no gráfico anterior), os novos pólos de MF:
>> plot( real(polesMF), imag(polesMF), 'r+')
>> % O terceiro parâmetro "r+" significa cor red (vermelho) com marcador "+"

Até este ponto, teremos um gráfico dos plano-s para este sistema, parecido com:

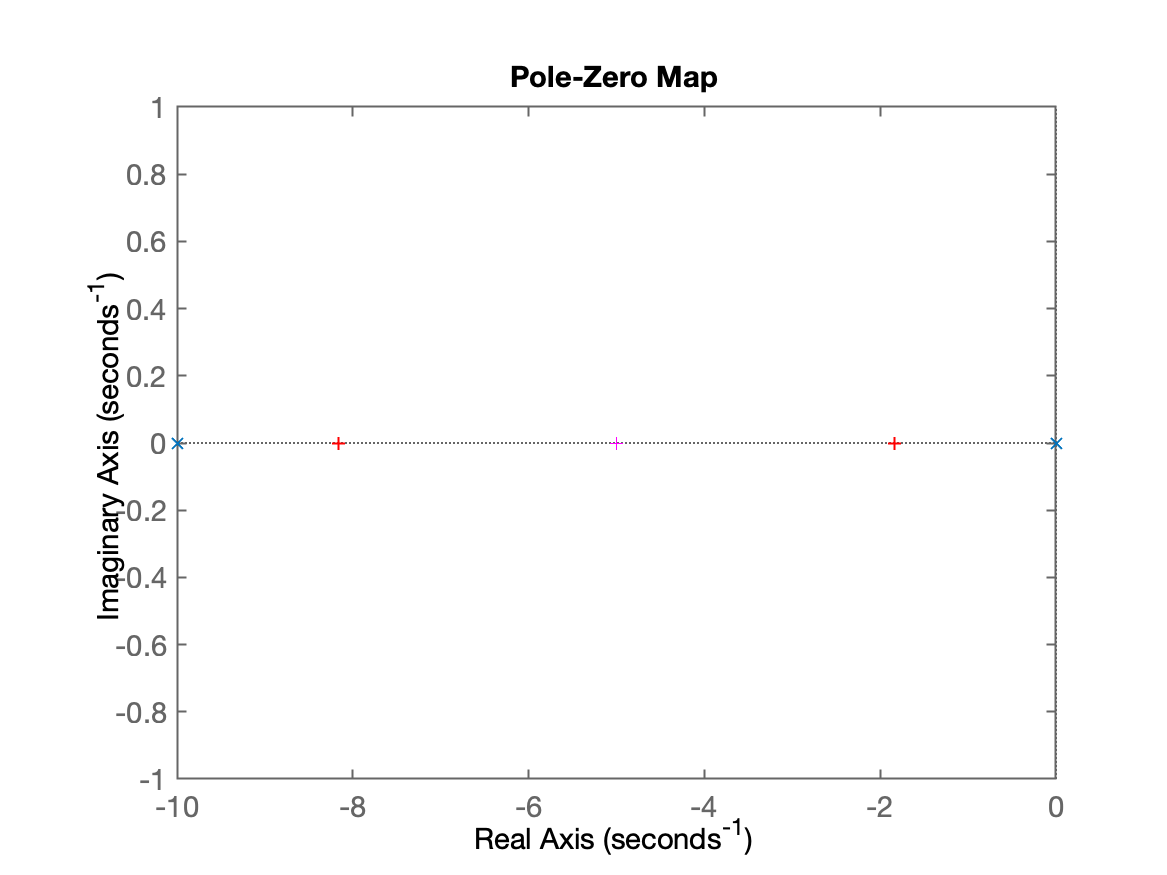
Mas nós não estamos interessados em apenas em plotar o root-locus.

Queremos entender a relação dos pólos de MF com a resposta temporal de um sistema quando o submetemos à uma malha fechada e o submetemos à uma entrada (referência), do tipo degrau.

Na prática, queremos fazer:

$FTMA(s)=K \cdot G(s)$

$FTMF(s)=\dfrac{K \cdot G(s)}{1 + K \cdot G(s) \cdot H(s)}$

No nosso caso, $H(s)=1$ (também dito "realimentação unitária"), e então a malha-fechada se simplifica para:

$FTMF(s)=\dfrac{K \cdot G(s)}{1+ K \cdot G(s)} = \dfrac{FTMA(s)}{1+FTMA(s)}$

Se queremos ter idéia de resposta temporal de um sistema de MF quando submetido à entrada degrau, então ncessitamos realizar algo como:

$Y(s) = \underbrace{R(s)}_{\text{Degrau}} \cdot FTMF(s)$

Mas não queremos $Y(s)$ e sim $y(t)$, então necessitamos realiar a transformada inversa de Laplace sobre o $Y(s)$ calculando anteriormente, ou em outras palavaras:

O cálculo anterior pressupõe analiticamente o uso de expansão em frações parciais. Mas, para nossa "sorte", o Matlab facilita numericamente os cálculos anteriores, gerando diretamente o gráfico de $y(t)$, uma vez repassada a $FTMF(s)$ à sua função step(<FTMS>):

xxxxxxxxxx
>> figure;      % força abertura de nova janela gráfica (para preservar o pzmap anterior)
>> step(ftmf)

E você deve ter obtido algo como gráfico:

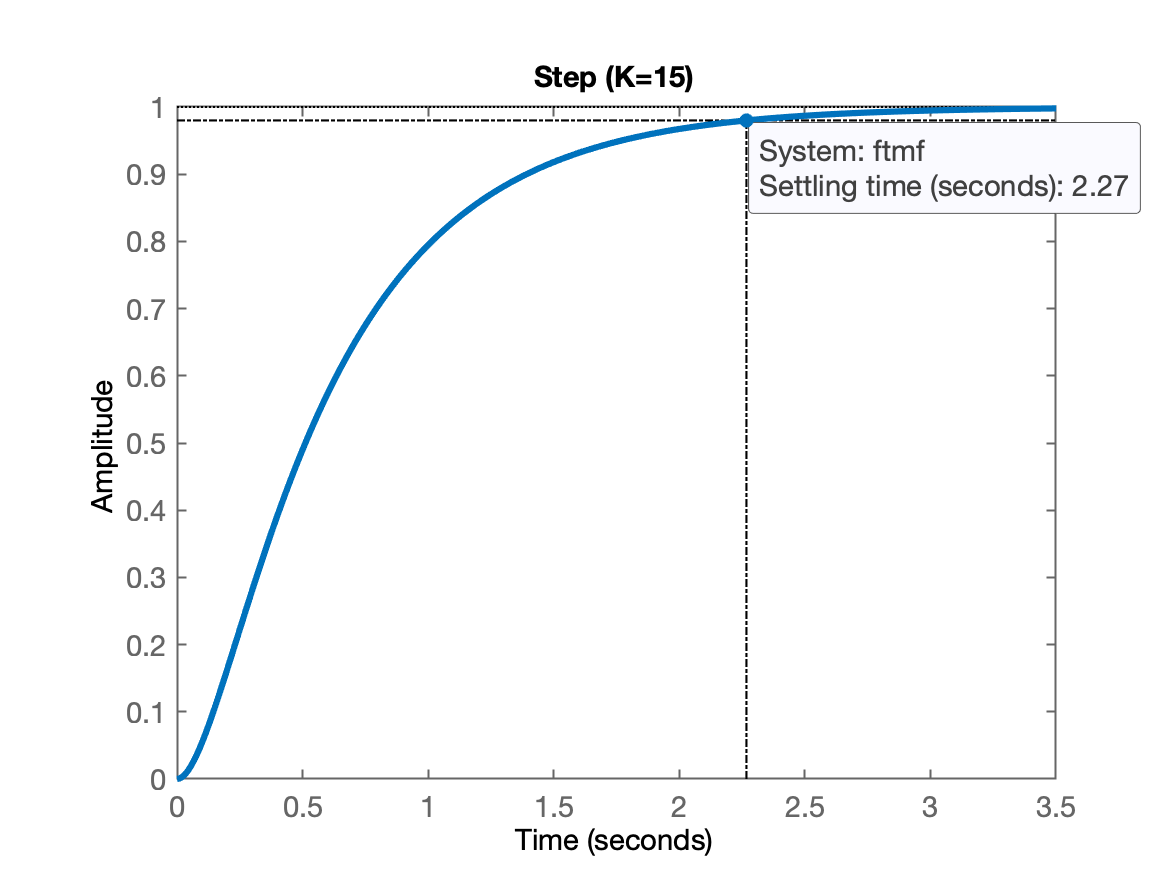
Ou reunindo informações:

RL	Step

Podemos complementar melhor nosso entendimento sobre o root-locus e sua relação com a resposta temporal de um sistema, variando o ganho, calculando as posições assumidas pelos pólos de MF para cada novo valor de ganho, e, para cada valor de ganho, usar a função step() para entender o papel dos pólos de MF na resposta temporal do sistema em MF depois que o mesmo é fechado com certo valor de ganho.

xxxxxxxxxx
>> ftmf=feedback(25*G, 1);      % Este valor de ganho gera pólos duplos (e ainda reais)
>> polesMF=pole(ftmf)
polesMF =
    -5
    -5
>> figure(1)    % voltando o "foco" do Matlab para primeira janela, a do "pzmap"
>> plot(real(polesMF),imag(polesMF),'m+')   % plotando local destes pólos de MF
>> figure;      % nova janela para resposta temporal correspondente à estes pólos
>> step(ftmf)   % plota a resposta temporal
>> title('Step (K=25)')     % Acrescentando título à esta janela gráfica

Até este ponto, se tudo deu certo, você deve ter obtido algo como:

RL	Step

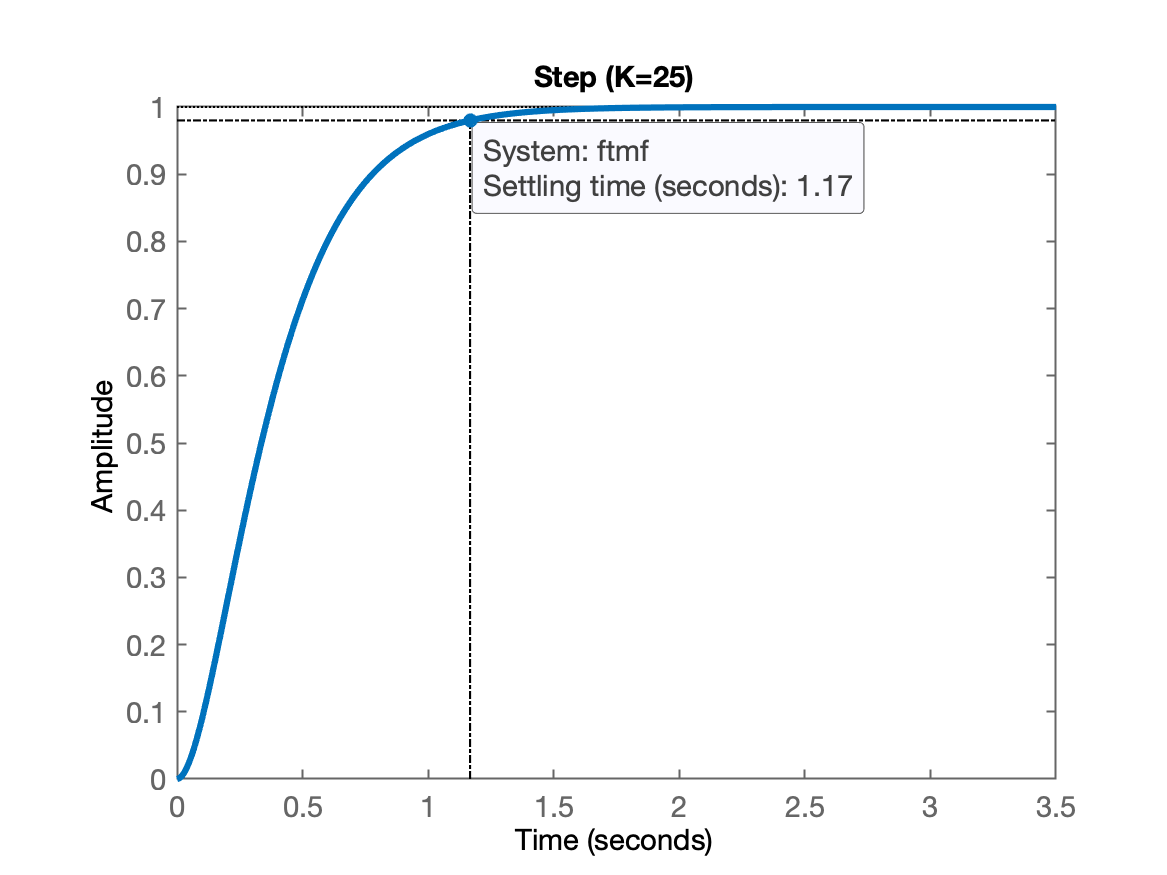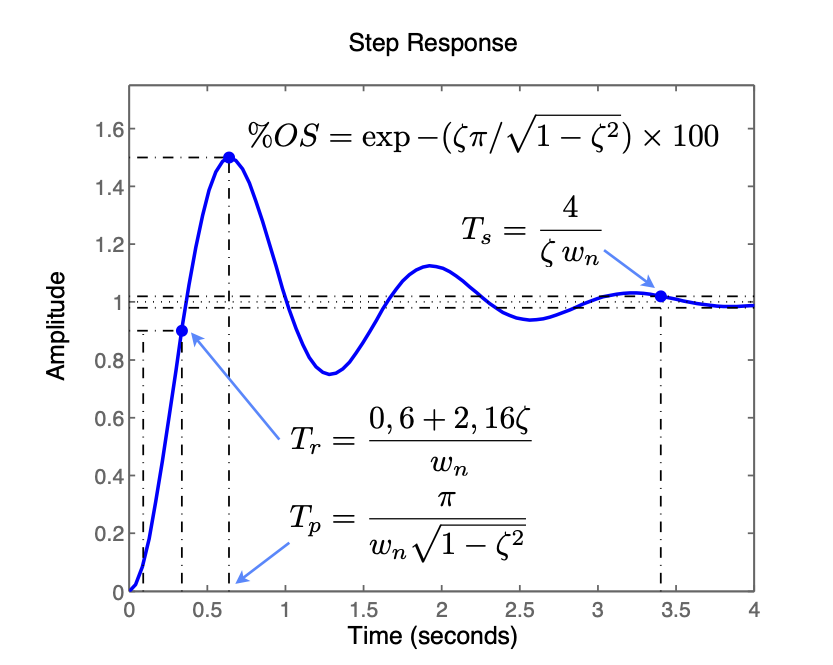
Completando a idéia para outros valores mais de ganho. E.. (não menos importante), comprovando que pólos de MF reais geram respostas super-amortecidas (sem sobressinal) e pólos de MF complexos (isto é, com parte imaginária diferente de zero), geram respostas suub-amortecidas, com certo fator de amortecimento $\zeta$ ($0 < \zeta <1$) e frequência de oscilação, $\omega_n$. Lembre que a amplitude do sobre-sinal (ou overshoot, $\%OS$) está diretamente associado com o valor de $\zeta$.

xxxxxxxxxx
>> % Aumentando o ganho para obter pólos de MF complexos
>> ftmf=feedback(40*G, 1);
>> polesMF=pole(ftmf)
polesMF =
           -5 +      3.873i
           -5 -      3.873i
>> % Como esperado, finamente obtemos pólos de MF com partes imaginárias diferentes de 0
>> figure(1);   % "desenhando" estes novos pólos de MF do plano-s da primeira figura
>> hold on
>> plot(real(polesMF),imag(polesMF),'b+')
>>
>> % Neste ponto, provavelmente você poderá afirmar que o último comando não gerou
>> % nenhum resultado visível. Mas repare que no primeiro "pzmap", o eixo Y variou
>> % apenas entre [-1, +1] e agora a parte imaginária dos pólos de MF alançaram os
>> % valores [-3.873, +3.7873]. Necessitamos forçar o Matlab a aumentar o "range"
>> % vertical do gráfico do "pzmap". Vamos usar a função: axis() para isto:
>> % axis([xmin xman ymin ymax])
>> axis([-11 1 -5 5])

Continuando... Falta comprovar a resposta temporal para nossos primeiros pólos de MF com parte imaginária diferente de zero:

xxxxxxxxxx
>> figure; step(ftmf)
>> title('Step (K=40)')

Até este ponto você deve ter algo como:

RL	Step

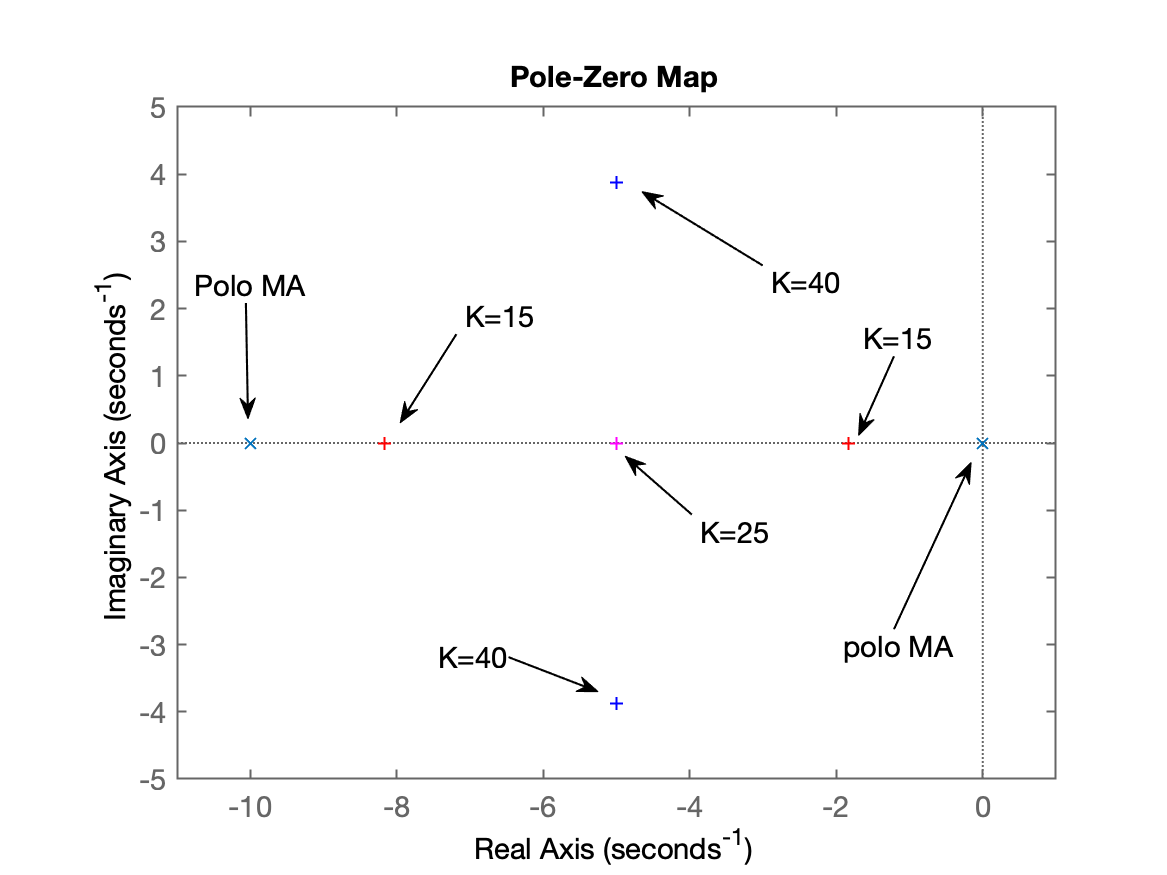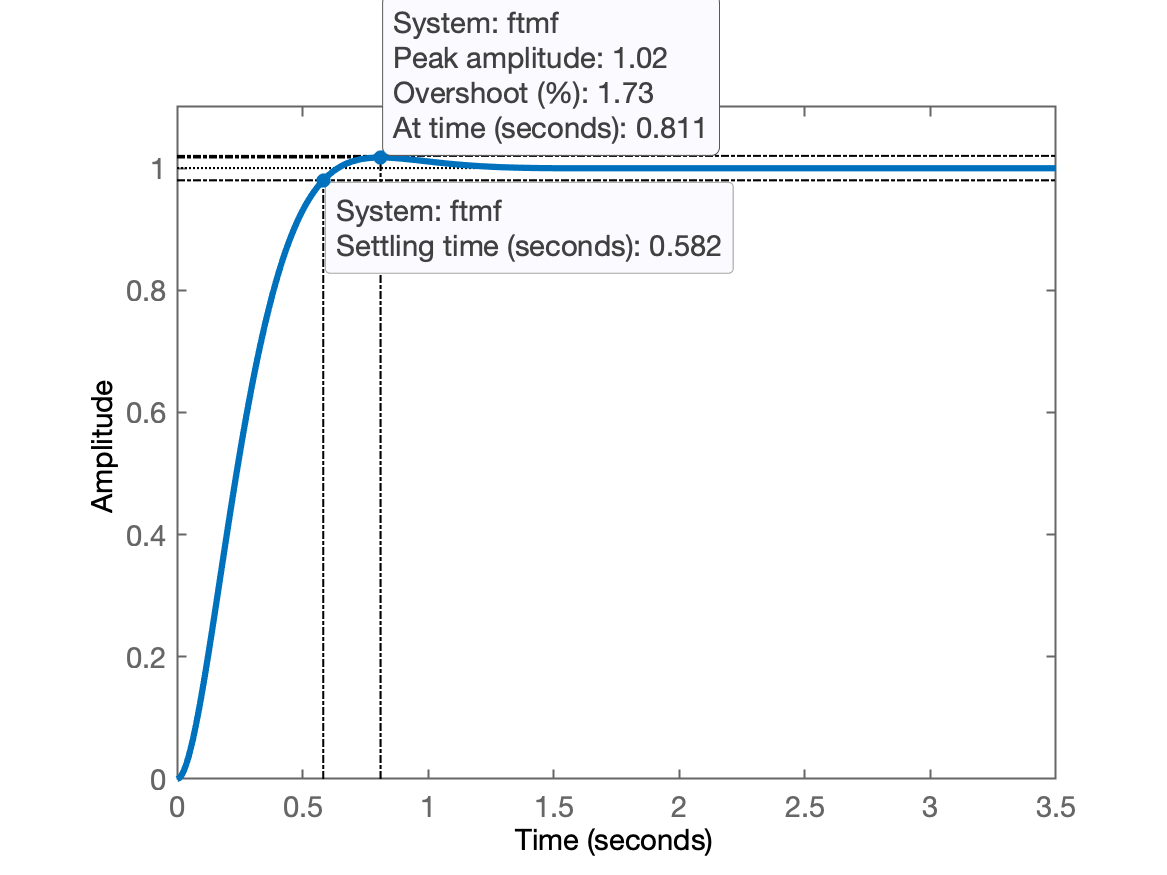Percebemos que a resposta começou a ficar sub-amortecida, com %OS bem baixo ainda.

Continuando o processo para valores ainda maiores de ganho:

xxxxxxxxxx
>> ftmf=feedback(150*G, 1);
>> polesMF=pole(ftmf)
polesMF =
           -5 +      11.18i
           -5 -      11.18i
>> figure(1)
>> plot(real(polesMF),imag(polesMF),'g+')
>> axis([-11 1 -12 12])     % Ajustando range novamente no gráfico do pzmap
>> axis equal               % para escala no eixo X = eixo Y
>> % Completando com resposta temporal
>> figure;step(ftmf)
>> title('Step (K=150)')

Agora, você deve ter obtido algo como:

RL	Step

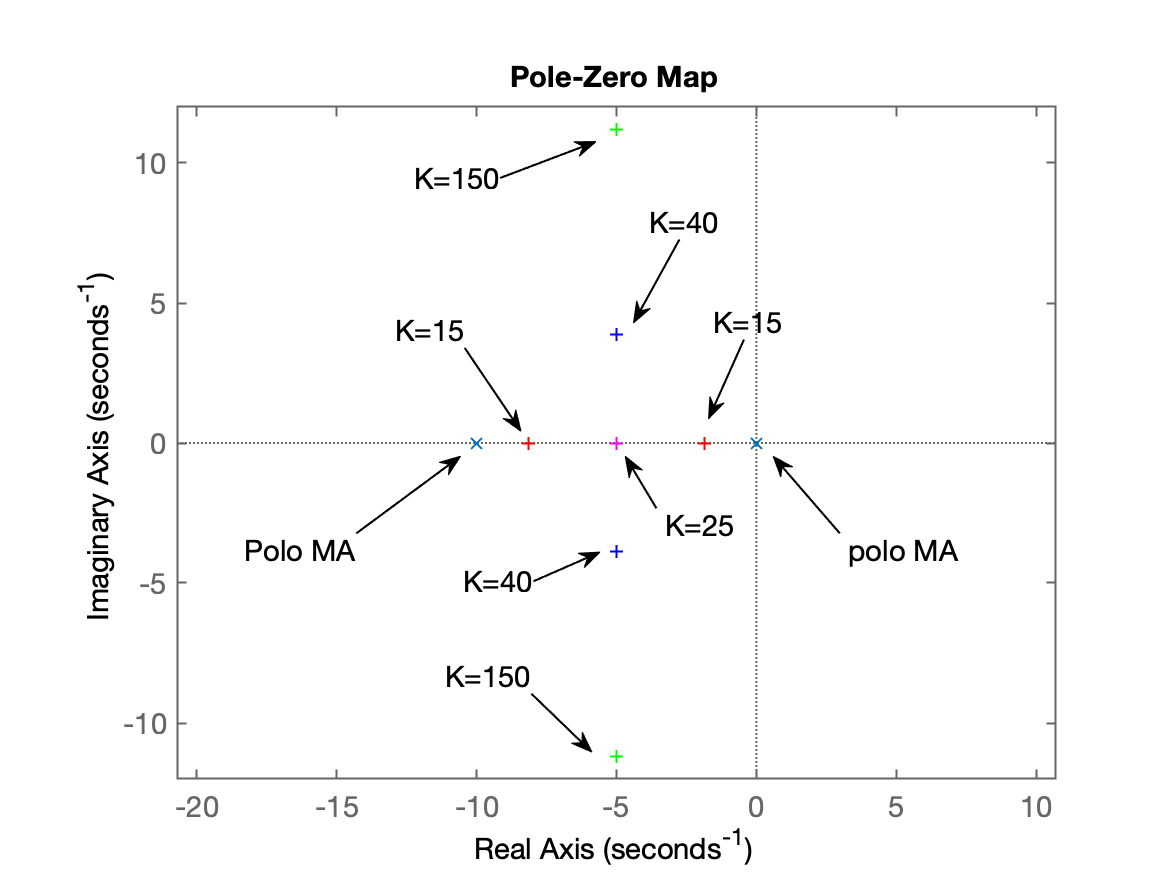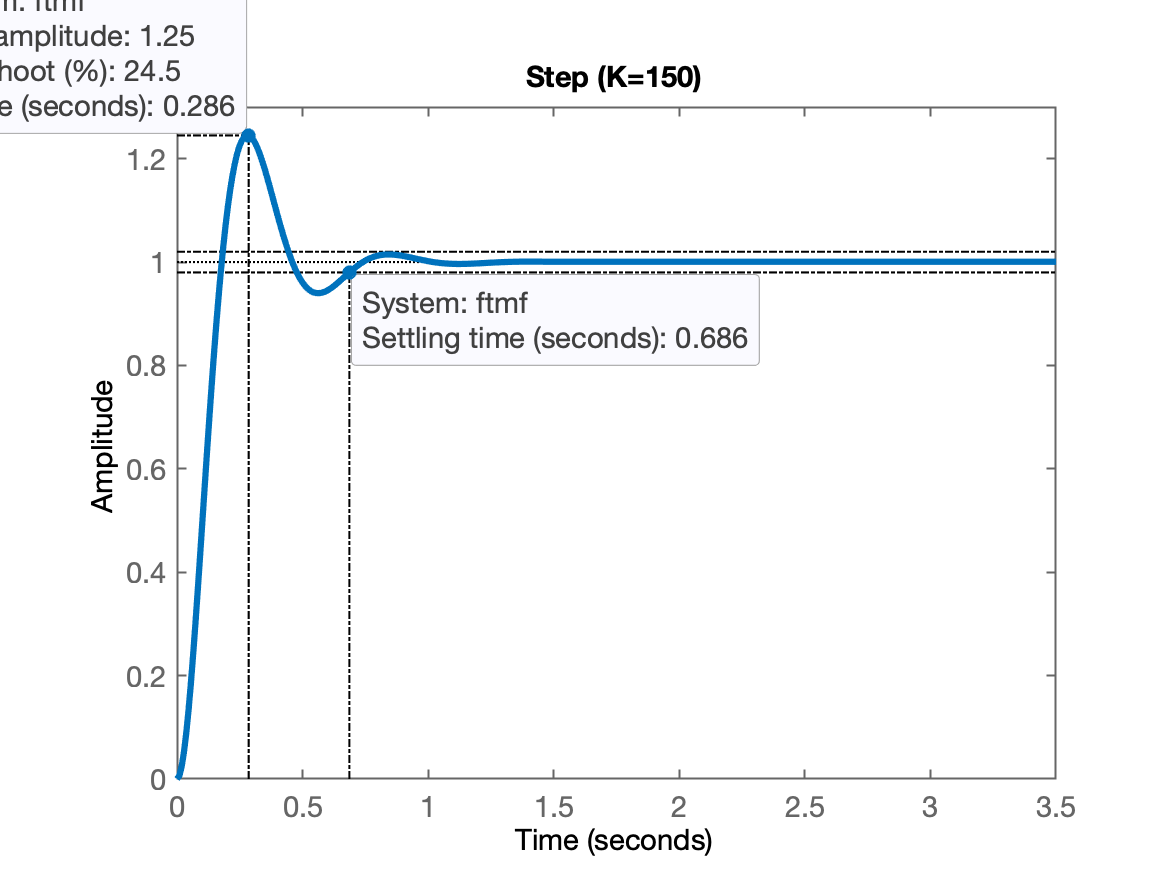Em resumo, o RL deve ter ficado algo como:

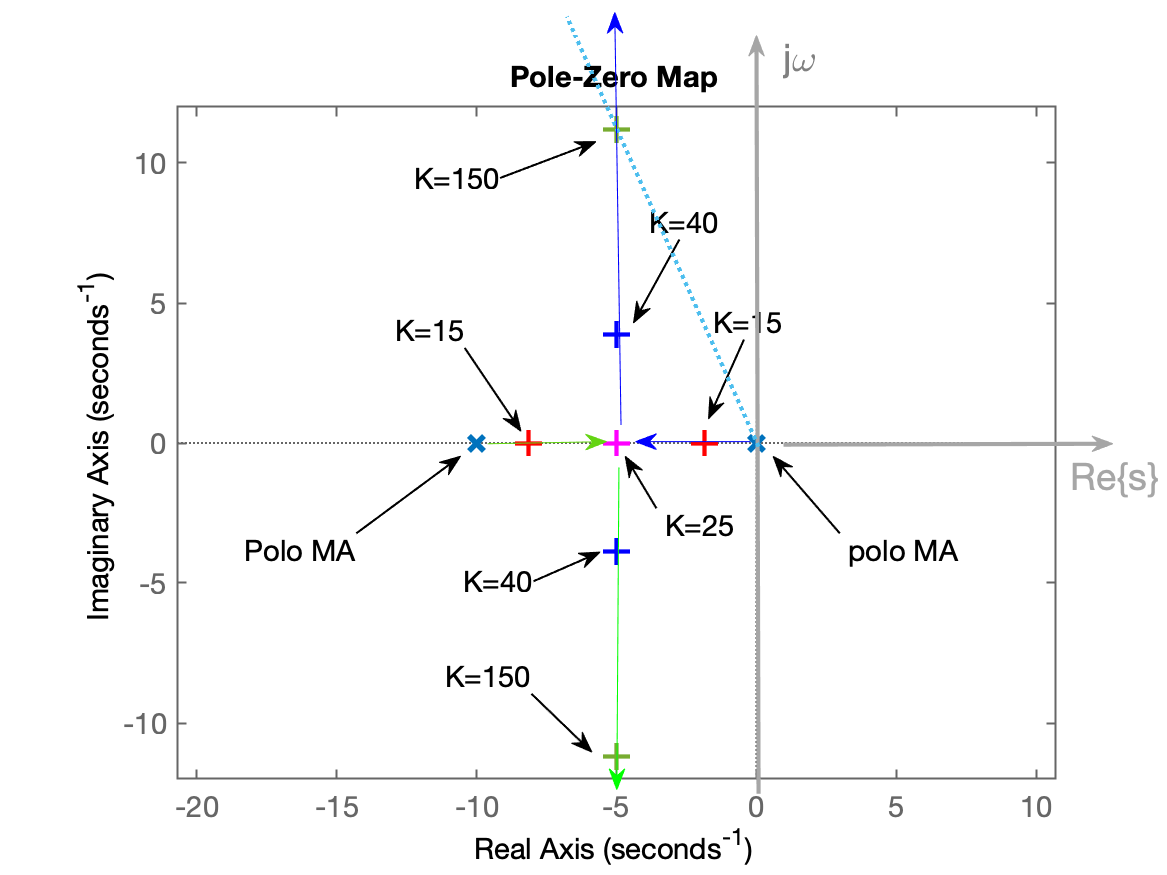
Fim... 🕦 ​para esta aula

Sugere-se tornar hábito que ao final de cada seção de trabalho, você faça ainda:

xxxxxxxxxx
>> save aula_26042024      % gera arquivo aula_26042024.mar (dados)
>> diary off               % encerra arquivo de registro iniciado no início deste doc
>> quit

💾 Arquivos gerados disponíveis: aula_26042024.txt, aula_26042024.mat e aula_26042024.md (já convertido para UTF8).

Sugestões para próxima aula:

Na próxima aula, vamos tentar continuar à partir deste ponto e comprovar mais detalhes sobre respostas temporais de sistemas de 2a-ordem com raízes complexas (ver Respostas Transitórias de Sistemas Lineares):

$FTMF(s)=\dfrac{b}{s^2+as+b}=\dfrac{K}{(s+p_1)(s+p_2)}=\dfrac{\omega_n^2}{s^2+2\zeta \omega_n + \omega_n^2}$

ou seja, fizemos:

Caso o sistema possua pólos complexos ($0 < \zeta <1$) $\rightarrow$, a resposta sub-amortecida para entrada degrau fica:

Pólos de MF: $p_{1,2}=\sigma \pm j \omega_d$

ou graficamente:

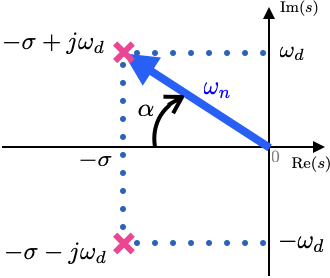
parte real: $\sigma = \omega_n \cos(\alpha) = \omega_n \zeta$ parte imaginária: $\omega_d=\omega_n \sin(\alpha)=\omega_n \sqrt{1-\zeta^2}$

$\alpha=\tan^{-1}\left( \dfrac{\omega_d}{\sigma} \right)$

Fator amortecimento: $\zeta=\cos(\alpha) = \dfrac{|\sigma|}{\omega_n} = \dfrac{a/2}{\omega_n}$ $\sin(\alpha) = \sqrt{1-\zeta^2}$

A resposta em MF para este sistema fica:

$Y(s)=R(s) \cdot FTMF(s)=\dfrac{K}{s(s+p_1)(s+p_2)}=K \left[ \dfrac{\omega_n^2}{s(s^2+2\zeta \omega_n^2+\omega_n^2)} \right]$

$Y(s) = \dfrac{K_1}{s} + \dfrac{K_2 s+K_3}{s^2+2\zeta \omega_n^2+\omega_n^2}$

A transformada inversa de Laplace para $Y(s)$ fica:

$y(t)=1-A \text{e}^{-\zeta \sigma t} \cos(\omega_d t - \phi)$

onde: $A=\dfrac{1}{\sqrt{1-\zeta^2}}$ $\phi=\tan{-1}\left( \zeta \big/ \sqrt{1-\zeta^2} \right)$

Podemos prever o valor do sobresinal, ou overshoot:

$\%OS=\exp\left( \dfrac{-\zeta \pi}{\sqrt{1-\zeta^2}} \right) \times 100\%$

Podemos calcular o $\alpha$ para o caso do último ganho adotado e comprovar o $\zeta$ obtido e correspondente $\%OS$ usando as equações anteriores...

Ou resumidamente:

🎈🎈🎈👋

Fernando Passold, em 26/04/2024

xxxxxxxxxx
​