# Entendendo Root Locus

A idéia aqui é usar comandos simples do Matlab para entender como o *root locus* é formado e qual a relaçao entre os pólos de malha-fechada e respostas temporais de um processo.

Se sugere fortemente uma eventual revistida do material [Respostas Transitórias de Sistemas Lineares]()

% G = tf(num,den)
num=1;
den=[1 10 0];
G = tf(num,den)

G =
 
      1
  ----------
  s^2 + 10 s
 
Continuous-time transfer function.

zpk(G)

ans =
 
     1
  --------
  s (s+10)
 
Continuous-time zero/pole/gain model.

root(den)
{Undefined function 'root' for input
arguments of type 'double'.} 
roots(den)
ans =
     0
   -10
pole(G)
ans =
     0
   -10
% ftmf=feedback(K*G, H, -1) 
ftmf=feedback(G, 1)

ftmf =
 
        1
  --------------
  s^2 + 10 s + 1
 
Continuous-time transfer function.

pole(ftmf)
ans =
       -9.899
     -0.10102
ftmf=feedback(0.01*G, 1);
pole(ftmf)
ans =
       -9.999
   -0.0010001
ftmf=feedback(5*G, 1);
pole(ftmf)
ans =
      -9.4721
     -0.52786
ftmf=feedback(15*G, 1);
pole(ftmf)
ans =
      -8.1623
      -1.8377
ftmf=feedback(25*G, 1);
pole(ftmf)
ans =
    -5
    -5
ftmf=feedback(15*G, 1);
pzmç
 pzmç
    
{Error: Invalid text character. Check for
unsupported symbol, invisible character, or
pasting of non-ASCII characters.
} 
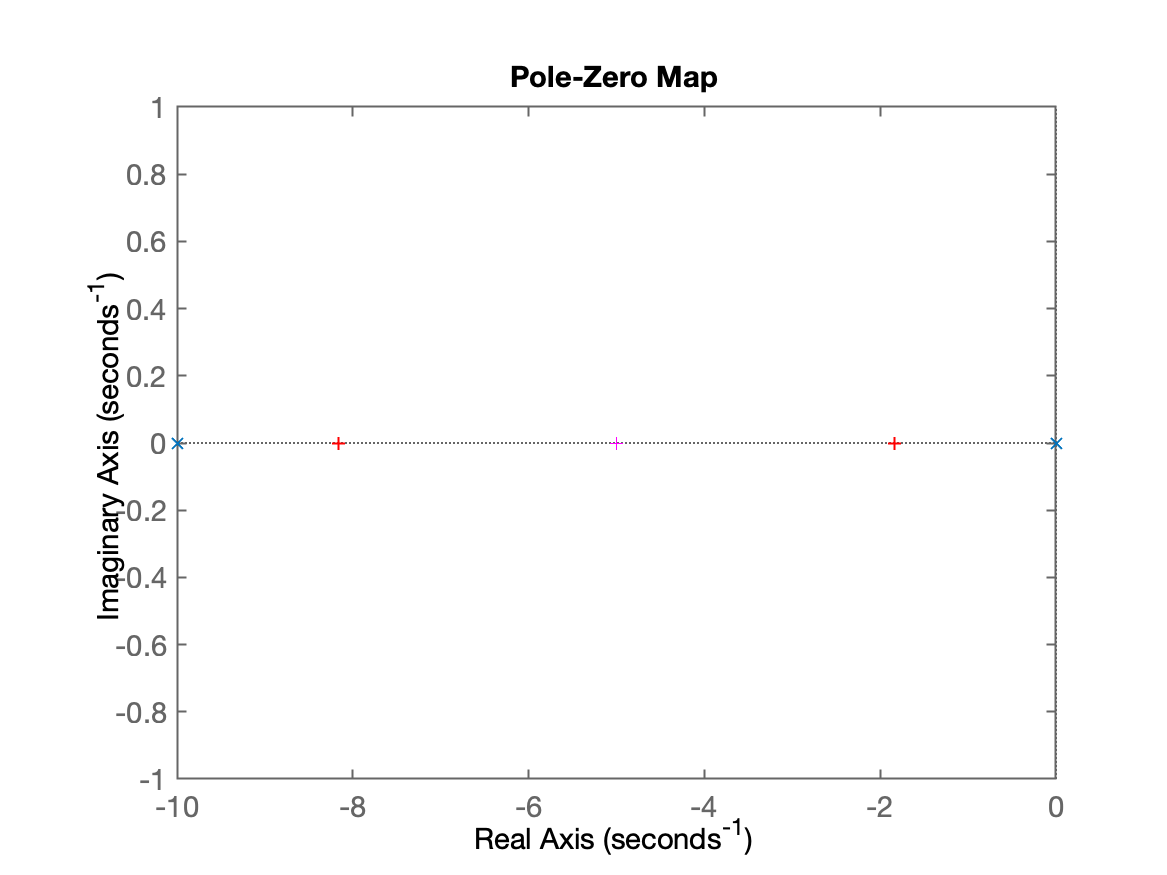
pzmap(G)
hold on % "segura as pontas"
pzmap(pole(ftmf))
{Error using <a href="matlab:matlab.internal.language.introspective.errorDocCallback('pzmap', '/Applications/Matlab_R2019b.app/toolbox/control/ctrlobsolete/pzmap.m', 66)" style="font-weight:bold">pzmap</a> (<a href="matlab: opentoline('/Applications/Matlab_R2019b.app/toolbox/control/ctrlobsolete/pzmap.m',66,0)">line 66</a>)
Wrong number of input arguments.} 
polesMF=pole(ftmf)
polesMF =
      -8.1623
      -1.8377
real(polesMF)
ans =
      -8.1623
      -1.8377
imag(polesMF)
ans =
     0
     0
plot(real(polesMF),imag(polesMF),'r+')
figure; step(ftmf)
ftmf=feedback(25*G, 1);
polesMF=pole(ftmf)
polesMF =
    -5
    -5
figure(1)
plot(real(polesMF),imag(polesMF),'m+')
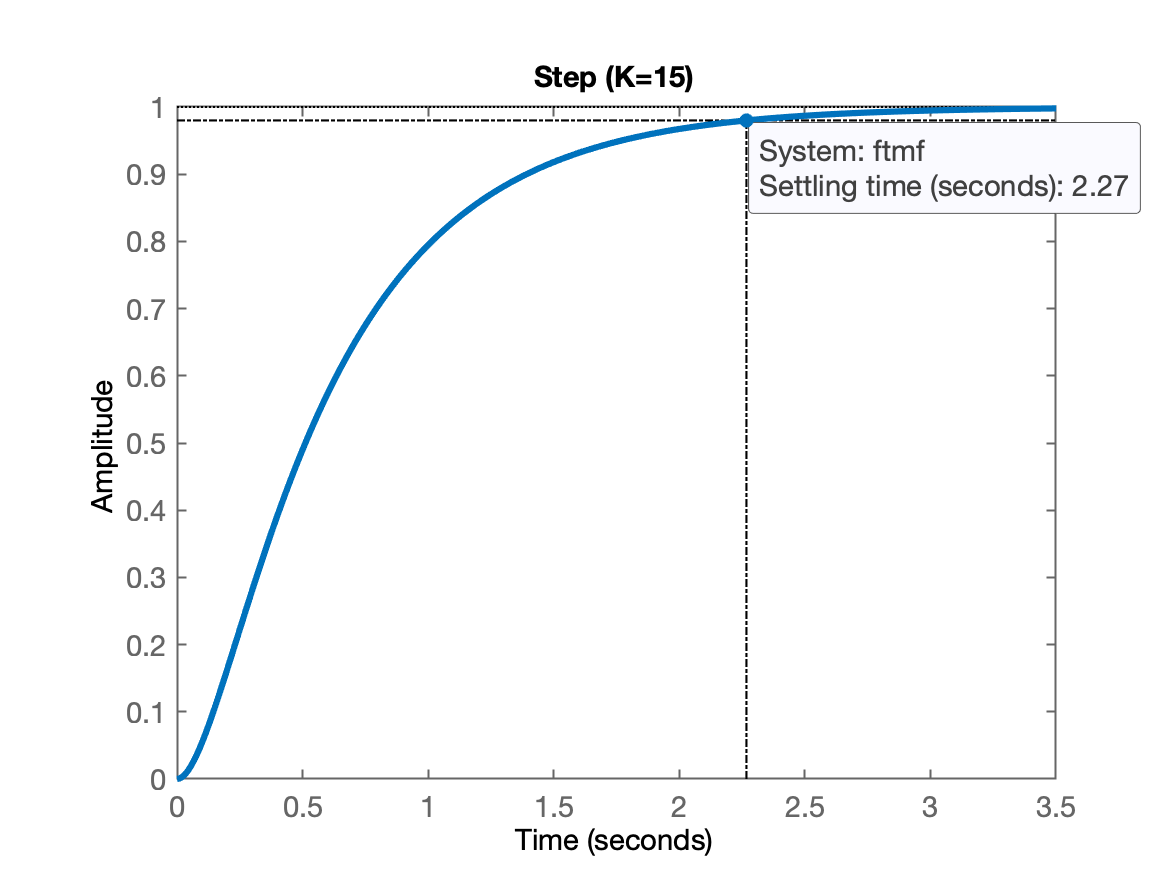
title('Step (K=15)')
figure; step(ftmf)
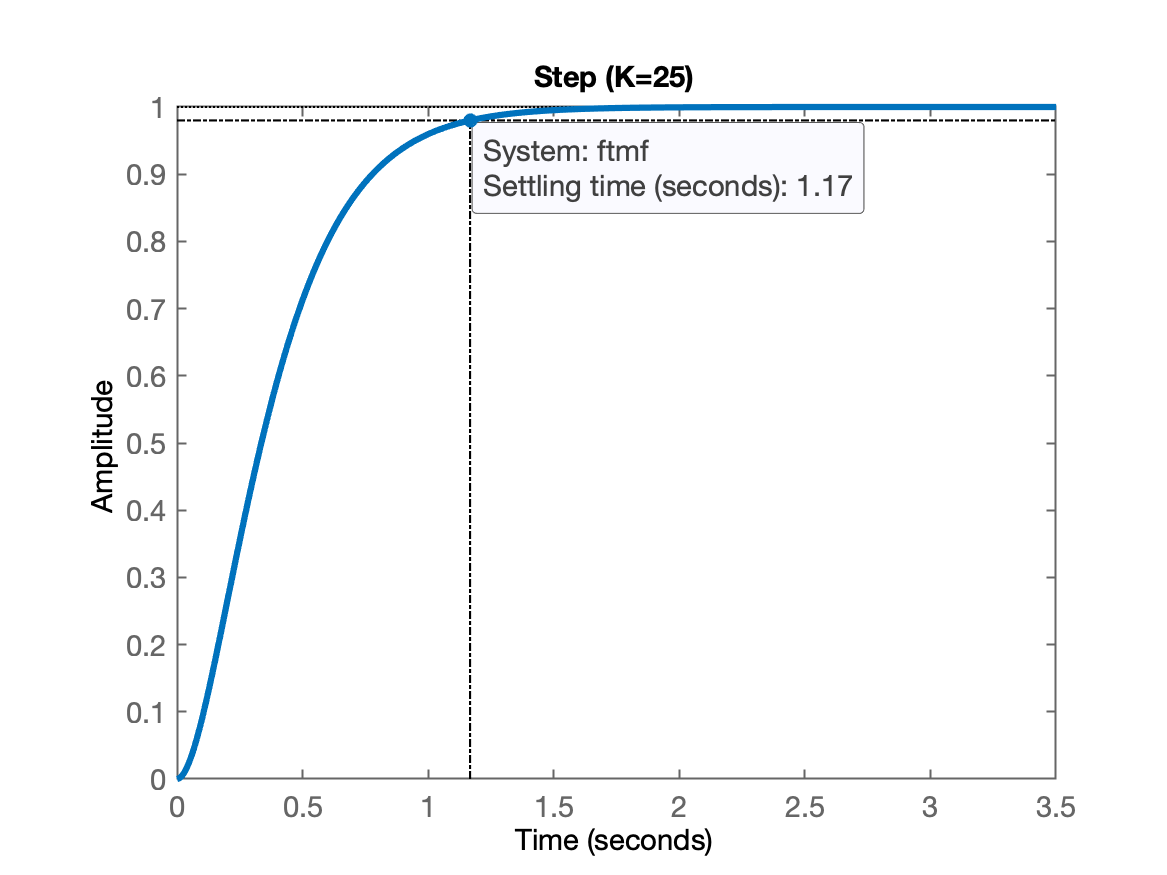
title('Step (K=25)')
save aula_26041024
diary off

% ![rl_planta_teste_1](rl_planta_teste_1.png)

title('Step (K=15)')
title('Step (K=25)')

% ![step_planta_teste_1_K15.png](step_planta_teste_1_K15.png)

% ![step_planta_teste_1_K25.png](step_planta_teste_1_K25.png)

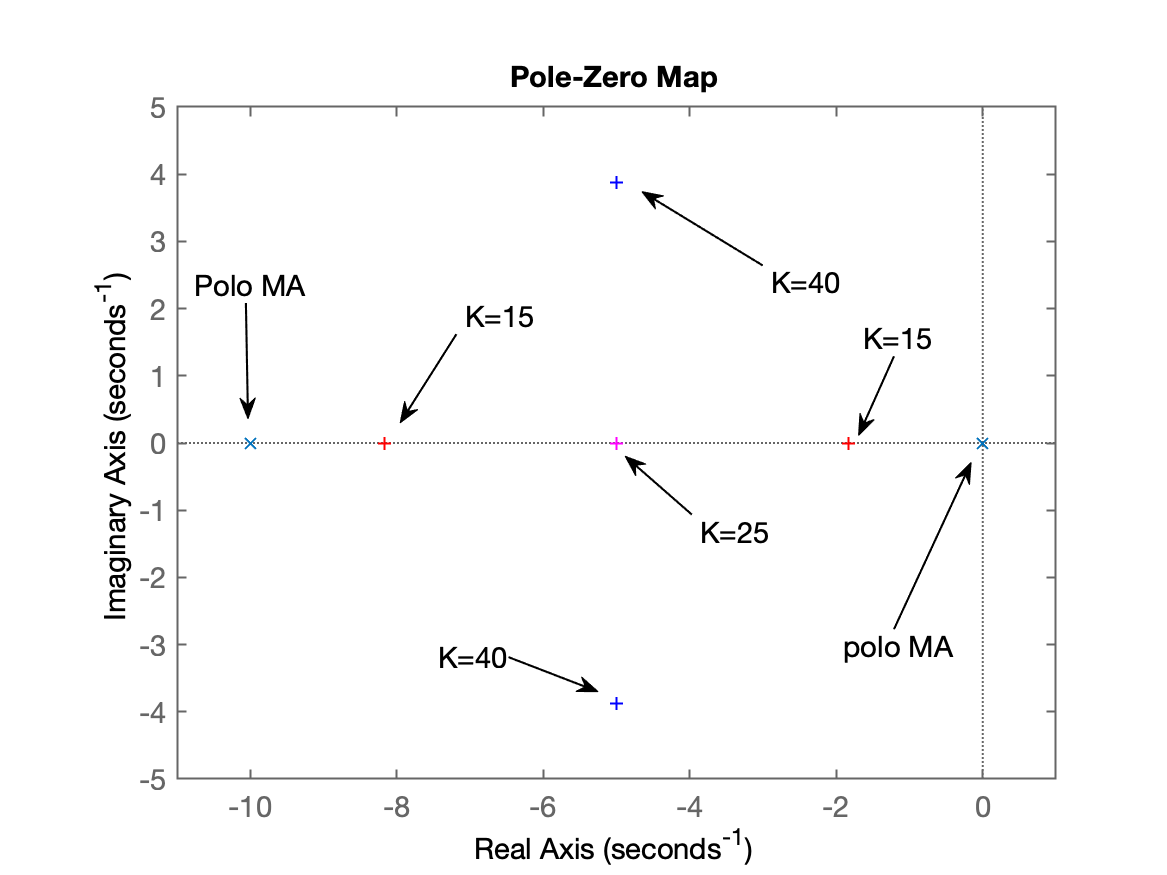
ftmf=feedback(40*G, 1);
polesMF=pole(ftmf)
polesMF =
           -5 +      3.873i
           -5 -      3.873i
figure(1);
hold on
plot(real(polesMF),imag(polesMF),'b+')
% axis([xmin xman ymin ymax])
axis([-11 1 -5 5])

% ![rl_planta_teste_1_2.png](rl_planta_teste_1_2.png)

40
ans =
    40
figure; step(ftmf)
title('Step (K=40)')
figure; step(ftmf)
title('Step (K=40)')
[Warning: Error occurred while executing the
listener callback for event WindowMouseMotion
defined for class matlab.ui.Figure:
Invalid or deleted object.
Error in
matlab.graphics.shape.internal.PointDataTipController.dragOrientation] 
[Warning: Error occurred while executing the
listener callback for event WindowMouseMotion
defined for class matlab.ui.Figure:
Invalid or deleted object.
Error in
matlab.graphics.shape.internal.PointDataTipController.dragOrientation] 
[Warning: Error occurred while executing the
listener callback for event WindowMouseMotion
defined for class matlab.ui.Figure:
Invalid or deleted object.
Error in
matlab.graphics.shape.internal.PointDataTipController.dragOrientation] 
[Warning: Error occurred while executing the
listener callback for event WindowMouseMotion
defined for class matlab.ui.Figure:
Invalid or deleted object.
Error in
matlab.graphics.shape.internal.PointDataTipController.dragOrientation] 
[Warning: Error occurred while executing the
listener callback for event WindowMouseMotion
defined for class matlab.ui.Figure:
Invalid or deleted object.
Error in
matlab.graphics.shape.internal.PointDataTipController.dragOrientation] 
[Warning: Error occurred while executing the
listener callback for event WindowMouseMotion
defined for class matlab.ui.Figure:
Invalid or deleted object.
Error in
matlab.graphics.shape.internal.PointDataTipController.dragOrientation] 
ftmf=feedback(150*G, 1);
polesMF=pole(ftmf)
polesMF =
           -5 +      11.18i
           -5 -      11.18i
figure(1)
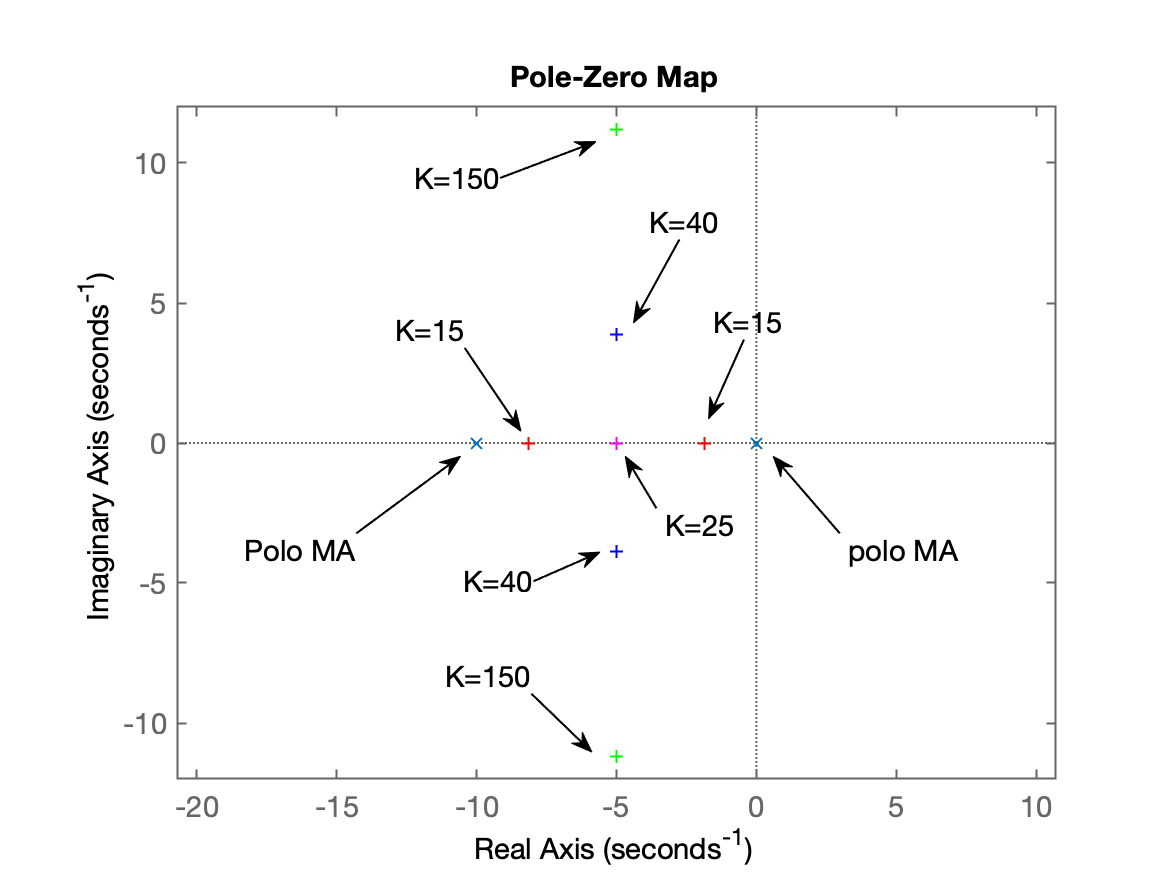
plot(real(polesMF),imag(polesMF),'g+')
axis([-11 1 -12 12])
axis equal

% ![rl_planta_teste_1_3.png](rl_planta_teste_1_3.png)

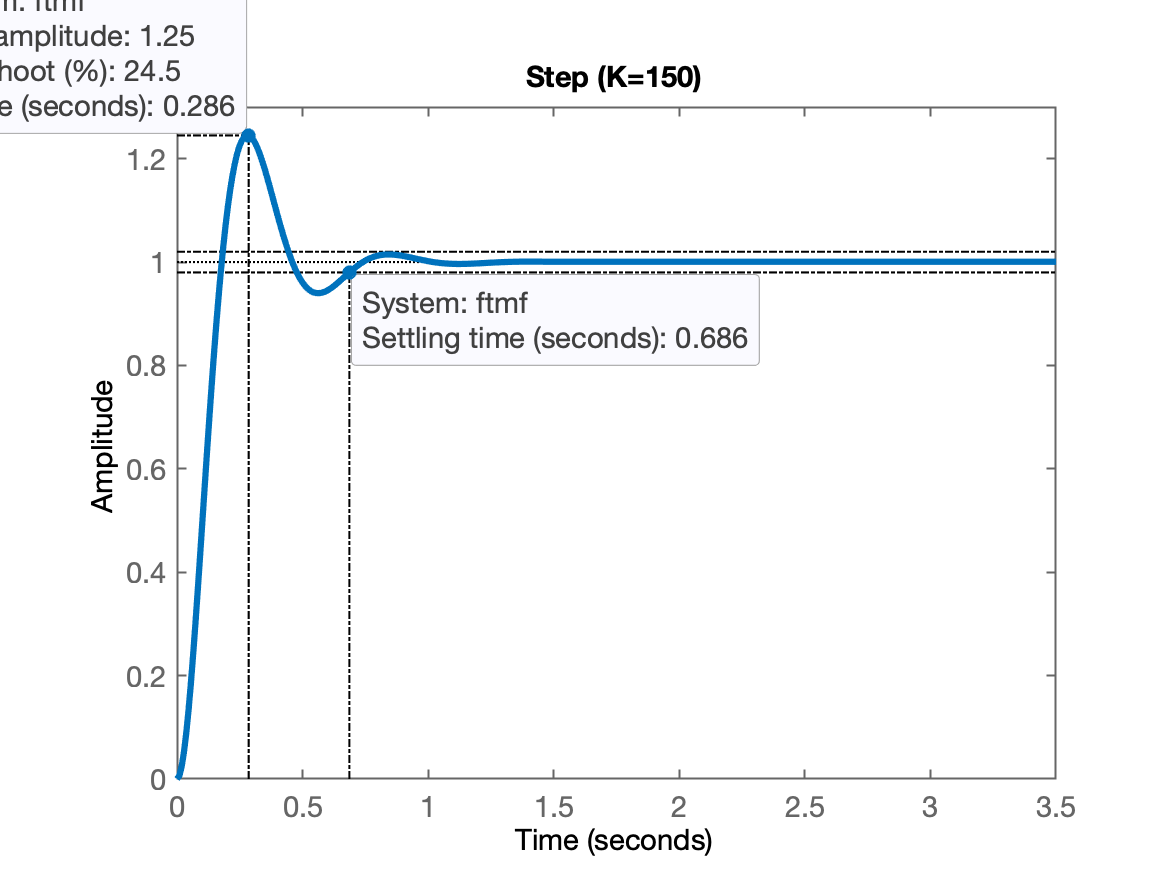
figure;step(ftmf)
title('Step (K=150)')

% ![step_planta_teste_1_K150.png](step_planta_teste_1_K150.png)

save aula_26041024
diary off