Trabalho #1

Sobre Teorema de Amostragem e Transformada-$\mathcal{Z}$.

1. (70%) Suponha uma onda senoidal de 1 Volt de pico, oscilando na frequência de 100 Hz.

   Demonstre matematicamente (50%) e considere os teoremas de amostragem (50%), para explicar o que acontece quando:

   a) Este sinal é amostrado à $f_s=$ 200 Hz;

   b) Este sinal é amostrado à $f_s=$ 400 Hz;

   c) Este sinal é amostrado à $f_s=$ 1 KHz;

   Faça acompanhar equações, cálculos, tabelas e gráfico mostrando na mesma figura, duas curvas: uma do sinal original contínio no tempo e outra (sobreposta) sinal amostrado.

2. (30%) Considere agora que seu sistema está amostrando uma onda quadrada oscilando na frequência de 100 Hz, e que você resolveu amostrar a mesma à $f_s=$ 500 Hz. Você é capaz de:

   a) Recorde da Série de Fourier e verifique o espectro (harmônicas e amplitudes) de uma onda quadrada. Considere este sinal e mostre uma tabela mostrando harmônica (sua frequência) x amplitude (de cada harmônica). Sugere-se plotar este gráfico.

   b) Suponha que seu sistema de aquisição seja precedido de um filtro passa-baixas ideal com frequência de corte, $f_c=$ 250 Hz. Explique o que ocorre com o sinal original depois de passar por este filtro.

   c) Aplique o teorema da amostragem sobre o sinal anterior. Não é necessário considerar a função Sampling e seu efeito na modulação da amplitude do sinal amostrado envolvido. Pode ser considerado uma amostragem ideal.

   d) Considere que seu sistema de amostragem apenas aplica um ganho unitário sobre o sinal adquirido e que a saída D/A do mesmo é acompanhada do mesmo filtro passa-baixas do item (b).

   e) Complete uma tabela como a mostrada abaixo

   Harmônica	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
   Frequência (Hz)	100	200	300	400	500	600	700	800	900	1000	1100	1200	1300	1400	1500	1600	1700
   Amplitude (pico)	_	_	_	_	_	_	_	_	_	_	_	_	_	_	_	_	_

   para:

   e.1) A onda quadrada original (não filtrada, não amostrada);

   e.2) O resultado da onda quadrada depois que passa pelo filtro passa-baixas (antes do A/D);

   e.3) O resultado da onda do item (2) depois que é amostrada (eventualmente considere a função Sampling; neste caso: $\tau=T$);

   e.4) O resultado da onda reconstituída (depois que passa pelo filtro passa-baixas depois do D/A).

   f) Use os resultados numéricos obtidos na tabela anterior para mostrar num mesmo gráfico, o que aconteceu com o espectro original da onda quadrada.

   g) Use o Matlab (ou outro software) para recompor e mostrar num gráfico, o sinal reconstituído (sinal amostrado à 500Hz) sobreposto ao sinal original da onda quadrada (sintetizada usando série de Fourier até a 17a-harmônica).

   h) Explique o que aconteceu.

   Ref:

   • Síntese de Onda Quadrada usando Série de Fourier (e Matlab);
   • Amostragem de Onda Dente de Serra (uso de Matlab).

Obs.: Sugere-se o uso do Matlab para cálculos e composição dos gráficos.

Exemplo de códigos Matlab:

Por exemplo, a figura abaixo mostra uma onda senoidal de 1 Hz, amostrada à 5 Hz:

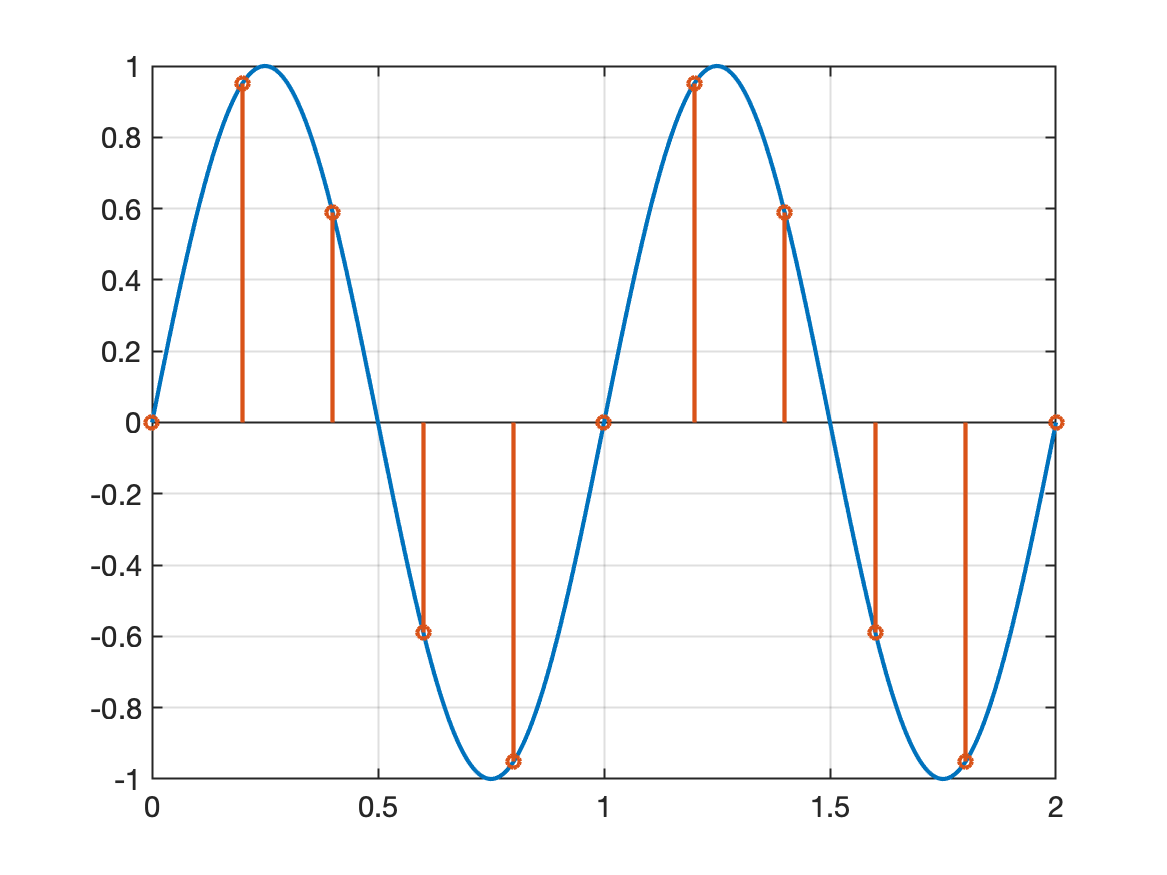
Código Matlab:

xxxxxxxxxx
>> f=1;         % freq. original do sinal em Hz
>> w=2*pi*f;    % freq angular em rad/s
>> Toriginal=1/f;
>> t=0:Toriginal/200:Toriginal*2;   % cria vetor tempo para 2 ciclos do sinal continuo, 200 pontos por ciclo
>> y=sin(w*t);  % calcula vetor do sinal original
>> plot(t,y)    % mostra gráfico do sinal original
>> fs=2;        % amostragem à 2 Hz
>> fs=5;        % amostragem à 5 Hz
>> T=1/fs       % calcula período de amostragem (em segundos) e mostra resultado
T =
​
          0.2
>> kT=0:Toriginal/fs:Toriginal*2;   % cria vetor tempo das amostras 
>> size(kT)                         % tamanho do vetor - qtdade amostras geradas em 2 ciclos
ans =
     1    11
>> yd=sin(w*kT);  % cria vetor do "sinal digital"
>> hold on        % comando para permitir sobreposição de gráficos
>> stem(kT,yd)    % plota sinais amostrados
>> grid

Você pode trocar a linha do comando stem(kT,yd) por stairs(kT,yd) e acrescentar o comando legend('y(t)','y[kT]'), o que resultará em:

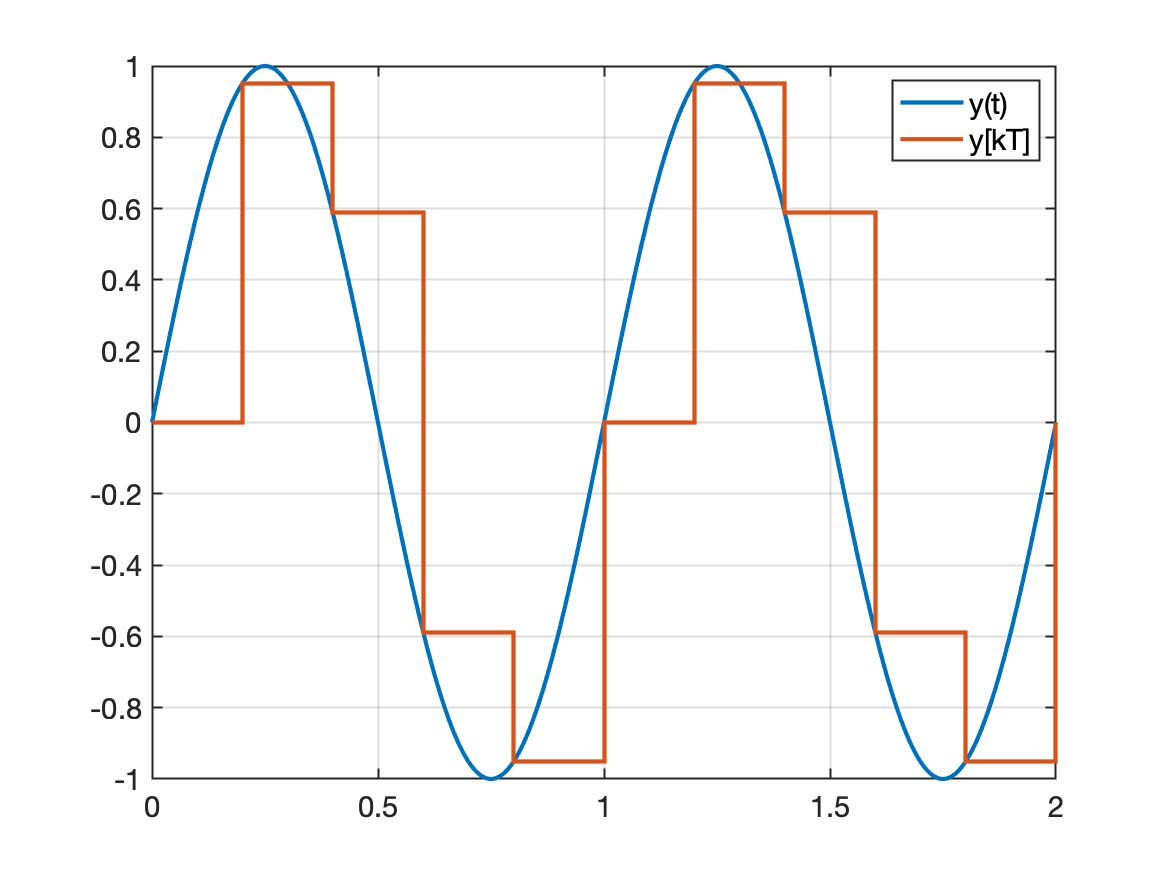
Fernando Passold, em 11/03/2024.