Teste verificando Teorema de Amostragem

Síntese de uma Onda Dente de Serra

Seja o sinal com o qual queremos testar o período de amostragem, uma onda dente de serra ("swatooth wave'') do tipo mostrada na próxima figura:

Se esta onda levar $2L$ segundos para completar um ciclo, podemos descrevê-la como:

$f(t)=\dfrac{t}{2L}$

onde $L$ corresponde ao tempo que a mesma leva para completar seu ciclo. No caso da figura, esta onda levou 2 segundos ( $L=2$ ).

Vamos supor que queremos uma onda dente de serra oscilando à 100 Hz, então neste caso: $2L=T$ , como $T=1/f$ teremos: $2L=1/100$ e finalmente $L=1/(2 \cdot 100)=0,005$ segundos (o período de tempo de um ciclo da onda).

Série de Fourier

Vamos sintetizar esta onda usando Série de Fourier.

A dedução da série de Fourier para este tipo de onda leva à seguinte equação:

$f(t)=\dfrac{1}{2} - \dfrac{1}{\pi} \sum_{n=1}^{\infty} \sin{\left( \dfrac{n \, \pi \, t}{L} \right)} \qquad$ (Ref.: Wolfram MathWorld: Fourier Series -- Sawtooth Wave)

Um rápido teste para comprovar a equação anterior pode ser feito no MATLAB.

Neste caso, vamos gerar uma onda dente-de-serra na frequencia de 1 Hz apenas e pretendemos acompanhar na tela os 2 primeiros ciclos da onda (2 segundos):

>> t=0:1/200:2; % cria vetor tempo, 2 segundos divididos em 100 intervalos/segundo
>> y=1/2-1/pi*( 1*sin(1*2*pi.*t/1) + 1/2*sin(2*2*pi.*t/1) + 1/3*sin(3*2*pi.*t)/1 + 1/4*sin(4*2*pi.*t/1) + 1/5*sin(5*2*pi.*t)/1 );
>> plot(t,y)

Deve ter sido gerado um gráfico semelhante à:

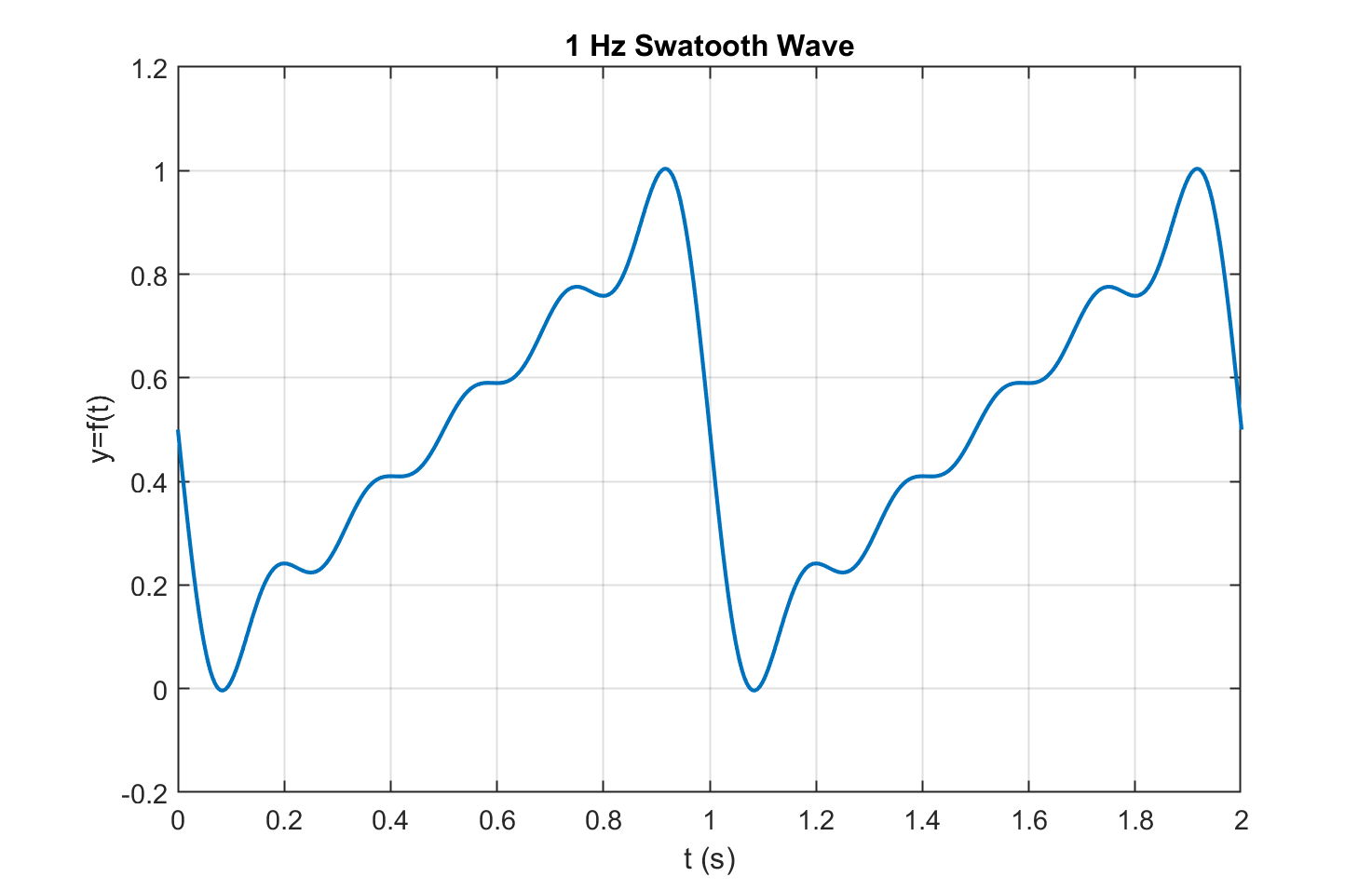
Note que sintetizamos apenas os primeiros 5 termos da série de Fourier para esta onda ( $n=5$ ). Se usarmos mais termos, mais nos aproximaremos da forma de onda original.

Note os componentes de frequência desta onda:

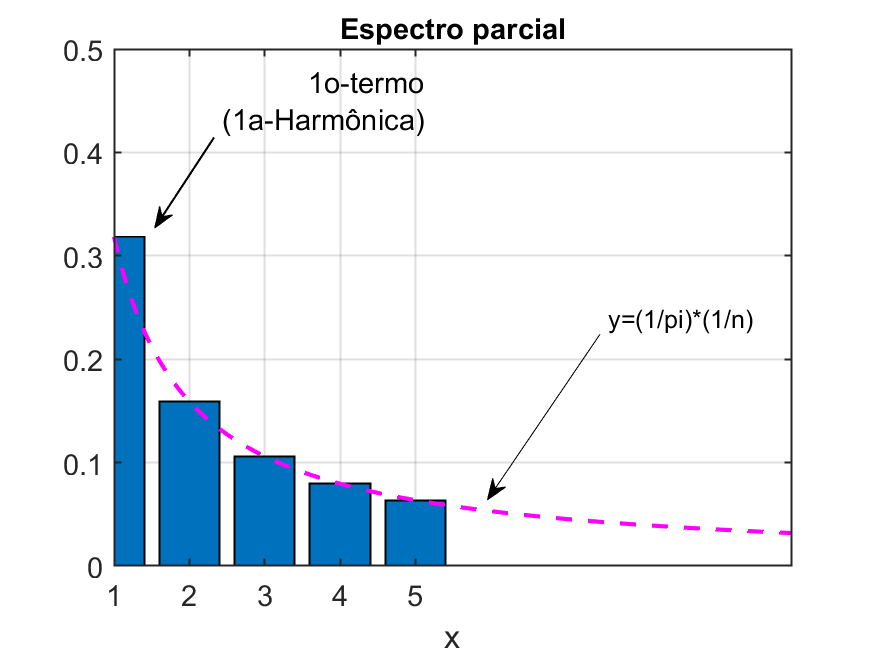ou na forma de uma tabela:

Termo	Freq (Hz)	Amplitude
1	1	0.31831
2	2	0.15915
3	3	0.1061
4	4	0.079577
5	5	0.063662

A tabela acima foi obtida executando no Matlab:
> n=1:5;
> A=(1/pi)*(1./n);
> [n' A']

Note que a linha com a expressão para cálculo de $y=f(t)$ é algo longa para ser digitada à mão. Podemos melhorar isto codificando uma pequena rotina que já considera o período de tempo total desejado, a frequencia desejada para a onda e o número de termos que devem ser usados para sua síntese. A rotina dente_serra.m segue abaixo:

% Gera dente de serra
% Fernando Passold, em 11/03/2023

clear t y % limpa estas variaveis da memória

disp('Gerador de Dente de Serra')

n = input('Qtdade de termos desejados   (n=)  ? ');
f = input('Freq. desejada para a onda (f= Hz) ? ');

T=1/f;
t_final=2*T; % periodo de tempo para 2 ciclos do sinal

t=0:T/100:t_final; % cria vetor tempo.

nn = 1:n; % termos
A=(1/pi)*(1./nn); % amplitude de cada termo isolado

index = 0; % indice para cada termo calculado de y=f(t)
num_termos = length(t); % tamanho do vetor t

while index < num_termos
  index = index + 1; % instante tempo atual == t(index)
  % lembrar que matlab inicia indices vetores em 1 
  % Calculando amplitudes em cada instante de tempo
  sum = 0;
  for k=1:n % calculando composição dos n-termos
    sum = sum + A(k)*sin( (2*k*pi*t(index))/T );
  end
  y(index) = 1/2 - sum;
end

figure; % abre nova janela gráfica
plot(t,y)
y_max=1.1*max(y);
aux=num2str(f);
titulo=['Dente de Serra ' aux ' (Hz)'];
title(titulo)
xlabel('tempo (s)')
ylabel('Amplitude (Volts)')

figure; % novo gráfico com espectro do sinal
nn=f*nn; % termos em Hz
stem(nn,A);
axis([0 (n+1)*f 0 y_max])
title('Espectro parcial')
xlabel('Freq. (Hz)')
ylabel('Amplitude (Vp)')
aux=num2str([nn' A']);
[lin,col]=size(aux);
% matlab deixa 4 espacos em branco entre nn e A
%     1234
msg='f    A(f)';
% então falta completar string com m espacos
u=length(msg);
m=col-u;
for k=1:m
  msg=[msg ' ']; % agregando espaco extra faltante
end
% acrescentando um "divisor" na tabela
msg2='-'; % traço divisor
for k=1:col-1
  msg2=[msg2 '-'];
end
% colunas_size(msg) == colunas_size(aux)
aux=[msg; msg2; aux];
text(0.7*n*f,0.7,aux)

Executando esta rotina para $f=2$ Hz e 9 termos:

>> dente_serra
Gerador de Dente de Serra
Qtdade de termos desejados   (n=)  ? 9
Freq. desejada para a onda (f= Hz) ? 2

Obtemos os gráficos:

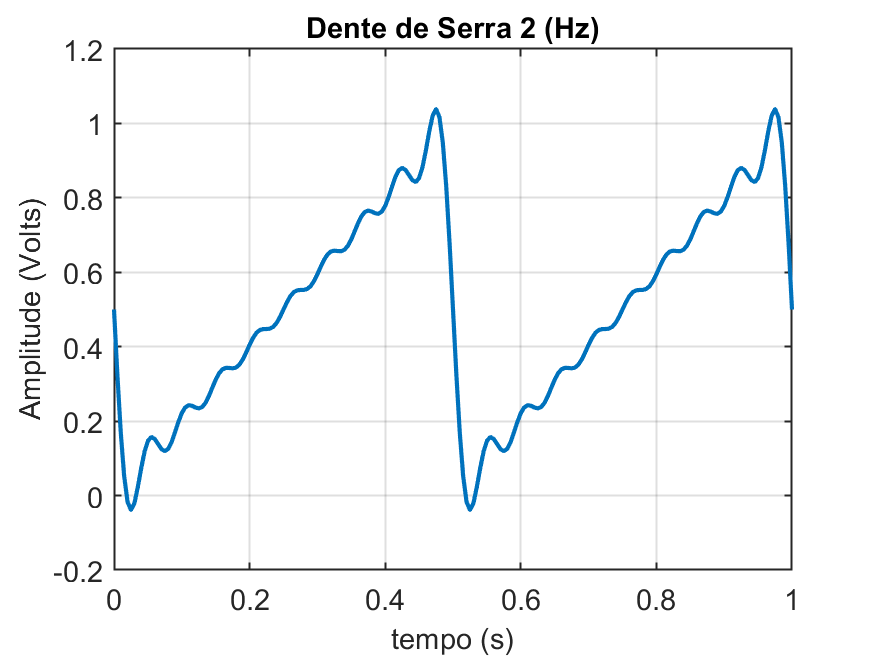
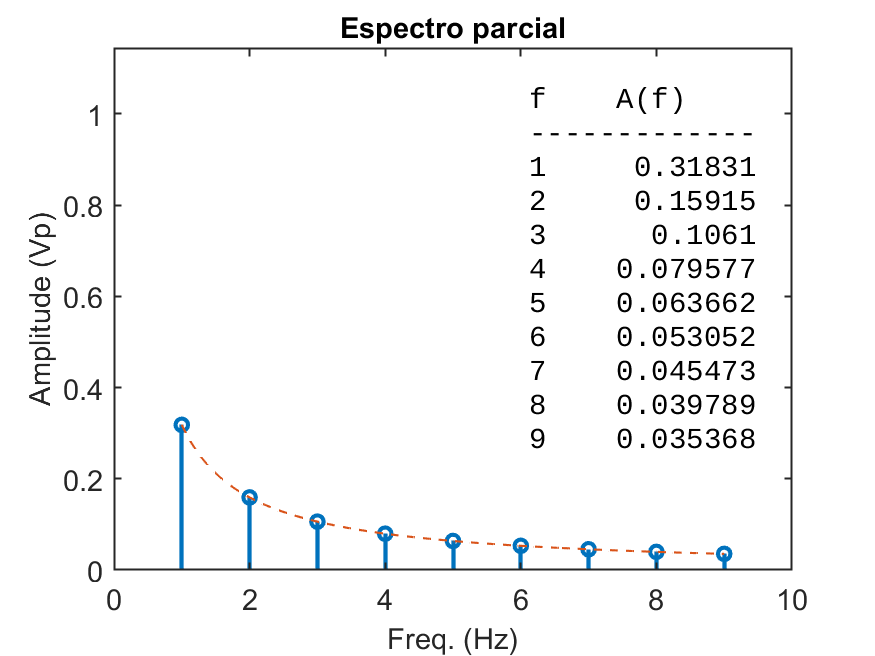
Digitalizando a Dente de Serra

Suponha que vamos digitalizar uma onda dente de serra variando na frequência de 100 Hz, onde o conversor A/D trabalha com frequência de amostragem de $f_s=400$ Hz, ou seja, 4 vezes a frequência máxima do sinal (na realidade $4 \times$ a freq. fundamental, da 1a-harmônica, deste sinal). Este conversor vêm precedido por um filtro passa-baixas (FPB) ideal com frequência de corte em 250 Hz (pouco acima da metade de $f_s$ ). Suponha que vamos nos restringir até o $10^{\underline{o}}$ (décimo) termo para síntese da onda dente de serra.

Pergunta: -- Como este final ficará amostrado por esta forma de amostragem?

Resposta:

Note que apesar da onda estar variando na $f=100$ Hz e ser amostrada à $f_s=400$ Hz, parece que estamos respeitando o teorema de amostragem e que não vamos perder informação neste sinal... Será?

Mas notamos que os 100 Hz correspondem apenas a 1a-harmônica deste sinal (sua frequência fundamental). Na realidade, este sinal é rico em mais harmônicas. Isto significa que estaremos perdendo informação das harmônicas de mais alta ordem.

Note que é importante, preceder o conversor A/D de um filtro passa-baixas para ``truncar'' as componentes do sinal e evitar replicação do espectro no momento da amostragem.

Executando mais uma vez a rotina dente_serra.m notamos o seguinte espectro de sinal:

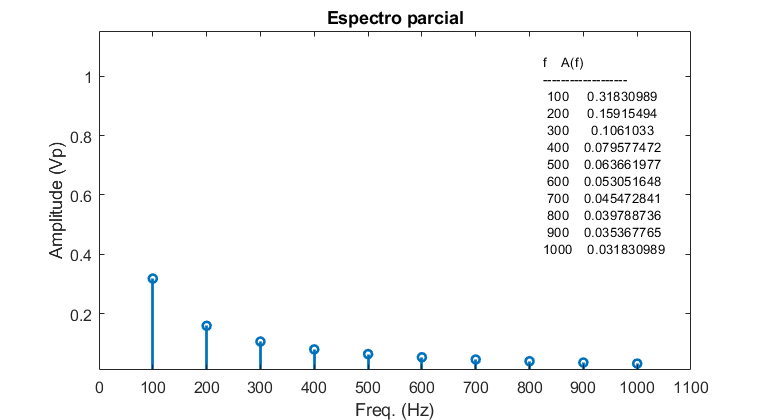
Como o A/D é precedido de um FPB com $f_c=250$ Hz. Então teremos algo como:

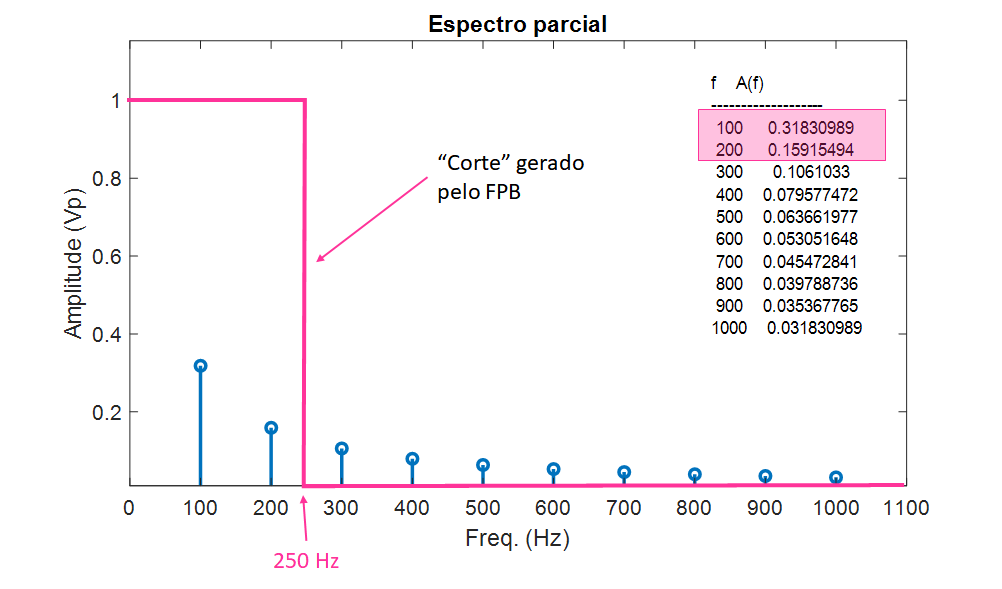
Note (está destacado) na figura anterior, que apenas os 2 primeiros componentes do sinal serão capturados (as frequências de 100 Hz e 200 Hz). Todos os outros componentes serão eliminados (ou atenuados no caso de um FPB real).

Considerando ainda a função Sampling que permite prever a queda de amplitude (ou ganho) do sinal amostrado em determinada frequência, podemos prever as amplitudes que serão capturadas pelo conversor A/D.

Então:

\vert S(jw) \vert = \dfrac{\sin(\omega T /2)}{\omega T /2}

Estamos considerando para este caso, sustentador de ordem zero, ou seja, $\tau=T$ .

Apenas esta última equação gera um gráfico como:

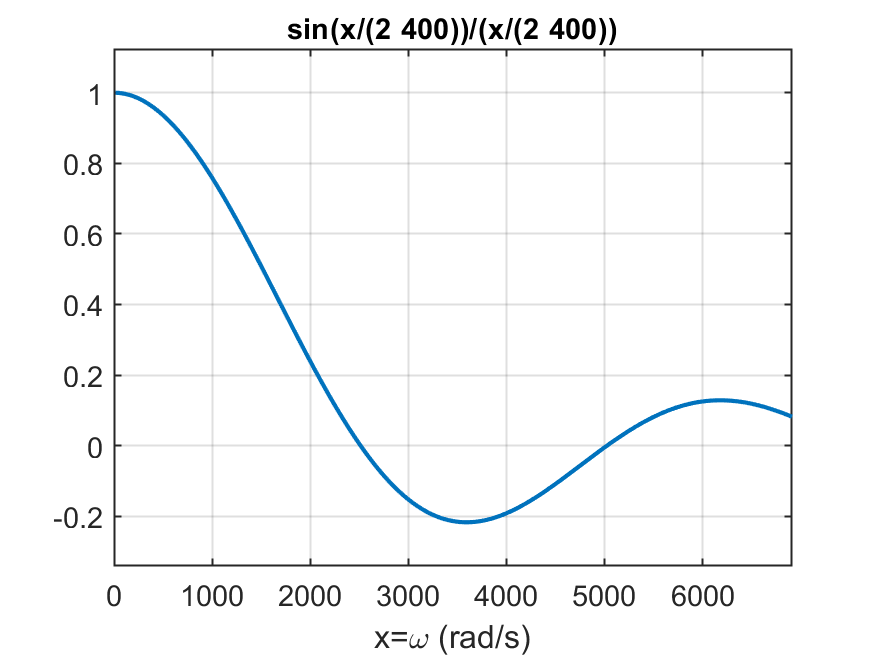
O gráfico anterior foi realizado usando Maltab:

>> figure; ezplot('sin(x/(2*400))/(x/(2*400))',[0 2*pi*1100])
>> 2*pi*1000
      ans =
           6283.2

A eq. e gráficos anteriores levam em conta $\omega$ em rad/s e não Hz. Como $\omega=2\pi f$ , modificando a eq. anterior para:

\vert S(jw) \vert = \dfrac{\sin(\pi f T)}{(\pi f T)}

podemos obter um gráfico como:

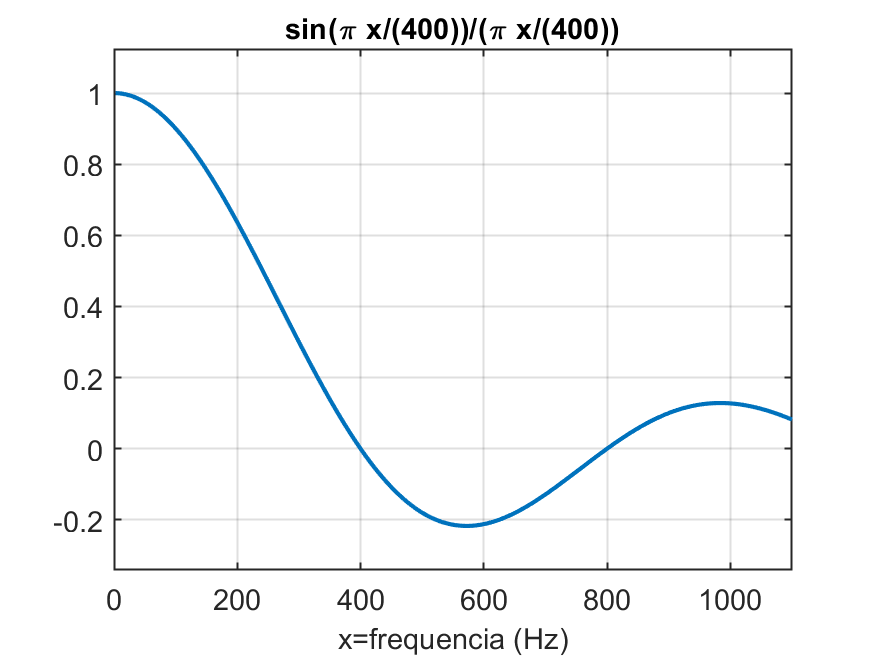
Este gráfico pode ser sobreposto ao nosso sinal de entrada, a onda dente de serra e então vamos ter algo como:

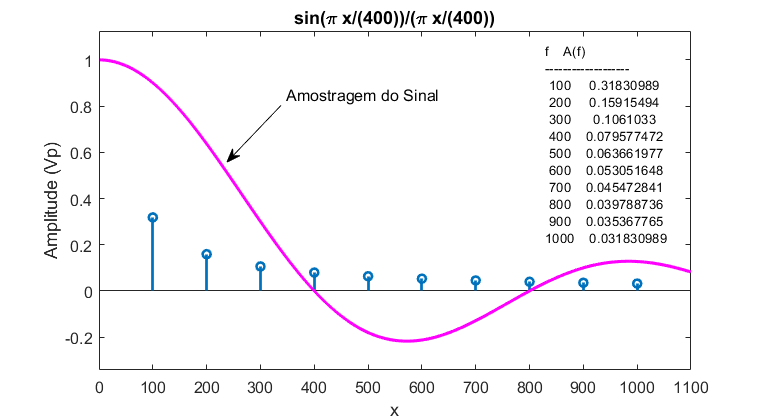
Obs.: Na figura anterior, não aparece o espectro "truncado" do sinal gerado pelo FPB, que "cancela" os componentes acima de 250 Hz.

Isto significa que nas frequências de 100 e 200 Hz, nosso sinal original (excetuando o FPB que foi considerado ideal), irá sofrer uma leve atenuação. Calculando a atenuação sofrida inerente ao processo de amostragem:

>> G1=sin(pi*100/400)/(pi*100/400) % atenuação do 1o-componente em 100 Hz
G1 =
      0.90032
>> G2=sin(pi*200/400)/(pi*200/400) % atenuação do 2o-componente em 200 Hz
G2 =
      0.63662
>>

Note a maior atenuação de sinal será sofrida pelo componente em 200 Hz (63,66% da amplitude original será mantida).

Considerando a forma inicial como calculamos as amplitudes da onda dente de serra, podemos acrescentar agora a atenuação sofrida nos seus 2 primeiros componentes:

>> n=1:10; % originalmente 10 componentes consideradas
>> A=(1/pi)*(1./n); % amplitude de cada componente
>> [n' A']
ans =
            1      0.31831
            2      0.15915
            3       0.1061
            4     0.079577
            5     0.063662
            6     0.053052
            7     0.045473
            8     0.039789
            9     0.035368
           10     0.031831
>> B(1)=A(1)*G1 % resultado atenuação primeiro componente
B =
      0.28658
>> B(2)=A(2)*G2 % resultado atenuação segundo componente
B =
      0.28658      0.10132
>> f=n*100; % criando vetor frequencia
>> % agrupando os resultados obtidos
>> [n(1:2)' f(1:2)' A(1:2)' B']
ans =
            1          100      0.31831      0.28658
            2          200      0.15915      0.10132
>> % n = No. do componente
>> % f = frequencia do componente
>> % A(n) = Amplitude orignal componente n
>> % B(n) = Amplitude amostrada componente n

Podemos tentar sobrepor o gráfico da onda sintetizada usando 10 termos com a onda amostrada contendo apenas 2 termos.

Executando primeiro dente_serra.m obtemos um primeiro gráfico do sinal usando 10 componentes. Aplicando então o comando >>hold on depois de focar na janela gráfica da forma de onda, fazemos ainda:

>> dente_serra
Gerador de Dente de Serra
Qtdade de termos desejados   (n=)  ? 10
Freq. desejada para a onda (f= Hz) ? 100
>> % colocar foco no primeiro gráfico, da onda no tempo
>> hold on % para sobrepor próximo gráfico
>> t=0:1/(100*20):2*1/100; % criando vetor tempo, 20 amostras/ciclo de sinal; 2 ciclos
>> y_amost=1/2-B(1)*sin(1*2*pi*f.*t) - B(2)*sin(2*2*pi*f.*t);
>> plot(t,y_amost,'m-')
>> legend('Sinal original', 'Sinal Amostrado')

Deve ser obtido algo como:

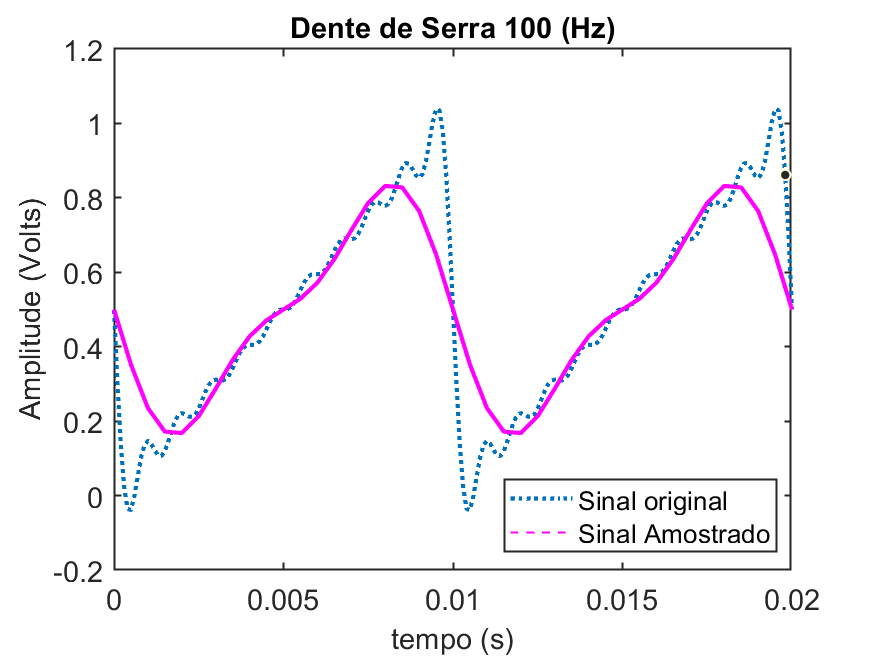
Note como o sinal amostrado perdeu informações do sinal original.

Note os pontos nos quais o sinal original foi amostrado:

>> t_amost=0:1/400:2*1/100;
>> t_amost'
ans =
            0
       0.0025
        0.005
       0.0075
         0.01
       0.0125
        0.015
       0.0175
         0.02

É possível sobrepor os pontos amostrados na onda original digitalizada, fazendo-se ainda:

>> y_amost2 = 1/2 - B(1)*sin(1*2*pi*f.*t_amost) - B(2)*sin(2*2*pi*f.*t_amost);
>> hold on % sobre a figura anterior, vamos acrescentar "terceiro" gráfico
>> plot(t_amost,y_amost2,'mo')
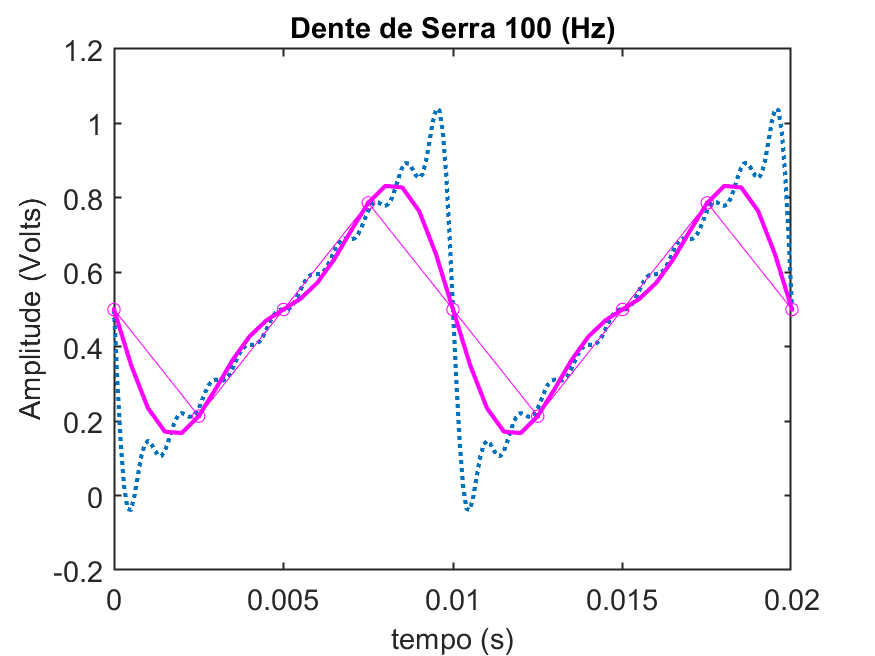
>> plot(t_amost,y_amost2,'m.-')

Perceba neste último gráfico obtido, os pontos com os marcadores circulares. Estes são os pontos que foram amostrados (capturados) do sinal original e serão processados pelo microcontrolador ou outro sistema embarcado.

Fim.

Fernando Passold, em 11/03/2023