Síntese de Onda Quadrada

Uma onda quadrada pode ser sintetizada usando série de Fourier [1, 2 ]:

onde: $n=1,3,5,\ldots,\infty$, somente números ímpares, correspondem as harmôincas ímpares do sinal (uma onda quadrada possui somente os componentes/harmônicas ímpares); $f=$ frequência da onda quadrada (em Hz); $A=$ Amplitude de pico da onda quadrada; $t=$ variável tempo (em segundos).

Para acompanhar a dedução completa se sugere uma visita à: Math is Fun >> Advanced >> Fourier Series Graph Tool.

Assim sendo, nossa onda quadrada pode ser sintetizada aplicando a eq.:

considerando que a mesma vá oscilar entre $-1$ até $+1$ Volts ($A=1$).

Obs.: este tipo de onda possui apenas harmônicas ímpares.

No Matlab, podemos reproduzir esta síntese em gráficos:

>> % Exemplo de síntese temporal de onda quadrada
>> f=10; % 10 Hz
>> T=1/f; % periodo da onda
>> t=0:T/100:2*T; % criando vetor tempo, 2 ciclos, 100 amostras/ciclo
>> y1=1*sin(2*pi*f.*t); % 1a-harmônica (fundamental)
>> y3=(1/3)*sin(2*pi*3*f.*t); % 3a-harmônica
>> y5=(1/5)*sin(2*pi*5*f.*t); % 5a-harmônica
>> y7=(1/7)*sin(2*pi*7*f.*t); % 7a-harmônica
>> y9=(1/9)*sin(2*pi*9*f.*t); % 9a-harmônica
>> y11=(1/11)*sin(2*pi*11*f.*t); % 11a-harmonica
>> % Plotando apenas 1a-harmonica, na freq. fundamental
>> figure; plot(t,y1)
>> title
>> % Acrescentando a 3a-harmônica:
>> y=y1+y3;
>> figure; plot(t,y)
>> title('Onda quadrada (até 3a-harmonica)')
>> % Acrescentando a 5a-harmônica:
>> y=y+y5;
>> figure; plot(t,y)
>> title('Onda quadrada (até 5a-harmonica)')
>> % Acrescentando a 7a-harmônica:
>> y=y+y7;
>> figure; plot(t,y)
>> title('Onda quadrada (até 7a-harmonica)')
>> % Acrescentando 9a-harmônica:
>> y=y+y9;
>> figure; plot(t,y)
>> title('Onda quadrada (até 9a-harmonica)')
>> % Acrescentando a 11a-harmonica
>> y=y+y11;
>> figure; plot(t,y)
>> title('Onda quadrada (até 11a-harmonica)')

Obs.: No código anterior, não foi considerado o fator $\left( \dfrac{4\,A}{\pi} \right)$ que deveria ser usado para escalar o valor de cada harmônica sendo processada. Neste caso: $\left( \dfrac{4\,A}{\pi} \right) = \dfrac{4}{\pi}=1,2732$, o que vai implicar numa onda que não oscila exatamente sobre $-1$ e $+1$. Volts.

A execução dos comandos acima rende os seguintes gráficos:

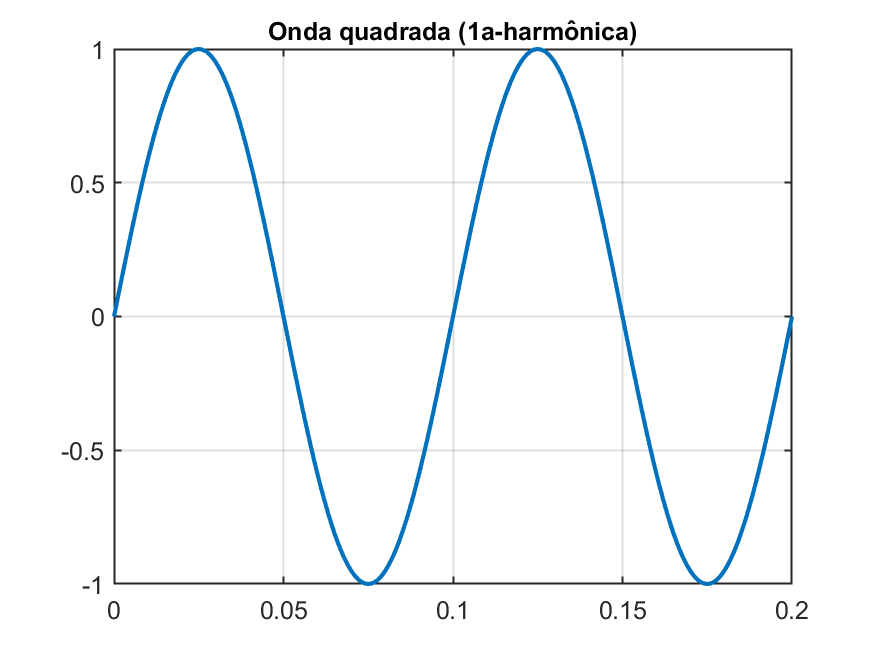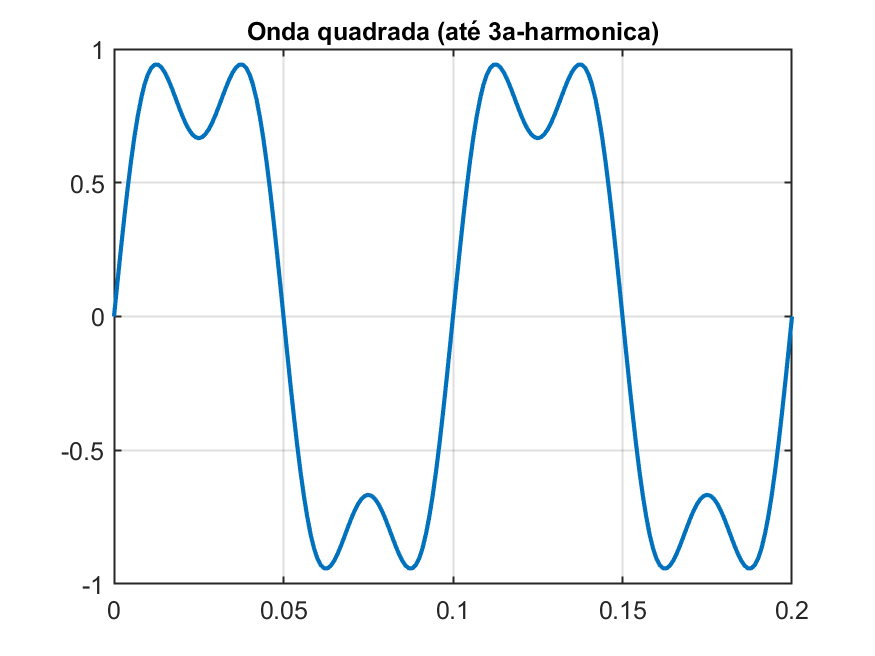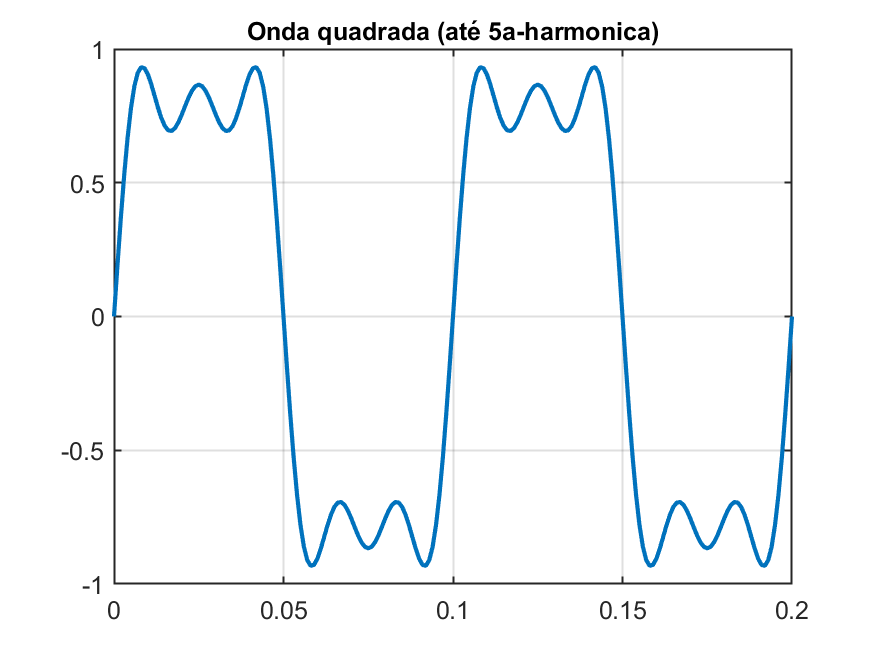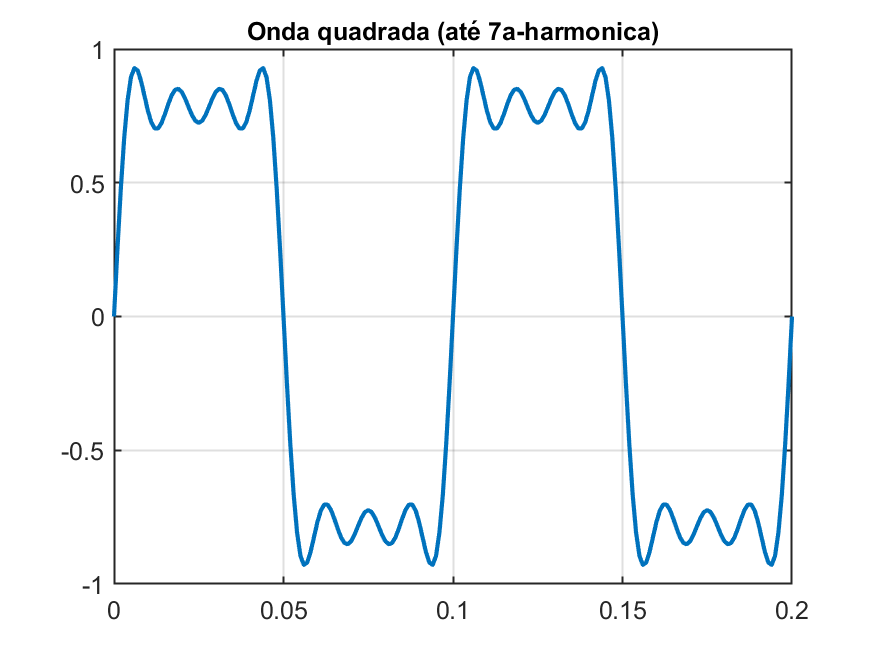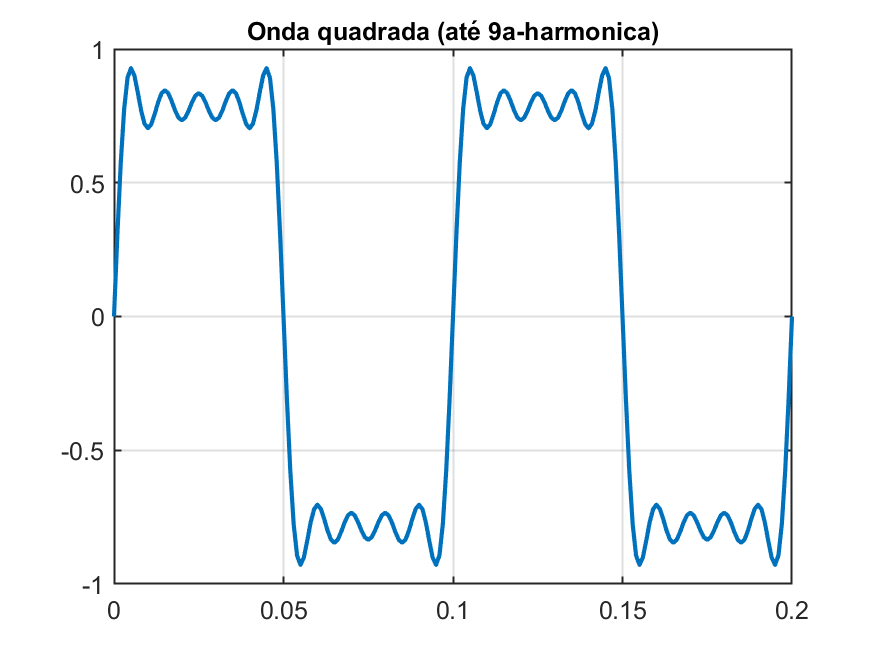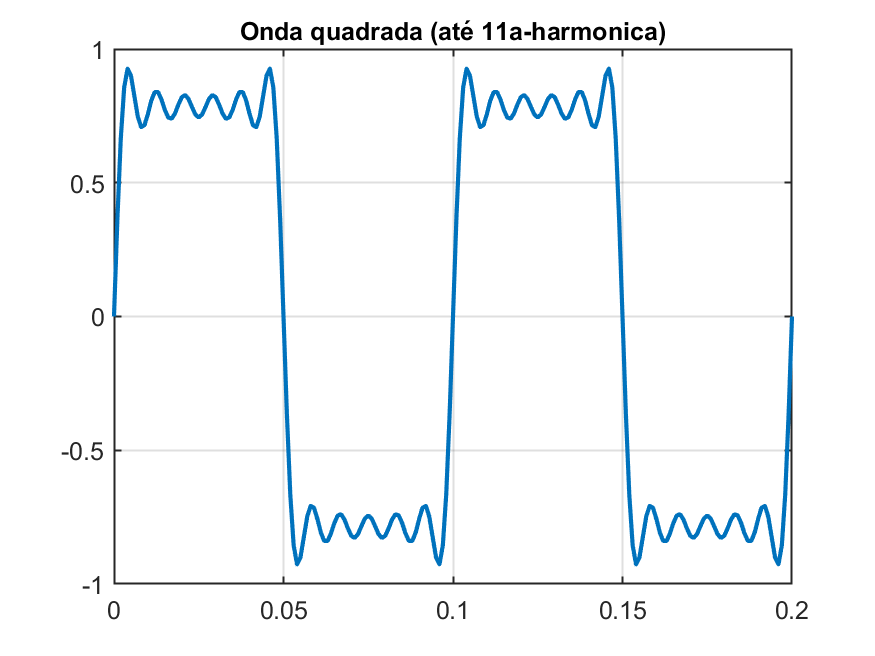Fica fácil reparar que quanto maior o número de harmônicas, mais a onda resultante se assemelha a uma onda quadrada.

Podemos mostrar uma "tabela" e gráfico das amplitudes das harmônicas (gráfico espectral), fazendo:

xxxxxxxxxx
>> %  1 2 3   4 5   6 7   8 9   10 11  12 13  14 15  16 17 - harmônicas
>> Y=[1 0 1/3 0 1/5 0 1/7 0 1/9 0 1/11 0 1/13 0 1/15 0 1/17]; % amplitudades cada harmonica
>> h=1:17; % criando vetor h
>> F=f.*h; % criando vetor F: freqs das harmonicas
>> figure; stem(F,Y) % cada ponto do gráfico é uma linha vertical com marcador
>> xlabel('Freq. (Hz)');
>> ylabel('Amplitude (Abs)');
>> title('Espectro Onda Quadrada')
>> grid
>> % Acrescentando texto referente ao número da harmõnica nas linhas geradas:
>> h=h'; % apenas transposta de h
>> h_text=num2str(h); % transforma cada linha do vetor h numa string (array de char)
h_text =
  17×2 char array
    ' 1'
    ' 2'
    ' 3'
    ' 4'
    ' 5'
    ' 6'
    ' 7'
    ' 8'
    ' 9'
    '10'
    '11'
    '12'
    '13'
    '14'
    '15'
    '16'
    '17'
>> text(F,Y,h_text) % acrescenta o texto à cada pico da harmônica
>> axis([0 180 0 1.1]) % melhora área vizualização

Gráfico resultante:

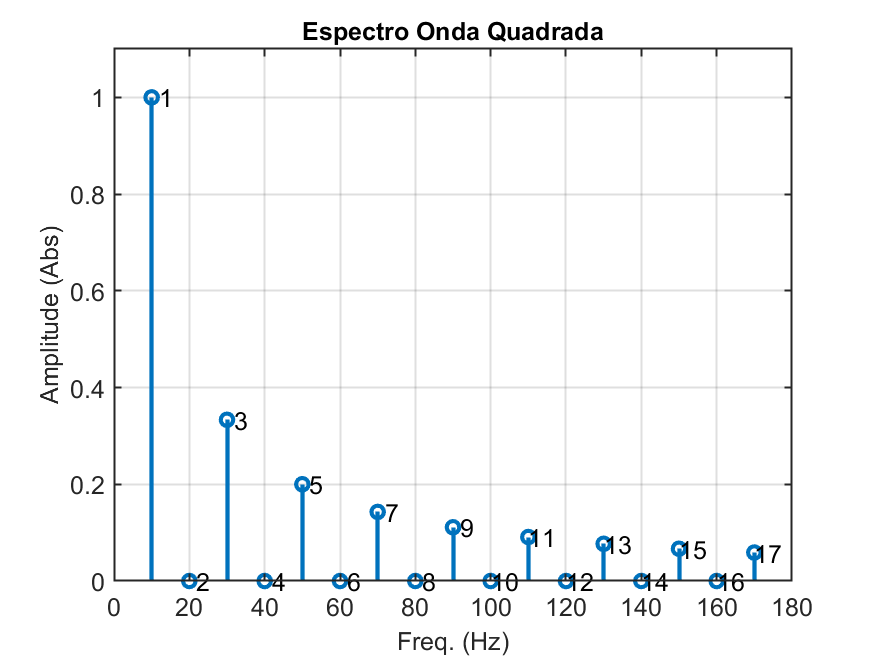
Referências:

[1] Fourier Series (mathsisfun.com), acessado em 25/03/2023;

[2] Fourier series - Wikipedia, acessado em 25/03/2023.