Filtro Digital Passa-Baixa Primeira Ordem

Intro à Filtro Digital

Depois que um sinal contínuo passa por uma conversão analógico para digital, filtragem digital adicional pode ser aplicada para melhorar a qualidade do sinal. Se o sinal está sendo usado em um aplicativo em tempo real ou foi coletado para uma análise posterior, implementar um filtro digital via software é bastante simples. Já os vimos sendo usados casualmente em alguns dos meus posts anteriores, como MCP3008 com Raspberry Pi. Agora, vamos analisar esses tipos de filtros com mais detalhes. Para os exemplos, usaremos as funções de processamento de sinal do pacote SciPy Python.

Uma das desvantagens da filtragem digital (ou filtragem analógica, para esse assunto) é a introdução de um atraso de fase no sinal filtrado.

Acompanhe pelos gráficos abaixo:

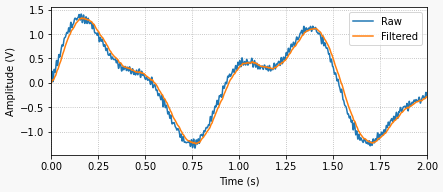
1a-figura: sinal bruto e filtrado (com atraso de fase):

2a-figura: sinal bruto e filtrado (sem atraso de fase):

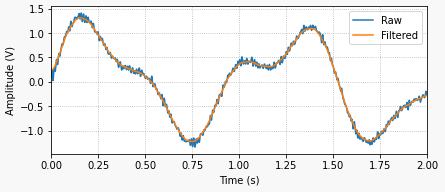
Os gráficos anteriores ilustram como seria um sinal filtrado real e seu atraso de fase (1a-figura), em contraste com um sinal filtrado ideal sem atraso (2a-figura). Embora a situação ideal não possa ser alcançada com o processamento de sinais em tempo real, ela pode ser alcançada ao processar sinais que já estão amostrados e armazenados como uma sequência discreta de valores numéricos.

Como a sequência do início ao fim está disponível, a ideia é filtrá-la uma vez (causando uma mudança de fase) e, em seguida, filtrar a sequência resultante para trás (causando uma mudança de fase novamente). Como a filtragem é feita tanto para frente quanto para trás, as mudanças de fase se cancelam, resultando em um sinal filtrado de fase zero!

Para ver como isso é feito, confira o script filtfilt.py (mais abaixo) e os exemplos de aplicação na documentação do SciPy. Você também pode acessar o código usado para gerar os gráficos baseado na página GitHub: Things-DAQ-Code/Digital-Filtering.

Em GitHub: Things-DAQ-Code/Digital-Filtering, estão disponíveis:

xxxxxxxxxx
/Things-DAQ-Code-main/Digital-Filtering/
├── post_digital_filtering_bandpass.py
├── post_digital_filtering_butterworth.py
├── post_digital_filtering_phase_delay.py
├── post_digital_filtering_response.py
└── utils.py
​
1 directory, 5 files

A rotina filtfilt faz parte dos esforços de processamento de sinal. Há muitas informações que podem ser extraídas de um sinal depois de "limpá-lo" um pouco. Se o alinhamento temporal entre os eventos for crítico, evitar uma mudança de fase é o caminho a seguir.

Antes de entrarmos na aplicação em tempo real de filtros digitais, vamos falar brevemente sobre como eles são implementados.

Equação de Diferenças

Vou me concentrar em filtros que podem ser descritos como a equação de diferença abaixo:

$\displaystyle\sum_{k=0}^{N} a_k y[n-k] = \displaystyle\sum_{k=0}^{M} b_k x[n-k]$

Onde $x[n]$ é a sequência de entrada (sinal bruto, de entrada) e $y[n]$ é a sequência de saída (sinal filtrado). Antes de você abandonar esta página da web, deixe-me reescrever a equação para que possamos começar a trazê-la para uma forma mais aplicável. Já que a ideia é encontrar a saída $y[n]$. Em função de seus valores anteriores e da entrada, podemos escrever:

$a_0 y[n] = -a_1 y[n-1] - \ldots - a_N y[n-N]\quad+\quad b_0 x[n]+b_1 x[n-1] + \ldots + b_M x[n-M]$

É comum normalizar os coeficientes, então $a_0=1$.

Filtro de 1a-ordem

Para simplificar, considere um filtro de primeira ordem que, em termos de equações de diferença, depende apenas dos valores das amostras atuais e da amostra anterior, ou respectivamente: $[n]$ e $[n-1]$. Assim:

$a_0 y[n] = -a_1 y[n-1] + b_0 x[n] + b_1 x[n-1]$

Então, para construir um filtro digital passa-baixa de primeira ordem, tudo o que precisamos fazer é determinar os coeficientes: $a_1$, $b_0$ e $b_1$ (considerando que $a_0=1$, está normalizado). Felizmente para nós, as funções de design de filtro SciPy MATLAB-Style retornam esses coeficientes, reduzindo nossa tarefa para a implementação do filtro usando Python. Antes de revisarmos alguns exemplos de código, vamos examinar um filtro de primeira ordem que eu uso bastante. Ver também A função filter() do Matlab/Octave.

Filtro Passa Baixas Digital de 1a-ordem

Passar do domínio tempo contínuo para o domínio tempo discreto envolve uma transformação em que aproximamos uma variável contínua por seu equivalente discreto (transformada-Z).

No caso de um filtro passa-baixo de primeira ordem, podemos analisar seu comportamento no tempo contínuo, mais especificamente a resposta a uma entrada degrau unitário. A figura à seguir ilustra a aplicação de um filtro passa-baixa de 1a-ordem sobre um sinal exponencial de entrada:

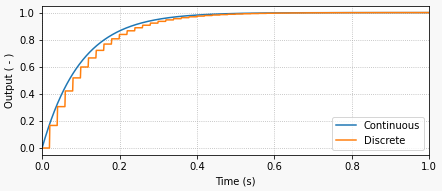
A resposta contínua do sistema à entrada constante $x(t)=u(t)$ (degrau unitário) é dado por: $y(t)=1-e^{-t/\tau}$, onde $\tau$ é o tempo de resposta do filtro (constante de tempo do filtro) e está relacionado à frequência de corte do filtro, $f_c$:

$\tau_c=\dfrac{1}{2 \pi f_c}$

O tempo de resposta do filtro é o tempo que leva para a saída atingir aproximadamente 63% do valor final. No caso do gráfico acima, o tempo de resposta é de 0,1 segundo. Se você está se perguntando de onde isso vem, basta calcular a resposta do sistema usando $t=\tau$.

A equação diferencial que corresponde ao sistema contínuo de primeira ordem em questão é:

$\dfrac{\partial y}{\partial t}=\dfrac{1}{\tau} x(t) - \dfrac{1}{\tau} y(t)$

E aqui é onde nossa aproximação discreta (equação de diferenças) de $\partial y/ \partial t$ usando relação de Euler (também conhecida como "regra retangular direta ou forward rectangular rule"), incluindo o período de amostragem $T_s$, fica:

$\dfrac{\partial y}{\partial t} \cong \dfrac{y[n]-y[n-1]}{T_s}$

Aplicando esta aproximação no termos $y(t)$ e $x(t)$ em suas contrapartes discretas $y[n]$ e $x[n]$, podemos chegar à equação de diferenças abaixo, que representa o filtro digital passa-baixa de primeira ordem, onde usamos a relação de Euler para aproximar $\partial y/\partial t$. Lembre-se: $[n]$ e $[n-1]$ são as amostras discretas no instante de amostrragem atual e no instante de amostragem anterior (respectivamente).

$\dfrac{y[n]-y[n-1]}{T_s} = \dfrac{1}{\tau}x[n] - \dfrac{1}{\tau}y[n]$

Finalmente, isolando $y[n]$ resultra numa equação muito semelhante à que vimos no final da seção anterior. Observe que os coeficiente $a_1$ e $b_0$ são uma ponderação envolvendo uma relação entre taxa de amostragem e constante de tempo do filtro ($b_1=0$ neste caso em particular):

$y[n]=\left( \dfrac{\tau_c}{\tau_c+T_s} \right) y[n-1] + \left( \dfrac{T_s}{\tau_c+T_s} \right) x[n]$

O interessante nesta abordagem de implementação é que é fácil perceber que a saída $y[n]$ é uma "média ponderada" entre seu valor anterior $y[n-1]$ e o valor de entrada atual $x[n]$.

Note: quanto menor o tempo de resposta do filtro ($\tau_c << T_s$), mais rápido o filtro (maior frequência de corte) e mais ele segue o valor de entrada. Por outro lado, num filtro mais lento ($\tau_c >> T_s$), a saída só leva em conta o valor anterior de saída do próprio filtro.

Filtro Exponencial Digital

Em outras abordagens semelhantes deste tipo de filtro (ver: "Filtro Exponencial Digital" em Controle com Ação Derivativa), é comum se usar o termo $\alpha$, onde:

$\alpha=\left( \dfrac{T_s}{\tau_c+T_s} \right)=\dfrac{1}{\dfrac{\tau_c}{T_s}+1}$

e a equação de diferenças anterior é re-escrita como:

$y[n]=\alpha x[n] + (1-\alpha)y[n-1]$

Onde: $0 < \alpha < 1$.

Tipicamente é empregado o valor $\alpha=0,1$ (o que implica que a constante de tempo do filtro é $10 \times$ menor que o período de amostragem adotado para o filtro).

Note:

$\left\{ \begin{array}{lclcl} \text{Se } \alpha=1 & \Rightarrow & y[n]=x[n] & \therefore & \text{Não existe filtragem!}\\ \text{Se } \alpha=0 & \Rightarrow & y[n]=0 & \therefore & \text{O sinal original é ignorado!} \end{array} \right.$

Exemplo de Código em Python

O código Python abaixo mostra como implementar este filtro, colocando-o dentro de um loop de execução e executando uma excitação de entrada de etapa através dele. Ele produzirá o gráfico mostrado no início desta seção. Convido você a experimentar diferentes tempos de resposta (frequências de corte) e períodos de amostragem.

> Segue script filtro.py :

x
import numpy as np
import matplotlib.pyplot as plt
​
# Criando matriz de tempo para sinal "contínuo"
tstop = 1       # Duração do sinal (s)
Ts0 = 0.001     # Passo de tempo "Contínuo" (s)
Ts = 0.02       # Período de amostragem (s)
t = np.arange(0, tstop+Ts0, Ts0)
​
# Resposta contínua do sistema de primeira ordem para entrada degrau
tau = 0.1       # Tempo de resposta (s)
y = 1 - np.exp(-t/tau)  # y(t)
​
# Pré-alocação de arrays de sinal para filtro digital
tf = []
yf = []
​
# Inicializando valores anteriores e atuais
xcurr = 1   # x[n] (entrada degrau)
yfprev = 0  # y[n-1]
yfcurr = 0  # y[n]
​
# Execução 
tprev = 0
tcurr = 0
while tcurr <= tstop:
    # Fazendo cálculos de filtro a cada `Ts` segundos
    if (np.floor(tcurr/Ts) - np.floor(tprev/Ts)) == 1:
        yfcurr = tau/(tau+Ts)*yfprev + Ts/(tau+Ts)*xcurr
        yfprev = yfcurr
    # Atualizando arrays de saída
    tf.append(tcurr)
    yf.append(yfcurr)
    # Atualizando etapas de tempo "contínuas" anteriores e atuais
    tprev = tcurr
    tcurr += Ts0
​
# Criando a figura Matplotlib
fig = plt.figure(
    figsize=(6.3, 2.8),
    facecolor='#f8f8f8',
    tight_layout=True)
# Adicionando e configurando eixos
ax = fig.add_subplot(
    xlim=(0, max(t)),
    xlabel='Time (s)',
    ylabel='Output ( - )',
    )
ax.grid(linestyle=':')
# Plotando sinais
ax.plot(t, y, linewidth=1.5, label='Continuo', color='#1f77b4')
ax.plot(tf, yf, linewidth=1.5, label='Discreto', color='#ff7f0e')
ax.legend(loc='lower right')
​
​

Fim.

🌊 Fernando Passold 📬 ,