Sintonia PID (Método do Relé

Sintonia PID (Método do Relé - Parte II)

Na parte I, foi estudada a teoria associada com este método. Resumindo:

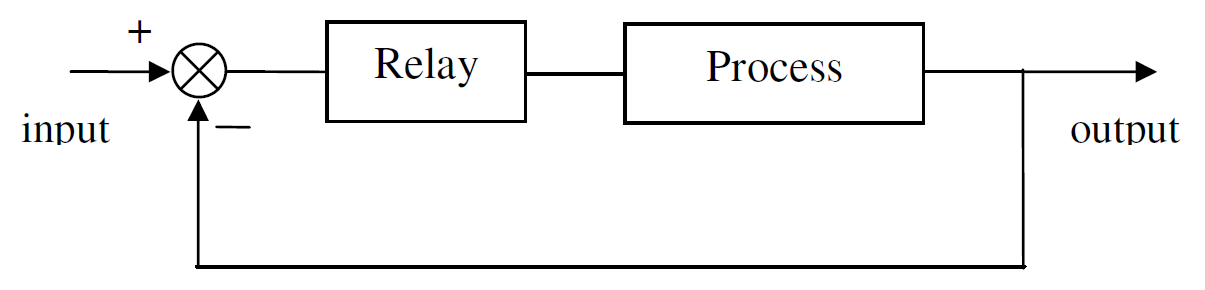
Astrom e Hagglund (1984) propuseram um poderoso método de variação de auto-sintonia (ATV = Auto-Tune Variation) para obter o ganho final, $K_u$ e o período final, $T_u$ . O método consiste em colocar um relé em série com o sinal de erro alternando o sinal na entrada do processo em $\pm d$ na detecção da travessia zero (zero crossing). Isso é esquematicamente ilustrado na próxima figura:

A ação do relé fará a entrada do processo alternar ao redor do estado estável $\pm d$ para cada cruzamento em zero do sinal de erro correspondente à saída cruzando o set-point especificado (a referência estabelecida). Isto faz o sistema oscilar de maneira sustentada (estável) colocando o sistema num ciclo limite como aparece na próxima figura:

O período de oscilações corresponde ao período final, $T_u$ . A amplitude $a$ das oscilações de saída e a amplitude das oscilações do relé, $d$ , permitem determinar o ganho final $K_u$ como sendo:

K_u = \dfrac{4 \cdot d}{\pi \cdot a}

Vantagens: O método ATV tem vantagens sobre os outros métodos. Este método encontra automaticamente a frequência crítica (ou período) de oscilação do processo. Além disso, grandes desvios longe do estado estável são evitados, pois este é um teste de loop fechado. Eventualmente os valores do ciclo limite do relé podem ser definidos pelo usuário, alimentando a planta com os valores máximos $U_{max}$ e $U_{min}$ em malha-aberta. Assim se pode prever a possível excursão do sinal de saída da planta, antes mesmo de aplicar este método, evitando-se assim que a planta oscile assumindo amplitudes muito elevadas.

A ideia agora é Implementar o método do relé no Matlab/Simulink...

Simulação usando Simulink

Seja a planta:

G(s)=\dfrac{1}{(s+1)(s+2)(s+10)}

Implementando o metódo do relé para este planta no Matlab/Simulink, podemos chegar à (arquivo: planta_ajuste_metodo_rele.slx):

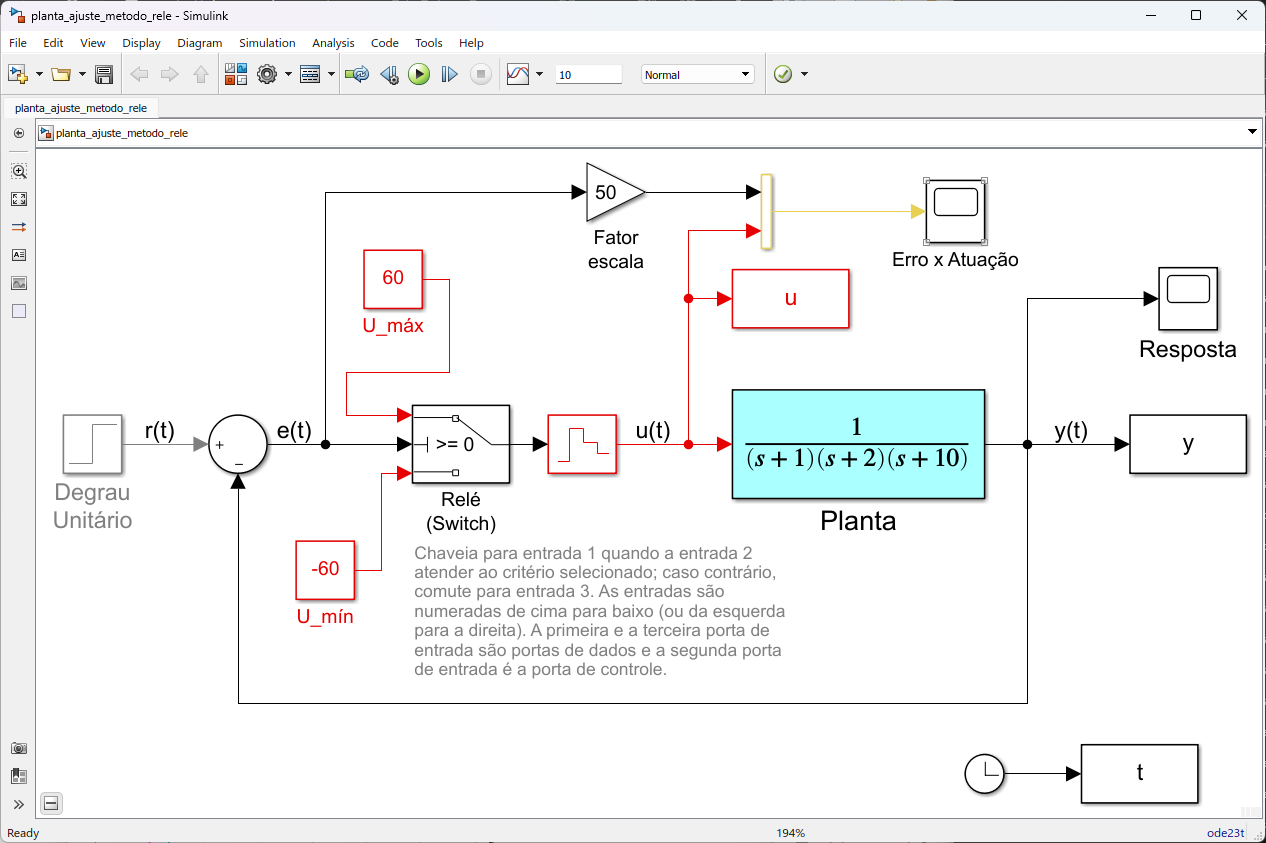
Note alguns detalhes:

A referência estabelecida foi um sinal degrau (constante de amplitude $=1$ ).
O ganho DC ( $y(\infty)|_{degrau}$ ) desta planta é bem baixo:
```
>> G=tf(1,poly([-1 -2 -10]));
>> zpk(G)

       1
------------------
(s+10) (s+2) (s+1)
>> dcgain(G)
      0.05
```
ou: $y(\infty)|_{degrau}=\lim_{s \to 0} \; s \cdot \left( \dfrac{1}{s} \right) \cdot \left( \dfrac{1}{(s+1)(s+2)(s+10)} \right)$ $y(\infty)|_{degrau}=\dfrac{1}{(1)(2)(10)}=\dfrac{1}{20}=0,05$ . Motivo pelo qual, para as amplitudes dos sinais de atuação/controle, à serem gerados pelo relé, foi optado pelo valor 60:
```
>> dcgain(G)*60
ans =
3
```

Resultados obtidos com esta simulação:

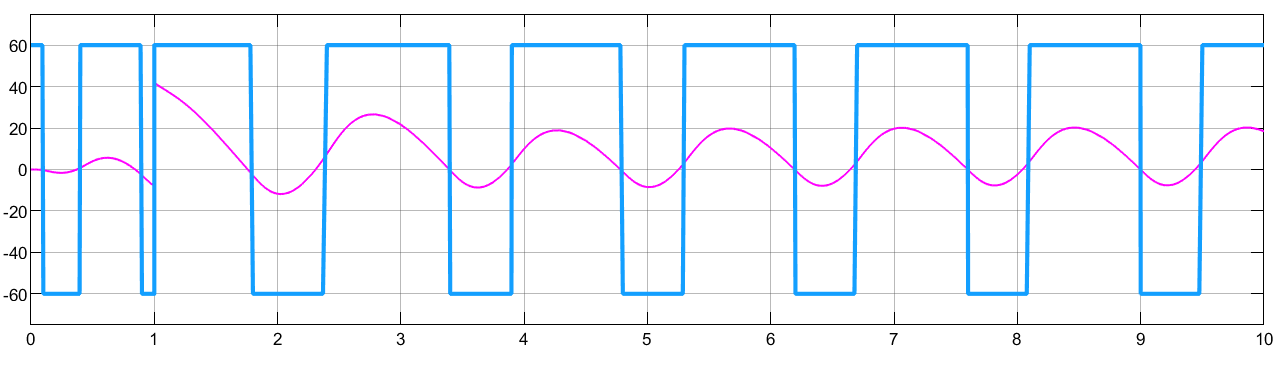
Gráfico do sinal de erro $\times$ saída do relé (saída do atuador):

Gráfico da resposta (saída) do sistema:

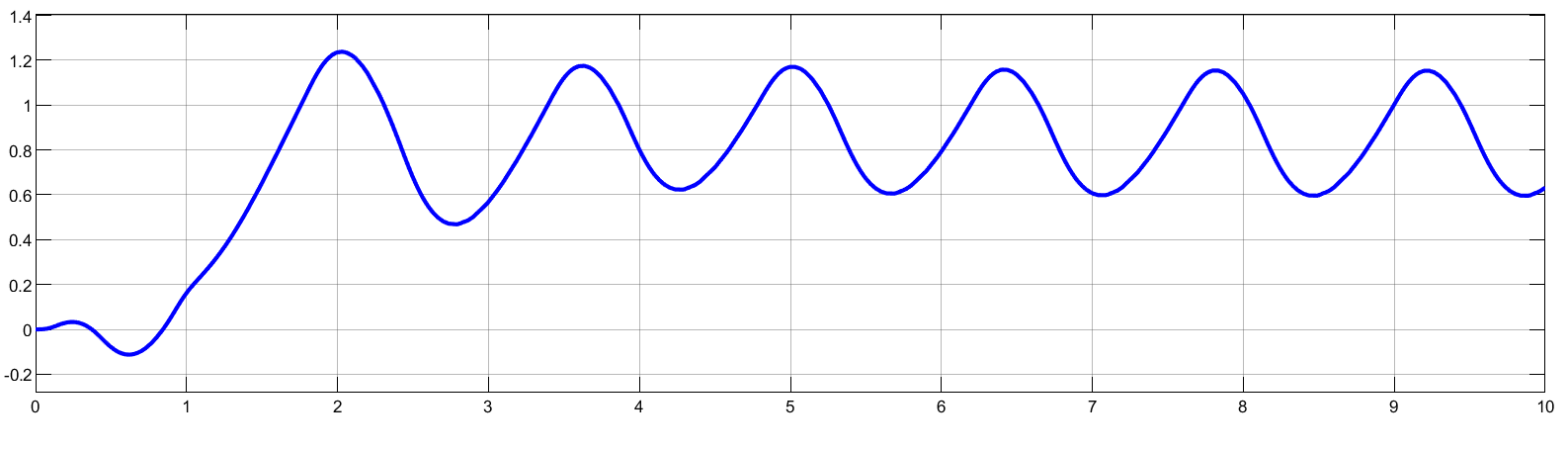
Necessitamos agora caputar as informações que nos interessam:

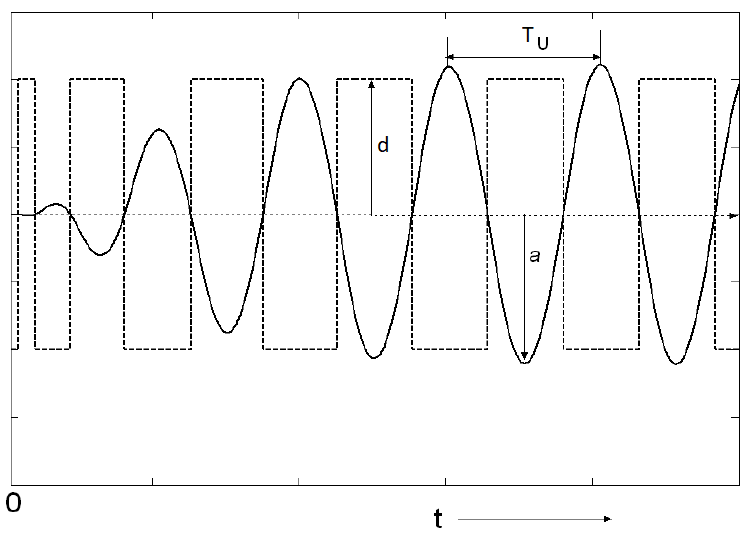
Extraíndo a informação do período de oscilação, 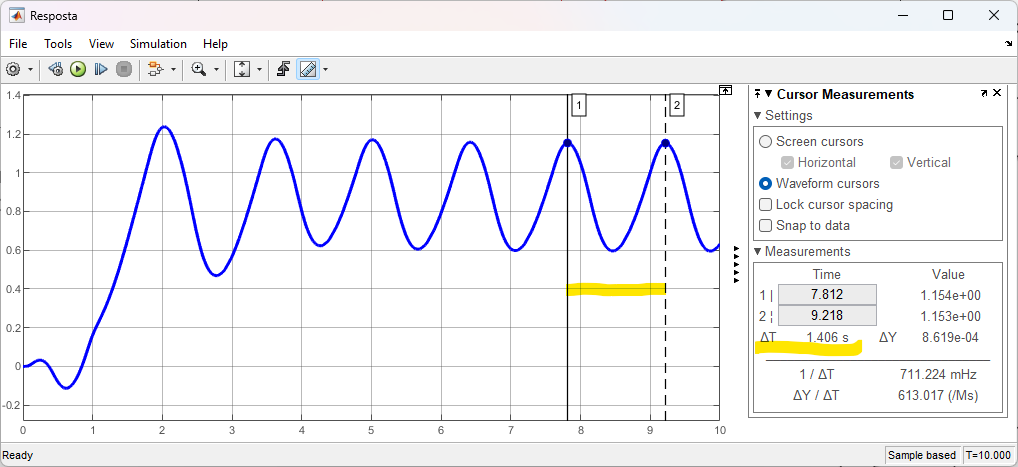$T_U$ : Da figura percebemos que $T_u= 1,406$ segundos.

Extraíndo a informação referente à amplitudade da oscilação, 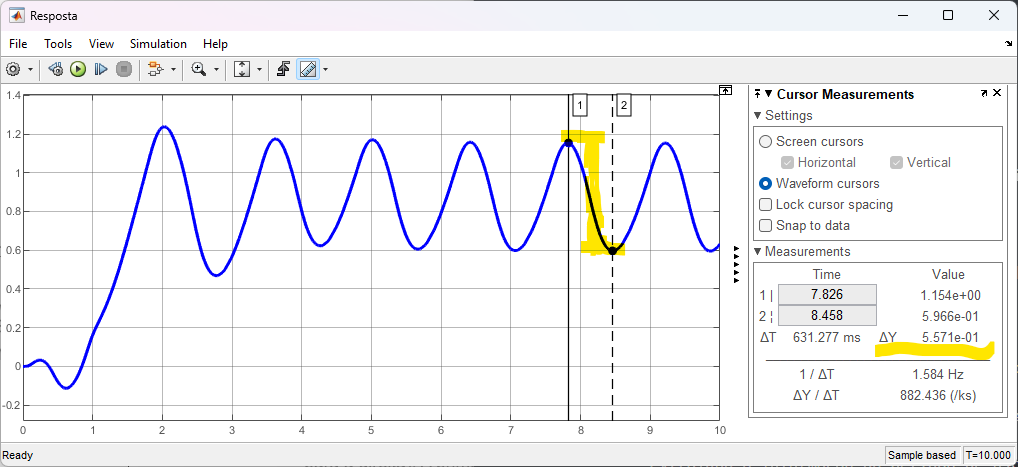$a$ : Da figura, temos que $2a=5,571 \times 10^{-1}=0,5571$ , então: $a=$

>> a=0.5571/2
a =
      0.27855

Extraíndo informação referente ao sinal gerado pelo relé: 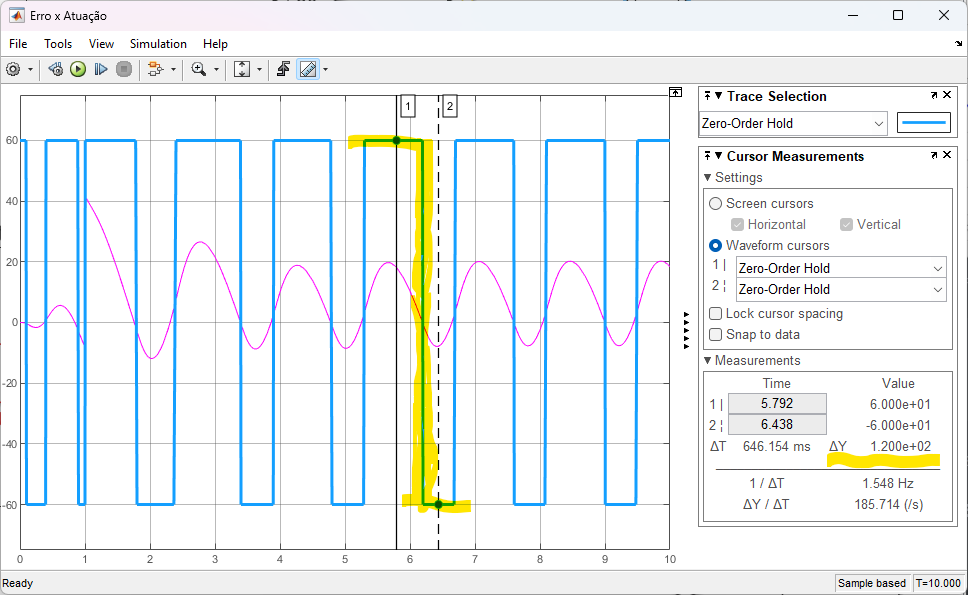Da figura, temos que $2d=1.2 \times 10^2=120 \quad \therefore \quad d=60$ .

Completando os cálculos de estimativa do $K_u$ , obtemos:

>> d=60;
>> Ku=(4*d)/(pi*a)
Ku =
       274.26

Calculando os parâmetros para o PID usando a tradicional tabela de Zigler-Nichols:

>> Tu=1.406;
>> Kp=.6*Ku
Kp =
       164.55
>> Ki=1.2*(Ku/Tu)
Ki =
       234.07
>> Kd=0.074*Ku*Tu
Kd =
       28.535

Aplicando no PID do Matlab/Simulink (arquivo: planta_2_PID.slx):

Os parâmetros usados foram:

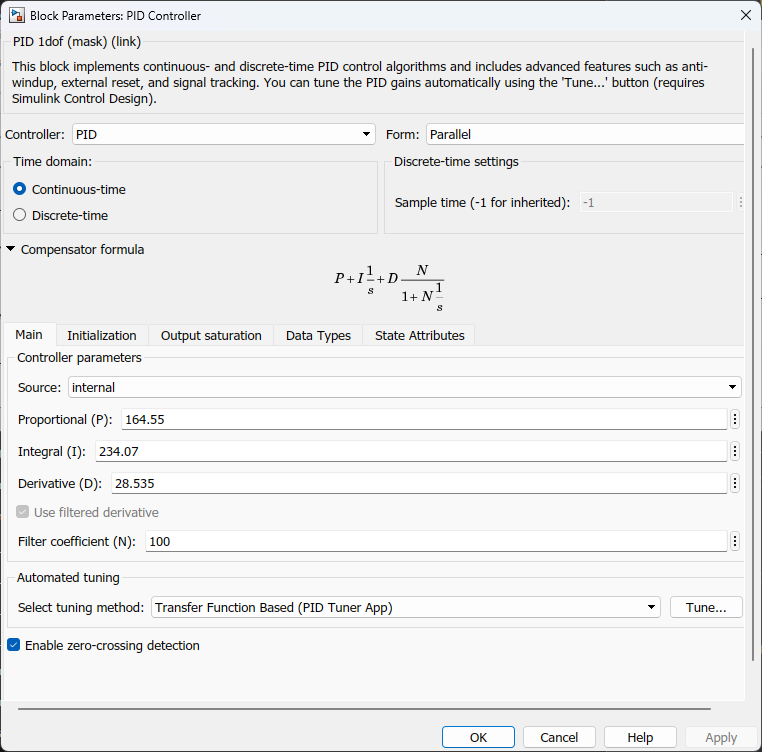
Obs.: deixado parâmento $N$ do filtro derivativo em 100.

Obtemos as seguintes respostas:

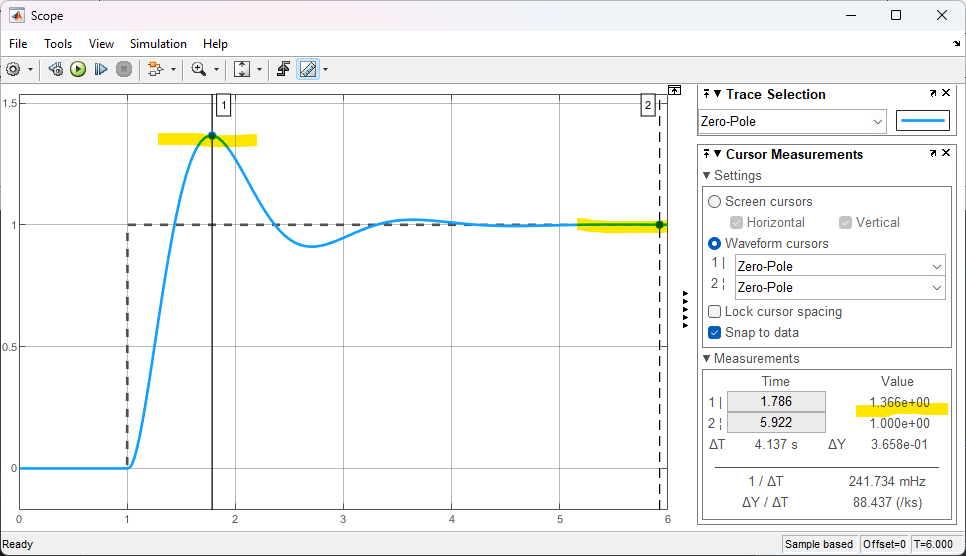ou seja um overshhot de $\%OS=36,6\%$ .

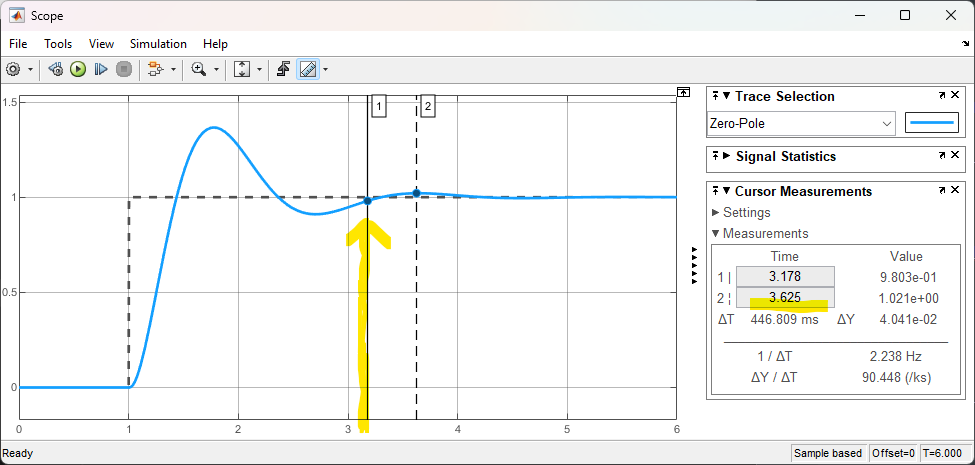e um tempo de assentamento, $t_s = 3,625$ segundos.

Este PID pode ser melhorando re-ajustando valores de $K_p$ (reduzir), $K_i$ (reduzir) e $K_d$ (manter igual).

Trabalho I

Prof. Fernando Passold, em 27.10.2022, 21/03/2023