Projeto de Controladores (Cont)
Controladores com Ação Derivativa
Aula de 20/10/2023 Dados desta aula podem ser recuperados à partir de planta.mat
Projeto de PD
Recuperando dados da aula passada:
>> load planta
Lembrando da equação genérica do PD(ver "Dedução Controladores PD & Lead) (arquivo PDF; Aula de 21/05/2020)"):
A única incógnita é a posição do zero do PD:
Podemos adotar o mesmo raciocínio empregado em "Projeto de Controlador PD (Aula de 28/05/2020)".
Lembrando da nossa planta:
>> zpk(BoG)
ans =
0.00046711 (z+3.27) (z+0.2335)
--------------------------------
(z-0.9608) (z-0.9048) (z-0.6703)
Sample time: 0.02 seconds
Discrete-time zero/pole/gain model.
Seguindo este mesmo raciocínio, parece ser melhor localizar o zero do PD entre os 2 pólos mais dominantes (mais lentos) da planta:
>> z_PD=(0.9608+0.9048)/2 % Calculando o valor geométrico médio entre os 2 pólos
z_PD =
0.9328
>> z_PD=0.93;
>> C_PD1 = tf([1 -z_PD],[1 0], T)
C_PD1 =
z - 0.93
--------
z
Sample time: 0.02 seconds
Discrete-time transfer function.
>> ftma_PD1 = C_PD1*BoG;
>> zpk(ftma_PD1)
ans =
0.00046711 (z+3.27) (z-0.93) (z+0.2335)
---------------------------------------
z (z-0.9608) (z-0.9048) (z-0.6703)
Sample time: 0.02 seconds
Discrete-time zero/pole/gain model.
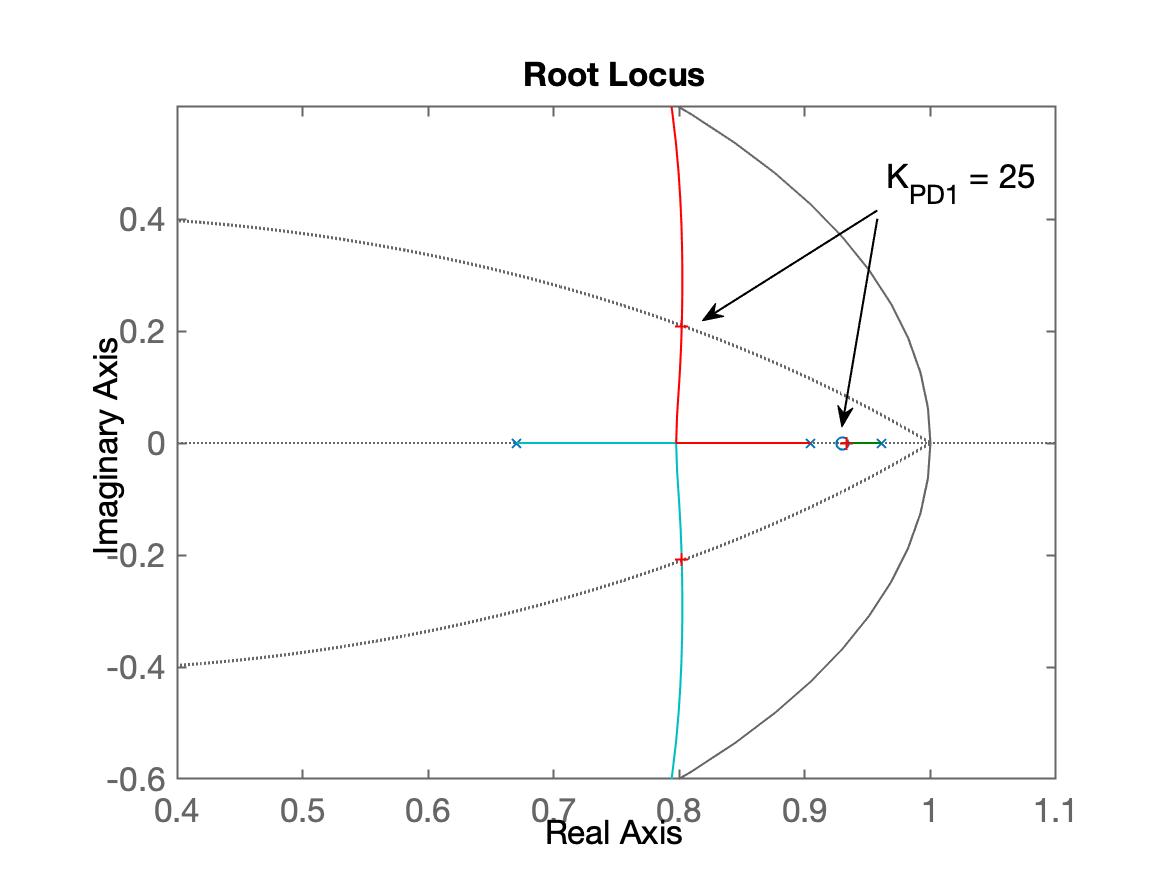
>> rlocus(ftma_PD1)
>> hold on; zgrid(zeta,0)
>> axis([0.4 1.1 -0.6 0.6])
>> [K_PD1,polosMF_PD1] = rlocfind(ftma_PD1)
Select a point in the graphics window
selected_point =
0.80225 + 0.20805i
K_PD1 =
25.218
polosMF_PD1 =
0.93332 + 0i
0.80195 + 0.20805i
0.80195 - 0.20805i
-0.013055 + 0i
>> K_PD1 = 25;
O RL para este PD fica:
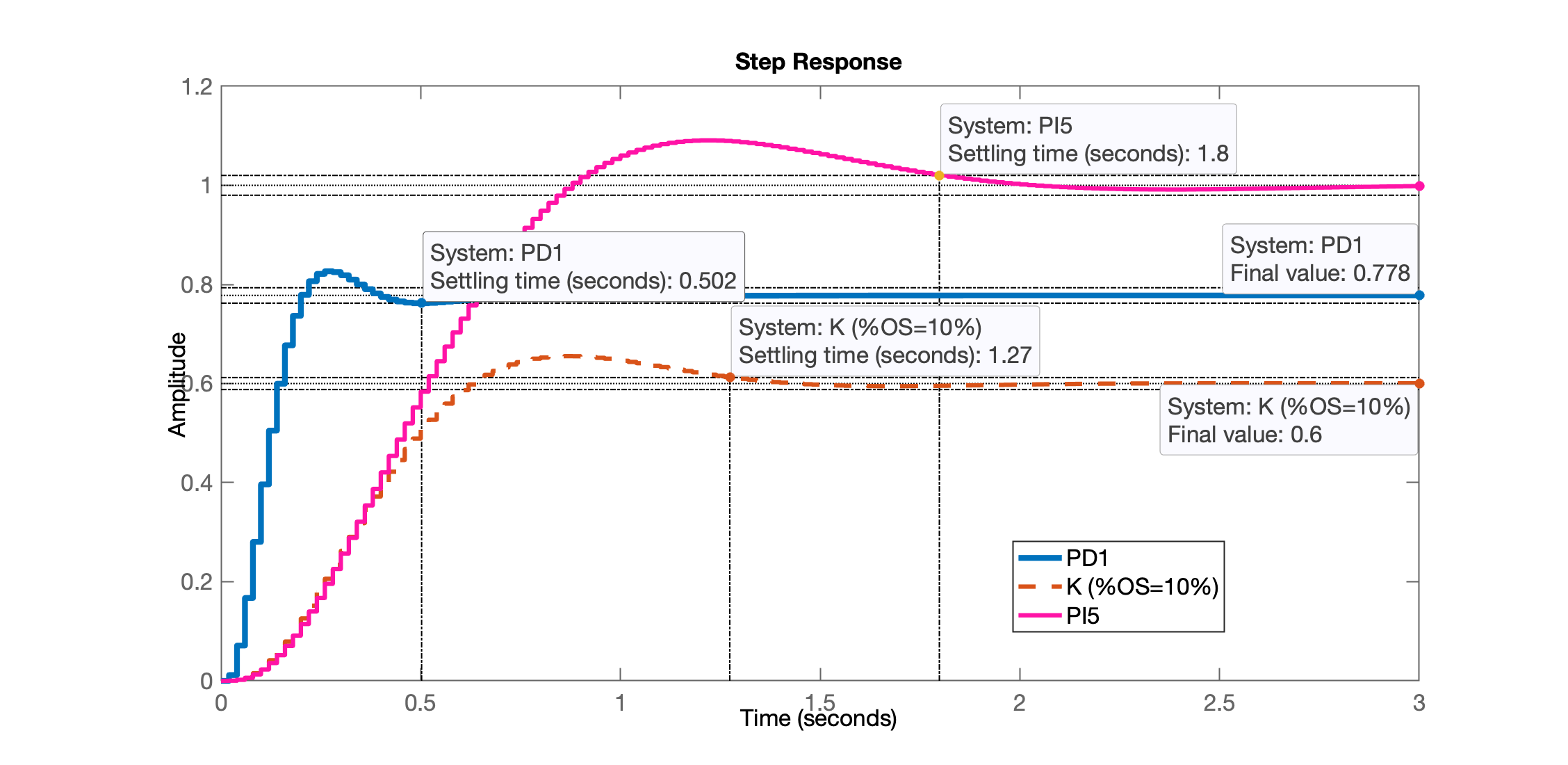
Fechando a malha com o ganho encontrado:
>> ftmf_PD1 = feedback(K_PD1*ftma_PD1, 1);
>> figure; step(ftmf_PD1, ftmf_K_OS10, ftmf_PI5)
>> legend('PD1', 'K (%OS=10%)', 'PI5')
Vamos obter o seguinte resultando, já comparando este PD (PD1) com a resposta obtida no projeto de outros controladores:
Melhorando o PD usando App Control System Designer
Podemos melhorando projeto com App Control System Designer.
Lembrando de fazer alguns ajustes iniciais:
Importando o controlador PD1 já realizado:
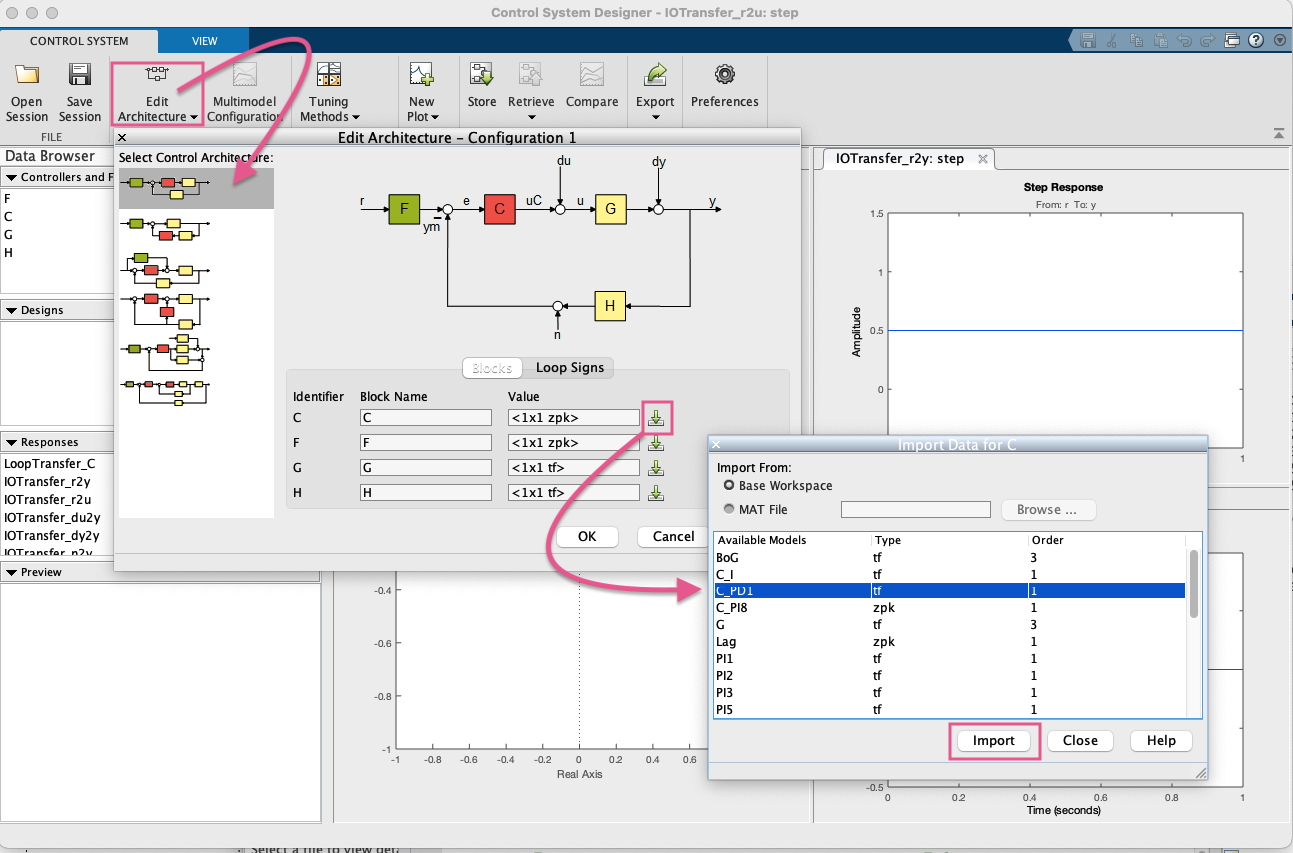
Não esquecendo de importar a planta (principalmente):
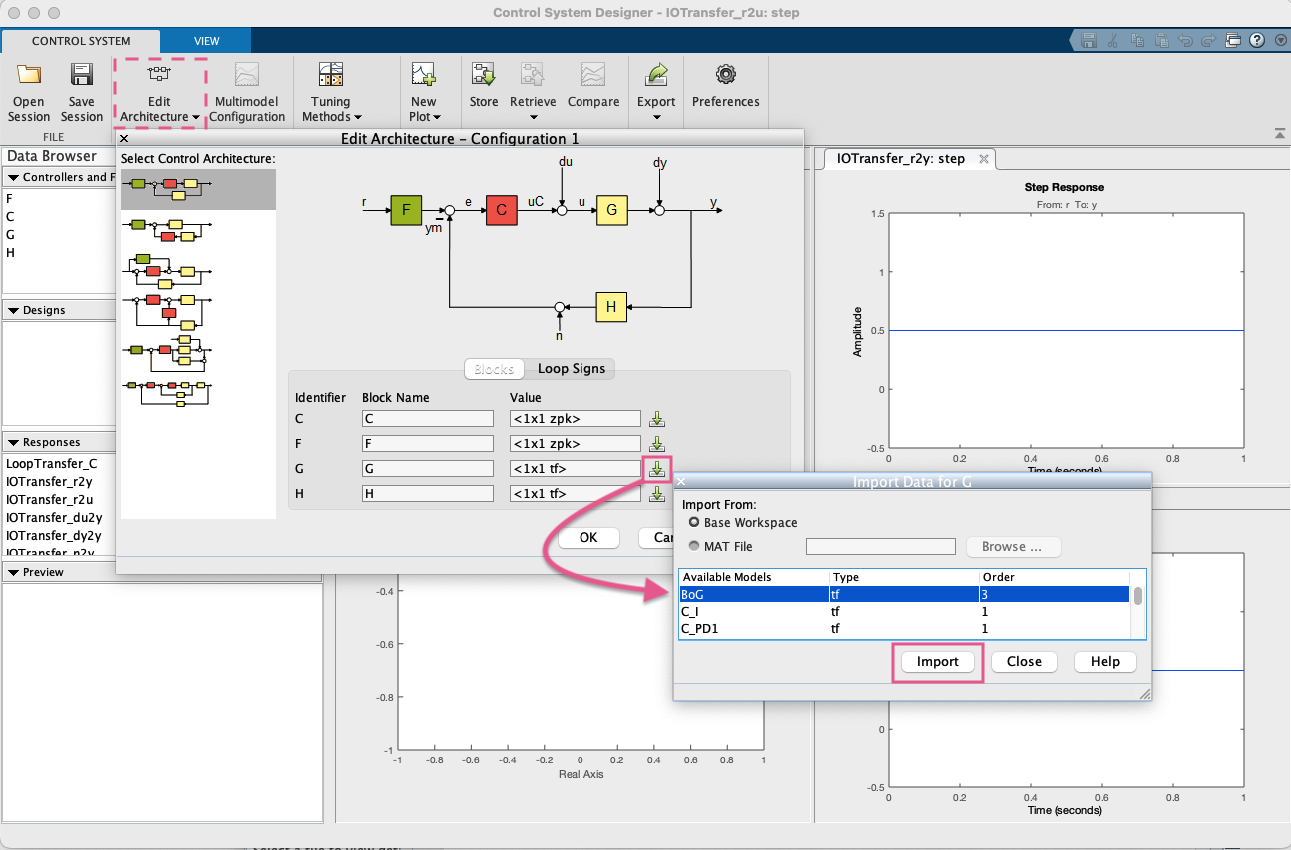
Editando o ganho do controlador:
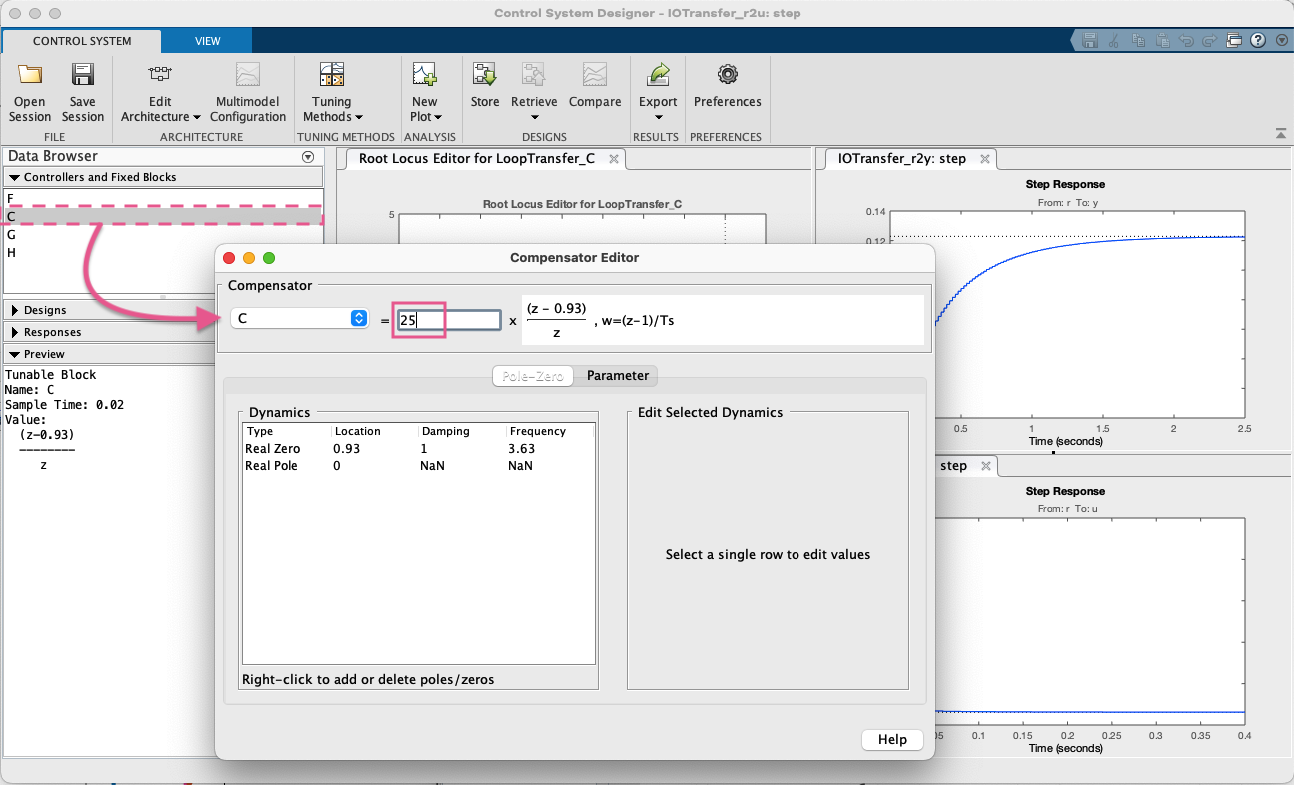
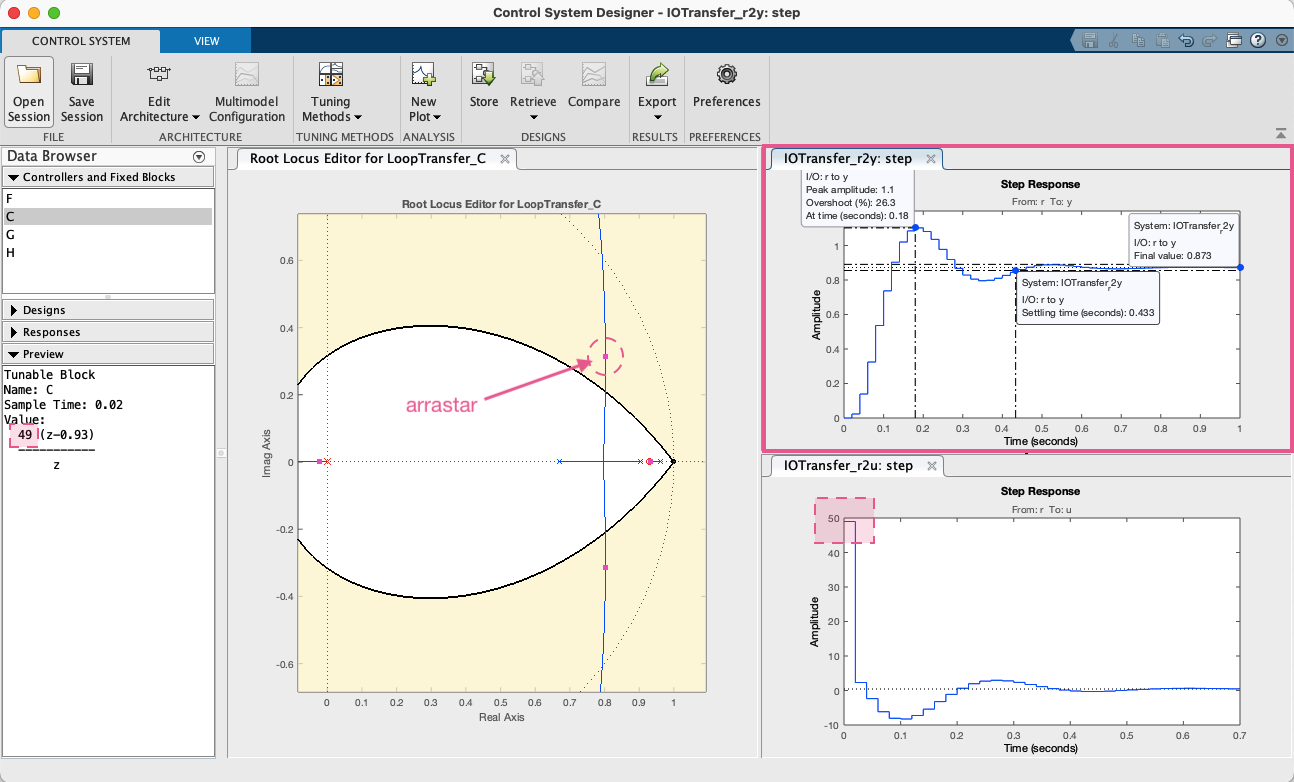
Aumentando o ganho para 49:
Exportando a equação deste PD para a janela de comandos do Matlab:
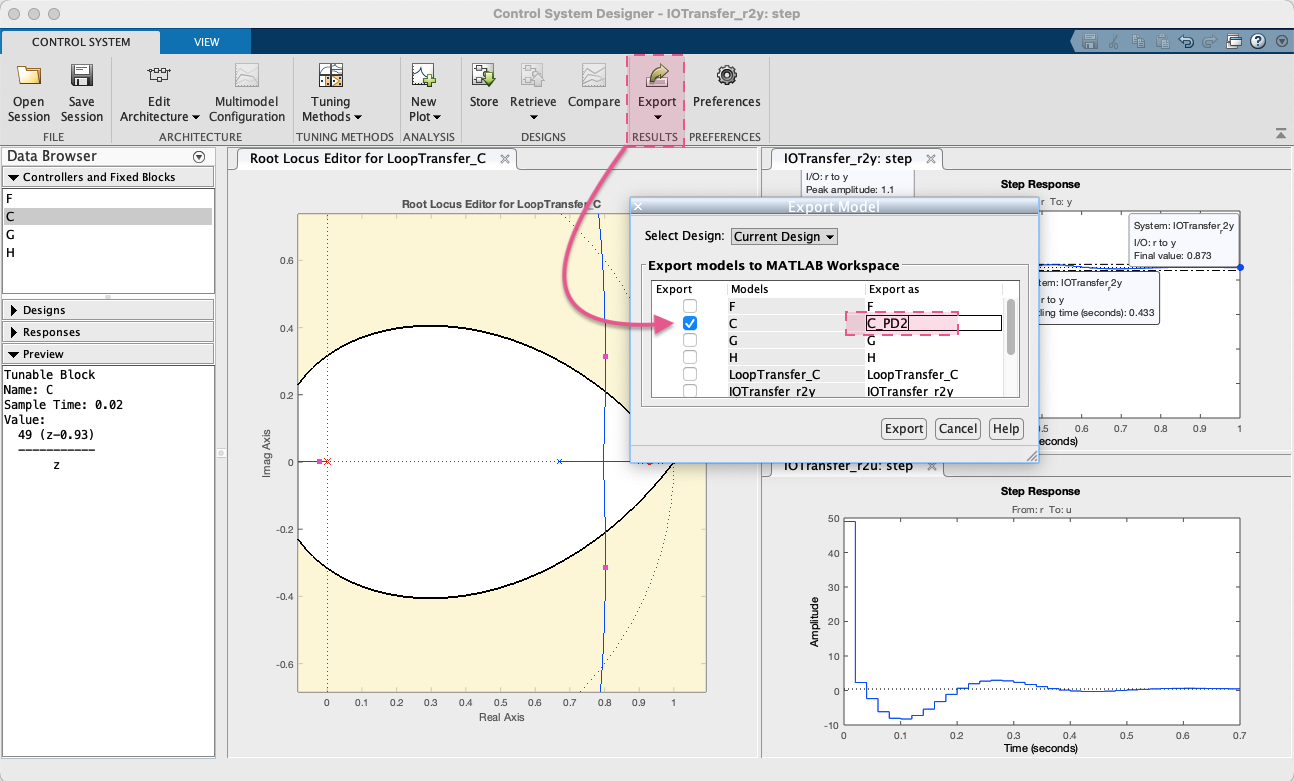
>> zpk(C_PD2)
ans =
49 (z-0.93)
-----------
z
Name: C
Sample time: 0.02 seconds
Discrete-time zero/pole/gain model.
Conclusão: Aumentar o ganho implicou reduzir o erro em regime permanente (como esperado).
PD cancelando um dos pólos da planta
Suponha que agora vamos cancelar o 2o-polo mais lento da planta com o zero do PD3:
Ajustando o zero do PD3:
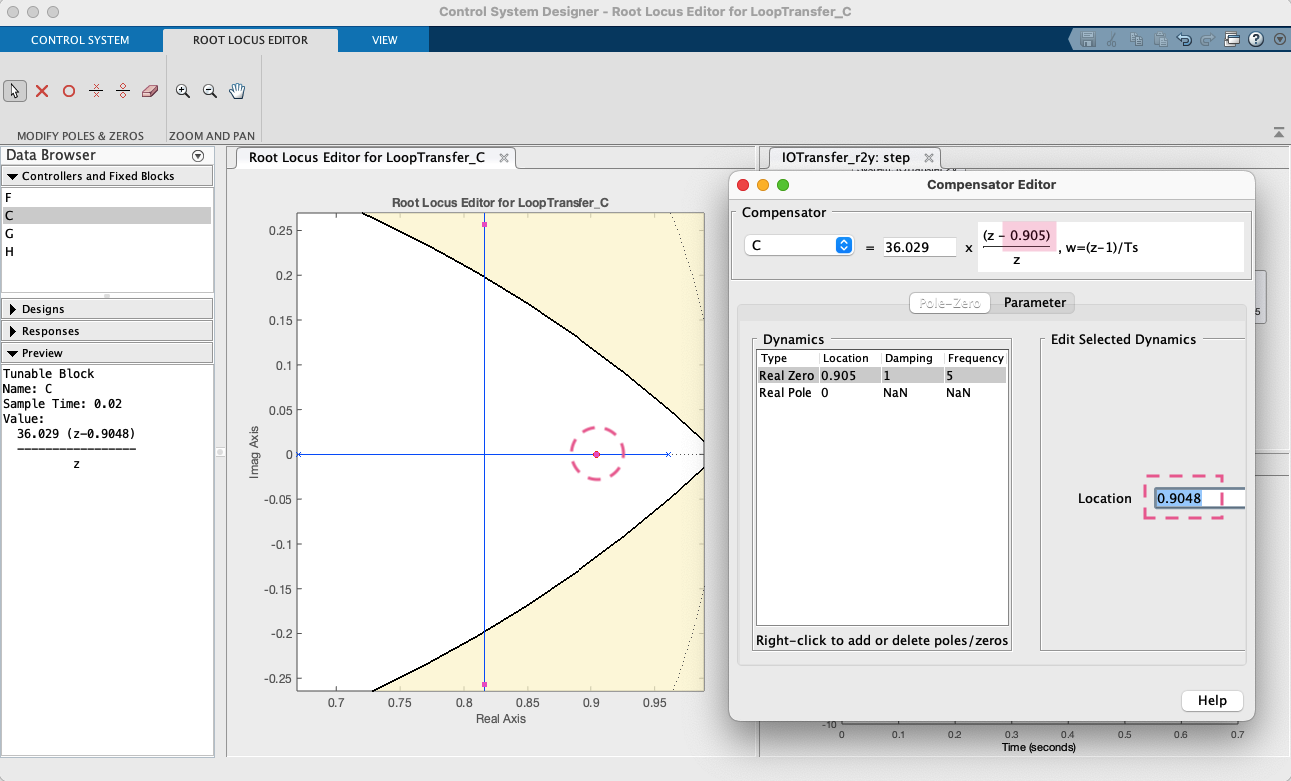
Resultado final obtido:
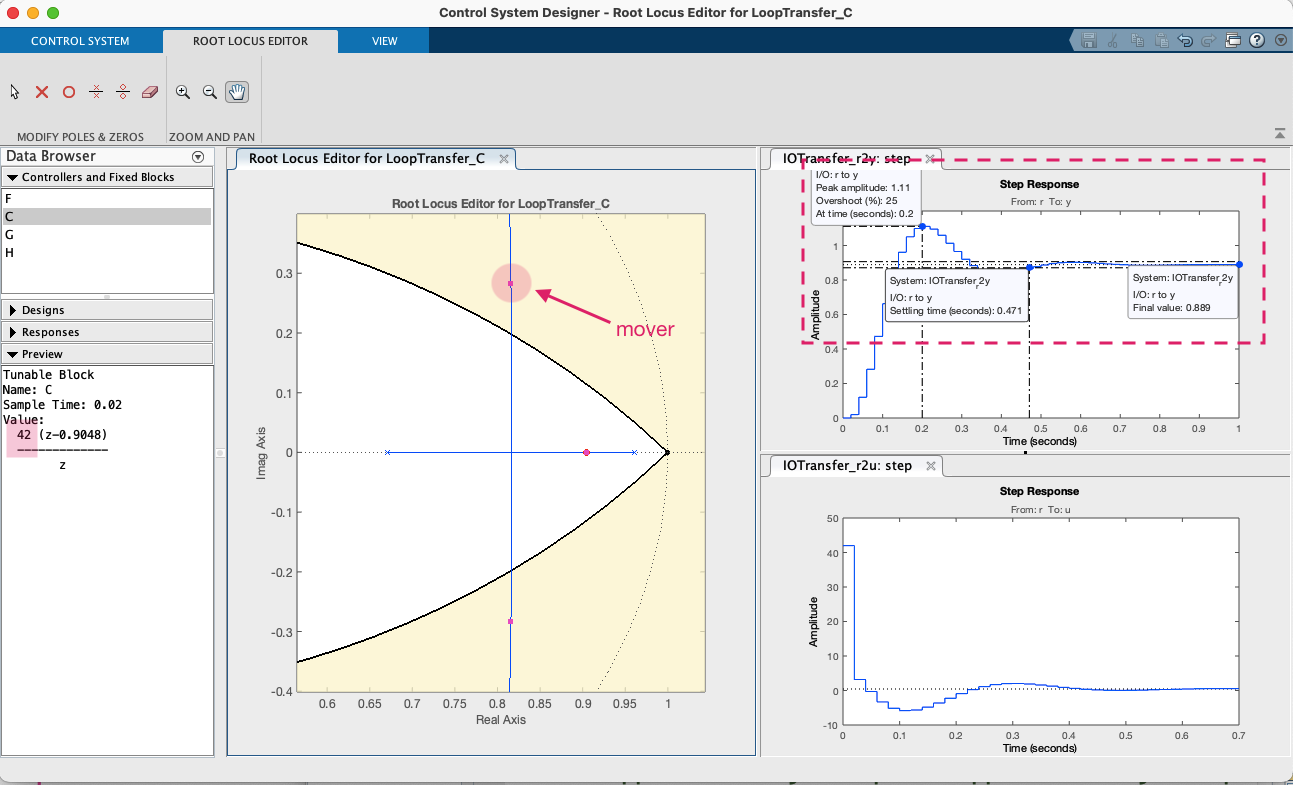
Exportando controlador como PD3:
zpk(C_PD3)
ans =
42 (z-0.9048)
-------------
z
Name: C
Sample time: 0.02 seconds
Discrete-time zero/pole/gain model.
Conclusão: Este seria o PD mais rápido possível de poder ser realizado (em teoria) para esta planta.
Salvando seção de trabalho do App Control System Designer em: ControlSystemDesignerSession_PD.mat.
Salvando dados de todos os projetos já realizados:
>> save planta
>> % Encerrando o "diary"
>> diary off
>> quit
Fernando Passold, em 20/10/2023