Projeto de Controladores usando técnica de Resposta em Frequencia

Intro

Material teórico:

• Parte 1: Revisão Diagramas de Bode + Conceitos Área Controle;
• Parte 2: Ajuste de Ganho usando Resposta em Frequência.

Projeto de Controlador Proporcional (ou Ajuste de Ganho)

Este tipo de controlador permite atender no máximo ao $\%OS$ especificado para o sistema em MF. A idéia pode ser resumida na figura:

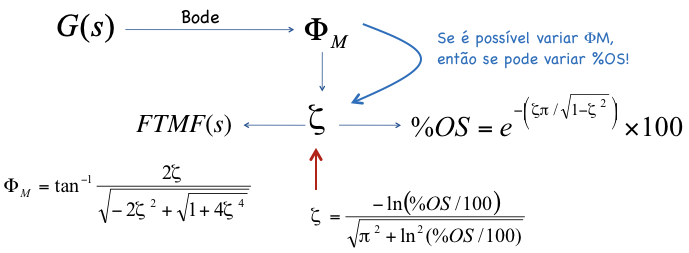
Tabelas $\zeta \times \Phi_m \times \%OS$

Segue tabelas relacionando $\zeta \times \Phi_m \times \%OS$:

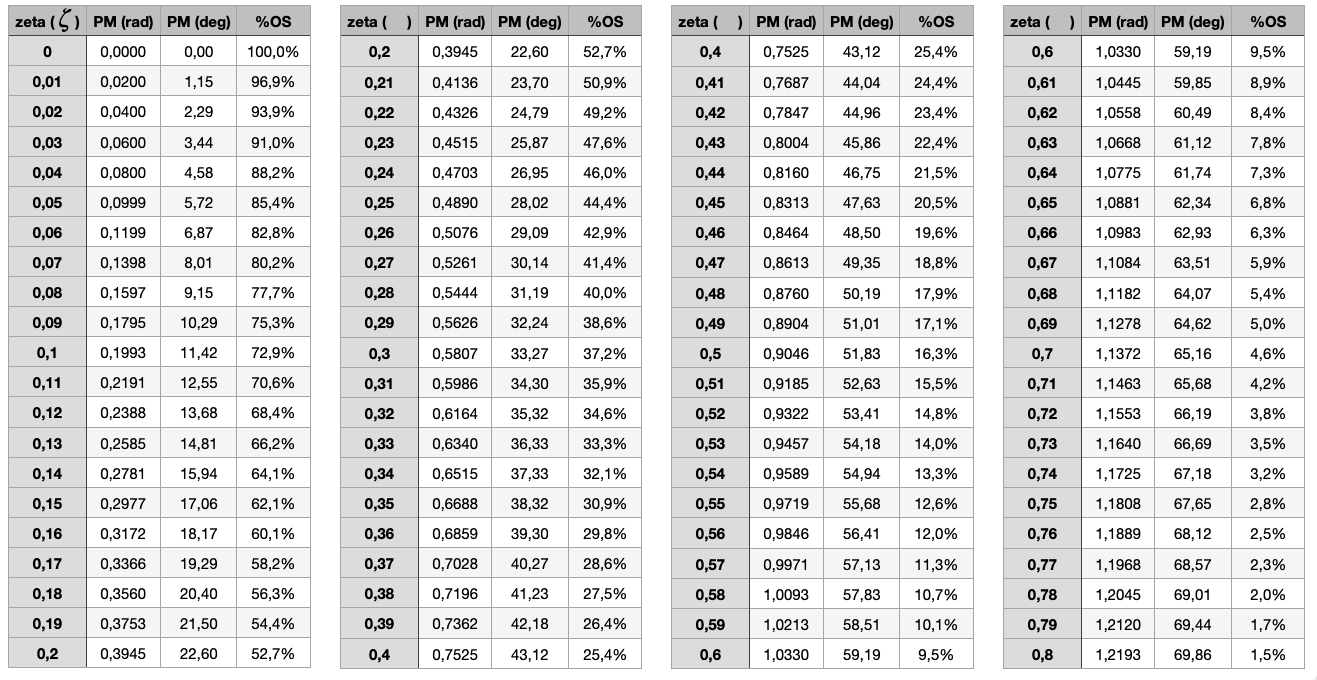
Gráficos $\%OS \times \zeta$ e $\%OS \times \Phi_M$

Alguns gráficos como referência de valores:

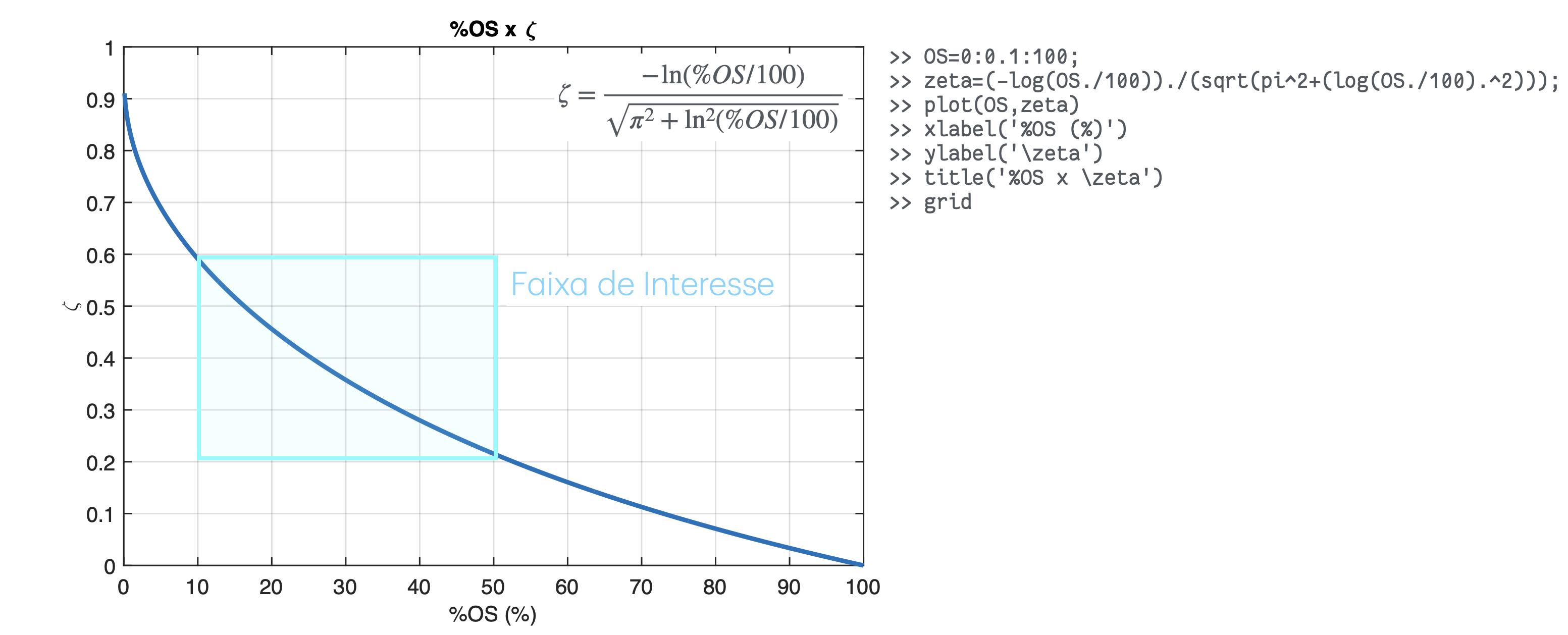
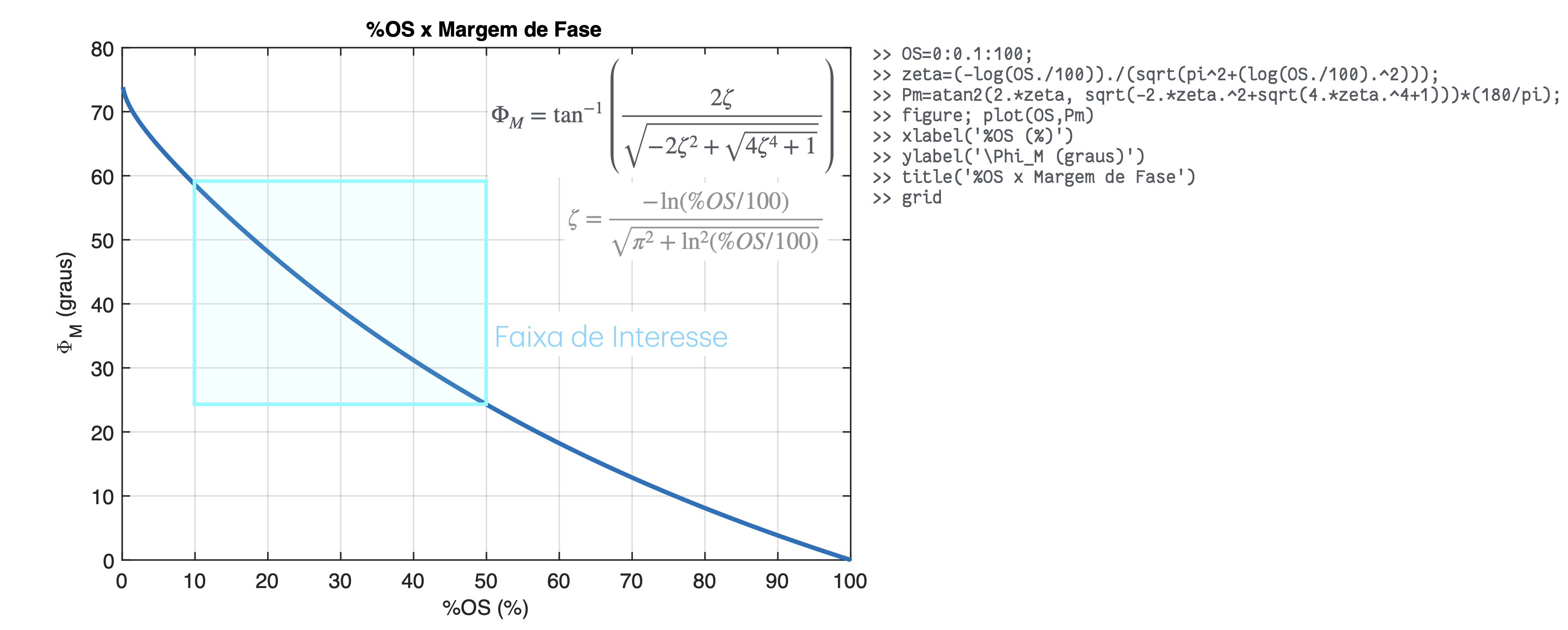
Procedimento geral

1. Em função do $\%OS$ desejado, calcular o correspondente fator de amortecimento, $\zeta$:

No Matlab:

xxxxxxxxxx
>> OS=10;   % exemplo
>> zeta=(-log(OS/100))/(sqrt(pi^2+(log(OS/100)^2)))
zeta =
    0.5912

2. Tendo o valor de $\zeta$, calcular a margem de fase requerida, $\Phi_m$ (ou Pm):

No Matlab:

xxxxxxxxxx
>> Pm=atan2(2*zeta, sqrt(-2*zeta^2 + sqrt( 1+4*zeta^4) ) )
Pm =
    1.0226
>> % Resposta em radianos!
>> Pm_deg=Pm*180/pi     % convertendo para graus
Pm_deg =
   58.5931

3. Identificar no Diagrama de Bode do sistema, a frequencia $\omega_{\Phi_M}$ na qual ocorreria a margem de fase desejada, $\Phi_M$. Eventualmente fica mais fácil descobrir $\omega_{\Phi_m}$ no Diagrama de Fase após realizar o cálculo: $\theta=180^o-\Phi_m$, onde $\theta$ corresponde aos ângulos assumidos por $\angle{FTMA(j\omega)}$. Note que você deve realizar algo como:

   

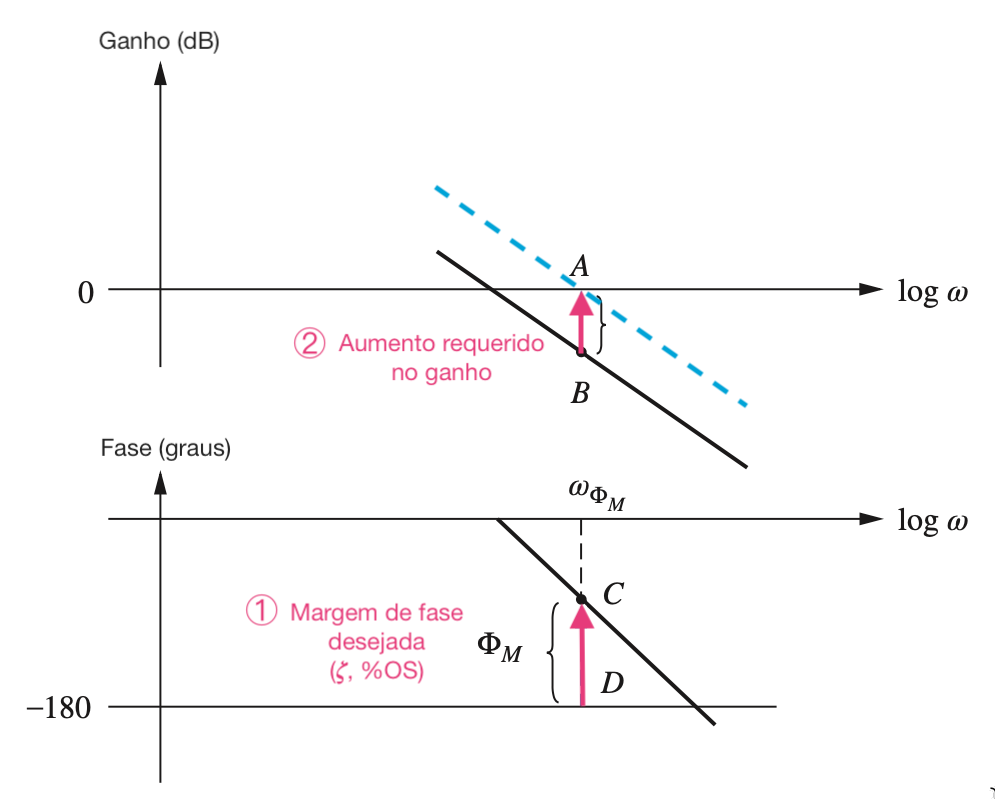
4. Modificar o ganho do sitema (ajustar o valor de $K$ do ccontrolador proporcional) de forma à que o ponto na qual a frequencia $\omega_{\Phi_M}$ se transforme na margem de fase requerida para este sistema. Para tanto, neste ponto (frequencia = $\omega_{\Phi_M}$), o ganho final do sistema em MF (considerando o ganho $K$) deve ser igual à 1 (ou 0 dB).

Exemplo 1: Exemplo 11.1 de NISE

Seja uma planta caracterizada pela função transferência (baseado no exemplo 11.1, de NISE, Norman S., Control Systems Engineering, 7th Edition, Wiley & Sons, 2024. pág 616), para este sistema, encontrar $K$ para obter $\%OS=9,5\%$ para entrada degrau:

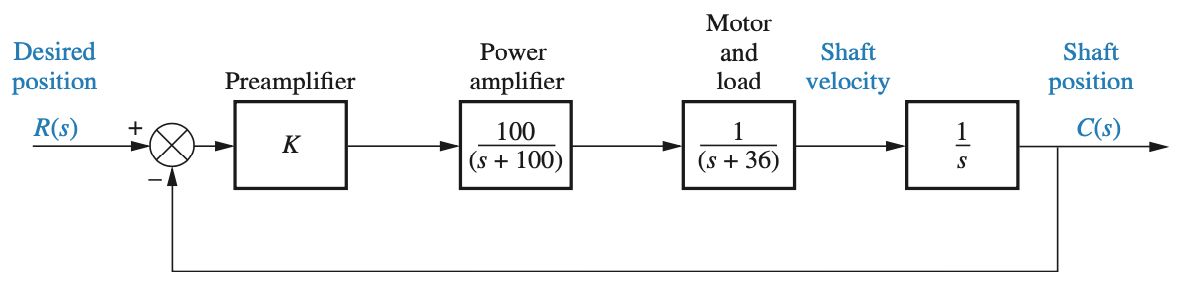
Note que este sistema em especial é do tipo 1 (possui 1 integrador: pólo na origem em $s=0$). Neste caso, o erro em regime permanente deste sistema, em malha fechada, para entrada degrau, sempre será nulo.

Continuando...

Entrando com dados no Matlab e levantando Diagrama de Bode deste sistema:

x
>> G=tf(100,poly([0 -36 -100]));
>> zpk(G)   % verificando introdução correta dos dados
​
ans =
 
        100
  ----------------
  s (s+100) (s+36)
 
Continuous-time zero/pole/gain model.
​
>> bode(G)

O que rende o gráfico (Diagrama de Bode):

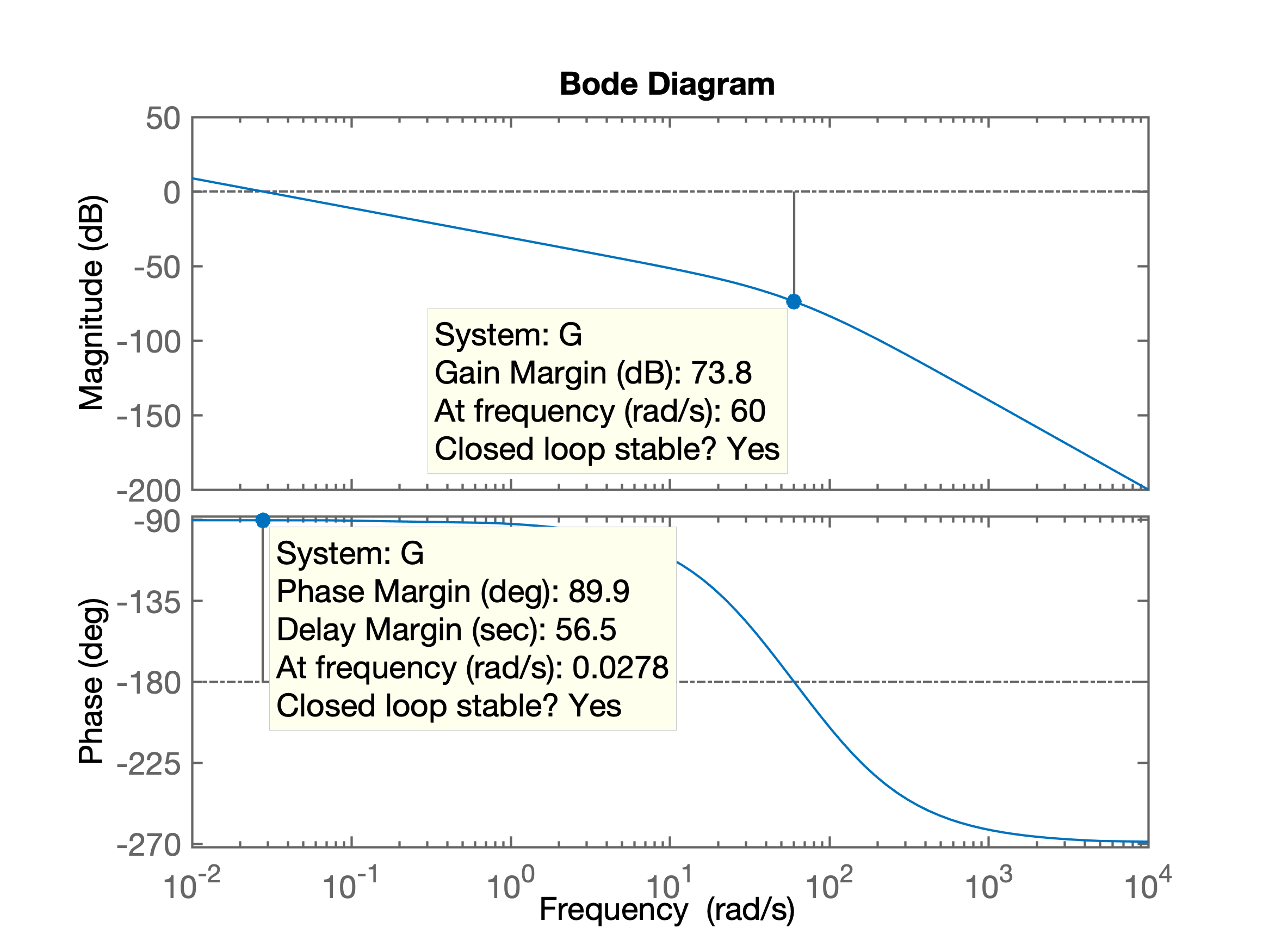
Obs.: Se eventualmente o Matlab não iníciar o diagrama de fase para frequêcias abaixo de $10^0$ (1 rad/s), usar o comando: bode(G, {0.01, 10000}) para forçar diagramas de magnitude e fase na faixa de $\omega=[0.01, \quad 1000]$ (rad/s).

Também podemos usar a função margin(.) do Matlab:

xxxxxxxxxx
>> margin(G)

que gera um Diagrama de Bode ligeiramente modificado como o mostrado abaixo:

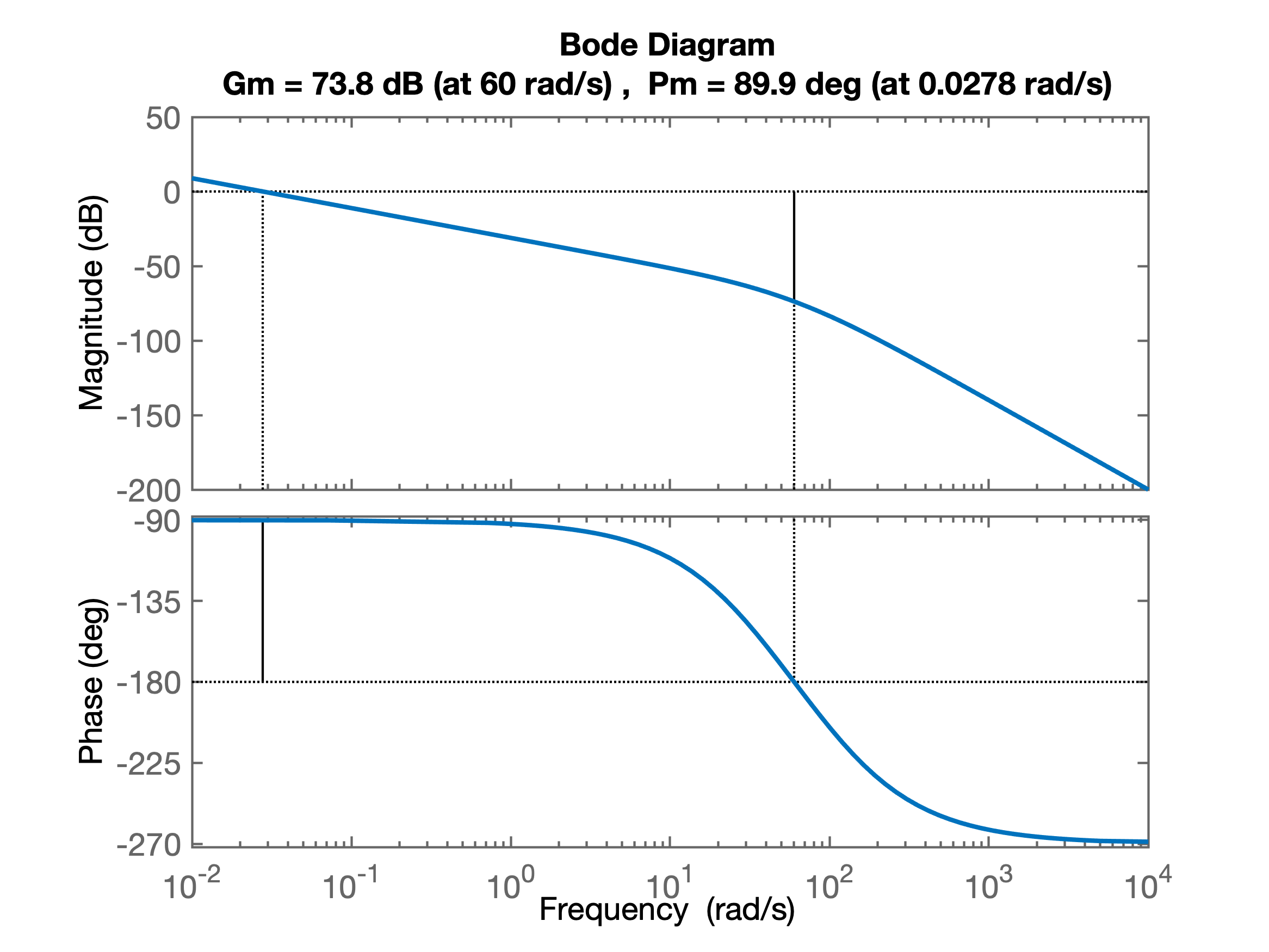
Porém note que tomar conhecimento das margens de ganho e de fase do sistema original, não importa para a sintonia do controlador Proporcional. Estas informações permanecem apenas como "curiosidades".

Mas... o digrama de Bode nos interessa.

NISE preferiu "fixar" ganho unitário ($|FTMA(j\omega)|=1$ ou 0 dB) na frequência $\omega=$ 0,1 rad/s, fazendo o $K=3,6$. Note o resultado obtido nas próximas figuras:

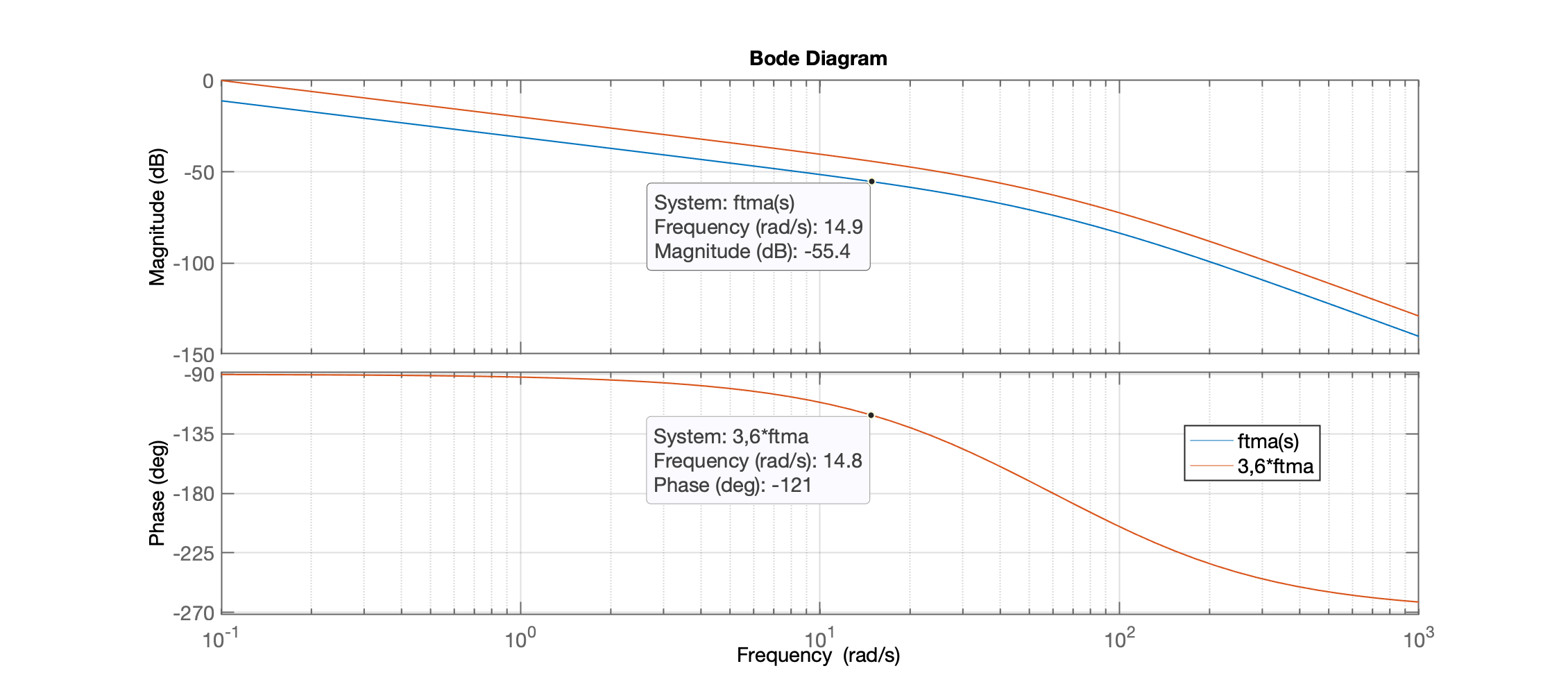
NISE percebeu que na frequência de $\omega=0,1$ rad/s, o ganho original do sistema, $|FTMA(j\omega)|$ era de $-11,1$ dB (você pode confirmar isto, criando um "DataTip" no Diagrama de Magnitude no ponto $\omega=0,1$ rad/s). Note que NISE aumentou o ganho de forma a fazer o Diagrama de Magnitude passar por 0 dB na frequência $\omega=0,1$ rad/s. Note que aumentar o ganho de 11,1 dB equivale à:

$|FTMA(j\omega)|\vert_{dB}=20 \log_{10}(|FTMA(j\omega)|)$,

ou ao valor absoluto:

$|FTMA(j\omega)|=10^{11,1/20} \cong 3,6$:

Note que ao fazer $K=3,6$, o gráfico da magnitude cruza o ganho unitário (ou de 0 dB) em $\omega=0,1$ rad/s, e então até podemos confirmar que a margem de fase, $\Phi_M \cong 90^o$. Acompanhe pela figura anterior onde foram usados os comandos:

x
>> 11.1/20
ans =
        0.555
>> 10^ans
ans =
       3.5892   % valor do ganho necessário (valor adimensional)
>> % Testando:
>> 20*log10(3.6)
ans =
       11.126   % valor do ganho em dB
>> % Traçados de Diagramas de Bode
>> ftma = tf(100, poly([0 -36 -100]));
>> ftma2= ftma*3.6;
>> figure; bode(ftma, ftma2, {0.1, 1000})
>> legend('ftma(s)', '3,6*ftma')
>> grid

Voltando ao projeto...

No caso deste projeto é desejando $\%OS=9,5\%$. Isto Implica na seguinte margem de fase desejada, Pm:

xxxxxxxxxx
>> OS=9.5; % overshoot de 9,5%
>> zeta=(-log(OS/100))/(sqrt(pi^2+(log(OS/100)^2)))
zeta =
      0.59962
>> Pm=atan(2*zeta/ (sqrt(-2*zeta^2+sqrt(1+4*zeta^4))))*(180/pi)
Pm =
       59.162

⚠️ Obs.: Note que a eq. original para cálculo da margem de fase em função de $\zeta$ resulta num ângulo em rad/s. Na expressão acima para cálculo de Pm foi acrescentando o termo *(180/pi) para transformar rad/s para graus!

Agora para forçar que a margem de fase seja de $59,162^o$ necessitamos fazer com que o gráfico de magnitude passe por 0 dB na frequência angular ($\omega$) na qual o Diagrama de fase passa por: $(180^o-59,162^o)=120,84^o$, ou:

xxxxxxxxxx
>> 180-Pm
ans =
       120.84

Buscamos no Diagrama de Bode, a frequencia onde o diagrama de Bode, parte da Fase, passe por $\cong 120^o$:

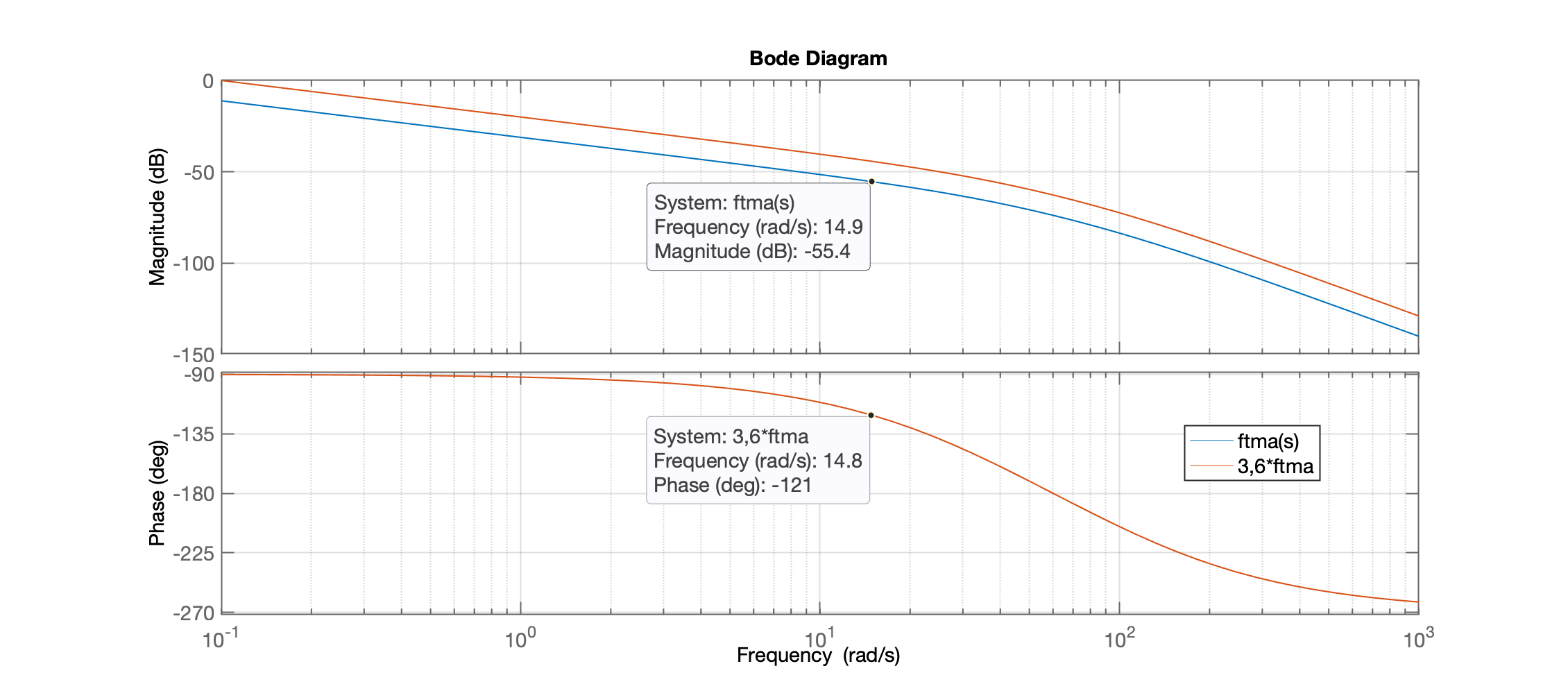
O diagrama de fase passa por $\cong 120^o$ na frequência $\omega \cong 15$ rad/s. Nesta mesma frequência, o diagrama de magitude passa pelo valor de ganho de $-55,4$ dB. Para esta frequência corresponder ao ponto onde deveria ocorrer a Margem de Fase, o Diagrama de Ganho deveria passar por 0 dB (ganho unitário), o que significa que para este caso, necessitamos aplicar um ganho (o "$K$") de $+55,4$ dB, ou em termos de ganho absoluto:

xxxxxxxxxx
>> 55.4/20
ans =
         2.77
>> K=10^ans
K =
       588.84
>> 20*log10(K)  % verificando
ans =
         55.4

Fechando a malha com este valor de ganho, teremos:

xxxxxxxxxx
>> ftmf=feedback(K*G, 1);
>> figure; step(ftmf)

Que gera a figura:

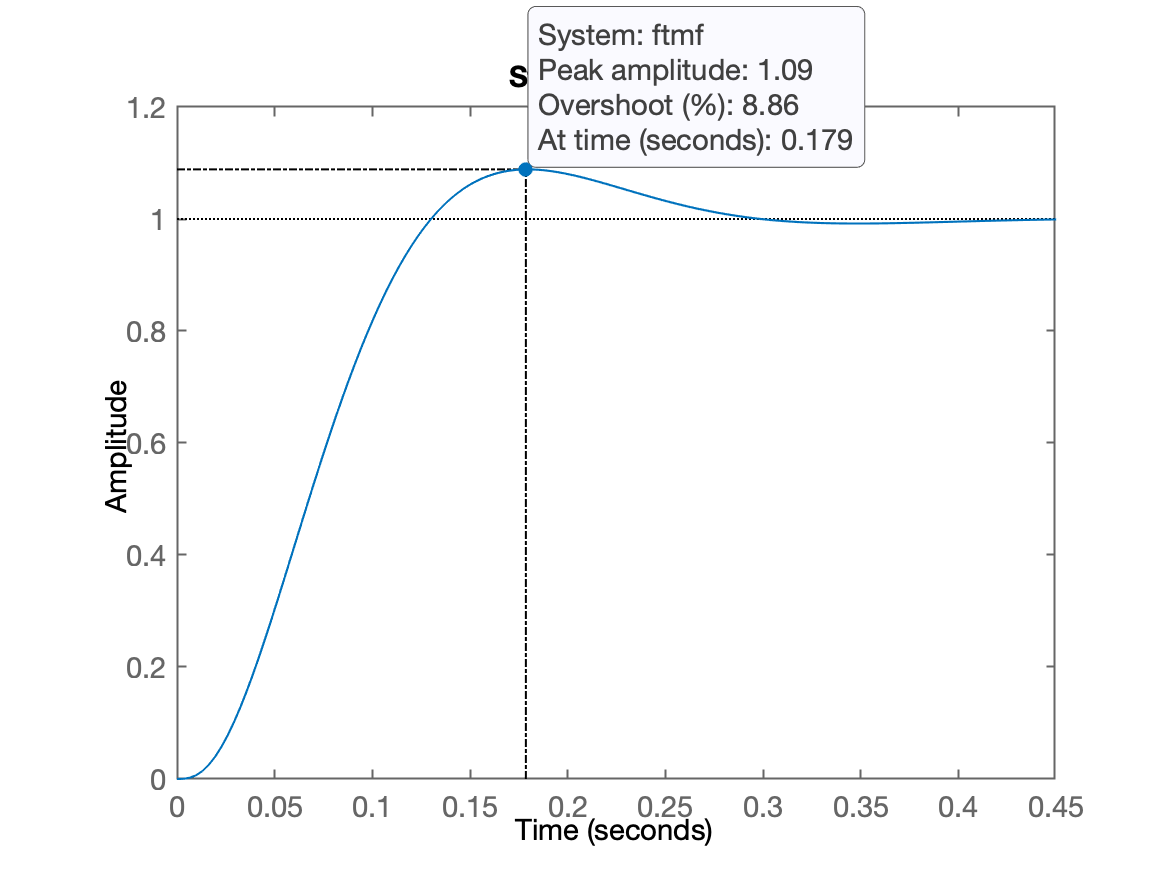
Notamos que o $\%OS$ ficou abaixo dos 9,5% desejados. Mas temos que lembrar que as equações que definem (estimam), $\%OS$, $\zeta$ e $\Phi_M$ foram desenvolvidas para sistemas que em MF resultam em sistemas de 2a-ordem com apenas 2 pólos complexos conjugados. Neste caso, temos um sistema de 3a-ordem:

xxxxxxxxxx
zpk(ftmf)
​
ans =
 
               58884
  --------------------------------
  (s+107.6) (s^2 + 28.36s + 547.1)
 
Continuous-time zero/pole/gain model.

A título de curiosidade, repare o que acontece com o Diagrama de Bode quando consideramos o ganho $K=588,84$:

xxxxxxxxxx
>> ftma3=ftma*K
ftma3 =
 
         5.888e04
  ----------------------
  s^3 + 136 s^2 + 3600 s
 
Continuous-time transfer function.
​
>> figure; bode(ftma, ftma3, {0.1, 1000})
>> grid

E temos o gráfico:

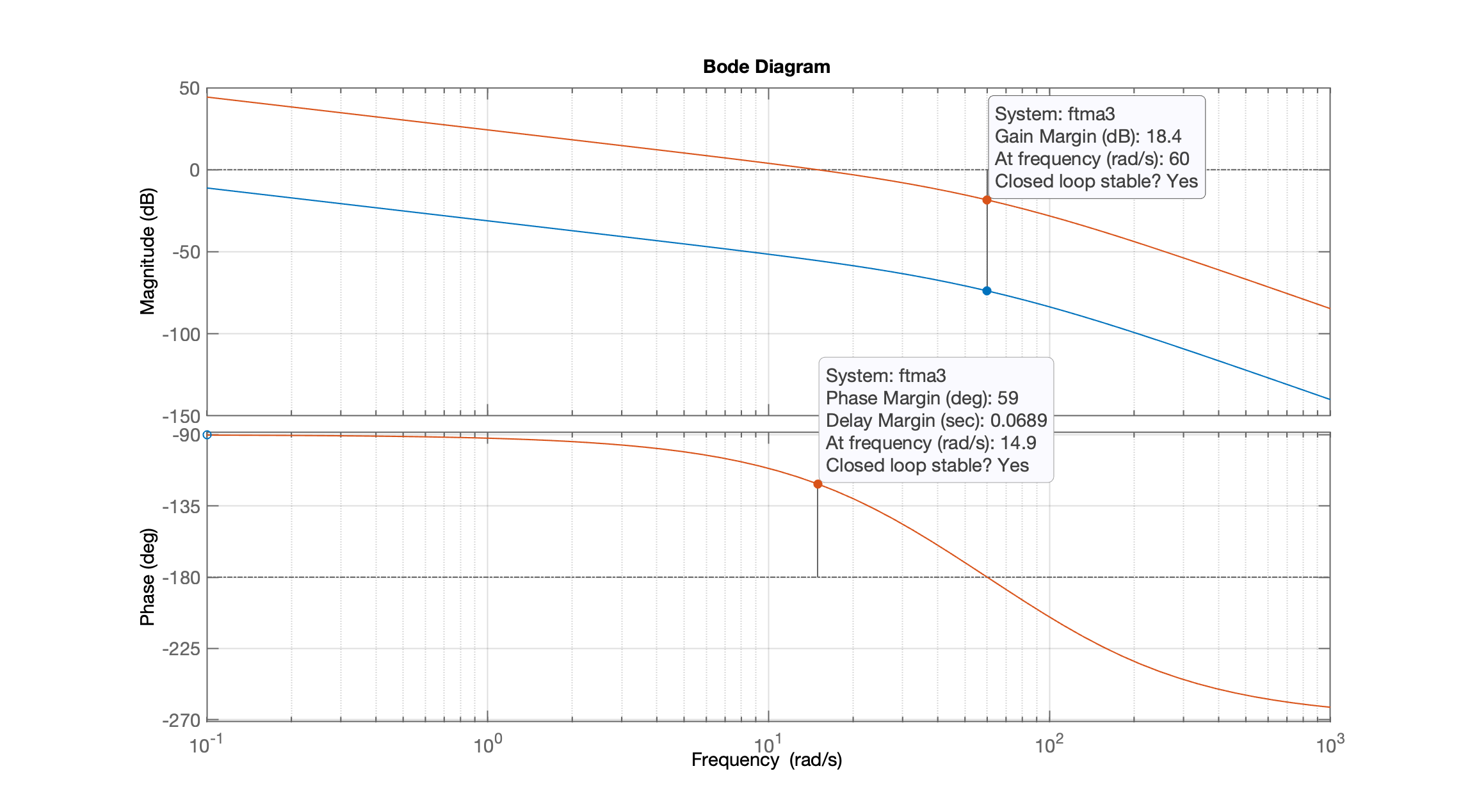
A curva em azul se refere ao Diagrama de Bode do sistema original (com $K=1$) e a curva alaranjada se refere ao sistema adotando o ganho de $K=588,84$.

Resumo

Segue resumo do procedimento adotado:

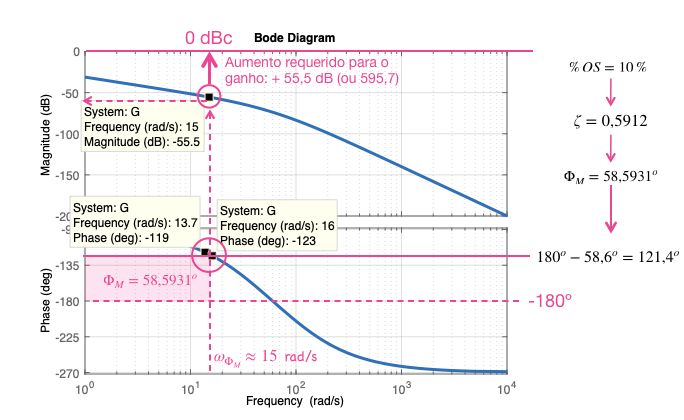
Note que a função transferência desta planta incluia um integrador. Isto significa que o procedimento para projeto de Controlador com Ação Integrativa Pura segue o mesmo procedimento já mostrado anteriormente. ⚠️

Automatizando o cálculo usando script ch11p1_fer.m

Todo este procedimento foi "automatizado" por NISE na forma de um script para o Matlab.

Segue código fonte de ch11p1_fer.m (modificado para incluir gráficos mostrando o procedimento).

% Nise, N.S. 
% Control Systems Engineering, 3rd ed. 
% John Wiley & Sons, New York, NY, 10158-0012
%
% Control Systems Engineering Toolbox Version 3.0 
% Copyright � 2000 by John Wiley & Sons, Inc.
%
% Chapter 11: Design via Frequency Response
%
% (ch11p1) Example 11.1: We can design via gain adjustment on the Bode plot using 
% MATLAB. You will input the desired percent overshoot from the keyboard. MATLAB 
% will calculate the required phase margin and then search the Bode plot for that 
% phase margin. The magnitude at the phase-margin frequency is the reciprocal of 
% the required gain. MATLAB will then plot a step response for that gain. Let us 
% look at Example 11.1 in the text.
%
% Atualizado por fpassold em 21.10.2019
​
disp('(ch11p1) Example 11.1 - Controlador Proporcional')       % Display label.
​
%% ---- Entre com a função transferência da planta no bloco abaixo
%
numg=[100];                         % Define numerator of G(s).
deng=poly([0 -36 -100]);            % Define denominator of G(s).
G=tf(numg,deng)                     % Create and display G(s).
​
%% Seguem cálculos associados com o projeto
pos=input('Input %OS ?: ');          % Input desired percent overshoot.
z=(-log(pos/100))/(sqrt(pi^2+log(pos/100)^2));
                                    % Calculate required damping ratio.
fprintf('\nRequired damping ratio (zeta): %6.4f\n', z)
Pm=atan(2*z/(sqrt(-2*z^2+sqrt(1+4*z^4))))*(180/pi);
                                    % Calculate required phase margin.
fprintf('Required phase margin, Pm = %7.4f\n', Pm)
​
%% Criando vetores associados com Diagrama de Bode
w=0.1:0.01:100;                     % Set range of frequency from 0.01 to 
                                    % 1000 in steps of 0.01.
[Mag,P]=bode(numg,deng,w);          % Gets Bode data.
​
figure;                             % Plot Bode diagram
subplot(2,1,1)
h1 = semilogx(w, 20.*log10(Mag));   % h1: current figure handle
fig1 = gcf; % current figure handle
grid
title('Open Loop Freq. Response')
ylabel('Magnitude (dB)');
​
%% ajustando propriedades da figura
set(h1,'LineWidth', 2);
ax = gca; % current axes
ax.FontSize = 14;
​
subplot(2,1,2)                  % Diagrama de fase
h2 = semilogx(w, P);
grid
ylabel('Phase (deg)')
xlabel('Frequency (rad/sec)')
​
%% ajustando propriedades da figura
set(h2,'LineWidth', 2);
ax = gca; % current axes
ax.FontSize = 14;
escY=min(P);
​
Ph=-180+Pm;                         % Calculate required phase angle.
fprintf('Required phase angle: %7.2f^o\n', Ph)
u=length(P);
for k=1:1:u;                        % Search Bode data for required phase
                                    % angle.
  if P(k)-Ph<=0;                    % If required phase angle is found,
                                    % find the value of 
    M=Mag(k);                       % magnitude at the same frequency.
    fprintf('Found Pm at w = %5.2f (rad/s)\n', w(k))
    fprintf('with magnitude = %5.2f dB (%5.2g)\n', 20*log10(M), M)
    new_K=1/M;                      % Calculate the required gain.
    subplot(2,1,2)
    hold on
    % Marca no diagrama o ponto onde ocorre a Margem de Fase, Pm
    semilogx([w(1) w(u)], [-180 -180], 'k-.', 'LineWidth', 2)   % linha guia -180o
    semilogx([w(k) w(k)], [-180 Ph], 'm-', 'LineWidth', 6)     % mostra Pm
    aux=[num2str(Pm,'%4.1f') '^o'];
    aux2=-180+Pm/2;
    text((w(k)), aux2, aux, 'FontSize',14)    
    
    semilogx([w(k) w(k)], [Ph  0], 'm--', 'LineWidth', 2)
    semilogx([w(1) w(u)], [P(k) P(k)], 'm--', 'LineWidth', 2)
    aux=[num2str(w(k),'%3.2f') ' rad/s'];
    text((w(k)),0 , aux, 'FontSize',14)
    subplot(2,1,1)
    hold on
    % Marca no diagrama do ganho, os pontos que correspondem à Pm
    semilogx([w(k) w(k)], [0 20.*log10(Mag(k))], 'm-', 'LineWidth',6)  % Mostra altura ajuste do ganho
    semilogx([w(k) w(k)], [20.*log10(Mag(k)) 20.*log10(Mag(u))], 'm--', 'LineWidth',2)
    semilogx([w(1) w(u)], [20.*log10(Mag(k)) 20.*log10(Mag(k))], 'm--', 'LineWidth',2)
    aux=[num2str(-20*log10(M),'%5.2f') ' dB'];
    aux2=20.*log10(Mag(k))/2;
    text((w(k)), aux2, aux , 'FontSize',14)
    break                           % Stop the loop.
  end                               % End if.
end                                 % End for.
​
fprintf('Then, required K = %6.2f\n', new_K)
k_final=new_K;
fprintf('Then, final required K = %6.2f\n', k_final)
T=feedback(k_final*G,1);                  % Find T(s) using the calculated K.
figure; step(T);                          % Generate a step response.
title(['Closed-Loop Step Response for K= ',num2str(k_final)]) % Add title to step response.
ax = gca; % current axes
ax.FontSize = 14;
​
%% verificando diagrama de Bode compensado
adjusted_g=k_final*G;
figure; bode(G,adjusted_g)
hold on;    % sobrepondo dados de margens
margin(adjusted_g)

Explicação:

O script ch11p1_fer.m automatiza o processo, usando a função [M,P]=bode(G,w) para estocar valores de ganho e fase do diagrama de Bode para este sistema, $G$, nos vetores $M$ e $P$, em função dos valores de frequencia passados via vetor $w$ (que variou entre $0,01 \le \omega \le 1000$ rad/s, com passo de 0,01 rad/s). Então se calcula o ângulo de fase pelo qual deve passar a planta para alcançarmos a margem de fase desejada, na linha: Ph = -180+Pm, onde Pm corresponde à margem de fase desejada, ou $\Phi_M$. Depois, um laço for percorre os valores do vetor de fase P buscando a frequencia onde teríamos a marge da fase caso o ganho do sistema fosse igual à 1 ou 0 dB, via teste: if P(k)-Ph <= 0. Quando este ponto é encontrado, o valor do ganho é estocado na variável M e a compensação de ganho requerrida é calculada na variável K, K=1/M. Notar que tanto o vetor M quanto a variável M guardam valores de ganho absolutos e não na escala de dB. A declaração break dentro do if anterior, "quebra" o laço for que varria as frequencias. O restante são cálculos fechando a malha e realizando o teste.

Execução:

xxxxxxxxxx
ch11p1_fer
(ch11p1) Example 11.1 - Controlador Proporcional
​
G =
 
           100
  ----------------------
  s^3 + 136 s^2 + 3600 s
 
Continuous-time transfer function.
​
Input %OS ?: 9.5
​
Required damping ratio (zeta): 0.5996
Required phase margin, Pm = 59.1621
Required phase angle: -120.84^o
Found Pm at w = 14.84 (rad/s)
with magnitude = -55.33 dB (0.0017)
Then, required K = 584.18
Then, final required K = 584.18
​
>>

Exemplo 2: Planta do Estudo de Caso

Pode-se usar o script ch11p1_fer.m com outro tipo de planta, desde que seus dados sejam ingressados no mesmo.

A planta neste caso é:

x
>> load planta      % carregado os dados da última aula
>> zpk(G)           % verificando tf da planta
​
ans =
 
          20
  ------------------
  (s+10) (s+4) (s+1)
 
Continuous-time zero/pole/gain model.

As linhas do script ch11p1_fer.m devem ser editadas contemplando os dados de outra planta:

xxxxxxxxxx
>> edit ch11p1_fer.m

Editar as linhas abaixo:

xxxxxxxxxx
%% ---- Entre com a fun��o transfer�ncia da planta no bloco abaixo
%
% numg=[100];                         % Define numerator of G(s).
numg = 20;
% deng=poly([0 -36 -100]);            % Define denominator of G(s).
deng = poly([-1 -4 -10]);
G=tf(numg,deng);                      % Create and display G(s).
zpk(G)
​

Executando, temos agora:

xxxxxxxxxx
>> ch11p1_fer
(ch11p1) Example 11.1 - Controlador Proporcional
​
ans =
 
          20
  ------------------
  (s+10) (s+4) (s+1)
 
Continuous-time zero/pole/gain model.
​
Input %OS ?: 10
​
Required damping ratio (zeta): 0.5912
Required phase margin, Pm = 58.5931
Required phase angle: -121.41^o
Found Pm at w =  2.82 (rad/s)
with magnitude = -17.62 dB ( 0.13)
Then, required K =   7.61
Then, final required K =   7.61
​
>>

Repare que as seguintes figuras são geradas:

Figura 1: Diagrama de Bode inicial mostrando ajustes para alançar Margem de Fase desejada:

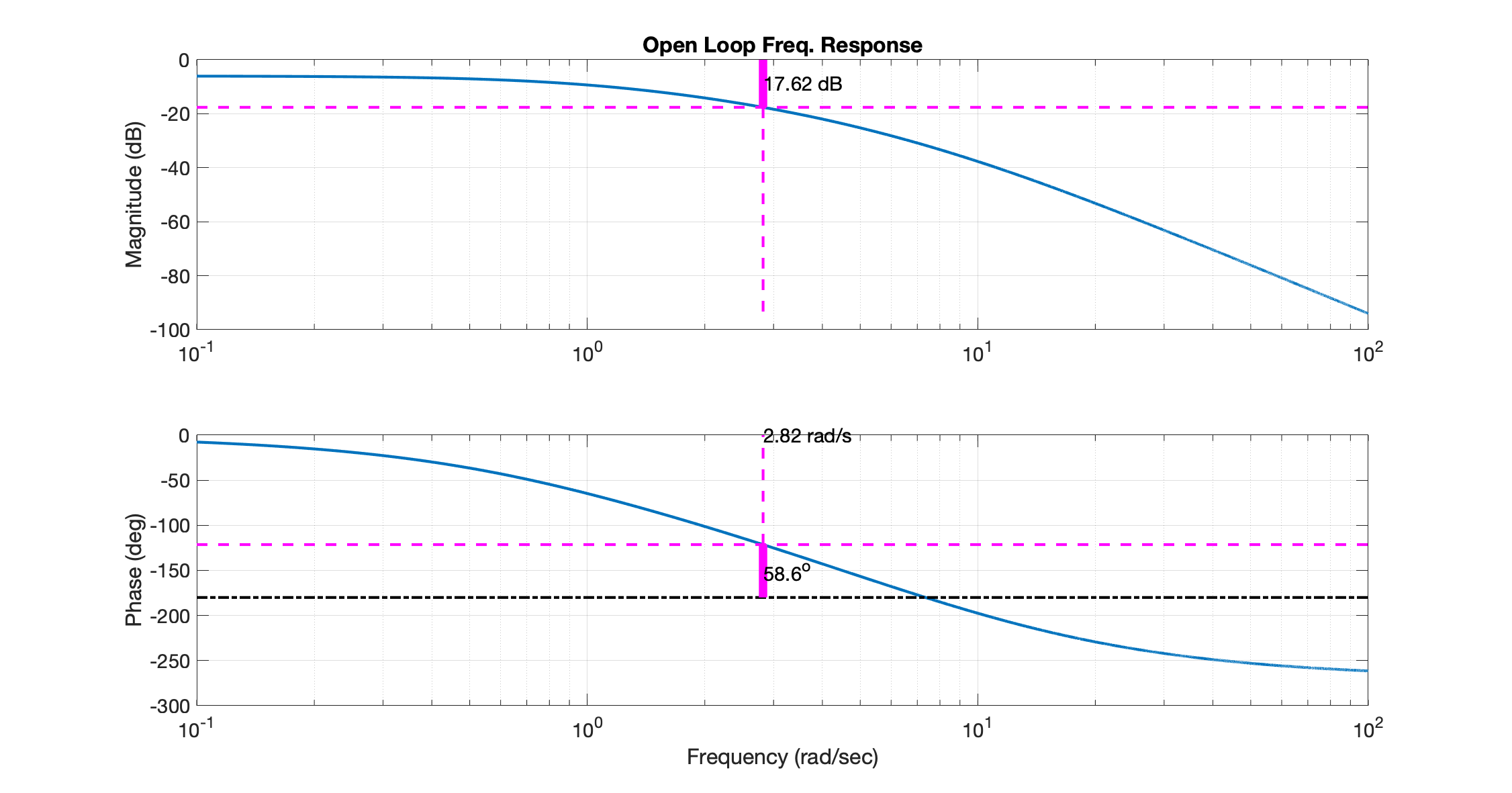
Figura 2: Resposta ao Degrau unitário para sistema em MF adotando ganho encontrado anteriormente ($+17,62$ dB ou 7,61):

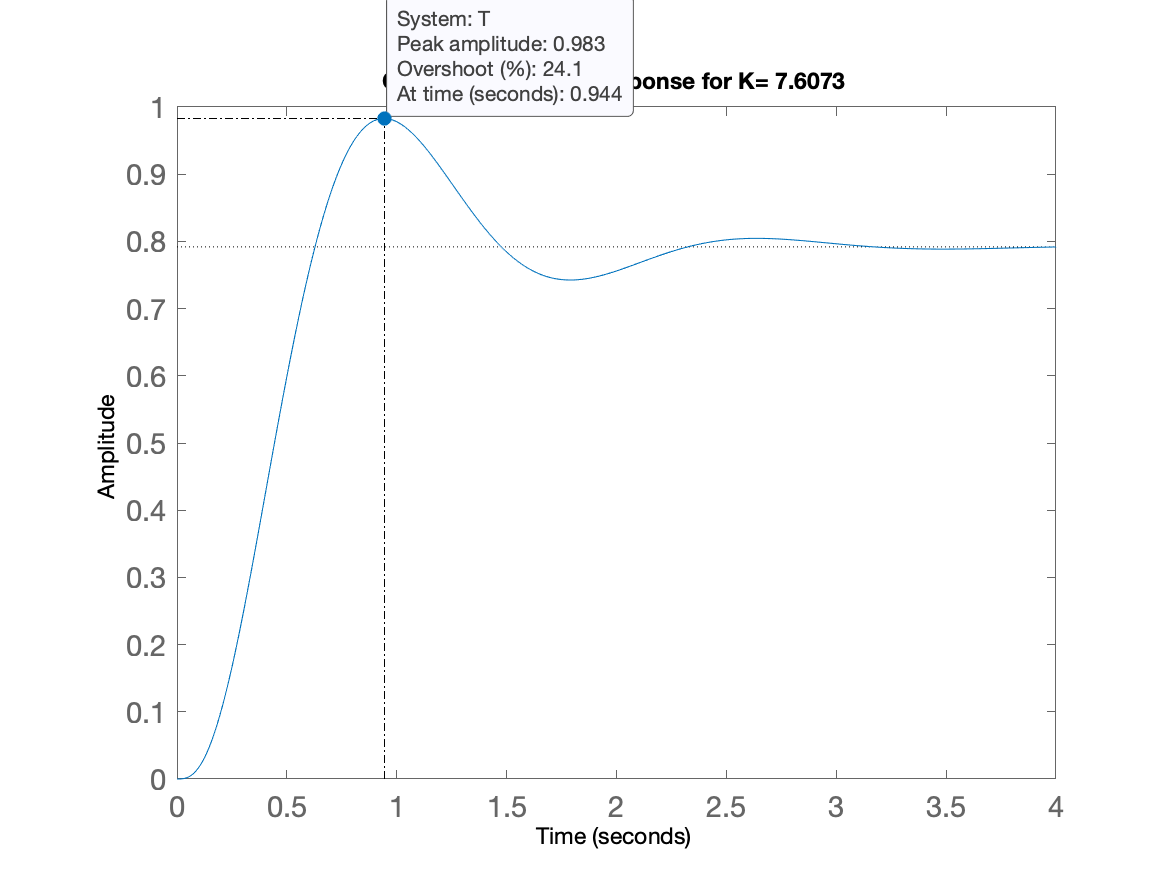
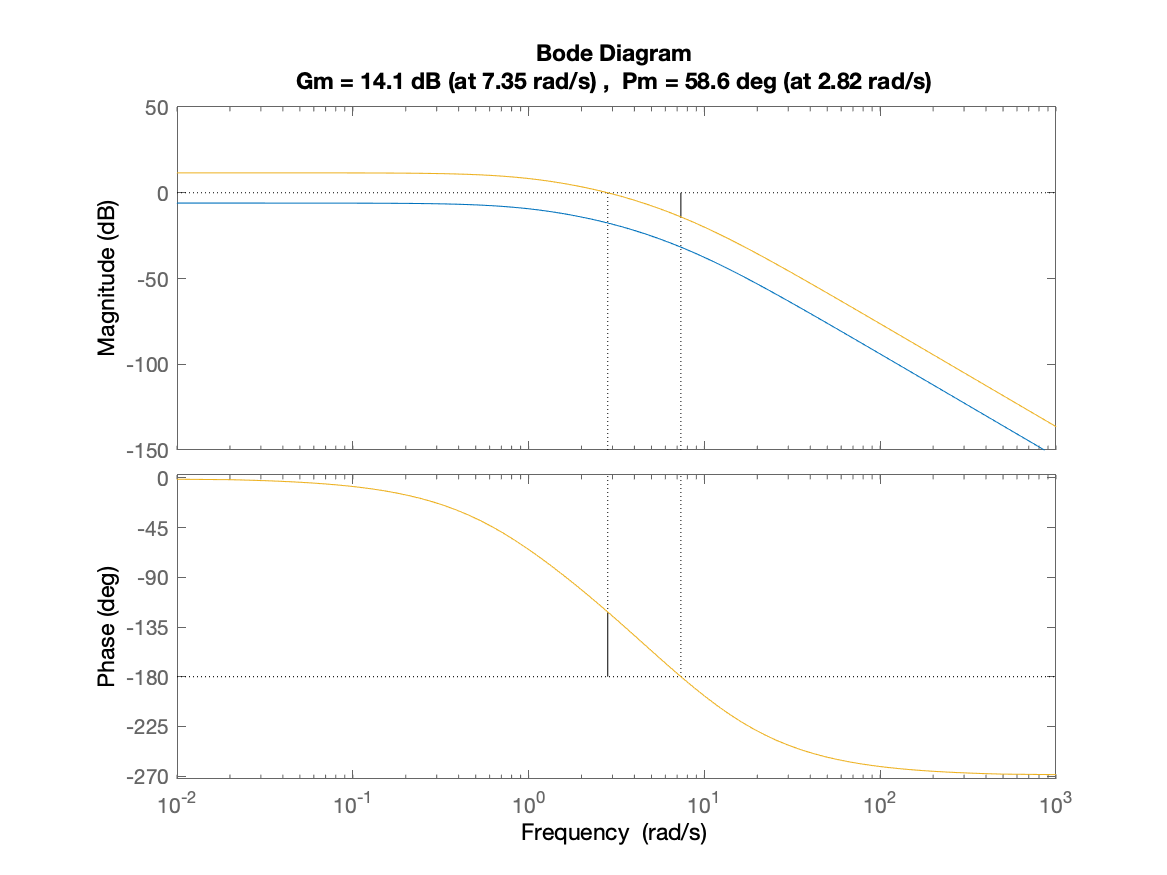
Figura 3: Diagramas de Bode original x Sistema Modificado com novo valor de ganho:

🎧

🌊 Fernando Passold 📬 ,