Projeto Controladores usando RL

🎵

Projeto de PID

Base teórica

Um PID ou controlador por Avanço-Atraso de fase ("Lead-Lag") implica acrescentar um sistema de 2a-ordem ao que se deseja controlar. A equação genétrica do controlador fica:

$C_{PID}(s)=\dfrac{K(s+z_{PI})(s+z_{PD})}{s}$

que representa o caso de um PID teórico, com implementação analógica de uma ação derivativa pura (impossível na prática: implica ganho $\infty$ conforme a frequência $\uparrow$). Para revisar questões sobre ação derivativa, clique em: (1) Ação Derivativa na presença de sinal ruidoso e (2) Teoria à respeito de Compensador por Avanço de Fase (Lead). Caso seja considerado um PID com Ação Derivativa filtrada (realizável na prática), teremos algo como:

$C_{PID_2}(s)=\dfrac{K(s+z_{PI})(s+z_{PD})}{s(s+p_{PD})}$

onde o pólo do PD, $p_{PD}$, corresponde ao pólo do filtro passa-baixa usado para limitar o ganho de uma ação derivativa pura. Note: PD $+$ FPB $=$ Lead.

Já a eq. de um controlador "Lead-Lag" fica como:

$C_{Lead-Lag}(s)=\dfrac{K_{Lead-Lag}(s+z_{Lead})(s+z_{Lag})}{(s+p_{Lead})(s+p_{Lag})}$

Note que estes controladores possuem muitas incógnitas além do ganho geral $K$ que pode ser definido com auxílio do RL. Em alguns casos necessitamos definir: 2 zeros e 1 pólo (considerando PID com ação Integral "pura", isto é, com 1 pólo na origem). E então fica complicado tentar imaginar diferentes combinações de posições de zeros e pólos destes controladores (mesmo garantindo ação "PI" $+$ "PD" -- a "ordem" dos pólos e zeros importa).

Uma abordagem mais fácil adotada para resolver esta questão é dividir o projeto em 2 estapas. Primeiramente realizamos o projeto de um PD/Lead para atender requisitos temporais e depois executamos o projeto do PI/Lag (para atender critérios de erro), levando em conta o PD/Lead projetado na etapa anterior. Isto é possível porque na prática estaríamos como que "cascateando" um controlador PD/Lead com um controlador PI/Lag.

Em resumo, a idéia é fazer algo do tipo:

Exemplo 9.5 (NISE)

Ver: Exemplo de projeto de PID, baseado no exemplo 9.5 (seção PID Controller Design), do livro: Nise, Norman S., Control System Engineering, 6th ed. 2011, John Wiley & Sons, Inc.

Planta deste exemplo:

$G(s)=\dfrac{s+8}{(s+10) (s+6) (s+3)}$

Requisitos de controle:

• $t_s \le \dfrac{2}{3} t_s \vert_{Prop}$ (reduzir em 2/3 $t_s$ de Controlador Proporcional simples adotado com a planta);
• $\%OS \le 20%$.

Executando o script: example_9_5.m.

xxxxxxxxxx
>> example_9_5
Este script resolve o exemplo 9.5:
PID Controller Design, do livro:
Nise, Norman S., Control System Engineering,
6th ed. 2011, John Wiley & Sons, Inc.
Planta a ser compensada:
​
ans =
 
        (s+8)
  ------------------
  (s+10) (s+6) (s+3)
 
Continuous-time zero/pole/gain model.
​
Maximo percentual overshoot tolerado (%OS): ? 20

Obs.: Ingressado o valor 20 (para $\%OS=20\%$). O script prossegue com:

xxxxxxxxxx
Fator de amortecimento (zeta): 0.4559
​
Observe o RL da FTMA(s) do Contr. Prop. + Planta... (Figure 1)...
Realize um zoom sobre a area de interesse e
pressione qualquer tecla para continuar 

Neste instante é aberta a primeira figura com o RL para completar o projeto o Controlador Proporcional. Necessária esta etapa porque no exemplo, não foi informado o ganho $K$ adodato para o sistema. O script espera que o usuário realize um "zoom" sobre a região de interesse para posterirmente definir o ganho do controlador (proporcional):

xxxxxxxxxx
Select a point in the graphics window
selected_point =
      -5.4147 +     10.526i
k =
       120.61
poles =
      -5.4149 +     10.526i
      -5.4149 -     10.526i
      -8.1702 +          0i

Neste caso, o RL para este controlador, já com o ganho escolhido fica como mostra a figura abaixo (Figure 1):

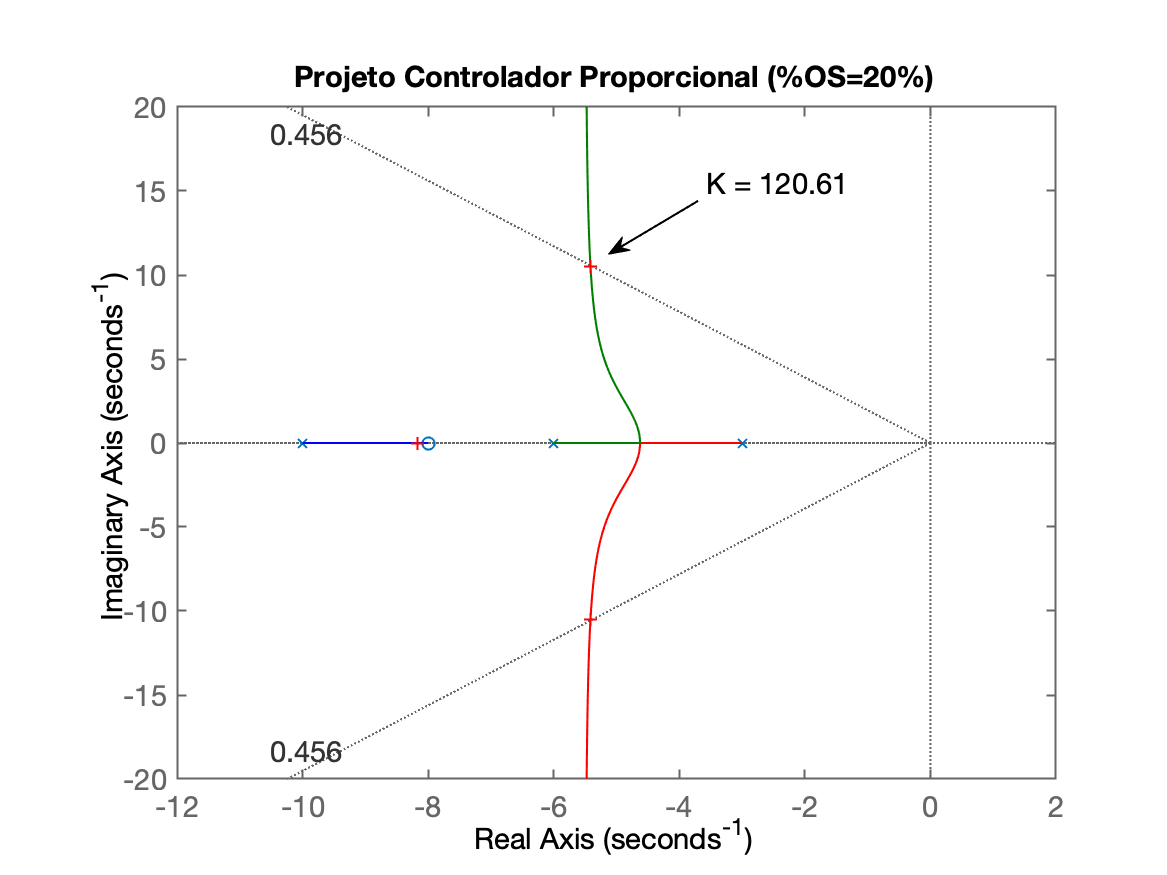
Em seguida o script continua estimando o $t_s$ e $t_p$ em função do par de pólos complexos encontrados com este valor de ganho. Note que esta estimativa (equações) não consideram a ordem real deste sistema (3a-ordem, contra as equações definidas para sistemes de 2a-ordem; haverá uma certa "imprecisão").

Além disso o script já calcula o novo $t_s$ necessário (2/3 do valor do $t_s$ encontrado para o controlador Proporcional) e segue os cálculos para 1a-etapa do projeto de um PID: projeto do PD, usando contribuição angular para definir o local necessário para o zero do PD. Lembrando da eq. do PD:

$C_{PD}(s)=K_{PD}(s+z_{PD})$

Note que o script se detêm monstrando o resultado do cálculo das contribuições angulares:

xxxxxxxxxx
Estimando tempo de assentamento, t_s: 0.7387
Estimando tempo do pico, t_p: 0.2985
​
Novo tempo de tipo (desejado), t_p: 0.1990
​
theta (cos(zeta)): 62.8739^o
180^o-theta: 117.1261^o
​
Polos de MF desejados em: s = -8.0889 +j15.7895
​
Contribuicoes angulares dos polos do sistema em malha-aberta:
p(1) = -10 --> 83.0989^o
p(2) = -6 --> 97.5365^o
p(3) = -3 --> 107.8641^o
Soma das contribuicoes dos polos: 288.4994^o
​
Contribuicoes angulares dos zero do sistema em malha-aberta:
z(1) = -8 --> 90.3228^o
​
Somatorio total das contribuicoes angulares (polos e zeros): 198.1767^o
​
Angulo resultante para o zero do PD: 18.1767^o
Posicao do zero do PD: em s = -40.0009
Equacao do PD (variavel "c"):
​
ans =
 
  (s+40)
 
Continuous-time zero/pole/gain model.
​
Levantando RL da FTMA(s) do sistema com o PD...
Observe o RL da FTMA(s) do PD + planta (Figure 4)...
Realize um zoom sobre a area de interesse e
pressione qualquer tecla para continuar 

Segue RL ainda do Controlador Proporcional, mas mostrando onde deveriam ficar os pólos de MF desejados em função do $t_p$ requerido (Figure 2):

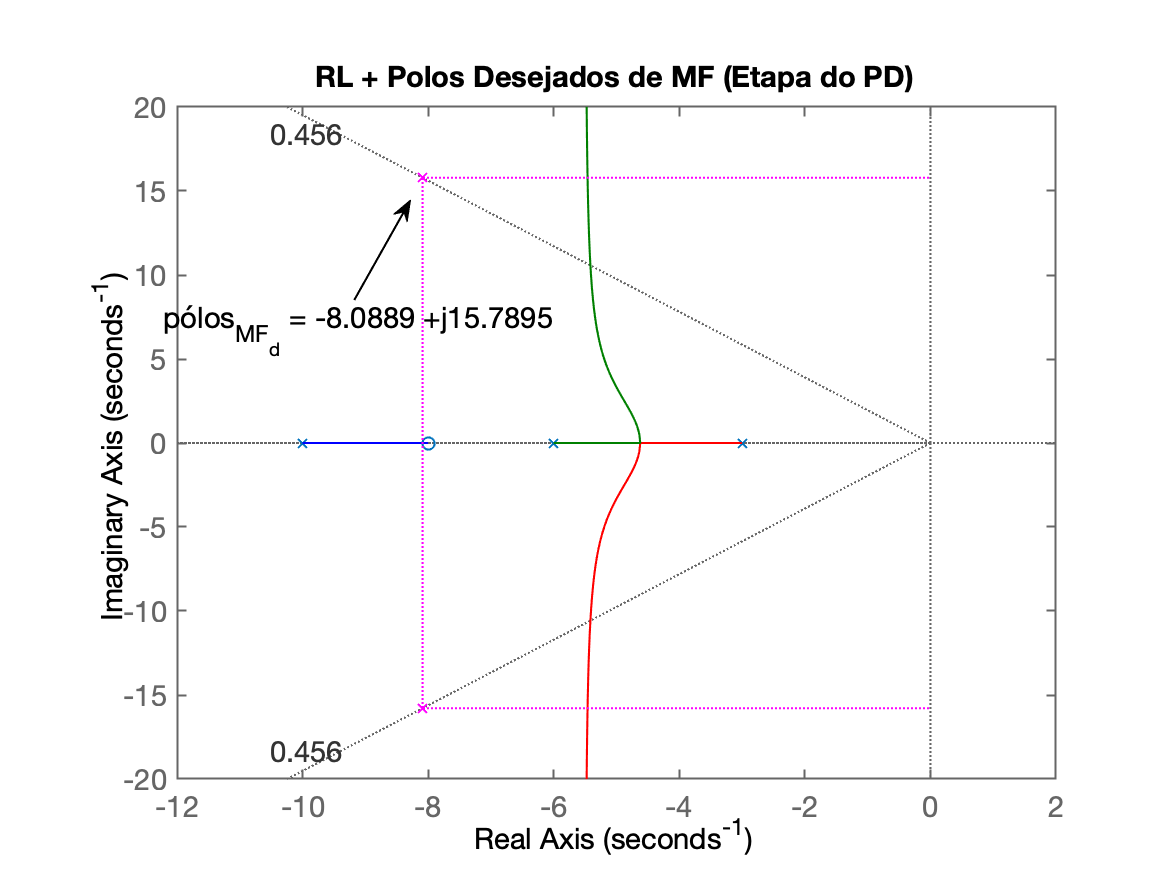
Note que o local desejado para os pólos de MF, "sobe" em diagonal no plano-s em relação ao ponto escolhido antes para o controlador proporcinal. Note que: $t_p \downarrow$ quando $j\omega \uparrow$ (parte imaginária do pólo aumenta, ou "sobe"), e que $t_s \downarrow$ quando $\sigma \to -\infty$; onde $s=\sigma+j\omega$ se refere a certa posiçao para pólo de MF no plano-s.

Segue Figure 3 com resultado dos cálculos da contribuição angular) usados para determinação do local do zero do PD:

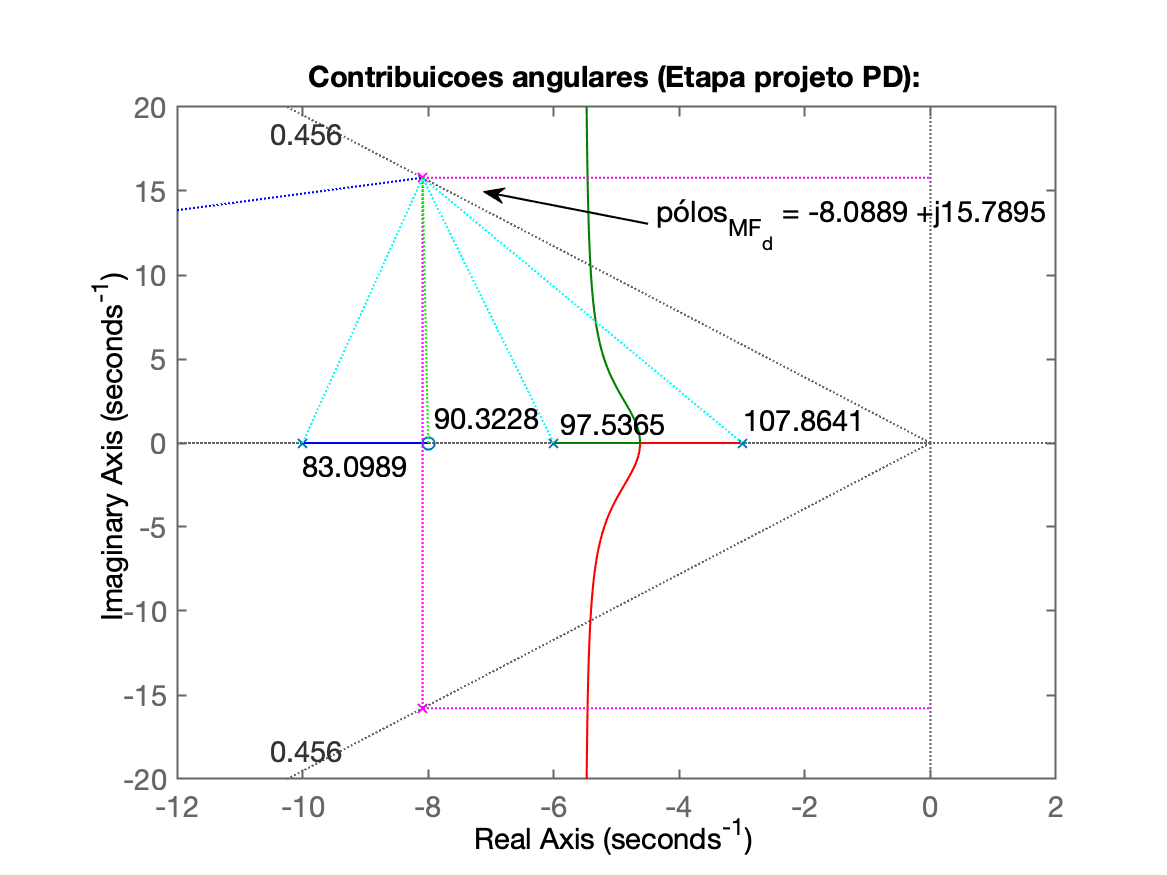
Confira com os valores calculados e mostrados pelo script (ver acima).

Em seguinda o script se detêm no RL do PD esperando que o usuário realize um "zoom" na região de interesse para posteriormente definir o ganho do PD:

xxxxxxxxxx
Select a point in the graphics window
selected_point =
      -10.456 +     17.717i
K_pd =
         10.1
poles_pd =
      -10.519 +     17.679i
      -10.519 -     17.679i
      -8.0627 +          0i

O RL já com "zoom" e ponto de ganho escolhido para este PD aparece abaixo (Figure 4):

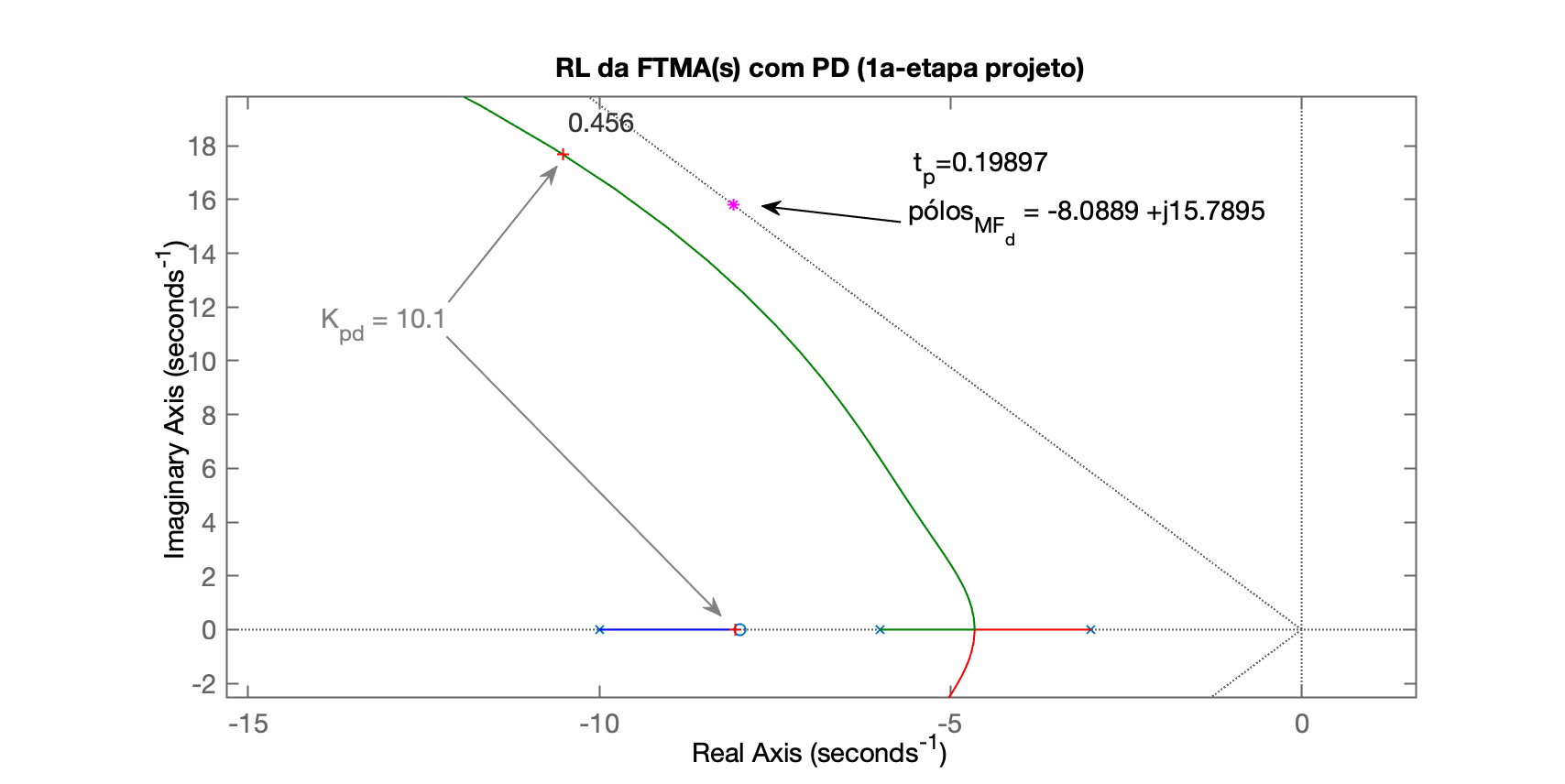
O script mostra ainda como ficaria a resposta ao degrau unitário para este PD (Figure 5):

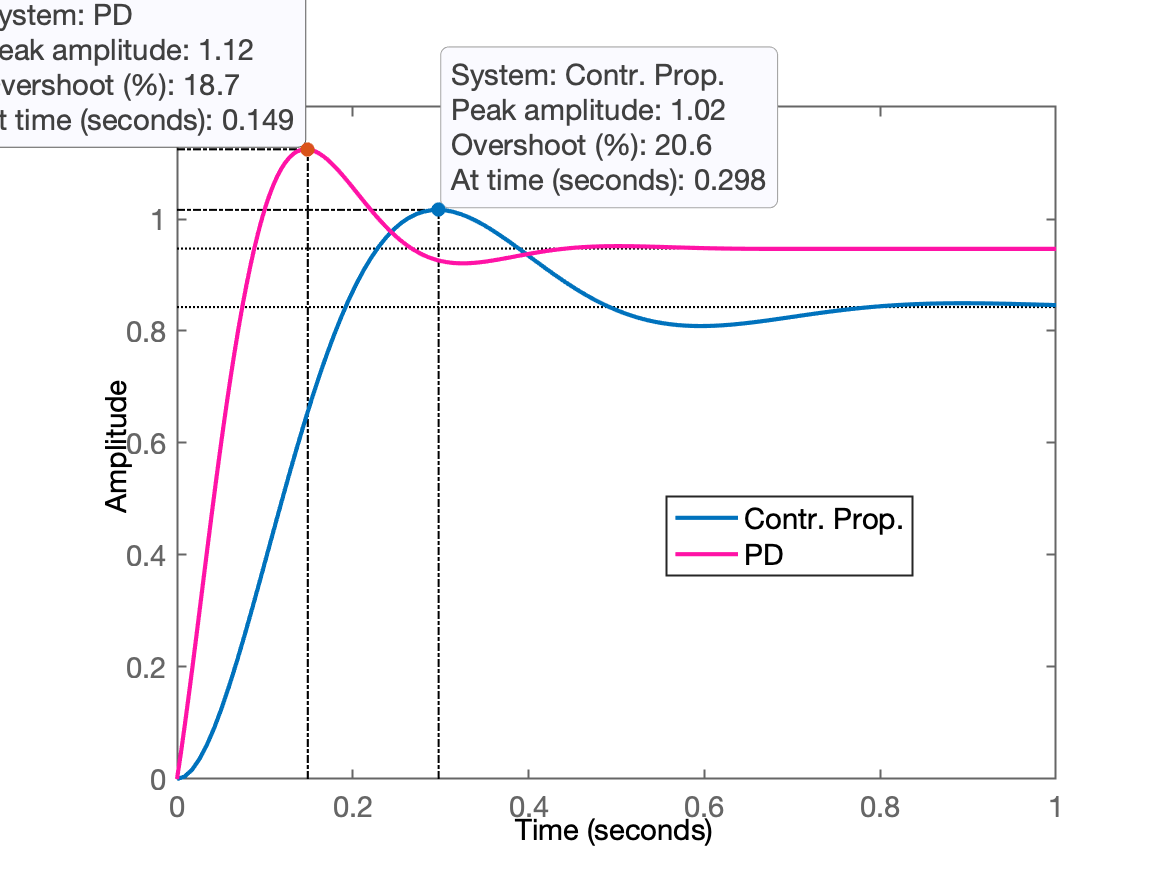
Percebe-se que este PD alcançou um $t_p$ menor que o desejado e calculado ($t_s \le 0,1990$). E é bom que tenha sido encontrado um valor menor, já que na 2a-etapa do projeto do PID, quando for acrescentada a ação integral, a tendência é que o $t_s$ aumente em função do atraso introduzido pela ação integral.

O script segue informando a eq. final do PD (incluindo seu ganho) e parte para 2a-etapa: Projeto do PI. Neste caso, poderia ter sido feito um novo cálculo de contribuição angular, mas NISE optou por simplesmente arbitrar uma posição para o zero do PI (no código original ele simplesmente fixa este zero em $s=-0,5$; mas estas versão foi modifica para permitir que o usuário indique outro local para o zero do PI, além de acrescentar gráficos extras).

Lembrando a eq. do PI:

$C_{PI}=\dfrac{ K_{PI} (s+z_{PI}) }{s}$

Percebe-se que justamente falta definir a posição do zero do PI. Note que nesta execução optamos por colocar o zero do PI em $s=-2$, mais próximo do pólo mais lento da planta localizado em $s=-3$ (isto vai resultar num traçado de RL que fará o pólo mais dominante real, se afastar da origem do plano-s (onde está o pólo do integrador) e "caminhar" na direção de $s \to \infty$, neste caso, encontrando o zero do próprio controlador -- repare isto no próximo RL que será apresentado).

O script continua com:

xxxxxxxxxx
Selecione uma posicao para o zero do PI (em: -3 <= s < 0) [-0.5]: ? -2
Equacao do PID (ainda sem ganho):
​
ans =
 
  (s+40) (s+2)
  ------------
       s
 
Continuous-time zero/pole/gain model.
​
FTMA(s) do PID + Planta (variavel "PIDg"): 
​
ans =
 
   (s+40) (s+8) (s+2)
  --------------------
  s (s+10) (s+6) (s+3)
 
Continuous-time zero/pole/gain model.
​
Observe o RL da FTMA(s) do PID + planta (Figure 6)...
Realize um zoom sobre a area de interesse e
pressione qualquer tecla para continuar 

Mais uma vez o script se detêm mostrando o RL final do PID completo (Figure 6), esperando que o usuário realize um "zoom" sobre a região de interesse para que em seguinda, possa ser definido o ganho genérico do PID. Lembrando que:

$C_{PID}(s)=\dfrac{K_{PID}(s+z_{PD})(s+z_{PI})}{s}$

Segue RL já mostrando o ganho adotado para o PID (Figure 6):

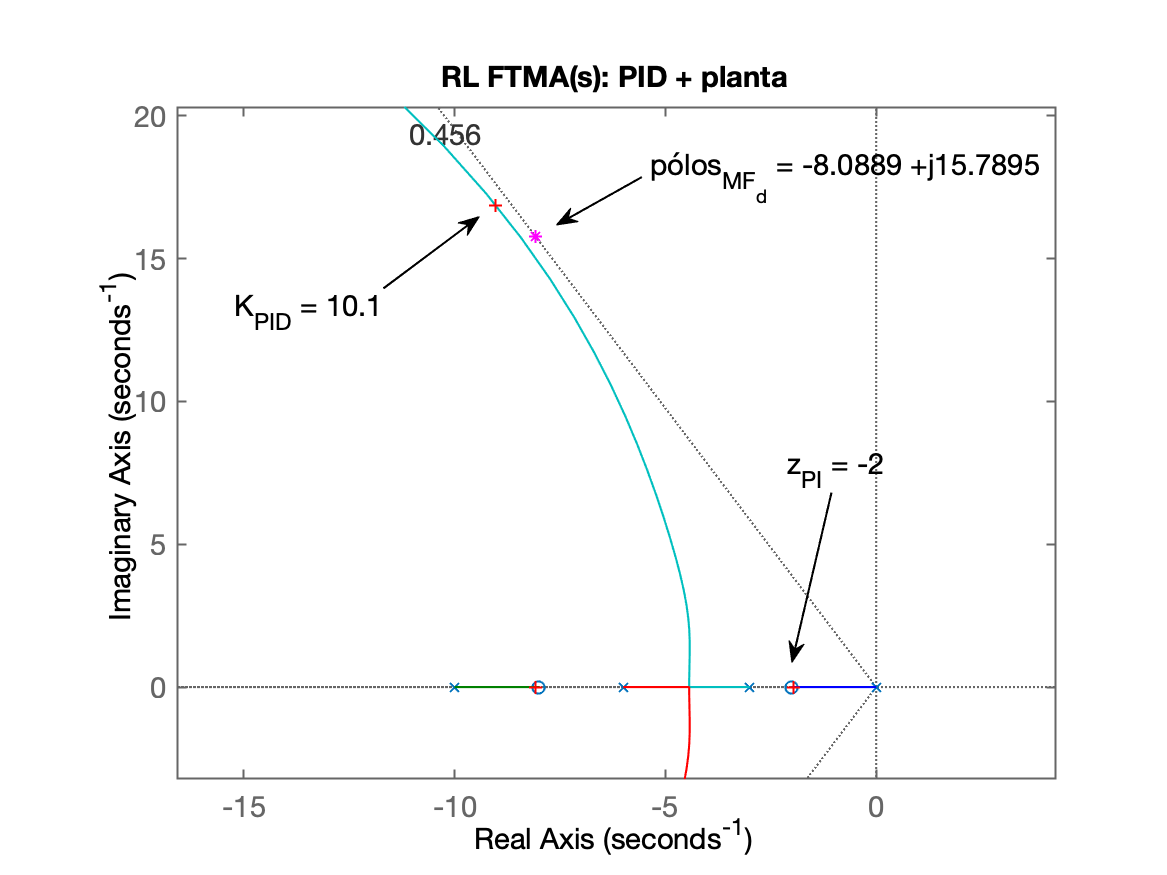
O script então finaliza os cálculos mostrando os últimos resultados e a resposta ao defrau btida para o PID (Figure 7).

xxxxxxxxxx
Select a point in the graphics window
selected_point =
      -9.0519 +     16.849i
k_PIDg =
       9.1068
poles_PIDg =
      -9.0227 +     16.865i
      -9.0227 -     16.865i
      -8.0929 +          0i
      -1.9685 +          0i
Equacao final (completa) do PID (variaval "PID2"):
​
PID2 =
 
  9.107 s^2 + 382.5 s + 728.6
  ---------------------------
               s
 
Continuous-time transfer function.
​
Kp =
       382.49
Ki =
       728.56
Kd =
       9.1068
>> 

Segue resposta ao degrau do PID recém projetado (Figure 7):

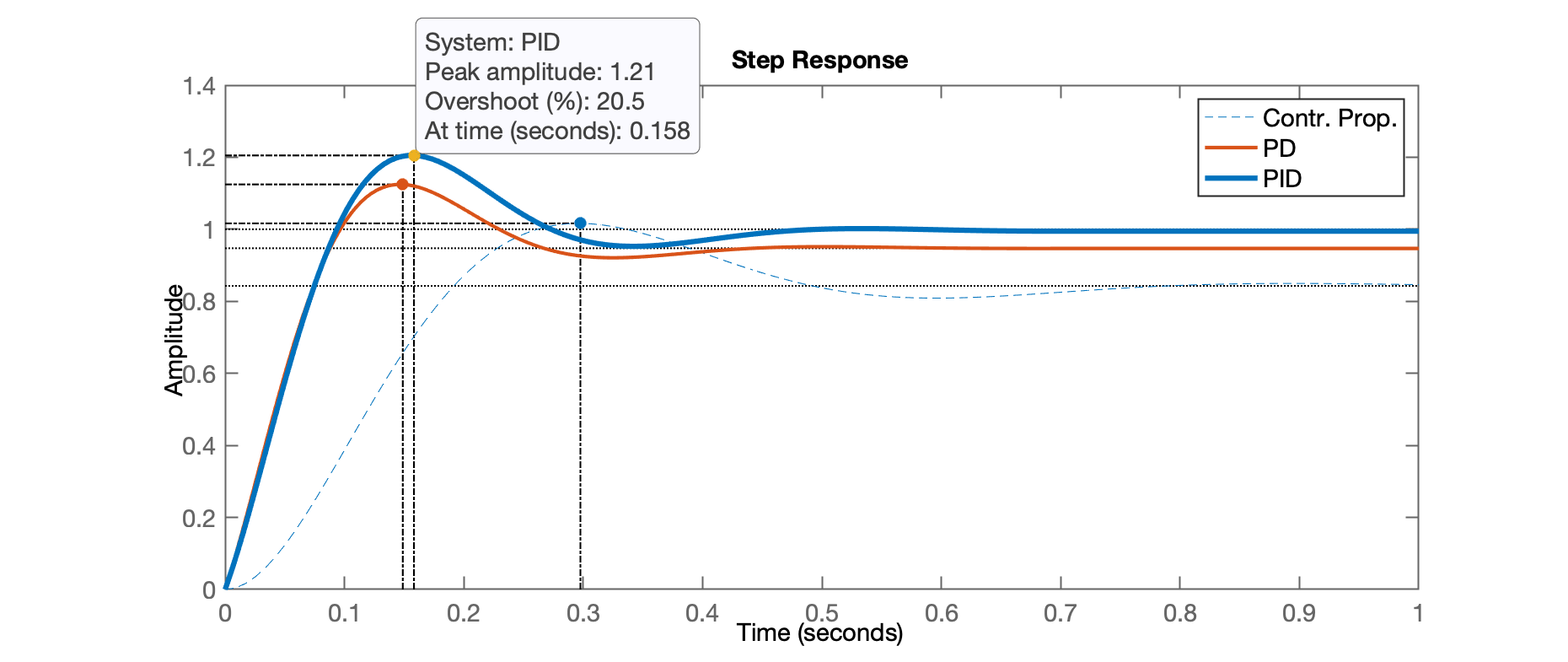
Considerações finais: Este PID provavelmente pode ficar ainda melhor, se o zero do PI for propositalmente colocado sobre o pólo mais lento da planta em $s=-3$. Isto vai acabar resultando numa redução de complexidade do sistema. Isto é, em MF, com o acréscimo do PID, ao invés de ficarmos um sistema em MF de 4a-ordem, vamos acabar com um sistema de 3a-ordem (consequentemente um RL com menos traçados, mais simples e com pólos dominantes mais afastados do eixo $j\omega$ e portanto, mais rápidos):

Antes:

$FTMA(s)=C_{PI}(s) \cdot G(s)=\dfrac{K_{PID}(s+z_{PD})(s+z_{PI})}{s} \cdot \dfrac{s+8}{(s+10) (s+6) (s+3)}$

Depois, com o zero do PI em $s=-3$:

$FTMA(s)=C_{PI}(s) \cdot G(s)=\dfrac{K_{PID}(s+z_{PD}) \cancel{(s+3)} }{s} \cdot \dfrac{s+8}{(s+10) (s+6) \cancel{(s+3)}}$

Problema Proposto 1

Refaça o projeto anterior, definindo como nova posição para o zero do PI, o valor: $s=-3$, propositalmente cancelando o pólo mais lento da planta. Comente/justifique o que acontece apresentando e explicando os resultados obtidos.

Projeto do PID Planta Estudo de Caso

A idéia agora é testar a abordagem de NISE mas não necessariamente usando script de NISE, mas usando outro script para facilitar cálculos de contribuição angular (find_polo_zero.m), para realizar a etapa 1: projeto do PD e etapa 2: projeto do PI, finalizando então com o controlador PID.

Revisando Requisitos de Controle

De todas as formas, necessitamos revisar requisitos de controle que serão adotados para o projeto do PID para a planta do estudo de caso, até como um "fator baliza" necessário para definir o projeto do PID.

Revisando valores obtidos anteriormente (principalmente nos projetos envolvendo ação derivativa), notamos que:

• $\%OS \le 10\%$;
• $0,5 < t_s < 0,827 \text{ (PD)}\quad \Rightarrow \quad t_s \le 0,8$;
• $e(\infty) \le 10\%$.

1a-Etapa: Projeto do PD

Usando script: find_polo_zero.m:

xxxxxxxxxx
>> help find_polo_zero
  find_polo_zero.m
  
  Angular contribution routine to find out where to locate pole or zero 
  of the controller depending on the desired location for MF poles
 
  Use:
  This routine already expects a tf named "ftma_aux"
    ftma_aux(s)=C(s)'*G(s);
  where: C(s)' is almost the full tf of the controller, 
         except for the pole or zero that this routine is expected to 
         determine using angular contribution.
  
  This routine uses angular contribution to find the position of the pole
  or the zero that is necessary to complete the tf of the controller.
  It asks almost at the end, whether the user wants to find out the 
  position of the pole or the zero that is missing.
 
  Fernando Passold, 14/10/2020, 20/10/2020, 30/10/2022, 30/11/2022.
​
>> 

Notamos que necessitamos definir a variável ftma_aux em função do tipo do controlador desejado, no caso, um PD:

$C_{PD}=\dfrac{K(s+z_{PD})}{1}$

onde a incógnita é o zero do PD ($z_{PD}$).

A variável ftma_aux deve considerar parte da eq. do controlador menos a parcela que envolve a incógnita. Neste caso, resulta simplesmente em:

$\text{ftma_aux}=K\cdot G(s)$

Preparando esta variável e executando o script:

xxxxxxxxxx
>> find_polo_zero
​
Routine to determine the position of the pole or zero
that is missing to complete controller design
​
%OS$ (desired Overshoot, in %): ? 10
  ts_d (desired settling time): ? 0.8
Desired MF poles must be located at:
    s = -5 ± j6.82188
​
Evaluating the pole(s) contribution angle(s):
  Pole 1) in s=-10 + j(0)   | angle: 53.76^o
  Pole 2) in s=-4 + j(0)    | angle: 98.34^o
  Pole 3) in s=-1 + j(0)    | angle: 120.39^o
            Sum(angle{poles}) = 272.49^o
​
Evaluating the zero(s) contribution angle(s):
            Sum(angle{zeros}) = 0.00^o
​
Determining pole or zero location of the controller:
Select: [p]=pole or [z]=zero, for the controller ? z
​
Angle contribution required for controller: 92.49^o
This means that the controller 
    ZERO must be at s = -4.70387
​
To finish the project, note that:
​
ftma =
 
     20 (s+4.704)
  ------------------
  (s+10) (s+4) (s+1)
 
Continuous-time zero/pole/gain model.
​
Find the controller gain with the command:
​
    >> K_ = rlocfind(ftma)
​
>>

A figura mostrando os cálculos da contribuição angular para este PD, aparece abaixo:

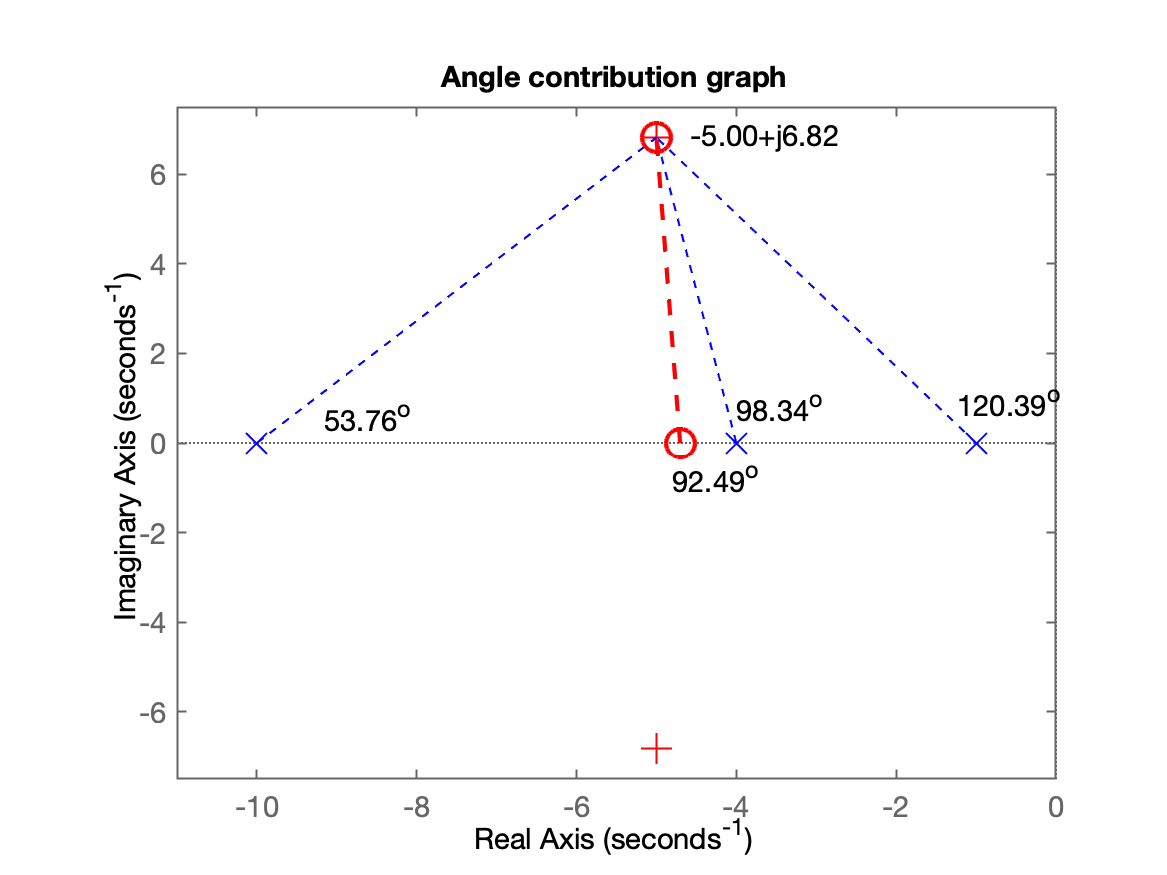
Note o zero do PD calculador em $s=-4,704$.

O script finaliza mostrando outros dados e o RL da $FTMA(s)$ (variável ftma) já incluindo o zero do controlador recém calculado, para que o usuário "sintonize" (defina o ganho do controlador):

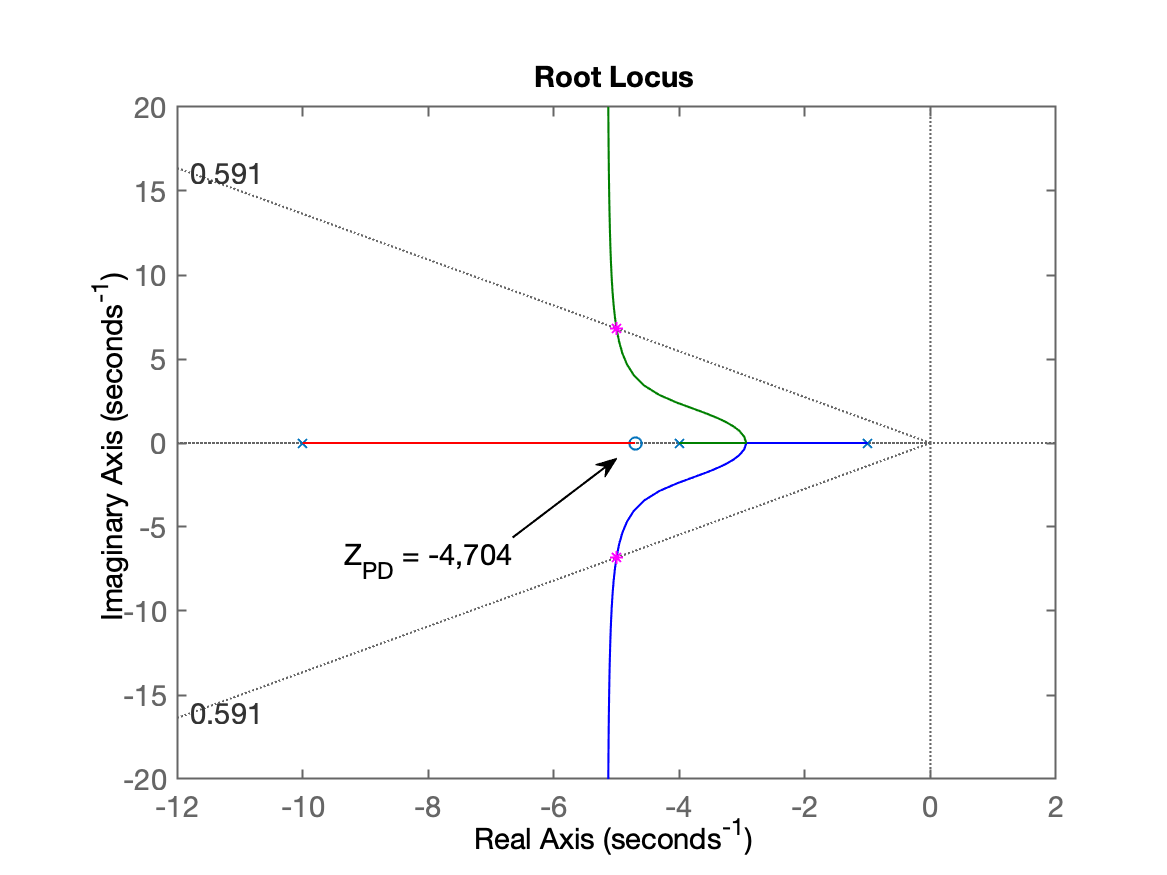
Note que não é necessário definir o ganho do PD, umaz vez que na 2a-etapa, vamos cascatear ao PD recém definido, um controle PI, culminando no PID final desejado. E neste caso, novos RLs podem ser visualizados enquanto se finaliza o projeto, mas apenas o RL final do PID completo é que será usado para definir o ganho geral do PID, não importando se foram definidos ganhos para o PD (da 1a-etapa) ou PI (da 2a-etapa).

Porém, é de bom tom, "guardar" em alguma variável a função transferência do PD recém projetado:

>> C_PD1a_etapa = tf( [1 -zero_c], 1)
​
C_PD1a_etapa =
 
  s + 4.704
 
Continuous-time transfer function.
​
>>

2a-Etapa: Projeto do PI

Agora partimos para a 2a-etapa, lembrando da eq. do PI:

$C_{PI}=\dfrac{ K_{PI} (s+z_{PI}) }{s}$

Como vamos seguir usando o script find_polo_zero.m, necessitamos definir um novo conteúdo para variável ftma_auxpara poder realizar o projeto deste controlador. Neste caso, temos que fazer algo como:

$\text{ftma_aux}=\underbrace{\dfrac{K_{PI}}{s}}_{\text{Parte do PI}} \cdot \underbrace{C_{PD}(s) \cdot G(s)}_{PD + Planta}$

onde a incógnita à ser determinada com o auxílio do script é o local do zero do PI. Note que estamos continuando o projeto do controlador, então o PD recém determinado (com excessão do seu ganho), deve ser considerado na sequência dos cálculos (sim, a complexidade do sistema vai aumentando).

Continuando o projeto:

xxxxxxxxxx
>> C_aux = tf(1, [1 0]);            % somente um integrador (parte do PI)
>> ftma_aux = C_aux*G*C_PD1a_etapa; % não esquecer de acrescentar PD já definido antes!
>> zpk(ftma_aux)                    % apenas para verificação
​
      20 (s+4.704)
--------------------
  s (s+10) (s+4) (s+1)
​
Continuous-time zero/pole/gain model.
​
>> find_polo_zero
​
Routine to determine the position of the pole or zero
that is missing to complete controller design
​
%OS$ (desired Overshoot, in %): ? 10
  ts_d (desired settling time): ? 0.8
Desired MF poles must be located at:
    s = -5 ± j6.82188
​
Evaluating the pole(s) contribution angle(s):
  Pole 1) in s=0 + j(0) | angle: 126.24^o
  Pole 2) in s=-10 + j(0)   | angle: 53.76^o
  Pole 3) in s=-4 + j(0)    | angle: 98.34^o
  Pole 4) in s=-1 + j(0)    | angle: 120.39^o
            Sum(angle{poles}) = 398.72^o
​
Evaluating the zero(s) contribution angle(s):
  Zero 1) in s=-4.70387 + j(0)  | angle: 92.49^o
            Sum(angle{zeros}) = 92.49^o
​
Determining pole or zero location of the controller:
Select: [p]=pole or [z]=zero, for the controller ? z
​
Angle contribution required for controller: 126.24^o
This means that the controller 
    ZERO must be at s = 0
​
To finish the project, note that:
​
ftma =
​
     20 s (s+4.704)
--------------------
  s (s+10) (s+4) (s+1)
​
Continuous-time zero/pole/gain model.
​
Find the controller gain with the command:
​
    >> K_ = rlocfind(ftma)
​
>>

Segue figura com resultado da contribuição angular associado com o projeto deste PI:

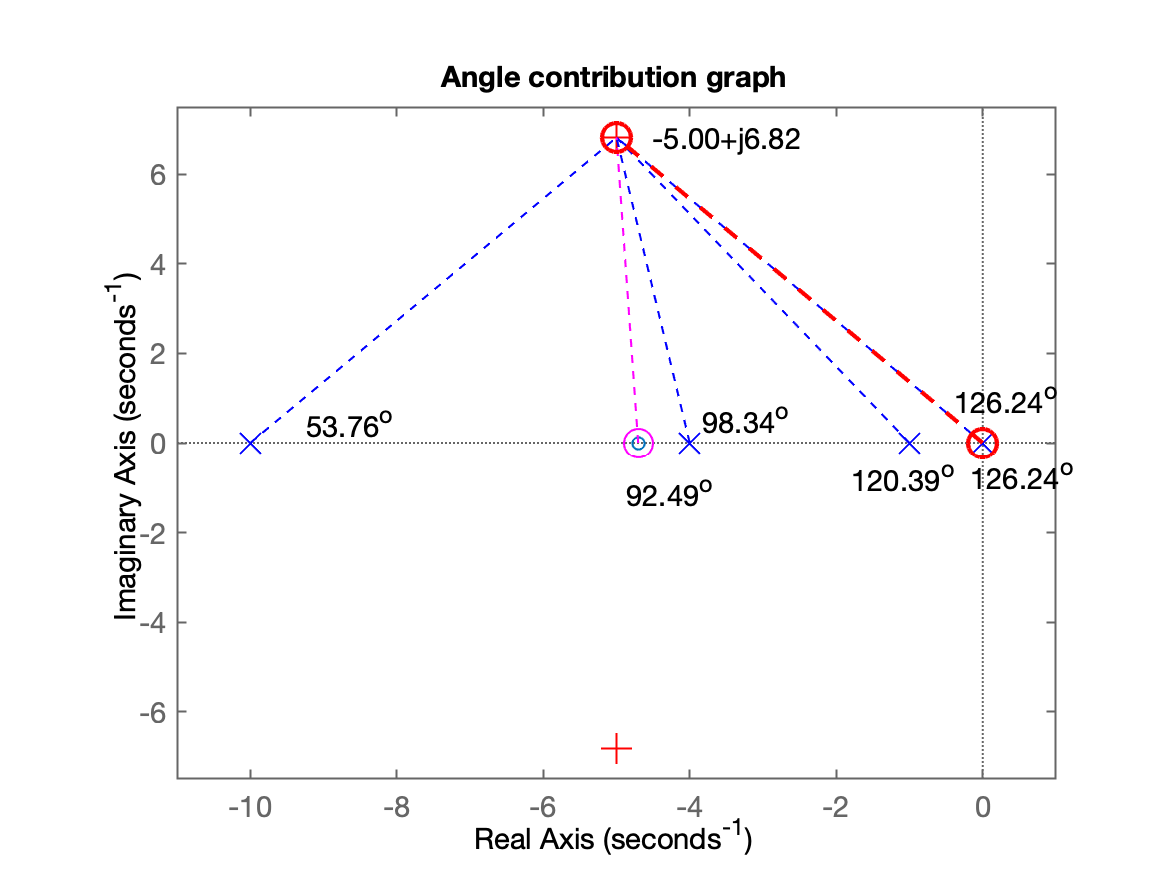
E segue o gráfico do RL final obtido, ou seja, do RL para o PID:

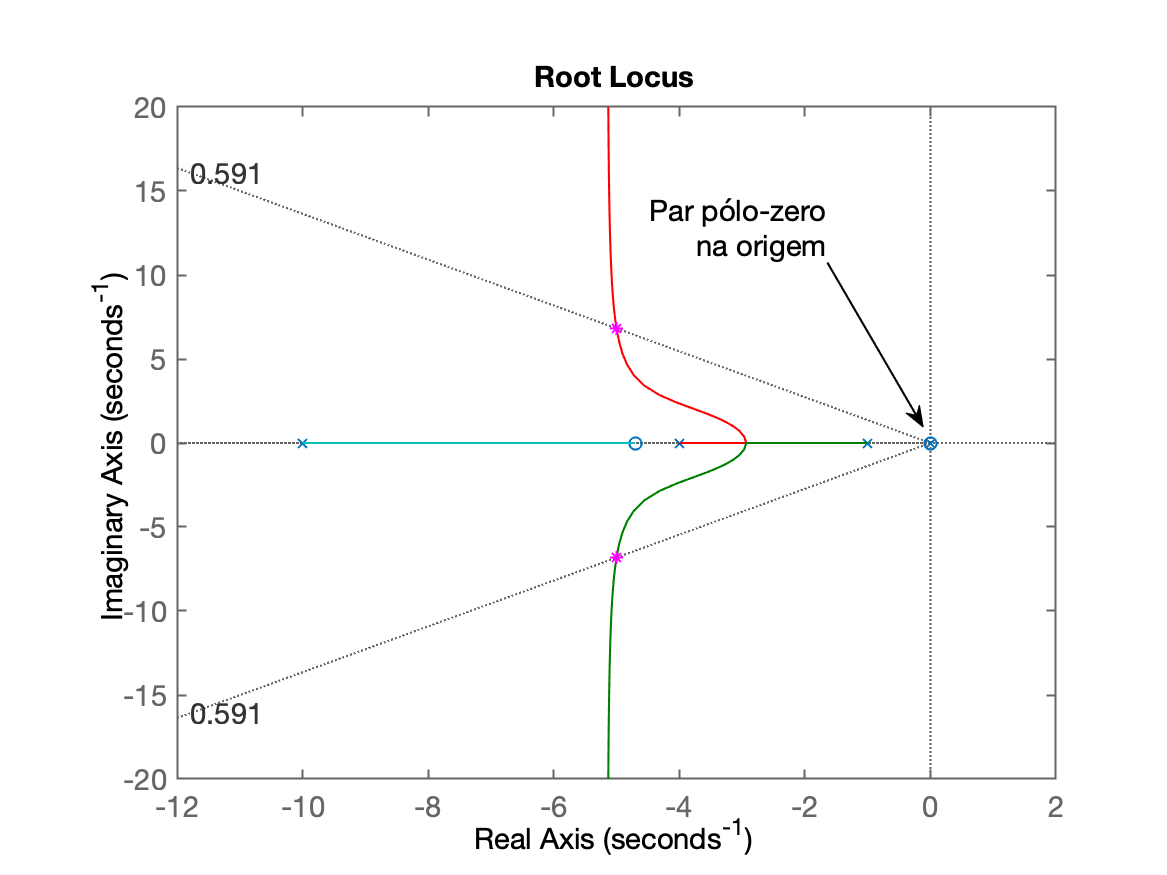
Note o resultado interessante... O zero calculado do PI coincidiu om o próprio pólo do PI, ou seja, não existe mais ação "PI". restou apenas ação "PD". Isto é, este controlador, não é mais um PID e acabou sendo um simples PD. Compare este RL com o RL do controlador PD calculado antes:

RL do PD	RL do PID

Provavelmente isto ocorreu porque o $t_s$ especificado e adotado para o projeto deste PI é algo reduzido ("ousado"), fazendo com o zero do PI acabasse por ser colocado sobre o próprio pólo integrador.

Provavelmente se o $t_s$ especificado tivesse sido ainda menor, teria resultado num zero para o PI na parte real positiva do plano-s (zero de MA "instável"), o que implicaria num RL final para o PID onde o pólo integrador caminharia na direção deste zero (parte real positiva do plano-s), inevitavelmente levando a um pólo de MF real positivo ou sistema instável.

Este resultado indica que o valor especificado: $t_s \le 0,8$ segundos é algo exagerado (e provavelmente impossível de ser obtido) colocando um PID para esta planta.

Solução: refazer projeto do PD usando $t_s$ mais baixo que o especificado. Até porque no momento de acrescentar o PI, o $t_s$ obtido para o PD vai ser ampliado em função do atraso causado pela ação integral. E se isto não resolver, aumentar o valor originalmente proposto.

Refazendo o PD

Nesta 2a-tentativa, vamos fazer o $t_s$ especificado para o projeto do PD, menor que o $t_s$ especificado para o PID completo. Esperemos que $t_s \cong 0,8$ segundos ainda possa ser obtido para um PID para esta planta. Este novo projeto vai permitir confirmar se isto é possível ou não.

Neste caso, vamos definir $t_s=0,65$ segundos para o projeto do PD:

xxxxxxxxxx
>> ftma_aux = G;    % refazendo `ftma_aux` para etapa do PD
>> find_polo_zero
​
Routine to determine the position of the pole or zero
that is missing to complete controller design
​
%OS$ (desired Overshoot, in %): ? 10
  ts_d (desired settling time): ? 0.65
Desired MF poles must be located at:
    s = -6.15385 ± j8.39616
​
Evaluating the pole(s) contribution angle(s):
  Pole 1) in s=-10 + j(0)   | angle: 65.39^o
  Pole 2) in s=-4 + j(0)    | angle: 104.39^o
  Pole 3) in s=-1 + j(0)    | angle: 121.54^o
            Sum(angle{poles}) = 291.32^o
​
Evaluating the zero(s) contribution angle(s):
            Sum(angle{zeros}) = 0.00^o
​
Determining pole or zero location of the controller:
Select: [p]=pole or [z]=zero, for the controller ? z
​
Angle contribution required for controller: 111.32^o
This means that the controller 
    ZERO must be at s = -2.87713
​
To finish the project, note that:
​
ftma =
​
     20 (s+2.877)
------------------
  (s+10) (s+4) (s+1)
​
Continuous-time zero/pole/gain model.
​
Find the controller gain with the command:
​
    >> K_ = rlocfind(ftma)
​
>> C_PD1a_etapa = tf( [1 -zero_c], 1)   % fazendo "backup" da eq. do controlador
​
C_PD1a_etapa =
​
  s + 2.877
​
Continuous-time transfer function.
​
>>

Segue gráfico mostrando resultados do cálculo da contribuição angular associados com o projeto desta 2a-versão do PD:

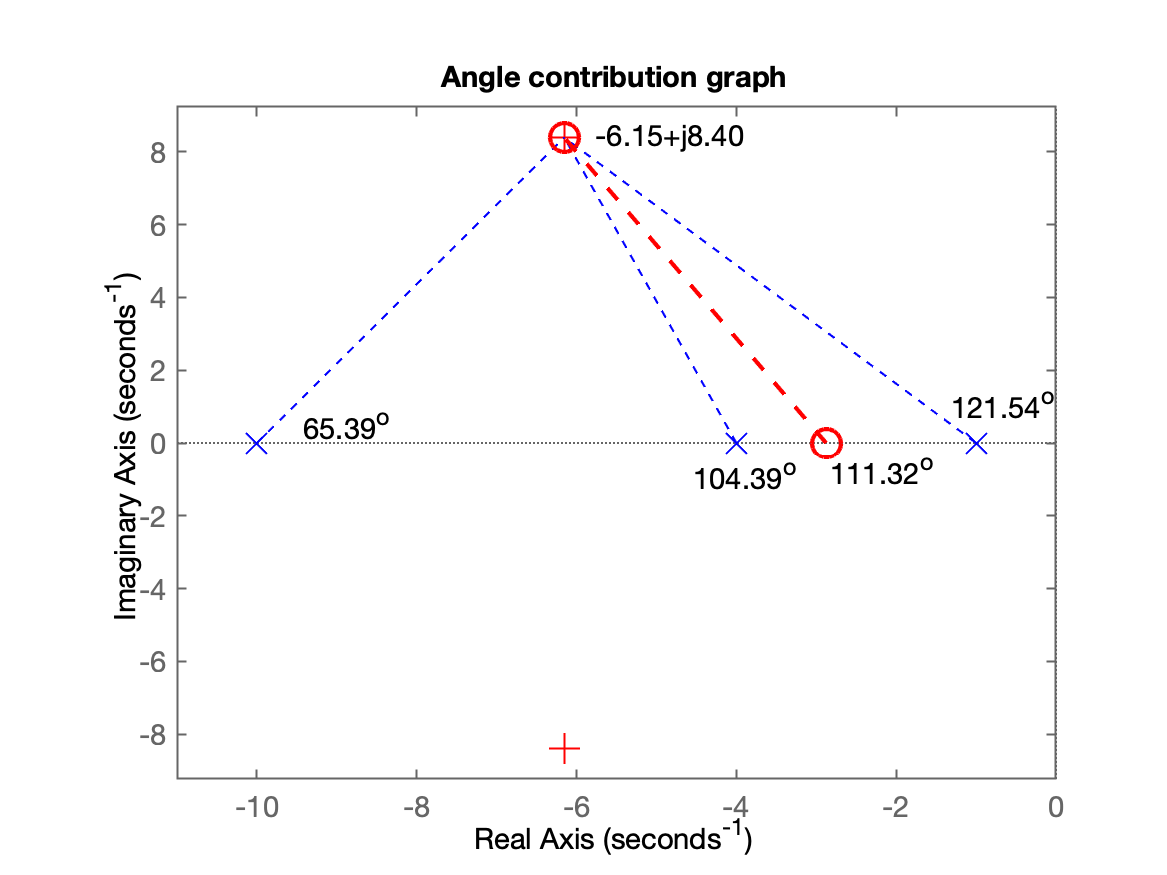
Note que o zero deste PD mudou de lugar em comparação com o primeiro PD proposto!

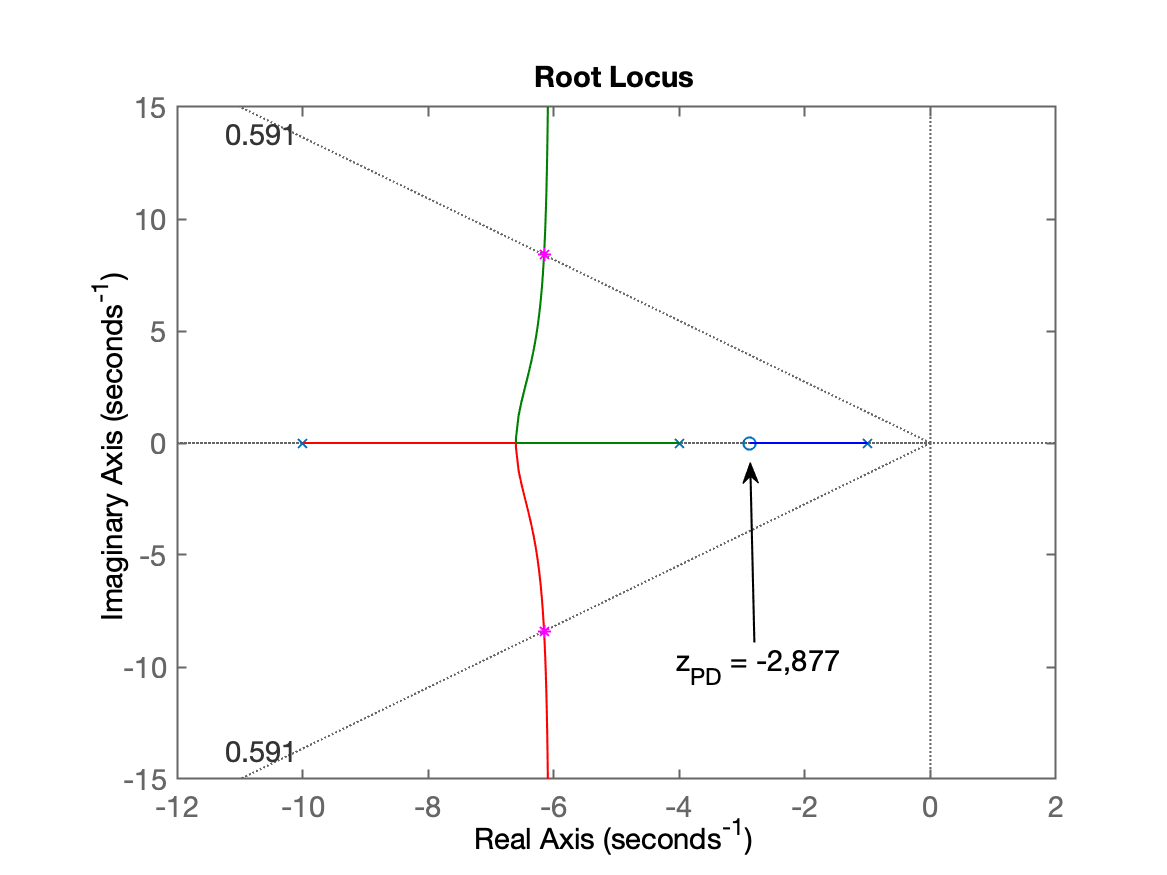
Segue o RL para este PD:

Refazendo o PI

Terminando 2a-etapa do projeto do PID.

Neste caso, ao executar novamento o script find_polo_zero.m para o projeto do PI, vamos voltar a usar $t_s=0,8$; valor especificado para o PID:

xxxxxxxxxx
>> ftma_aux = C_aux*G*C_PD1a_etapa;     % remontando `ftma_aux` 
>> zpk(ftma_aux)                        % para verificação
​
      20 (s+2.877)
--------------------
  s (s+10) (s+4) (s+1)
​
Continuous-time zero/pole/gain model.
​
>> find_polo_zero
​
Routine to determine the position of the pole or zero
that is missing to complete controller design
​
%OS$ (desired Overshoot, in %): ? 10
  ts_d (desired settling time): ? 0.8
Desired MF poles must be located at:
    s = -5 ± j6.82188
​
Evaluating the pole(s) contribution angle(s):
  Pole 1) in s=0 + j(0) | angle: 126.24^o
  Pole 2) in s=-10 + j(0)   | angle: 53.76^o
  Pole 3) in s=-4 + j(0)    | angle: 98.34^o
  Pole 4) in s=-1 + j(0)    | angle: 120.39^o
            Sum(angle{poles}) = 398.72^o
​
Evaluating the zero(s) contribution angle(s):
  Zero 1) in s=-2.87713 + j(0)  | angle: 107.29^o
            Sum(angle{zeros}) = 107.29^o
​
Determining pole or zero location of the controller:
Select: [p]=pole or [z]=zero, for the controller ? z
​
Angle contribution required for controller: 111.44^o
This means that the controller 
    ZERO must be at s = -2.32115
​
To finish the project, note that:
​
ftma =
​
  20 (s+2.877) (s+2.321)
  ----------------------
   s (s+10) (s+4) (s+1)
​
Continuous-time zero/pole/gain model.
​
Find the controller gain with the command:
​
    >> K_ = rlocfind(ftma)
​
>> 

Desta vez, o zero do PI não cancelou seu próprio pólo integrador, indicativo de que este projeto é viável e que resultará num PID.

Segue figura mostrando o gráfico dos cálculos da contribuição angular e local do novo zero para PI:

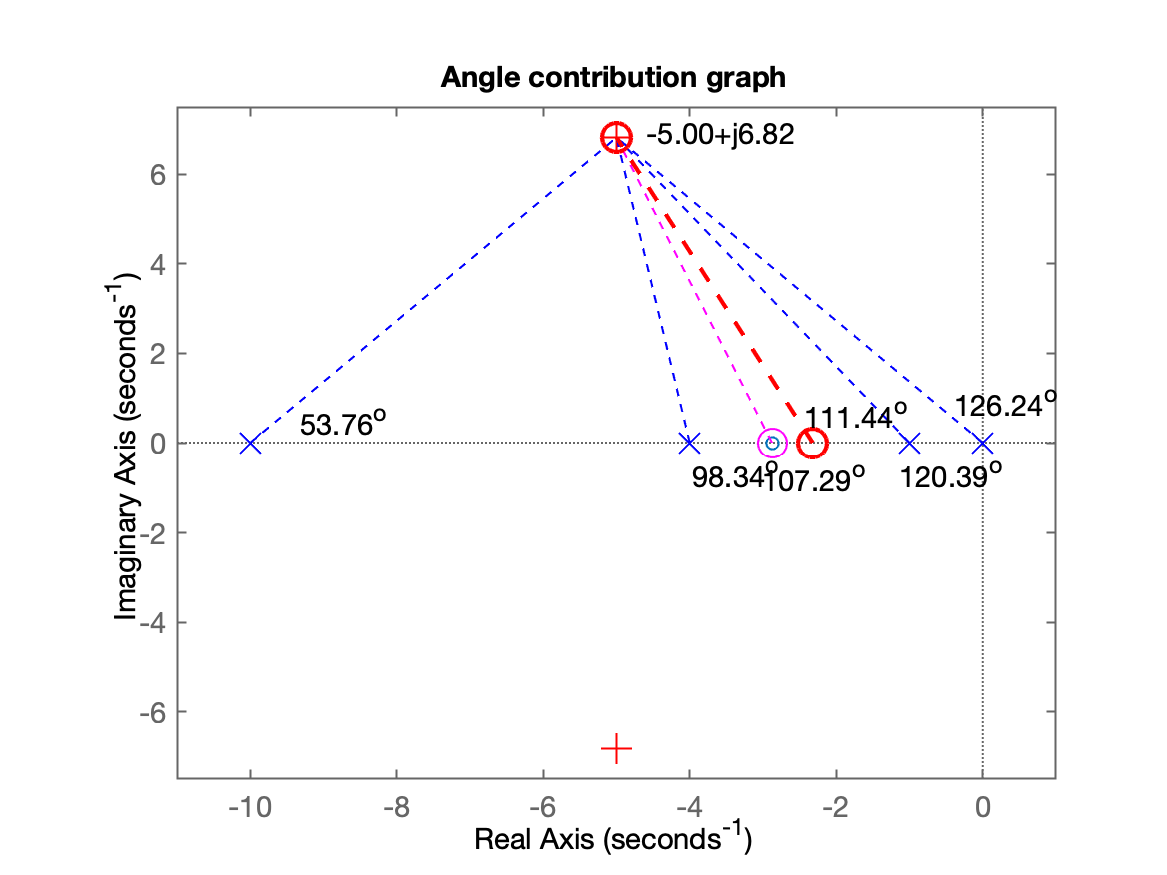
Continuando...

x
>> C_PI2a_etapa=C_aux*tf( [1 -zero_c], 1)   % "backup" da eq. deste controlador
​
C_PI2a_etapa =
​
  s + 2.321
  ---------
      s
​
Continuous-time transfer function.
​
>> 

Finalizando

xxxxxxxxxx
>> PID1 = C_PD1a_etapa * C_PI2a_etapa;  % montando eq. completa do PID
>> zpk(PID1)
​
  (s+2.877) (s+2.321)
  -------------------
           s
​
Continuous-time zero/pole/gain model.
​
>> zpk(ftma)    % aproveitando/verificando o último RL traçado
​
  20 (s+2.877) (s+2.321)
  ----------------------
   s (s+10) (s+4) (s+1)
​
Continuous-time zero/pole/gain model.
​
>> ftma_PID1 = ftma;    % "backup" da ftma(s) com o PID
>> [K_PID1,polosMF] = rlocfind(ftma)    % "sintonizando" PID
Select a point in the graphics window
selected_point =
      -4.9834 +     6.7802i
K_PID1 =
       3.6967
polosMF =
      -5.0015 +     6.7808i
      -5.0015 -     6.7808i
      -2.4985 +    0.84389i
      -2.4985 -    0.84389i

RL do PID já mostrando o ganho definido para o mesmo:

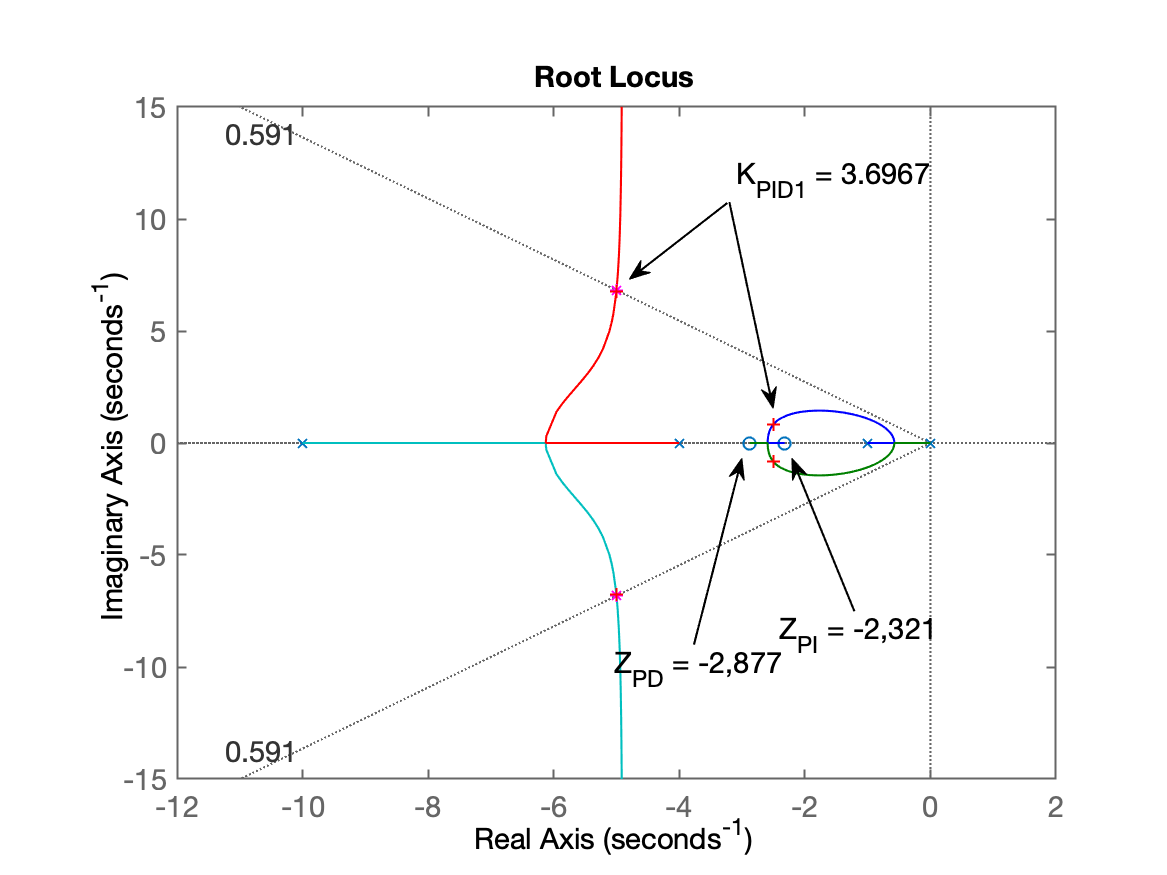
Note no RL anterior, que a "complexidade" deste sistema aumentou: são 4 pólos de MF (4 traçados de RL), com 2 pares de pólos complexos, cada par interagindo com o outro, já que estão relativamente próximos. Terminamos com um sistema de 4a-ordem:

xxxxxxxxxx
>> zpk(ftma)
​
ans =
 
  20 (s+2.877) (s+2.321)
  ----------------------
   s (s+10) (s+4) (s+1)
 
Continuous-time zero/pole/gain model.
​

Note que o zero do PI acabou ficando próximo do zero do PD. Mas eles continuam compondo um PD e um PI colocados em cascata para resultar no PID.

Fechando a malha...

xxxxxxxxxx
>> ftmf_PID1 = feedback(K_PID1*ftma_PID1, 1);
>> figure; step(ftmf_PID1)

Segue figura com resposta ao degrau obtida para o PID:

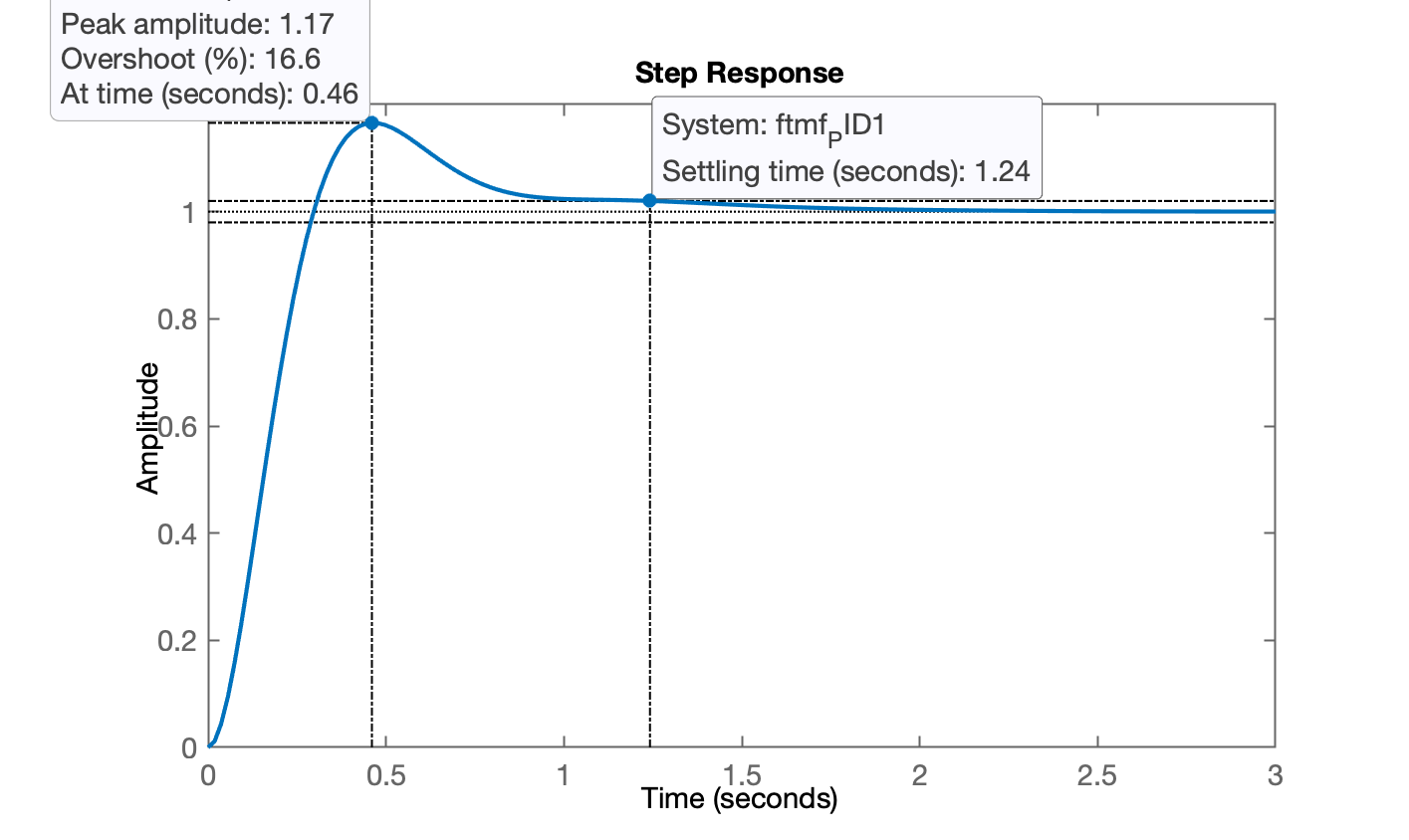
Considerações Finais

Não conseguimos atender os requisitos de controle. Tanto $\%OS$ foi ultrapassado e $t_s$ resultou maior que o desejado (quase o dobro).

Para melhorar este PID teríamos que "arrastar" o zero do PD e o zero do PI para a direção $s \to \infty$. Mais fácil fazer isto usando o App Control System Designer. Tema para próxima aula...

Problema Proposto 2

Melhore o projeto do PID anterior a fim de tentar satisfazer os requisitos de controle. Dica: use o App Control System Designer para realocar novas posições para os zeros do PD e do PI. Comente/justifique sua estratégia, apresente e explique os novos resultados obtidos.

😅 Ufa, esta aula (21/10/2024) terminou com "apenas" 16 janelas gráficas abertas...

Finalizando os trabalhos desta aula:

xxxxxxxxxx
>> save planta
>> diary off
>> quit

Arquivo disponível: planta.mat.

🌊 Fernando Passold 📬 ,