Ações Derivativas

Note que um PD é acrescentado num sistema para acelerar o tempo de resposta do mesmo, mas deve ser percebido alguns “efeitos colaterais” da ação Derivativa:

• Expressivas amplitudes para a ação de controle. Os valores gerados na teoria podem ser aplicados na prática?
• Um Derivador possui tendência à amplificar componentes de alta frequencia.

Sobre esta última parte, vamos supor um sinal de referência simples, oscilatório, sobre o qual se apresenta ruídos com amplitude de 1% em relação à amplitude da oscilação original que queremos derivar. Então temos algo como:

$f(t)=\underbrace{1 \sin(2 \pi 1 \, t)}_{\text{Sinal original}} +\underbrace{\frac{1}{100} \sin (2 \pi 60 \, t) + \frac{1}{100} sin (2 \pi 20K \, t)}_{\text{Ruídos}}$

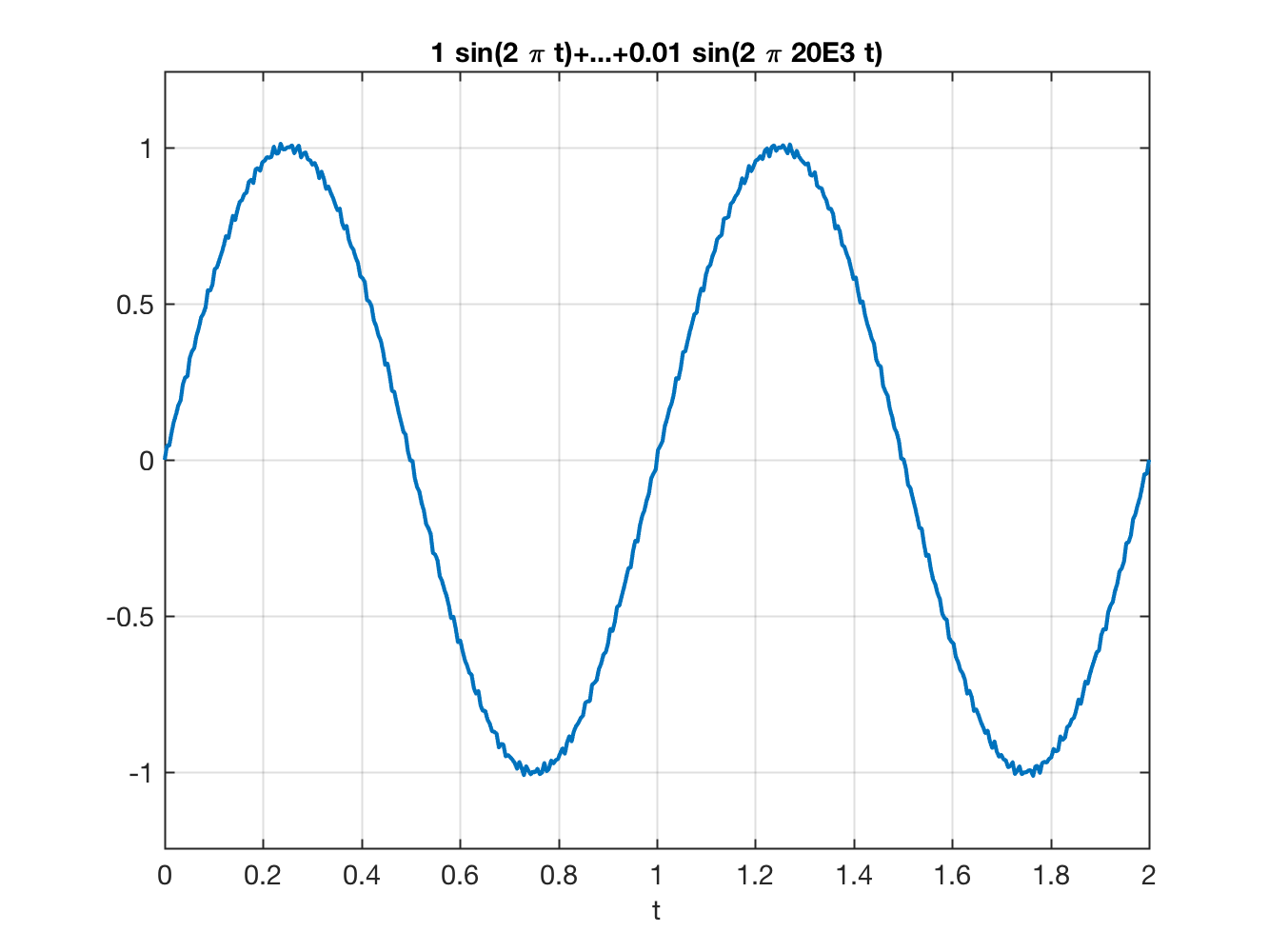
note que o sinal original está oscilando com amplide de $\pm 1$; e sobreposto ao mesmo aparece o ruído: um sinal induzido da rede (60 Hz) com amplitude de 1% em relação ao sinal original $+$ sinal induzido de uma fonte chapeada na frequência de 20 KHz, mesma amplitude reduzida de 1% em relação ao sinal origina.

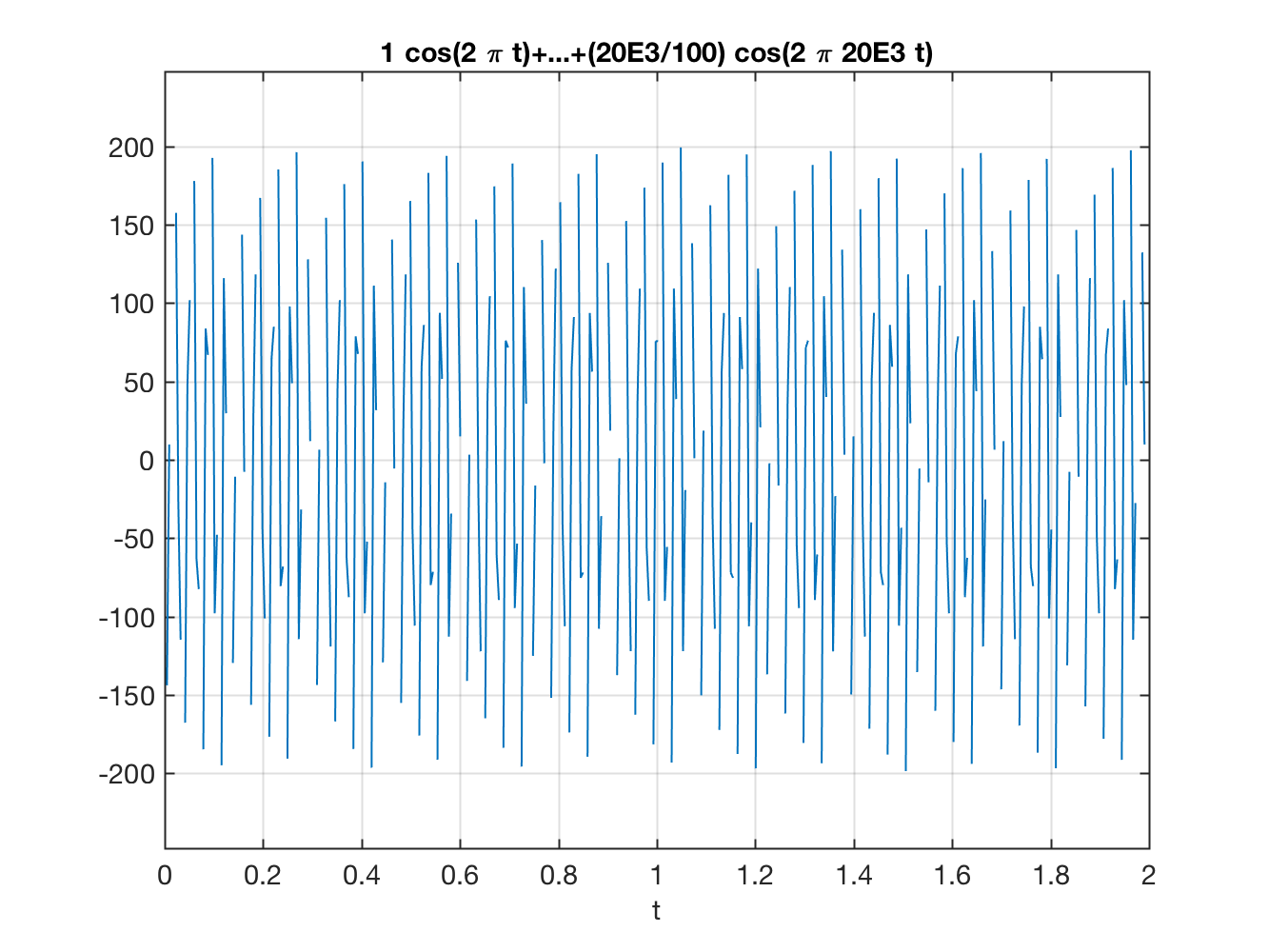
O que ocorre com este sinal quando realizamos sua derivada: $v(t)=\dfrac{\partial f(t)}{\partial t}$ ?

Por definição termos:

$v(t)=1 \cos(2\pi \,t)+\dfrac{60}{100} \cos(2 \pi 60 \, t) + \dfrac{20000}{100} \cos (2 \pi 20K \, t)$

$v(t)=1 \cos(2 \pi \, t)+0,6 \cos(2 \pi 60 \,t) + 200 \cos(2 \pi 20K \, t)$

Note que sobre a derivada do sinal original que continua variando entre $\pm 1$, temos agora a derivada do ruído da rede, cuja amplitude alcança 60% da amplitude do sinal que queremos derivar; e pior que isto,, há a derivada do ruído da fonte chaveada, cuja amplitude acabaou sendo $200 \times$ maior que a própria deriva que gostaríamos de medir.

Em termos mais práticos, podemos gerar a seguinte figura:

Sinal original (com ruído)	Derivada do sinal da esquerda

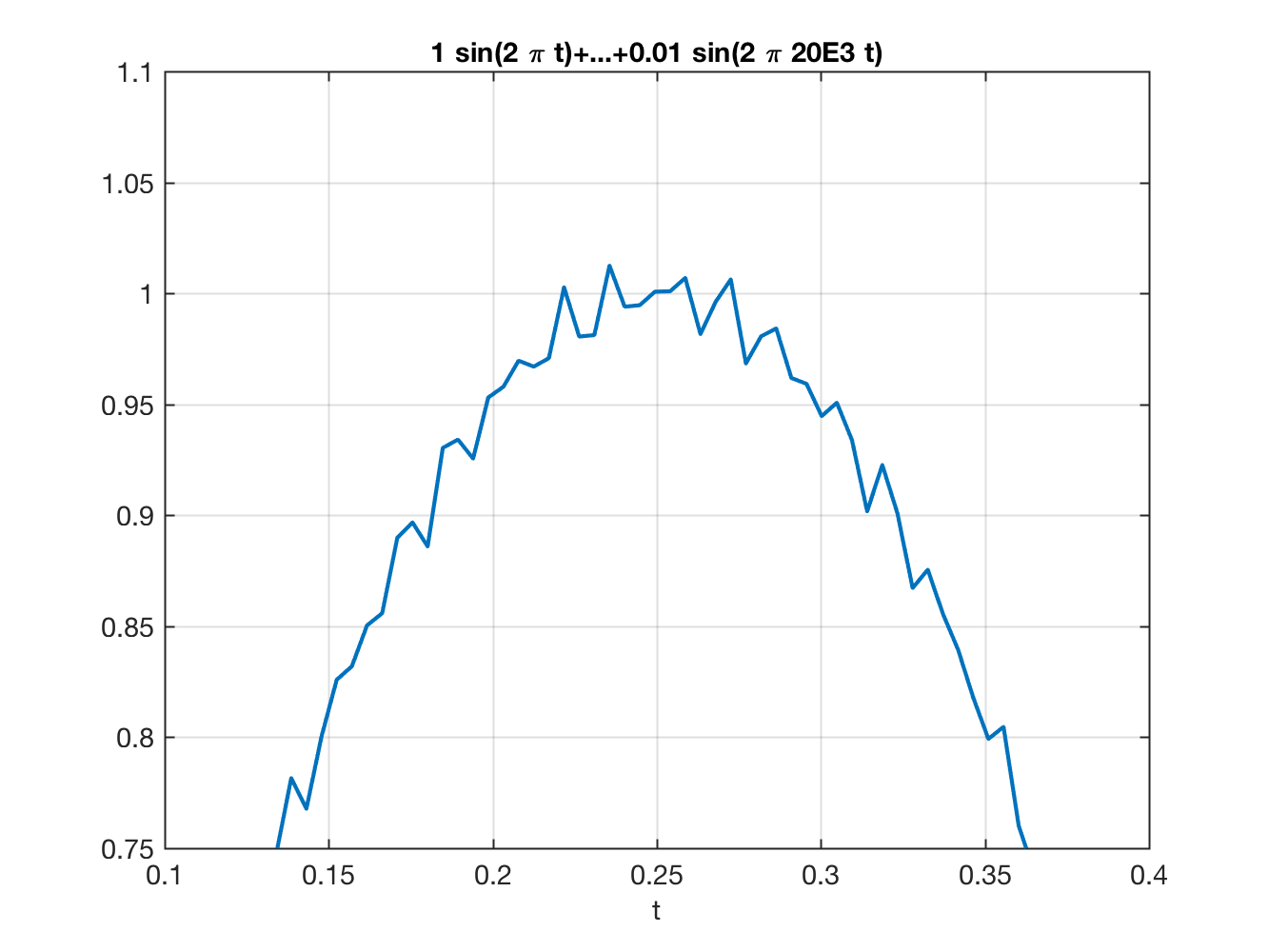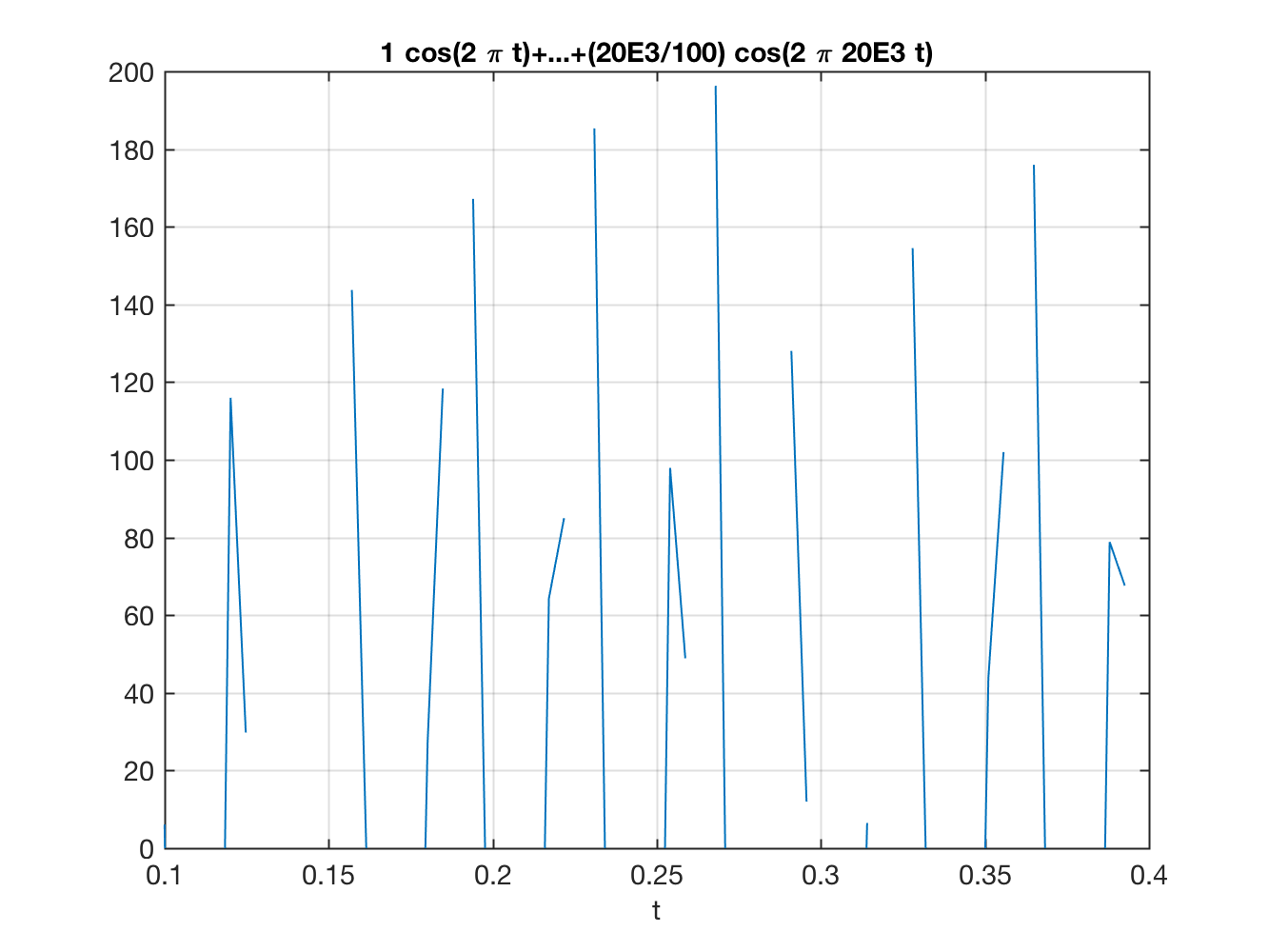Código usado na Matlab para a simulação (gráficos anteriores):

>> t_fim=2*1; % fim do período de simulação para 2 ciclos sinal original 1 Hz
>> figure;
>> ezplot('1*sin(2*pi*t)+0.01*sin(2*pi*60*t)+0.01*sin(2*pi*20E3*t)', [0 2]) % sinal antes da derivada
>> figure; 
>> ezplot('1*cos(2*pi*t)+(60/100)*cos(2*pi*60*t)+(20E3/100)*cos(2*pi*20E3*t)', [0 2])

Note o que era esperado:

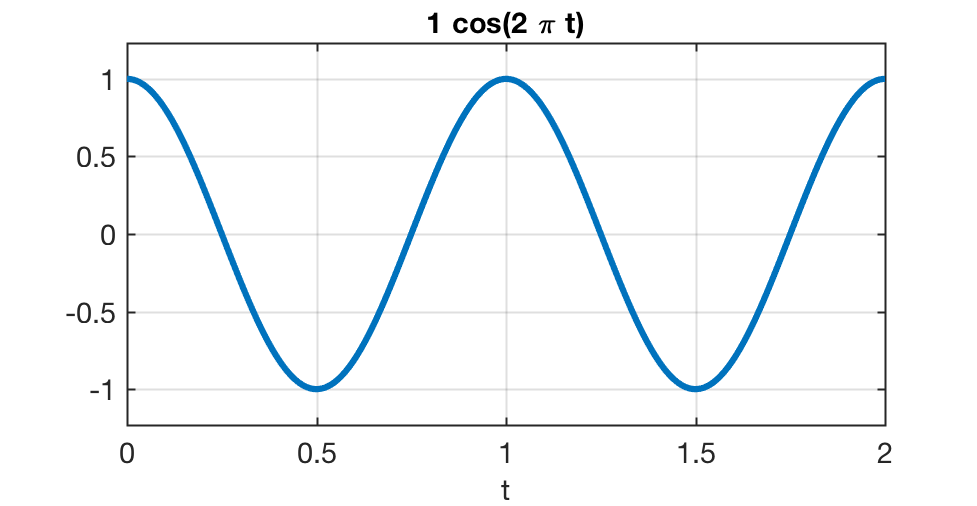
Obviamente que estamos muito distantes do desejado devido ao ruído. A questão é a forma como o derivador funciona. Por exemplo, atente para o diagrama de Bode, sua parte de amplitude para um Derivador Puro:

$v(t)=\dfrac{\partial{f(t)}}{\partial{t}}$

$V(s)=s \cdot F(s)$

$\frac{V(s)}{F(s)}= 1 \cdot s$

Cujo diagrama de Bode rende:

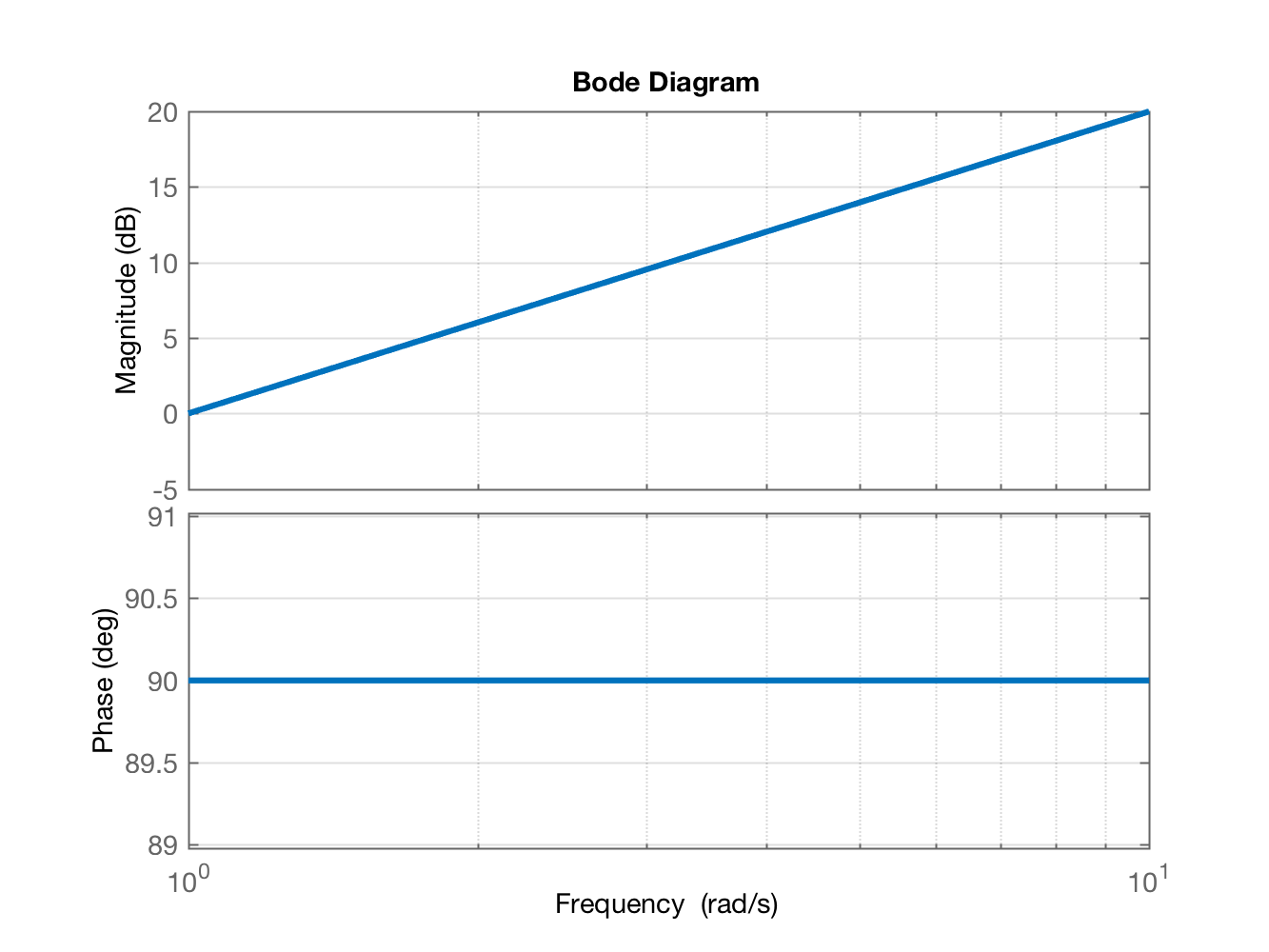
Então percebe-se claramente que um Derivador Puro amplifica enomermente componentes de alta frequência.

Uma forma de solucionar o problema é incorporar m filtro passa-baixas (FPB) no sinal de erro que passará pelo bloco derivador, o que vai resultar num controlador por Avanço de Fase (Lead), algo como:

Exemplo:

Supondo o que muda quando partimos para um controlador PD, consideramos agora outra planta já abordada anteriormente:

Para a mesma foi realizado um projeto de PD que rendeu:

Lembrando da eq. do PD, temos:

$C_{PD}(s)=K_d \left( s+ \dfrac{K_p}{K_d} \right)= K_p + K_d \, s$

E então teríamos: $K_d=42$ e $K_p=3,5 \cdot 42=147$.

E um Lead para este sistema poderia ser:

onde o pólo seria resultado do acréscimo de um Filtro Passa-Baixa, $FPB(s)$, à ação derivativa, considerando-se neste caso, uma frequencia de corte de $f_c=5$ (Hz) (ou $\cong 32$ (rad/s)).

Note: só a equação do filtro (com ganho DC unitário) resultaria em:

$FPB(s)=\dfrac{32}{s+32}$

O diagrama de Bode deste Lead ficaria:

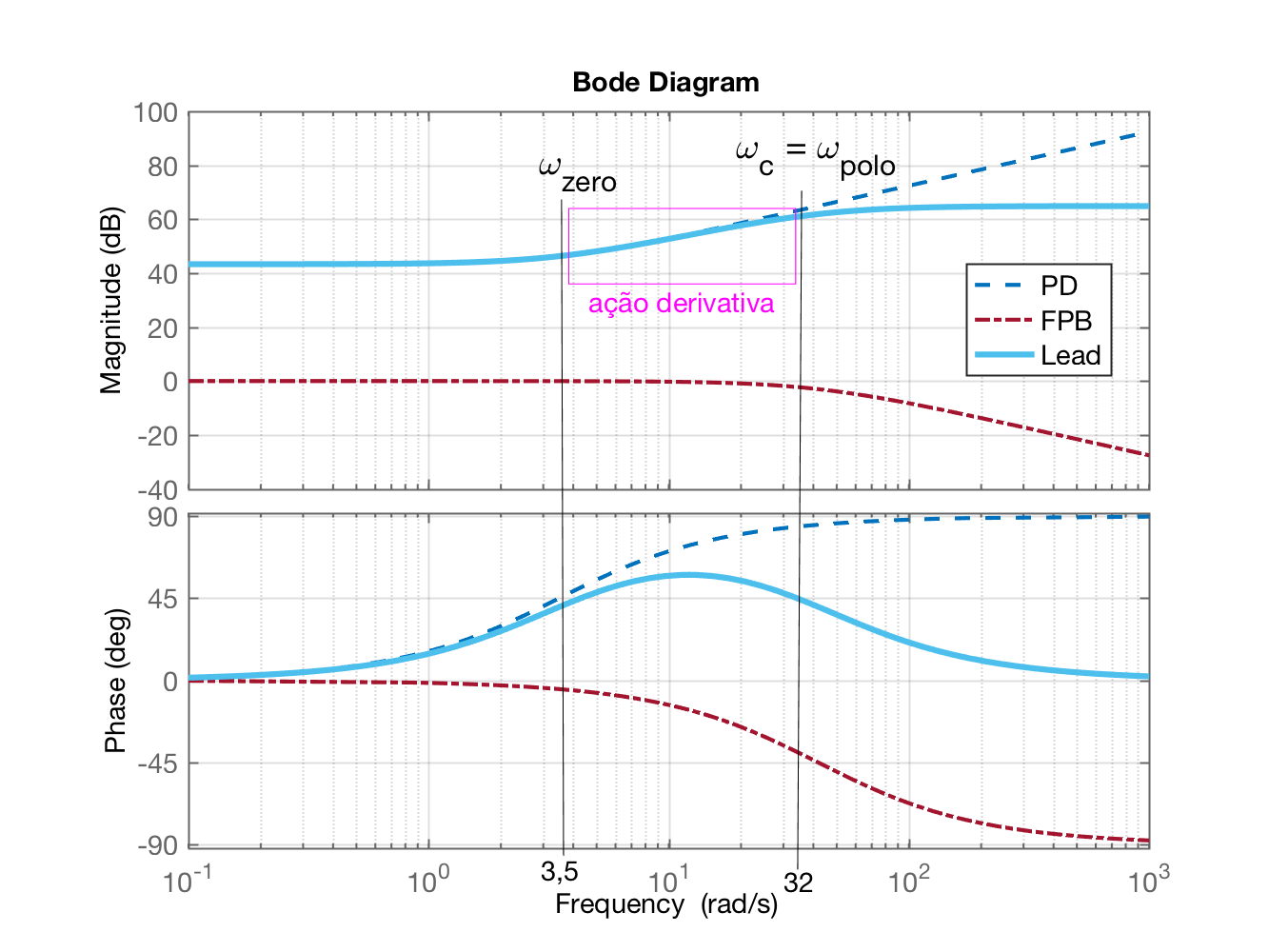
Note o “avanço” (subida) na fase provocado por este tipo de controlador (o caracteriza seu nome) e note que usando um simples Filtro Passa-Baixas de 1a-ordem, o ganho fica limitado após a frequência de corte do filtro (em $f_c=32 (rad/s)=5 Hz$). A atuação do filtro seria ainda mais eficaz de o mesmo fosse de 2a-ordem; neste caso, teríamos um decaimento de -20 dB/déc à partir desta frequência de corte, o que significa que não estaríamos mais amplificando derivadas de sinais à partir dos 5 Hz.

Este sistema, a FTMA(s) simulado com um ruído do tipo ..., resultaria em ....:

<<Sorry: não houve tempo para terminar esta simulação>>

Dados salvos como “teste.mat"

Fernando Passold, em 02.06.2021