Aplicação Prática de Diagramas de Bode

Ação Derivativa de Sinal Ruidoso

Interpretando o diagrama de Bode para uma ação puramente derivativa:

G(s)=s

O diagrama de Bode da função transferência acima rende:

>> G=tf([1 0],1)

G =
 
  s
 
>> bode(G,[0.01 100])

Gráfico gerado:

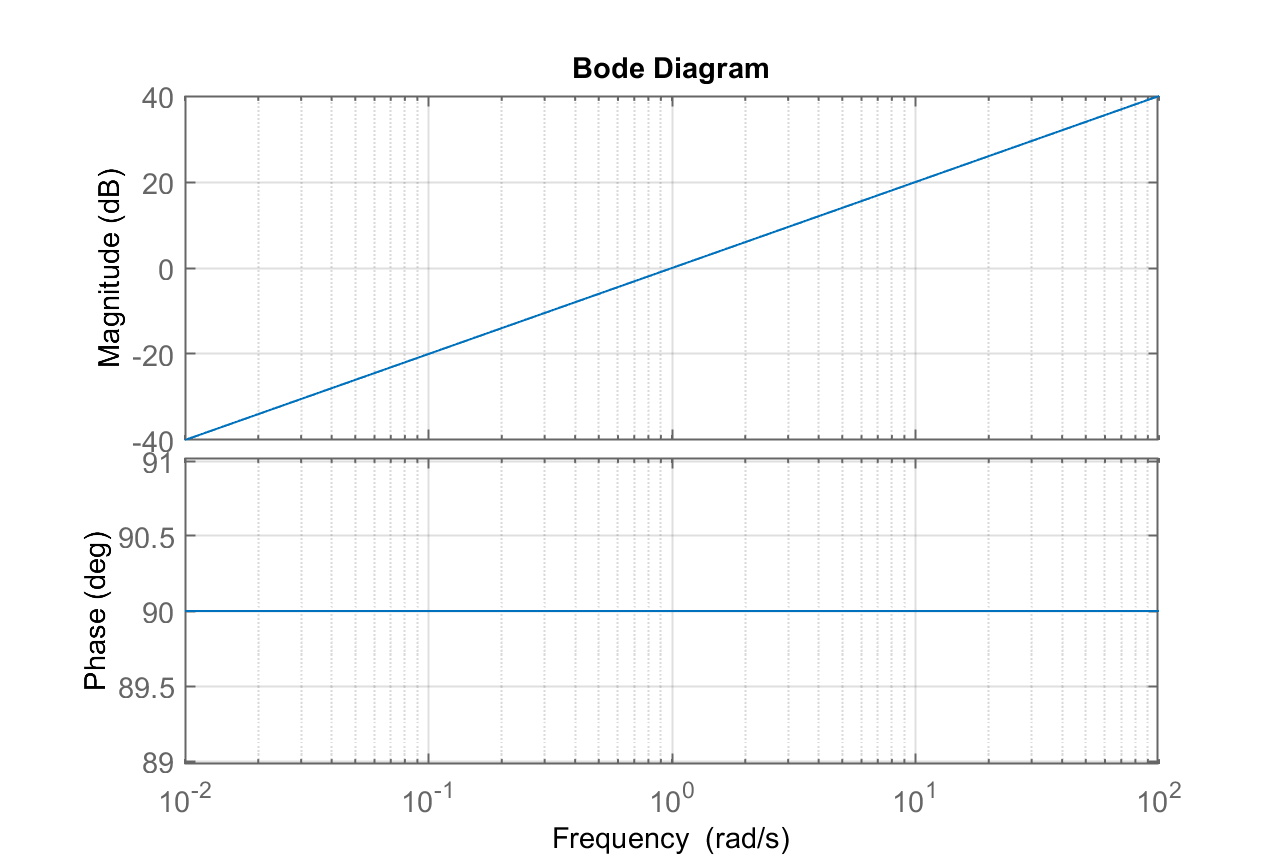
Este gráfico significa que um sinal senoidal com frequência = 1 rad/s ( $2\pi=6.2832$ Hz) sofrerão um “ganho” $K=1$ ou:

$|G|=|j \omega|=\sqrt{\omega^2}=\omega$

$|G|_{\text{dB}}=20log_{10}(\omega)$ ,

onde $\omega=$ frequência em rad/s.

Então na frequencia de 1 rad/s teremos:

$K\vert_{\text{dB}}=20\log_{10}\left(\dfrac{V_{out}}{v_{in}}\right)=20\log_{10}(1)=0)$ dB.

Note que o gráfico anterior também permite saber que componentes acima da frequência de 1 rad/s sofrenão um ganho considerável e SEM nenhuma limitação.

Como isto pode afetar um circuito?

Suponha que você esteja tentando construir um circuito eletrônico puramente derivativo. Suponha que este circuito consiga sintetizar a expressão $G(s)=s$ . O que acontece quando ele é submetido a um sinal senoidal real de 1 Hz, 1 Vpp, num laboratório, na vida real?

Bom, na vida real, sobreposto a este sinal, temos componentes de alta frequência, o que chamamos comumente de “ruído”. Vamos supor que então além da senoide de 1 Hz, 1 Vpp que estamos injetando no nosso circuito, o mesmo também está recebendo ruido. Algo como:

ruído da rede, sobreposto ao gerado, na frequência de 60 Hz, 10 mVpp;
ruído de "ripple" mal filtrado de uma fonte de alimentação analógica que usa retificação em onda completa e que está induzindo no circuito uma tensão de 7 mVpp (a 120 Hz);
ruído gerado por fonte chaveada (algum reator de lâmpada "eletrônica"), trabalhando na frequência de 4 KHz, induzindo um ruído de 1 mVpp;
ruído de outra fonte chaveada trabalhando em 20 KHz, também na faixa de 1 mVpp;
mais um ruído de outra fonte chaveada, esta trabalhando à 40 KHz, na faixa de 1 mVpp.

O que ocorre se tentarmos derivar este tipo de sinal?

Do pondo de vista do Diagrama de Bode, e interpretando o mesmo, notamos que os componentes acima de 1 Hz vão ser amplificados da seguinte forma:

Na frequência de 60Hz, sinais aplicados neste circuito sofrerão um ganho de:

Ganho(60\text{ Hz})\vert_{^\text{dB}} = 20*log_{10}(2\pi60)=51.527 \text{ (dB)}

Automatizando este cálculo com o auxílio do Matlab paras os ruídos nas outras frequencias podemos fazer:

>> format shortg                  % formato mais "amigável" de print de casas decimais
>> freq=[60 120 4E3 20E3 40E3];   % cria vetor com freq's dos ruídos (em Hz)
>> freq_rad=2*pi*freq;            % calculando freq's anteriores em rad/s
>> Ganho_dB=20*log10(freq_rad);   % calcula ganho em dB para cada faixa de freq anterior
>> % Verificando os resultados obtidos:
>> [freq' Ganho_dB']
ans =
           60       51.527
          120       57.547
         4000       88.005
        20000       101.98
        40000          108
>> % Calculando o valor do ganho em termos absolutos e não em dB
>> Ganho=10.^(Ganho_dB/20);
>> % "Tabulando" os resultados obtidos:
>> [freq' Ganho_dB' Ganho']
ans =
           60       51.527       376.99
          120       57.547       753.98
         4000       88.005        25133
        20000       101.98   1.2566e+05
        40000          108   2.5133e+05
>> Amp=[0.01 7E-3 1E-3 1E-3 1E-3]; % criando vetor com amplitude de cada ruído
>> Amp_out=Amp.*Ganho;             % calculando amplitude de saída
>> % Tabulando os novos resultados obtidos
>> [freq' Ganho_dB' Ganho' Amp_out']
ans =
           60       51.527       376.99       3.7699
          120       57.547       753.98       5.2779
         4000       88.005        25133       25.133
        20000       101.98   1.2566e+05       125.66
        40000          108   2.5133e+05       251.33
>>

Percebemos então o ganho absurdo (251.327,41 vezes = 108 dB) que incide sobre o ruído de apenas 1 mVpp que ocorre na frequência de 40 KHz. Isto é, este sinal que originalmente oscilava à 0,001 Vpp, uma vez derivado neste circuito, vai passar a oscilar à 251,33 Vpp!!!

Perceba então que o Diagrama de Bode indica simplesmente isto, que o ganho será cada vez maior, quanto maior for a frequência do sinal na entrada deste circuito. Você entende agora porque não existe circuito eletrônico derivativo puro? Se um amplificador operacional for montado para tentar executar uma derivada pura sobre seu sinal de entrada, qualquer componente de frequência elevada vai implicar num ganho tão elevado que o mesmo fatalmente vai saturar na tensão de alimentação adotada para o mesmo (tensão negativa ou positiva se for considerada alimentação simétrica para o Amp. Op.).

Circuito ideal	Circuito funcional

$\dfrac{V_{out}(s)}{V_{in}(s)}=-\dfrac{Z_2(s)}{Z_1(s)}$	$\dfrac{V_{out}(s)}{V_{in}(s)}=-\dfrac{Z_2(s)}{Z_1(s)}$
$\dfrac{V_{out}(s)}{V_{in}(s)}=-\dfrac{ \frac{R_2}{1} }{ \frac{1}{sC_1} }$	$\dfrac{V_{out}(s)}{V_{in}(s)}=-\dfrac{ \frac{R_2}{1+sR_2C_2} }{ R_1 + \frac{1}{sC_1} }$
$\dfrac{V_{out}(s)}{V_{in}(s)}=-sR_2C_1$	$\dfrac{V_{out}(s)}{V_{in}(s)}=-\dfrac{sR_2C_1}{(1+sR_1C_1)(1+sR_2C_2)}$
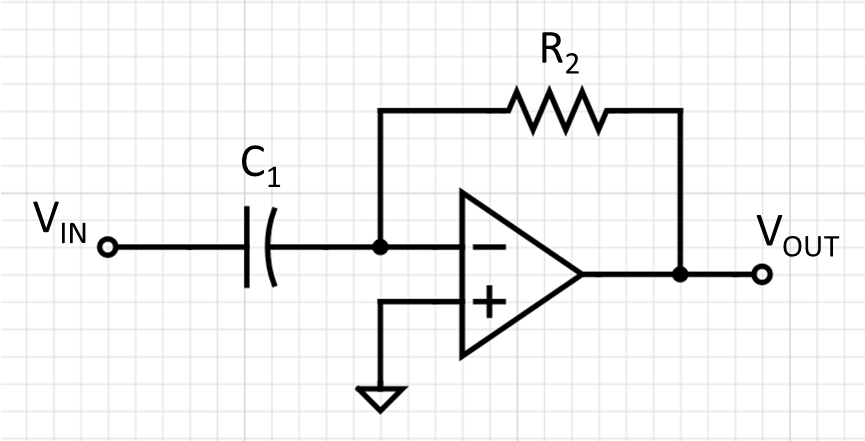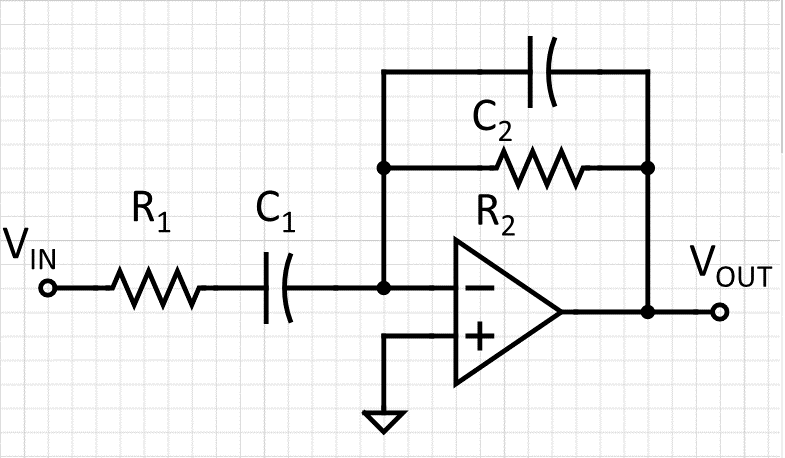(não funciona)	(viável na prática)
Fig 1 (a)	Fig 1 (b)

Referência sugerida: EDN: The practical op-amp differentiator is quite versatile.

Se por acaso, fosse possível construir um circuito puramente derivativo, poderíamos simular (usando Matlab ou outro software), tanto o sinal de entrada (com ruído), quanto o sinal de saída (derivada pura). Resultaria algo como:

>> ezplot('sin(2*pi*1*t)+0.01*sin(2*pi*60*t)+0.007*sin(2*pi*120*t)+1E-3*sin(2*pi*4E3)+1E-3*sin(2*pi*20E3*t)+1E-3*sin(2*pi*40E3*t)',[0 2])
>> hold on;
>> ezplot('sin(2*pi*1*t)+3.7699*sin(2*pi*60*t)+5.2779*sin(2*pi*120*t)+25.133*sin(2*pi*4E3)+125.66*sin(2*pi*20E3*t)+251.33*sin(2*pi*40E3*t)',[0 2])
>> legend('Sinal original (com ruído)', 'Derivada do sinal')

Gráficos gerados:

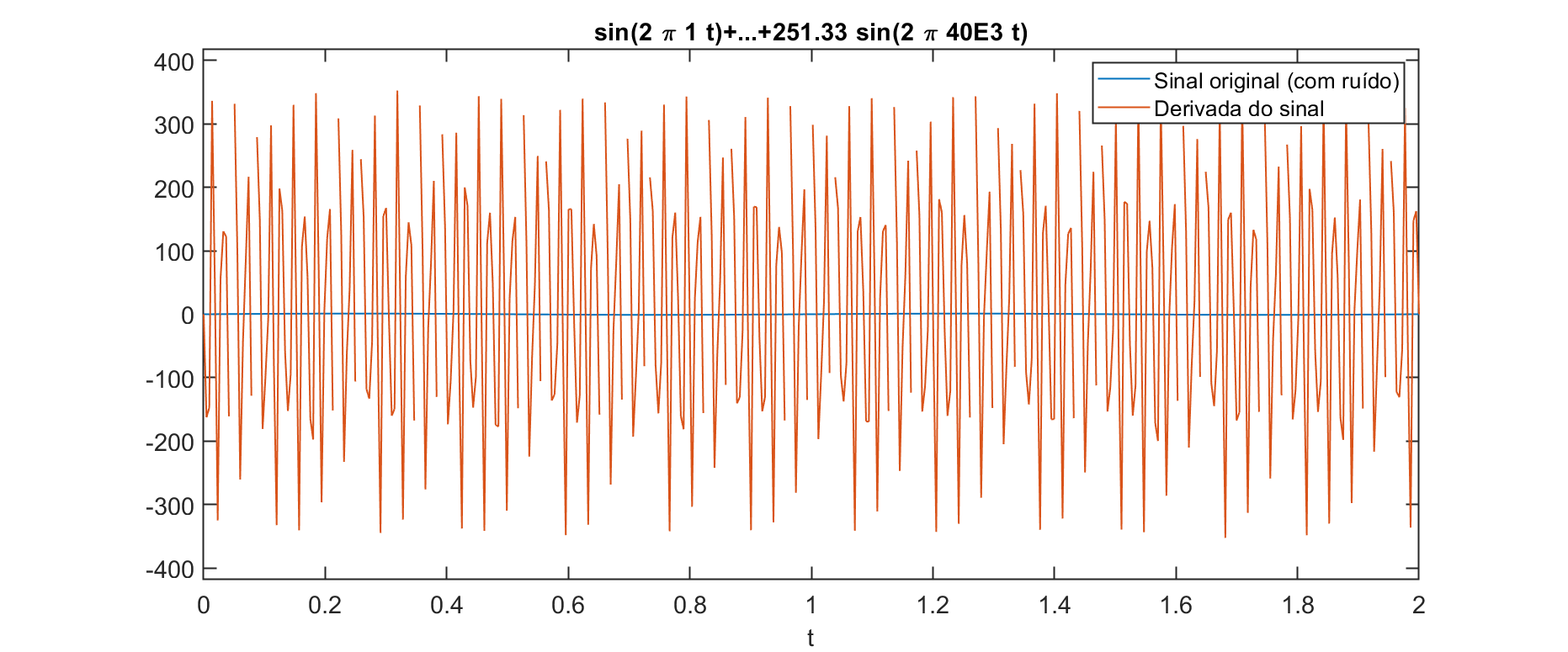
O sinal original apenas com ruído resulta algo mais simples:

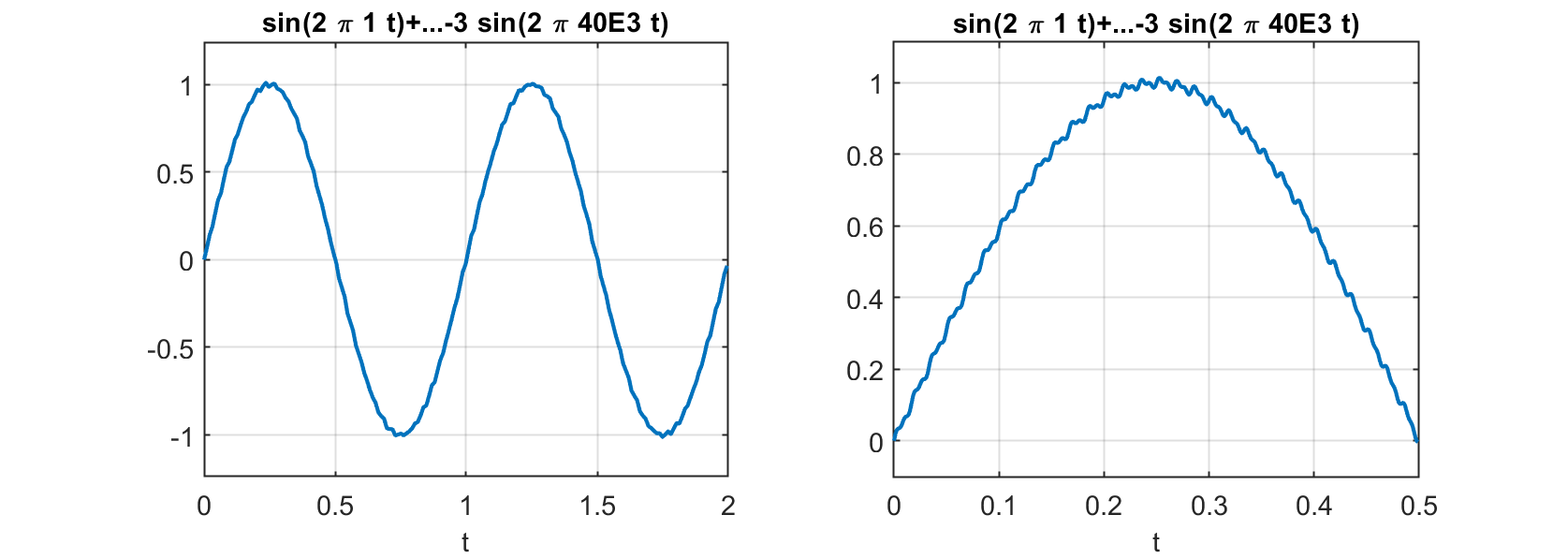
Analise os gráficos e ficará evidente o problema. Note que o sinal de saída parece oscilar entre $\pm$ 350 Vpp! Mas atenção, não consideramos nesta simulação que o sinal derivado vai ser defasado em $+90^o$ em relação ao sinal original, o que significa:

$\sin(x+90^o)=\cos(x)$

$\dfrac{\partial\sin(x)}{\partial x}=\cos(x)$

Esclarecendo as relações trigonométricas anteriores de forma gráfica:

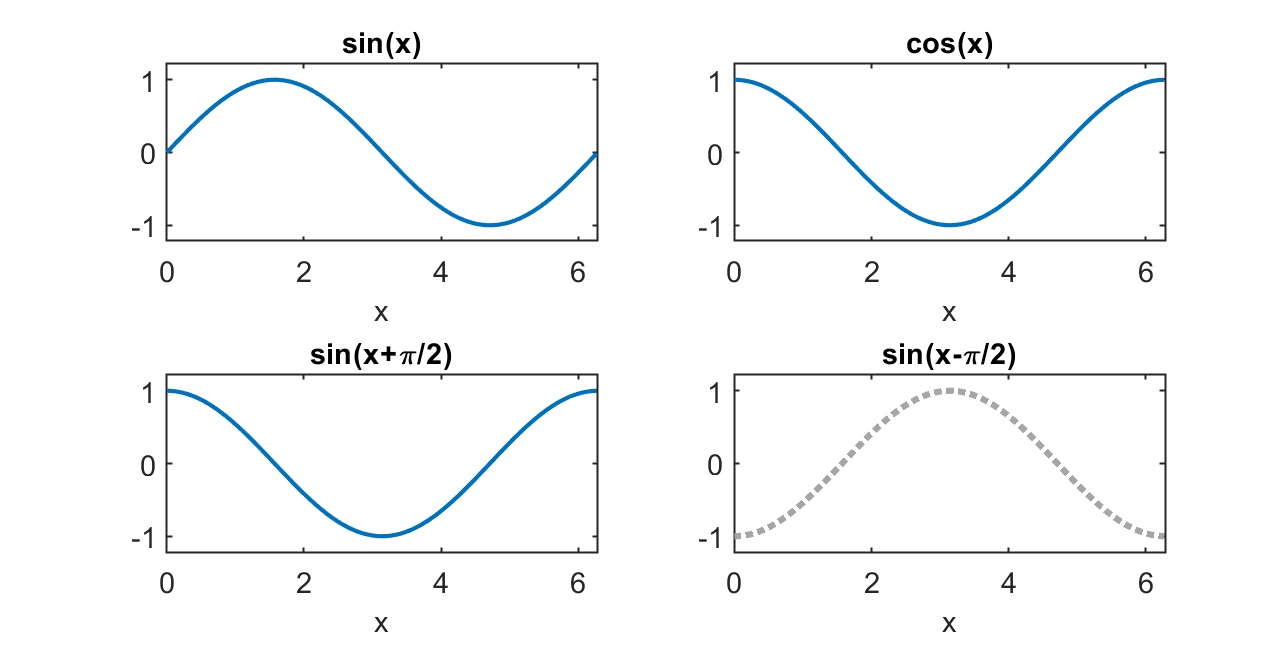
Podemos corrigir o gráfico envolvendo a derivada do sinal ruidoso incluindo a defasagem de $+90^o$ e vamos obter então:

>> close all
>> ezplot('sin(2*pi*1*t)+0.01*sin(2*pi*60*t)+0.007*sin(2*pi*120*t)+1E-3*sin(2*pi*4E3)+1E-3*sin(2*pi*20E3*t)+1E-3*sin(2*pi*40E3*t)',[0 2])
>> hold on
>> ezplot('cos(2*pi*1*t)+3.7699*cos(2*pi*60*t)+5.2779*cos(2*pi*120*t)+25.133*cos(2*pi*4E3)+125.66*cos(2*pi*20E3*t)+251.33*cos(2*pi*40E3*t)',[0 2])

Gráfico corrigido:

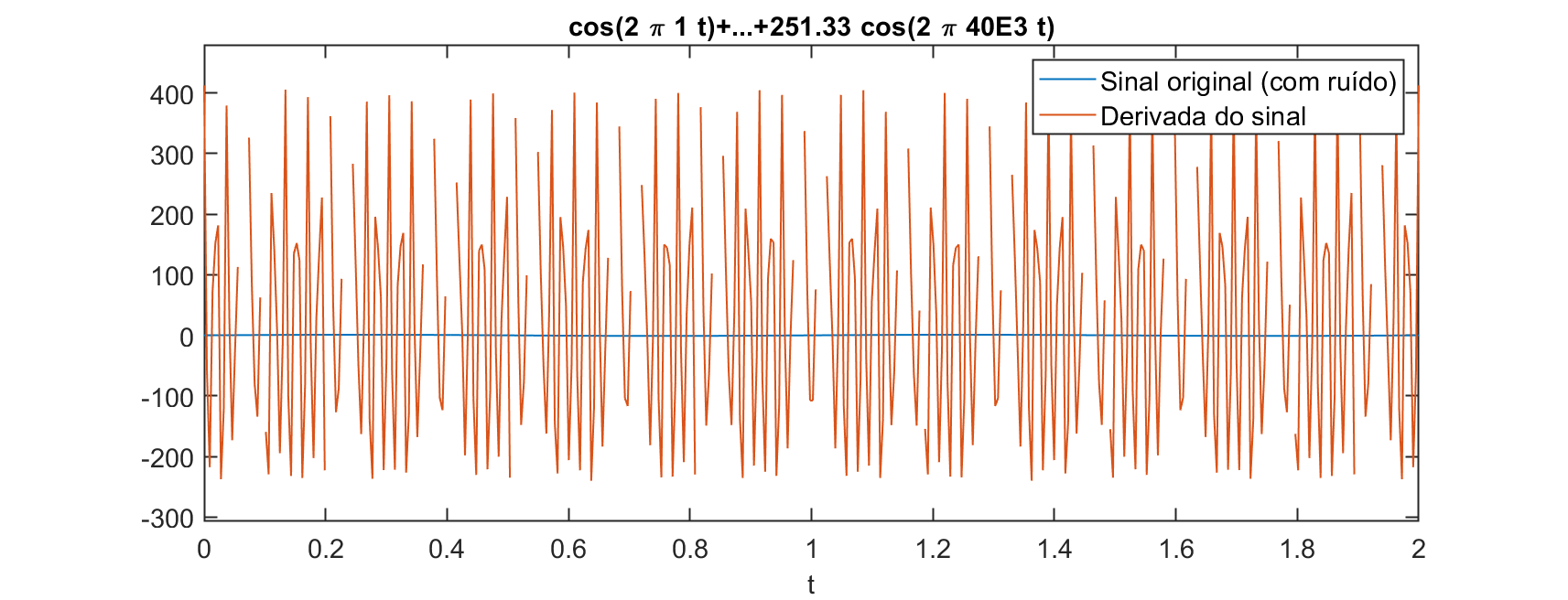
Porém perceba que o gráfico gerado desta forma pelo próprio Matlab possui descontinuidades entre certos períodos de tempo.

Note que eventualmente este último gráfico mão está tão correto assim, afinal de contas, você não indicou no comando ezplot() o incremento de tempo que o Matlab deveria ter adotado para gerar os pontos para traçar estes gráficos. Mas podemos tentar “forçar” o Matlab neste ponto.

Considere que o passo (ou incremento) para o variável t nas funções ezplot() anteriores deve ser muito menor que 1 segundo. Considere que dentro do intervalo de 1 segundo, um sinal senoidal de 40 KHz, possui 40.000 picos positivos. Então começa a parecer óbvio que não podemos simular este sinal usando como passo algo que gere 40.000 pontos num segundo, porque mesmo assim, estaríamos apenas calculando 1 ponto da onda senoidal de 40 KHz dentro de seu ciclo de trabalho. Raciocinando desta forma, é justo pensar que este passo deve ser muito menor. Vamos supor que queremos simular 10 pontos da onda senoidal de 40 KHz, então deveríamos variar este passo/incremento numa frequência $10 \times$ maior, ou seja, fazer varir o passo da variável t em 400 KHz. Mas como precisamos definir o valor deste passo em segundos e não em Hz, o valor do passo que deveríamos adotar neste caso, deveria ser de: $T_s=1/400.000$ . Fazendo este cálculo no Matlab e executando novamente os gráficos ezplot() considerando este passo teremos:

>> figure
>> Ts=1/400E3
Ts =
      2.5e-06
>> % Note: o incremento de tempo a ser usado corresponde a 2,5 ns
>> t=0:Ts:2;
>> ezplot('sin(2*pi*1*t)+0.01*sin(2*pi*60*t)+0.007*sin(2*pi*120*t)+1E-3*sin(2*pi*4E3)+1E-3*sin(2*pi*20E3*t)+1E-3*sin(2*pi*40E3*t)',[0:Ts:2])
>> hold on;
>> ezplot('cos(2*pi*1*t)+3.7699*cos(2*pi*60*t)+5.2779*cos(2*pi*120*t)+25.133*cos(2*pi*4E3)+125.66*cos(2*pi*20E3*t)+251.33*cos(2*pi*40E3*t)',[0:Ts:2])
>>

Infelizmente este novo gráfico resulta igual ao anterior. Descontinuidades ainda estão presentes. O "erro" se deve ao fato de que o Matlab quando comandado com ezplot(fun,[a,b]) realiza o gráfico para $fun(x)$ com $a < a < b$ ; mas note que o Matlab não permite especificar o passo/incremento exigido para a variável $x$ .

Consultando a documentação do Matlab, mesmo a função similar fplot(x,y,lims) não permite especificar o passo para incremento na variável $x$ . Então temos que partir para a “força bruta”, sintetizando o vetor $t$ da forma como queremos mais o sinal original com ruído e o sinal filtrado, realizando cálculos sobre o vetor $t$ gerado antes.

>> Ts=1/400E3
Ts =
      2.5e-06
>> t=0:Ts:2;
>> size(t)
ans =
           1      800001
>> % Note: agora foi gerado um vetor de +800.000 pontos
>> sinal_original=sin(2*pi*1*t)+0.01*sin(2*pi*60*t)+0.007*sin(2*pi*120*t)+1E-3*sin(2*pi*4E3)+1E-3*sin(2*pi*20E3*t)+1E-3*sin(2*pi*40E3*t);
>> size(sinal_original)
ans =
           1      800001
>> derivada_sinal=cos(2*pi*1*t)+3.7699*cos(2*pi*60*t)+5.2779*cos(2*pi*120*t)+25.133*cos(2*pi*4E3)+125.66*cos(2*pi*20E3*t)+251.33*cos(2*pi*40E3*t);
>> size(derivada_sinal)
ans =
           1      800001
>> figure; plot(t,derivada_sinal,'r-', t,sinal_original,'b-')

O que resulta no gráfico:

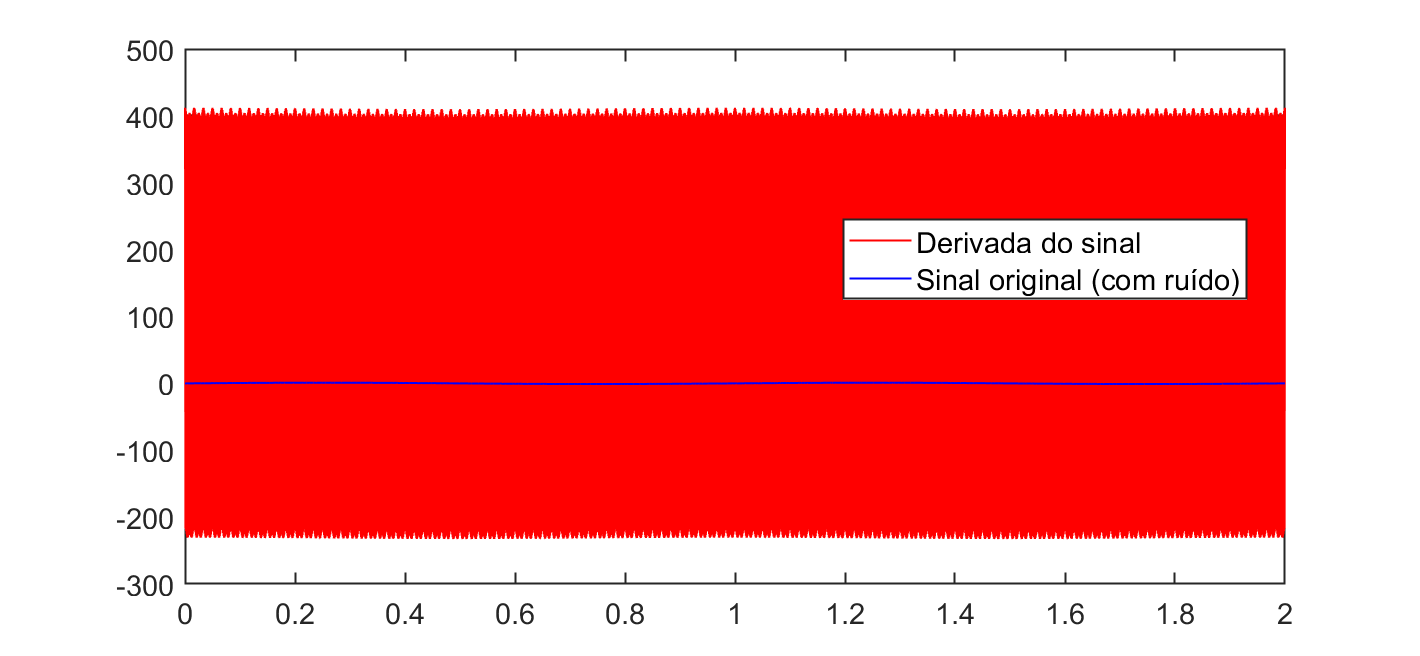
Obs.: na sequencia de entrada dos vetores para o plot() do último gráfico, propositalmente foi invertida a ordem de exibição das 2 curvas, caso contrário, o gráfico da derivada do sinal iria "tampar" completamente o gráfico do sinal original (com ruído).

Fica mais nítido neste último gráfico que a amplitude do sinal derivado oscila entre -200 até +400 Volts.

Esta falta de "simetria" em relação à tensão nula (referência = zero) se deve ao fato de que coincidiu que no momento de compor o somatório de ondas cossenoidas, mais picos positivos de sinais ocorreram que somas de picos negativos. Lembrar que a derivada do sinal que estamos plotando se assemelha (quase), a uma Série de Fourier, que na realidade preconiza que o sinal qualquer pode ser composto realizando um somatório de ondas cossenoidas com ondas senoidasis (ou mais simples: somas de ondas senoidas com diferentes defasagens), onde as frequênicas dos cossenos e senos correspondem às harmônicas deste sinal:

f(t)=\dfrac{1}{2}a_0 + \sum_{n=1}^{\infty} a_n \, \cos(n \, t) + \sum_{n=1}^{\infty} a_n \, \sin(n \, t)

ou:

f(t)=\dfrac{1}{2}a_0 + \sum_{n=1}^{\infty} a_n \, \cos(n \, t - \varphi_n)

onde $\varphi$ representa o deslocamento de fase para determinando componente (frequencia) do sinal.

Sobre Séries de Fourier ver:

Wolfram MathWorld: Fourier Series.

Wikipedia: Fourier series

Voltando ao nosso gráfico, fica evidente que o sinal de alta frequência foi bastante amplificado, fato que cria uma "cortina" vermelha de fundo no gráfico anterior; como a frequência é elevada, não percebemos mais os 40.000 pontos/ciclo $\times$ 2 ciclos (2 segundos).

Realizando um "zoom" sobre um pequeno intervalo de tempo para figura anterior:

>> % 10 ciclos onda 40 Khz:
>> periodo_tempo=10*1/40E3
periodo_tempo =
      0.00025
>> pontos=periodo_tempo/Ts
pontos =
   100
>> plot(t(1:pontos),derivada_sinal(1:pontos),'r-', t(1:pontos),sinal_original(1:pontos),'b-')
>> % notar que este gráfico não é muito elucidativo, melhorando um pouco...
>> figure;
>> subplot(211);
>> plot(t(1:pontos),derivada_sinal(1:pontos),'r-', t(1:pontos),sinal_original(1:pontos),'b-')
>> legend('Derivada do sinal', 'Sinal original (com ruído)')
>> grid
>> sinal_puro=sin(2*pi*1*t);
>> subplot(212);
>> plot(t(1:pontos),sinal_original(1:pontos),'b-', t(1:pontos),sinal_puro(1:pontos),'k--')
>> title('Sinal original (com ruído)')
>> grid

Segue o novo gráfico com um "zoom" mostrando os primeiros 250 ns do sinal original (com ruído) $\times$ sua derivada.

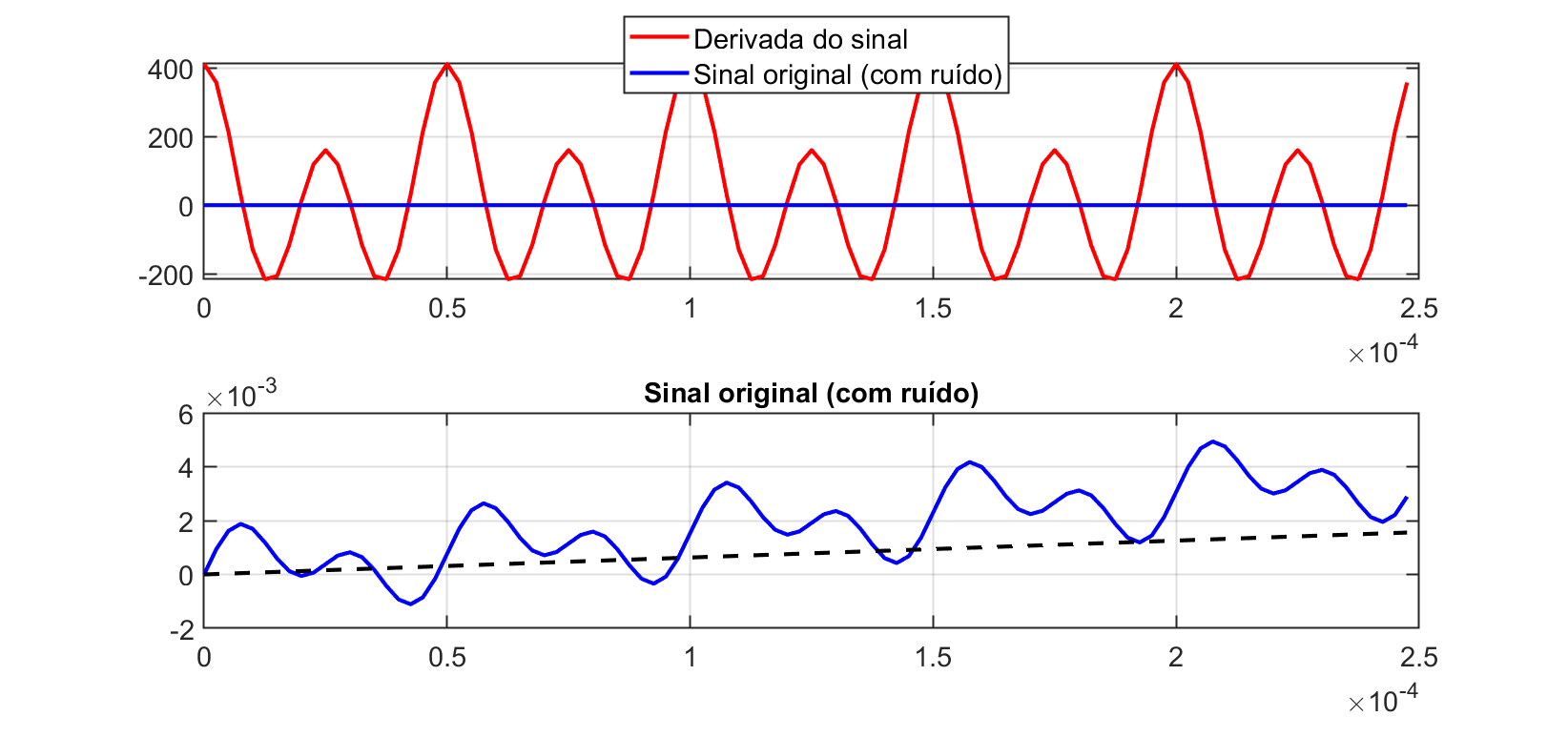
Note que estes últimos gráficos são bem mais “precisos”, mas seu resultado não desmente o que ocorre quando se tenta aplicar derivada pura num sinal com ruído.

Solução para a Derivada de Sinal ruidoso?

É por este motivo que o circuito de um amplificador operacional derivativo puro é modificado para limitar o ganho para componentes de alta frequência. Entenda que o problema não é realizar a derivada, mas limitar o ganho para componentes de alta frequência. E esta limitação pode ser realizada, incorporando um Filtro passa baixas na malha de realimentação derivativa do circuito com amplificador operacional. Isto também significa que é o próprio usuário deste circuito que deve saber indicar até que frequência do sinal do entrada deseja realizar uma derivada? Na área de controle, é comum sistemas reais trabalharem na banda de frequência de 0,01 Hz até 10 Hz. Então é importante acrescentar um filtro passa baixas, acima da frequência máxima. Com isto, já estaríamos limitando o ganho aplicado por este novo circuito, até para o ruído da rede ocorrendo nos 60 Hz, já que se supõe que componentes nesta frequência e frequências superiores não correspondem a variações rápidas de resposta do próprio processo sobre o qual se queira aplicar uma ação derivativa.

Por exemplo, um circuito com ação derivativa até os 20 Hz resultaria em algo como:

>> G=tf(2*pi*20*[1 0],[1 2*pi*20])

G =
 
   125.7 s
  ---------
  s + 125.7

>> % o "ganho" de 125.7 = 2*pi*20 é necessário para resultar 0 dB em 1 rad/s.
>> bode(G)
>> grid

E agora temos o gráfico:

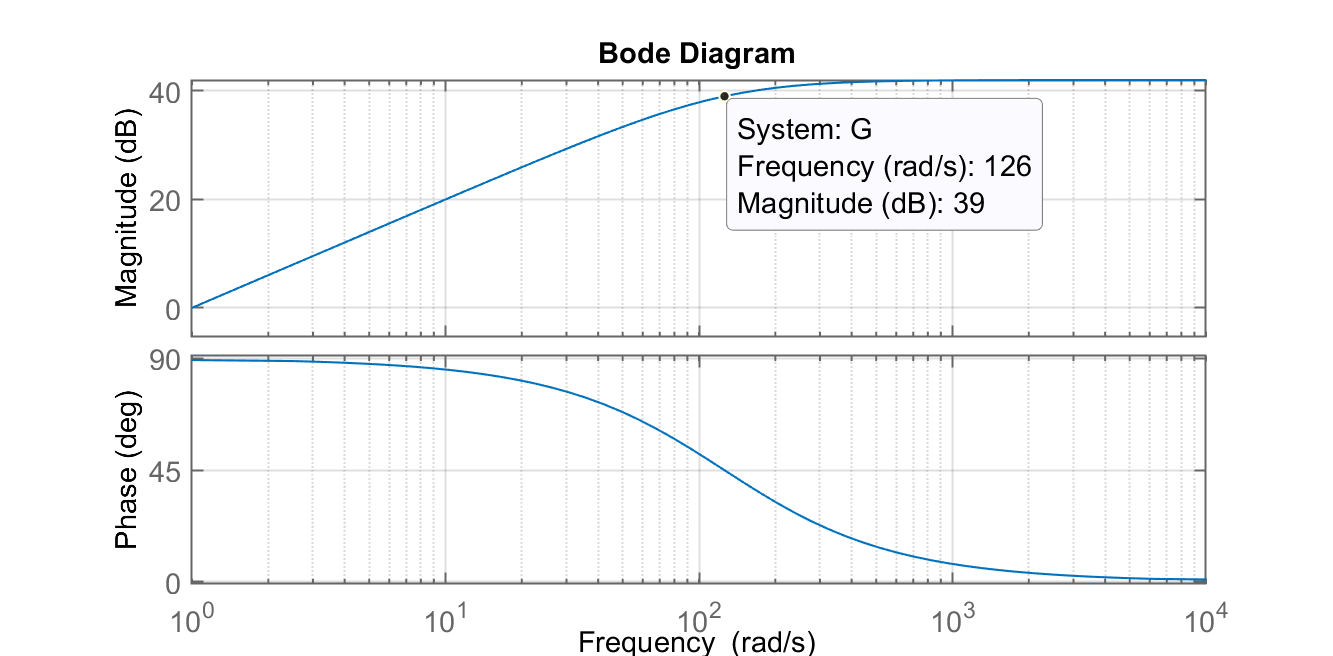
Note que a partir dos 20 Hz (125,6 rad/s), o ganho deste circuito fica limitado à 40 dB. Isto significa, que este ultimo circuito, realiza derivada sobre sinais de entrada até a faixa de 20 Hz (neste caso). O melhor seria até incluir um filtro duplo (de 2a-ordem = -40 dB/déc) na frequência de 20 Hz, para forçar uma queda de -20 dB/déc na amplitude dos ruídos (frequências superiores à 20 Hz).

Um circuito derivador real, ficaria ainda mais interessante, se além de apenas limitar o ganho à partir de derterminada frequência, atenuasse o ganho para altas frequências, resultado num Diagrama de Ganho semelhante ao mostrado à seguir:

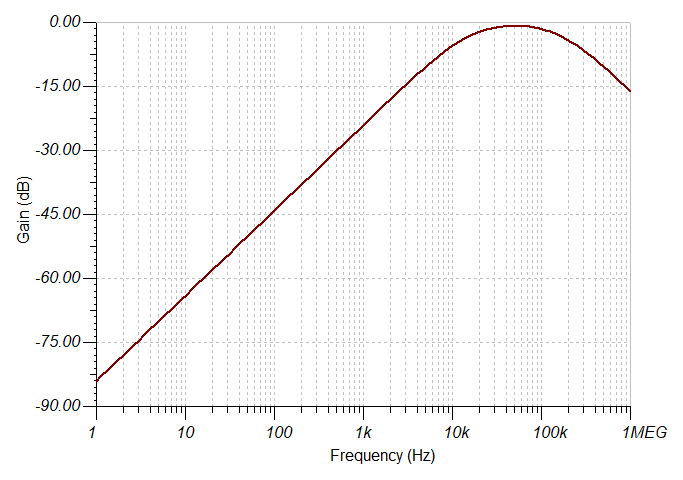
Isto pode ser obtido escolhendo um valor apropriado para o capacitor C $_2$ no circuito apresentado antes na fig 1 (b). Para se aprofundar mais, se sugere a leitura de “EDN: The practical op-amp differentiator is quite versatile”.

Fim.

Prof. Fernando Passold, em 10/11/2022.