Trabalho sobre Diagramas de Bode

Sugere-se ler antes o tópico:

• Diagramas de Bode: https://fpassold.github.io/Controle_1/Diagramas_Bode_1.pdf

e opcionalmente:

• Exemplo de uso com Matlab: https://fpassold.github.io/Controle_1/testes_bode_1.html
• A Tool for Construction of Bode Diagrams from Piecewise Linear Asymptotic Approximations, Erik Cheever and YueLi: https://www.ijee.ie/OnlinePapers/Interactive/Cheevers/EACWebPaper/ , associado com a ferramenta BodePlotGui (ver mais abaixo).

Itens do Trabalho

1. Traçar os diagramas de Bode para as funções transferência abaixo:

   a) $G_a(s)=\dfrac{20\,s}{s+10}$

   b) $G_b(s)=\dfrac{2000s+4000}{s^2+220s+4000}$

   c) $G_c(s)=\dfrac{40}{s^2+0,5s+40}$

   d) $G_d(s)=\dfrac{s^3+2001s^2+1.002.000s+1.000.000}{10s^3+2100s^2+120.000s+1.000.000}$

   Observações:

   1. Relacionado à cada diagrama de Bode deve ser mostrado:

      a) O cálculo (determinação) da "linha de base" (ganho de "partida" ou ganho DC);

      b) As frequências e assíntotas associadas com cada pólo e zero da função transferência (indicar taxa de aumento ou redução do ganho; o mesmo para o diagrama de fase)

      c) No caso de pólos ou zeros complexos, deve ser calculada ainda a frequência do pico da ressonância ($\omega_n$) e determinado o valor do ganho ou atenuanção que ocorre nesta frequência (eventualmente o fator de amortecimento, $\zeta$, pode ser mostrado).

   2. Você pode usar as ferramentas:

      • echeever/BodePlotGui (ou baixar diretamente de https://github.com/echeever/BodePlotGui)
      • https://github.com/milanofthe/Interactive_BodePlot
      • https://en.wikipedia.org/wiki/Bode_plot

    

2. Seja uma onda senoidal oscilando na frequência de 1 Hz @ 1,0 Vpp (Volts de pico (amplitude da senoide). Se este sinal passar pelo filtro representado pela função: $H(s)=G_c(s)=\dfrac{40}{s^2+0,5s+30}$ Este sinal será atenuado (ganho negativo em dB) ou incrementado (ganho positivo em dB).

   Justificar a resposta realizando cálculos e apresentando uma simulação no tempo mostrando o sinal orignal (em linha tracejada) e como fica o sinal filtrado (linha contínua). Esperado um gráfico como:

   

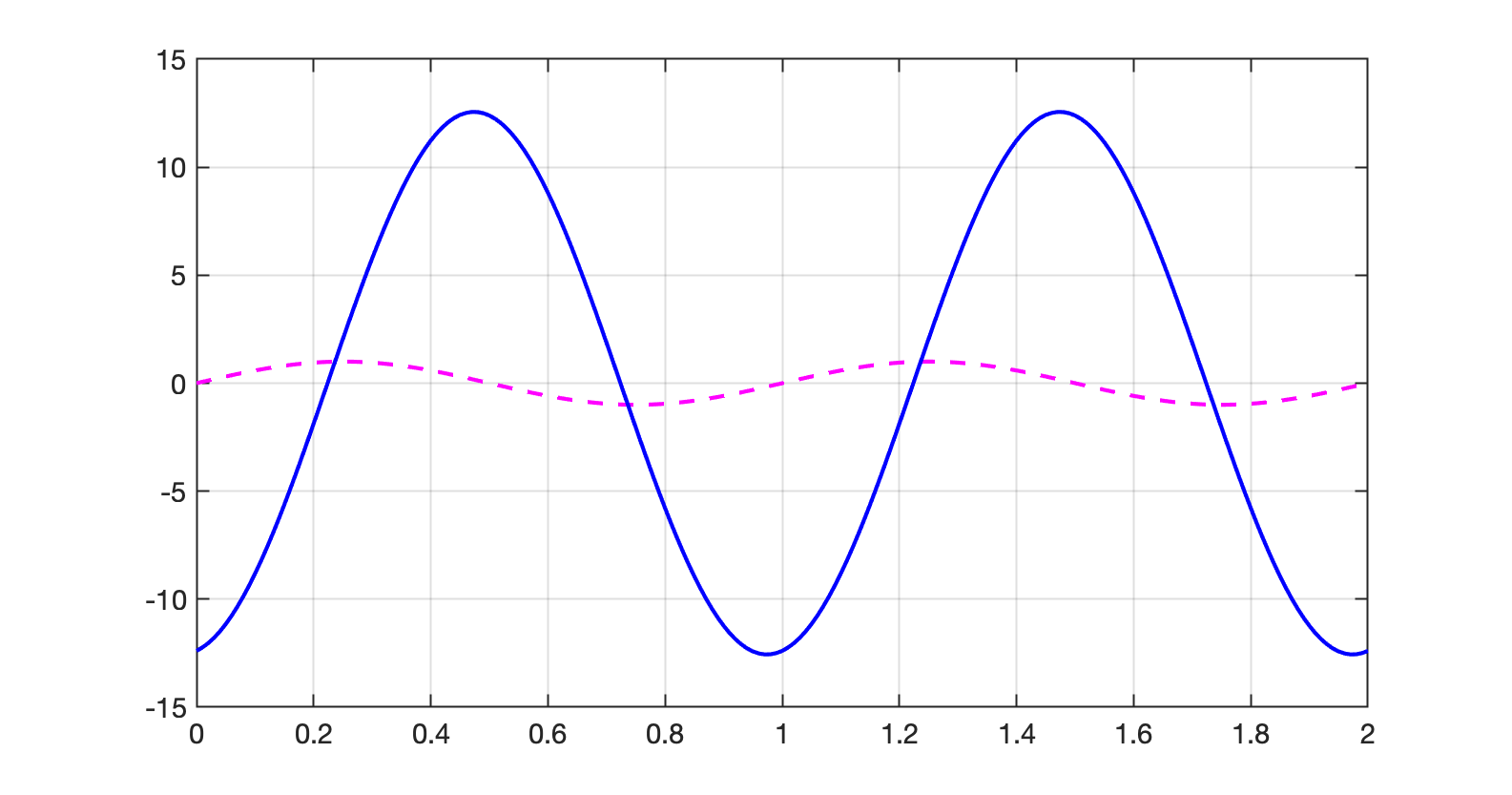
   Obs: resposta válida apenas se demonstrar o cálculo do ganho e defasagens sofridos pela senóide quando a mesma passar por este filtro. Adicionalmente pode ser apresentado o diagrama de Bode correspondente à este filtro.

   Dica: eventualmente, vocé pode usar os comandos:

   xxxxxxxxxx
   >> h=bodeplot(H);
   >> setoptions(h,'FreqUnits','Hz','MagUnits','abs')
   

   Para gerar o diagrama de Bode com frequência variando em Hz ao invés de rad/s e para mostrar as magnitudes em valores absolutos (aon invés de ser em dB).

    

3. Suponha agora que certos sinais passarão pelo filtro cuja equação é mostrada abaixo: $\begin{array}{rcl}H(s)=G_d(s)&=&\dfrac{s^3+2001s^2+1.002.000s+1.000.000}{10s^3+2100s^2+120.000s+1.000.000}\\&=&\dfrac{s^3 + 2001 s^2 + 1.002e06 s + 1e06}{10 s^3 + 2100 s^2 + 120000 s + 1e06}\\&=&\dfrac{0.1 (s+1000)^2 (s+1)}{(s+100)^2 (s+10)}\end{array}$

   Mostre (demonstrando cálculos e valores encontrados) o que acontece quando os seguintes sinais passam por este filtro:

   a) Senóide de 30 Hz @ 1,0 Vpp; (este sinal será amplificado ou atenuado? Demonstrar com cálculos)

   b) Senóide de 80 Hz @ 1,0 Vpp; (este sinal será amplificado ou atenuado? Demonstrar com cálculos)

   c) O sinal agora é composto pela soma de 2 senóides: $x_1(t)$ oscilando à 30 Hz @ 0,4 Vpp $+$ $x_2(t)$ oscilando à 80 Hz @ 0,4 App. Neste caso em particular, mostre num gráfico a composição do sinal $x(t)=x_1(t)+x_2(t)$ (3 curvas diferentes devem aparecer devidamente identificadas através de uma legenda). Mostre depois num segundo gráfico, como fica este sinal $x(t)$ depois de passar pelo filtro $-$ sugere-se mostrar o impacto do filtro causado no sinal $x_1(t)$ e o mesmo em relaçao ao sinal $x_2(t)$. Dica: Vocé terá que calcular o ganho/atenuação ($G_1$ e $G_2$) e defasagens angulares ($\phi_1$ e $\phi_2$) aplicados pelo filtro em cada sinal e usar estes valores para sintetizar o sinal na saída do filtro, algo como: $y_1(t)=G_1 \cdot 0,4 \cdot \sin{(2\pi \cdot 30 \cdot t + \phi_1)}$, o meso para $y_2(t)$ e depois calcular $y(t)=y_1(t)+y_2(t)$. O resultado deve ser algo semelhante à:

   

    

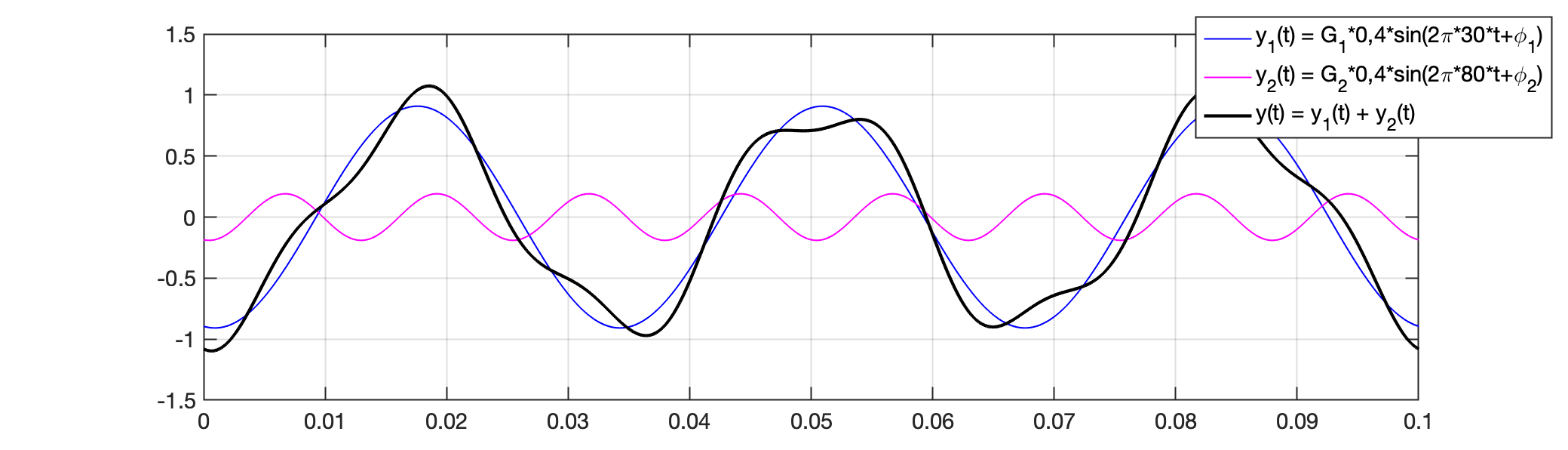
   Adicionalmente vocé pode apresentar o Diagrama de Bode deste sinal e apontar na figura o que acontece com cada sinal, além de mostrar e realizar outros cálculos para justificar o que se pede nos items (a), (b) e (c).

Anexo

i. Cálculo de Ganhos e Defasagens

Você pode calcular os ganhos e defasagens sobre cada sinal aplicando equações como mostrado abaixo:

x
>> f=____       % é aqui que você entra com o valor desejado
>> w=2*pi*f     % transformando freq de entrada f (em Hz) para (rad/s)
>> s=j*w        % ponto no plano-s (depende da frequência)
>> G=(s^3+2001*s^2+1002000*s+1E6)/(10*s^3+2100*s^2+120E3*s+1E6) % Função Gd(s)
G = 
    -0.39534 - 2.2365i
>> % Note que Matlab retorna número complexo (como esperado)
>> ganho=abs(G) % calculando magnitude (valores absolutos)
ganho =
    2.2712
>> fase_rad=angle(G) % defasagem (resulado em rad/s)
fase_rad =
    -1.7458
>> fase_deg=rad2deg(fase_rad) % defasagem em ângulo decimal
fase_deg =
    -100.02

ii. Diagramas no tempo (simulação dos sinais)

Para simular os gráficos do sinal de entrada $x(t)$ e sinal de saída num filtro $y(t)$, você pode fazer:

xxxxxxxxxx
>> T=1/f                % período do sinal de entrada acontece na frequencia f
>> t=0:T/100:1.5*T;     % gera vetor t, de 0 até 1,5 ciclos sinal entrada, 100 amostras/ciclo
>> x=1.0*sin(2*pi*f*t); % sintetiza onda de entrada, vetor x(t)
>> y=ganho*1.0*sin(2*pi*f*t+fase_rad); % sintetiza onda de saída, y(t)
>> figure; plot(t,x,'m--', t,y,'b-')

Que gera algo como: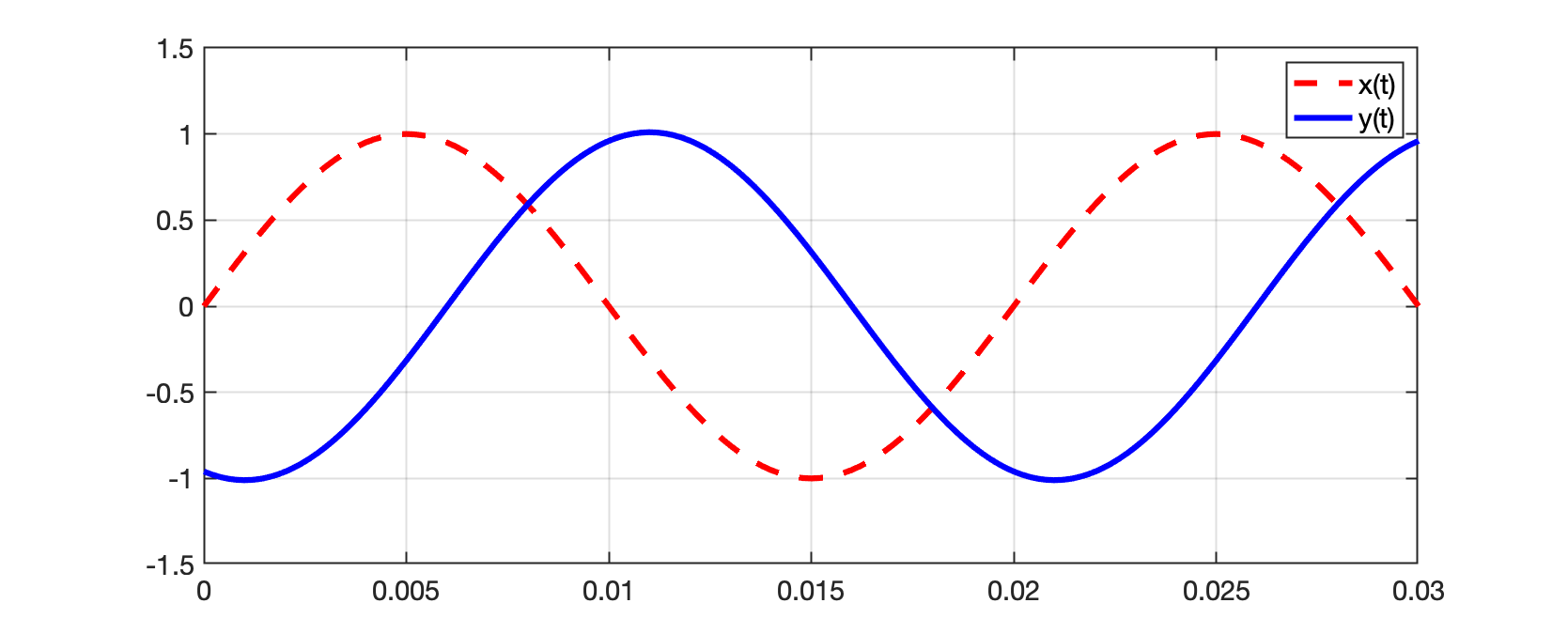

Fernando Passold @ 2025/1.