Intro::RNs
Intro::RNsIntrodução2.1 Redes Neurais ArtificiaisInspiração biológica...Modelo de Nerônio...Funções Ativação...Tipos (topologias) de RNs...Aprendizado supervisionado e não-supervisionadoRede MLP ou Back-PropagationRegra de Aprendizado Delta Generalizado...Treinamento...Épocas de treinamento...Taxa de Aprendizado e Momentum…Inicialização da rede..."Energia" da rede durante treinamento...Mínimos locais globais...Treinando uma rede...Dimensões da rede MLP...Qualidade conjunto de treinamento...Backpropagation em redes com várias camadas invisíveisRNs pré-treinadasMais Referências:
Introdução
Introdução à RNs, extraído de:
- Passold, Fernando, Cap 2.1 Redes Neurais Artificiais, pp 25—44, In: Sistema especialista hibrido em anestesiologia para pacientes criticos/problematicos, Dissertação (Mestrado), Preograma de Pós-Graduação em Engenharia Elétrica, UFSC, 209 p., 1995, URL: https://repositorio.ufsc.br/xmlui/handle/123456789/111563
Implementação (codificação) baseada nas referências:
- ALEKSANDER, I., MORTON, H., An Introduction to Neural Computing. London (UK): Chapman & Hall, 1990, p. 22-159.
- MAREN, A. J., 7. Multilayer Feedforward Neural Networks I: Delta Rule Leaming, In: -, HARSTON, C. T., PAP, R. M. (eds.), Handbook of Neural Computing Applications. San Diego (California): Academic Press, Inc., Cap. 7, p. 85-105, 1990a.
- MAREN, A. J., Neural Network Structures: Form Follows Function, In: -, HARSTON, C. T., PAP, R. M. (eds.), Handbook of Neural Computing Applications. San Diego (Califomia): Academic Press, Inc.,Cap. 4, p. 45-57, 1990b
- LAWRENCE, J., Introduction to Neural Networks and Expert Systems, Nevada City (Califórnia): California Scientific Software, 1992.fornia Scientific Software, 1992.
- KNIGHT, K., Comectionist, Ideas and Alogorithms, Communications of the ACM, v. 33, n. 11, p. 59-74, November, 1990.
Obs.: o livro Handbook of Neural Computing Applications, pode ser encontrado (para consulta), no site: https://archive.org/details/handbookofneural0000mare (acessado em 14/03/2025). Este livro estava disponível na Biblioteca Central da UFSC. Ou tente aqui. 👈📘
2.1 Redes Neurais Artificiais
Inspiração biológica...
Redes neurais artificiais são biologicamente inspiradas. Um neurônio biológico consiste de um núcleo, axônio e dendritos. As junções entre neurônios constituem as sinapses. Um neurônio artificial, ou elemento processador (processing element, PE), modela os axônios e dendritos de sua contraparte biológica através de conexões e as sinapses utilizando ponderações ou pesos de ajuste. A figura 4 mostra dois neurônios biológicos interconectados através de sinapses.
| Figura 4: Células nervosas ou neurônios interconectados (ALEKSANDER, 1990). |
|---|
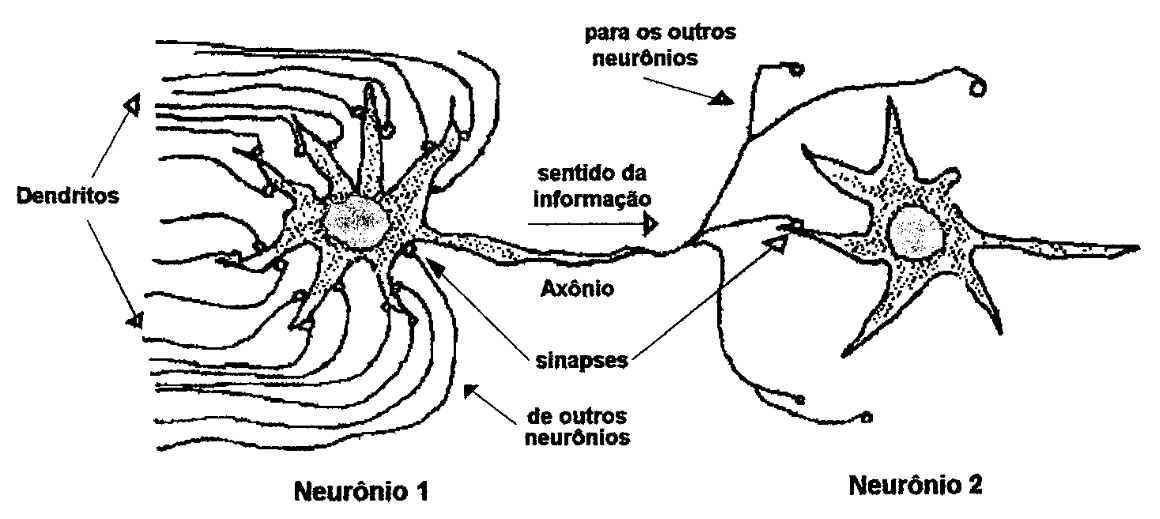 |
Todos os sinais que constantemente chegam a um neurônio via dendritos (que podem ser considerados como canais de entrada) são somados e quando esta soma atinge um certo limiar, faz com que o neurônio dispare um sinal para os outros, via axônio (que pode ser comparado a um canal de saída). A soma dos sinais é realizada no núcleo. Através de sinapses, (conexões com outros neurônios), os dendritos recebem sinais inibitórios ou excitatórios. As sinapses regulam a forma como a informação passa pelos neurônios, biologicamente através de uma forma de comunicação química realizada por transmissores químicos ou melhor, neurotransmissores (LAWRENCE, 1992; GANONG, 1973; GUYTON, 1973).
Cada célula nervosa possui um "encaixe" de entrada para suas informações, ou seja, não é qualquer informação presente na sua entrada que se propaga para a saída. É necessário uma combinação correta de receptores nervosos com transmissores nervosos. Uma vez que este encaixe tenha sido feito de maneira eficaz, esta célula dispara, ou seja, propaga a informação para o próximo neurônio, liberando seus neurotransrnissores. A eficácia deste encaixe é determinada pela presença em quantidade suficiente do neurotransmissor correto na conexão nervosa. Dependendo da compatibilidade com o neurotransmissor, a saída de um neurônio pode excitar ou inibir a entrada de outro, numa seqüência complexa de encaixes - maiores detalhes são explorados em LAWRENCE (1992) e GANONG (1973).
Numa rede neuronal biológica, as várias células nervosas que a compõem, ajustam suas sinapses primeiramente baseado no seu genótipo (informações presentes no DNA das células de qualquer organismo vivo desde o momento de seu nascimento) e posteriormente através do treino ou aprendizado ao longo da sua vida. No decorrer da vida de um organismo vivo, novas conexões são realizadas enquanto outras são ajustadas (de modo inibitório ou excitatório), caracterizando o que se conhece como o aprendizado.
O cérebro humano é uma intrincada rede neuronal composta por mais de 100 bilhões de células nervosas (l00.000.000.000 ou ) com mais de 10 quatrilhões de interconexões (ou sinapses) (LAWRENCE, 1992; OLIVEIRA, 1991; SOUCEK, 1989; WALNUM, 1993). Algumas evoluíram com o tempo, caracterizando o que se conhece como aprendizado, outras já vieram de "fábrica" (no nosso genoma por exemplo, o sistema nervoso central). Muitos processos cognitivos humanos não levam mais do que poucas centenas de milisegundos, enquanto que isoladamente os neurônios do cérebro humano processam informações numa velocidade tão baixa quanto a execução de uma simples instrução num computador digital. O elevado poder de processamento do cérebro humano advém do seu massivo processamento paralelo .
[1]: Atualmente, a simulação digital (computacional) de redes neurais (tecnologia também conhecida como neurocomputação, se restringe a atualizar os sinais entre cada neurônio artificial de maneira discreta, e não contínua e concorrentemente como ocorre no modelo biológico real (OBERMEIER, 1989; SOUCEK, 1989).
Verificar se isto continua válido para computadores NeuroTrópicos...
Modelo de Nerônio...
Um modelo de rede neural artificial é caracterizado pelos seus neurônios (ou elementos processadores) isoladamente, as conexões entre eles (arquitetura ou topologia da rede) e seu esquema de aprendizado (MAREN, 1990; LAWRENCE, 1992).
Uma rede neural artificial pode ser comparada a um grafo orientado composto por um certo número de nós ou elementos processadores interconectados que operam em paralelo. Cada elemento processador (ou neurônio artificial) possui um certo número de entradas e somente um único sinal de saída que se propaga pela através das conexões com os outros elementos processadores. A cada entrada de um elemento processador está associado um peso "sináptico" que pode ser excitatório (positivo) ou inibitório (negativo), normalmente variando de à . A figura 5 mostra um modelo de neurônio artificial. O sinal de entrada pode assumir uma variação contínua (desde -1 até +1) ou discreta (restrito aos valores binários ou O ou l). Um valor contínuo poderia significar o grau de veracidade (ou possibilidade) associado a uma entrada, e no caso discreto, se a entrada é falsa ou verdadeira (LAWRENCE, 1992).
[3]: Este "grafo" é implementado nos dias atuais na forma de "tensores" derivando a famosa biblioteca
tensorflow…. Complementar…
| Figura 5: Neurônio artificial simplificado (ou PE). |
|---|
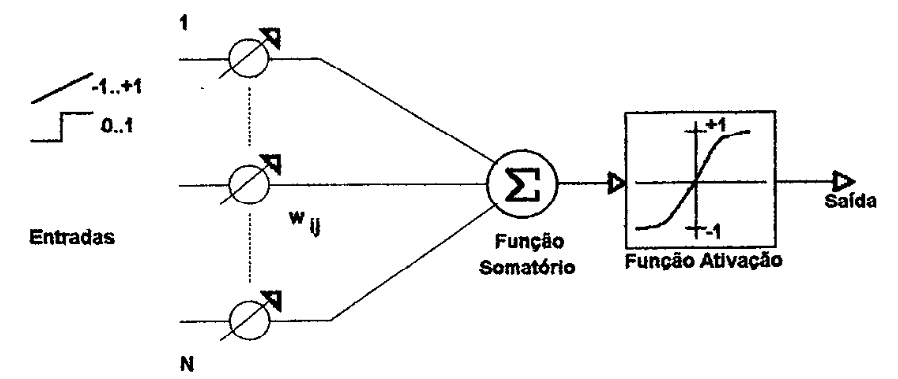 |
O elemento processador avalia seus sinais de entrada realizando um somatório ponderado das suas entradas (através dos pesos sinápticos associados a cada entrada), seguindo a equação:
onde: . representa a soma ponderada dos sinais (conexões) de entrada do neurônio , representa o valor do peso sináptico associado à conexão entre o neurônio e e , representa a saída do ésimo neurônio. De uma maneira mais simplificada, isto significa somar todos os sinais de entrada que chegam a um neurônio levando em consideração o peso das conexões envolvido em cada sinal de entrada.
O sinal de saida do elemento processador é encontrado aplicando-se o somatório ponderado das suas entradas numa função ativação que determinará seu valor de saída (nível de ativação):
onde: função ativação do neurônio .
Entrada de Bias: alguns modelos de RNs MLP consideram uma entrada fixa com valor , associada com um peso sináptico. Neste caso, a eq. (2) anterior seria modificada para:
onde peso sinático associado com a entrada de "bias".
Funções Ativação...
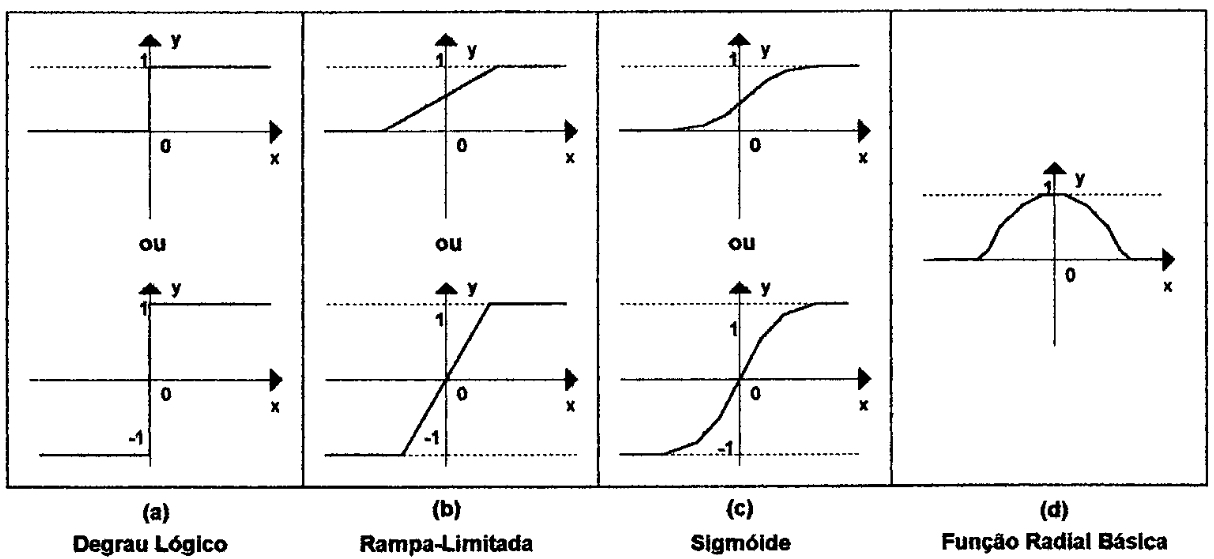
A figura 6 ilustra algumas formas de função ativação ou função transferência de um neurônio. Esta função pode caracterizar o neurônio em linear ou não-linear. O modelo não-linear mais simples está mostrado na figura 6(a), nestes caso quando o somatório ponderado de suas entradas atinge um certo valor (threshold), normalmente zero, este neurônio "dispara", é ativado - este modelo mais simples é também conhecido como perceptron ou neurônio binário (KNIGHT, 1990; MAREN, 1990).
| Figura 6: Típicas funções transferências empregadas em redes neurais (MAREN, 1990). |
|---|
 |
Obs.: Atualmente existem mais funções transferência. Por exemplo: ReLU, Leaky ReLU, Sigmoid, Tanh, Softplus, ELU, SELU, Swish e GELU. Recomenda-se assistir ao video no YouTube: A Review of 10 Most Popular Activation Functions in Neural Networks, Machine Learning Studio, 25 fev 2023, 13.625 visualizações (acessado 01/03/2025), 15:58.
A função sigmóide é normalmente a mais utilizada nos neurônios não lineares (KNIGHT, 1990; MAREN, 1990; LAWRENCE, 1992), a sua saida é proporcional à soma ponderada das suas entradas, e é a que mais se aproxima da função ativação de um neurônio real (LAWRENCE, 1992; GANONG, 1973). A tabela 1 faz uma comparação entre um neurônio biológico e um neurônio artificial.
| Rede neural natural ou biológica | Rede neural artificial (RNA) |
|---|---|
| Dendritos | Pontos de entrada (inputs) |
| Axônios | Elementos de saída (output) |
| Núcleo | Elemento processador (PE) |
| Conexão inibitória | Peso negativo associado à conexão |
| Conexão excitatória | Peso positivo associado à conexão |
| Neurotransmissor | Valor positivo ou negativo propagado |
| Somatório das entradas | Função somatório das entradas |
| Ativação do neurônio | Função ativação (ou função transferência) |
Uma rede neural completa é organizada na forma de camadas. Uma rede neural pode possuir neurônios na camada de entrada, neurônios na camada seguinte e assim sucessivamente até a camada final, de saída. Uma rede com mais de uma camada pode ser caracterizada como uma rede multicamadas.
<Faltou alguma figura!?>
Tipos (topologias) de RNs...
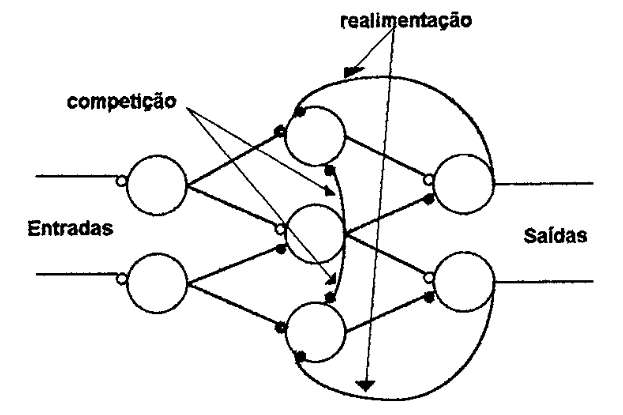
A forma pela qual os neurônios estão conectados uns aos outros (topologia ou arquitetura da rede) causa um enorme efeito na operação da rede neural. Sua topologia determina o tipo de processamento que irá acontecer. Algumas redes possuem elos de realimentação e outras não. Outras estruturas de redes podem envolver conexões inibitórias entre um neurônio e o restante dos outros naquela camada, minimizando o número de neurônios ativos numa espécie de competição (LAWRENCE, 1992; MAREN, 1990; OBERMEIER, 1989; ALEKSANDER, 1990). As vezes ainda, ocorrem redes ondes os neurônios da camada de saída atuam como entradas dos neurônios da camadalanterior. A figura 7 mostra uma rede neural com elos de realimentação e competição. Realimentações estão presentes em redes do tipo Hopfield (LAWRENCE, 1992; LIPPMAN, 1987; KNIGHT, 1990). Estruturas de competição estão presentes em redes do tipo Kohonen e counter-propagatíon (LAWRENCE, 1992).
| Figura 7: Rede neural com conexões de realimentação e competitivas (LAWRENCE, 1992). |
|---|
 |
A figura 8 apresenta algumas estruturas de redes neurais. Uma rede back propagation é como a da figura 8(a), a da figura 8(b), uma rede do tipo Hopfield, a figura 8(c) representa uma rede BAM (Bidirectional Associatíve Model) (LAWRENCE, 1992; MAREN, 1990).
| Figura 8: Estruturas de redes neurais (MAREN, 1990). |
|---|
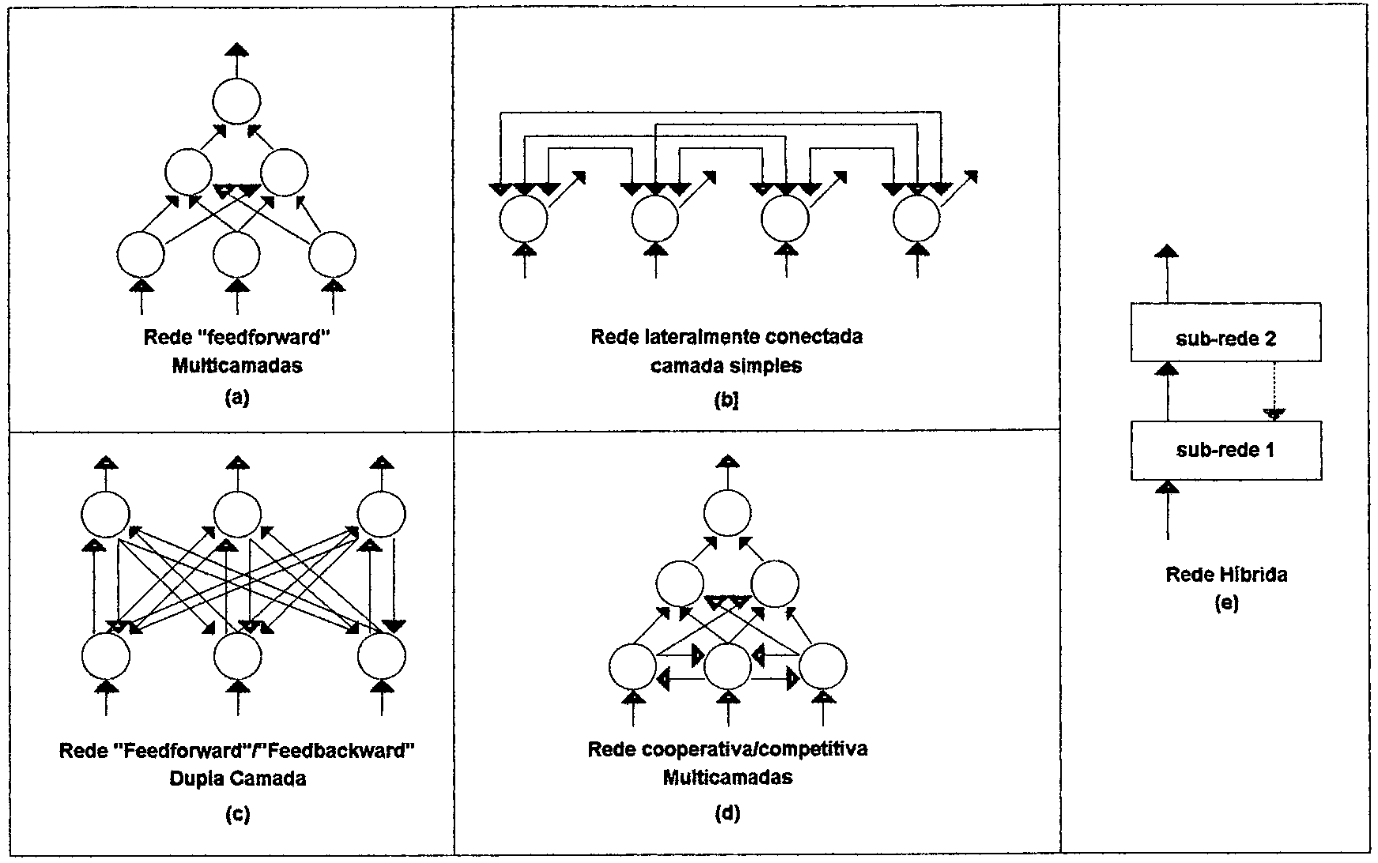 |
Como demonstrado na figura 8 existem dois tipos de ideias básicas em arquiteturas de redes. De maneira simplificada, se a saída de um neurônio não depende nunca de valores anteriores, a rede é dita feedforward, os seus sinais se propagam num único sentido e as saídas dependem somente dos sinais que estão chegando dos outros neurônios - não há laços neste sistema (MAREN, 1992). Uma vez treinadas, estas redes produzem sempre o mesmo resultado de saída para a mesma entrada (LAWRENCE, 1992).
Em redes retropropagadas ou feedback, a saída de um neurônio está sempre relacionada a algum valor prévio de saída da rede, existem laços de realimentação entre um neurônio e outro.
Obs.: Atualmente existe muito mais estruturas/arquiteturas de redes neurais, ditas "modelos". Consultar:
- DeepAI Docs: Glossary (acessado em 13/03/2025).
- Neural Networks as Cybernetic Systems (3rd and revised edition) - Part 2 — Brains, Minds & Media (Bielefeld University, Germany, 1990; acessado em 13/05/2025)
Aprendizado supervisionado e não-supervisionado
E finalmente as redes neurais podem ainda ser classificadas pelo seu algoritmo (ou regra) de aprendizado que normalmente ou é supervisionado ou não-supervisionado (KNIGHT, 1990; MAREN, 1990; LAWRENCE, 1992).
No método de aprendizado supervisionado, se fornece à rede pares de entrada e saída casados isto é, para cada entrada é apresentado a saida esperada e a rede monitora a si própria corrigindo associações incorretas através de um processo de realimentação pela rede (correção dos pesos sinápticos). Este método caracteriza o que os psicólogos classificam como aprendizado associativo (LAWRENCE, 1992). Já uma rede não- supervisionada não possui acesso à saida desejada, esta rede deve aprender por mecanismos de estímulo-reação, comparável a forma como as pessoas inicialmente aprendem uma linguagem: somente pela audição repetida de certas palavras em momentos particulares, as pessoas aprendem a fazer associações entre ideias e palavras (LAWRENCE, 1992). Neste caso não existe ninguém (um "professor") para indicar se associação feita está correta. A rede se encaminha interativamente num processo intemo próprio de categorização da informação entrada, também conhecido como data clustering (OBERMEIER, 1989; SOUCEK, 1989).
[2]: Teorias de aprendizado estudadas em psicologia, que analisam o aprendizado de redes neurais sob um enfoque behaviorista ou cognitivo, podem ser vistos em LAWRENCE (1992), HARSTON (1990), COLTHEART (1994), KRUSCHKE (1993), LATIMER (1994), SCHRETER (1994), WATSON (1994), WILES (1994) e JOHNSON (1994). Pode-se incluir aqui a rede do "Chapeuzinho Vermelho"...
Uma rede neural aprende modificando suas respostas conforme a entrada se modifique. Os pesos são ajustados conforme o método (regra) de aprendizado utilizado. O valor dos pesos sinápticos varia somente durante a etapa de treinamento da rede neural, sendo ajustados de forma a acumular mais conhecimento que fica distribuído pelos seus pesos sinápticos, no seu emaranhado de conexões (LAWRENCE, 1992).
Treinar uma rede neural é uma questão de ajuste de pesos, que pode ser feito tanto manualmente quanto automaticamente (algoritmos computacionais). Uma rede neural simulando uma porta lógica OU exclusiva (XOR) pode ter seus pesos sinápticos facilmente determinados manualmente - como demonstrado em LAWRENCE (1992), KNIGHT (1990), JONES (1987), MAREN (1990) e TOURETZKY (1989).
Obs.: Sobre "RN XOR" recomenda-se ver:
- ???
A capacidade de aprendizado, processamento e informação inteligente estocada numa rede neural é determinada pela sua arquitetura (topologia) das conexões da rede e pelo algoritmo de treinamento utilizado (GUERRIERE, 1991; JOSIN, 1987). O comportamento de uma rede é detemiinado pelos pesos das suas conexões, que são estabelecidos durante o processo de treinamento. As regras (algoritmos) de aprendizado descrevem como cada neurônio deve interpretar a informação vinda dois outros neurônios à ele conectados e assim, qual sinal distribuir pelo restante da rede (JOSIN, 1987). Existem muitas regras de aprendizado baseados em inúmeros fatores como dependência ao estado anterior da rede, limiares estáveis ou variantes e à particularidades da função transferência utilizada (JOSIN, 1987). As redes neurais não trabalham com símbolos discretos, mas alguns autores afirmam que a rede realiza um processamento sub- simbólico pela associação de padrões que realiza de forma a representar o conhecimento (JOSIN, 1987; CAUDIL, 199lb). A importância das conexões numa rede ,deu a esta área de estudo, o seu nome: conexionismo (RYAN, 1991). As redes neurais agem sobre seus dados detectando alguma forma de organização desconhecida; desta forma, elas podem reconhecer relações especiais (útil no processamento de imagens), temporais (em sistemas de controle) e desempenhar algumas tarefas de classificação, previsão e estimativa de funções (HAMMERSTROM, ANTSAKLIS, 1992; CAUDIL, 1991a).
Rede MLP ou Back-Propagation
A rede neural baseada no algorimto de aprendizado back-propagation é a tipo mais difundida (HAMMERSTROM, 1993; TOURETZKY, 1989; MAREN, 1990; ANTSAKLIS, 1992; SOUCEK, 1989), uma rede perceptron (não-linear) de multicamadas ƒeedforward, onde nenhuma infomiação é retropropagada durante sua operação (ANTSAKLIS, 1992). É assim denominada pelo seu esquema de aprendizado supervisionado, no qual um sinal de erro de saída é retropropagado pela rede modificando o peso das conexoes de forma a minimizar este erro (HAMIVIERSTROM, 1993; MAREN, 1990; TOURETZKY, 1989).
Uma rede back-propagatíon requer no mínimo três camadas (uma das camadas é "invisível") que são usualmente referenciadas como camada de entrada, invisível ou intermediária, e de saída. A camada de entrada é meramente passiva, isto é, somente recebe os padrões de entrada (vetores de entrada). Diferentemente da camada de entrada, as camada invisível e de saída processam ativamente os dados. A camada de saída como sugere seu nome, apresenta os resultados da rede, um conjunto de variáveis contínuas de saida (vetores de saída), um valor para cada nó.
Os nós da camada de entrada se conectam somente aos nós da camada invisível, e os nós da camada invisível somente com os da camada de saída, não existindo nenhuma conexão direta entre nós da camada de entrada e de saida. Nomialmente os nós entre as camadas são completamente interligados.
Uma rede back-propagation (assim como outras redes ƒeedforward) possui estágios separados para aprendizado e operação. Uma vez que a rede tenha sido treinada, o processo de aprendizado se encerra e os pesos são armazenados (em arquivos). Durante a operação, nenhuma informação é retropropagado, o termo back propagation se refere exclusivamente a fase de aprendizado.
Seu algoritmo de aprendizado exige que a função transferência para cada nó seja uma função contínua e diferenciável. Esta fiinção deve ser assintótica tanto para valores infinitamente positivos quanto infinitamente negativos (com relação a sua variável independente, , ou a soma ponderada das entradas de uma neurônio). Estas condições levam a uma curva com formato de S, conhecido como função sigmóide, como mostrado na figura 9.
| Figura 9: A função transferência sigmóide e sua derivada. | |
|---|---|
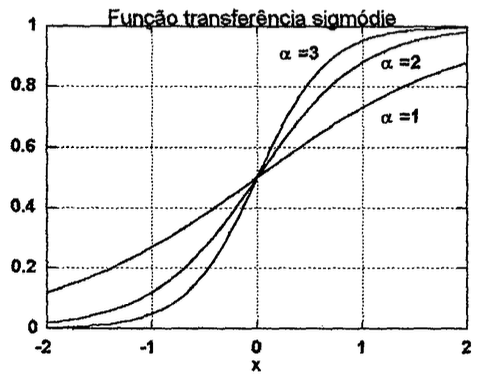 | 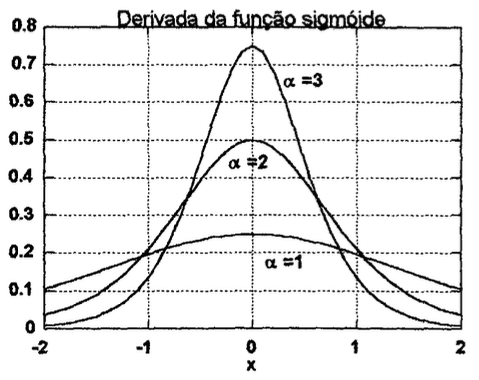 |
| neste caso, representa o ganho do neurônio e normalmente é ajustado em 1 |
Obs.: A derivada da função sigmoidal não é monotônica, isto é, é capaz de produzir o mesmo resultado, por exemplo, saída (considerando ) tanto para entrada qunato para — o que pode paralizar o treino da rede quando usado algoritmo de treinamento baseado em derivada ou gradiente descendente. Motivo pelo qual este função pode ser trocada pela Swish (ver XX). Note ainda que a função sigmoidal excursiona sua saída na faixa: . Se for desejada uma função de ativação capaz de gerar valores negativos e positivos, na faixa de , pode ser usada a função tangente hiperbólica, definida como:
Esta função possui un formato muito semelhante à função sigmoidal com excessão de que gera valores negativos máximos tendendo à para entradas muito negativas e valores positivos tendendo à no caso de entradas muito positivas. Mas sua derivada é igualmente não monotônica.
Mais sobre Funções de Ativação, ver: YouTube: A Review of 10 Most Popular Activation Functions in Neural Networks, Machine Learning Studio, 25 fev 2023, 13.625 visualizações (acessado 01/03/2025), 15:58.
Este tipo de função caracteriza uma das principais diferenças para com seus modelos predecessores (redes perceptron, ADALINE) que utilizavam funções transferências mais simples, limitando sua habilidade em problemas de reconhecimento de padrões mais complexos, ver figura 10 (MAREN, 1990; KNIGHT, 1990).
| Figura 10: Espaços de solução linearnente separáveis correspondentes a uma rede de perceptrons lineares (MAREN, 1990). |
|---|
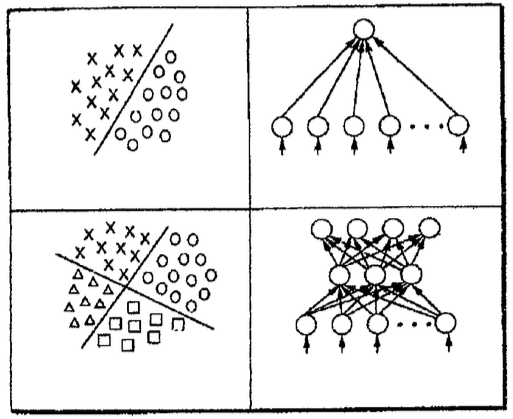 |
Regra de Aprendizado Delta Generalizado...
A regra de aprendizado da rede back-propagation é conhecida como regra Delta generalizada, uma forma generalizada da regra do mínimo erro médio quadrático, de Widrow e Hoif, uma técnica de minimização dos erros cujas equações de erro operam sobre funções diferenciais baseadas numa heurística de gradiente descendente (KNIGHT, 1990; JONES, 1987; MAREN, 1990).
Treinamento...
O treinamento da rede requer uma série (conjunto) de padrões de entrada com suas correspondentes saídas, sobre as quais se deseja que a rede faça a associação. Durante o treinamento, a rede passa cada padrão de entrada da camada de entrada para a camada de saída, modo conhecido como forward, figura 11(a). Inicia-se então o modo backward da rede, em que os erros são retropropagados da camada de saída para a camada de entrada. A rede compara a resultado atual com a saída desejada, a diferença é o erro da camada de saída, figura 11(b).
O objetivo (matemático) por traz do aprendizado é minimizar a chamada "função custo" (normalmente asosciada ao erro médio quadrático da rede — ver adiante). Então, genericamente se pode dizer que:
A saída de certo neurônio da camada pode genericamente ser retratado como sendo: Onde: camada da rede, que varia de até camadas invisíveis;
Padrão/sinal de entrada para um neurônio ou PE; conjunto de pesos associados com a conexão entre o neurônio atual (na camada ) e os outros neurônios da próxima camada; bias de entrada para certo neurônio associado com a camada atual ): função de ativação do(s) neurônio(s) da camada atual ;
Quando se deseja treinar uma rede, se está tentando minimizar a função custo, algo como: Onde: Função relacionada com erro da rede, ou simplesmente loss function; medida do erro para padrão de treino , que varia de 1 até número total de padrões de treinamento; saída calculada para padrão de entrada ; saída esperada para o padrão de entrada .
Normalmente é usado o erro quadrático médio para inferir o erro da rede:
| Figura 11: Treinamento de uma rede neural back propagatíon. |
|---|
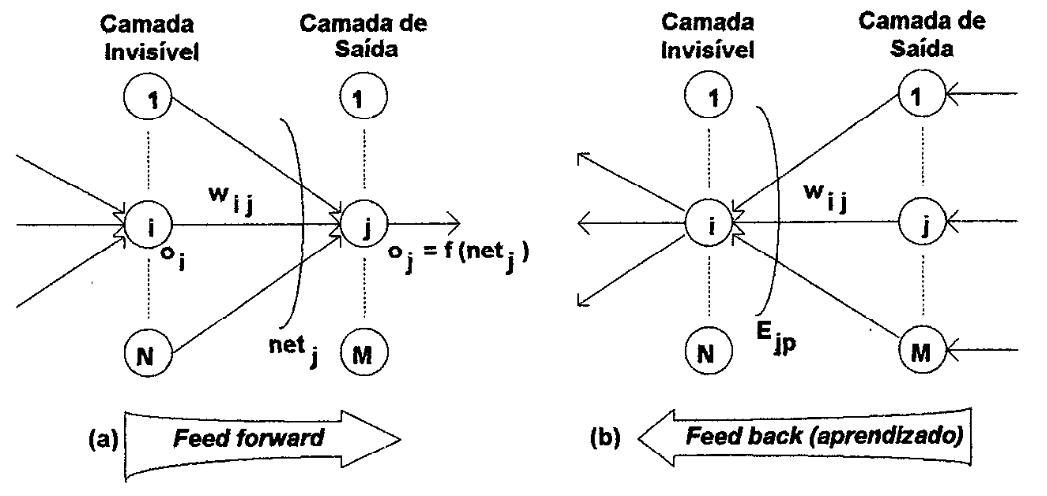 |
Cada neurônio da camada de saída evolui seu erro, figura 11(b):
onde: Erro linear na saída referente ao padrão ; saída desejada para a saída rereferente ao padrão ; saída computada pela RN para o padrão .
Se deseja que a rede seja capaz de relacionar padrões de treinamento (pares de entrada- saída), de tal forma que:
A qualidade da aproximação realizada pode ser medida pelo erro quadrático da saída. O erro quadrático "instantâneo", para o padrão , neurônio é então:
Obs.: Este "fator qualidade" e equação associada é conhecida nos dias atuais como função custo.
Este valor () é utilizado para atualizar os pesos da rede de forma que padrão por padrão de treinamento apresentado à rede, o erro seja minimizado, pelo método de gradiente descendente ou steepest descent gradient, deslocando o vetor das sinapses numa mesma direção, método conhecido como regra delta generalizada.
Obs.: Nos dias atuais, com o "advento" das redes neurais profundas, compostas por várias camadas invisíveis, este algoritmo usado de forma simples ("pura"), padece do problema do "waninsh gradient" — à respeito disto ver RNs > Vanishing Gradient. Existem formas de tentar minimizar este problema, ver material do MIT 6.S191 course: Introduction to Deep Learning.
A cada passo de treinamento, cada sinapse sofre uma atualização:
onde corresponde ao "passo do treinamento" ou taxa de aprendizado.
O acréscimo realizado em cada sinapse corresponde à:
onde: gradiente do valor esperado do erro.
O gradiente do erro é proporcional à derivada da função transferência:
Assim:
Os próprios pesos já atualizados são então usados para retropropagar os erros da camada da saída para as predecessoras e provocar o ajuste de pesos da camada invisível (KNIGHT, 1990; MAREN, 1990; SOUCEK, 1989; LIPPMAN, 1987; JONES, 1987; LAWRENCE, 1992) — processso conhecido como método da cadeia.
Faltou introduzir regra da cadeia!?
Épocas de treinamento...
A regra Delta generalizada é um processo de minimização dos diferentes erros para os diferentes padrões. Devido a quantidade de padrões de treinamento, não se pode simplesmente ajustar a derivada de em relação a , à zero, e sim tentar se aproximar dos melhores valores para de forma incrementalmental, padrão por padrão.
Costuma-se dizer que depois que todos os padrões de entrada e saída forma apresentados à rede, uma época (eppoch) do treinamento foi completada (KNIGHT, 1990).
O algoritmo back-propagation é conhecido por demandar muito tempo (time consumíng algorithm) (SOUCEK, 1989; MAREN, 1990; KNIGHT, 1990), o tempo de aprendizado é aproximadamente num computador serial (CPUs comuns) e num sistema de computação paralela (GPU´s com núcleos CUDA) que utiliza um processadores (núcleos de cálculo) separado para cada conexão; onde é o número de conexões da rede e , o número de padrões de treinamento e , a função que relaciona e (SOUCEK, 1990). Outros como MORSE (1989), sugerem a seguinte equação: ).
Taxa de Aprendizado e Momentum…
A velocidade do treinamento pode ser incrementada por uma pequena modificação na equação de ajuste dos pesos, com a adição do termo momento (momentum), :
Normalmente, o treinamento de uma rede é iniciado com valores próximos de para a taxa de aprendizado e para o termo momento, e durante o treinamento são adotados valores menores (decrescentes) para a taxa de aprendizado e maiores para o termo momento, por exemplo, alcançando valores como: e (KNIGHT, 1990; LIPPMAN, 1987).
Inicialização da rede...
A rede ainda é inicializada com seu conjunto de pesos sinápticos randomizado (preferência por distribuição normal) numa faixa variando de à (KNIGHT, 1990).
Mas estudos mais recentes, de Glorot & Bengio (2010) e He & Zhang & Sun (2015) propões outras formas de inicializar uma rede MLP, garantindo convergência mais rápida e estável da rede, principalmente se a mesma contiver muitas camadas ocultas — ver RNs > Inicialização de pesos.
"Energia" da rede durante treinamento...
Durante o treinamento de uma rede back propagatíon espera-se que seu erro (, também tratado como "energia" da rede) diminua, conforme pode ser visto na figura 12, de forma que os pesos alcancem os melhores valores (mínima energia), ponto que se conhece como mínimo global (www) (MAREN, 1990; KNIGHT, 1990; LAWRENCE, 1992).
| Figura 12: Estado energético de uma rede neural (LAWRENCE, 1992). |
|---|
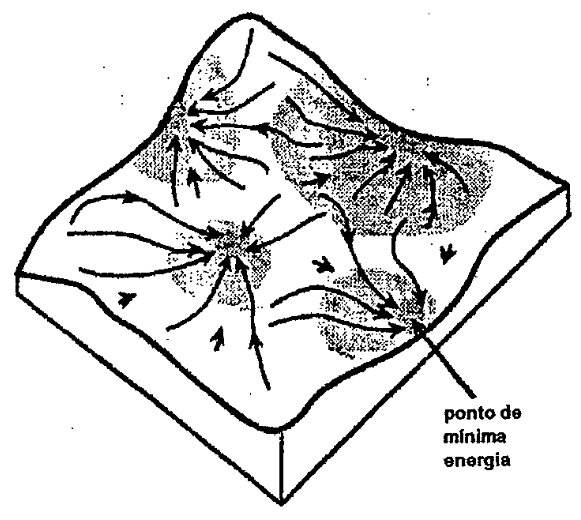 |
Mínimos locais globais...
Entretanto a rede pode entrar num estado de paralisia durante seu treinamento, causado pelo próprio processo de otimizaçao do erros pelo método do gradiente. Pelo próprio formato não monotônico da derivada da função transferência, se é deslocado numa região de gradiente pequeno, o treinamento praticamente paraliza num ponto conhecido como mínimo local, representado na figura 13 como , o que não é o desejável , ou mínimo global.
| Figura 13: Mudança na energia dos pesos da(s) conexão(ões) de um sistema neural (ALEKSANDER, 1990). |
|---|
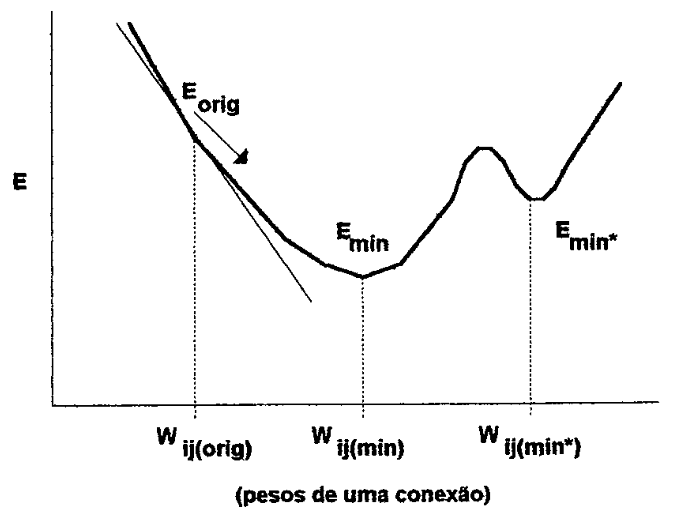 |
O termo momento atenua o problema do mínimo global, fazendo a rede escapar de alguns mínimos locais, pela orientação na atualização dos pesos numa mesma direção (KNIGHT 1990), mas a introdução de ruído randômico à rede numa técnica conhecida como simulated annealing é mais conhecida pois provoca pequenos "saltos" nos valores das sinapses, permitindo o deslocamento dos pesos para "va1es" mais profimdos, conforme pode ser observado na figura 14 (KNIGHT, 1990; SZU, 1990; ALEKSANDER, 1990; LAWRENCE, 1992; GARCIA, 1992).
| Figura 14: Uma bola "ruidosa" numa superficie montanhosa (ALEKSANDER, 1990). |
|---|
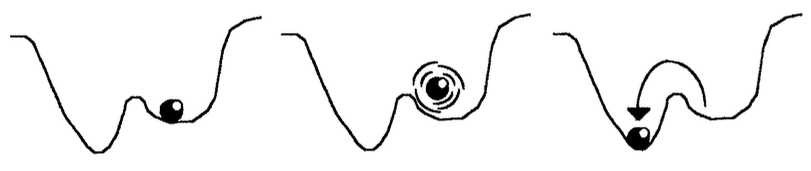 |
Obs.: Atualmente existem métodos que visam combater este problema do mínimo local como:
- algoritmo estocástico associado com cálculo do gradiente do erro;
Não confundir com o problema do "waninshing grandiet" que pode ser evitado de outras formas.
Sobre outros algoritmos de aprendizado, clique aqui.
Treinando uma rede...
Durante o treinamento da rede é importante monitorar-se seu desempenho para evitar que um treinamento prolongado demais leve a rede a um estado de sobre-aprendizado (overtrainig, overlearning ou overfitting), ocasião em que a rede perde sua capacidade de generalização, tentando memorizar individualmente os pares entrada/saida utilizados no treinamento (KNIGHT, 1990; HOLDAWAY, 1990).
Um método para reduzir o sobreaprendizado é acompanhar o desempenho da rede sobre um conjunto separado de teste, durante o seu processo de treinamento. Isto é feito, apresentando-se periodicamente o conjunto de teste à rede e avaliando-se os resultados obtidos, sem passar pela fase de retropropagação dos erros e ajuste dos pesos. Nomalmente este teste é executado depois que todo o conjunto de treino (ou uma época) foi apresentado à rede, caracterizando uma parte do processo de treinamento conhecido como "recall" (KNIGHT, 1990; HOLDAWAY, 1990).
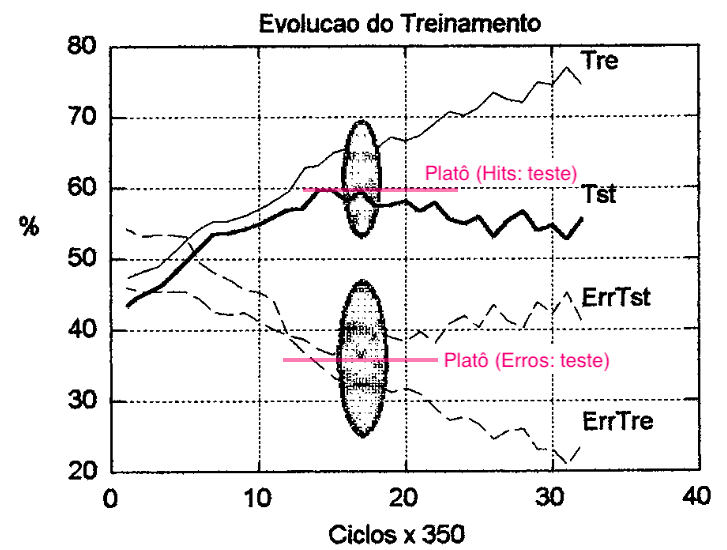
Deve ser adotado um critério para se estabelecer o ponto de parada ou melhor ponto do treinamento da rede, antes que se alcance o sobreaprendizado. A figura l5(a) mostra a evolução no treinamento de uma rede. A eficiência da rede para o conjunto de treino e teste vai aumentando desde a fase inicial do treinamento, devido ao ajuste dos pesos, até que se atinge um platô, em tomo do qual os pesos ficam oscilando, procurando a melhor direção para aumentar sua eficiência sobre o conjunto de treino. Quando este platô é encontrado a rede está começando à se especializar sobre o conjunto de treino entrando no sobreaprendizado.
Se o treinamento persiste, a eficiência para o conjunto de treino atinge um máximo, enquanto que para o conjunto de teste piora, justamente porque a rede perde sua capacidade de generalização. A introdução de ruído na rede (técnica de simulated annealing), durante a fase de platô, contribui para evitar que a rede memorize os padrões de treino, mas neste caso, o ruído deve ser controlado o suficiente para não confundir a rede (KNIGHT, 1990).
KNIGHT (1990) sugere que se pare o treinamento quando a rede atingir a região de platô, na suposição de que qualquer avanço possa inviabilizar o treinamento. Ver figura 15.
| Figura 15: Efeito típico da generalização no treinamento de uma rede. |
|---|
 |
Obs.: Esta implementação requer que cada vez que um novo nível mínimo de energia da rede seja alcançado, todo o conjunto de pesos sinápticos deva ser gravado (na prática anexando ao nome do arquivo a data e horário daquele instante). Assim, uma vez comprovado que o platô foi ultrapassado é possível recuperar os pesos já gravados da rede no ponto do platô (uma forma de "retroceder" no treinamento, salvando arquivos de pesos temporários — sugere-se criar um arquivo de "log" para indicar a que corresponde cada novo arquivo de pesos gerados). Este procedimento requer um pouco mais de habilidade em termos de programação no algoritmo de treinamento. Eventualmente o "nível de desempenho" da rede pode ser observado calculando-se à cada passo do treinamento o "erro quadrático médio" (ver próximo parágrafo), tanto para o conjunto de treino quanto para o conjunto de testes (ou validação) — Ver figuras 16 e 16a.
Exemplo deste tipo de procedimento é mostrado em Treino de RN MLP (Exemplo de Implementação).
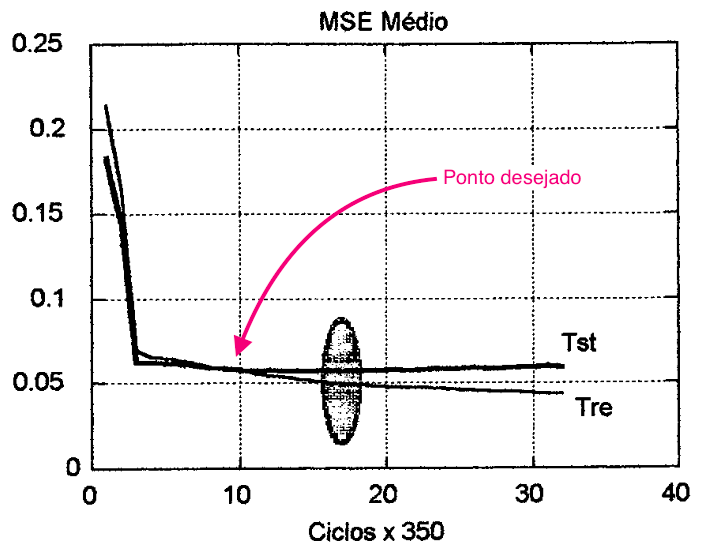
HAMMERSTROM (1993), sugere que se monitore a generalização da rede para cada época do treinamento, calculando-se o erro quadrático médio para cada padrão, somando os erros médios para todos os padrões apresentados e finalmente então calculando-se a sua média, tanto para os padrões de treino quanto de teste.
O erro médio quadrático para o conjunto de treino e teste normalmente decresce rapidamente no início do treinamento até que as duas curvas alcançam um platô, quando após, o erro para o conjunto de treino continua vagarosamente a baixar enquanto que o erro para o conjunto de teste aumenta. Neste caso, é sugerido que se para de treinar a rede no momento em que é alcançado o menor erro médio quadrático residual para o conjunto de testes, como mostra a figura 16. Já HOLDAWAY (1990) sugere um teste quantitativo e qualitativo dos erros, tanto para o conjunto de treino quanto para o conjunto de teste.
| Figura 16: Verificando a eficiência da rede durante o treinamento pela curva de MSE médio do conjunto de teste. |
|---|
 |
Quantitativamente o processo é semelhante ao já descrito por KNIGHT (1990) e HAMMERSTROM (1993), só que contabilizando-se agora os erros ao invés dos acertos.
Qualitativamente, os erros são divididos em três grupos:
- Erros otimistas;
- Erros pessimistas, e;
- Erros graves (ou "hard”).
As primeiras duas categorias se referem ao caso em que a rede erra na classificação do padrão por uma posição, ou seja, um exemplo de erro "otimista" é o caso em que rede assinala a saída 1 quando o correto para o padrão seria 2. Um erro grave se refere aos casos em que a rede assinala a saída 1 quando deveria ser a saída 3 ou vice-versa.
Pode-se perceber pelas linhas tracejadas na figura 15 que a percentagem de erros graves para o conjunto de teste (ErrTst) diminui, estabiliza e volta a aumentar depois que o platô foi atingido, enquanto que para o conjunto de treino (ErrTre) a tendência é de baixa.
| Figura 15: Efeito típico da generalização no treinamento de uma rede. |
|---|
 |
Dimensões da rede MLP...
Alguns fatores influenciam o processo de aprendizado de uma rede neural: o número de camadas invisíveis, o número de neurônios nas camadas invisíveis e o formato do conjunto de treino (KNIGHT, 1990; LAWRENCE, 1992; JONES, 1987).
As camadas invisíveis podem ser referenciadas como detectores de características por aprendizado (learned-feature detectors) ou unidades de representação internas (8re-representation units8), uma vez que os padrões ativamente codificados na camada invisível retratam características da entrada que a rede considerou significativas(KN1GHT, 1990; LIPPMAN, 1987; TOURETZKY, 1989; JONES, 1987, LAWRENCE, 1992). Idealmente a rede acumula conhecimento nas suas camadas invisíveis, abstraído das informações contidas nos padrões de entrada apresentados para treinamento (MAREN, 1990).
O conhecimento abstraído fornece a base para a classificação de padrões em alguma categoria na camada de saída. A camada invisível pode ser treinada para detectar a presença de caracteristicas nos padrões de entrada. A camada de saída pode até mesmo aprender à responder na ausência de características de um padrão, isto dá as redes neurais uma característica de tolerância à faltas (fault tolerant), capacidade para lidar com dados incompletos (JOSIN, 1987; HAMMERSTROM, 1993a; OBERMEIER, 1989).
Pode-se tomar árduo descobrir exatamente que características estão sendo representadas na camada invisível, mas depois de treinada, pode ser feita uma análise de sensibilidade sobre os pesos da rede de forma a tentar identificar as características da entrada que estão sendo mapeadas, detectando-se quais nós se tomam mais ativos em resposta a certos padrões de treino (MAREN, 1990; KLISMASAUSKAS, 1991).
Obs.: Nos dias atuais, a "análise de sensibilidade" foi substituída por técnicas de prunning, ou "podas" controladas nos pesos da rede. A idéia é a que se, o valor de um peso é muito baixo, ele pode ser simplesmente zerado, o que, tanto na fase de forward quanto na fase de backward da rede possa ocorrer economia em cálculos computacionais (sim, trata-se de um método de otimização). Esta técnica é válida em sistemas otimizados (bibliotecas matemáticas otimizadas) capazes de acelerar (e escalonar) multiplicações de várias matrizes, além de ser capaz de lidar com matrizes esparças (que contêm elementos zerados no seu interior).
Notar que: bibliotecas como
NumPy(com extensões comoSciPy),CuPy,PyTorcheTensorFlowsão capazes de realizar multiplicações otimizadas de matrizes esparsas, evitando operações desnecessárias com zeros e escalonando as operações para núcleos CUDA em GPUs. Para matrizes esparsas, é recomendável usar bibliotecas especializadas comoscipy.sparse,CuPyou frameworks comoPyTorcheTensorFlow, que oferecem suporte nativo a GPUs. A bibliotecaSciPy(scipy.sparse) Realiza multiplicações de matrizes esparsas de forma otimizada, evitando operações com zeros. A bibliotecaCuPyoferece uma interface semelhante ao NumPy, mas com suporte a GPUs via CUDA. Suporta matrizes esparsas e pode realizar operações como multiplicações em GPUs, aproveitando a paralelização. A bibliotecaPyTorch(com suporte a CUDA) também suporta operações com matrizes esparsas e oferece suporte a GPUs via CUDA e pode ser usado para multiplicações eficientes de matrizes esparsas. A bibliotecaTensorFlow(com suporte a CUDA) também suporta matrizes esparsas e operações em GPUs. É amplamente utilizada em aprendizado de máquina e oferece otimizações para operações com matrizes esparsas.Ver: Python e Bibliotecas matemáticas mais avançadas para ML e Bibliotecas C++ avançadas para ML.
Inicia-se o treinamento de uma rede com apenas uma camada invisível, verificando-se seu desempenho (LAWRENCE, 1992). Mais de uma camada invisível revela-se útil para o processamento de informações temporais (ANTSAKLIS, 1992) e para problemas de representações espaciais ou geométricas (TOURETZKY, 1989), entretanto mais camadas invisíveis demandam maior tempo de treinamento para a rede. Para grande parte das aplicações, redes neurais back-propagatíon com uma camada invisível é o suficiente, segundo o que demonstra o teorema desenvolvido por Kolmogorov de mapeamento do espaço QJPPMAN, 1987; SOUCEK, 1989; JOSIN 1987).
A capacidade de mapeamento de padrões complexos aumenta com o aumento da camada invisível, entretanto isto acarreta um aumento considerável no tempo de treinamento necessário para a rede (JONES, 1987; KNIGHT, 1990). E um aumento exagerado do número de elementos da camada invisível pode fazer que a rede assinale para cada categoria de saída à ser mapeada, um elemento da camada invisível, tomando a camada de saída redundante (KNIGHT, 1990; OBERMEIER, 1989; MORRES RJ., 1989; MURATA, 1992).
Normalmente, aumenta-se gradativamente o número de elementos da camada invisível monitorando-se o desempenho da rede (LAWRENCE, 1992; OBERMEIER, 1989). MURATA (1992) propõe o uso de técnicas estatisticas analisando a relação entre a capacidade de generalização da rede (erros durante o treinamento) e o número de exemplos utilizados para treinamento, como forma de se detemiinar o número de elementos invisíveis.
Qualidade conjunto de treinamento...
Um dos principais aspectos relacionados ao aprendizado indutivo deve ser a qualidade do conjunto de treinamento utilizado. Mesmo com sua sofisticada capacidade e habilidade matemática para fazer generalizações, não se pode esperar que os modelos conexionistas possam descobrir informações que não estejam presentes nos exemplos de treinamento (HART, 1989).
Normalmente os conjuntos de treinamento são preparados seguindo uma distribuição randômica de padrões, entretanto, HOLDAWAY (1990), sugere que se siga uma mesma proporcionalidade entre os padrões de treino, num esforço para evitar que a rede desenvolva um aprendizado preferencial, dando preferência para os padrões mais freqüentes (JOSIN, 1987; KNIGHT, 1990).
É desejável que o conjunto de treinamento seja completamente representativo das entradas utilizadas para a rede durante sua aplicação (BARNARD, 1992). Um conjunto de treino que represente somente certas características da aplicação pode comprometer a capacidade de interpolação da rede entre as amostras de treinamento ou sua capacidade de extrapolação de informações (BARNARD, 1992). Nem sempre é possível se montar um conjunto de treinamento capaz de caracterizar completamente o problema da aplicação no sentido de conter amostras similares à todas as entradas possíveis. Normalmente é preferível que a rede tenha capacidade de extrapolação (BARNARD, 1992).
Existem estudos para aprimoramento de redes neurais back propagation, seja de forma a acelerar seu treinamento (ALLRED, 1989; TRESP, 1993), seja utilizando função transferência baseada em lógica difusa (KELLER, 1985), seja introduzindo métodos estocásticos no algoritmo de aprendizagem (SOUCEK, 1989) ou mesmo modificando sua estrutura para redes neurais óiftzsas MACHADO, 1992b).
Backpropagation em redes com várias camadas invisíveis
Anteriormente foi mostrado algo do algoritmo de aprendizado para redes MLP, mas ressaltando as equações usadas apenas da camada de saída (resultados) para a última camada invisível da rede. Note que os pesos da rede devem ser retropropagados (atualizados) baseado em algum método de aprendizado, "retrocedendo" da camada de saída até a camada de entrada, isto requer a aplicação da regra da cadeia para ir retropropagando os pesos a medida que ser regride da última camada invisível da rede para as outras camadas predecessoras. Aqui, as coisas podem ficar mais "complicadas", mas lembro que geralmente os método usados acabam usando derivada da função transferência. A derivada da função transferência sigmoidal e tangente hiperbólica são fáceis de obter, simplificar e incorporar num algorimto computacional, enquanto outras funções como ReLU, Leaky ReLu e SoftPlus são bem mais fáceis de usar e eventualmente por este mesmo motivo, são mais usadas em redes "deep" mais profundas de forma a tanto garantir convergência quanto acelerar o aprendizado (mesmo assim, se a quantidade de padrões de treinamento for elevada, recomenda-se fortemente a adoção de bibliotecas matemáticas otimizadas que ativam núcleos CUDA de placas GPU ou então se seugre a contratação de serviços do tipo AWS da Amazon).
Para saber mais sobre isto, incluindo a regra da cadeia, ver: Retro-propagação (Backpropagation) e RNs / Regra Delta Generalizada.
RNs pré-treinadas
É comum estar disponível em repositório todo o modelo de uma certa rede, disponibilizado para uso ou testes. Este modelo concentra os dados da rede: ou seja, informações sobre sua topologia (número de PEs em cada camada, quantidade de camadas, funções transferência usadas em cada camada) e os conjuntos de pesos sinápticos já sintonizados para a rede com base em algum repositório de dados. Mas as vezes se faz necessário completar o conjunto de treino com novos padrões de treinamento, situação na qual, se aplicam técnicas de Transfer Learning — para mais detalhes, clicar aqui.
Mais Referências:
- Redes Neurais Artificiais: 3.1 Modelo MLP, de Pedro H. A. Konzen (autor do site: https://notaspedrok.com.br/: interessante site com tutoriais em diferentes área de Cálculo, RNs, programação em Python e em C++): (acessado em 14/03/2025);
- PSI5892: A rede perceptron multicamada (PSI 5892 = Fundamentos de Adaptação e Aprendizado de Máquina, de Magno T. M. Silva e Renato Candido, USP — acessado em 14/03/2025).
- Perceptrons multicamadas em aprendizado de máquina: Um guia abrangente (Sejal Jaiswal, DataCamp, Tutorias > Aprendizado de Máquina, 24/10/2024) (acessado em 14/03/2025).
Opções: seguir para:
- Montagem do conjunto de treinamento de uma RN;
- Automatizando etapas de treinamento e testes de uma RN.
13/05/2025