Projeto de Controladores Digitais

🎵 Aula de 22/04/2024.

Iniciando da seção anterior Aula de 08/04/2024 (arquivo planta.mat) 🚀:

xxxxxxxxxx
>> diary aula_22042024.txt      % iniciando novo registro
>> load planta                  % carregando dados da aula passada
>> zpk(BoG)                     % verificando dados da planta
​
ans =
 
   0.0020446 (z+2.867) (z+0.2013)
  --------------------------------
  (z-0.9048) (z-0.8187) (z-0.4493)
 
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.
​
>> 

Controlador Proporcional - Projeto 4

Suponha que os requisitos de controle sejam:

• $\%OS \le 20\%$ (overshoot ou sobresinal máximo);
• $e(\infty) \le 20\%$ (errro de regime permanente).

Realizando o projeto no Matlab:

x
>> OS=20;
>> zeta=(-log(OS/100))/(sqrt(pi^2+(log(OS/100)^2)))
zeta =
      0.45595
>> close all % fechar todas as figuras
>> rlocus(BoG)
>> hold on;
>> zgrid(zeta,0)
>> % fazendo zoom na região de interesse
>> axis([-0.7 1.1 -0.3 1.1])
>> % sintonizando o controlador
>> [K_OS2,polosMF]=rlocfind(BoG)
Select a point in the graphics window
selected_point =
      0.88033 +    0.18328i
K_OS2 =
       1.9896
polosMF =
       0.8798 +    0.18337i
       0.8798 -    0.18337i
      0.40923 +          0i
>> 

Obtemos o seguinte root-loucs já ressaltando o ganho encontrado usando comando rlocfind():

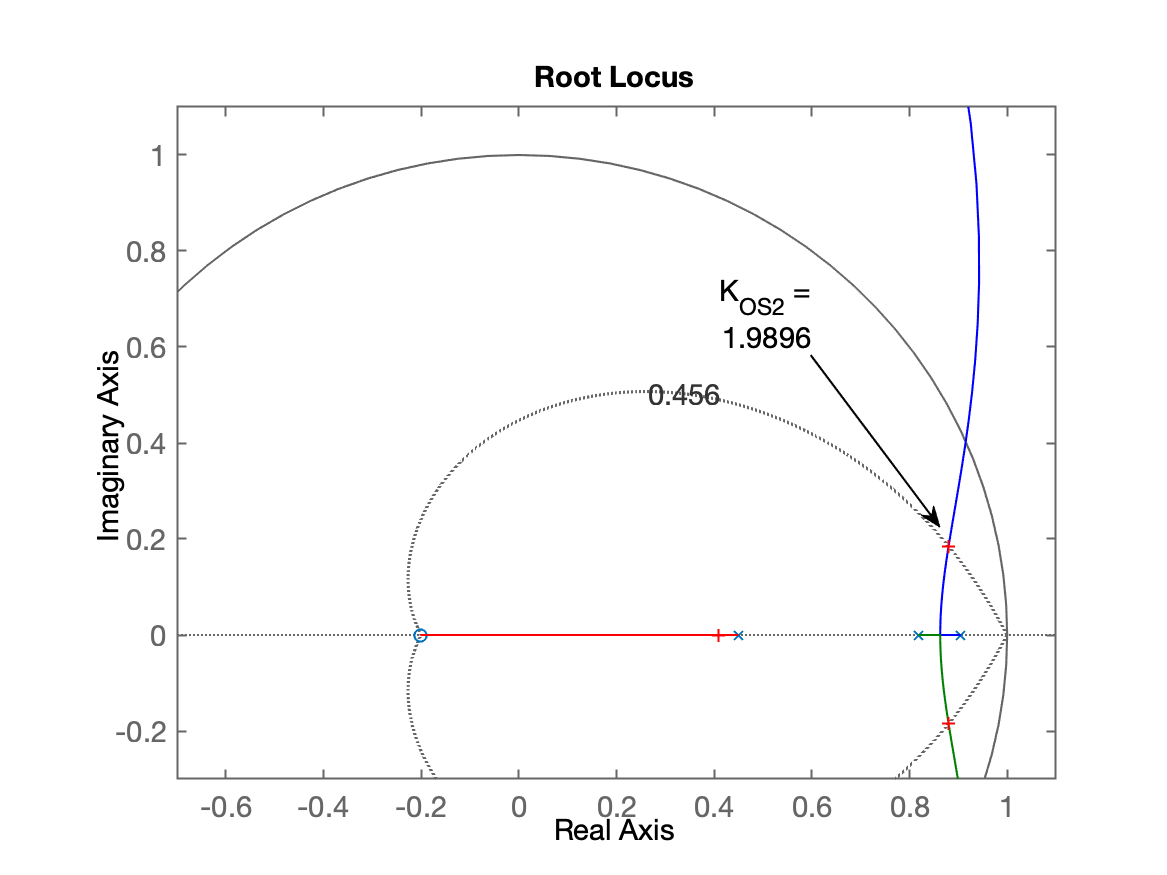
Fechando a malha com um ganho ligeiramente superior...

xxxxxxxxxx
>> K_OS2=2;
>> ftmf_K_OS2=feedback(K_OS2*BoG,1);
>> pole(ftmf_K_OS2)
ans =
      0.87987 +    0.18383i
      0.87987 -    0.18383i
      0.40906 +          0i
>> figure; step(ftmf_K_OS2)

E temos a figura que mostra a resposta para entrada degrau:

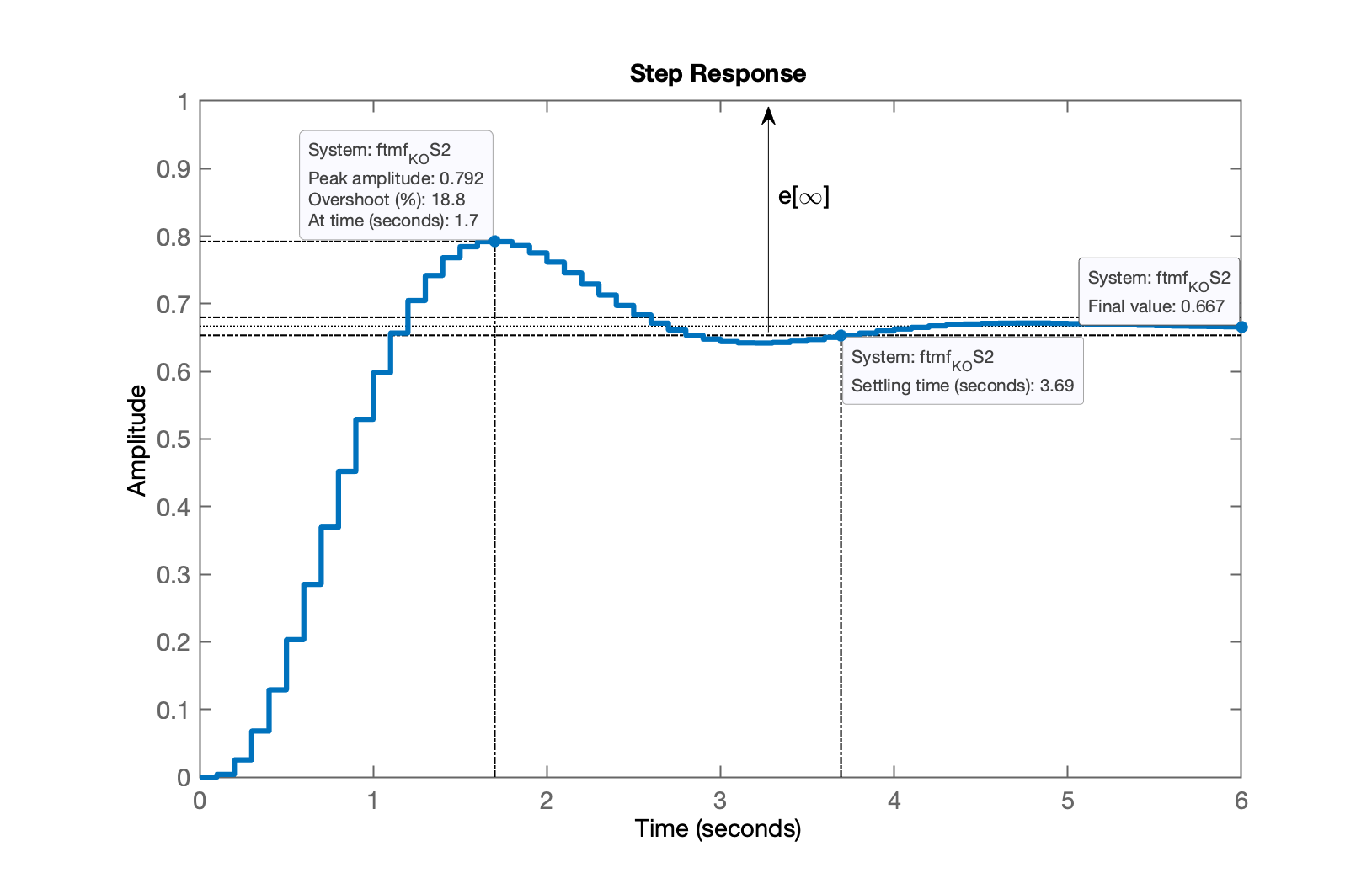
E percebemos alguns detalhes:

• Valor de pico da saída do sistema, $Max\{y[k]\}=$ 0,792; no tempo $t_p=$ 1,7 segundos; ($\%OS=$ 18,8% em relação ao valor atingido em regime permanente pela planta, $y[\infty]=$ 0,667);
• Valor em regime permanente atingido pela planta, $y[\infty]=$ 0,667. Note que a referência era uma entrada degrau, o que significa que o desejado era $y[\infty] \to 1,0$.

Notamos um erro de regime permanente, $e[\infty]$:

>> dcgain(ftmf_K_OS2)
ans =
      0.66667
>> erro=((1-dcgain(ftmf_K_OS2))/1)*100
erro =
       33.333

Algumas conclusões:

• O erro está acima do desejado (que era $\le$ 20%);
• Podemos aumentar o ganho porque $Max\{y[k]\}=$0,792 e poderia ter alcançado o valor 1,2 (20% de 1,0 do degrau unitário).

Aumentando o ganho "manualmente"... para tanto vamos observar o root-locus:

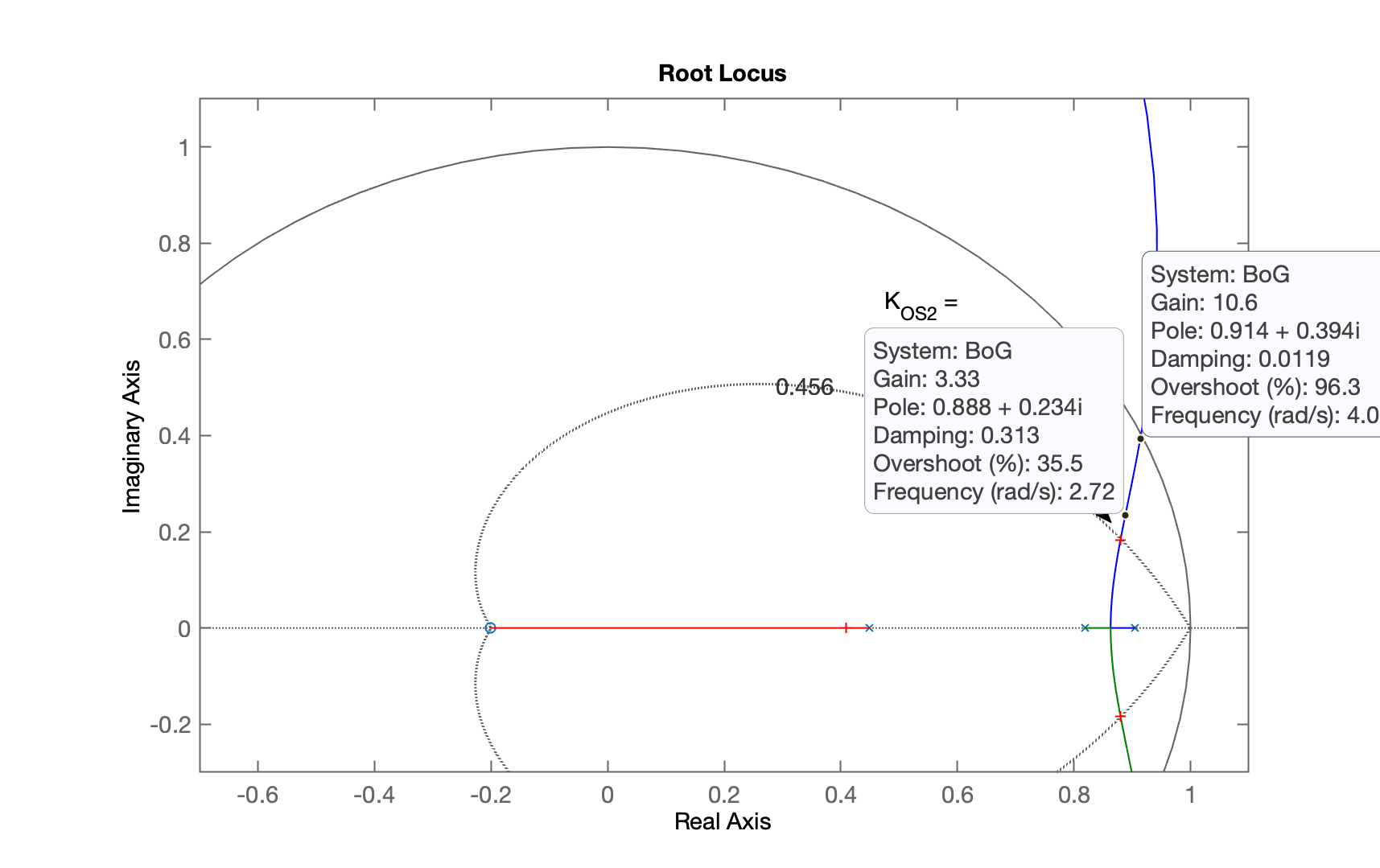
xxxxxxxxxx
>> K_2=3.5;
>> ftmf_K2=feedback(K_2*BoG,1);
>> figure; step(ftmf_K2)

Percebemos que com este ganho:

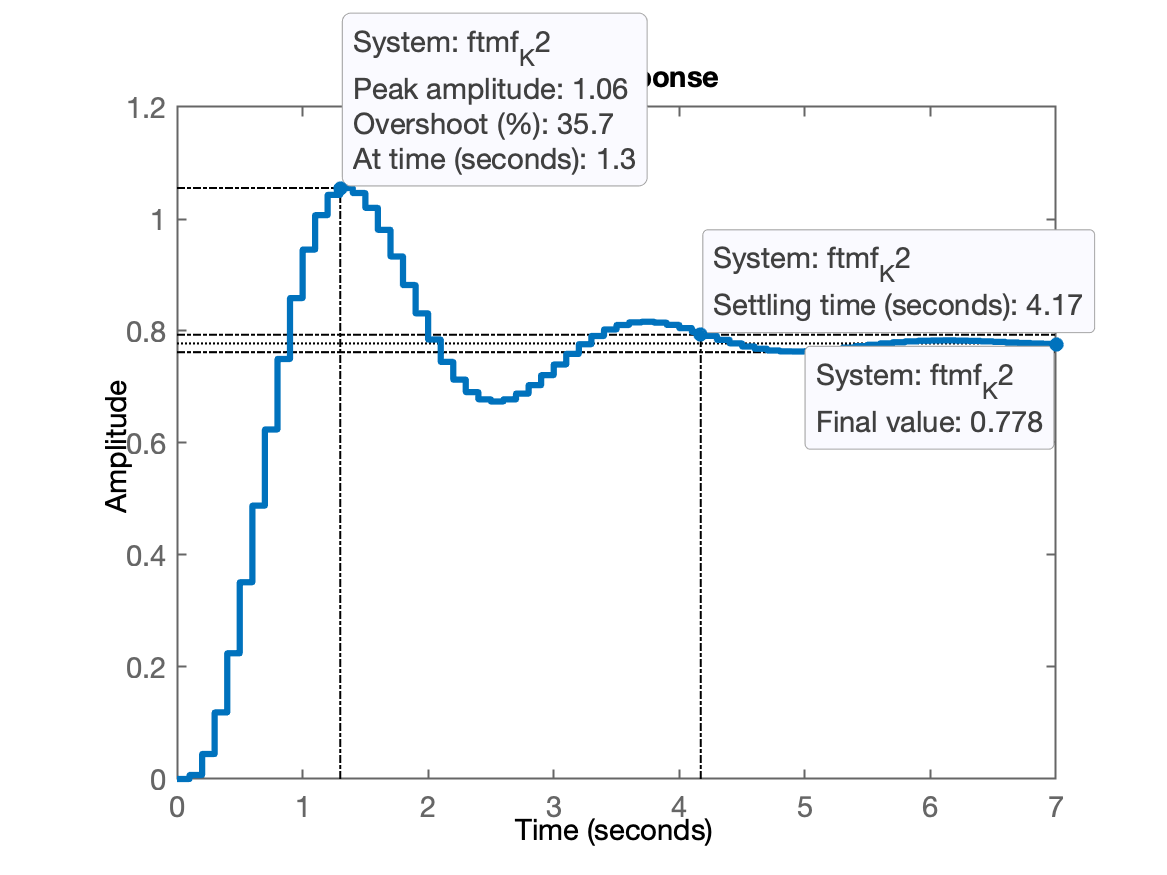
Aumentando o ganho ocorreu:

• $Max\{ y[k] \}=$ 1,06 (lembrando que poderia ter alcançado 1,2) $\rightarrow$ $\%OS=6\%$;
• o erro baixou, pois $y[\infty]=$ 0,778, ou seja:

xxxxxxxxxx
>> dcgain(ftmf_K2)
ans =
      0.77778
>> erro=((1-dcgain(ftmf_K2))/1)*100
erro =
       22.222

Determinando o valor do ganho de maneira mais determinística

Usando a Teoria do erro para determinar que valor de ganho deveria usar para manter $e[\infty] \le$ 20%.

O cálculo do erro é determinado por:

$e_{Step}(\infty)=\dfrac{1}{1+K_p}$ (eq. (1))

onde: $K_p=$ constante (de erro estático) de posição:

$K_p = \displaystyle\lim_{z \to 1} FTMA(z)$.

Calculando o $K_p$ necessário para este caso: $e[\infty]=20\%$. Note: $e[\infty]=20\%=0,2$. Então substituindo o valor do erro na eq. (1) encontramos o valor necessário para $K_p$:

$0,2=\dfrac{1}{1+K_p}$

$0,2(1+K_p)=1$

$0,2 K_p = 1 - 0,2$

$K_p=\dfrac{1-0,2}{0,2}$

xxxxxxxxxx
>> Kp=(1-0.2)/0.2
Kp =
     4

Necessitamos calcular o $\displaystyle\lim_{z \to 1} FTMA(z)$:

$\displaystyle\lim_{z \to 1} FTMA(z) =\displaystyle\lim_{z \to 1} K \cdot BoG(z) = \displaystyle\lim_{z \to 1} K \left[ \dfrac{0.0020446 (z+2.867) (z+0.2013)}{(z-0.9048) (z-0.8187) (z-0.4493)} \right]$

$\displaystyle\lim_{z \to 1} FTMA(z)=K \left[ \dfrac{0.0020446 (1+2.867) (1+0.2013)}{(1-0.9048) (1-0.8187) (1-0.4493)} \right]$

No Matlab, podemos usar a função dcgain() para determinar o limite $\displaystyle\lim_{z \to 1} FTMA(z)$:

xxxxxxxxxx
>> limite=dcgain(BoG)
limite =
            1

Então temos:

$e_{Step}[\infty]=\dfrac{1}{1+K_p}$

$K_p = \displaystyle\lim_{z \to 1} FTMA(z)$

$K_p = K \cdot \underbrace{\displaystyle\lim_{z \to 1} BoG(z)}_{=1}$

$K_p=K \cdot 1$

dai concluímos que:

$K=K_p=4$.

Fechando a malha com $K=4$:

xxxxxxxxxx
>> K4=Kp
K4 =
     4
>> ftmf_K4=feedback(K4*BoG,1);
>> figure; step(ftmf_K4)

O que rende a seguinte resposta:

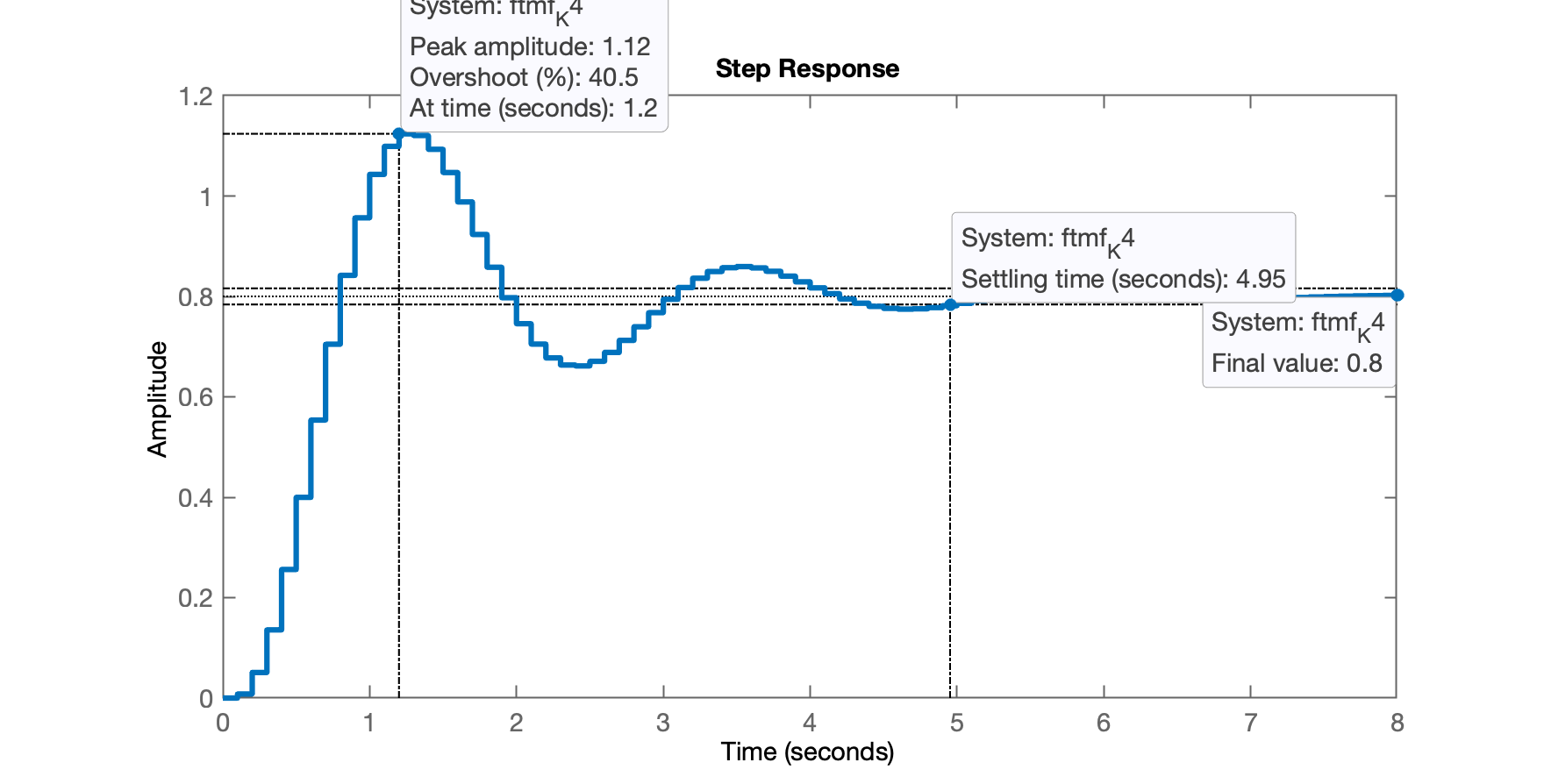
E notamos que atendemos aos requisitos de controle desejados.

Notamos que apenas com controle proporcional numa planta tipo 0, não conseguimos garantir erro nulo para regime permanente. Se fez necessário incoporar ação integral à equação de malha direta do sistema.

Controle com Pura Ação Integral

Lembrando da teoria do erro, a ação integral se caracteriza por um pólo em $z=1$. Então a equação de um controlador com ação integral pura fica:

$C_I(z)=K_i \cdot \left( \dfrac{1}{z-1} \right)$

onde $K_i$ corresponde ao ganho adotado para o controlador.

Realizando o projeto usando Matlab:

xxxxxxxxxx
>> C_I=tf(1,[1 -1], T)
​
C_I =
 
    1
  -----
  z - 1
 
Sample time: 0.1 seconds
Discrete-time transfer function.
​
>> ftma_I = C_I*BoG;
>> zpk(ftma_I)
​
ans =
 
      0.0020446 (z+2.867) (z+0.2013)
  --------------------------------------
  (z-1) (z-0.9048) (z-0.8187) (z-0.4493)
 
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.
​
>> rlocus(ftma_I)
>> axis equal
>> % realizando um zoom na região de interesse
>> axis([-4 2 -1.5 1.5])

O RL para este sistema (de 4a-ordem) fica:

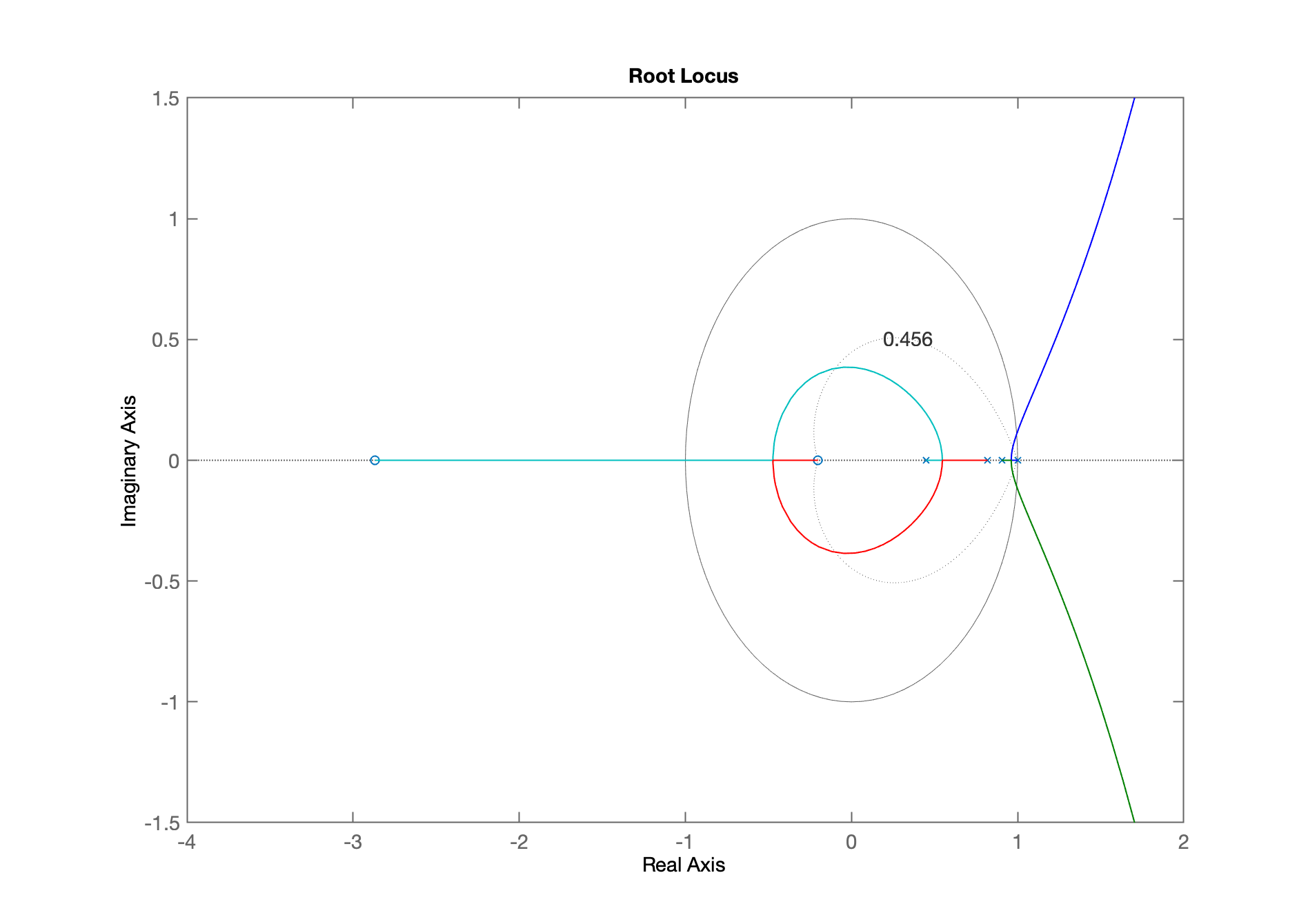
Realizando um zoom na área de interesse e acrescentando a linha guia para mesmos valores de $\zeta$ correspondendo ao $\%OS=$ 20%:

xxxxxxxxxx
>> hold on;
>> zgrid(zeta,0)
>> axis([0.7 1.05 -0.2 0.2])
>> [K_I,polosMF]=rlocfind(ftma_I)
Select a point in the graphics window
selected_point =
      0.97085 +   0.053215i
K_I =
     0.047198
polosMF =
      0.97039 +   0.053366i
      0.97039 -   0.053366i
      0.78049 +          0i
      0.45162 +          0i

Teremos um RL ressaltando este valores de ganho como o mostrado na próxima figura:

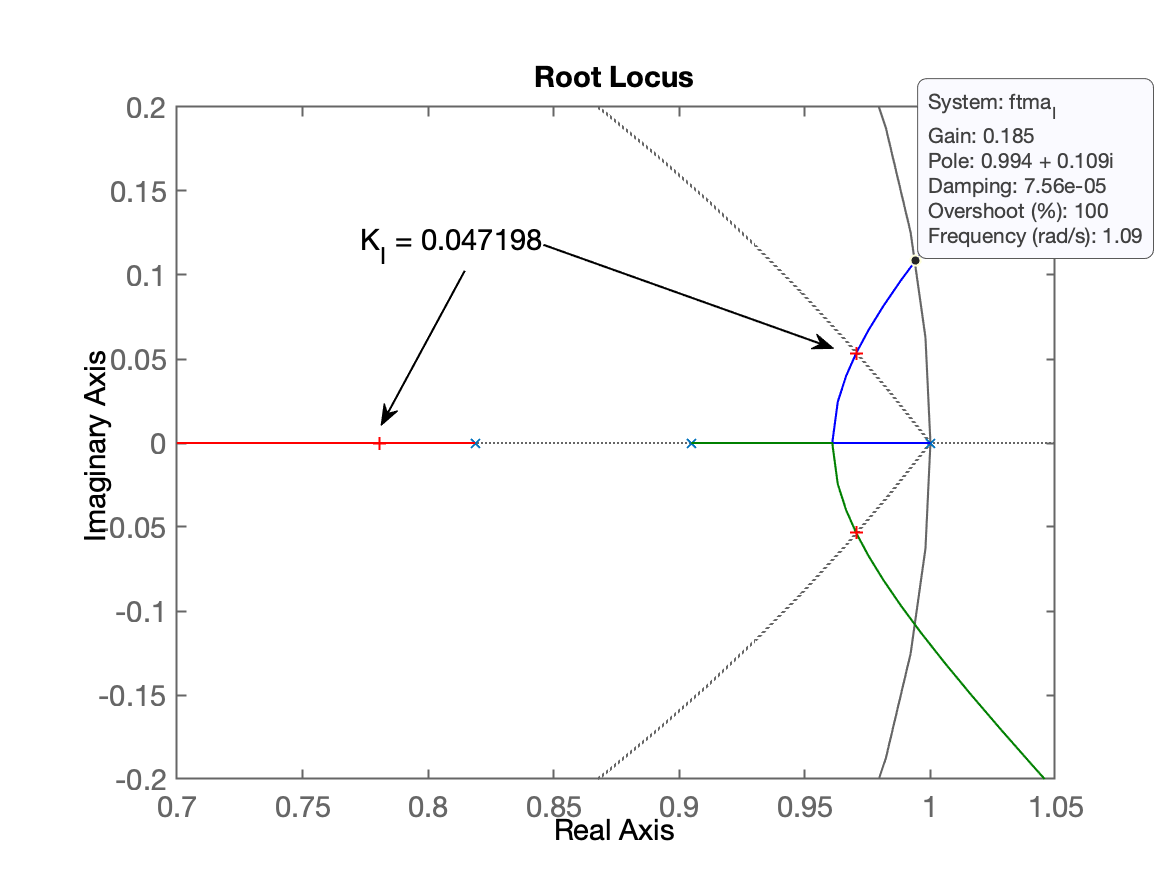
Fechando a malha com $K=0,05$ (note que é um valor muito baixo; impraticável provavelmente):

>> K_I=0.05;
>> ftmf_I=feedback(K_I*ftma_I,1);
>> pole(ftmf_I)
ans =
      0.97111 +   0.055534i
      0.97111 -   0.055534i
      0.77891 +          0i
      0.45176 +          0i
>> figure; step(ftmf_I)

E obtemos a seguinte resposta à entrada degrau:

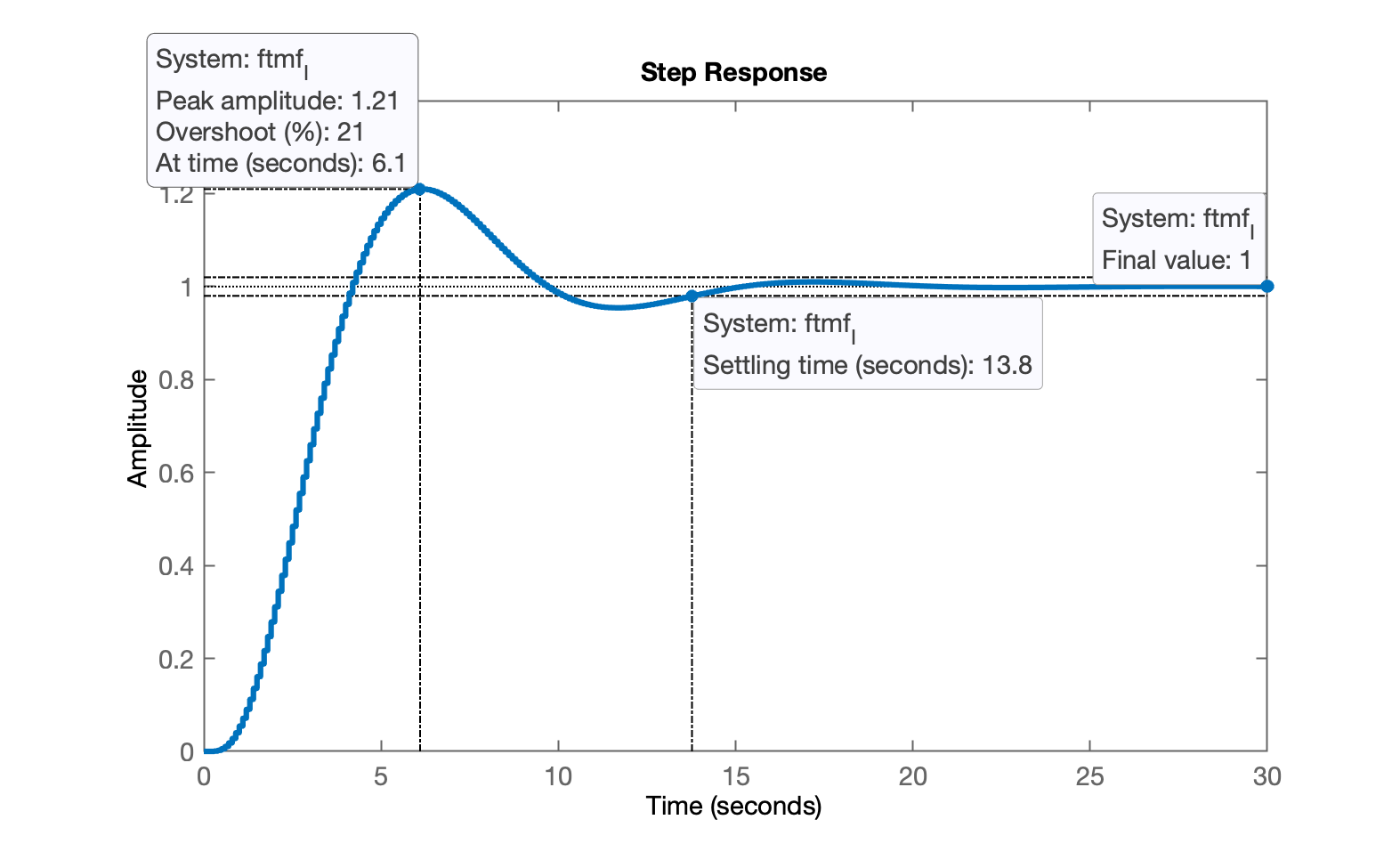
Repare que o erro de regime permanente agora é nulo. E perceba o $\%OS=$ 21%.

Mas... comparando a resposta deste controlador com o anterior (simples ganho Proporcional):

xxxxxxxxxx
>> figure; step(ftmf_K4, ftmf_I);
>> legend('Kp (e[\infty]=20%)', 'Integrador Puro')

Obtemos então:

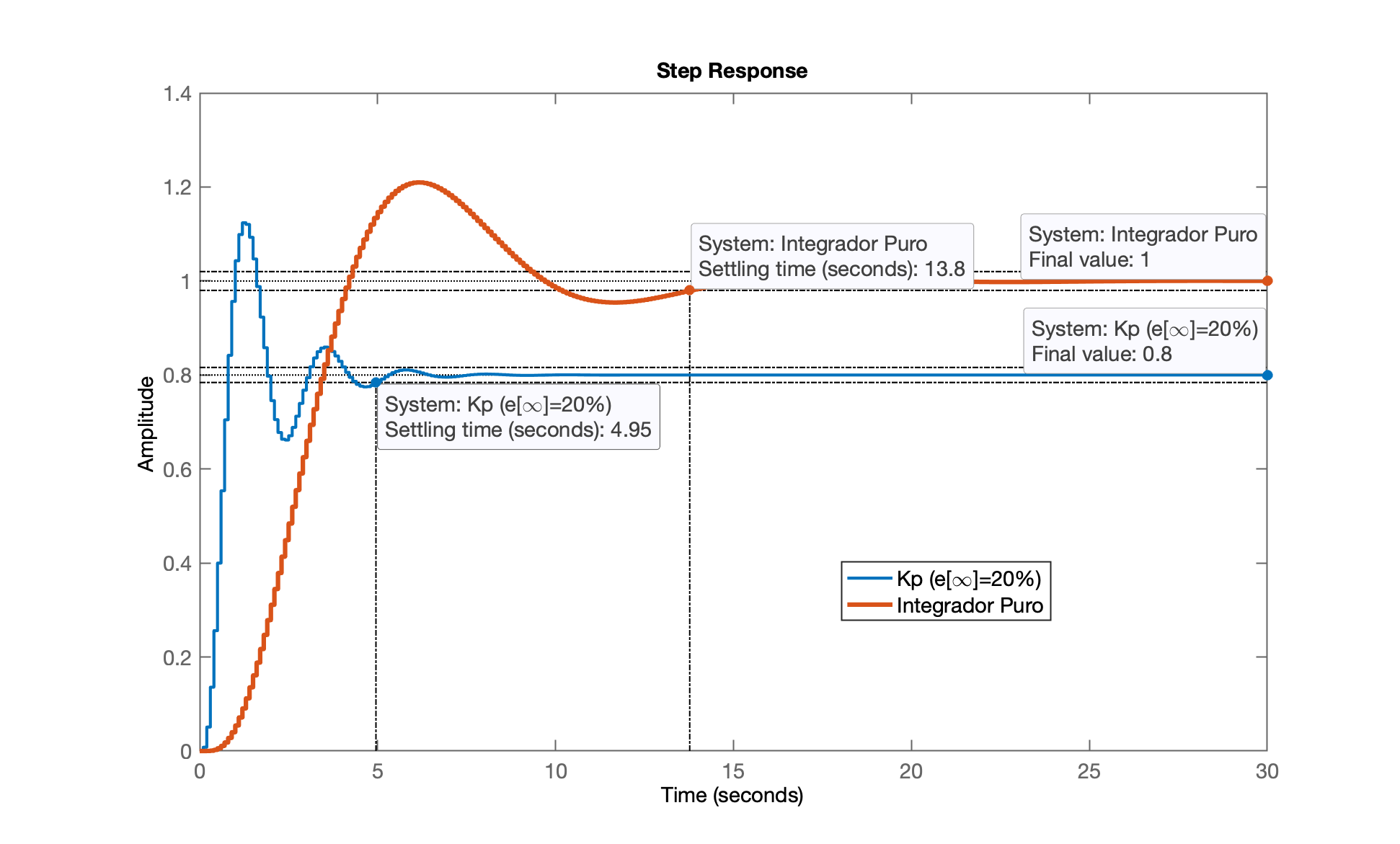
Percebo que o controlador com ação inregral pura permitiu zerar o erro de regime permanente, mas aumentou consideravelmente o tempo de assentamento, $t_s$ (de 4,95 passamos para 12,8 segundos), atrasando a resposta do sistema quase 3 vezes ($13.8/4.95 = 2.7879$).

Fim...

Não esquecer de encerrar a seção de trabalho no Matlab fazendo:

xxxxxxxxxx
>> save planta      % salva dados para continuação na próxima aula
>> diary off        % encerra arquivo texto de registro dos comandos usados

Arquivo de dados atualizado: planta.mat.

Fernando Passold, em 22/04/2024.