Projeto de Controladores

Continuação da aula de 29/04/2024 depois de passar pelo Resumo de controladores com ação derivativa:


>> load planta

💾 Arquivo: planta.mat.

Projeto de PD

Equação genérica do PD:

$C_{PD}(z)=\dfrac{K(z-z_{PD})}{z}$

$z=0$ $z_{PD}$ .

A posição do zero do PD depende dos pólos e zeros da planta.

Lembrando da eq. da planta:


>> zpk(BoG)
 
   0.0020446 (z+2.867) (z+0.2013)
  --------------------------------
  (z-0.9048) (z-0.8187) (z-0.4493)
 
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.

$BoG(z)$ temos 3 opções em vista:

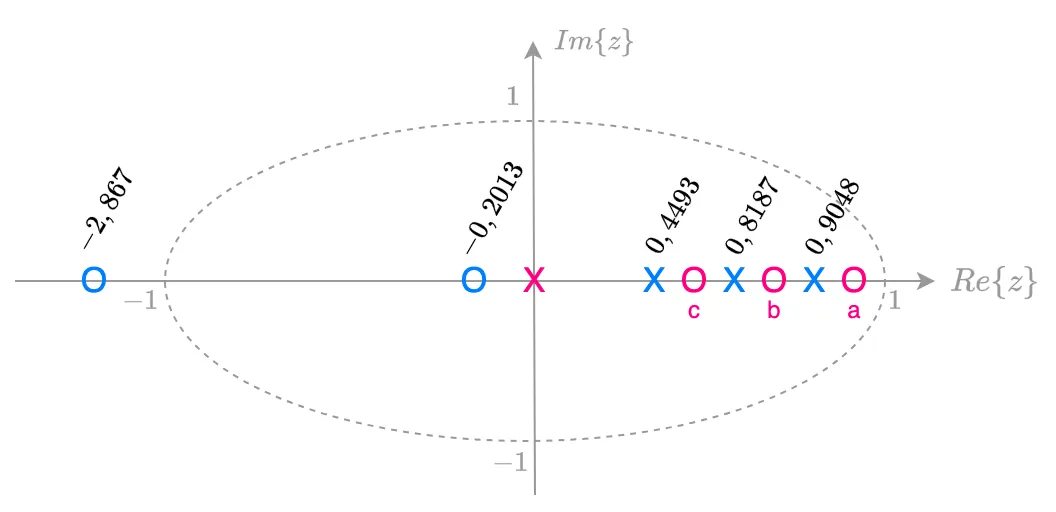
opcoes_zero_PD

Sendo as 3 opções:

$0,9048 < z < 1$ (entre o pólo mais lento da planta e o círculo unitário, mas sem estar sobre o círculo unitário);
$0,8187 < z < 0,9048$ (entre os 2 pólos mais lentos da planta);
$0,4493 < z < 0,8187$ (entre os 2 pólos não tão lentos da planta).

Graficamente:

A opção "a" resulta no RL similar ao mostrado abaixo:

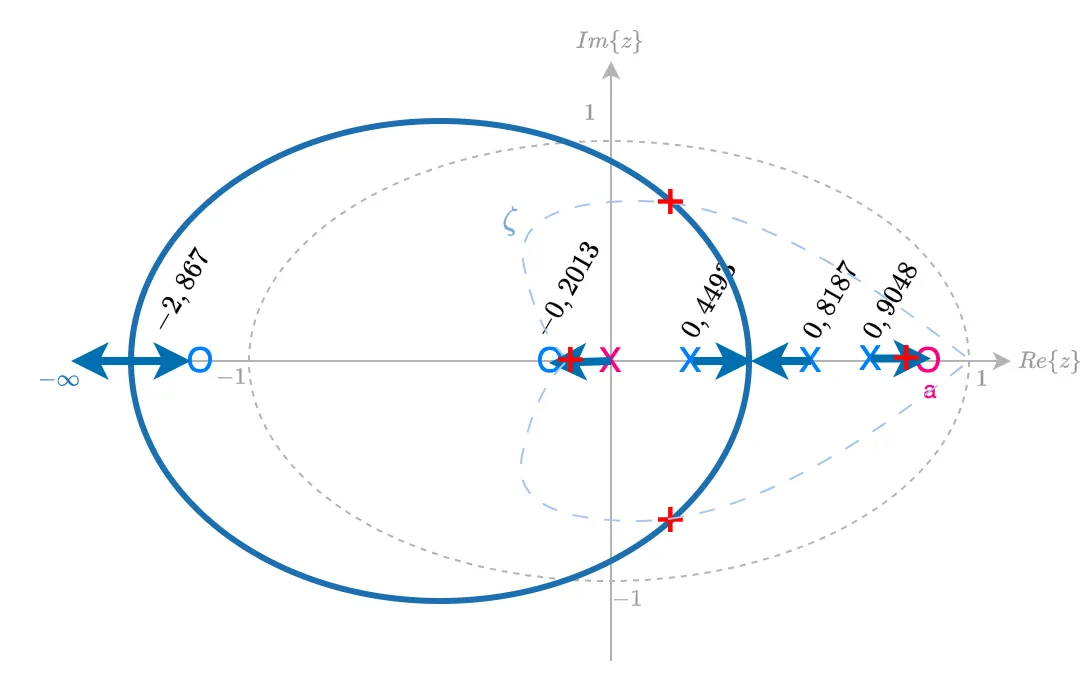
Notamos que ficamos com um pólo dominante em MF, real, muito próximo do círculo unitário (tendendo para a posição do zero do PD).

A opção "b" resulta neste outro RL:

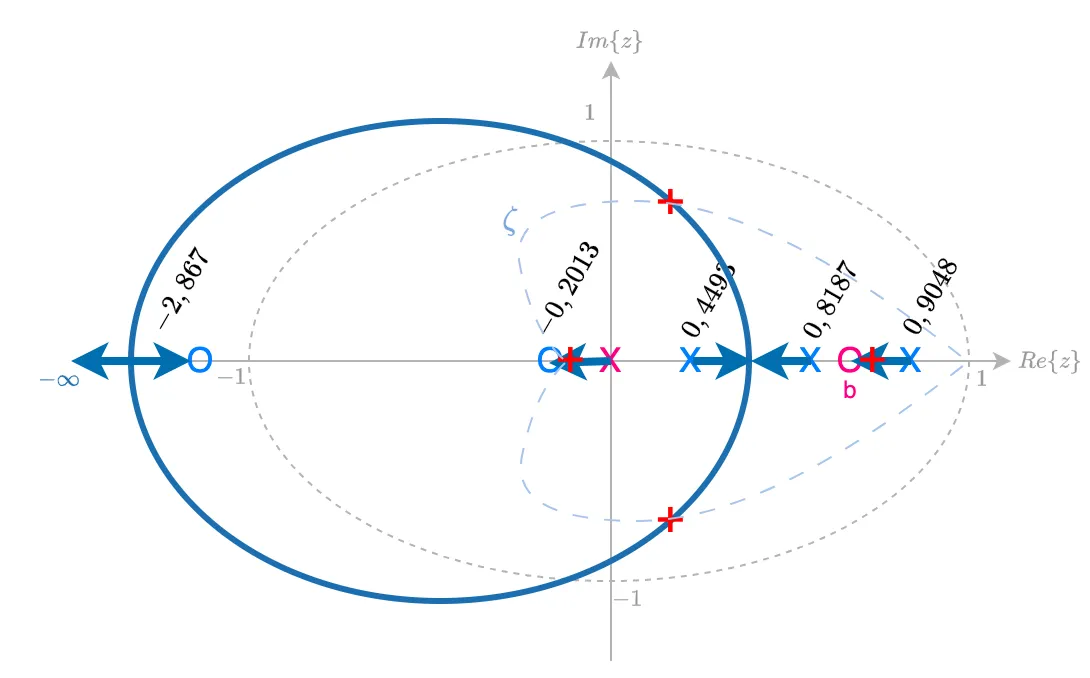
opcoes_zero_PDb

$z \to -\infty$ , o que garante uma resposta mais rápida em comparação com a opção "a".

E a opção "c" resulta no proximo RL:

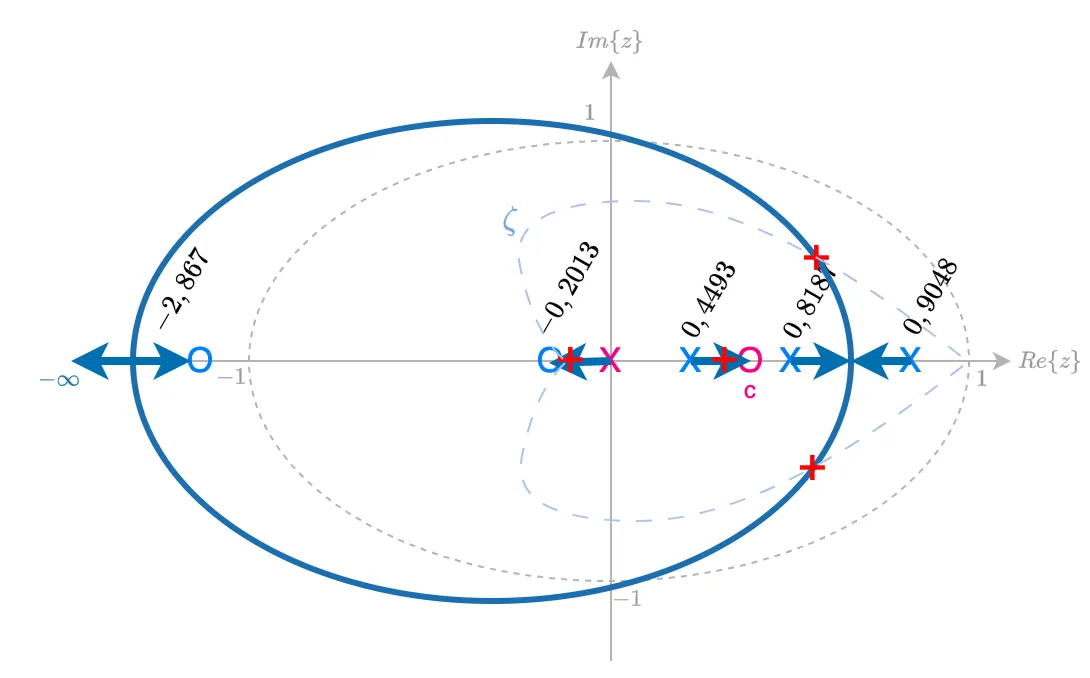
opcoes_zero_PDc

Esta opção cria um par de pólos de MF dominantes complexos, aparentemente mais próximos do círculo unitário (mais lentos) que em comparação com os pólos de MF dominantes da opção anterior "b".

4a-opção, opção"d" $z=0,9048$ ), colocando o zero do PD sobre o mesmo. Neste caso, temos um "ganho" extra que seria reduzir a complexidade do sistema. Com as outras opções obtemos um sistema de 4a-ordem em MF. Com esta opção, ficamos um sistema em MF de 3a-ordem. Este RL ficaria algo como:

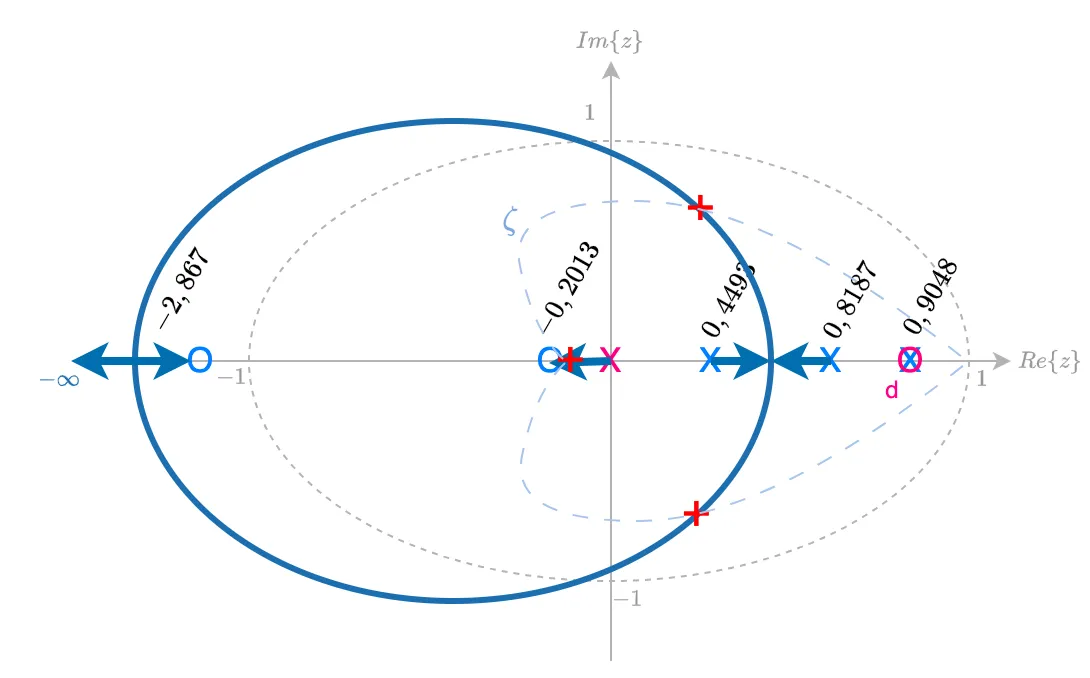
opcoes_zero_PDd

Esta opção parece a mais promissora. Reduz a complexidade do sistema, e garante um par de pólos complexos de MF dominantes, afastado do círculo unitário.

Projeto do PD "b"

$0,8187 \le z \le 0,9048$ (entre os 2 pólos + lentos da planta):


xxxxxxxxxx
>> ze_PD=(0.9048+0.8187)/2
ze_PD =
      0.86175
>> C_PDb=tf(poly(ze_PD),[1 0],T)
C_PDb =
 
  z - 0.8618
  ----------
      z
 
Sample time: 0.1 seconds
Discrete-time transfer function.
>> ftma_PDb=C_PDb*BoG;
>> zpk(ftma_PDb)
 
  0.0020446 (z+2.867) (z-0.8618) (z+0.2013)
  -----------------------------------------
     z (z-0.9048) (z-0.8187) (z-0.4493)
 
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.
>> rlocus(ftma_PDb)
>> hold on; zgrid(zeta,0)
>> axis([0.3 1.1 -0.2 0.6]) % zoom na região de interesse
>> [K_PDb,polosMF]=rlocfind(ftma_PDb)
Select a point in the graphics window
selected_point =
      0.65484 +    0.38453i
K_PDb =
        21.38
polosMF =
      0.86556 +          0i
      0.65366 +    0.38451i
      0.65366 -    0.38451i
    -0.043689 +          0i

RL deste PD:

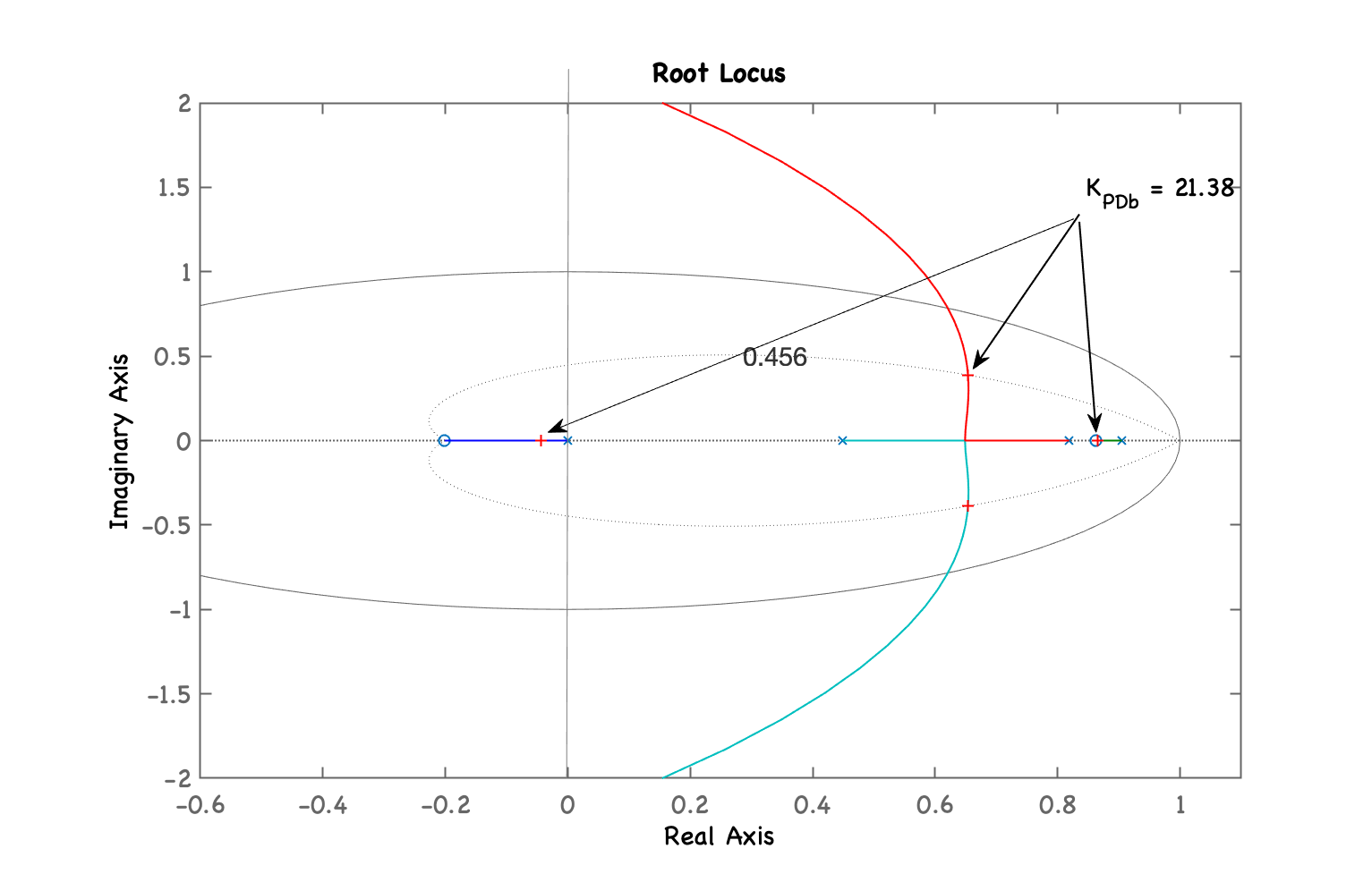
Temos o seguinte RL com "zoom" sobre região de interesse e ressaltando ganho adotado:

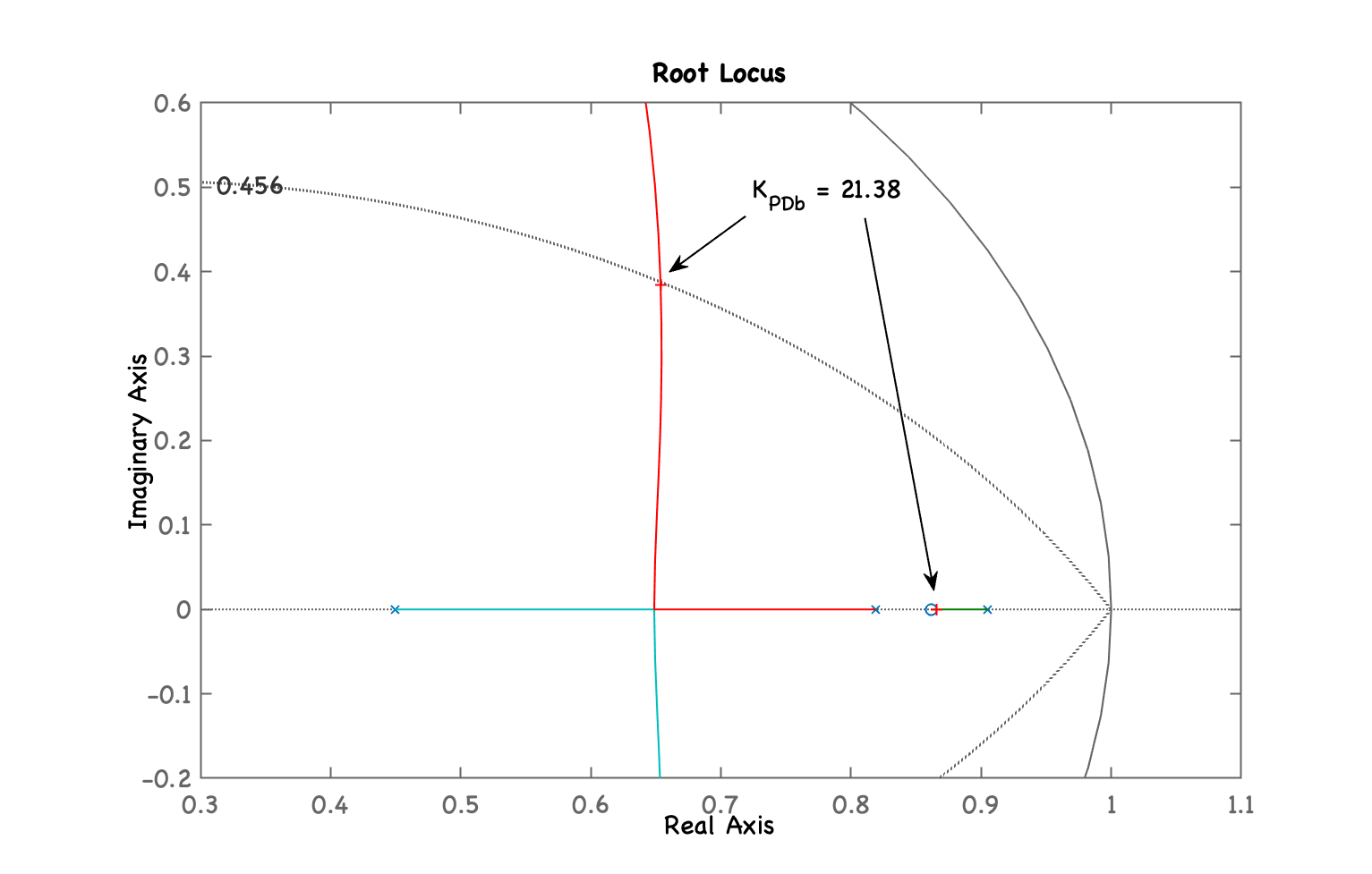
Fechando a malha:


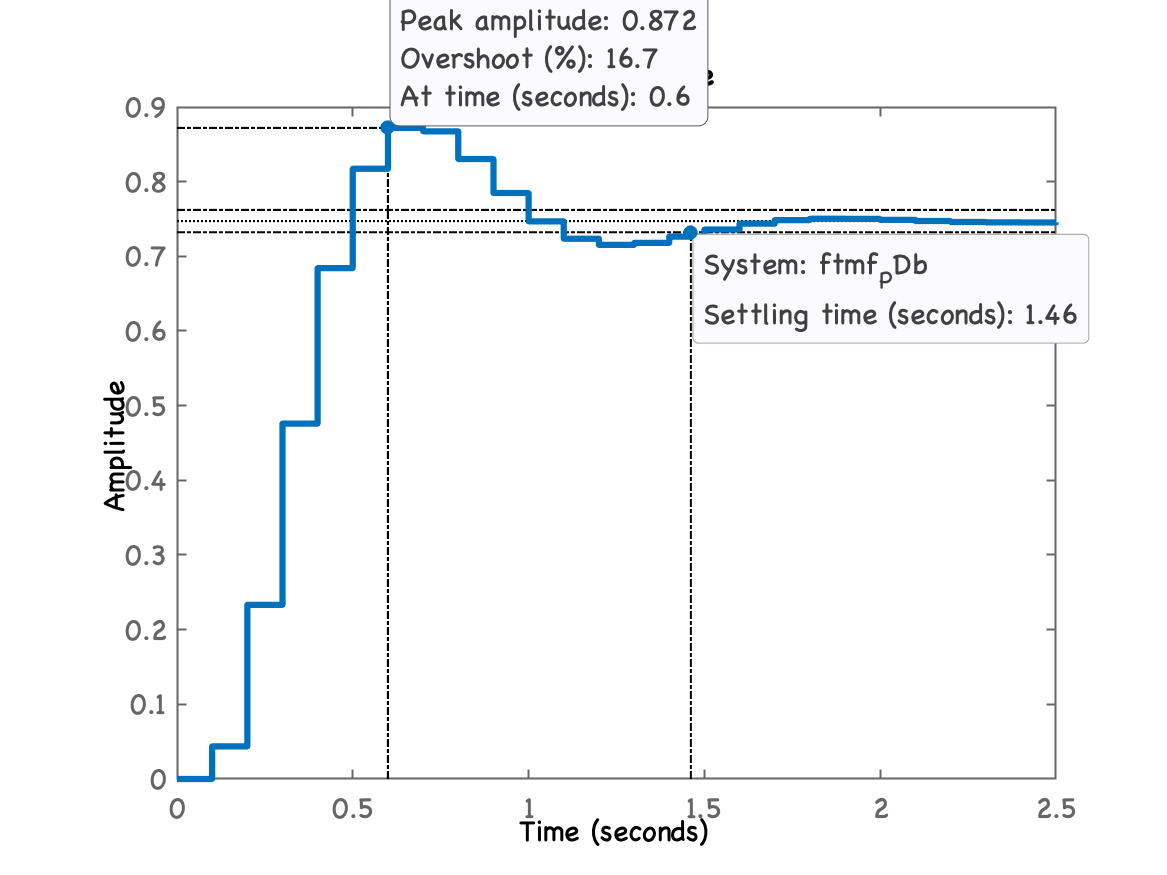
xxxxxxxxxx
>> ftmf_PDb=feedback(K_PDb*ftma_PDb, 1);
>> figure; step(ftmf_PDb)

E temos a seguinte resposta ao degrau:

Comparando com outros controladores


xxxxxxxxxx
>> figure; step(ftmf_K_OS2, ftmf_PId, ftmf_PDb)
>> legend('Prop', 'PId', 'PDb')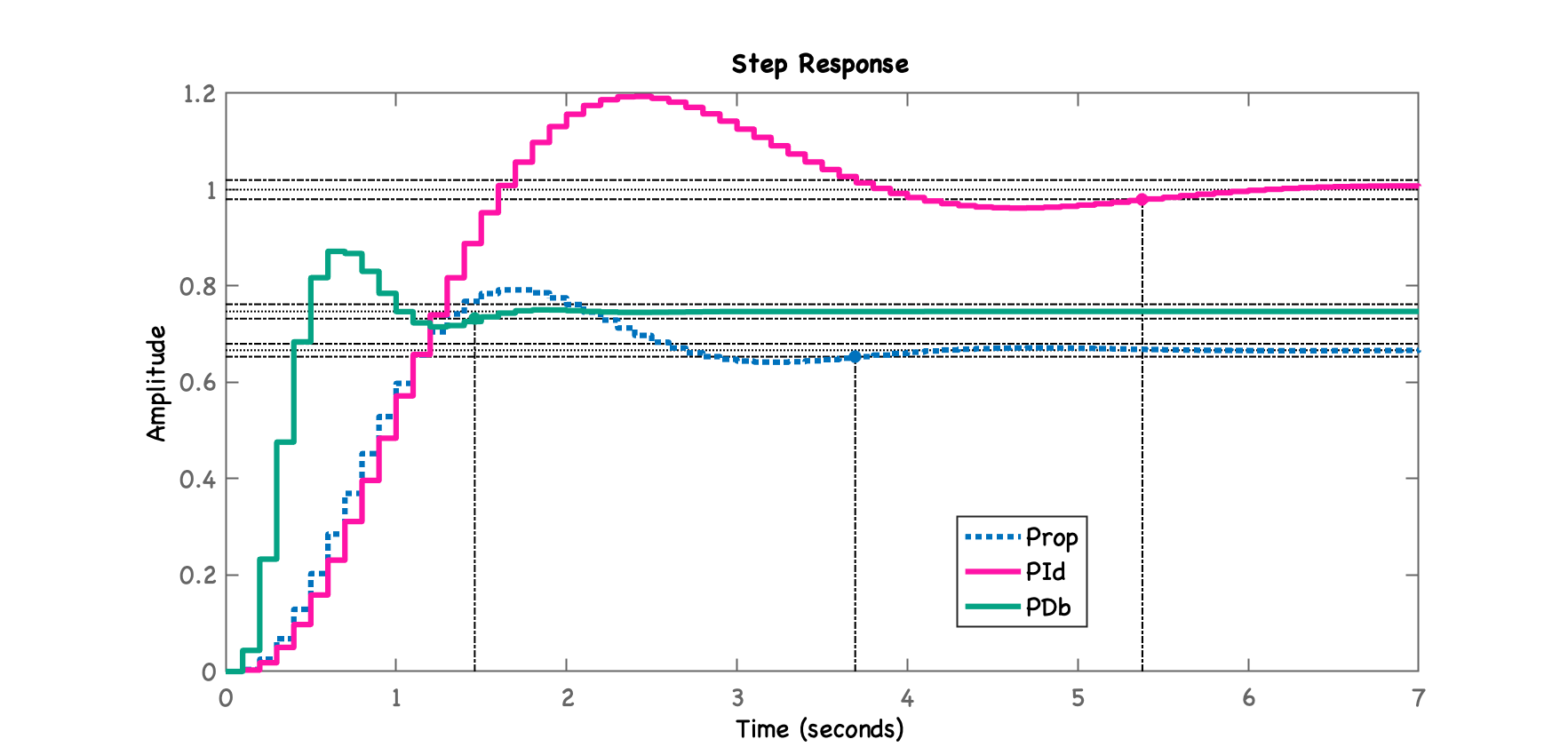

Projeto do PD "d"

Realizando o projeto do PD opção "d". Neste caso, analizando os RL's para as outras opções, percebemos uma 4a-opção: "d", neste caso, colocamos o zero do PD propositalmente sobre o pólo + lento da planta (provacando deliberadamente um cancelamento pólo-zero).


xxxxxxxxxx
>> polos_BoG=pole(BoG)
polos_BoG =
      0.90484
      0.81873
      0.44933
>> C_PDd=tf(poly(polos_BoG(1)),[1 0],T)
C_PDd =
 
  z - 0.9048
  ----------
      z
 
Sample time: 0.1 seconds
Discrete-time transfer function.
>> ftma_PDd=C_PDd*BoG;
>> figure; rlocus(ftma_PDd)
>> hold on; zgrid(zeta,0)
>> axis([0.3 1.1 -0.2 0.6])
>> [K_PDd,polosMF]=rlocfind(ftma_PDd)
Select a point in the graphics window
selected_point =
      0.63369 +    0.39825i
K_PDd =
       21.641
polosMF =
      0.90484 +          0i
      0.63466 +    0.39828i
      0.63466 -    0.39828i
    -0.045501 +          0i

Temos o RL com o mesmo "zoom" sobre região de interesse e ressaltando ganho adotado:

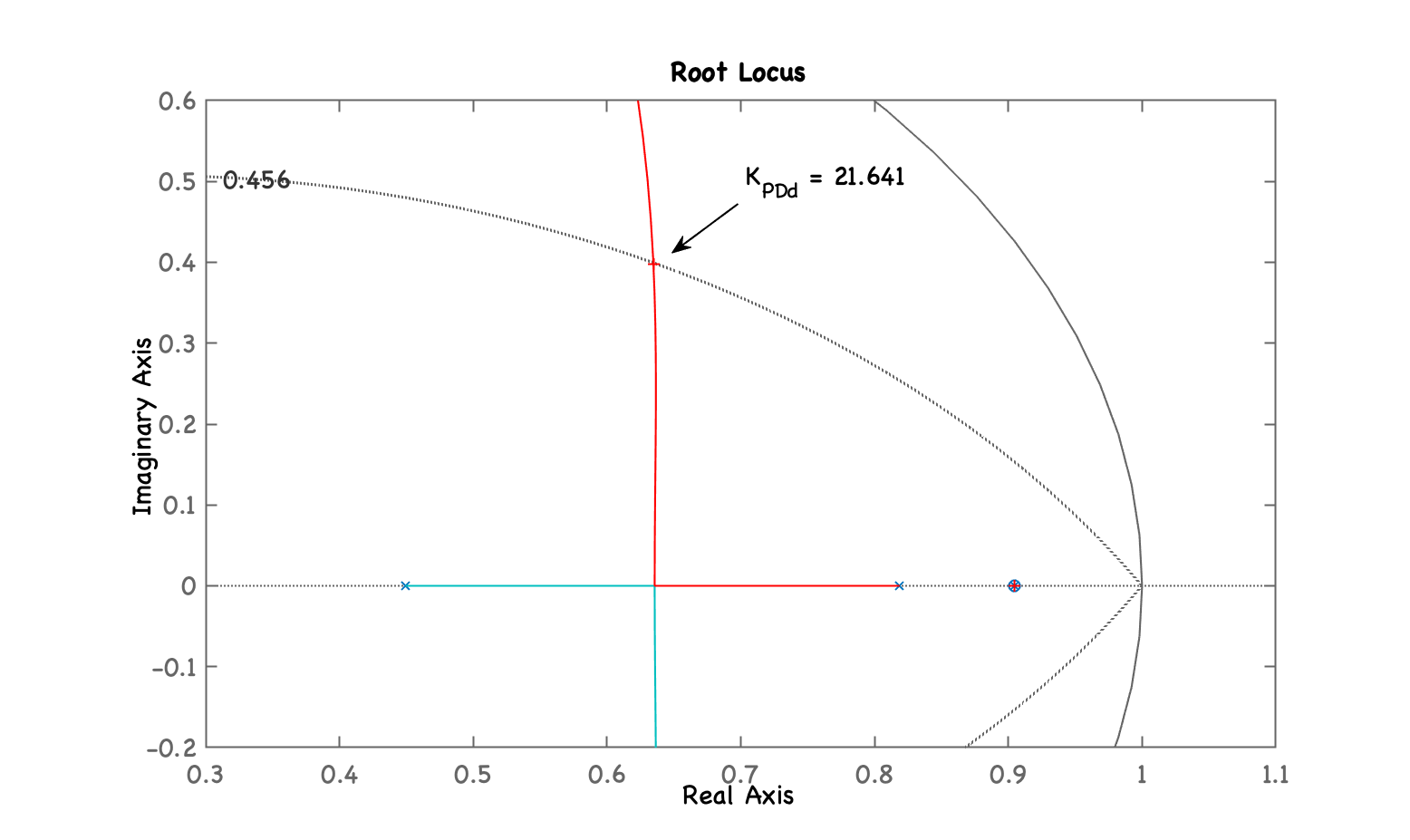
Fechando a malha...


xxxxxxxxxx
>> ftmf_PDd=feedback(K_PDd*ftma_PDd, 1);
>> figure; step(ftmf_PDb, ftmf_PDd)
>> legend('PD(b)', 'PD(d)')

Resposta à entrada degrau deste PD:


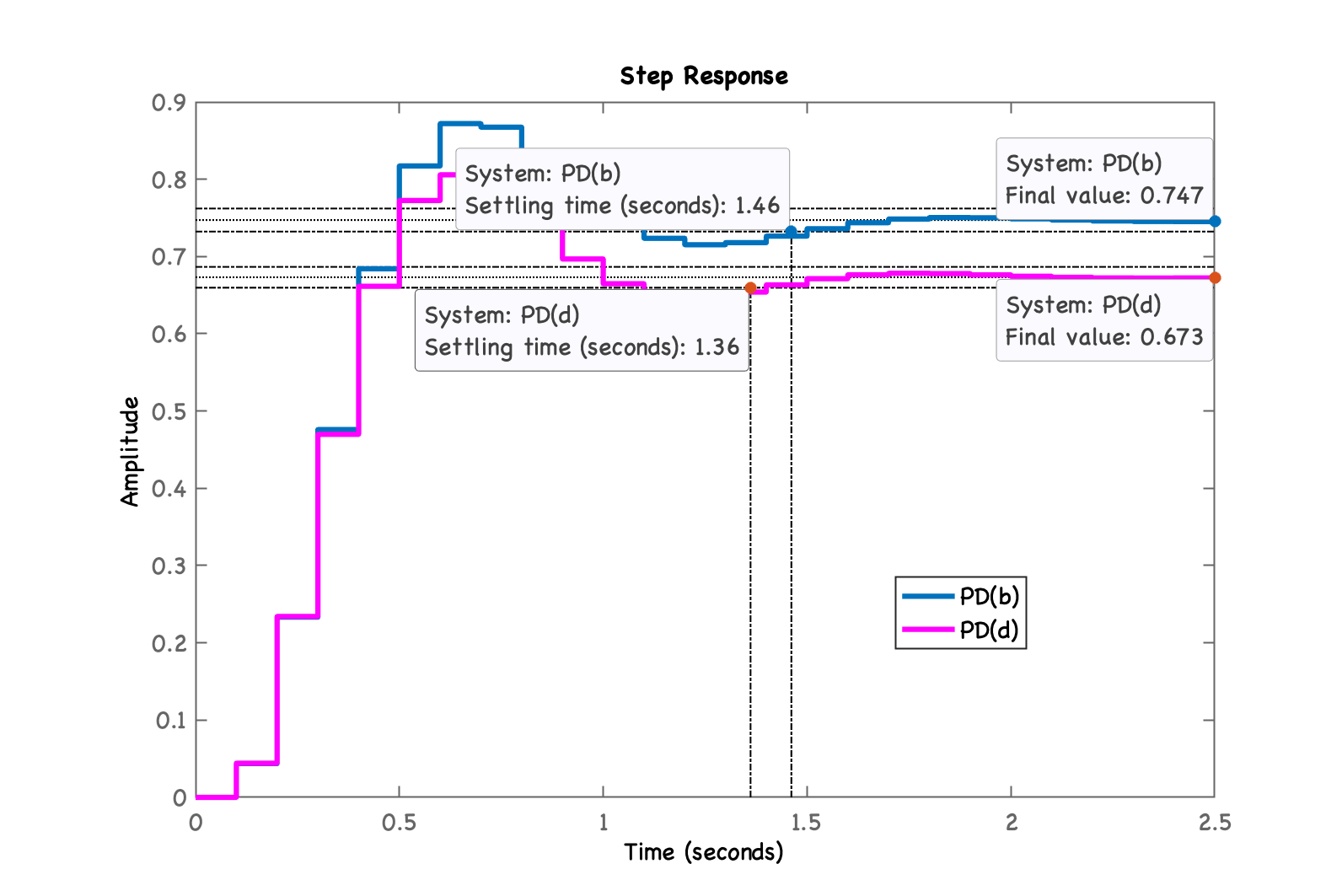
xxxxxxxxxx
>> stepinfo(ftmf_PDd)
        RiseTime: 0.2
    SettlingTime: 1.4
     SettlingMin: 0.64747
     SettlingMax: 0.80581
       Overshoot: 19.709
      Undershoot: 0
            Peak: 0.80581
        PeakTime: 0.6

O PD "d" é mais rápido que o PD "b", mas o erro é maior:


xxxxxxxxxx
>> erro_PDb=((1-dcgain(ftmf_PDb))/1)*100
erro_PDb =
       25.279
>> erro_PDd=((1-dcgain(ftmf_PDd))/1)*100
erro_PDd =
       32.686

Controlador Lead

$z=0,4493$ (pólo mais rápido da planta).

Lembrando da eq. do PD "b":


>> zpk(C_PDb)
 
  (z-0.8618)
  ----------
      z
 
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.

Usando a mesma posição do zero do PD "b" para o Lead:


xxxxxxxxxx
>> C_Lead=tf(poly(0.8618),[1 -0.2],T)
C_Lead =
 
  z - 0.8618
  ----------
   z - 0.2
 
Sample time: 0.1 seconds
Discrete-time transfer function.
>> ftma_Lead=C_Lead*BoG;
>> figure; rlocus(ftma_Lead)
>> hold on; zgrid(zeta,0)
>> axis([0.3 1.1 -0.2 0.6])
>> [K_Lead,polosMF]=rlocfind(ftma_Lead)
Select a point in the graphics window
selected_point =
      0.69005 +    0.36477i
K_Lead =
       15.397
polosMF =
      0.86586 +          0i
      0.68946 +    0.36481i
      0.68946 -    0.36481i
     0.096638 +          0i

Obtemos o seguinte RL:

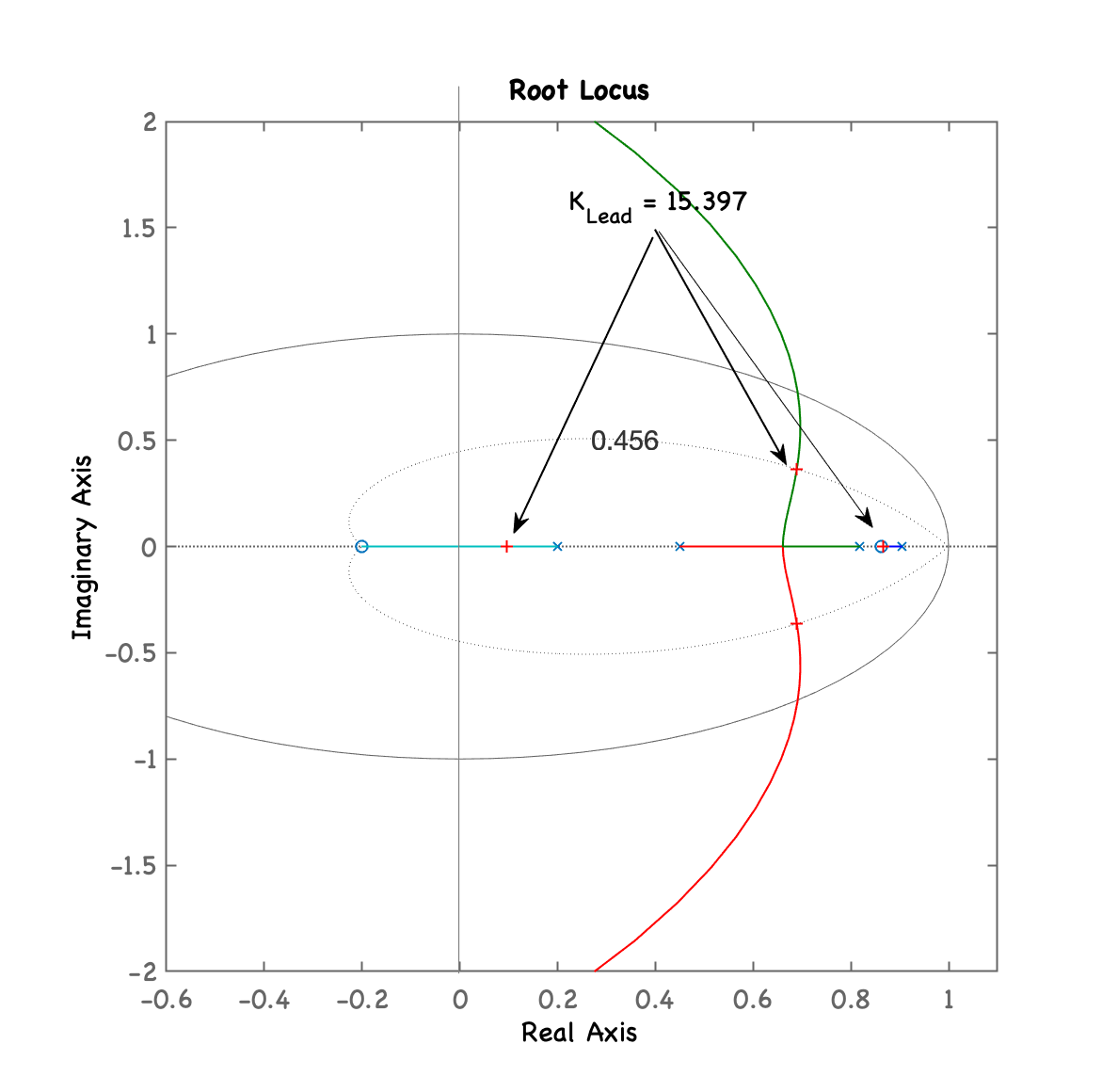
Repare que o pólo deste controlador está afastado da origem do plano-z.

O mesmo RL com zoom na região de interesse e mostrando ganho adotado:

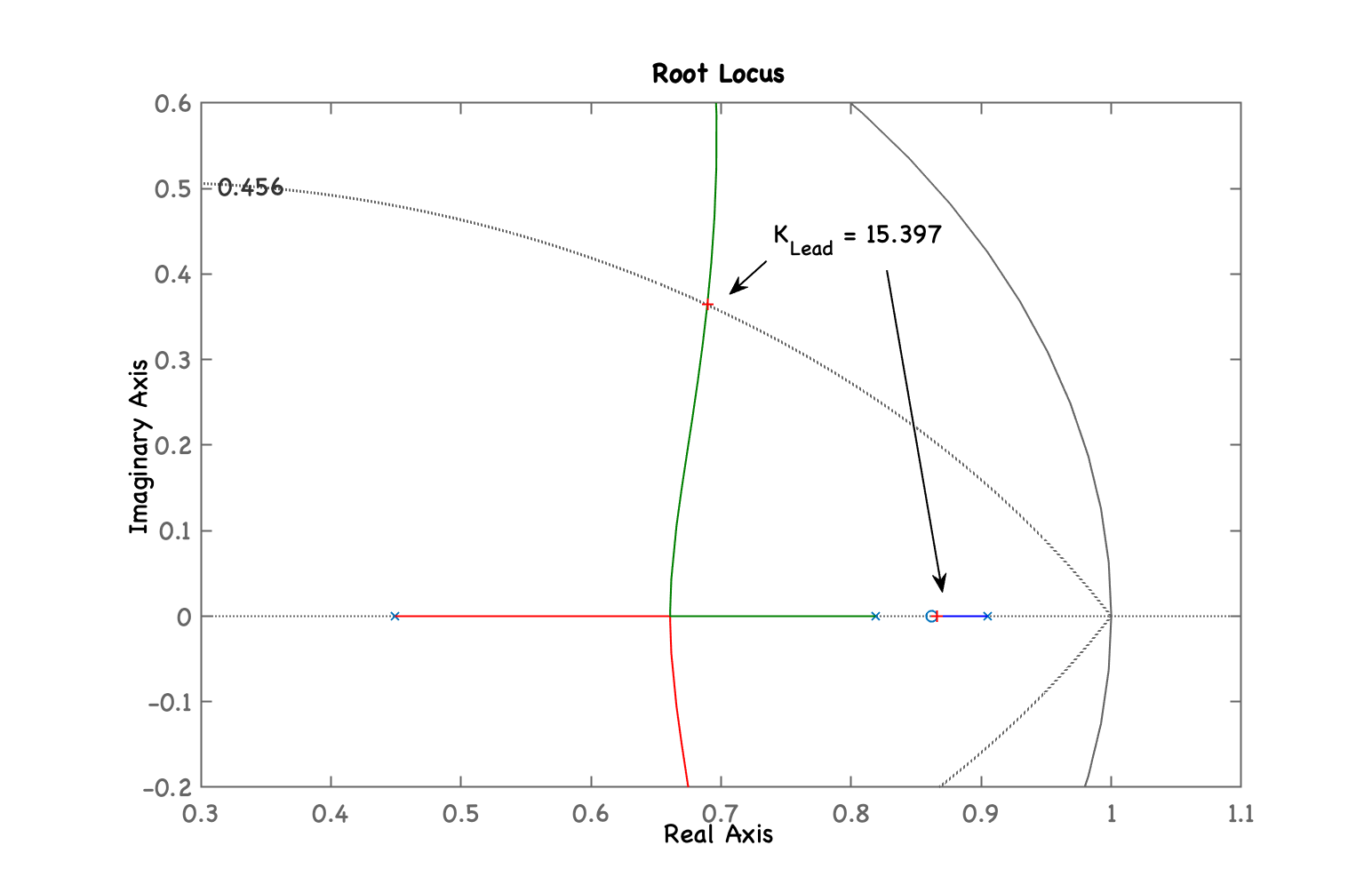
Fechando a malha...


xxxxxxxxxx
>> ftmf_Lead=feedback(K_Lead*ftma_Lead, 1);
>> figure; step(ftmf_Lead, ftmf_PDb)
>> legend('Lead', 'PD (b)')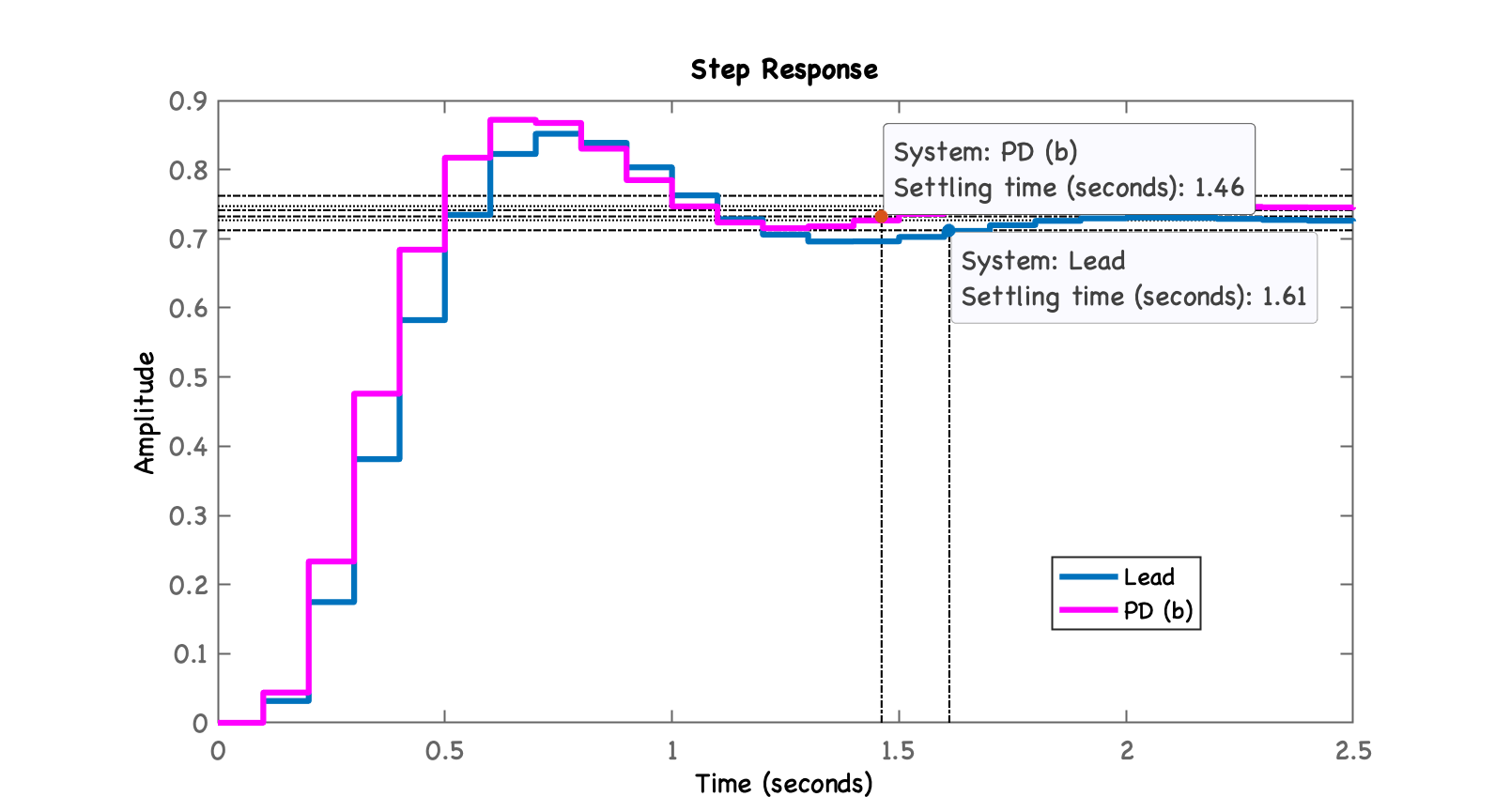

Calculando o erro de regime permanente


xxxxxxxxxx
>> dcgain(ftmf_Lead)
ans =
      0.72677
>> erro_Lead=((1-dcgain(ftmf_Lead))/1)*100
erro_Lead =
       27.323

Terminando esta seção de trabalho:


xxxxxxxxxx
>> save planta
>> diary off
>> quit