Considerações matemáticas

Conceitos Introdutórios

Propriedades físicas do ar

Apesar de insípido, inodoro e incolor, percebemos o ar através dos ventos, aviões e pássaros que nele flutuam e se movimentam; sentimos também o seu impacto sobre o nosso corpo. Concluímos que o ar tem existência real e concreta, ocupando lugar no espaço.

Compressibilidade do ar comprimido

O ar, assim como todos os gases, tem de ocupar todo o volume de qualquer recipiente, adquirindo o seu formato, já que não tem forma própria. Assim, podemos encerrá-lo num recipiente com volume determinado e, posteriormente, provocar-lhe uma redução de volume, usando uma de suas propriedades – a compressibilidade.

Ar-comprimido $\Rightarrow$$\Rightarrow$ compressível e elástico:

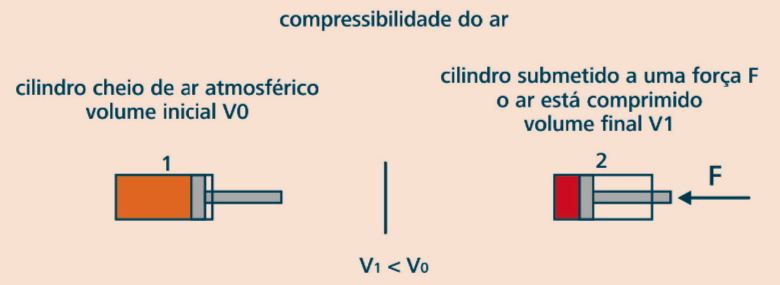
O ar atmosférico permite reduzir o seu volume quan- do sujeito à ação de uma força exterior.

Elasticidade

Propriedade que possibilita ao ar voltar ao seu volume inicial, uma vez extinto o efeito (força) responsável pela redução do volume.

Difusibilidade

Propriedade do ar que lhe permite misturar-se homogeneamente com qual- quer meio gasoso que não seja saturado.

Expansibilidade

Propriedade do ar que lhe possibilita ocupar totalmente o volume de qual- quer recipiente, adquirindo o seu formato.

Princípios Básicos

1. Pressão: no compressor;
2. Fluídos: comportamento;
3. Fluxo (de ar): pressão envolvida nos condutos;
4. Trabalho: que vai realizar cada cilindro;
5. Potência: requerida para realizar o trabalho.

Pressão

Atmosfera é a camada formada por gases, principalmente Oxigênio (O${}_2$$_2$) e Nitrogênio (N${}_2$$_2$), que envolve toda a superfície do planeta. Pelo fato de o ar ter peso, as camadas inferiores são comprimidas pelas camadas superiores. Assim, as camadas superiores são menos densas que as inferiores. Concluí- mos, portanto, que um volume de ar comprimido é mais pesado que o ar à pressão normal ou à pressão atmosférica.

Quando dizemos que um litro de ar pesa $1,293\times {10}^3$$1,293 \times 10^3$ kg ao nível do mar, significa que, em altitudes diferentes, o peso do ar tem valores diferentes.

A atmosfera exerce sobre nós uma força equivalente ao seu peso, mas não o sentimos, pois ela atua em todos os sentidos e direções com a mesma intensidade.

A pressão atmosférica varia proporcionalmente à altitude considerada.

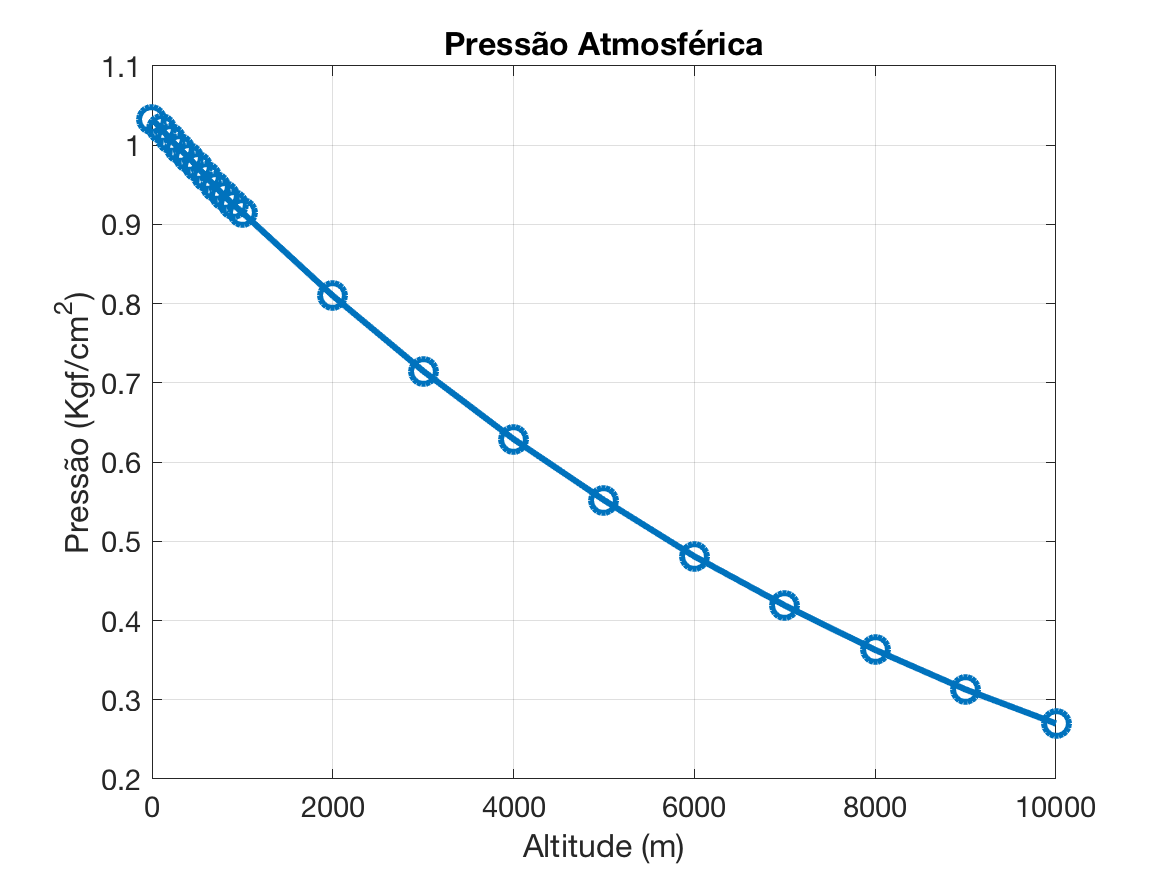
Definição:

$Pressão(P)={\displaystyle \frac{Força(F)}{Superfície(A)}}$$Pressão (P) = \dfrac{Força (F)}{Superfície (A)}$ = [Pa] (Sistema Internacional: Pascal)

Para expressar pressão de um gás ou líquido, se considera 3 tipos de pressão:

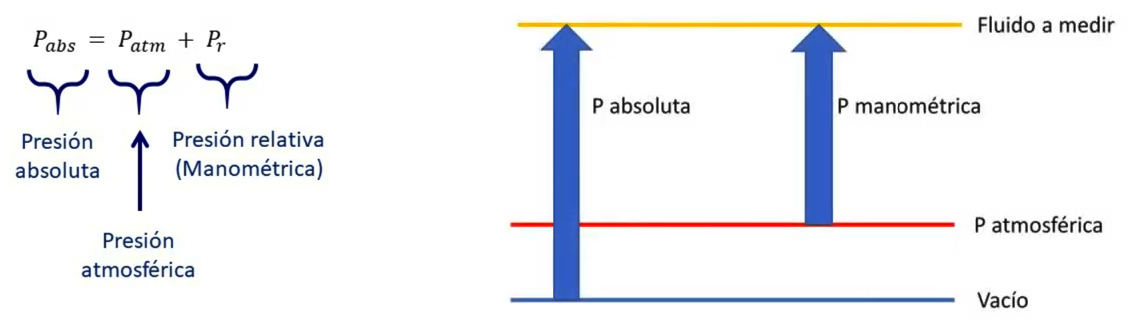
Pressão atmosférica:

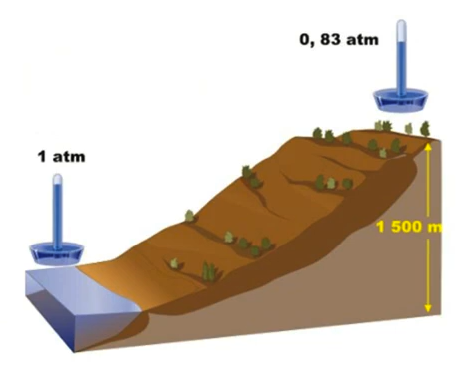
Unidades de Pressão:

São utilizadas diversas unidades de medida, conforme o país ou o tipo de ciência ou indústria.

kgf/cm2 – quilograma força por centímetro quadrado.

PSI – abreviatura de pounds per square inch – libras por polegada quadrada.

bar – é um múltiplo da Bária: 1 bar = 100 bárias. Bária é a unidade de pressão no sistema c, g, s, e vale uma dyn/cm2.

kPa – O pascal (símbolo: Pa) é a unidade padrão de pressão e tensão no SI. Equivale a força de 1 N aplicada uniformemente sobre uma superfície de 1 m2. O plural no nome da unidade pascal é pascals. O nome desta unidade é uma homenagem a Blaise Pascal, eminente matemático, físico e filósofo francês.

Torr = mm Hg – também chamado Torricelli, é uma unidade de pressão antiga, que equivale a 133,322 Pa. Surgiu quando Evangelista Torricelli inventou o barômetro de mercúrio, em 1643 e tem caído em desuso com o apare- cimento de tecnologia mais eficaz para a medição da pressão atmosférica e com a disseminação das unidades do sistema internacional de unidades.

Outra tabela:

Obs.: Pressão atmosférica se mede com um barômetro.

Pressão manométrica (relativa):

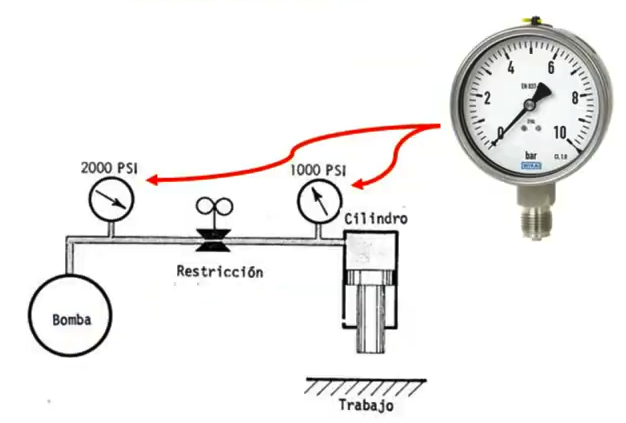
O ar é muito compressível sob ação de pequenas forças. Quando contido em um recipiente fechado, o ar exerce uma pressão igual sobre as paredes, em todos os sentidos.

Por exemplo, quando estamos apalpando uma bola de futebol, percebe-se a mesma pressão, uma pressão uniformemente distribuída, sobre qualquer parte da sua superfície.

Relações matemáticas, lei de Blaise Pascal:

$P={\displaystyle \frac{F}{A}}$$P=\dfrac{F}{A} \qquad$ ou $F=P\cdot A$$\qquad F=P \cdot A$

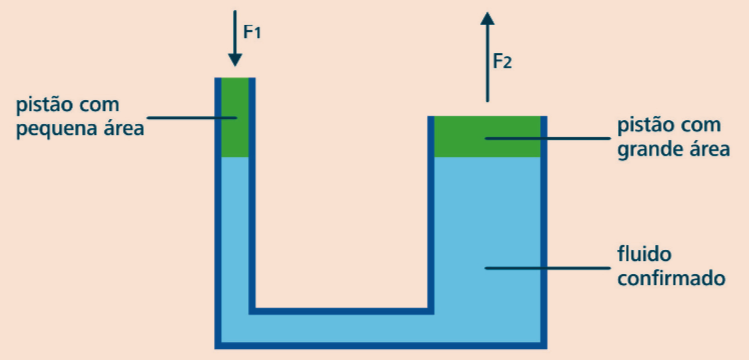
Onde:

Observações adicionais:

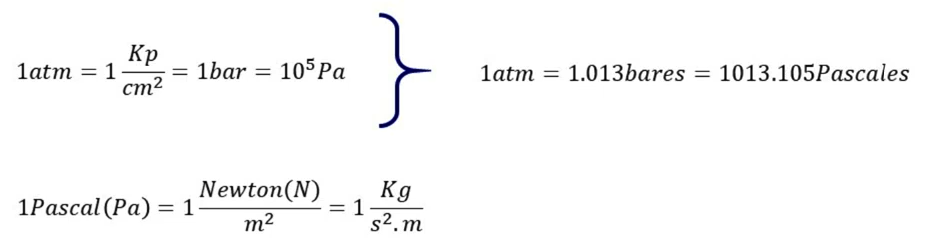
Nota: pressão atmosférica padrão = 101.325 Pa (sob condições normais de temperatura e pressão: $0^{o}C$$0 ^o C$ e 101.325 Pa (101325 Pa = 1,01325 bar = 1 atm = 760 mmHg).

Obs.: Atualmente a IUPAC (União Internacional de Química Pura e Aplicada) recomenda que o uso da pressão de 101.325 Pa seja descontinuado, recomendando desde 1982, o uso da atual pressão padrão, definida como uma pressão de 105 Pa (100.000 Pa exatamente).

Condições padrão de temperatura e pressão: mais atual, correspondem às condições de temperatura e pressão de 273,15 K (0 °C) e 100.000 Pa (100.000 Pa = 105 Pa = 100,0 kPa = 1 bar), respectivamente.

Diferentes sistemas de unidades:

Exemplo: Determinar a pressão absoluta Kgf/cm${}^2$$^2$ que se exerce ao aplicar uma força de 1,5 Kgf sobre um êmbolo que possui área de contato (superfície) de 0,001 cm${}^2$$^2$ ?

Solução:

Dados: $\begin{array}{c}\{\begin{array}{rcl}F& =& 1,5[Kgf]\\ A& =& 0,001[c{m}^2]\end{array}\end{array}$$\left\{ \begin{array}{rcl} F &=& 1,5 \; [Kgf]\\ A &=& 0,001 \; [cm^2]\end{array}\right.$

Aplicando as equações:

$P={\displaystyle \frac{F}{A}}={\displaystyle \frac{1,5[Kgf]}{0,001[cm]}}=1500[Kgf/c{m}^2]$$P=\dfrac{F}{A}=\dfrac{1,5 \; [Kgf]}{0,001 \; [cm]}=1500 \; [Kgf/cm^2]$

Esta é a pressão relativa, a pressão absoluta é dada por:

$P_{abs}=P_{atm}+P_r$$P_{abs}=P_{atm}+P_r$

então:

$P_{abs}=1\left[{\displaystyle \frac{Kgf}{c{m}^2}}\right]+1500\left[{\displaystyle \frac{Kgf}{c{m}^2}}\right]=1501\left[{\displaystyle \frac{Kgf}{c{m}^2}}\right]$$P_{abs}= 1 \; \left[\dfrac{Kgf}{cm^2} \right]+1500 \; \left[\dfrac{Kgf}{cm^2} \right]= 1501 \; \left[\dfrac{Kgf}{cm^2} \right]$

Sobre Força:

Definição moderna: Segunda lei de Newton: $\overrightarrow{F}={\displaystyle \frac{\mathrm{d}\overrightarrow{p}}{\mathrm{d}t}}$$\vec{F} = \dfrac{\mathrm{d}\vec{p}}{\mathrm{d}t}$, Onde: $\overrightarrow{p}$$\vec{p}$ se refere ao momento linear do sistema, e $\overrightarrow{F}$$\vec{F}$ a força resultante. Ambos são grandezas vetoriais. Num sistema com massa constante: $\overrightarrow{F}={\displaystyle \frac{\mathrm{d}\overrightarrow{p}}{\mathrm{d}t}}={\displaystyle \frac{\mathrm{d}\left(m\overrightarrow{v}\right)}{\mathrm{d}t}}$$\vec{F} = \dfrac{\mathrm{d}\vec{p}}{\mathrm{d}t} = \dfrac{\mathrm{d}\left(m\vec{v}\right)}{\mathrm{d}t}$ Onde: $m$$m$ se refere à massa e $\overrightarrow{v}$$\vec{v}$ se refere à velocidade.

Ou mais simplesmente:

$\overrightarrow{F}=m\cdot \overrightarrow{a}$$\vec{F}=m \cdot \vec{a}$

Unidades:

Sigla	Unidade	Obs
[N]	Newton	Unidade SI. 1 [N] = 1 Kg$\cdot$$\cdot$m/s${}^2$$^2$.
[Kgf]	Quilograma-força	Como a aceleração da gravidade é $\approx 9,8[m/s^2]$$\approx 9,8 \,[m/s^2]$, o peso de um corpo de 1 [Kg] é de aproximadamente 9,8 [N], ou seja: 1 [Kgf] = 9,8 [N].

 

Atenção:

Flambagem da haste

Algumas aplicações requerem atuadores de cursos longos. Se existe uma carga de compressão axial aplicada na haste, é preciso assegurar que os parâmetros de comprimento, diâmetro e carga estejam dentro dos limites de segurança para evitar a flambagem da haste.

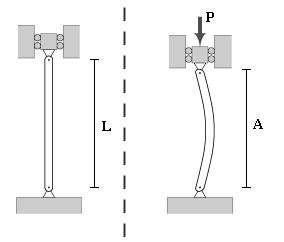
A flambagem ou encurvadura é um fenômeno que ocorre em peças esbeltas (peças em que a área de seção transversal é pequena em relação ao seu comprimento), quando submetidas a um esforço de compressão axial. A flambagem acontece quando a peça sofre flexão transversalmente devido à compressão axial. A flambagem é considerada uma instabilidade elástica, assim, a peça pode perder sua estabilidade sem que o material já tenha atingido a sua tensão de escoamento. Este colapso ocorrerá sempre em torno do eixo de menor momento de inércia de sua seção transversal. A tensão crítica para ocorrer a flambagem não depende da tensão de escoamento do material, mas sim de seu módulo de Young.

- carga crítica de flambagem: faz com que a peça comece a flambar. Unidade - N

• Equilíbrio estável: $P<P_{CR}$$P<P_{CR}$ - não há flambagem;
• Equilíbrio indiferente: $P=P_{CR}$$P=P_{CR}$;
• Equilíbrio instável: $P>P_{CR}$$P>P_{CR}$.

Quando a flambagem ocorre na fase elástica do material, a carga crítica ( $P_{CR}$$P_{CR}$ ) é dada pela fórmula de Euler :(para instabilidade elástica):

Onde: $E=$$E=$ módulo de elasticidade longitudinal do material, expressado em pascal; $I=$$I=$ menor dos momentos de inércia da secção em $m^4$$m^4$; $L_f=$$L_f=$ comprimento de flambagem da peça em metros.

Para determinar se uma peça irá sofrer flambagem ou compressão, temos que calcular o seu índice de esbeltez e compara-lo ao índice de esbeltez crítico. Esse índice de esbeltez é padronizado para todos os materiais.

Se o índice de esbeltez crítico for maior que o índice de esbeltez padronizado do material, a peça sofre flambagem, se for menor, a peça sofre compressão.

Determinação de $L_f$$L_f$:

O comprimento equivalente livre de flambagem $L_f$$L_f$ usado na fórmula é determinado pela instalação. Para pino articulado em um dos lados (Euler caso 2) o comprimento livre $L_f$$L_f$ é o mesmo $l$$l$ entre as juntas. Para uma montagem com um lado livre e o outro fixo (Euler caso 1): $L_f=2\cdot l$$L_f=2 \cdot l$:

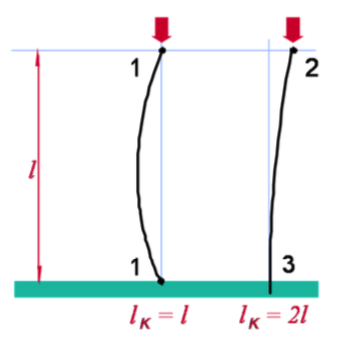
Outros casos:

Casos:	Observações
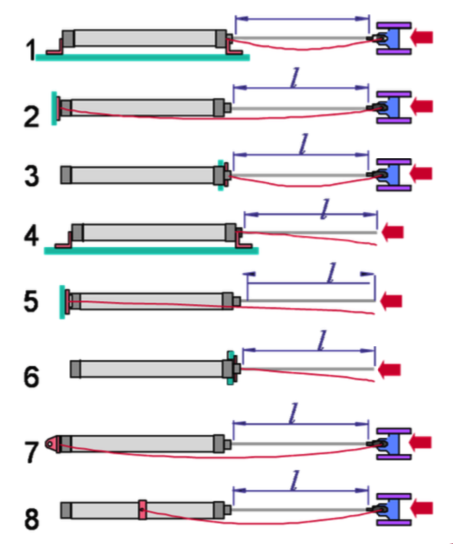	_Casos 1,2 e 3: uma haste entre mancais será considerada como articulada em um dos lados. Assumir $L_f=l$$L_f=l$ (Euler caso 2) _ Casos 4,5 e 6: o final da haste livre lateralmente assume $L_f=2l$$L_f=2l$ (Euler caso 1) - Caso 7: especial: $L_f<2l$$L_f<2l$ _ Caso 8: especial: $L_f<1,5l$$L_f<1,5l$ Obs.: Carga no avanço desenvolvida à pressão dada

Segue tabela exemplo de flambagem (fabricante IMI):

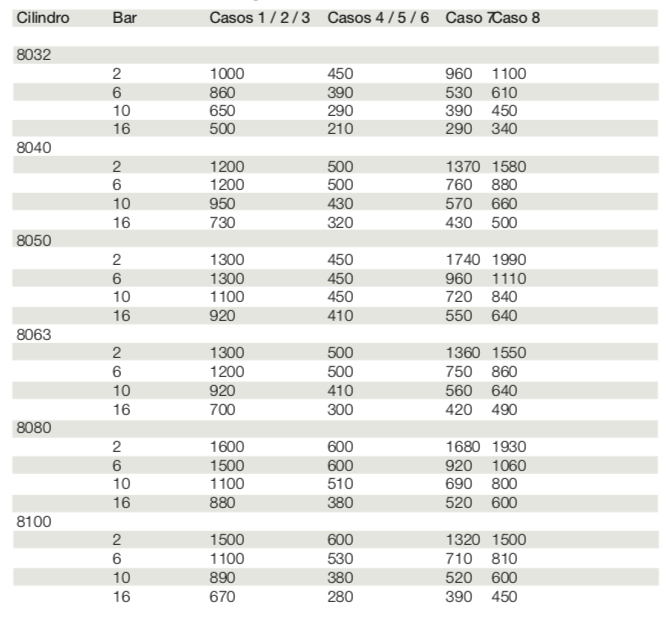
Obs: (1) Fator de segurança, "s" = 5; (2) Tabela dos curos máximos em [mm].

Fluídos

Para ar: equação geral dos gases:

$P\cdot V=n\cdot R\cdot T$$P \cdot V = n \cdot R \cdot T$

Onde: $P=$$P=$ Pressão (N/m${}^2$$^2$); $V=$$V=$ Volume (m${}^3$$^3$); $n=$$n=$ número de moles (quantidade de moléculas); $R=$$R=$ constante universal dos gases: $R=8,314\left[{\displaystyle \frac{J}{mol\cdot K}}\right]$$R=8,314 \; \left[\dfrac{J}{mol \cdot K}\right]$; $T=$$T=$ temperatura (Kelvin).

Propriedades de um sistema fechado baseado em gases (ar-comprimido; incompressível)

Isolando a cte $R$$R$ na eq.: $P\cdot V=n\cdot R\cdot T$$P \cdot V = n \cdot R \cdot T$ teremos:

$R={\displaystyle \frac{P\cdot V}{T\cdot n}}$$R=\dfrac{P \cdot V}{T \cdot n}$.

E então, num sistema de malha fechada, teremos:

${\displaystyle \frac{P_1\cdot V_1}{T_1\cdot n_1}}={\displaystyle \frac{P_2\cdot V_2}{T_2\cdot n_2}}$$\dfrac{P_1 \cdot V_1}{T_1 \cdot n_1}=\dfrac{P_2 \cdot V_2}{T_2 \cdot n_2}$

Casos que se apresentam:

• Processo isotérmico ($T=cte$$T=cte$): $P_1\cdot V_1=P_2\cdot V_2$$P_1 \cdot V_1=P_2 \cdot V_2$;
• Processo isobárico ($P=cte$$P=cte$): ${\displaystyle \frac{V_1}{T_1}}={\displaystyle \frac{V_2}{T_2}}$$\dfrac{V_1}{T_1}=\dfrac{V_2}{T_2}$;
• Processo isocora ($V=cte$$V=cte$): ${\displaystyle \frac{P_1}{T_1}}={\displaystyle \frac{P_2}{T_2}}$$\dfrac{P_1}{T_1}=\dfrac{P_2}{T_2}$

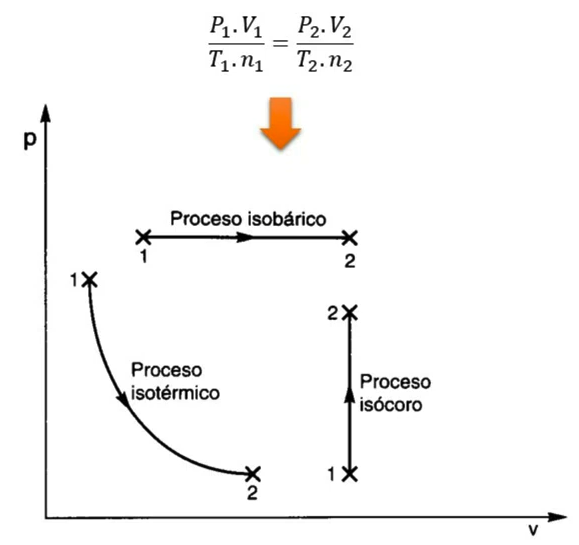
Exemplo: Seja um gás que inicialmente ocupava 15 cm${}^3$$^3$, é comprimido à uma temperatura constante até ocupar o volume final de 5 cm${}^3$$^3$. Se inicialmente se encontrava a uma pressão de 2 bares, qual será sua nova pressão depois que seu volume foi modificado?

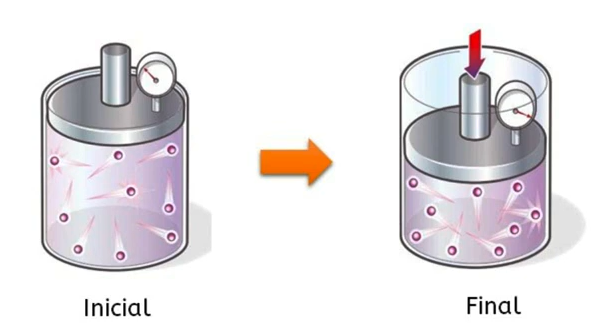
Solução:

Como a temperatura é constante (sistema isotérmico), se aplica a eq.:

$P_1\cdot V_1=P_2\cdot V_2$$P_1 \cdot V_1=P_2 \cdot V_2$

$2\cdot 15=P_2\cdot 5$$2 \cdot 15 = P_2 \cdot 5$

$P_2=6(bares)$$P_2=6 \; (bares)$

Lei geral dos gases perfeitos

As leis de Boyle-Mariotte, Charles e Gay Lussac referem-se às transformações de estado, nas quais uma das variáveis físicas permanece constante.

Geralmente, a transformação de um estado para outro envolve um relacio- namento entre todas. Assim, a relação generalizada é expressa pela equação:

De acordo com essa relação, são conhecidas as três variáveis do gás. Por isso, se qualquer uma das variáveis sofrer alteração, o efeito nas outras variáveis poderá ser previsto. Ver o Quadro 1.3, que relaciona o que acontece com a alteração de uma variável.

Note: Quando você enche uma bola ou pneu com uma bomba manual temos:

1. Volume – permanece constante.
2. Pressão – aumenta, pois a bola ou pneu fica mais “dura”.
3. Temperatura – aumenta. Isto pode ser notado na base da bomba, que esquenta.

Fluxo ($Q$$Q$)

Conceitos matemáticos...

Pode ser definido como:

$Q={\displaystyle \frac{Volume}{Tempo}}={\displaystyle \frac{V}{t}}$$Q=\dfrac{Volume}{Tempo}=\dfrac{V}{t}$

$V=S\cdot L$$V=S \cdot L$

onde: $V=$$V=$ Volume e $S=$$S=$ seção/superfície (m${}^2$$^2$); $L=$$L=$Comprimento.

$v={\displaystyle \frac{L}{t}}$$v=\dfrac{L}{t}$

Onde: $v=$$v=$Velocidade; $t=$$t=$tempo; $L=$$L=$Comprimento.

Lei da continuidade:

$Q={\displaystyle \frac{S\cdot L}{t}}=S\cdot v$$Q=\dfrac{S \cdot L}{t}=S \cdot v$

Exemplo: Um fluído corre dentro de um tubo e sai no duto No. 2 a uma velocidade de $v_2=5(cm/s)$$v_2=5 \; (cm/s)$ e pelo duto No. 3 com uma velocidade de $v_3=2(cm/2)$$v_3=2 \; (cm/2)$ . -- ver figura à seguir. Determine o fluxo do fluído no ponto No. 1. Dados: considera que as seções transversais sejam: $S_2=2(c{m}^2)$$S_2=2 \; (cm^2)$ e $S_3=6(c{m}^2)$$S_3=6 \; (cm^2)$.

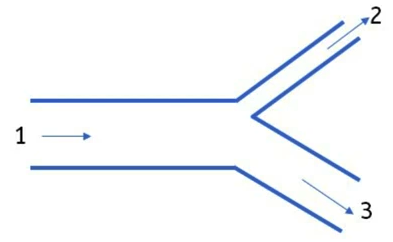
Solução:

Assumindo que não haja perdas:

$Q_1=Q_2+Q_3$$Q_1=Q_2+Q_3$

$Q_1=S_2\cdot v_2+S_3\cdot v_3$$Q_1=S_2 \cdot v_2 + S_3 \cdot v_3$

$Q_1=2(c{m}^2)\cdot 5(cm/s)+6(c{m}^2)\cdot 2(cm/s)$$Q_1=2 \;(cm^2) \cdot 5 \;(cm/s)+ 6 \;(cm^2) \cdot 2 \;(cm/s)$

$Q_1=22(c{m}^3/s)$$Q_1 = 22 \; (cm^3/s)$

Trabalho ($W$$W$)

$W=F\cdot d$$W=F \cdot d$

Onde: $W=$$W=$ trabalho; $F=$$F=$ Força; $d=$$d=$distância percorrida.

Se o trabalho for aplicado sobre um cilindo, então:

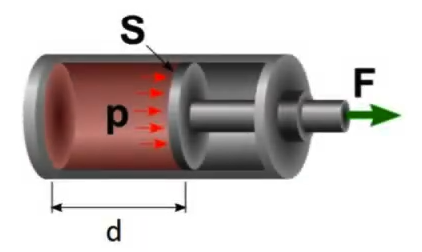
Da pressão se obtêm:

$P={\displaystyle \frac{F}{S}}$$P=\dfrac{F}{S} \quad$, então: $F=P\cdot S$$\quad F=P \cdot S$

Sendo que a Variação de volume: $\mathrm{\Delta }V=S\cdot d$$\Delta V = S \cdot d$

Levando à:

$W=P\cdot \mathrm{\Delta }V$$W = P \cdot \Delta V$

Trabalho $\Rightarrow 1(J)=1(N\cdot m)=1(Pa\cdot m^3)$$\Rightarrow 1 \;(J) = 1 \; (N \cdot m) = 1 \;(Pa \cdot m^3)$.

$(J)=$$(J)=$Joules.

Exemplo: Ao ingressar ar-comprimido num pistão de dublo efeito com pressão de 500 (KPa), este faz com que o êmbolo do cilindro se desloque 0,45 (m). Determinar o trabalho realizado pelo cilindro. Obs.: Considerar que a seção transversal do cilindro seja de $S=12(c{m}^2)$$S=12\;(cm^2)$.

Solução:

Dados: $P=500(KPa)d=0,45(m)S=12(c{m}^2)$$P=500 \;(KPa) \qquad d=0,45\;(m) \qquad S=12\;(cm^2)$

$W=P\cdot \mathrm{\Delta }V=P\cdot (S\cdot d)$$W=P \cdot \Delta V=P \cdot (S \cdot d)$

$W=500\times {10}^3(Pa)\cdot 12\times \underset{{10}^{-2}\cdot {10}^{-2}}{\underbrace{{10}^{-4}}}(m^2)\cdot 0,45(m)$$W=500 \times 10^3 \;(Pa) \cdot 12 \times \underbrace{10^{-4}}_{10^{-2}\cdot 10^{-2}} \;(m^2) \cdot 0,45 \;(m)$

$W=270(J)$$W = 270 \;(J)$

Potência ($P$$P$)

$P(Potência)={\displaystyle \frac{W(Trabalho)}{t(Tempo)}}$$P (Potência)= \dfrac{W (Trabalho)}{t (Tempo)}$

Útil para determinar a potência que se requer de um compressor para distribuir e realizar trabalho com o ar-comprimido.

Também:

$P(Potência)={\displaystyle \frac{p\cdot \mathrm{\Delta }V}{t}}=p\cdot \mathrm{\Delta }V\cdot f$$P (Potência)=\dfrac{p \cdot \Delta V}{t}=p \cdot \Delta V \cdot f$

Onde: $p=$$p=$Pressão; $f=$$f=$frequência ou número de ciclos/s.

Note: $1(W=Watt)={\displaystyle \frac{1(J)}{1(s)}}={\displaystyle \frac{1(Pa\cdot m^3)}{1(s)}}$$1 \;(W=Watt)=\dfrac{1 \;(J)}{1 \; (s)}=\dfrac{1 \; (Pa \cdot m^3)}{1 \; (s)}$

Exemplo: Ao ingressar ar-comprimido num pistão de dublo efeito com pressão de 500 (KPa), este faz com que o êmbolo do cilindro se desloque 0,45 (m). Determinar o trabalho realizado pelo cilindro e a potência utilizada se todo o processo leva 3 (s). Obs.: Considerar que a seção transversal do cilindro seja de $S=12(c{m}^2)$$S=12\;(cm^2)$.

Solução:

$W=P\cdot \mathrm{\Delta }V=P\cdot (S\cdot d)$$W=P \cdot \Delta V=P \cdot (S \cdot d)$

$W=500\times {10}^3(Pa)\cdot 12\times {10}^{-4}(m^2)\cdot 0,45(m)=270(J)$$W=500 \times 10^3 \;(Pa) \cdot 12 \times 10^{-4} \;(m^2) \cdot 0,45 \;(m)=270 \;(J)$

então: $P={\displaystyle \frac{W}{t}}={\displaystyle \frac{270(J)}{3(s)}}=90(W)$$P=\dfrac{W}{t}=\dfrac{270 \;(J)}{3 \;(s)}= 90 \;(W)$

Referências:

1. Pneumática Básica, IMI Precision Engineering, Norgren Limited, 2015.
2. Pavani, Sergio Adalberto; Comandos Pneumáticos e Hidráulicos, e-Tec Brasil (Escola Técnica Aberta do Brasil), Colégio Técnico Industrial de Santa Maria, UFSM, Santa Maria - RS, 3a. ed., 182 p., 2010.

Sugestões de tópicos: atuadores (ou cilindros pneumáticos, válvulas, sensores, simulações (parte I); Exercícios de especificações de componentes; Índice geral