Convolução

Material teórico: 3_Sistemas.pdf

Resumo:

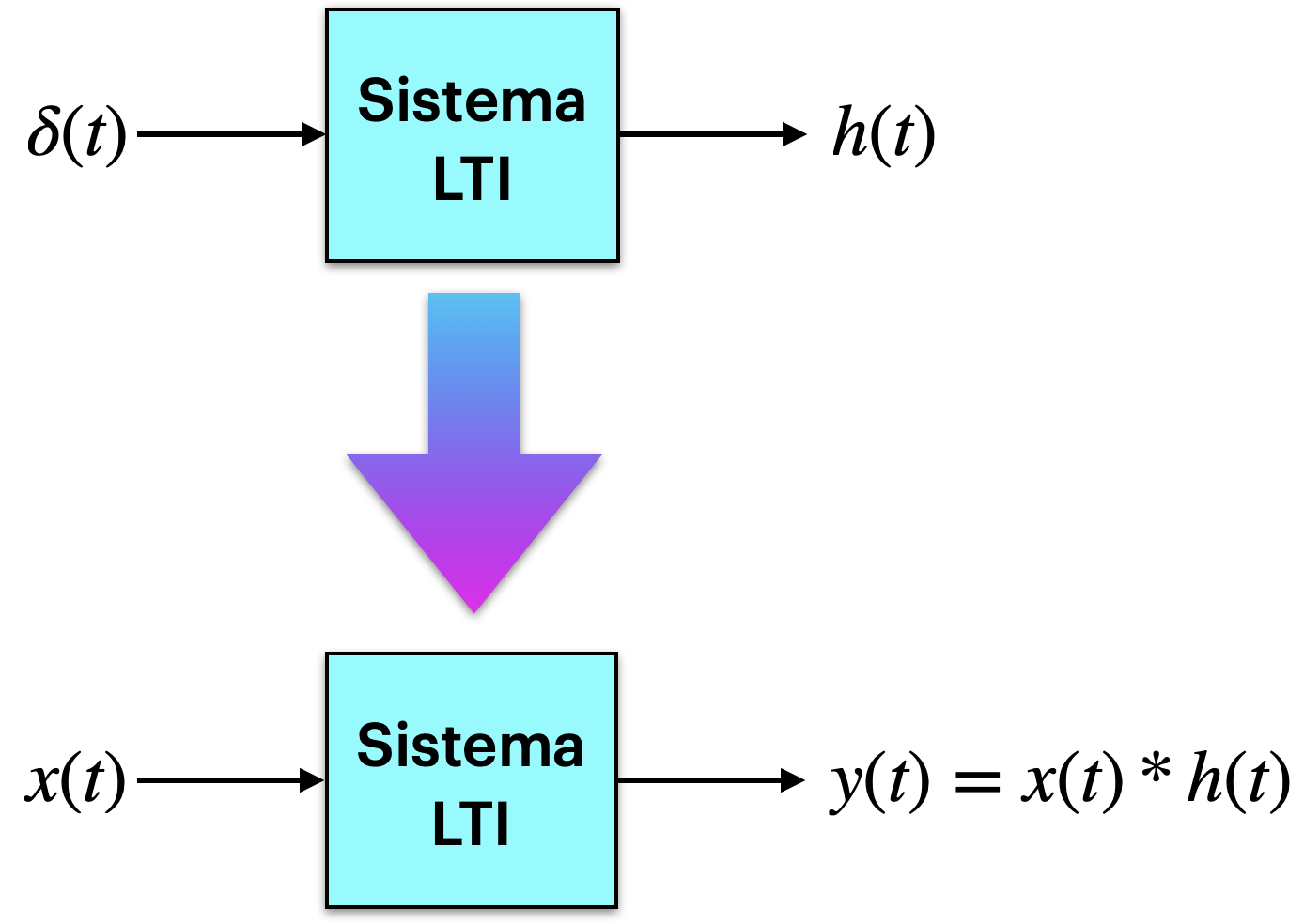
• Descreve a saída de um sistema, $h(t)$, quando um impulso unitário de Dirac, $\delta(t)$ (ou função delta) é aplicada à entrada de um sistema.
• A resposta ao impulso de um sistema LTI permite prever a saída, $y(t)$, para qualquer entrada arbitrária, , usando a teoria da convolução, ou:

Equações:

No tempo contínuo:

ou no tempo discreto

• A saída de qualquer sistema LTI pode ser determinada pela convolução do sinal de entrada $x(t)$, com sua resposta ao impulso unitário, $\delta(t)$, ou (na forma de um diagrama em blocos):

Cálculo:

1. Reversão temporal (rebatimento em relação ao eixo vertical) da resposta impulsiva $h(t)$ para se obter $h(t-\tau)$.
2. Multiplicação dos sinais $x(t)$ e $h(t_0-\tau)$ para todos os valores de $\tau$, com $t=t_0$.
3. Integração do produto $x(\tau)\cdot(t-\tau)$ para todos os valores de $\tau$, obtendo-se um valor unitário para $y(t_0)$.
4. Repetição dos passos anteriores para $-\infty<t<\infty$ para produzir a saída para todos os instantes de tempo,$x(t)$ .

Exemplos:

Ex_1: Seja $x(t)=u(t)$ (Degrau unitário) e $h(t)=e^{-at}u(t)$, com $a>0$ (função exponencial converge). Determine $y(t)$ .

• Resolução gráfica:

  Preparações	Resultados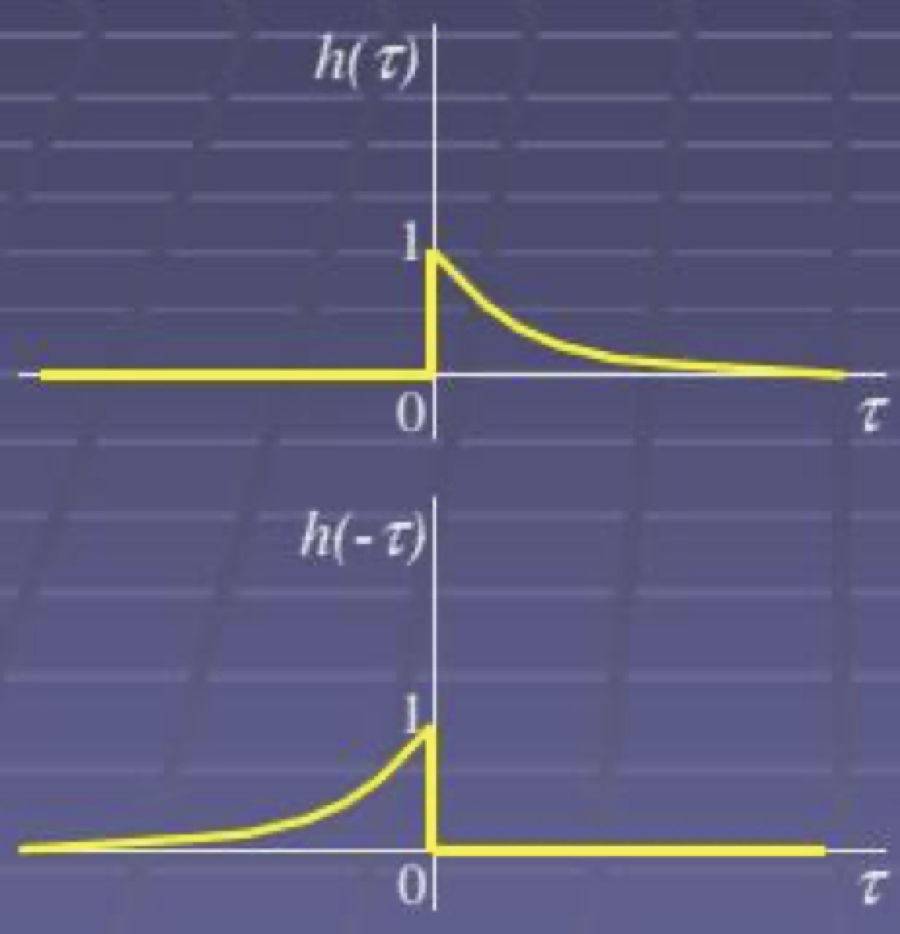

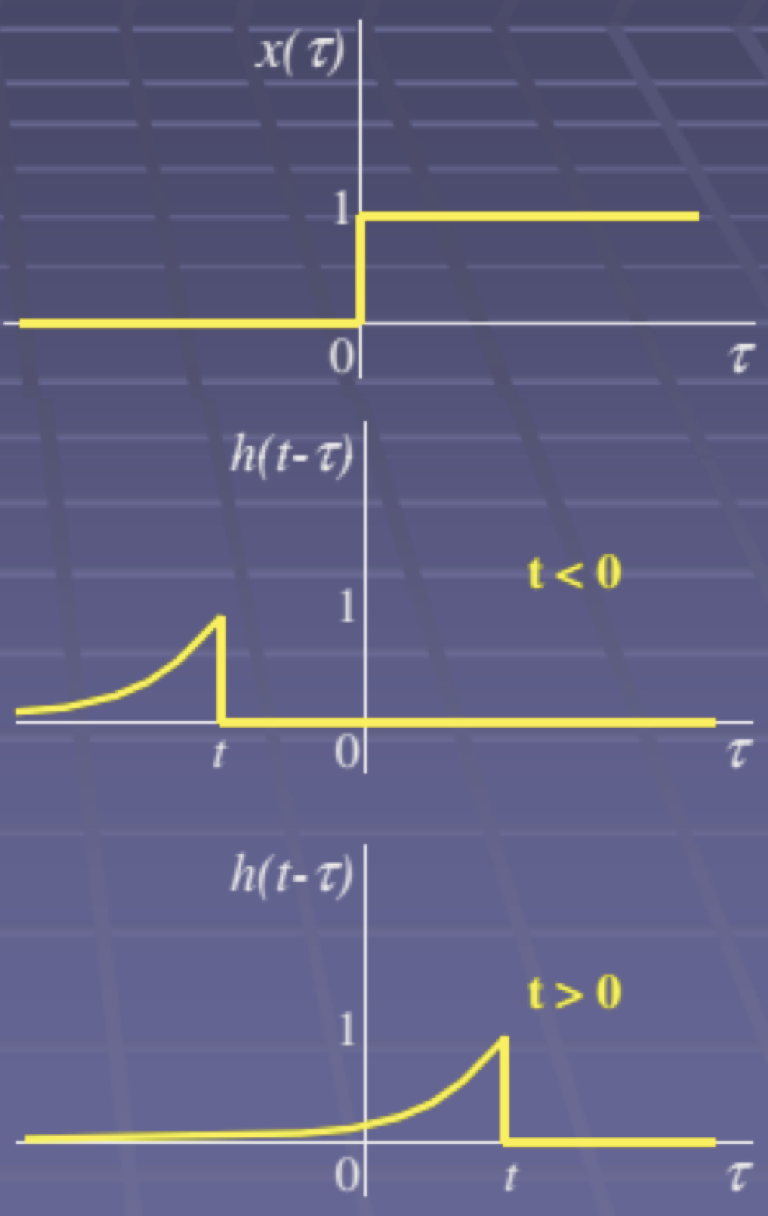
Resultado: $y(t)=\left( \frac{1-e^{-at}}{a} \right) u(t)$.

Ex_2: Animação_1:

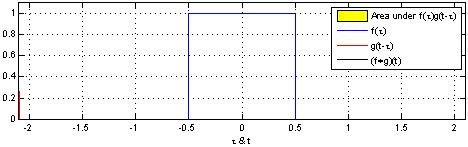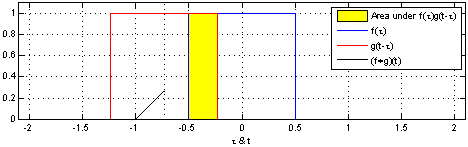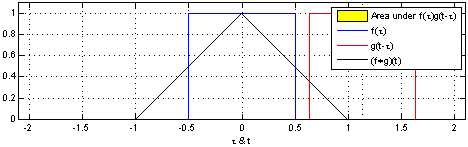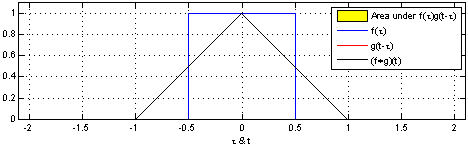
Ex_3: Animação_2:

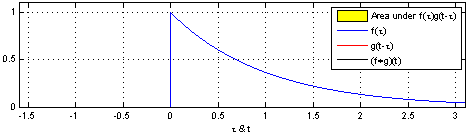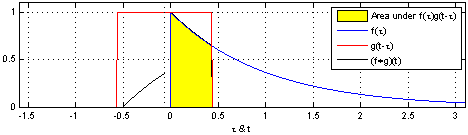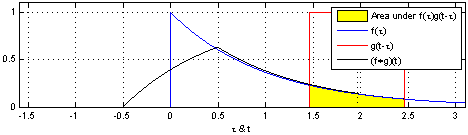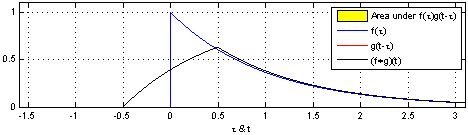
Referências externas:

• Matlab: xen0f0n/animateConvolutionD.m: https://gist.github.com/xen0f0n/088d5fda244f72af1fcdfd3618dfba54 (animateConvolutionD.m)
• Python: https://github.com/spatialaudio/signals-and-systems-lecture/blob/master/systems_time_domain/animation.py
• Matemathica/Wolfram: https://demonstrations.wolfram.com/DiscreteTimeConvolution/

Fernando Passold, em 08/09/2023.