
Projeto por Emulação
Projeto por EmulaçãoIntroduçãoMétodo da Correspondência Pólo-Zero (ou MPZ)Relações entre o plano-s e o plano-zMétodo de EulerExemplo_1: Caso de um Controlador de 1a-ordemExemplo_2: Caso de um Controlador por Avanço de FaseMétodo de TustinExemplo_1: Equação de diferenças usando o Método de TustinExemplo_2: Projeto de Controlador Digital usando o Método de TustinOutras Transformações BilinearesPara "imprimir" figuras de modelos do Simulink
Introdução
Um sistema contendo tanto um sinal contínuo no tempo quanto um sinal discreto é dito um sistema de dados amostrado 1.
Assumimos que o período de amostragem é fixo. Na prática, sistemas de controle digitais algumas vezes possuem períodos de amostragem variáveis e/ou diferentes períodos de amostragem entre seus ramos de realimentação. Normalmente, a lógica do computador inclui um sinal de clock que fornece um pulso, ou interrupção, a cada segundos, um conversor A/D envia uma sequencia numérica binária para o computador a cada instante de tempo que a interrupção ocorre. Outra alternativa de implementação, as vezes referenciada como free-running consiste em acessar o conversor A/D depois que cada ciclo de execução do código foi completada. No primeiro caso, o período de amostragem é preciso e fixo. No último caso, o período de amostragem depende do tamanho do código à ser executado, o qual eventuais laços de repetição e desvios condicionais (IFs) devem ser evitados, o que caso contrário, poderia fazer variar a quantidade de código à ser executada, fazendo variar o período de amostragem.
Também num sistema de controle digital deve estar presente um sampler (amostrador) e um conversor A/D para a entrada de comando (ou referência), , o que gera o sinal discretizado que juntamente com o saída amostrada do sistema, gera o sinal de erro discretizado: :
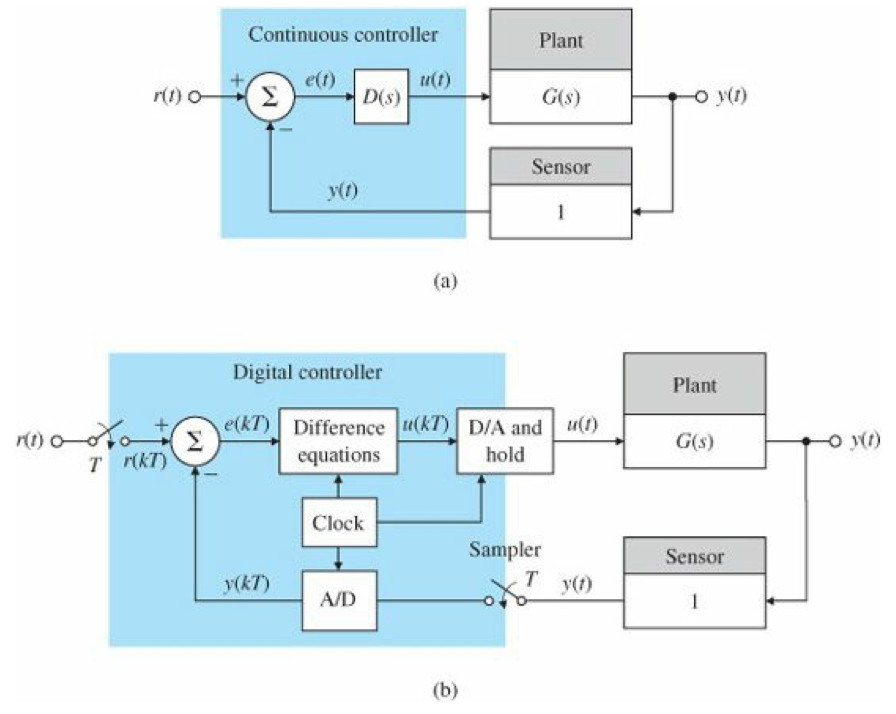
Um sistema contínuo de compensação pode ser aproximado por uma equação de diferenças que seria uma versão discreta de uma equação diferencial e pode ser adotado para emular o comportamento dinâmico de um compensador contínuo, , se o período de amostragem for curto o suficiente. O resultado desta equação de diferenças seria um sinal discreto a cada instante de amostragem. Este sinal seria convertido para o mundo contínuo, através de um conversor D/A e um sustentador (Holder). O conversor D/A converte o número binário numa tensão analógica e o sustentador manteria a última tensão analógica gerada durante os instantes de amostragem.
Existem duas técnicas básicas para determinar a equação de diferenças que define o controlador digital. Uma delas, chamada emulação, consistem em projetar o compensador contínuo no tempo, usando métodos clássicos de controle automático e então realizar uma aproximação de para uma representação discreta, usando um dos seguintes métodos:
- Método da Correspondência Pólo-Zero (MPZ = Matched Pole-Zero).
- Método de Euler;
- Método de Tustin;
Método da Correspondência Pólo-Zero (ou MPZ)
Este método, o da correspondência pólo-zero leva em conta a definição da transformada , extrapolando então a relação entre os planos e , obedecendo a relação:
(Pela definição)
como: , então teremos:
uma vez que: .
Desta forma, cada região do plano-s pode ser mapeada na correspondente região do plano-z.
Se tomamos a transformada da função amostrada , então os pólos de estão relacionados com os pólos de obedecendo a relação . O problema é que temos que considerar também que é a inversa de . Sendo assim, se temos e substituímos , obtemos como resultado da conversão para o plano. De modo simular, se temos e substituímos , obtemos como resultado da conversão para o plano. Infelizmente, ambas transformações podem ser levadas à caso, respeitando detalhes da complicada transformada mas conduzem a funções trancedentais (Cap. 13 de 2).
Relações entre o plano-s e o plano-z
A figura à seguir mostra as linhas de mapeamento resultantes para valores constantes de e para valores constantes de baseado na relação: :
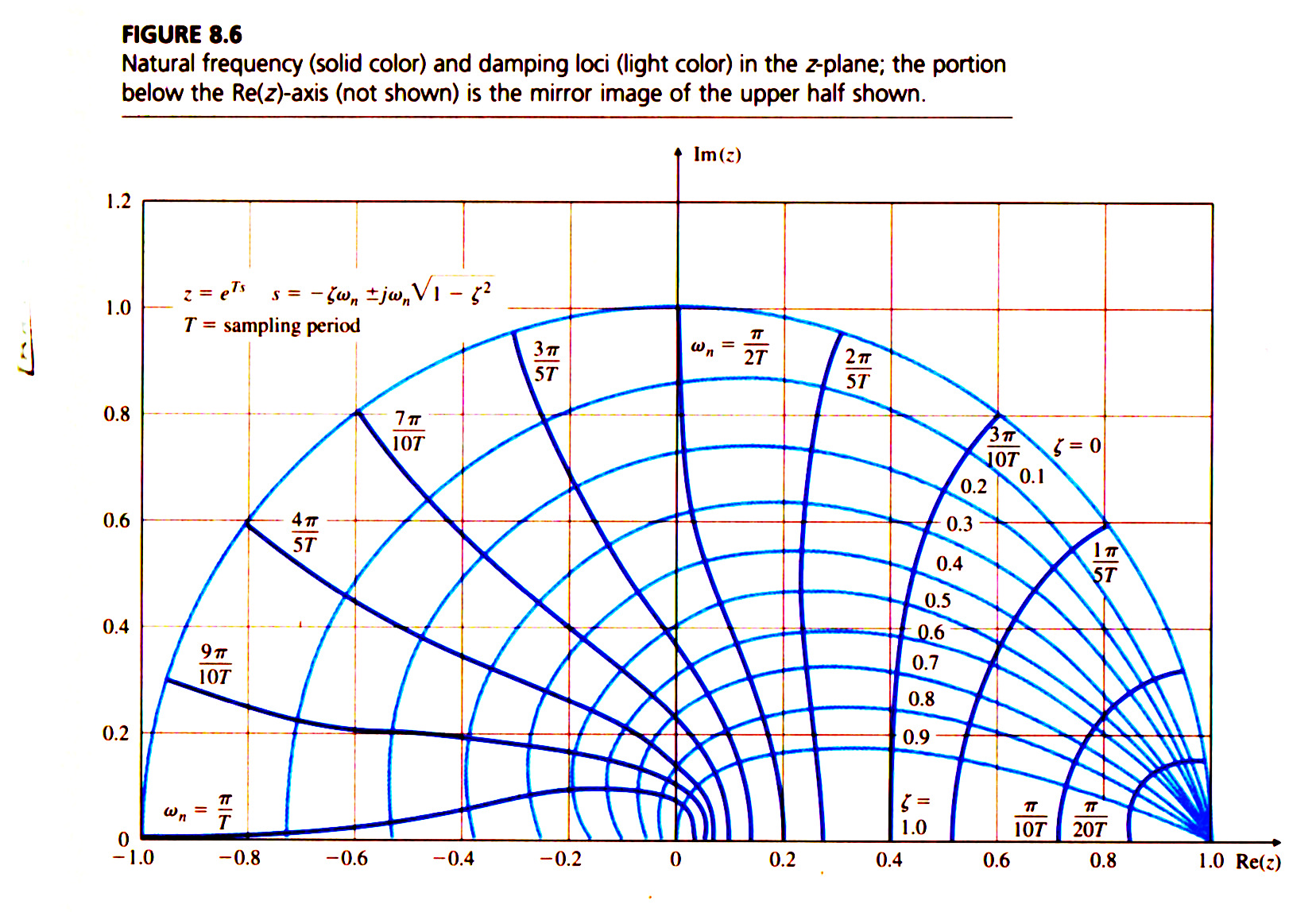
E a próxima figura mostra diferentes respostas no tempo resultantes para diferentes posições para um pólo em malha fechada.
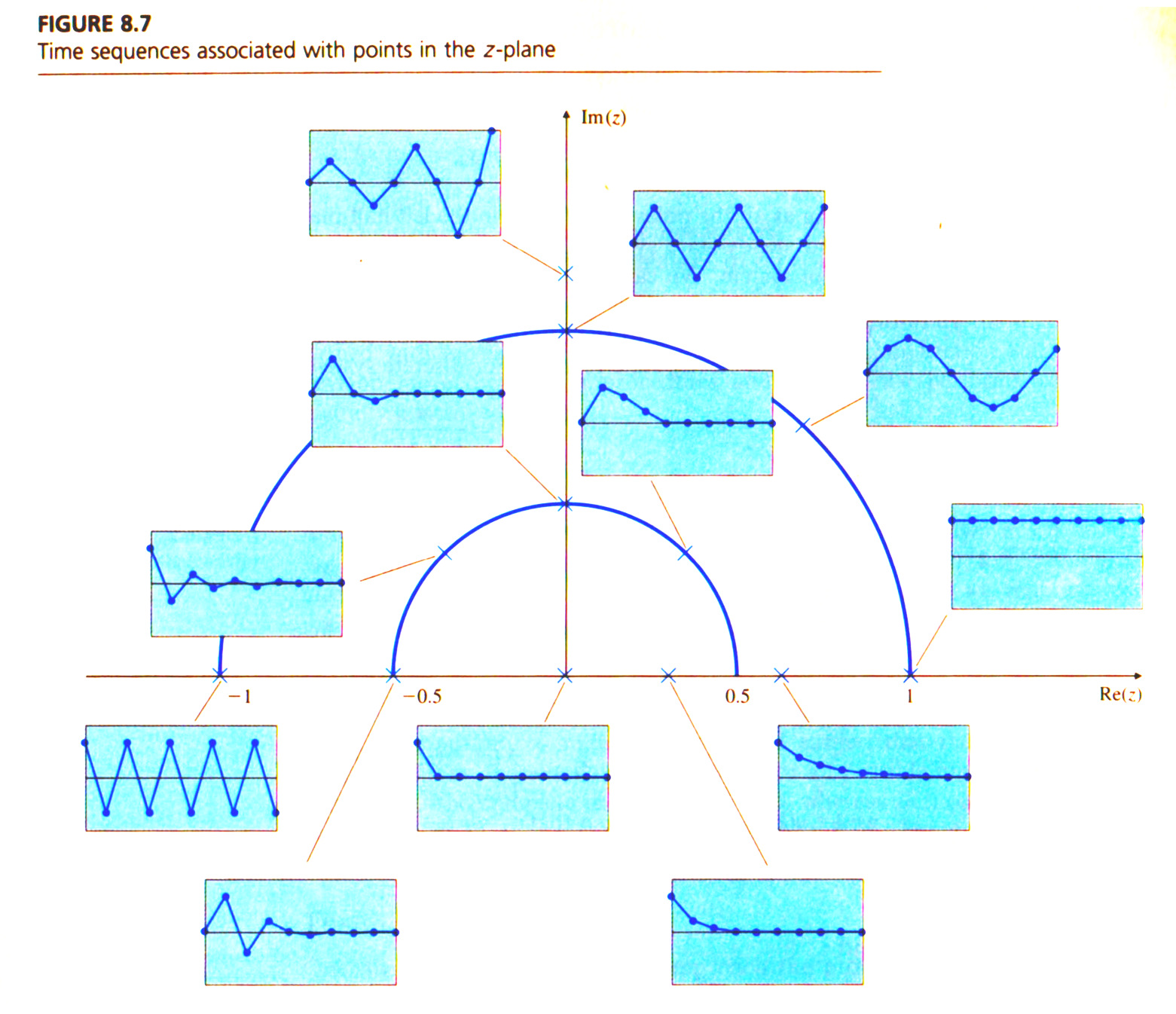
Método de Euler
Uma maneira particularmente simples de fazer com que um computador digital se aproxime da solução em tempo-real de uma equação diferencial é usar o método de Euler (também conhecido como regra retangular direta -- forward rectangular rule). Ela é resultado da seguinte aproximação:
que aplicada neste caso em particular resulta em:
onde: : corresponde ao período de amostragem (em segundos), ; : valor de no instante , ou ; : valor de no instante , ou .
Esta aproximação pode ser usada no lugar de várias derivadas que apareçam na equação diferencial do controlador e resulta num conjunto de equações que pode ser calculada por um computador digital. Estas equações de diferenças são resolvidas repetidamente a cada período de tempo. Para sistemas com margem de banda da ordem de uns poucos Hertz, taxas de amostragem resultam normalmente na ordem de 1 KHz, e assim os períodos de amostragem ficarão em torno de 1 ms e os erros envolvidos na aproximação resultarão bastante pequenos 1.
Exemplo_1: Caso de um Controlador de 1a-ordem
Usando o método de Euler, encontre a equação de diferenças que necessita ser programada num computador se é dado como:
Solução: Primeiro determinamos a equação diferencial que corresponde à :
por inspeção percebemos que a correspondente equação diferencial é:
Usando o método de Euler para aproximar a eq. (1) obtermos a seguinte equação de diferenças:
Rearrumando a eq. (2) obtemos:
A equação (3) determina o novo valor de controle, , uma vez conhecida a amostra passada do sinal de controle, e os novos e valores passados do sinal de erro, e .
Exemplo_2: Caso de um Controlador por Avanço de Fase
Encontre uma implementação digital para compensador de avanço de fase definido para a seguinte planta (Exemplo 5.13 de 1):
usando taxas de amostragem de: a) 20 e b) 40 Hz, simular as equações de controle para uma entrada degrau e comparar o resultado obtido entre o controlador analógico e o digital.
O sistema deve responder em malha-fechada com fator de amortecimento e com frequência natural (rad/s).
Na ocasião deste exercício foram feitas diferentes tentativas de pares pólo-zero para o compensador de avanço de fase como mostra a próxima figura:
| (a) | (b) |
|---|---|
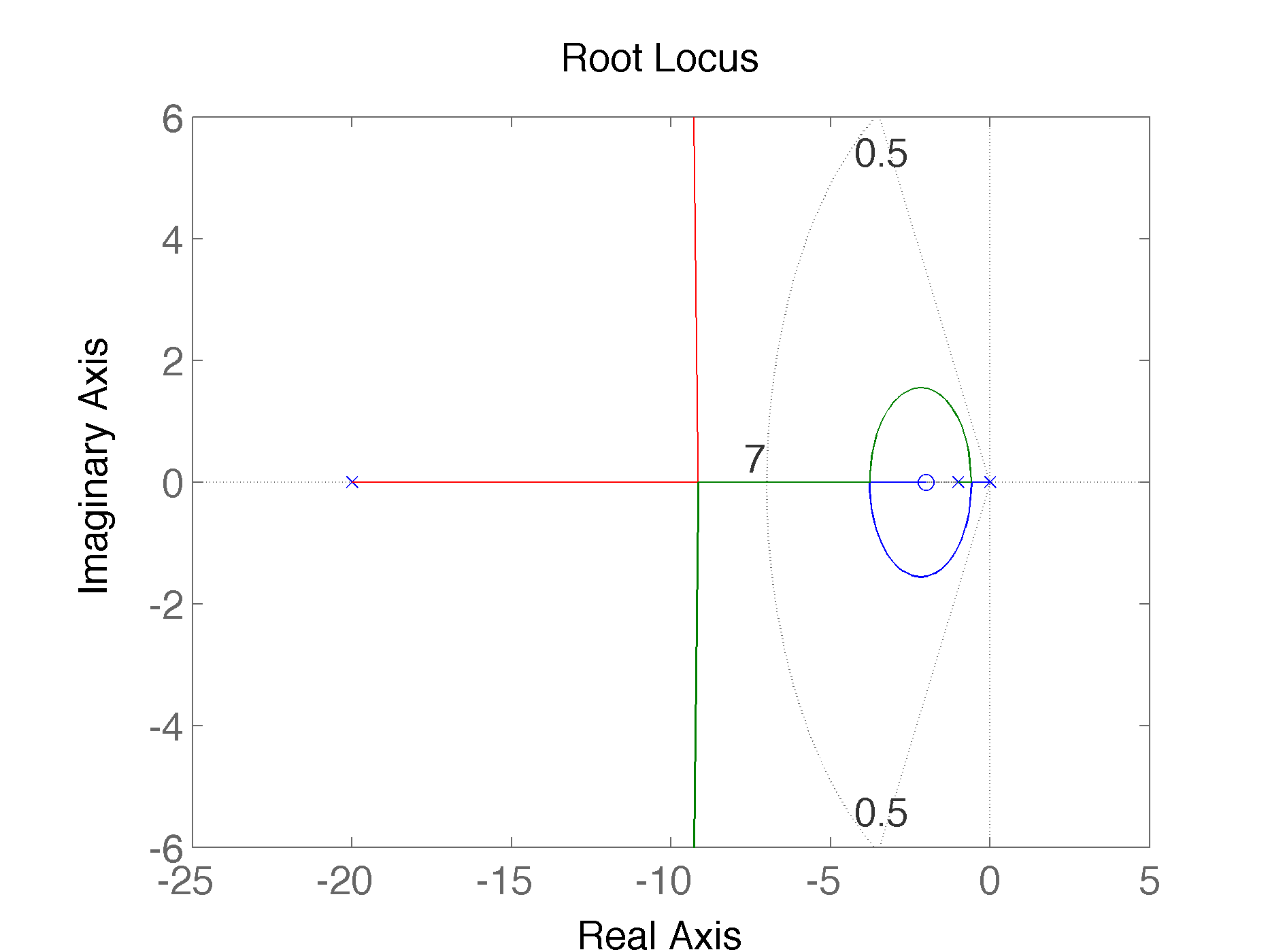 | 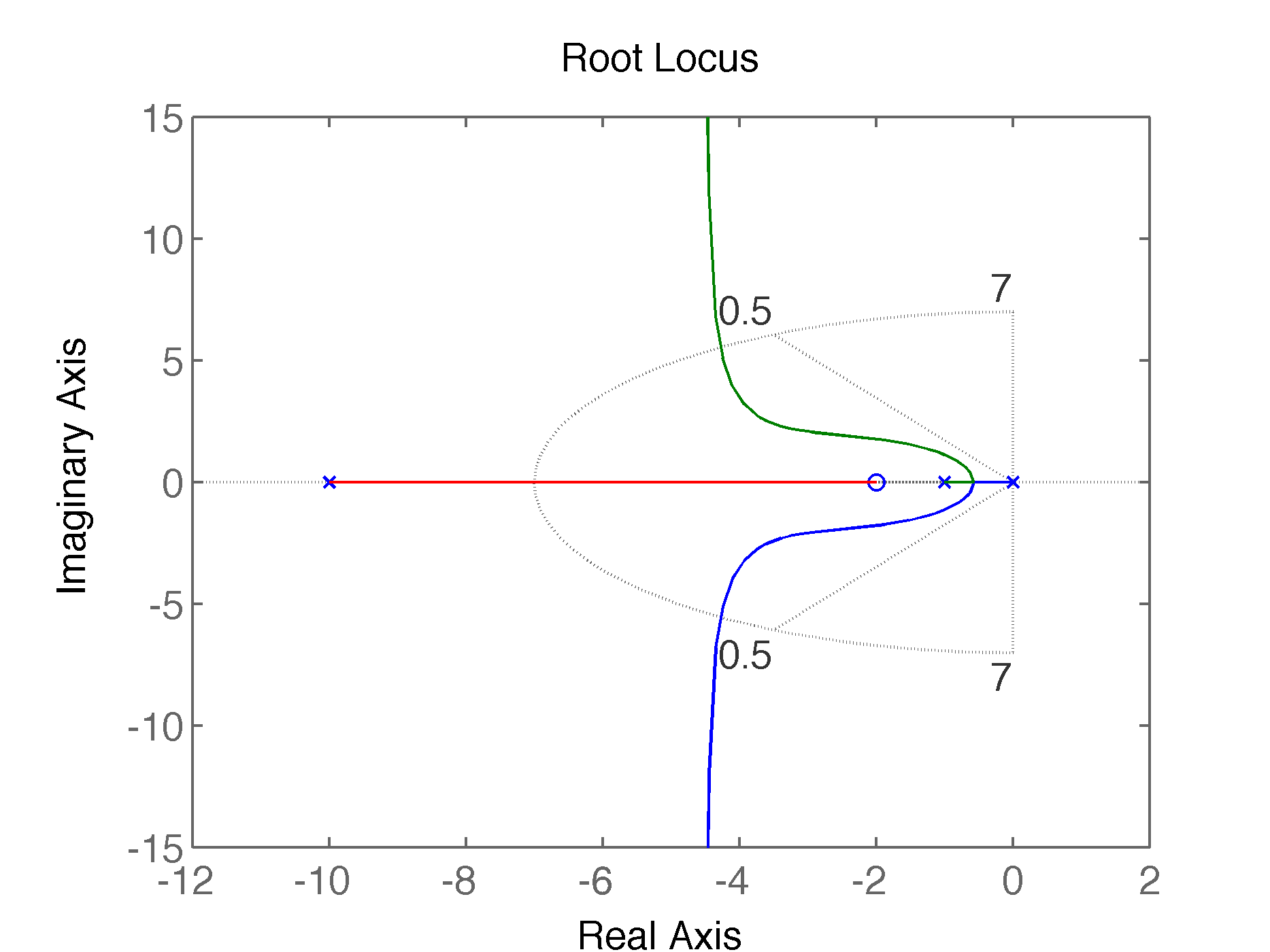 |
| (c) | |
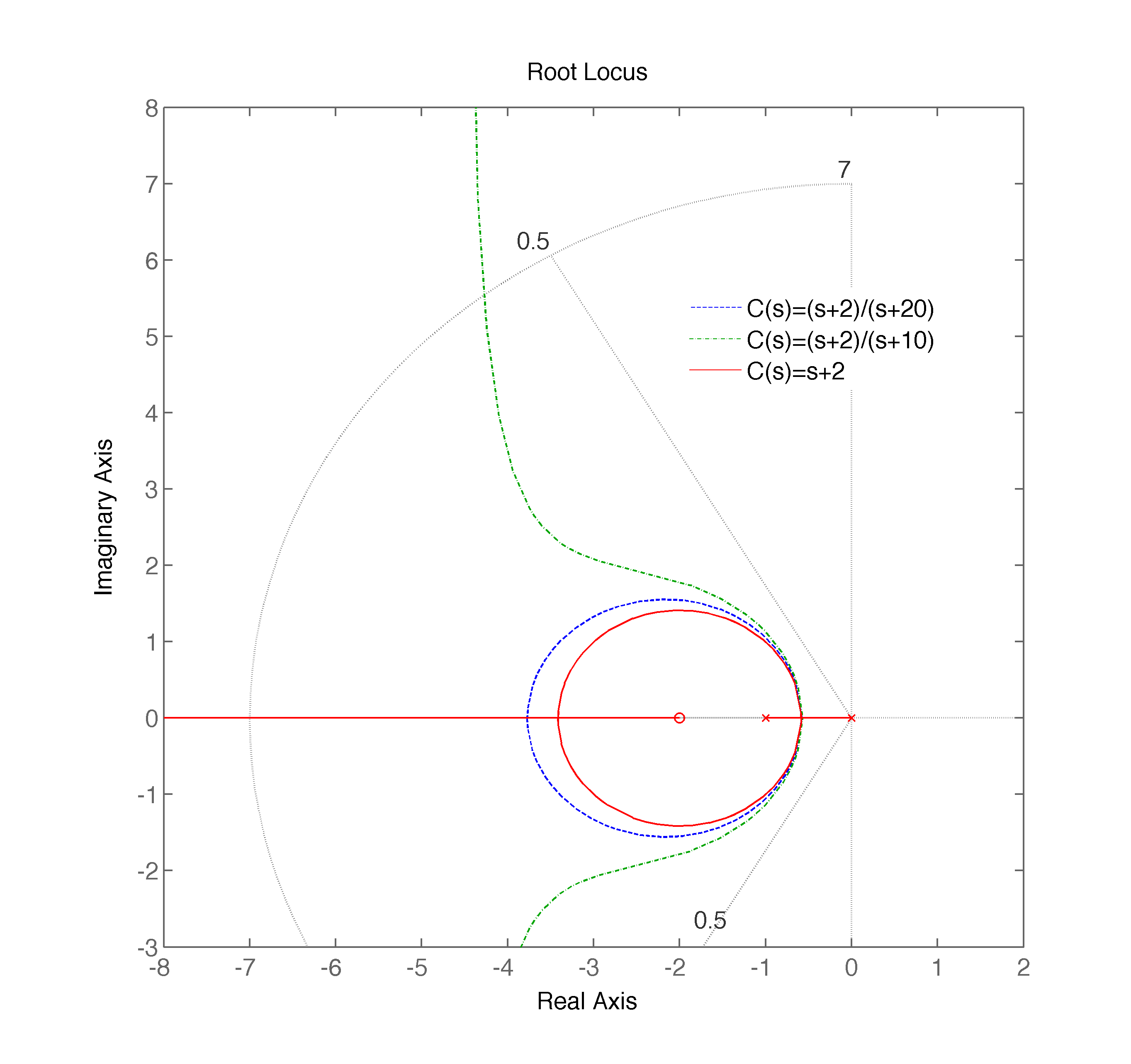 |
Na ocasião foi escolhido o controlador por atraso de fase:
A função transferência em malha aberta resulta:
onde . Este ganho resulta na resposta ao degrau mostrada na seguinte figura:
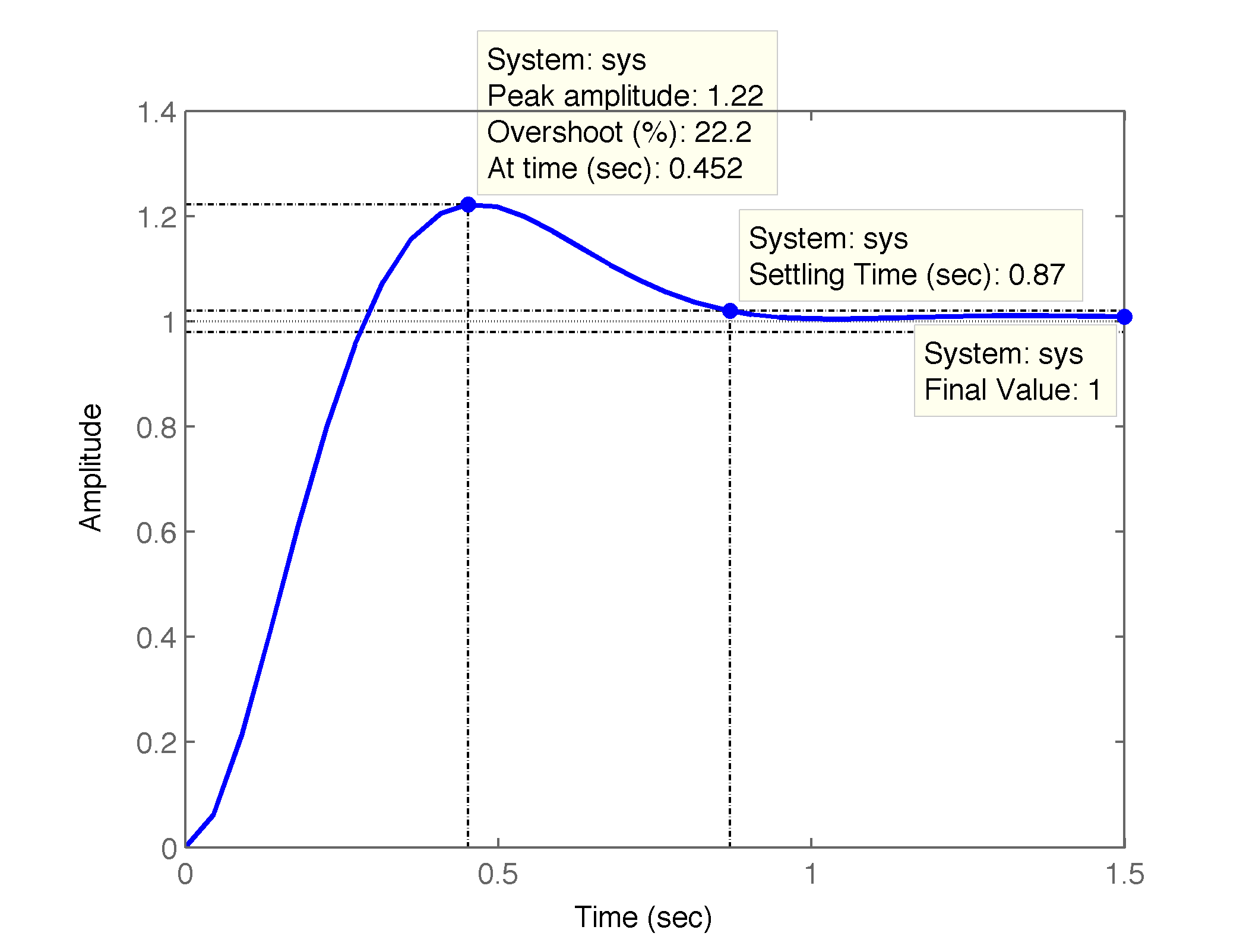
Solução: a função transferência do compensador de avanço de fase para esta planta fica (baseado no exemplo 5.13 de 1):
Desta forma, os parâmetros para a eq. (3) são , e .
a) Para a taxa de amostragem de 20 Hz, (segundos) e a eq. (3) pode ser simplificada para:
Colocando no formato de temos:
trabalhando a expressão anterior obtemos:
e então:
b) Para a taxa de amostragem de 40 Hz, (segundos), a eq. (3) simplificada resulta em:
Colocando no formato de obtemos:
O código no MATLAB para calcular a resposta contínua ao degrau fica:
xxxxxxxxxx>> num=70*[1 2]>> den=conv([1 1 0],[1 10])>> [numcl,dencl]=feedback(num,den,1,1)>> step (numcl,dencl)Que resulta no gráfico mostrado na seguinte figura anterior.
A próxima figura mostra o diagrama em blocos do sistema simulado usando tanto o compensador contínuo no tempo (a) quanto o simulador discreto (b).
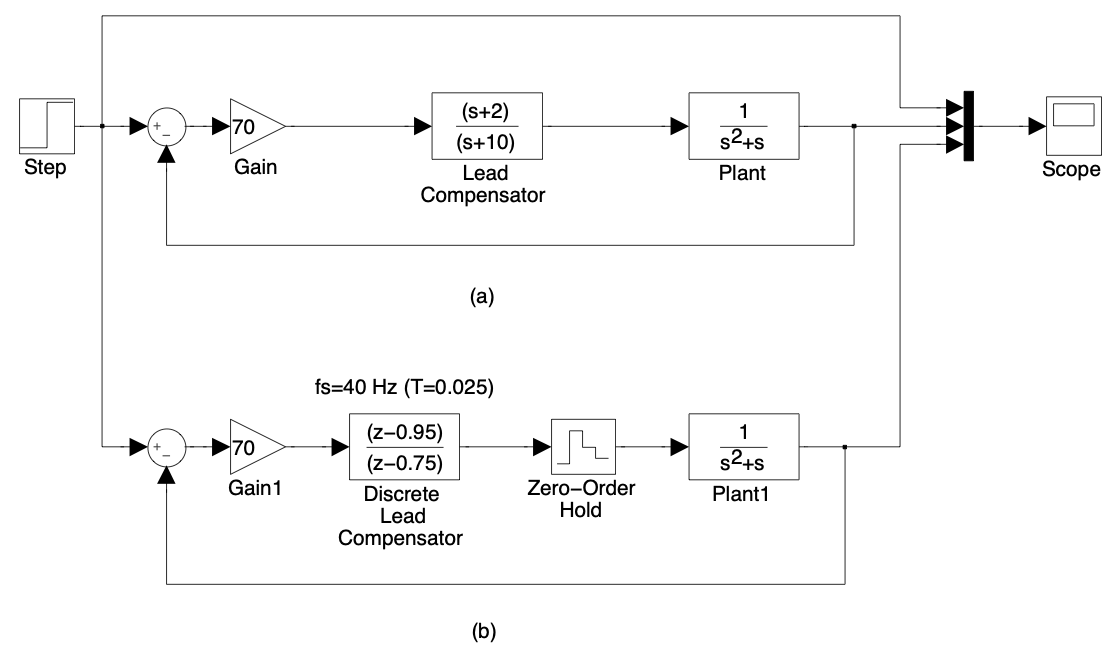
As respostas ao degrau para (a) T=0.05 e (b) T=0.025 aparecem na próxima figura:
| (a) [Hz] | (b) [Hz] |
|---|---|
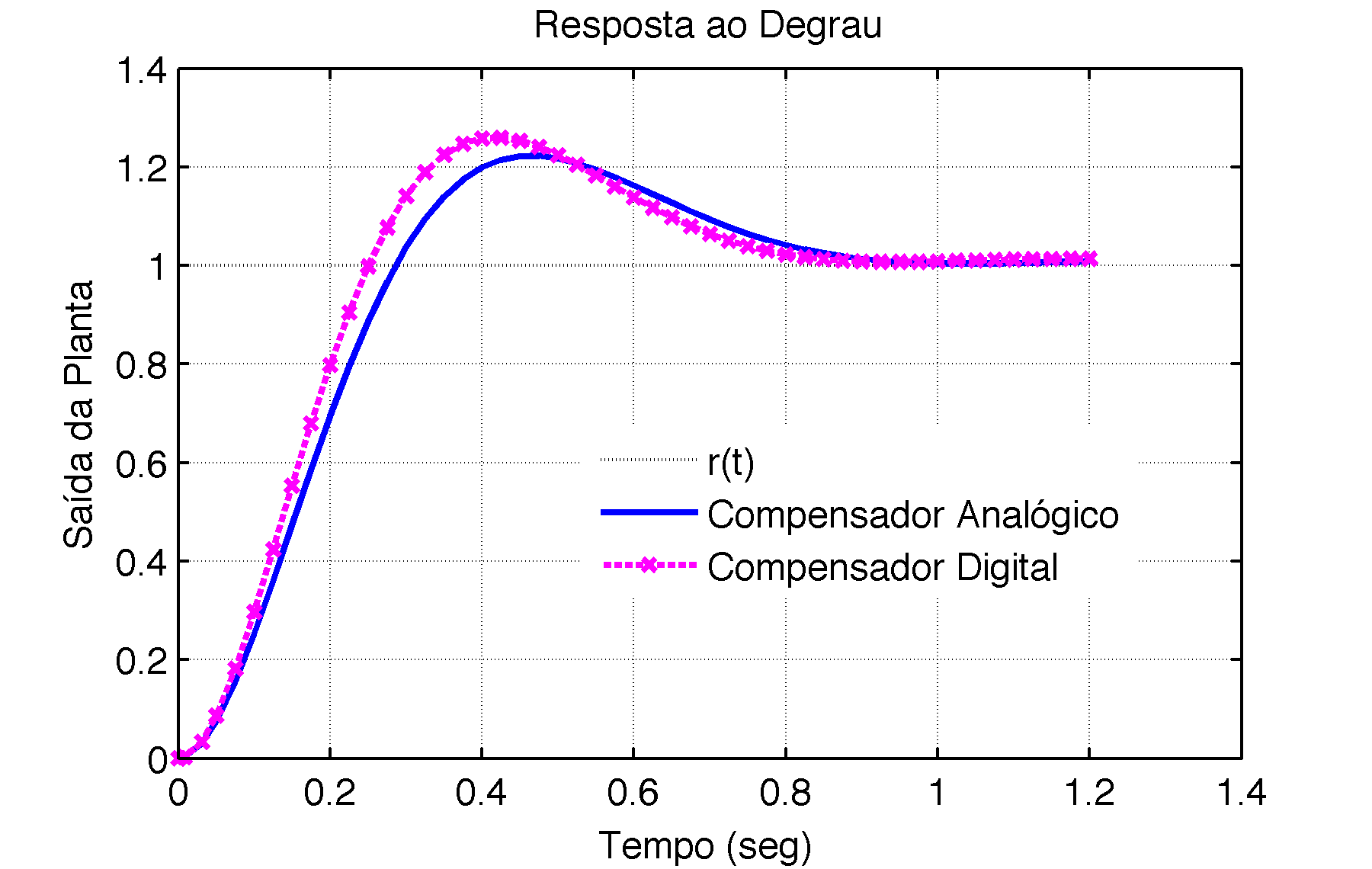 | 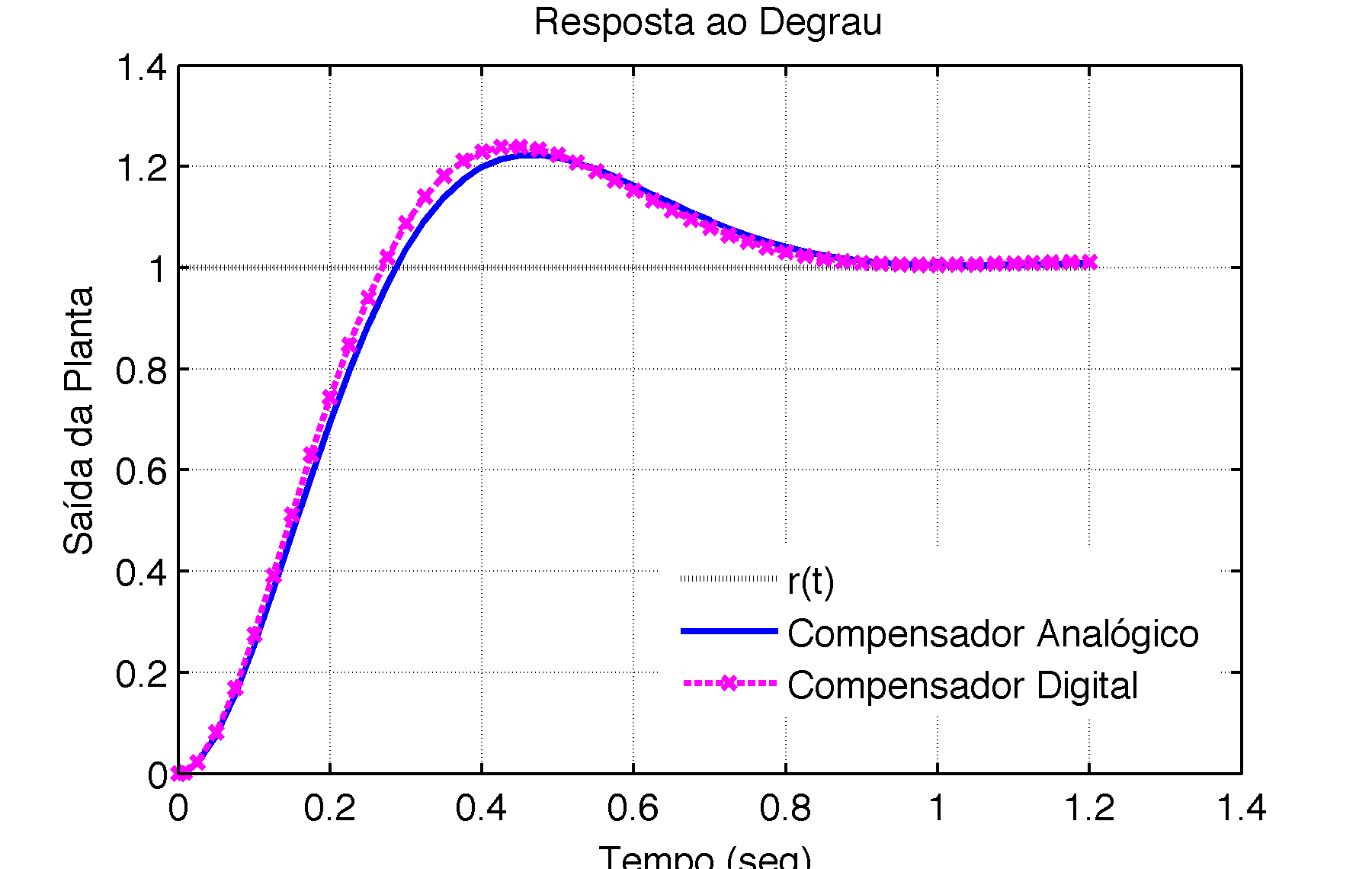 |
Conclusão: Este método (de Euler) é mais adequado quanto menor for o período de amostragem, . Para grandes valores de , este método pode resultar em instabilidade, mesmo quando o sistema sendo discretizado é estável no tempo contínuo.
Método de Tustin
Outro método de discretização é tratar o problema como uma integração numérica (aproximação).
Suponha que:
$o qual é uma integração. Assim sendo:
pode ser reescrito como:
área entre e período de amostragem atual
O método de Tustin realiza integração numérica trapezoidal a cada passo do período de amostragem, tentando aproximar através de uma linha direta entre dois instantes de amostragem:
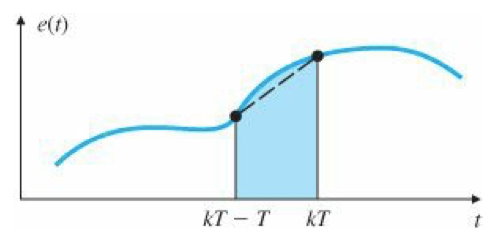
Ver PID Digital: Integração Trapezoidal, que resulta na mesma equação mostrada abaixo.
Reescrevendo como e como para simplificar a escrita, tra nsformamos a equação (4) em:
tomando a transformada da expressão anterior, obtemos:
Se: , aplicando esta aproximação para a integração resulta em:
Note que se substituírmos:
para cada ocorrência de em qualquer , obtemos baseado na equação da integração trapezoidal.
Este é o chamado método de transformação bilinear de Tustin 1. A idéia é a de que nos instantes amostrados, a transformação bilinear seja capaz de preservar o mesmo tipo (valor) da resposta de um controlador contínuo no tempo. Em resumo este tipo de transformação é usado para transformar um compensador contínuo no tempo, na sua versão digital, . Explicitamente a transformação bilinear de Tustin é dada por:
e sua inversa é dada por:
Quanto menor for o intervalo de amostragem, (ou maior a frequência de amostragem), mais a versão discretizada se aproxima do comportamento no domínio-frequência do compensador no domínio contínuo de tempo. A eq. (6) é a que entre os métodos de integração numérica, permite levar a um resultado mais próximo da resposta (em tempo e frequência) que realmente seria obtido usando o compensador no domínio contínuo de tempo.
Åström e Wittenmark3, propuseram uma referência para selecionar o período de amostragem à ser adotado. Eles concluíram que o valor de em segundos deve estar na faixa de até , onde corresponde a frequência (em rad/s) na qual o diagrama de magnitude da função transferência analógica do compensador mais planta passa por 0 dB (ganho unitário).
Exemplo_1: Equação de diferenças usando o Método de Tustin
Voltando ao exemplo da seção anterior e usando taxa de amostragem de [Hz], podemos usar o MATLAB para computar a aproximação de Tustin.
Solução: A forma contínua do compensador estudado na seção anterior era:
Usando declarações na linha de comandos do MATLAB, podemos fazer:
xxxxxxxxxx>> numc=70*[1 2];>> denc=[1 10];>> T=1/15;>> C=tf(numc,denc);>> zpk(C)Zero/pole/gain:70 (s+2)-------- (s+10)>> Cd=c2d(C,T,'tustin') Transfer function:56 z - 49--------- z - 0.5Sampling time: 0.066667>> zpk(Cd)Zero/pole/gain:56 (z-0.875)------------ (z-0.5)Sampling time: 0.066667>> que produz:
que pode ser transcrito para uma equação de diferenças resultando em:
que é similar a equação obtida usando o método de Euler.
Problema sugerido Comparar a resposta deste controlador usando o método de Tustin com os resultados obtidos quando o mesmo compensador contínuo no tempo foi discretizado usando o método de Euler (seção anterior). Para os mesmos 2 valores de período de amostragem: a) (Hz) e b) (Hz).
Simulando os controladores no Simulink, arquivo: Lead_Tustin_2a_ordem.slx:
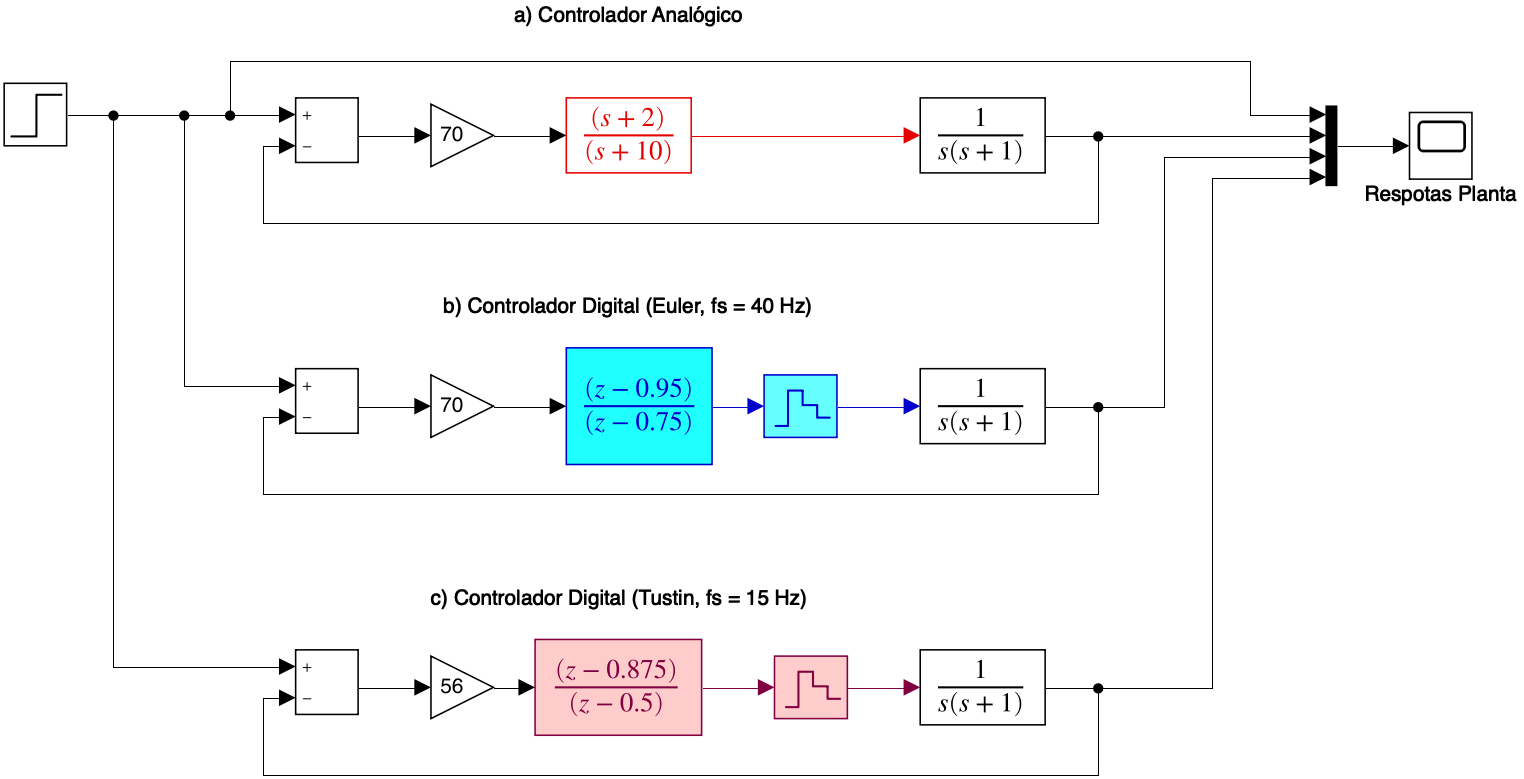
Resultados obtidos:
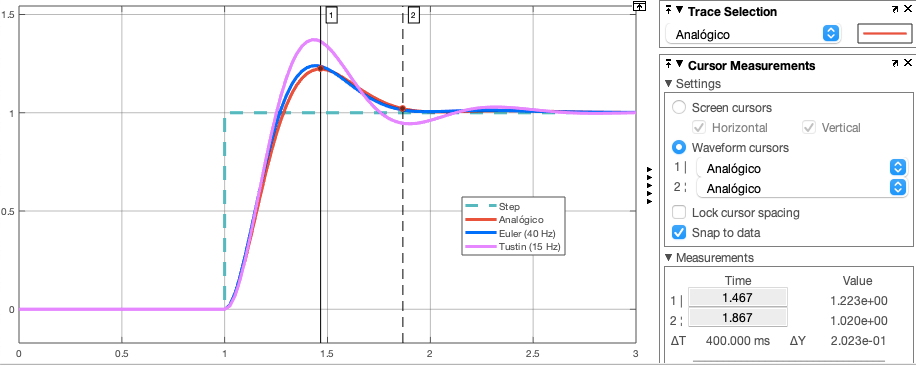
Exemplo_2: Projeto de Controlador Digital usando o Método de Tustin
Seja um sistema (planta) descrito pela equação (Exemplo 13.12, Cap 13 de 2):
onde o projeto de um compensador por avanço resultou num sistema compensado que opera com sobre sinal máximo de 20% e um tempo de acomodação de 1,1 segundos. Defina a equação de diferenças que corresponde ao compensador contínuo transformado para digital usando o método de Tustin. A equação do compensador é dada por:
Solução: Com base na eq. (8) e (8) se percebe que a frequência que corresponde à 0 dB, , para , é de 5,8 rad/s. Com base na linha guia proposta por 3, o menor valor recomendado para deveria estar na faixa de até segundos. Iremos adotar o valor de segundos.
Substituindo a eq. (6) na eq. (9) com segundos, leva à:
e a função transferência da planta usando sustentador de ordem zero (ZOH), com segundos resulta em:
Obs.: As equações anteriores foram obtidas usando o seguinte código no MATLAB:
xxxxxxxxxx>> num=1;>> den=poly([0 -6 -10]);>> G=tf(num,den);>> zpk(G) 1 -------------- s (s+10) (s+6) Continuous-time zero/pole/gain model.>> num_c=1977*[1 6];>> den_c=[1 29.1];>> C=tf(num_c,den_c);>> zpk(C) 1977 (s+6) ---------- (s+29.1) Continuous-time zero/pole/gain model.>> % convertendo para controle digital>> T=0.01;>> help c2d c2d Converts continuous-time dynamic system to discrete time. SYSD = c2d(SYSC,TS,METHOD) computes a discrete-time model SYSD with sampling time TS that approximates the continuous-time model SYSC. The string METHOD selects the discretization method among the following: 'zoh' Zero-order hold on the inputs 'foh' Linear interpolation of inputs 'impulse' Impulse-invariant discretization 'tustin' Bilinear (Tustin) approximation. 'matched' Matched pole-zero method (for SISO systems only). The default is 'zoh' when METHOD is omitted. The sampling time TS should be specified in the time units of SYSC (see "TimeUnit" property).>> Cd=c2d(C,T,'tustin');>> zpk(Cd) 1777.7 (z-0.9417) ----------------- (z-0.746)Sample time: 0.01 secondsDiscrete-time zero/pole/gain model.>> % convertendo a planta para o mundo digital usando ZOH:>> Gd=c2d(G,T)Gd = 1.602e-07 z^2 + 6.156e-07 z + 1.478e-07 --------------------------------------- z^3 - 2.847 z^2 + 2.699 z - 0.8521Sample time: 0.01 secondsDiscrete-time transfer function.>> zpk(Gd) 1.6016e-07 (z+3.586) (z+0.2574) ------------------------------- (z-1) (z-0.9418) (z-0.9048)Sample time: 0.01 secondsDiscrete-time zero/pole/gain model.>> ftma=series(C,G); % FTMA(s)>> ftmad=serires(Cd,Gd); % FTMA(z) com T=0,01 (s)>> ftmf=feedback(ftma,1); % FTMF(s)>> ftmfd=feedback(ftmad,1); % FTMF(z)>> [y,t]=step(ftmf); % resposta degrau, sistema contínuo>> plot(t,y)>> [yd1,td1]=step(ftmfd);>> hold on;>> stairs(td1,yd1,'m-')>> legend('FTMF(s)','FTMF(z) com T=0,01')>> title('Resposta ao Degrau');>> xlabel('Tempo (s)');>> ylabel('y^*(t)')>> gridA resposta para entrada degrau para o sistema compensando é mostrada na figura à seguir, que compara as respostas do compensador contínuo no tempo versus compensadores digitais usando segundos.
| (a) Resposta ao degrau. | (b) "Zoom'' sobre o gráfico (a). |
|---|---|
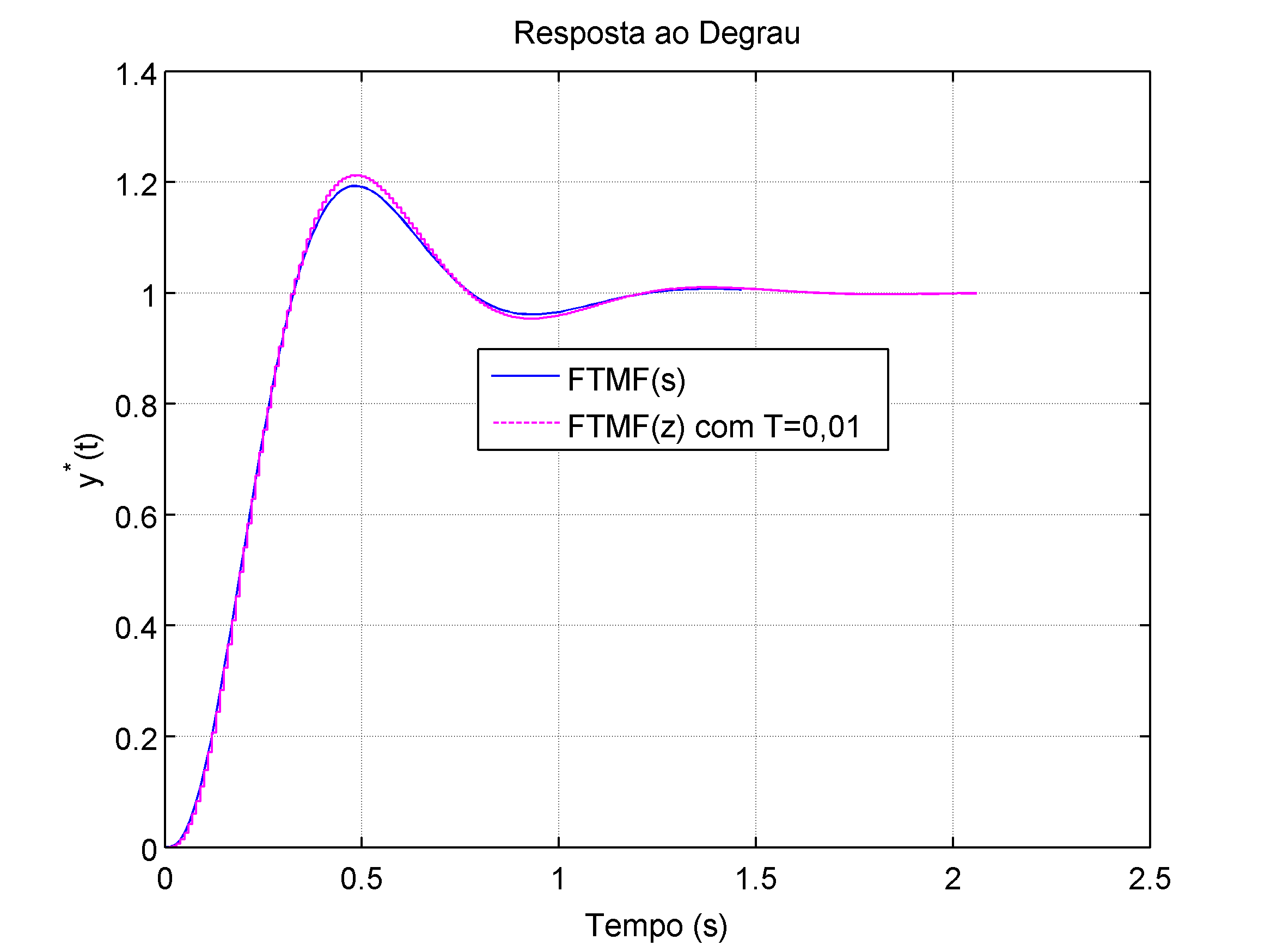 | 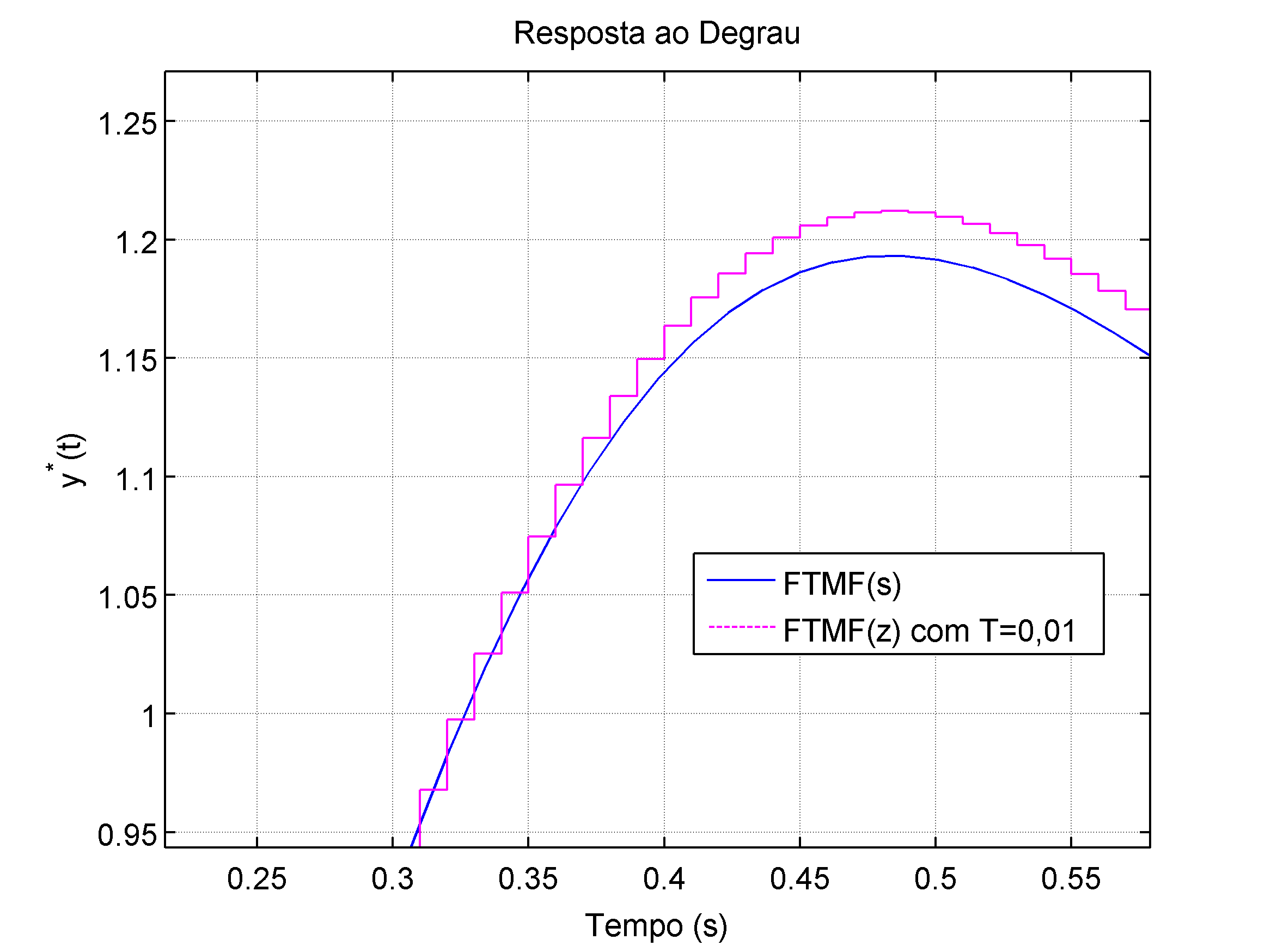 |
Outras Transformações Bilineares
Note que o método de Tustin trata-se de um caso específico da aplicação de um método de transformação bilinear do tipo:
e sua inversa:
A idéia é sempre buscar uma simples transformação capaz de atuar em ambos os lados (plano-s e plano-z) através de algum método de substituição direta (Cap 13. de 2).
Por exemplo, a transformação bilinear:
é proposta por Kuo4 para aproximar raízes presentes no interior do círculo unitário para o semi-plano esquerdo do plano-s. No caso, esta transformação recebeu o nome de transformação-R.
Outro tipo de transformação bilinear é a transformada-w onde:
tenta transformar o círculo unitário do plano-z para o eixo imaginário de outro plano complexo 5. Neste caso:
e sua inversa:
que é uma variação da proposta realizada pelo Ogata (Cap. 4: Design of Discrete-Time Control Systems by Conventional Methods, de 6):
Em comum as últimas 2 transformadas permitem realizar todo um projeto de controlador discreto usando o mapeamento em frequencia, tal qual se fazia usando Diagramas de Bode quando estávamos no plano-s (ou no mundo contínuo). Neste último caso, estas transformadas permitem converter em e lidar com o projeto do controlador tal qual se fazia antes usando Diagrama de Bode -- o que muda agora é que ao invés do Diagrama de Bode ser feito no plano- é realizado sobre o plano-.
Para "imprimir" figuras de modelos do Simulink
Você pode usar a linha de comandos para transformar numa figura, um modelo do Simulink sem recorrer a um print screen com resultados deploráveis (baixa resolução, 75 dpi). Para tanto:
xxxxxxxxxx>> print('-sLead_Tustin_2a_ordem', '-r150', '-dpng','Lead_Tustin_2a_ordem.png') % gera arquivo .png>> print('-sLead_Tustin_2a_ordem', '-r150', '-djpeg','Lead_Tustin_2a_ordem.jpg') % gera arquivo .jpg>> print('-sLead_Tustin_2a_ordem', '-r150', '-dpdf','Lead_Tustin_2a_ordem.pdf') % gera arquivo .pdfDetalhes:
print(-s<Model_Name>,...)indica que se deseja "imprimir" não uma janela gráfica, mas sim um modelo do Simulink;- a opção
'-r150', indica a resolução desejada, neste caso, 150 dpi; - o último parâmetro, se refere ao nome do arquivo.
Neste caso, foram gerados:
xxxxxxxxxx-rw-r--r-- 1 fernandopassold staff 79721 2 Jun 16:42 Lead_Tustin_2a_ordem.jpg-rw-r--r-- 1 fernandopassold staff 28346 2 Jun 16:43 Lead_Tustin_2a_ordem.pdf-rw-r--r-- 1 fernandopassold staff 66775 2 Jun 16:42 Lead_Tustin_2a_ordem.png
Fernando Passold (primeira publicação: 02/06/2014; atualizado em 02/06/2025)