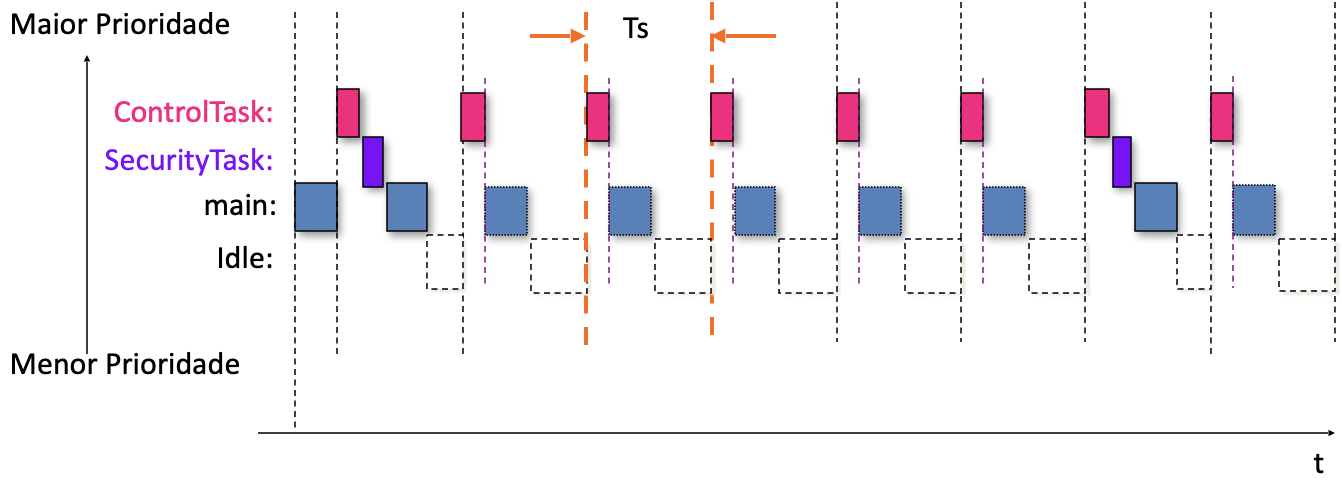1. PID Digital

1. PID Digital

1.1. Introdução

Equação tradicional de um PID no domínio tempo, formato paralelo:

$u(t) = K_p e(t) + K_i \displaystyle\int\limits_o^t {e(t)dt + K_d \frac{{\partial e(t)}}{{\partial t}}} \quad \quad$ [eq. (1)]

A eq. (1) retrata o PID no formato paralelo, conforme mostrado na figura à seguir:

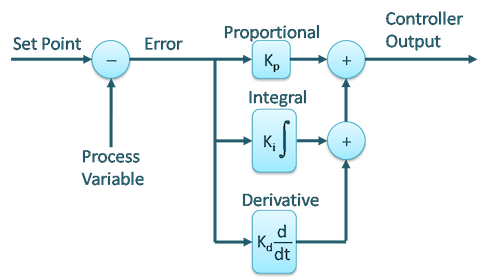
No formato paralelo do PID (eq. (1)), quando variamos certo parâmetro do PID ( $K_p$ ou $K_i$ ou $K_d$ ), a modificação de um parâmetro não afeta nenhum dos outros não alterados.

Repare porém que o PID pode ser implementado de outras formas, como no tradicional formato "ISA" como é mostrado na próxima figura:

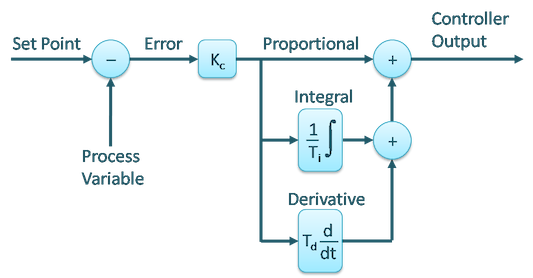
Porém no formato ISA, sua equação assume uma forma ligeiramente diferente:

$u(t) = K_c \left( e(t) + \dfrac{1}{T_i} \displaystyle\int e(t)dt + T_d \, \dfrac{\partial e(t)}{\partial t} \right)$

Neste caso:

$K_i=\dfrac{1}{T_i}$ e $K_d=T_d$ .

Porém, neste caso, quando variamos $K_c$ acabamos gerando um impacto nos outros parâmetros: $T_i$ e $T_d$ .

De qualquer modo, estamos interessados na versão digital, ou digitalizada do PID.

Para obter a equação no formato digital do PID poderímos recorrer a sua equação no plano-z, $U(z)$ e usar algum método de transformação bilinear como o "famoso" método de Tustin para obter sua equação no plano-z à partir da sua equação no plano-s e então obter sua equação de diferenças ( $u[kT]=\ldots$ ), considerando agora o período de amostragem, $T$ que será adotado para sua implementação. O problema destes métodos é que sua precisão varia com o valor do período de amostragem adotado: valores bem baixos (alta taxa de amostragem), conduz a melhores resultados.

Ou podemos partir diretamente para métodos numéricos que aproximam numericamente a ação integrativa e a ação derivativa.

1.2. Formas de Integração Numérica

Uma ação de integração numérica pode ser obtida de algumas formas:

Integração Retangular, ou;
Integração Trapezoidal, ou;
Método de Simpson, ou;
Outros métodos (ver Wikipédia: Integração Numérica).

1.2.1. Integração Retangular

Método mais simples de integração numérica. Acompanhe pela próxima figura:

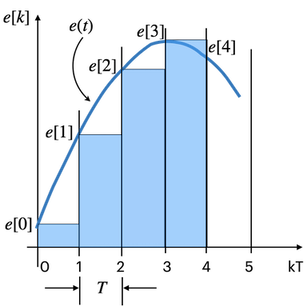
Suponha que $i[0]$ corresponda ao valor da integral no instante de amostragem zero, $k=0$ . Obviamente este valor é inicialmente nulo. Mas repara como o valor da integral varia conforma aumenta o instante da amostragem:

$\begin{array}{rcl} i[0] &=& 0\\ i[1] &=& i[0] + e[0] \cdot T\\ i[2] &=& i[1] + e[1] \cdot T\\ i[3] &=& i[2] + e[2] \cdot T\\ & \vdots & \\ i[k] &=& i[k-1] + e[k-1] \cdot T \end{array}$

onde: $i[k]=$ integral no instante de tempo atual, amostra atual, $k$ .

Notamos que a integral no instante atual atual, depende do seus valor no instante de amostragem anterior ( $i[k-1]$ ) e do valor de erro no instante de tempo anterior ( $e[k-1]$ ). E obviamente neste caso, fácil de acompanhar na figura, estamos realizando sucessivas somas de áreas retangulares.

Podemos realizar uma transformada-z sobre a última eq. genérica:

$\begin{array}{rcl} i[k] &=& i[k-1] + T \cdot e[k-1] \\ &\downarrow \mathcal{Z}&\\ I(z)&=&z^{-1} I(z) + T \cdot z^{-1} E(z)\\ I(z) - z^{-1}I(z) &=& T \cdot z^{-1} E(z)\\ I(z)\left( 1 - z^{-1}\right) &=& T \cdot z^{-1} E(z)\\ I(z) &=& \dfrac{T z^{-1}}{(1-z^{-1})} \; E(z)\\ & \text{ou:} &\\ I(z) &=& \dfrac{T}{(z-1)} \; E(z) \end{array}$

1.2.2. Integração Trapezoidal

Neste caso, vamos realizar sucessivas somas de áreas trapezoidais como mostra a próxima figura:

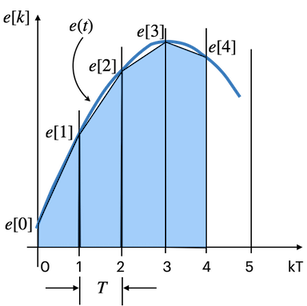
Lembrando que a área de um trapézio é calculada como:

$A=\left( \dfrac{B+b}{2} \right) \cdot h$

onde $B=$ base maior; $b=$ base menor e $h=$ altura do trapézio.

No nosso caso, $h$ será sempre igual à $T$ (período de amostragem adotado).

Levantando as equações, teremos:

$\begin{array}{rcl} i[0] &=& 0\\ i[1] &=& i[0] + T \left( \dfrac{e[0]+e[1]}{2} \right)\\ i[2] &=& i[1] + T \left( \dfrac{e[1]+e[2]}{2} \right)\\ & \vdots & \\ i[k] &=& i[k-1] + T \left( \dfrac{e[k-1]+e[k]}{2} \right) \\ &\downarrow \mathcal{Z}&\\ I(z) &=& \dfrac{T z^{-1}}{(1-z^{-1})} \; E(z)\\ I(z) &=& \dfrac{T}{2} \cdot \dfrac{(1+z^{-1})}{(1-z^{-1})} \cdot E(z)\\ & \text{ou:} &\\ I(z) &=& \dfrac{T}{2} \cdot \dfrac{(z+1)}{(z-1)} \cdot E(z) \end{array}$

Conclusão:

Note que não importa o método de integração adotado, sempre ocorrerá um pólo em $z=1$ .

1.3. Formas de Diferenciação Numérica

Uma derivada numérica pode ser obtida através de:

$\begin{array}{rcl} \dfrac{\partial e(t)}{\partial t} & \cong &\dfrac{e[k]-e[k-1]}{T}\\ \downarrow & & \\ D(z) &=& \dfrac{(1-z^{-1})}{T} \cdot E(z)\\ ou & & \\ D(z) &=& \dfrac{(z-1)}{T z} \cdot E(z) \end{array}$

1.3.1. O problema da Derivada de um sinal ruidoso

Para entender melhor o impacto da derivada sobre um sinal ruidoso, suponha que num sistema de controle, o sinal do erro seja dado por:

$e(t)=\sin(\omega t)+a_n \sin(n \omega t)$

onde:

$\omega=$ frequência angular do sinal original, cuja amplitude varia entre $\pm 1$ ;
$a_n=$ amplitude do ruído, e;
$n=$ fator-frequencia do ruído, isto é, quantas vezes a frequência do ruído é maior que a frequência do sinal original.

Suponha que a amplitude do ruído seja de apenas 1% da amplitude original do sinal, ou seja, $a_n=0,01$ .

Suponha que o ruído ocorra numa frequência $100 \times$ maior que a frequência original do sinal.

E vamos também supor que $\omega=$ 1 rad/s.

Então nosso sinal original (sem passar por derivada) corresponde à:

$e(t)=\sin(t) + 0,01\sin(100t)$

A derivada deste sinal leva à:

$\begin{array}{rcl} \dfrac{\partial e(t_)}{\partial t} &=& \cos(t) + (0,01 \cdot 100) \cos(100t)\\ &=& \cos(t) + \cos(100t) \end{array}$

ou seja, a amplitude original do ruído foi elevada e igualada (será considerada da mesma forma) que a amplitude do sinal original que queremos derivar, resultando numa onda sinosoidal com amplitude oscilando entre $\pm 2$ (note que originalmente estava restrito à $\pm 1,01$ ).

As próximas figuras ressaltam melhor o problema:

Sinal original (com o ruído):

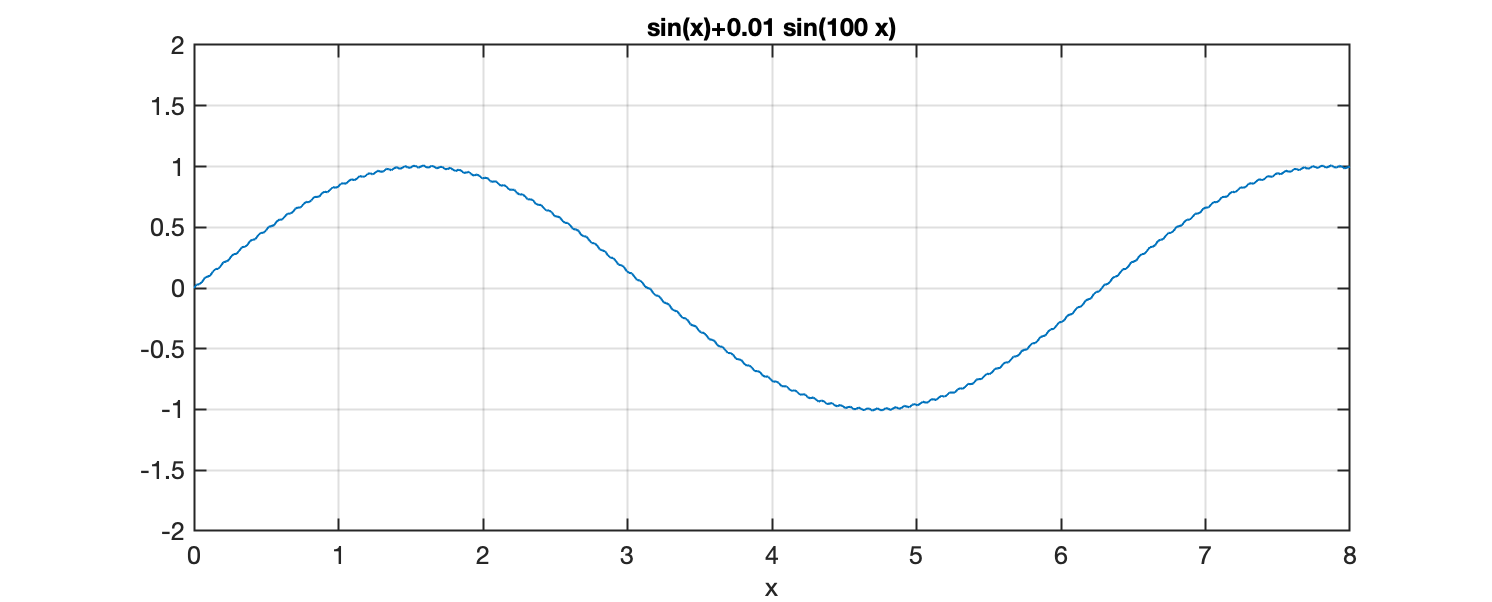
Derivada do sinal anterior (que continha ruído):

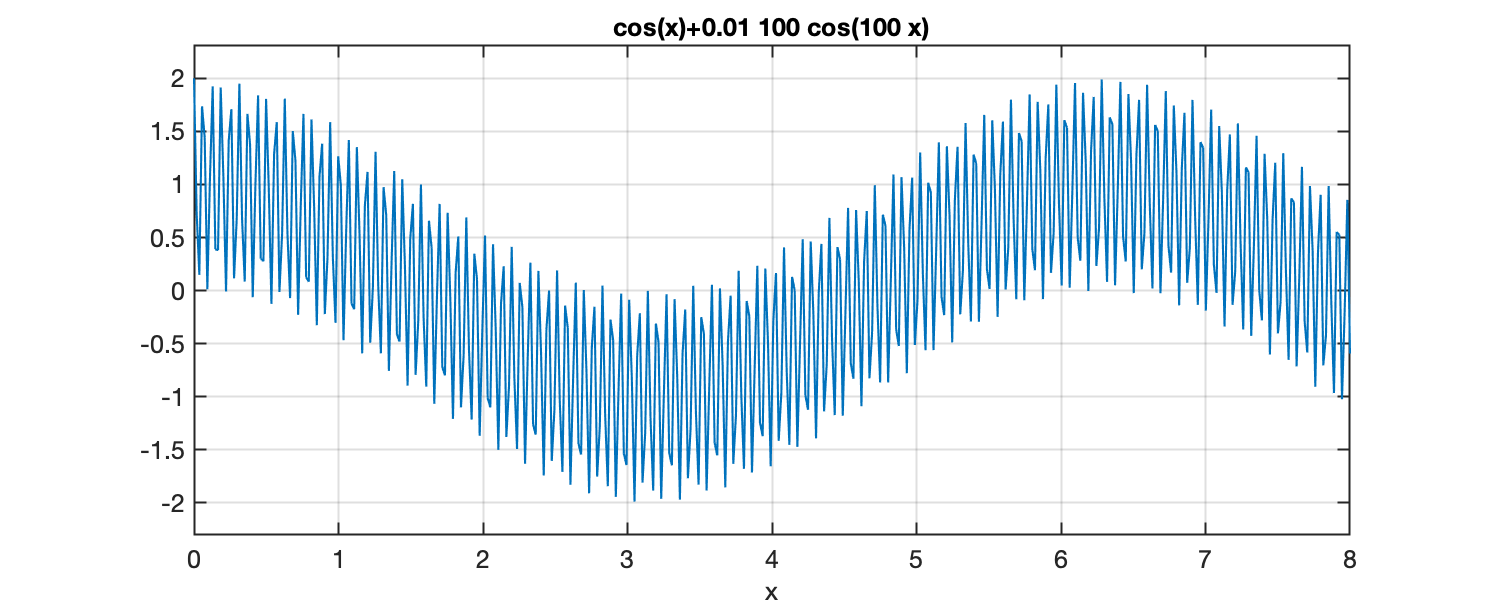
Código Matlab usado para gerar figuras anteriores:

>> ezplot('sin(x)+0.01*sin(100*x)',[0 8])
>> grid
>> axis([0 8 -2 2])
>> figure;
>> ezplot('cos(x)+0.01*100*cos(100*x)',[0 8])
>> grid

1.3.2. Ação derivativa filtrada

O problema (inerente à qualquer diferenciação) é que a derivada de um sinal ruidoso ressaltará sobremaneira a presença de ruídos presentes na malha de realimentação. Pior o resultado quanto maior for a frequência do ruído.

Solução?

Acrescentar à solução anterior um filtro derivativo, que pode ser tão simples quanto uma aproximação numérica de um filtro passa-baixa de 1a-ordem (resulta no "filtro exponencial digital de 1a-ordem").

A eq. da ação derivativa incluindo um filtro passa-baixa fica:

$D(s)=\dfrac{T_d\,s}{\alpha T_d \,s +1}$

onde tipicamente $\alpha=0,1$ .

1.3.2.1. Evitando ainda o "derivative kick"

Além disto, como é comum que os valores da referência se alterem de forma abrupta assumindo diferentes valores de constantes ao longo do tempo, realizar a derivada do sinal de erro:

$e(t)=r(t)-y(t)$ ,

costuma envolver grandes saltos (ou transições abruptas da referência), o que se chama de "derivative kicks", e que resulta numa ação derivativa muito "ruidosa".

Então se sugere fortemente que na eq. final do PID, a parte derivativa (preferencialmente com filtro), seja realizada apenas sobre a saída da planta, ou seja, que se faça algo como:

$\text{Nova Ação Derivativa}=T_d \left( \dfrac{\partial y(t)}{\partial t} \right)$ ,

ao invés de:

$\text{Ação Derivativa (original)}=T_d \left( \dfrac{\partial e(t)}{\partial t} \right)$ ,

1.3.3. Filtro Derivativo Exponencial de 1a-ordem

Então queremos filtrar o sinal do erro antes de calcular sua derivada e aplicar um ganho sobre o resultado. Ou seja, necessitamos implementar um filtro passa-baixas:

A eq. de um fitro passa-baixas de 1a-ordem pode ser descrita como:

$y(t) = x(t) + \tau_f \left( \dfrac{\partial x(t)}{\partial t} \right)$

ou:

$\dfrac{Y(s)}{X(s)}=\dfrac{1}{\tau_f \, s + 1}$

onde:

$\tau_f$ corresponde a constante de tempo do filtro;
$x(t)=$ sinal na entrada do filtro;
$y(t)=$ sinal na saída do filtro.

Note que:

$\tau_f = \dfrac{1}{2\pi\, f_c}$

onde: $f_c=$ frequência de corte do filtro (em Hz).

Obs.: recomenda-se fazer: $\tau_f < 0,1 \cdot \tau_{max}$ ; onde $\tau_f$ corresponde a maior constante de tempo da planta à ser controlada (polo mais lento/dominante), caso contrário, um substancial atraso no tempo será introduzido na malha de controle. Isto corresponde à colocar $f_c$ uma década acima da freq. mais lenta da planta.

A primeira eq. (a diferencial) repassada para um formato discreto resulta em:

$\dfrac{\partial x(t)}{\partial t} \cong \dfrac{x[k]-x[k-1]}{\Delta T}$

onde neste caso, $\Delta t$ corresponde ao período de amostragem $T$ adotado para implementar o filtro. Assim:

$y[k]=x[k]+\tau_f \left( \dfrac{x[k]-x[k-1]}{\Delta t}\right)$

que pode ser reescrita como:

$y[k]= \left( \dfrac{\Delta t}{\tau_f + \Delta t}\right)x[k] + \left( \dfrac{\tau_f}{\tau_f + \Delta t} \right)y[k-1]$

Se neste caso fizermos:

$\alpha = \left( \dfrac{\Delta t}{\tau_f + \Delta t} \right)$ , então:

$(1-\alpha)=1-\dfrac{1}{\tau_f/\Delta t+1}=\left( \dfrac{\tau_f}{\tau_f+\Delta t} \right)$

e então, a eq. do filtro resulta numa forma mais simples como:

$y[k]=\alpha \cdot x[k] + (1-\alpha) \cdot y[k-1] \qquad$ [eq. (2)]

onde:

$\alpha=\dfrac{2\pi \cdot T \cdot f_c}{2\pi \cdot T \cdot f_c+1}$ .

A transformada $\mathcal{Z}$ da eq. anterior resulta:

$\dfrac{Y(z)}{X(z)}=\dfrac{\alpha}{1-(1-\alpha)z^{-1}}$

ou:

$\dfrac{Y(z)}{X(z)}=\dfrac{\alpha \cdot z}{z-(1-\alpha)}$

Note na eq. (2), que:

Se $\alpha = 1 \quad \Rightarrow$ não há filtro: simplesmente: $y[k]=x[k]$ ;
Se $\alpha = 0 \quad \Rightarrow$ o sinal original (medição) é ignorado.

Por fim, note que a forma sugerida para o PID "ideal" fica algo como:

1.4. PID no formato Discreto

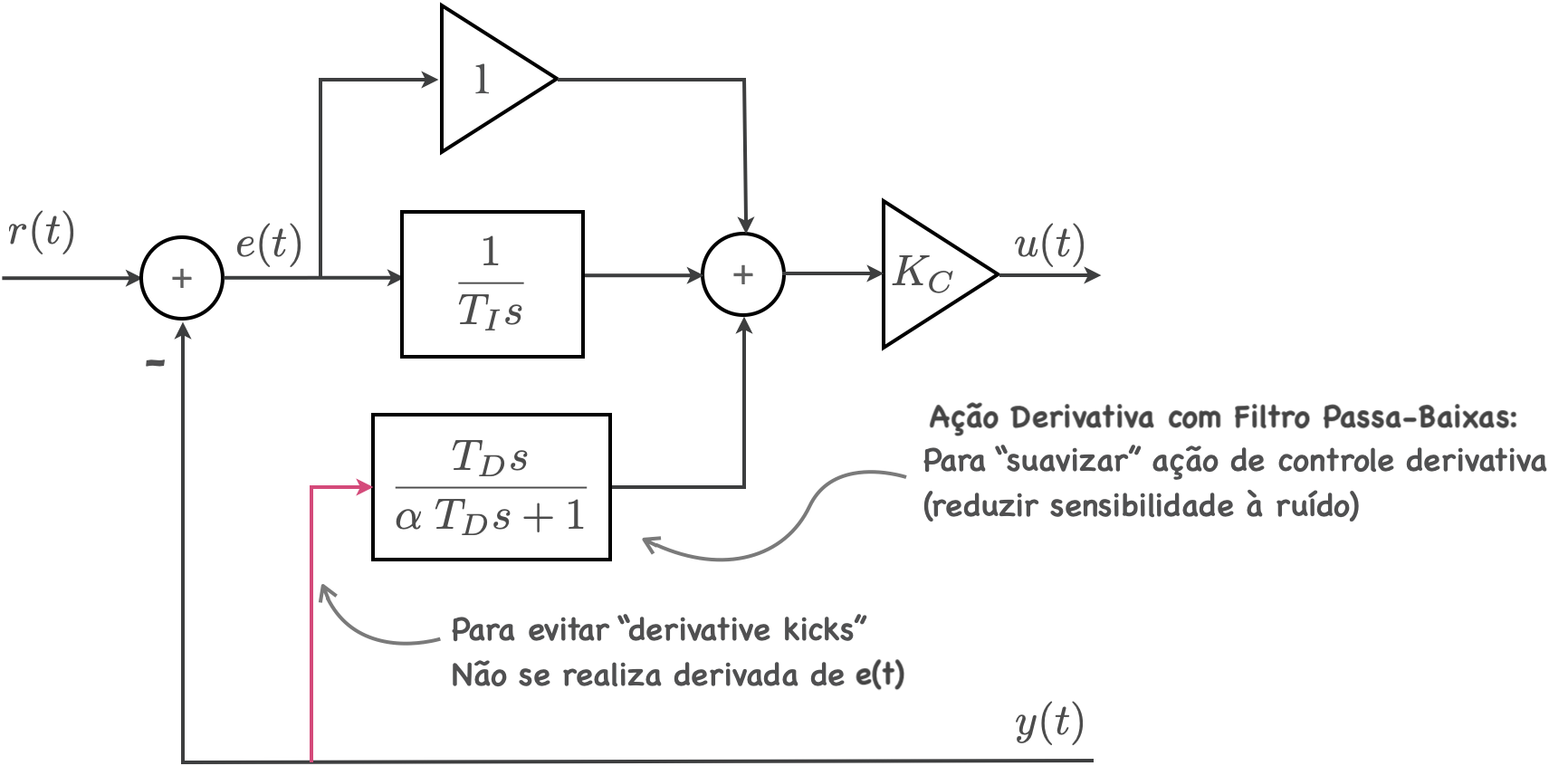
A eq. do PID no formato paralelo:

$u(t) = K_p e(t) + K_i \displaystyle\int\limits_o^t {e(t)dt + K_d \frac{{\partial e(t)}}{{\partial t}}}$

pode então ser repassada inicialmente para o formato discreto na forma:

$u[k] = K_p e[k] + K_i \displaystyle\sum\limits_{k = 0}^n {e[k]T} + K_d \left( \dfrac{e[k] - e[k - 1]}{T} \right)$

equação que também pode ser re-escrita para a forma:

$u[k] = K_c \left[ {e[k]+ \dfrac{T}{{\tau _i }}\displaystyle\sum\limits_{k = 0}^n {e[k]+ \dfrac{{\tau _d }}{T}\Big( {e[k] - e[k - 1]} \Big)} } \right]$

que corresponde ao formato ISA do PID.

De fato, qualquer uma das implementações anteriores, levam ao formato que se conhece como PID Discreto no formato de posição.

1.4.1. Modificações no PID no formato de posição

O problema associado com qualquer uma das formas anteriores está relacionado com o termo do somatório.

É fácil prever que este termo pode "saturar", efeito conhecido como de "saturação integral".

Ou seja, suponha um sistema em malha-fechada, onde o erro tarda a baixar. Neste caso, muitas áreas positivas de erro serão acumuladas, até que uma sucessão de áreas negativas (erros negativos) compense o acúmulo de áreas positivas. Neste ínterim, a variável associada com o termo somatório pode eventualmente ultrapassar o escopo da sua própria declaração (se foi declarada como int) ou pode assumir valores tão elevados (no caso de ter sido declarada como float) que se repassada como um valor (amplitude) para a ação de controle externa, irá saturar o drive de potência que comanda um motor.

Motivo pelo qual, é comum que o resultado desta implementação na versão digital da ação integral passe por um bloco "saturador", ou resulte num código do tipo:

sum = sum + e*T;
if (sum > 10000.0){
    sum = 10000.0;
}
if (sum < -10000.0){
    sum = -10000.0;
}

Exitem diferentes formas para contornar esta forma simplista de implementação da ação integral.

Um formato mais interessante de implementação, é conhecido como: PID no formato de velocidade, no qual, o que se computa, não é o valor de $u[k]$ , mas sim, que incremento deve ser dado no sinal de controle: $\Delta u[k]$ em cada instante de amostragem.

1.4.2. PID no formato de Velocidade

Neste formato, o que interesse é calcular:

$\Delta u[k] = u[k] - u[k-1]$

ou seja, qual seria a variação, $\Delta u[k]$ , evolvida no sinal de controle $u[k]$ .

Tomando a eq. do PID no formato ISA:

$u(t)=K_c\left[ e(t) + \dfrac{1}{T_i}\displaystyle\int_0^t e(t)dt + T_d \dfrac{\partial e(t)}{\partial t}\right]$

onde:

$\displaystyle\int_0^t e(t)dt \cong \sum_{k=1}^n e[k] \cdot T$

$\dfrac{\partial e(t)}{\partial t} \cong \dfrac{e[k]-e[k-1]}{T}$ .

Teremos então:

$\begin{array}{rcl} \Delta u[k] &=& + K_c \left[ e[k] + \dfrac{T}{T_i}\sum_{i=1}^{n}e[k]+\dfrac{T_d}{T}\Big(e[k]-e[k-1]\Big)\right] +\\ & & - K_c \left[ e[k-1] + \dfrac{T}{T_i}\sum_{i=1}^{n-1}e[k]+\dfrac{T_d}{T}\Big(e[k-1]-e[k-2]\Big)\right]\\ \Delta u[k] &=& K_c \left[ e[k]-e[k-1] + \dfrac{T}{T_i}e[k] + \dfrac{T_d}{T} \Big( e[k] -2e[k-1] + e[k-2] \Big) \right] \end{array}$

Como: $u[k] = u[k-1] + \Delta u[k]$

então finalmente obtemos a eq. do PID no formato de velocidade:

$u[k]=u[k-1]+K_c \left[ e[k] - e[k-1] + \dfrac{T}{T_i} e[k] + \dfrac{T_d}{T} \Big( e[k] - 2e[k-1] + e[k-2] \Big) \right] \qquad$ [eq. (3)]

Note que:

O termo $\sum$ "desapareceu";
$K_i=\dfrac{T}{T_i} \quad \longleftarrow \quad \uparrow T_i \; \Rightarrow \; \downarrow K_i$
$K_d=\dfrac{T_d}{T} \quad \longleftarrow \quad \uparrow T_d \; \Rightarrow \; \uparrow K_d$

A eq. de $\Delta u[k]$ do PID, no caso de opção pelo uso de integração trapezoidal, se modifica levemente para:

$\Delta u[k] = K_c \left[ e[k]-e[k-1] + \dfrac{T}{T_i}\left( \dfrac{e[k]+e[k-1]}{2}\right) + \dfrac{T_d}{T} \Big( e[k] -2e[k-1] + e[k-2] \Big) \right]$

O PID no formato de velocidade, arquitetura paralela fica:

$u[k]=u[k-1]+K_p \Big( e[k] - e[k-1] \Big) + K_i e[k] + K_d \Big( e[k] - 2e[k-1] + e[k-2] \Big) \qquad$ [eq. (4)]

onde:

$K_p = K_c$
$K_i = \dfrac{K_c \, T}{T_i}$
$K_d = \dfrac{K_c \, T_d}{T}$

1.5. Codificação do PID

A próxima figura mostra como ficaria o main() envolvendo programação de um sistema de controle:

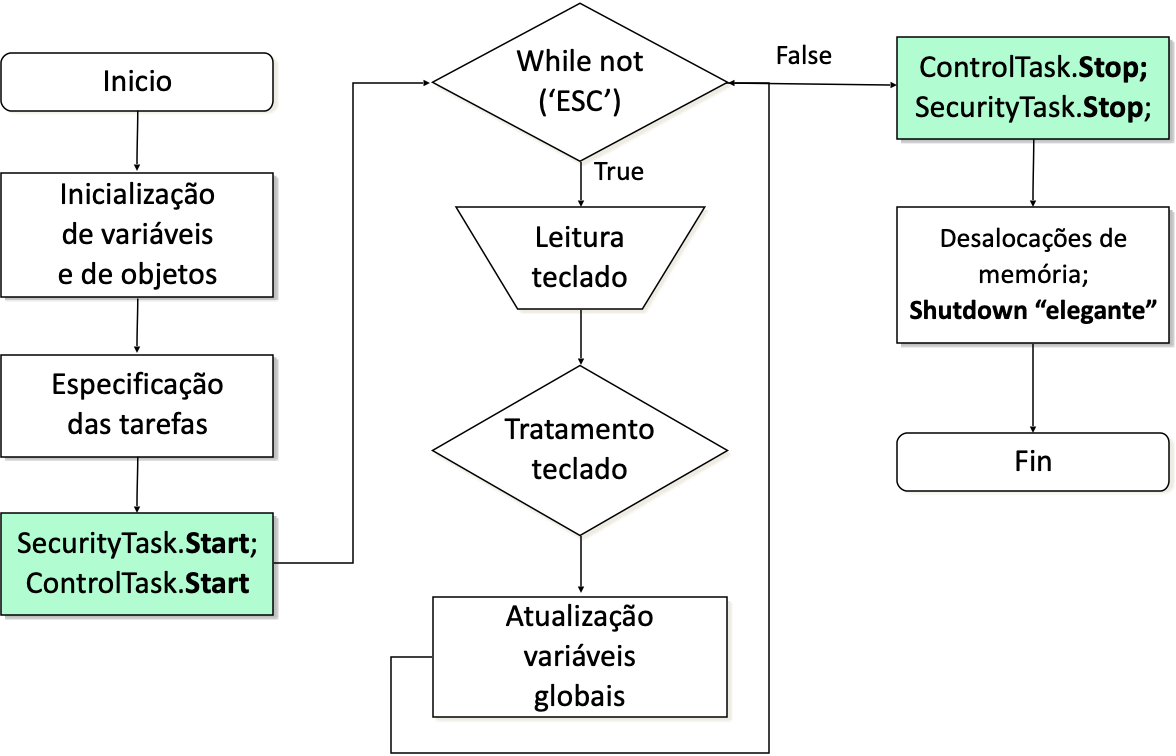
Note na figura anterior, que o algoritmo de controle, a rotina que inclui a eq. do controlador está prevista para ser implementada como uma task() síncrona (ControlTask) em sistemas de tempo-real ou como uma rotina de tratamento de interrupção (ISR) no caso de um sistema embarcado dedicado.

Note que na figura anterior, aparece também uma tarefa associada com a parte de segurança do equipamento (SecurityTask). Este tipo de rotina é responsável por monitorar chaves de fim de curso, botões de emergência, velocidades acima do normal na operação de um sistema, etc. Esta rotina desabilita a rotina de controle caso seja detectado um problema.

A próxima figura detalha o que se faria no bloco "Inicialização de variáveis e objetos":

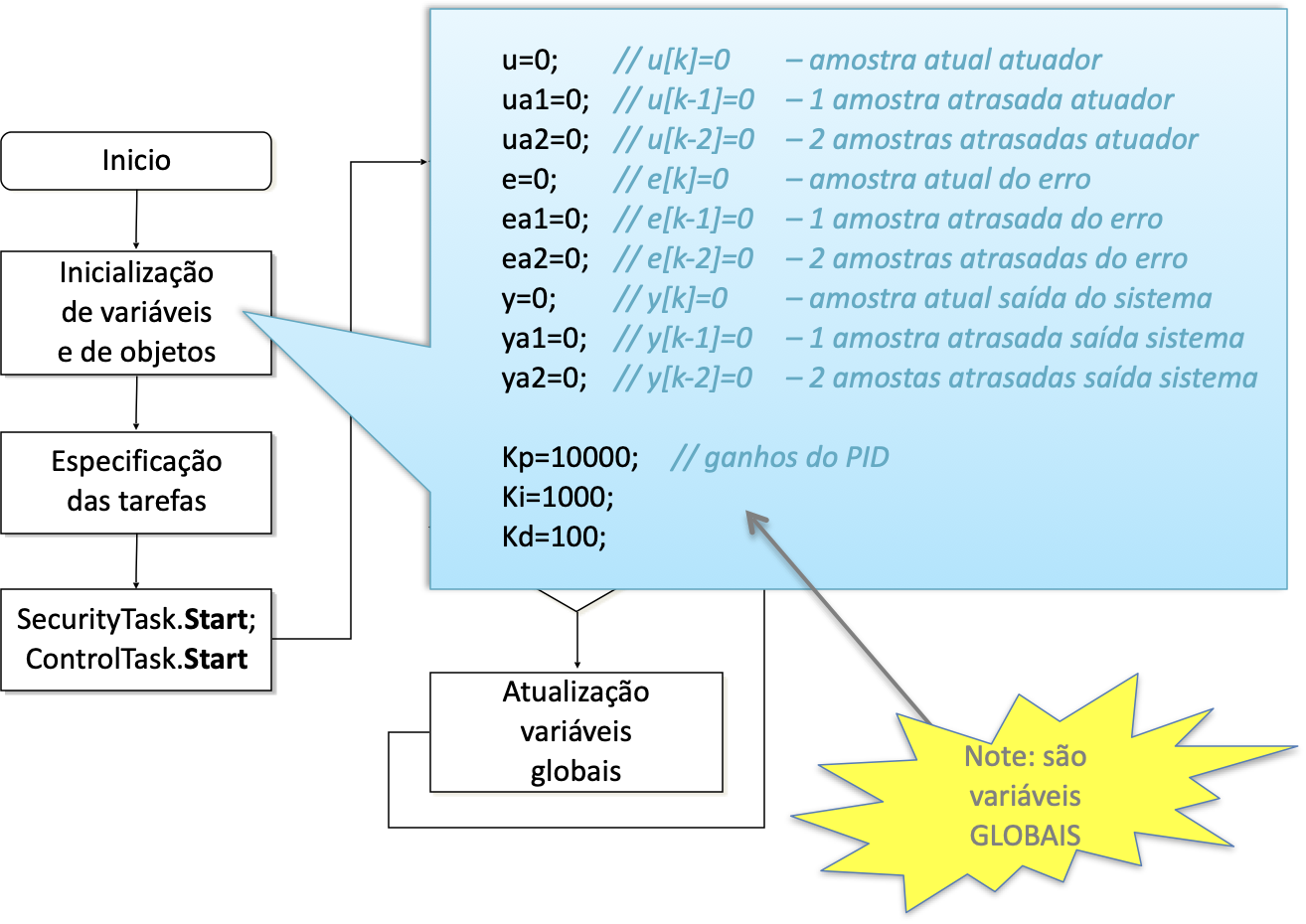
A próxima figura mostra o bloco em que se realizam os ajustes para funcionamento das tasks de tempo real (síncronas) ou no caso de microcontrolador, o bloco onde são ajustados os registradores para operação e associaçao de temporizadores para operação da interrupção por software causada por overflow de temporizador (ou simplesmente ISR):

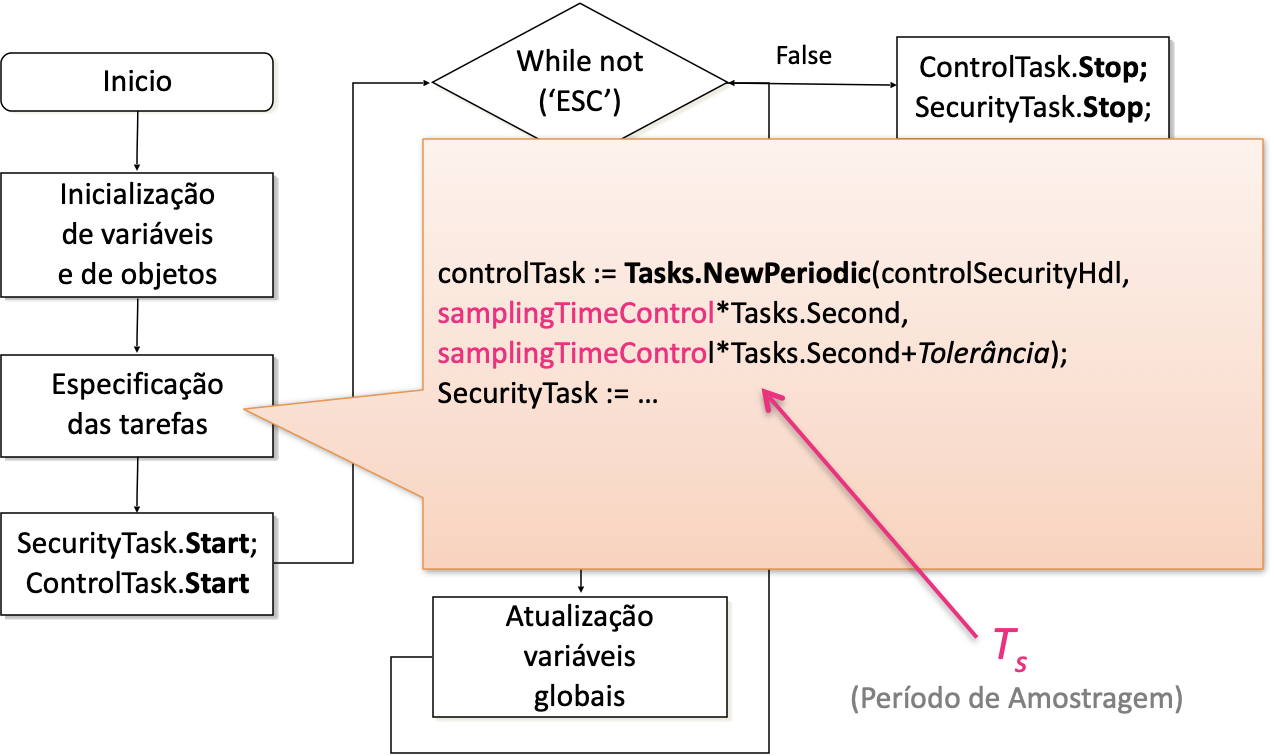
A próxima figura ilustra o que faz o bloco de "tratamento do teclado":

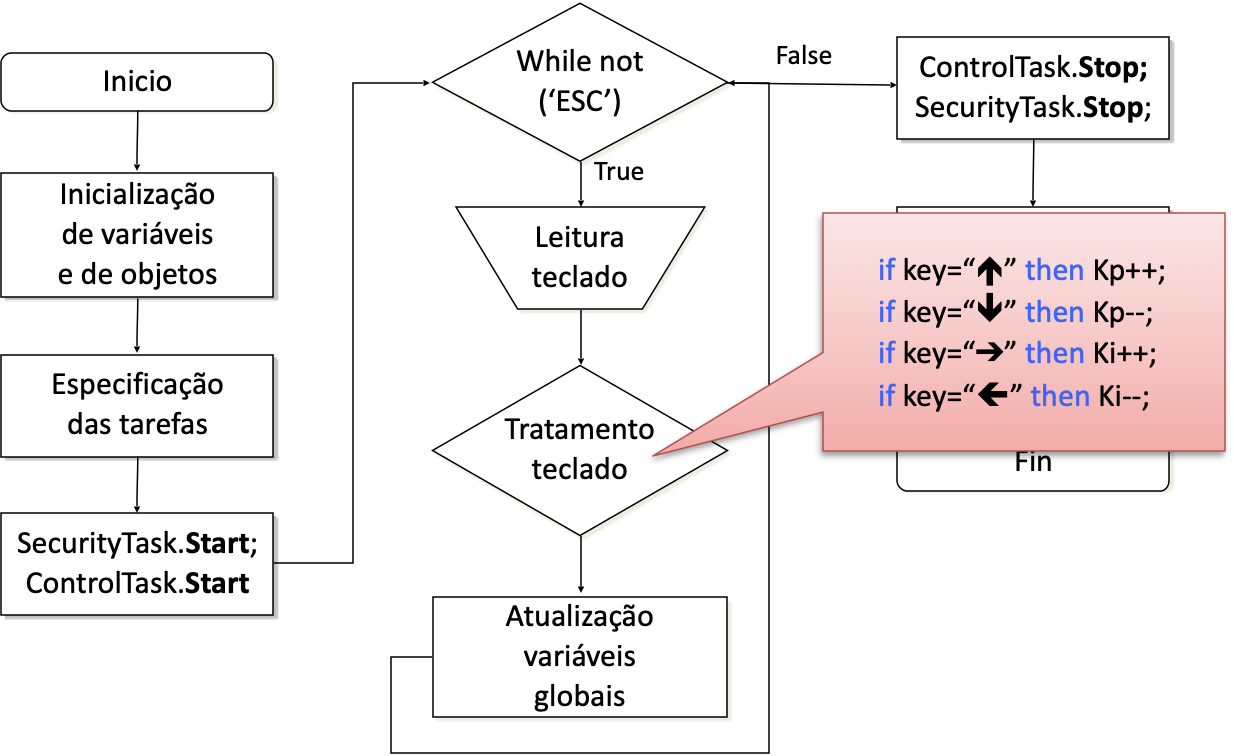
A seguinte figura mostra como deve ser programado na task (ou na ISR) associada com o controlador:

A lei de controle apresentada na figura anterior apenas foi mencionada à título de exemplo.

Exemplo: rotinas de controle num robô manipulador.

A próxima figura traz um diagrama mostrando como podem ser implementadas diferentes tasks para controle real de um robô manipulador:

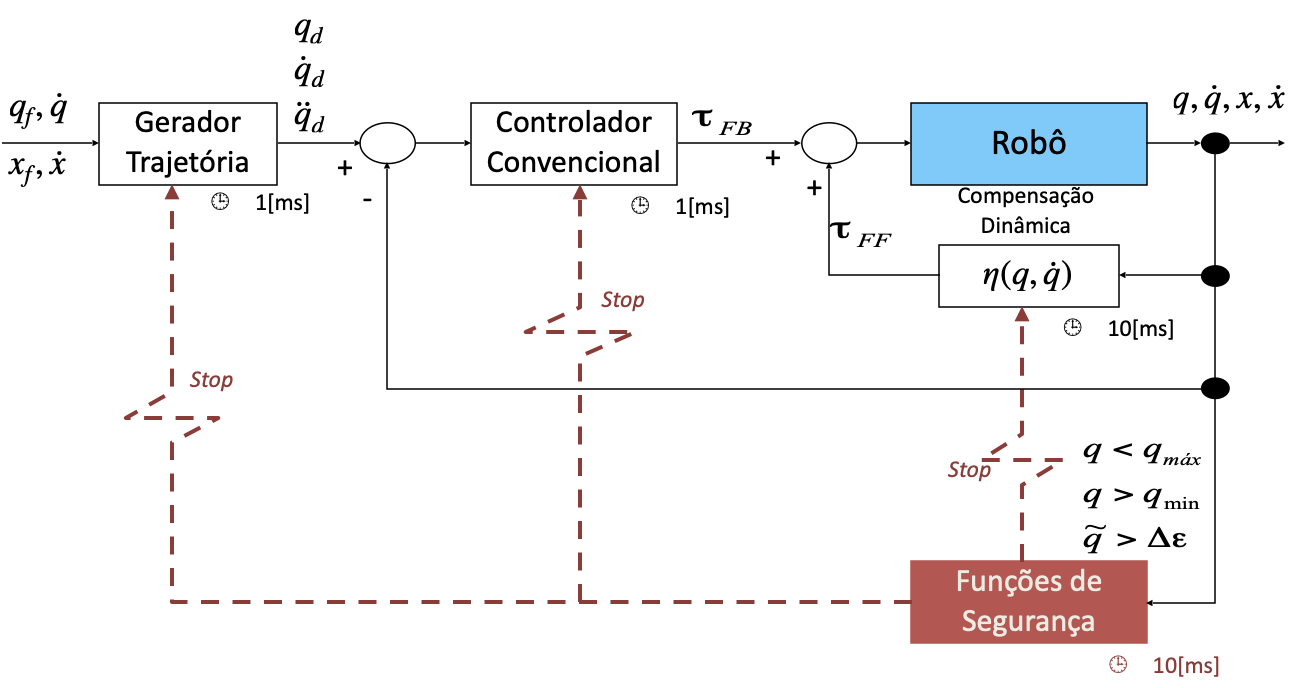
E a próxima figura passa uma idéia de como o tempo de processamento fica distribuído entre as diferentes rotinas que devem ser executadas pelo sistema (o ''tasks time slicing´´):

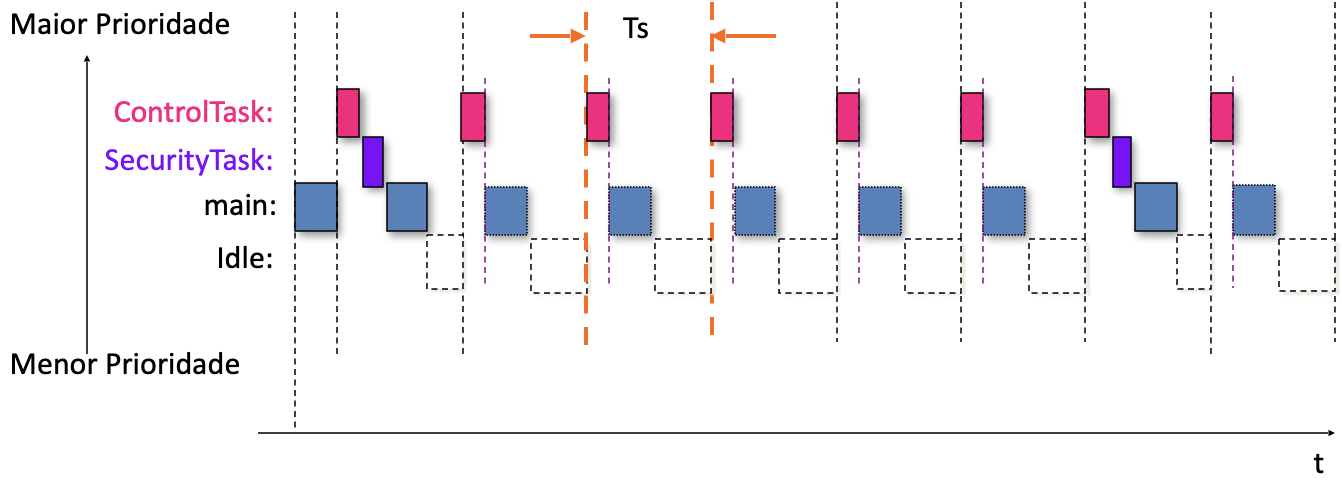
Fim.

Fernando Passold, em 24/04/2023.