
Projeto de Controlador Lead no domínio frequência
Projeto de Controlador Lead no domínio frequênciaEmbasamento TeóricoControladores do tipo Lead/LagControlador Lead (por Avanço de Fase)Procedimento para Projeto do Controlador LeadExemploExemploUsando App Control System Designer
Aula de 14.11.2019. Atualizado em 18.11.2024.
Embasamento Teórico
Controladores do tipo Lead/Lag
Equação genérica:
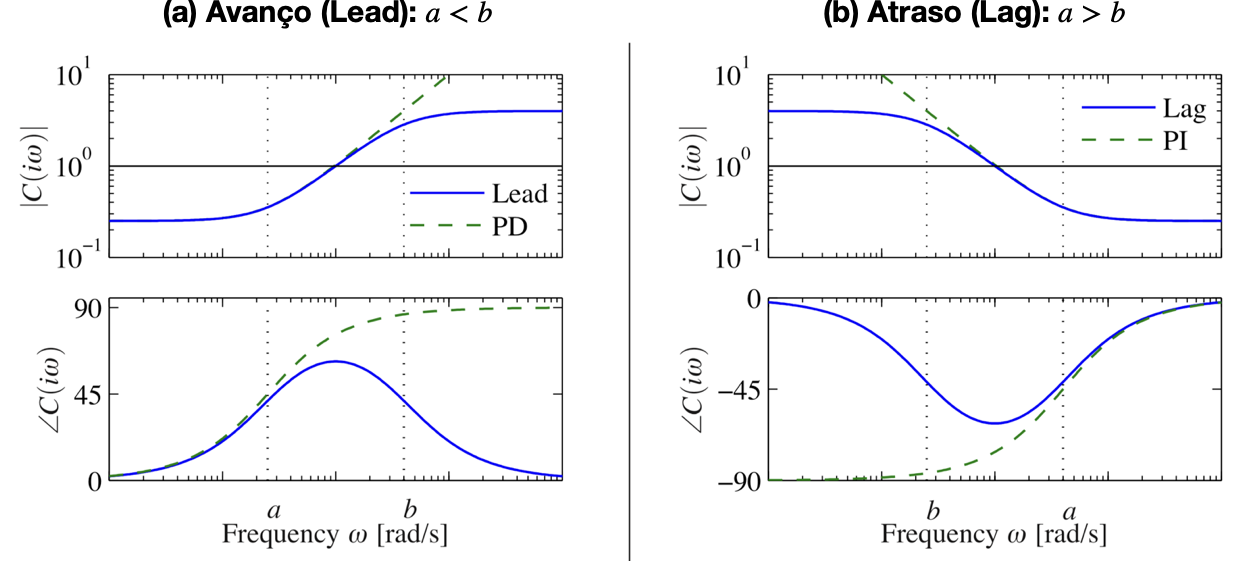
Baseado em: Karl Johan Aström, Richard M. Murray; Feedback Systems: An Introduction for Scientists and Engineers, Princeton University Press, Princeton, New Jersey, 2008.
Controlador Lead (por Avanço de Fase)
Uma equação genérica para este controlador pode ser:
Circuito usado para sintetizar um controlador por avanço de fase:
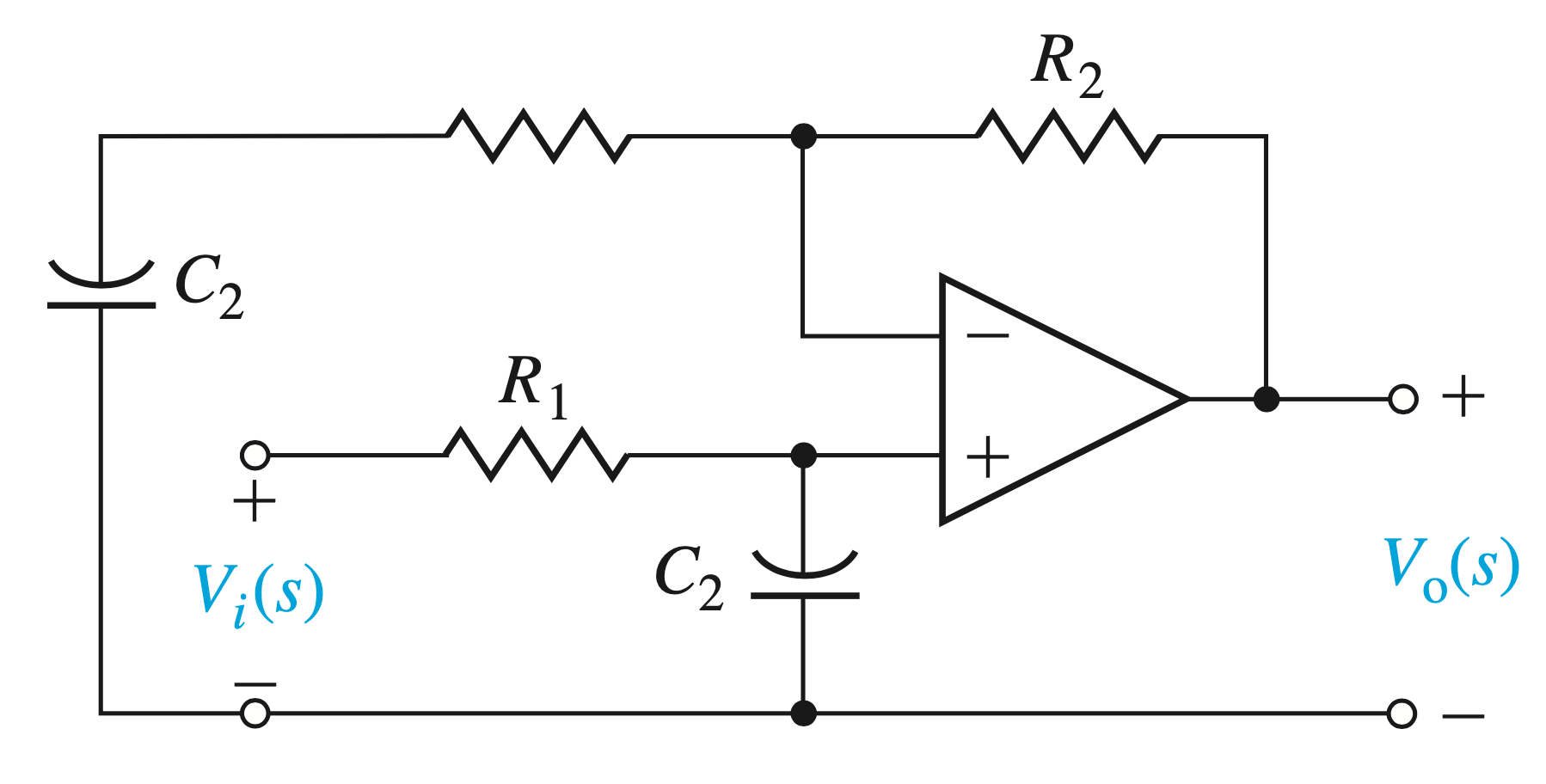
Ref.: Dorf, Richard C; Bishop, Robert H.; Modern Control Systems, 13th ed, (Chapter 8).
A equação anterior leva ao diagrama de Bode mostrado à seguir:
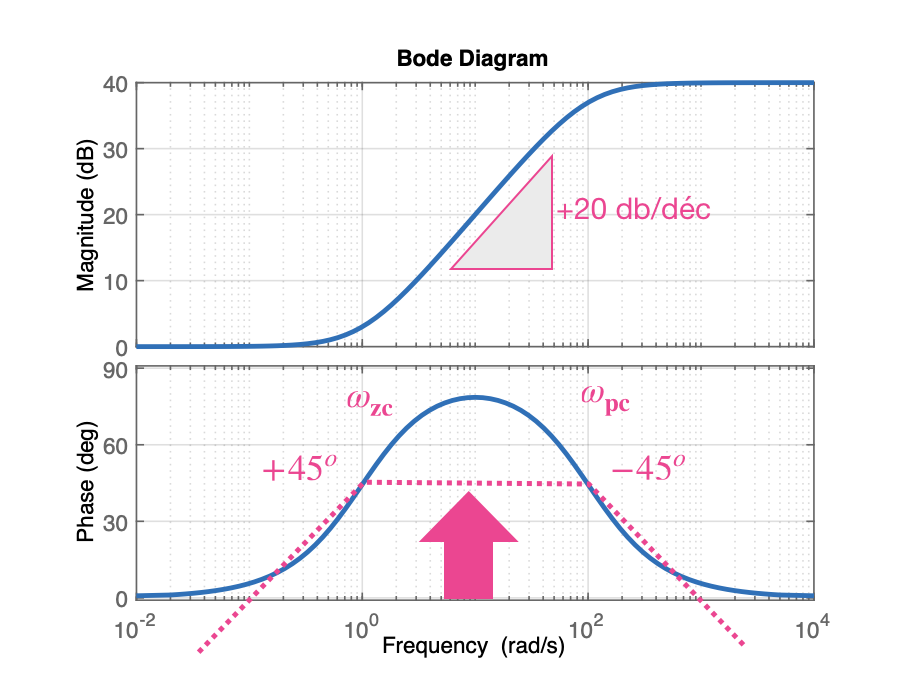
Detalhes:
- Zero próximo da origem (do plano-s).
Vantagens deste controlador (ou objetivos pretendidos com adoção do mesmo):
aumentar margem de fase, ; Lembrando que:
Se é possível variar então é possível variar .
(aproximação válida para: ):
Resposta temporal Relação: 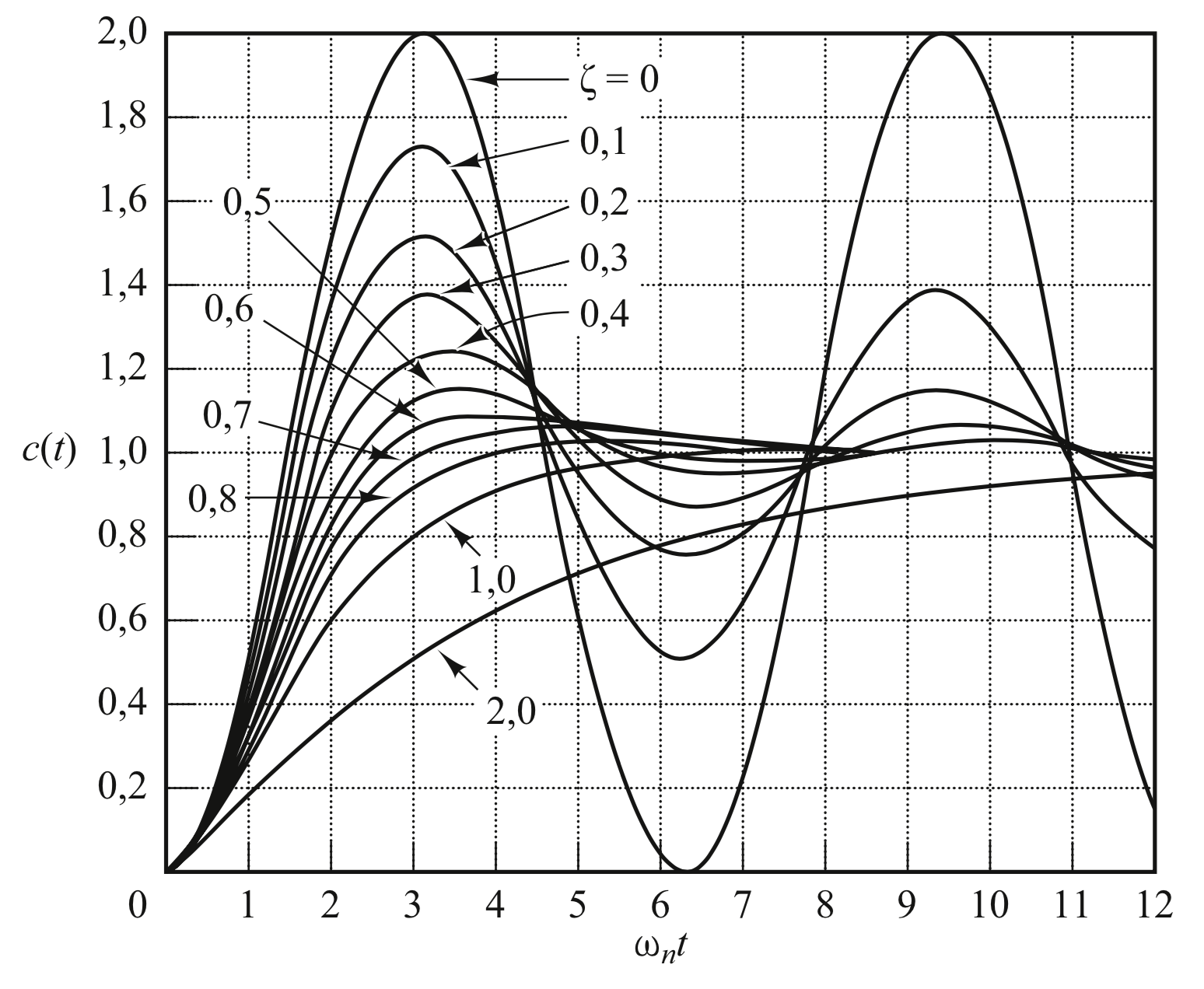
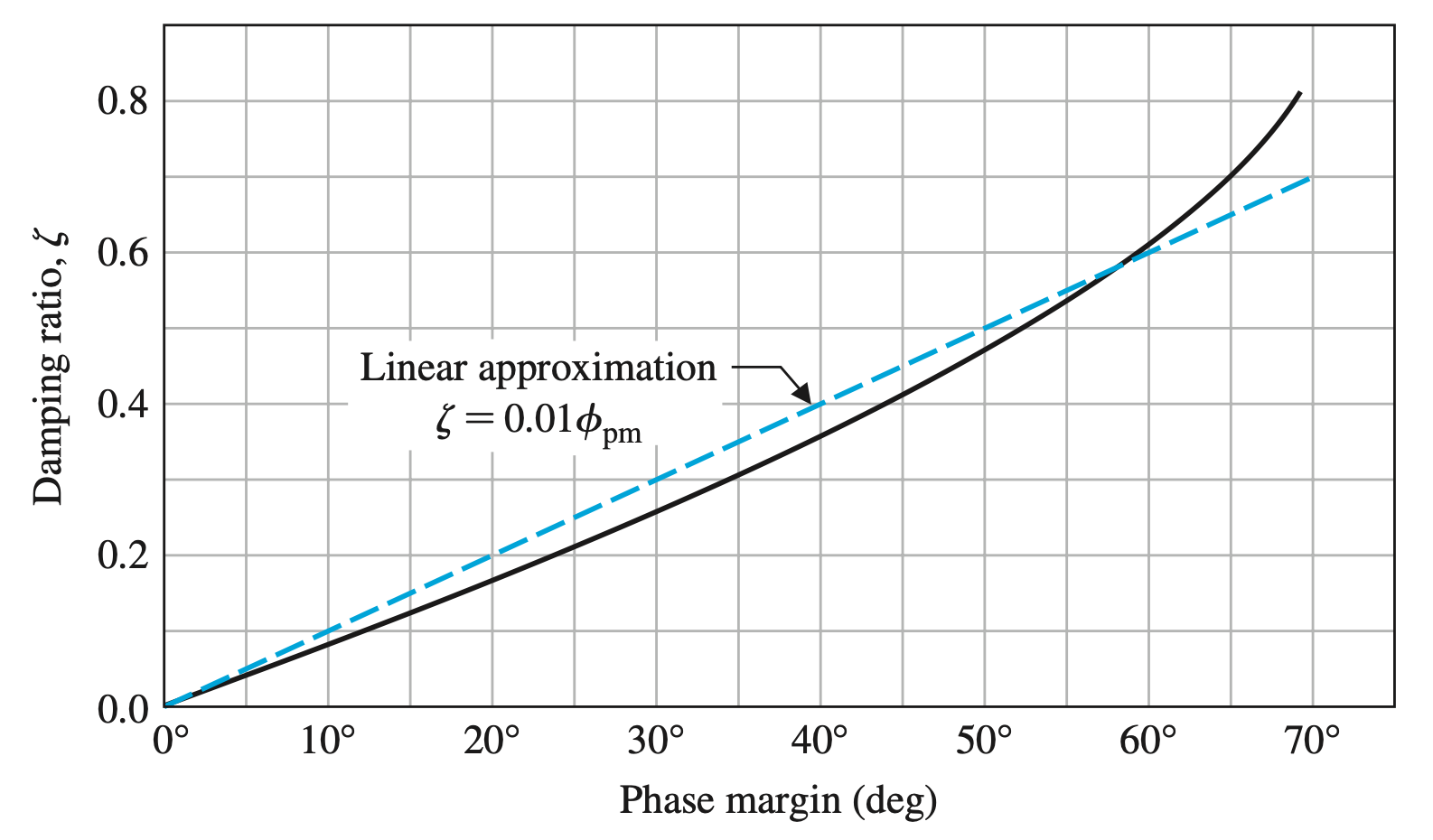
, e ; Lembrando de respostas de sistemas de 2a-ordem em malha fechada:
Quando ; quando (respostas sub-amortecidas), temos:
, ou
atua na faixa "alta" de frequências.
O problema é que esta eq. genérica não permite um estudo mais aprofundado ou facilita o projeto e aplicação deste controlador numa planta. A fim de melhorar a contribuição causada pela adoção deste controlador, modificaremos a eq. genérica do mesmo para:
Ref.: Katsuhiko Ogata, Engenharia de controle moderno, 5a. ed., p. 822. São Paulo: Pearson Prentice Hall, 2010; In [Capítulo 7 – Análise e projeto de sistemas de controle pelo método de resposta em frequência];
Detalhes:
- Note que define a relação ou "distância" entre o zero e pólo deste controlador. O pólo fica localizado numa frequência vezes superior à do zero.
- O valor mínimo de  é limitado pela construção física do compensador por avanço de fase. Esse valor mínimo de é geralmente adotado em torno de 0,05. Isso significa que o valor de avanço de fase máximo que pode ser conseguido é de aproximadamente . A eq. anterior rende o mesmo tipo de diagrama de bode que o já mostrado inicialmente, mas permite inferir informações mais interessantes para realização de um projeto adotando este tipo de controlador:
A próxima figura ressalta detalhes envolvendo o controlador por avanço de fase:
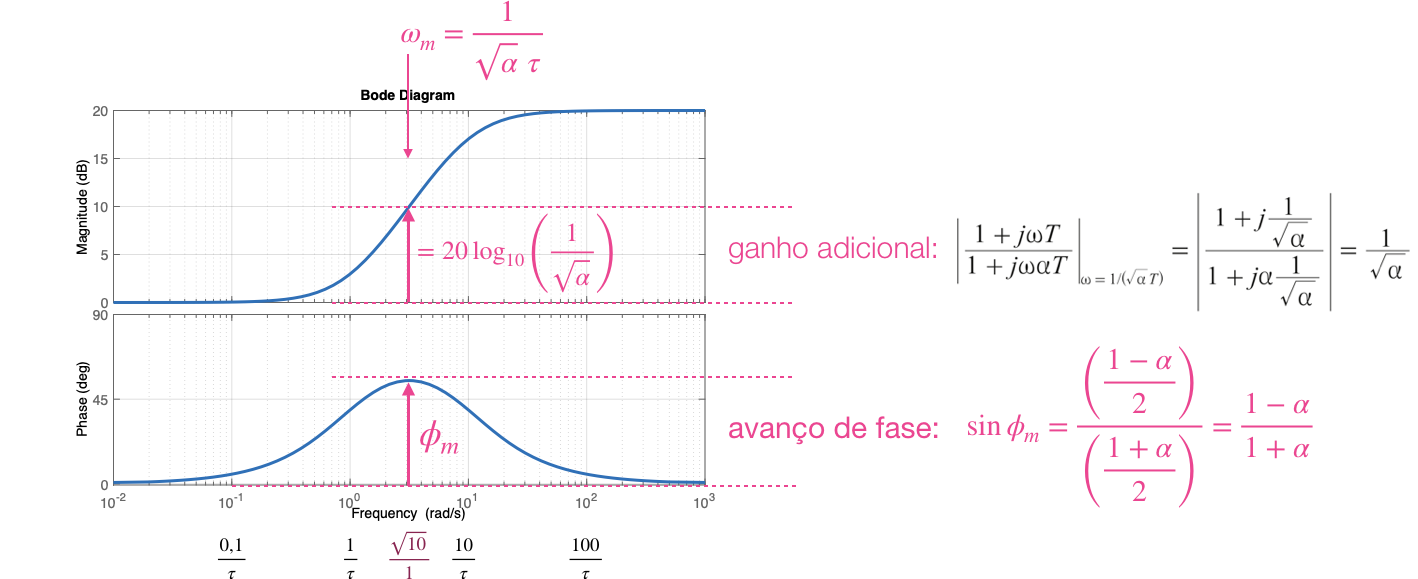
Esta figura ressalta as contribuições e alterações que serão provocadas no diagrana de Bode quando um controlador por Avanço de Fase for introduzido num sistema; corresponde à contribuição angular pretendida.
Notar:
A contribuição máxima (avanço de fase máximo) ocorre na frequenacia : onde corresponde à frequência onde fica localizado o zero () deste controlador, ou:
lembrando que:
Na frequência , a contribuição angular máxima, obtida, corresponde à relação: de onde podemos isolar :
Note que na frequência , o controlador por avanço de fase, vai acrescentar um ganho ao sistema no valor de: , ou
Procedimento para Projeto do Controlador Lead
Primeiramente defina o ganho que deve ser incorporado ao sistema em MF para que o mesmo atenda aos requisitos de erro em regime permanente especificados para o mesmo. Na prática, fazemos:
A fica:
onde: . Então, determine o ganho a fim de satisfazer o requisito de erro estático desejado ().
- Construir o Diagrama de Bode, com o ajustado. Avaliar a margem de fase original. Comparar com margem de fase desejada.
- Determinar o avanço de fase necessário (que deve ser acrescentado ao sistema): Adicionar à  ao ângulo assim determinado porque a adição do compensador, desloca um pouco a frequência de cruzamento de ganho () para a direita, reduzindo em algo a margem de fase.
- Determinar o fator de atenuação . Definir a freq. na qual o bloco não compensado passa pelo ponto . Selecionar esta freq. como nova freq. de cruzamento de ganho (), que corresponde à .
- Determinar as frequências do controlador:
- Usando o valor de determinado no item (1) e o de  na etapa (4), calcular a constante .
- Verificar a margem de ganho finalmente obitda para se certificar de que ela é satisfatória. Se não for, repita todo o processo modificando a localização do pólo e zero do controlador até alcançar o resultado desejado.
Exemplo
Considere uma planta caracterizada pela equação:
Deseja-se projetar un compensador para o sistema, de modo que a constante de erro estático de velocidade, , seja , a margem de fase seja pelo menos e a margem de ganho seja pelo menos 10 db.
Exemplo 7.26 extraido de Ogata, pag. 455
Solução
1) Primeiramente temos que ajustar o ganho do sistema em MF para atender às especificações do projeto em regime permanente ou seja, propiciar a constante de erro estático de velocidade requerida:
2) Traçamos o diagrama de Bode já considerando :
xxxxxxxxxx>> G1=tf(40, poly([ 0 -2]));>> zpk(G1) 40 ------- s (s+2) Continuous-time zero/pole/gain model.>> bode(G1)Diagrama de Bode para :
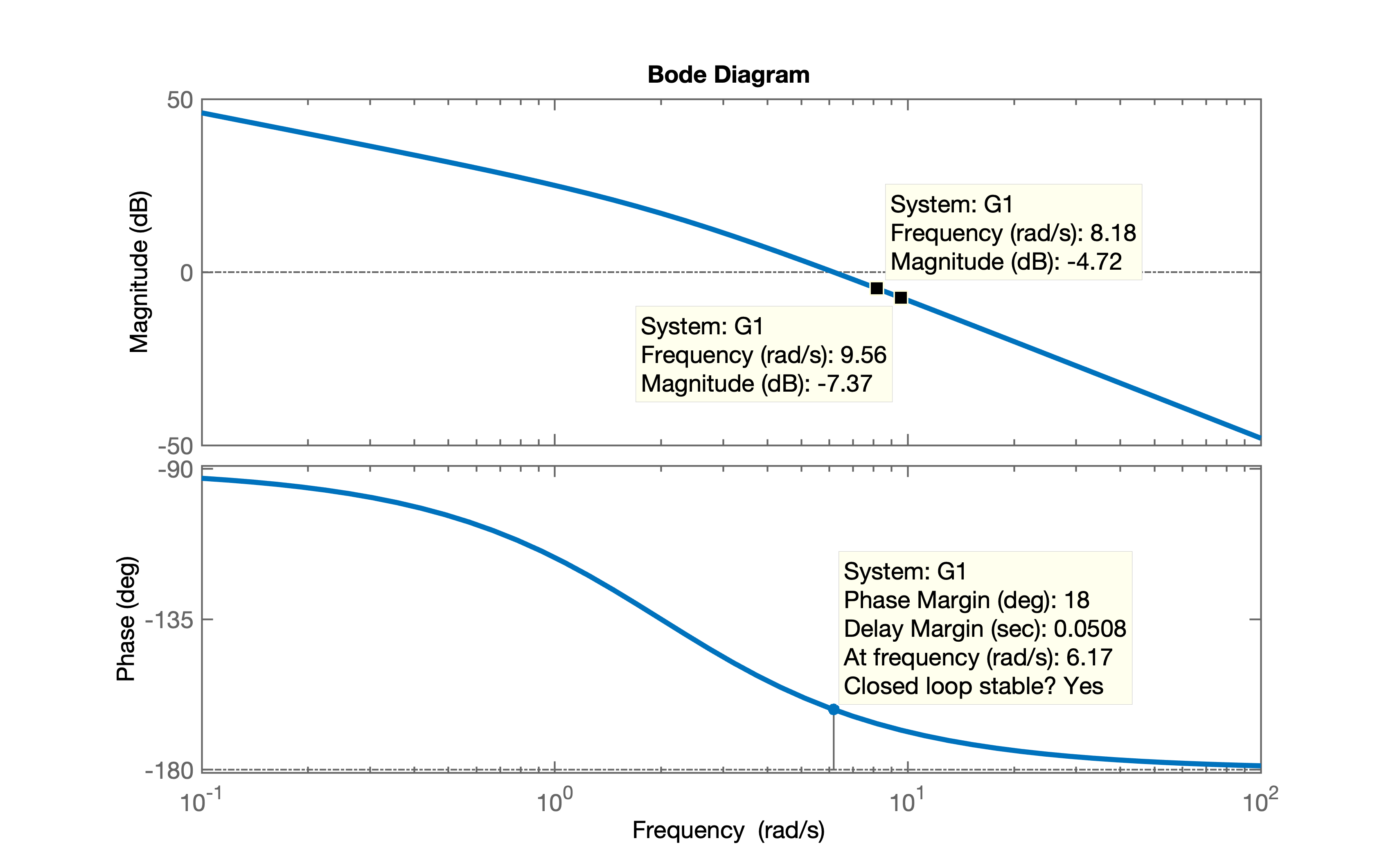
3) Analisando o diagrama de Bode anterior percebemos que a margem de fase do sistema (), realmente é muito baixa, apenas (o que implica overshoots elevados, fortes oscilações e bastante alongado).
Curiosamente, para
Como é desejado margem de fase mínima de () podemos inicialmente considerar o quanto é necessário aumentar esta margem de fase:
xxxxxxxxxx>> 50-18ans = 32Mas também temos que considerar que o acréscimo do controlador de avanço na planta, afeta um pouco tanto o diagrama de fase quanto ao ganho do sistema original. Para compensar esta ligeira distorção se costuma acrescentar de à na fase:
xxxxxxxxxx>> 32+5ans = 37Então, necessitamos que nosso controlador avance a fase em (esta seria a contribuição angular deste controlador).
4) Determinamos o fator , com base no desejado:
de onde podemos calcular :
xxxxxxxxxx>> aux=sin(37*pi/180) % lembrar que Matlab trabalha com radianos e não grausaux = 0.6018>> alpha=(1-aux)/(1+aux)alpha = 0.2486Agora falta considerar (e compensar) o ganho extra adicionado pelo controlador na frequência , que é igual à . Note que a nova frequência da margem de fase (onde o diagrama de Bode passa por 0 dB) será ligeiramenta deslocada para a direita. Alguns autores chamam este novo ponto de frequencia, de frequência de "cruzamento de ganho" ou .
O que se quer dizer é que, se queremos manter a margem de fase requerida, o ganho do sistema nesta frequencia, deveria ser de 0 dB, o que não ocorre porque a introdução do compensador de avanço de fase faz "subir" o ganho do sistema compensado. A idéia então é compensar esta subida, identificando a nova frequência onde o diagrama de Bode de "caia" o mesmo tanto que o compensaador fará "subir" o ganho.
Primeiramente temos que calcular o impacto no ganho causado pelo acréscimo do compensandor de Avanço:
xxxxxxxxxx>> ganho=1/sqrt(alpha)ganho = 2.0057>> 20*log10(ganho)ans = 6.0453Temos então que "caçar" este valor de ganho no diagrama de Bode. No caso, notar que obteremos um valor aproximado já que o matlab não calcula todos os valores possíveis de ganho para compor o diagrama de Bode. O matlab varia a frequencia do diagrama de forma não linear, logarítmica quando se usa a função bode(.):
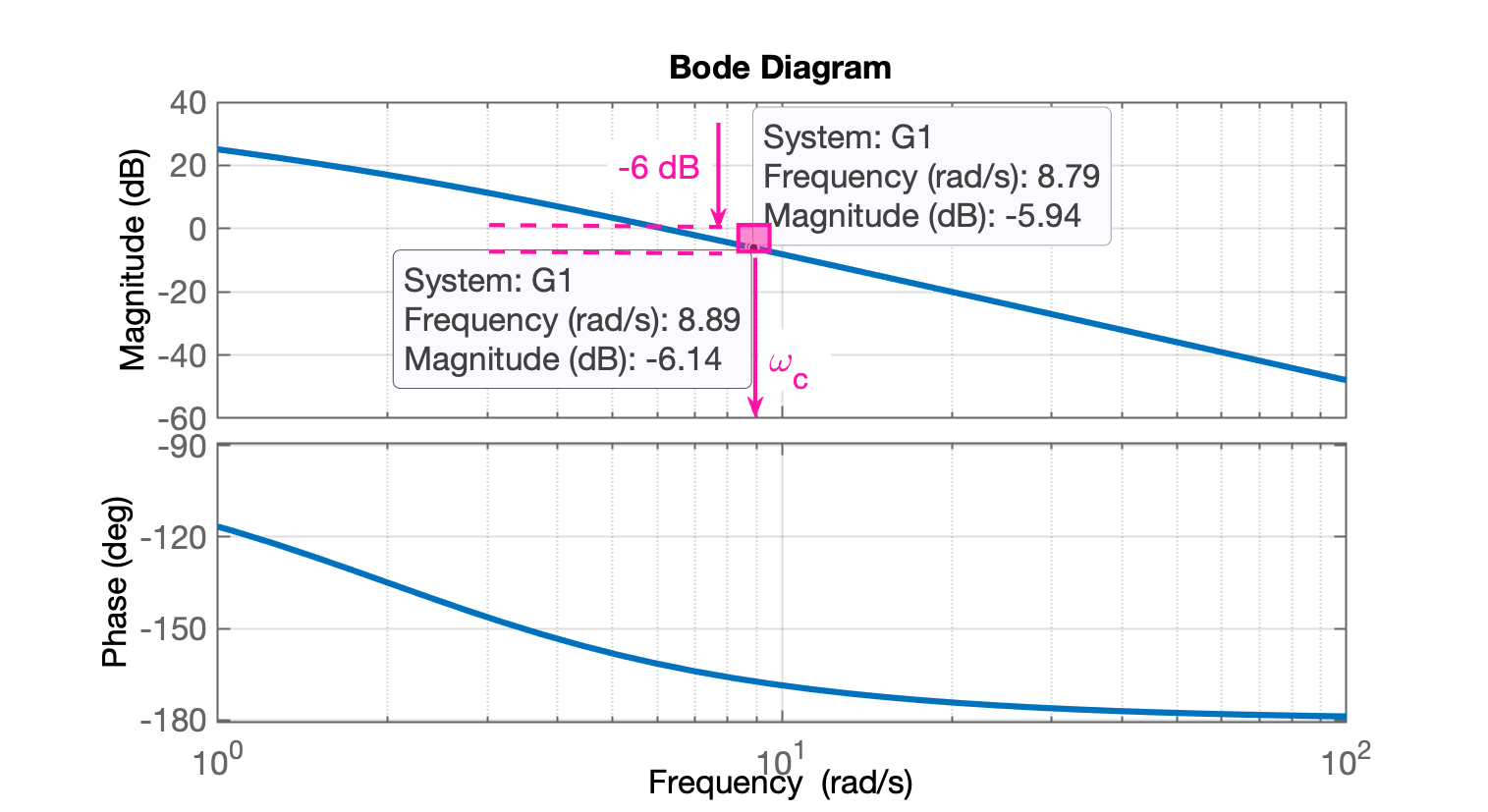
Neste caso, percebemos, via Datatips do Matab (ver figura anterior com diagrama de bode plotado), e temos acesso a 2 ponto próximos com a atenução desejada, ou ganho de dB rad/s, ou a frequência na qual , é aproximadamente (rad/s) (ver figura anterior).
5) De posse de e , agora podemos determinar as frequências para o zero e para o pólo do controlador:
Notar que não necessitamos calcular , já que:
então:
xxxxxxxxxx>> % wm (ou wc) final considerando Pm desejado fica em>> wm=9 % rad/swm = 9>> zero=sqrt(alpha)*wmzero = 4.4872>> polo=wm/sqrt(alpha)polo = 18.0512>> % Construindo a eq. do Controlador de Avanço>> C=tf( [1 zero], [1 polo] );>> zpk(C) % eq. do Lead (sem ganho) (s+4.487) --------- (s+18.05) Continuous-time zero/pole/gain model.6) Notar que falta definir o ganho do controlador. Para tanto, lembrar que o ganho final da (ou ) então:
e então:
xxxxxxxxxx>> K=10;>> Kc=K/alphaKc = 40.2279>> % Montando eq. final do Compensador, incluindo seu ganho:>> C=tf( Kc*[1 zero], [1 polo] );>> zpk(C) % eq. final do Lead com seu ganhoans = 40.228 (s+4.487) ---------------- (s+18.05) Continuous-time zero/pole/gain model.7) Avaliando o resultado final obtido:
xxxxxxxxxx>> G=tf(4, poly( [0 -2] ) );>> zpk(G) % eq. original da plantaans = 4 ------- s (s+2) Continuous-time zero/pole/gain model.>> ftma=C*G;>> figure; bode(G, G1, C, ftma)>> legend('G(s)', 'G1(s)', 'C(s)', 'ftma(s)')>> O que gera o Diagrama de Bode final:
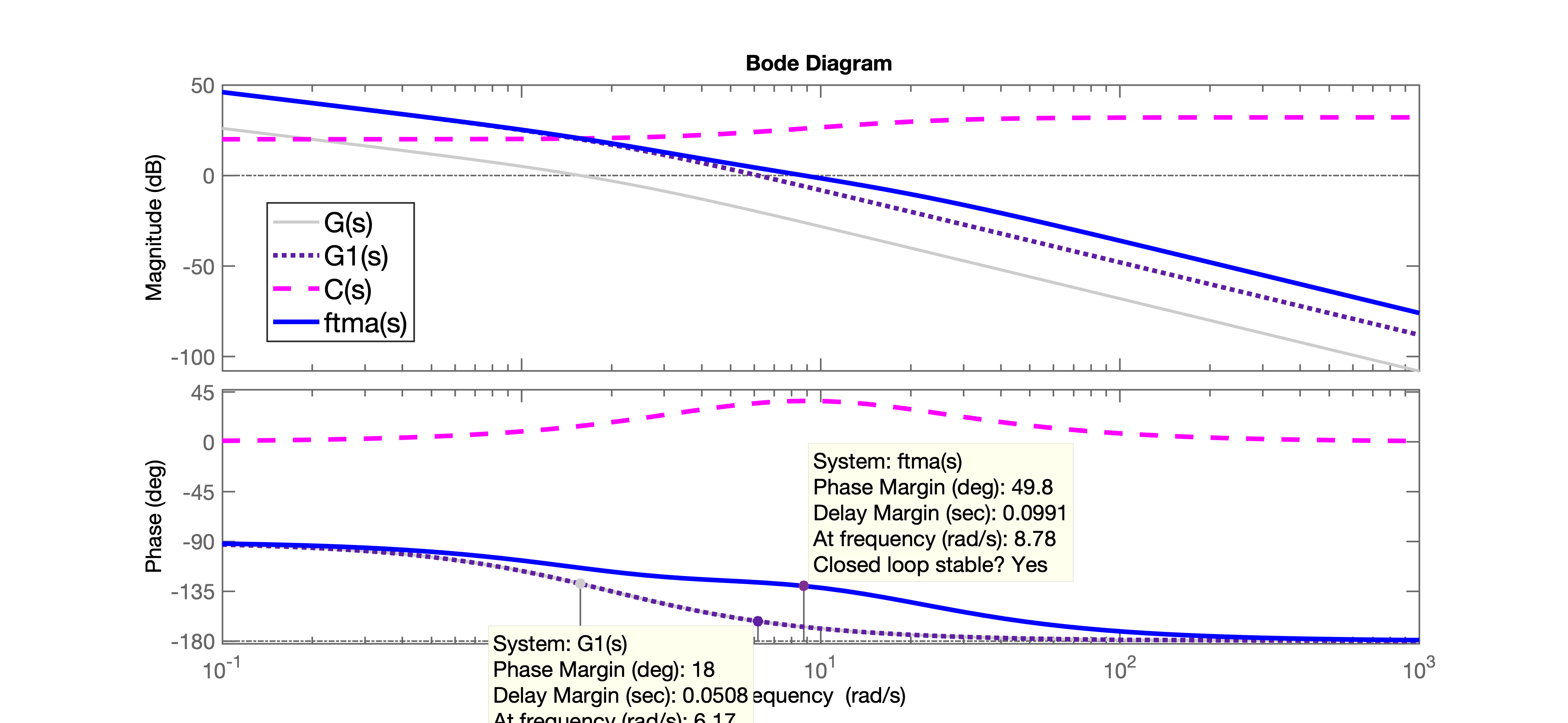
No diagrama de Bode anterior é possível se observar:
- A margem da fase original do sistema em ;
- A contribuição causada pelo compensador, maior no diagrama de fase e algo no diagrama de ganho;
- A margem final de fase: .
Exemplo
Projeto de Lead para controle posição de um motor CC. O circuito elétrico da armadura e o diagrama do corpo livre do rotor são mostrados na figura a seguir.
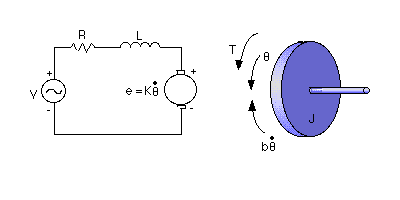
Neste exemplo, assumiremos os seguintes valores para os parâmetros físicos. Esses valores foram obtidos por experimento de um motor real no laboratório de controle de graduação da Carnegie Mellon University, usados para definir o Projeto de um Controle de Posição no Domìnio Frequência:
- momento de inércia do rotor, 3,22284E-6 kg.m^ 2 / s^2
- relação de amortecimento do sistema mecânico, 3.5077E-6 Nms
- constante de força eletromotriz, 0,0274 Nm / Amp
- resistência elétrica, 4 ohm
- indutância elétrica, 2,75E-6 H
- tensão de entrada, tensão da fonte
- output, ângulo posição do eixo
- Obs.: Supõe-se que o rotor e o eixo sejam rígidos.
Equações do sistema:
O torque do motor, , está relacionado à corrente da armadura, , por um fator constante . A f.e.m. contra, , está relacionada à velocidade de rotação, pelas seguintes equações:
No sistema internacional de unidades, (constante da armadura) é igual a (constante do motor).
A partir da figura anterior, podemos escrever as seguintes equações baseadas na lei de Newton combinada com a lei de Kirchhoff:
Usando transformadas de Laplace, as equações acima podem ser expressas em termos de :
Ao eliminar , podemos obter a seguinte função de transferência, onde a velocidade de rotação é a saída e a tensão é uma entrada:
No entanto, neste exemplo, veremos a posição como sendo a saída. Podemos obter a posição integrando a velocidade, , portanto, apenas precisamos dividir a função de transferência por :
e o diagrama de blocos do sistema se parece com:
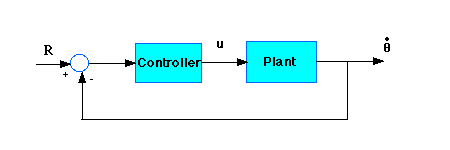
Com uma referência degrau de 1 rad/s, os critérios de projeto são:
- Tempo de assentamento inferior a 40 milissegundos;
- Ultrapassageam menor de 16%
- Nenhum erro de estado estacionário
- Nenhum erro de estado estacionário devido a um distúrbio na entrada
Obtendo o diagrama de Bode original:
x
>> J=3.2284E-6;>> b=3.5077E-6;>> K=0.0274;>> R=4;>> L=2.75E-6;>> num=K;>> den=[(J*L) ((J*R)+(L*b)) ((b*R)+K^2) 0];>> G=tf(num,den)>> zpk(G) 3.0862e+09 ------------------------ s (s+1.454e06) (s+59.23) Continuous-time zero/pole/gain model.>> % Falta acrescentar o integrador para controle de posição>> I=tf(1,[1 0])I = 1 - s Continuous-time transfer function.>> % incorporando ao modelo:>> G=I*G;>> zpk(G) 3.0862e+09 -------------------------- s^2 (s+1.454e06) (s+59.23) Continuous-time zero/pole/gain model.>> % Calculando alguns valores para algum "feeling" à respeito deste sistema...>> % contante de tempo elétrica:>> 1/1.454E6ans = 6.8776e-07 % segundos>> % = 0.6878 micro-segundos!>> % constante de tempo mecânica:>> 1/59.23ans = 0.0169>> ans*1000ans = 16.8833 % mili-segundos>> % conclusão: trata-se de um pequeno motor CC>>>> % Aproveitamos para levantar dados numéricos de Bode usando o próprio Matlab:>> [Gm,Pm,Wcg,Wcp] = margin(G) Warning: The closed-loop system is unstable. > In ctrlMsgUtils.warning (line 25) In DynamicSystem/margin (line 65) Gm = 0Pm = -5.7565Wcg = 0Wcp = 5.9703>> O diagrama de Bode para esta função transferência rende:
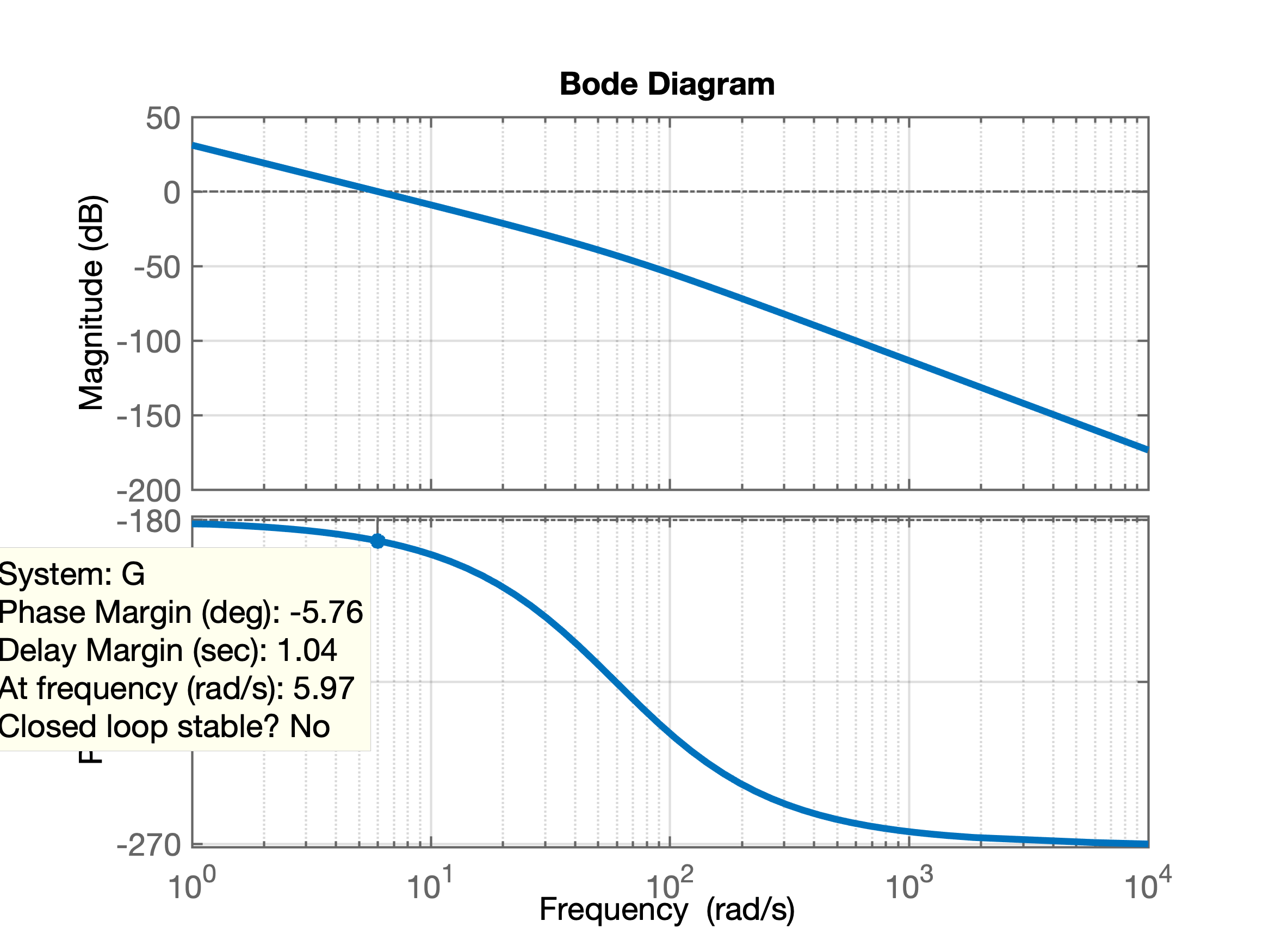
Perecebe-se uma margem de fase (original) muito baixa. Apenas .
Atendendo à especificações de ganho e margem de fase e design do controlador, temos:
- ;
- ;
- A partir do requisito de tempo de assentamento, podemos calcular a frequência de largura de banda desejada, .
Lembrando das equações:
e
e
ou:
Usando matlab para levantar estes valores, teremos:
xxxxxxxxxx>> OS=16;>> zeta=(-log(OS/100))/(sqrt(pi^2+(log(OS/100)^2)))zeta = 0.5039>> Pm_d=atan2(2*zeta, sqrt(-2*zeta^2 + sqrt( 1+4*zeta^4) ) )Pm_d = 0.9100>> Pm_d_deg=Pm_d*180/pi % para obter valor em graus (e não em radianos)Pm_d_deg = 52.1379>> % O diagrama de Bode deveria cair 3dB à partir de w_BW:>> w_BW=(4/(0.04*zeta))*sqrt((1-2*zeta^2)+sqrt(4*zeta^4-4*zeta^2+2))w_BW = 251.5743>> % Realizando alguns cálcuos preliminares>> % respeito ao avanço de fase necessário:>> Pm_d_deg-Pmans = 57.8945>> ans+5ans = 62.8945>> % Prevendo ajuste de ganho eem G(s) para respeitar -6,2 dB em w_BW=251 rad/s>> (79.1+75.1)/2ans = 77.1000>> ans-6.02 % considerando + 6,02 dB do Leadans = 71.0800>> Comparando os requisitos exigidos com o diagrama de Bode original do sistema percebemos que:
- Necessitamos ter pelo menos 58 graus de margem de fase ();
- O ganho deve cair entre -6 e -7,5 dB em alguma frequência após 250 rad/s (já considerando o acréscimo de ganho causado por um compensador de avanço de fase). Devemos acrescentar aproximadamente 71 dB de ganho na frequência de 251,57 rad/s:
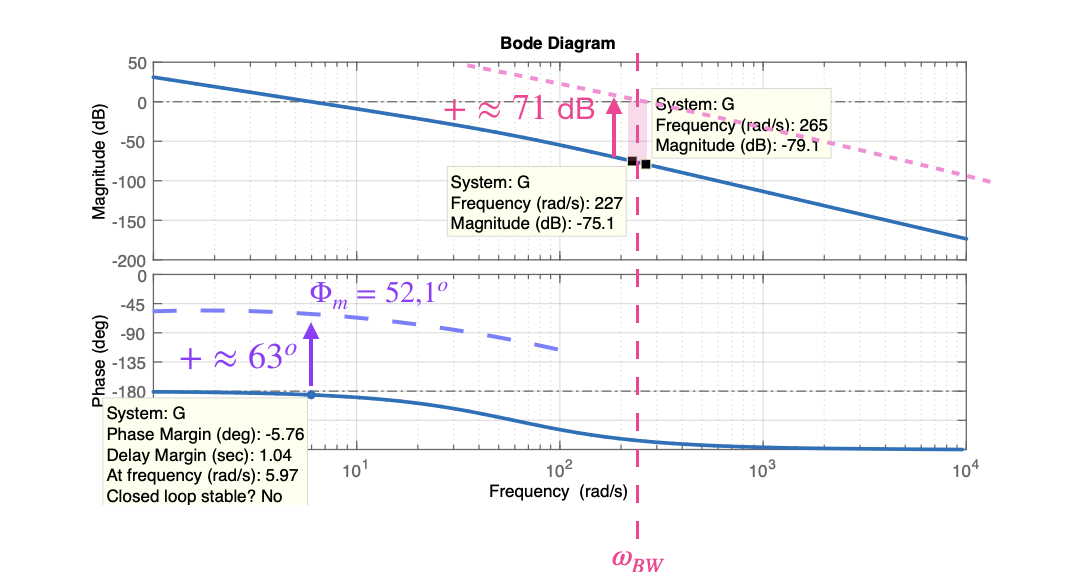
- O gráfico de ganho ficará entre -6 e -7,5 dB e após 244 rad/s. A partir da plotagem da fase Bode, podemos ver que existe um polo próximo a 60 rad/s. Usaremos um controlador PI para colocar um zero em s = 60 para "achatar" a curva de fase.
Considerações:
Note que foi acrescentado ação integral no modelo do controle de velocidade do motor, acrescentando arbitrariamente um zero em (rad/s).
No exemplo da Carnegie Mellon, estão aumentando a complexidade do controlador (isto é, aumentando sua ordem), resultando num sistema de 4a-ordem (necessário!?).
Últimas anotações:
x
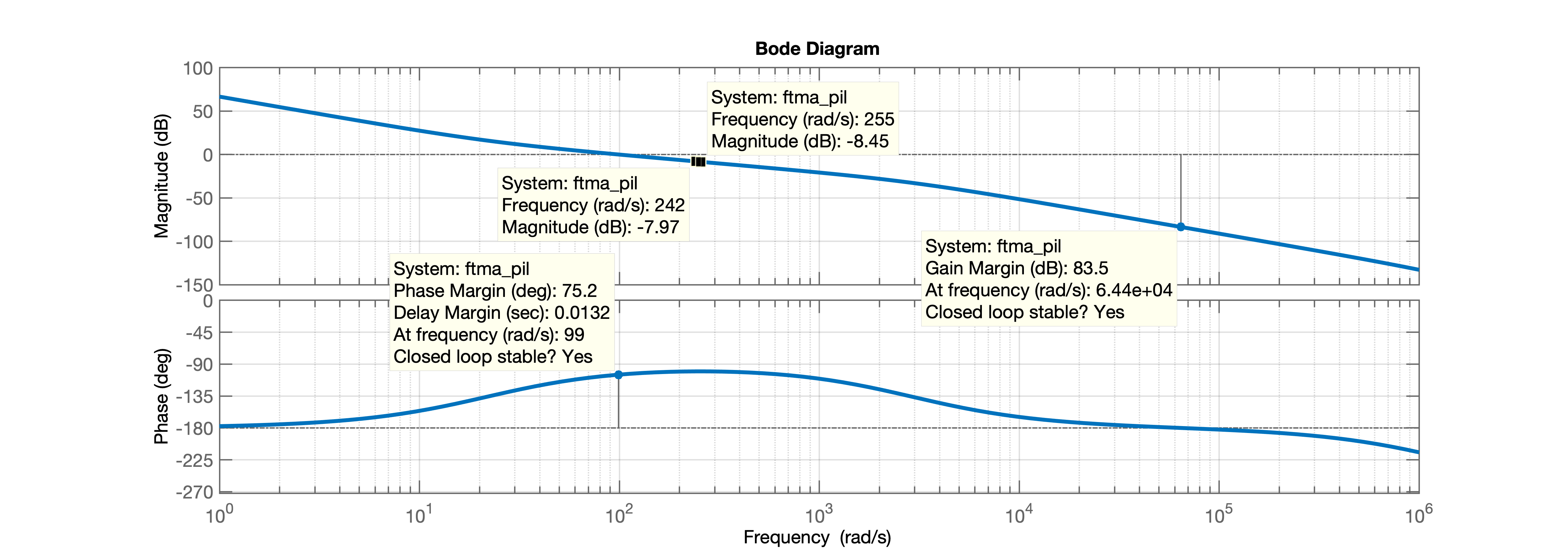
>> zpk(G) 3.0862e+09 -------------------------- s^2 (s+1.454e06) (s+59.23) Continuous-time zero/pole/gain model.>> % Até aqui Ok com exemplo da Carnegie Mellon>>>> PM=80;>> OS=16;>> zeta=(-log(OS/100))/(sqrt(pi^2+(log(OS/100)^2)))zeta = 0.5039>> Pm_d=atan2(2*zeta, sqrt(-2*zeta^2 + sqrt( 1+4*zeta^4) ) )Pm_d = 0.9100>> Pm_d_deg=Pm_d*180/piPm_d_deg = 52.1379>> >> wbw=(4/(0.04*zeta))*sqrt((1-2*zeta^2)+sqrt(4*zeta^4-4*zeta^2+2))wbw = 251.5743>> a=(1 - sin(PM*pi/180))/(1 + sin(PM*pi/180));>> aa = 0.0077>> T=1/(wbw*sqrt(a))T = 0.0454>> numpil = conv([1 60],[T 1]);>> denpil = [a*T 1];>> pil=tf(numpil,denpil);>> zpk(pil) 130.65 (s+60) (s+22.01) ----------------------- (s+2876) Continuous-time zero/pole/gain model.>> ftma_pil=pil*G;>> zpk(ftma_pil) 4.0321e11 (s+60) (s+22.01) ----------------------------------- s^2 (s+1.454e06) (s+2876) (s+59.23) Continuous-time zero/pole/gain model.>> figure; bode(ftma_pil)>> grid>> save motor_position_carnegie_mellon>> O diagrama de Bode deste "pil" rende:
Usando App Control System Designer
Uma versão mais atualizada deste último projeto usando o App Control System Designer no Domínio Frequência pode ser encontrado [aqui].
Prof. Fernando Passold, em 15.11.2019; 07.12.2020, 18/11/2024.