aula_21_11_2022.html

Scarf on the wind.
Photo by Marek Piwnicki on Unsplash

Aula de:	21/11/2022
Tema:	Projeto de Controladores por Avanço de Fase (“Lead“)

Projeto do Compensador por Avanço de Fase (“Lead”)
- Projeto do Lead2
- Projeto do Lead3
Amplitudes das Ações de Controle
- Calculando $u(t)$ …
- Problema para calcular $u(t)$ !?

Recuperando dados da aula passada (Projeto de Controladores PD, aula de 07/11/2022)), arquivo dados.mat:

>> pwd
ans =
    'C:\Users\fpassold\Documents\MATLAB\control2inf_2020_2'
>> % Recuperando dados da aula passada:
>> load dados

Projeto do Compensador por Avanço de Fase (“Lead”)

Sua equação genérica é:

C (s) = K ( s + z L e a d ) ( s + p L e a d )

$C(s)=K \dfrac{(s+z_{Lead})}{(s+p_{Lead})}$

onde $p_{Lead}=$ polo do controlador que corresponde ao filtro passa-baixas acrescentado a um controlador PD.

A questão continua sendo onde alocar o zero deste controlador. Já que o polo corresponde a frequência de corte de um filtro passa-baixas que deve estar localizado numa frequência superior ao polo mais rápido da planta (ou seja, no plano-s, este polo deveria estar próximo de $-\infty$ ). Recordando da equação da planta usada neste estudo de caso:

>> zpk(G) % confirmando a planta
ans =
          1
  ------------------
  (s+10) (s+2) (s+1)

percebemos que seu polo mais rápido está localizado em $s=-10$ . Então, localizar o pólo deste controlador em $s=-12$ parece ser uma boa localização (basta este pólo ser menor que $-10$ ).

Da aula passada (em 07/11/2022: Projeto de PD), quando foi realizado o projeto de controlador PD para esta planta, obtivemos os seguintes controladores:

	PD2	PD3
Equação	$C_{PD2}=55,0624(s+5.241)$	$C_{PD3}=143,6662(s+1.586)$
$t_s\vert_{\text{desejado}}$	1,3	0,7
RL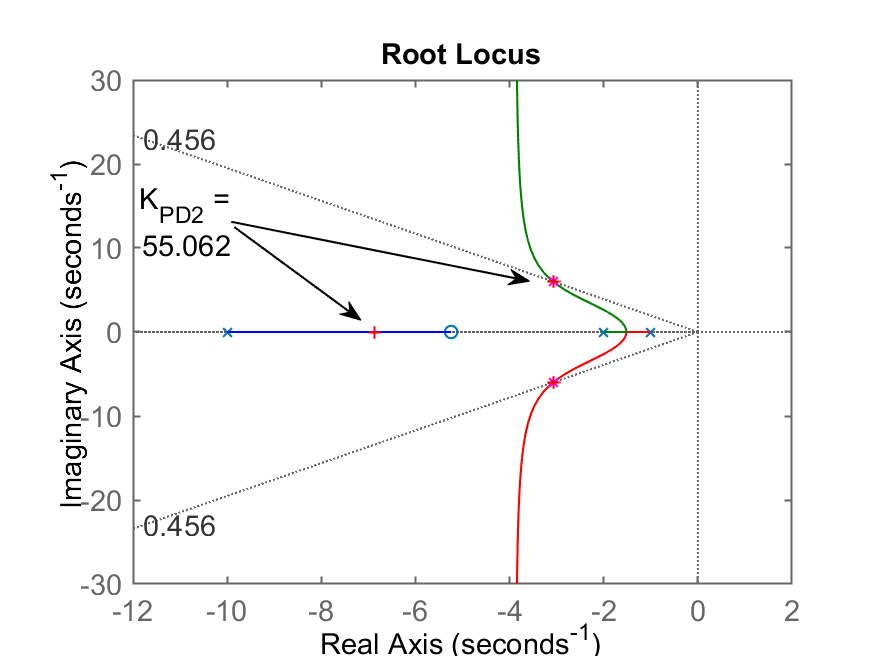
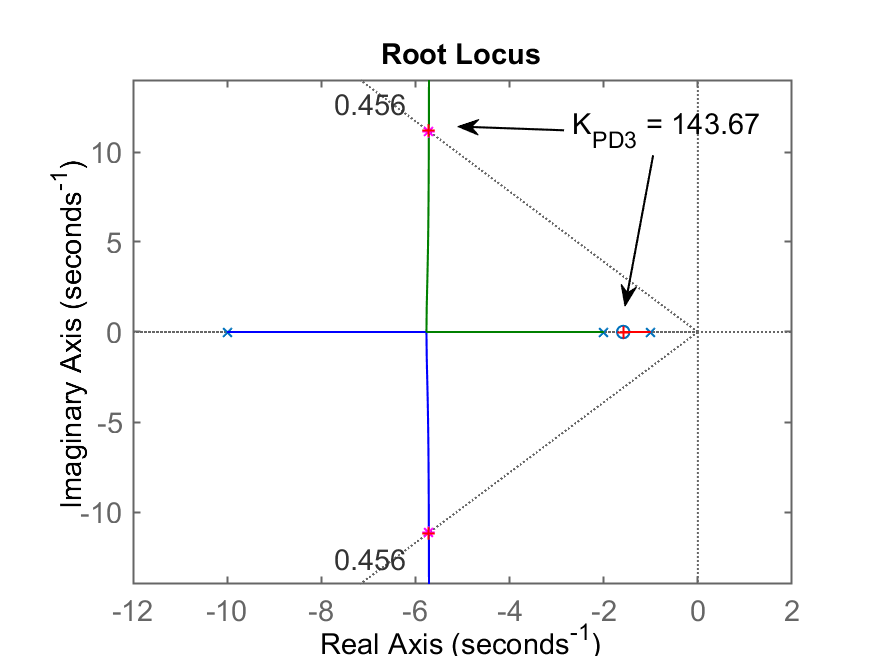Step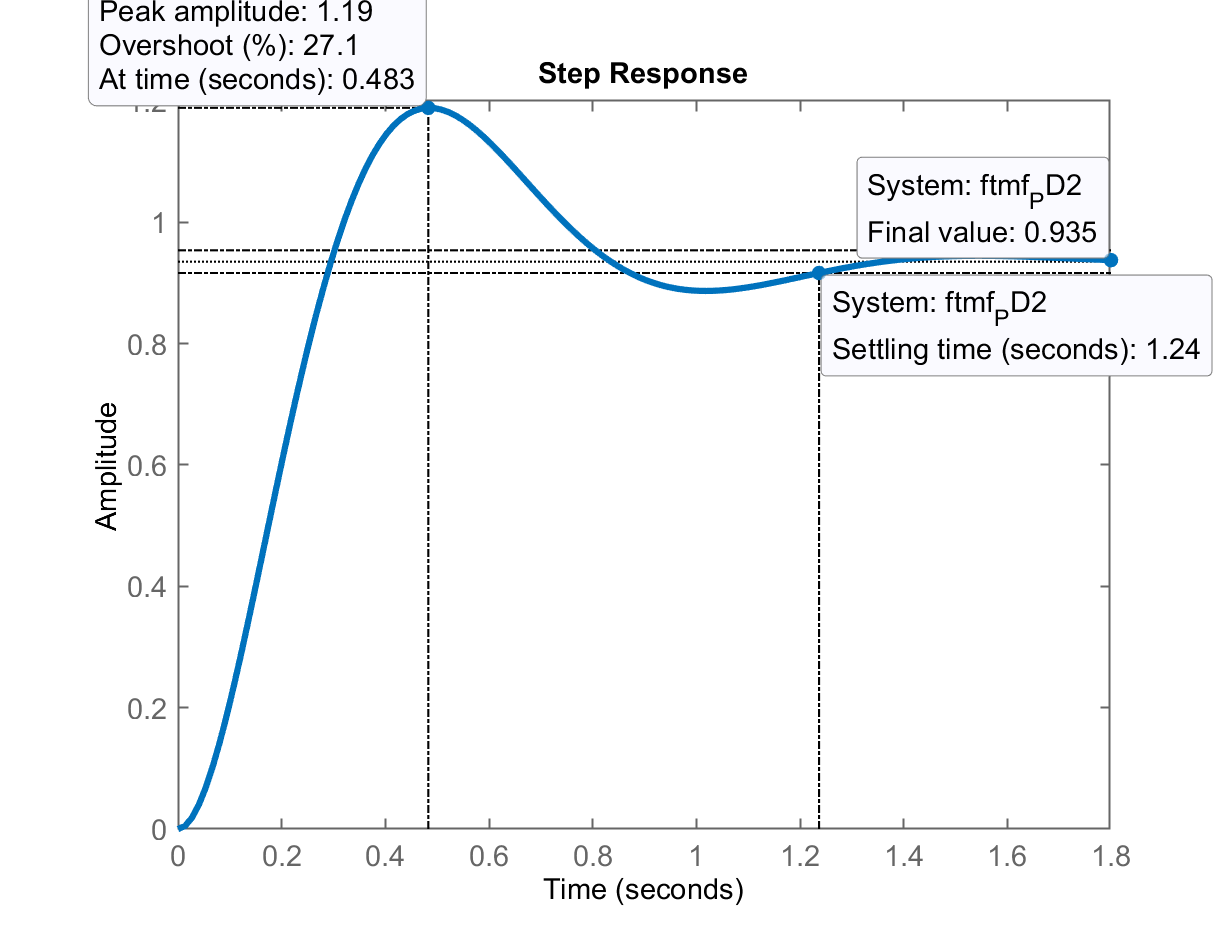
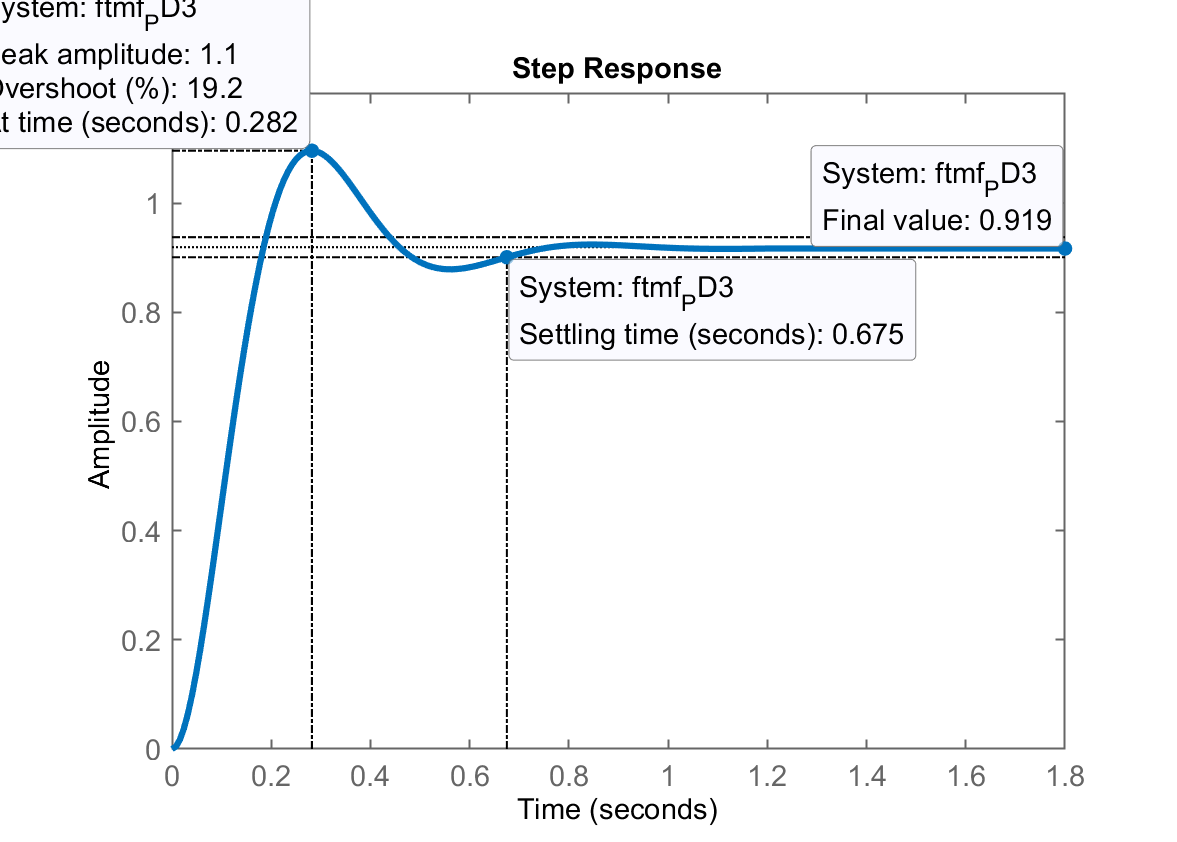$\%OS\vert_{u(\infty)}$	19%	10%
$t_s\vert_{\text{final}}$	1,24	0,675
$y(\infty)$	0,935	0,919
$e(\infty)$	6,5%	8,1%
Conclusão	Mais adequado Menor valor máximo do sinal atuador, e menor erro. (Note valor do $K_{PD2}=55,06$ )	Possível Mas elevados valores de atuação, e erro maior. (Note valor do $K_{PD3}=143,67$ )

Notamos que para o PD2, seu zero foi alocado em $s=-5,241$ ( $t_s \le 1,3$ segundos.), enquanto que para o PD3, o zero foi alocado em $s=-1,586$ ( $t_s < 0,7$ segundos). A princípio poderíamos partir o projeto do controlador Lead com o zero em alguma destas 2 opções e usar o script de cálculo de contribuição angular pare determinar o polo do controlador.

Mas… vamos reanalisar como fica (ou muda) o RL para este controlador em comparação ao PD.

Esboços rápidos de Root Locus, resultam em:

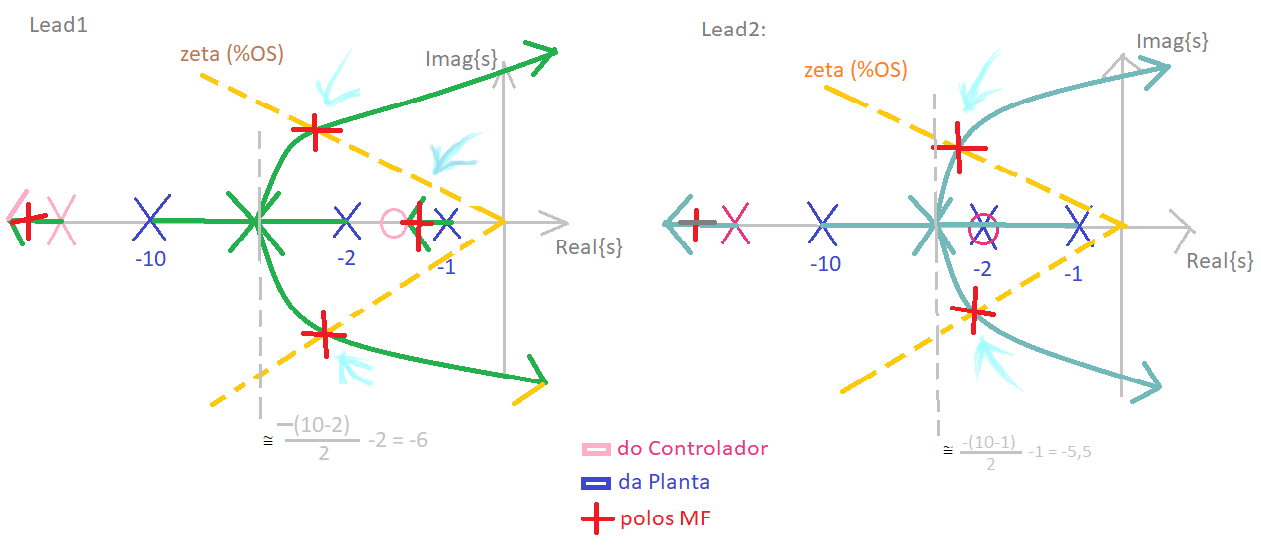
Analisando estes esboços podemos apostar em 2 posições para o zero deste controlador:

Lead1) com $z_{Lead1} = -1,6$ , entre os 2 poolos mais lentos da planta (em $s=-1$ e $s=-2)$ ;

Este local, gera um RL com ponto de partida para os polos complexos que provavelmente estará mais distante do eixo $j\omega$ em comparação com o Lead2, mas teremos um polo real dominante que estará localizado entre $z_{Lead1} < s <-1$ . E este polo está mais próximo do eixo $j\omega$ que os outros 2 polos complexos, o que vai “deteriorar” o $t_s$ que poderia ser obtido apenas em função dos polos complexos.
Lead2) com $z_{Lead2} = -2$ , propositalmente cancelando o segundo polo mais lento da planta em $s=-2$ .

Neste caso particular, note que a complexidade final do sistema é reduzida. O Lead1 aumenta a complexidade da $FTMA(s)$ para 4a-ordem, enquanto que o Lead2, ao contrário, reduz a complexidade do sistema para um de 3a-ordem. A questão (prática/real) é se este cancelamento realmente poderia ser obtido…

Só nos resta explorar estas opções para confirmar qual renderia melhores resultados. Testando…

>> Lead1=tf(poly(-1.6),poly(-12))
Lead1 =

  s + 1.6
  -------
  s + 12

>> Lead2=tf(poly(-2),poly(-12))
Lead2 =

  s + 2
  ------
  s + 12

>> % Comparando os RLs dos 2 Leads:
>> ftma_Lead1=G*Lead1;
>> ftma_Lead2=G*Lead2;
>> subplot(121); rlocus(ftma_Lead1);
>> hold on; sgrid(zeta,0)
>> % Lembrando posição desejada para polos de MF no caso
>> % de $t_s=1,3$ segundos e $\%OS=20\%$:
>> % em $s = -3.07692 \pm j 6.0061$.
>> % corresponde a variável `polos_MFd`
>> polos_MFd
polos_MFd =
      -3.0769 -     6.0061i
      -3.0769 +     6.0061i
>> plot(polos_MFd, 'md')
>> axis([-15 5 -10 10])
>> % Partindo para o outro RL
>> subplot(122); rlocus(ftma_Lead2)
>> hold on; sgrid(zeta,0);
>> plot(polos_MFd, 'md')
>> axis([-15 5 -10 10])

E assim obtemos:

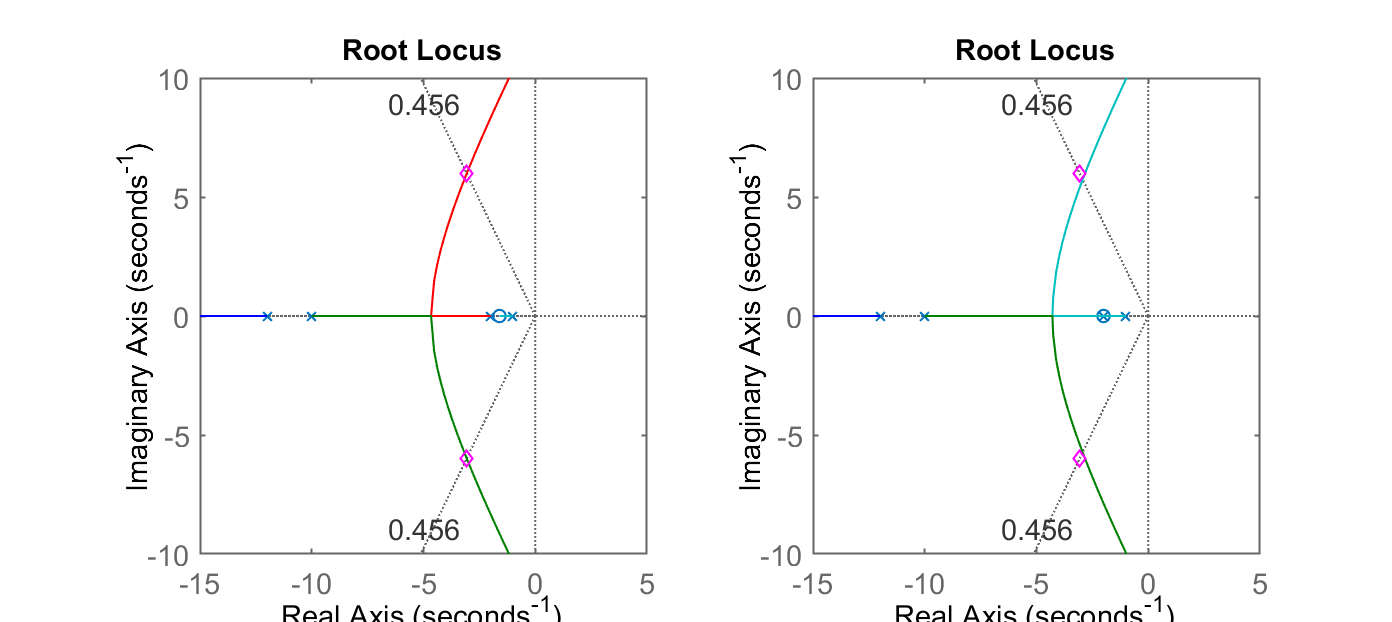
Pela anális dos RLs obtidos, o segundo controlador (Lead2) deve render melhores resultados porque só conterá polos dominantes complexos, enquanto o Lead1, além do polos complexos, sofrerá a influência do polo de MF entre $-1,6 < s < -1$ .

Projeto do Lead2

Continuando o projeto do Lead2, e usando o script find_polo_zero.m para calcular onde deveríamos localizar o polo deste controlador para $t_s \le 1,3$ segundos e $\%OS \le 20\%$ :

>> C_aux=tf(poly(-2),1); % eq. do controlador sem o polo
>> ftma_aux=G*C_aux;
>> zpk(ftma_aux)

        (s+2)
  ------------------
  (s+10) (s+2) (s+1)

>> find_polo_zero
%OS (desired Overshoot, in %): ? 20
 ts_d (desired settling time): ? 1.3
Desired MF poles in: s = -3.07692 \pm j 6.0061
Evaluating the pole(s) contribution angle(s):
  Pole 1 in s= -10 --> angle: 40.9432^o
  Pole 2 in s= -2 --> angle: 100.165^o
  Pole 3 in s= -1 --> angle: 109.076^o
Sum of the angle(s) of pole(s):
  $\sum \theta_{poles}=250.184^o$

Evaluating the zero(s) contribution angle(s):
  Zero 1 in s=-2 --> angle: 100.165^o
Sum of the angle(s) of zero(s):
  $\sum \theta_{zeros}=100.165^o$

Determining pole or zero location of the controller:
Select: [p]=pole or [z]=zero, for the controller ? p

Angle contribution required for controller: 487.865^o
The POLE of this controller must be at s = -13.4876
To continue the project, note that:

>> zpk(ftma) =

             (s+2)
  ----------------------------
  (s+13.49) (s+10) (s+2) (s+1)

Continuous-time zero/pole/gain model.

It is suggested to continue with the command:
>> K_ = rlocfind(ftma)

>> axis([-15 0 -2 7]) % realizando um "zoom" na região de interesse no gráfico da contrib angular.

O gráfico da contribuição angular resulta:

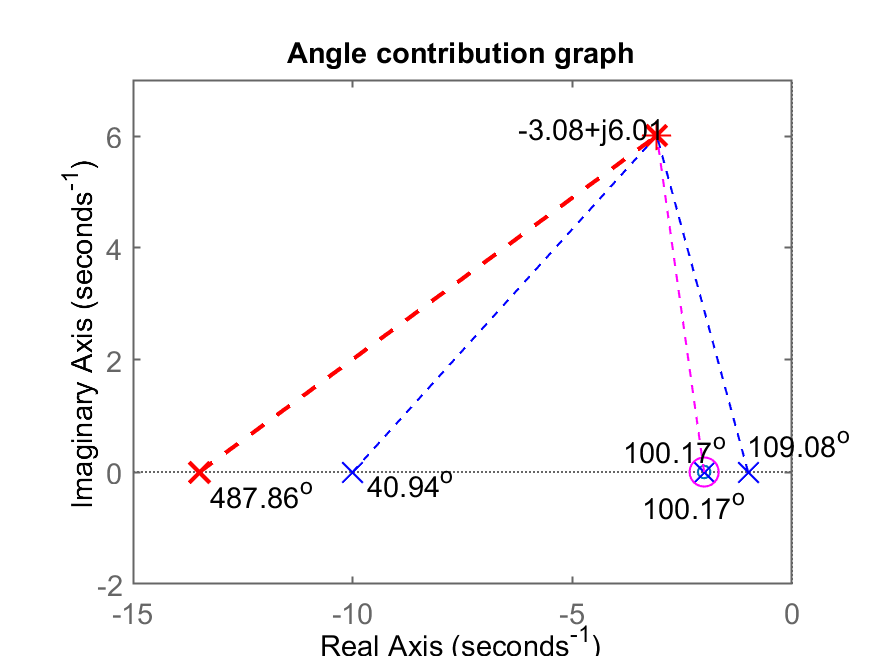
Descobrindo o ganho do Lead2…

>> axis([-15 2 -10 10]) % realizando zoom na região de interesse no RL do Lead2
>> K_Lead2=rlocfind(ftma)
Select a point in the graphics window
selected_point =
       -3.096 +     6.0062i
K_Lead2 =
        698.7

Segue o RL mostrando o ganho encontrado para o Lead2:

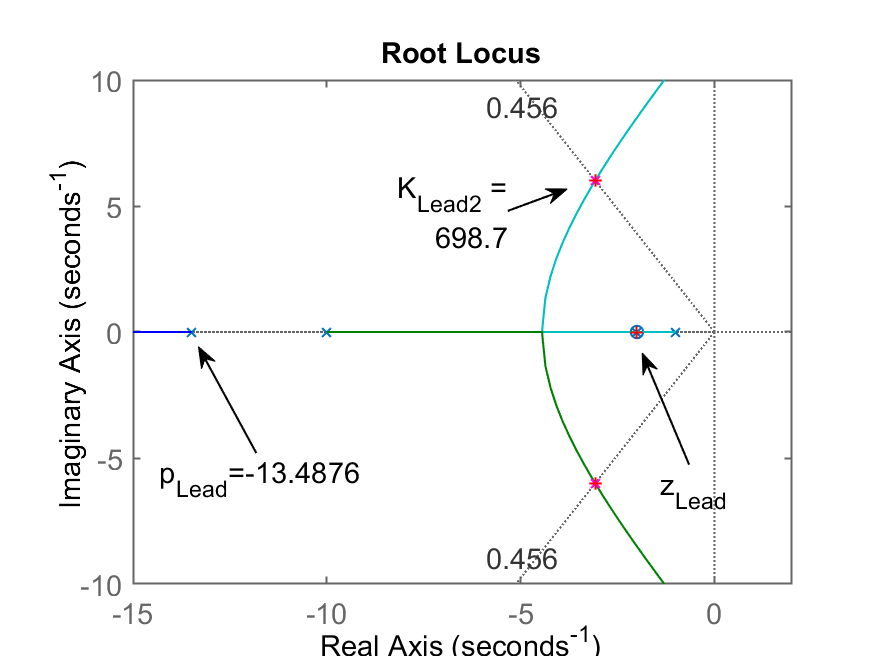
A equação final do Lead2 fica:

C L e a d 2 (s) = 698 , 7 ( s + 2 ) ( s + 13.4876 )

$C_{Lead2}(s)=\dfrac{698,7(s+2)}{(s+13.4876)}$

Fechando a malha e encontrando resposta ao degrau…

>> ftma_Lead2=ftma;
>> ftmf_Lead2=feedback(K_Lead2*ftma, 1);
>> figure; step(ftmf_Lead2)

Comparando com PD realizado antes para $t_s \le 1,3$ segundos:

>> zpk(PD2)
PD2 =

  s + 5.241

>> K_PD2
K_PD2 =
       55.062
>> ftma_PD2=PD2*G;
>> zpk(ftmf_PD2)

          55.062 (s+5.241)
  --------------------------------
  (s+6.866) (s^2 + 6.134s + 44.95)

>> figure; step(ftmf_PD2, ftmf_Lead2)
>> legend('PD_21', 'Lead_2')

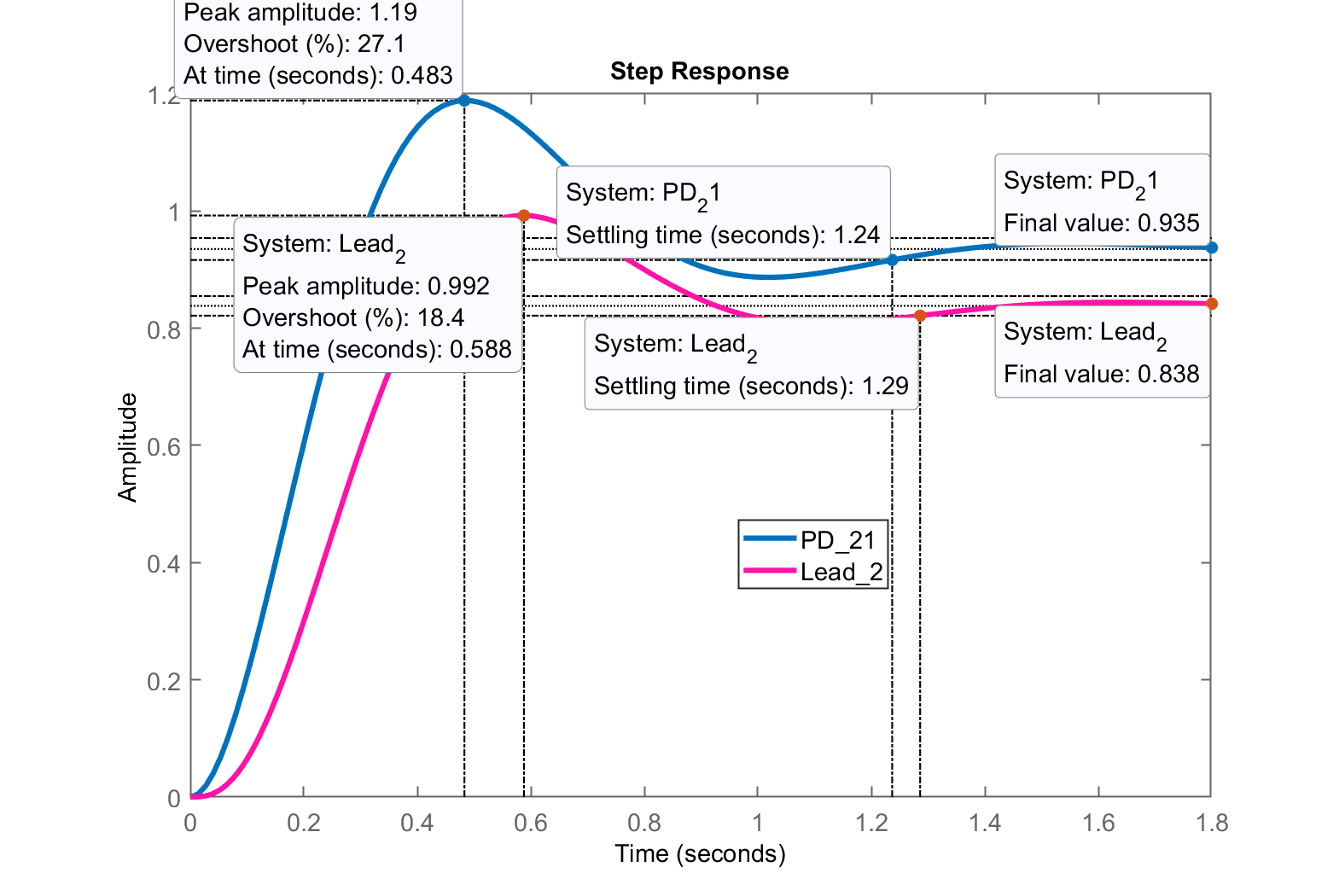
Pela figura nota-se que o erro do Lead2 é maior que o erro do PD2. Mas… o $\%OS$ do Lead2 é bem menor que o do PD2. Na realidade, considerando $r(\infty)=1$ (entrada degrau), $\%OS\vert_{Lead2}=0$ . Isto significa que pode-se aumentar o ganho do Lead2, o que deveria diminuir o erro e possivelmente reduzir o $t_s$ . Testando…

>> K_Lead2
K_Lead2 =
        698.7
>> K_lead2b=K_Lead2*1.1; % aumentando ganho em 10%
>> K_lead2b
K_lead2b =
       768.57
>> ftmf_Lead2b=feedback(K_lead2b*ftma, 1);
>> figure; step(ftmf_PD2, ftmf_Lead2b)
>> % Não houve uma melhora tão significativa. Aumentando ainda mais o ganho...
>> K_lead2b=K_Lead2*1.2 % aumentando ganho em 20%
K_lead2b =
       838.44
>> ftmf_Lead2b=feedback(K_lead2b*ftma, 1);
>> figure; step(ftmf_PD2, ftmf_Lead2b)

Comparando a resposta ao degrau do PD2 com o Lead2 com seu ganho aumentado em 20% (Lead2b):

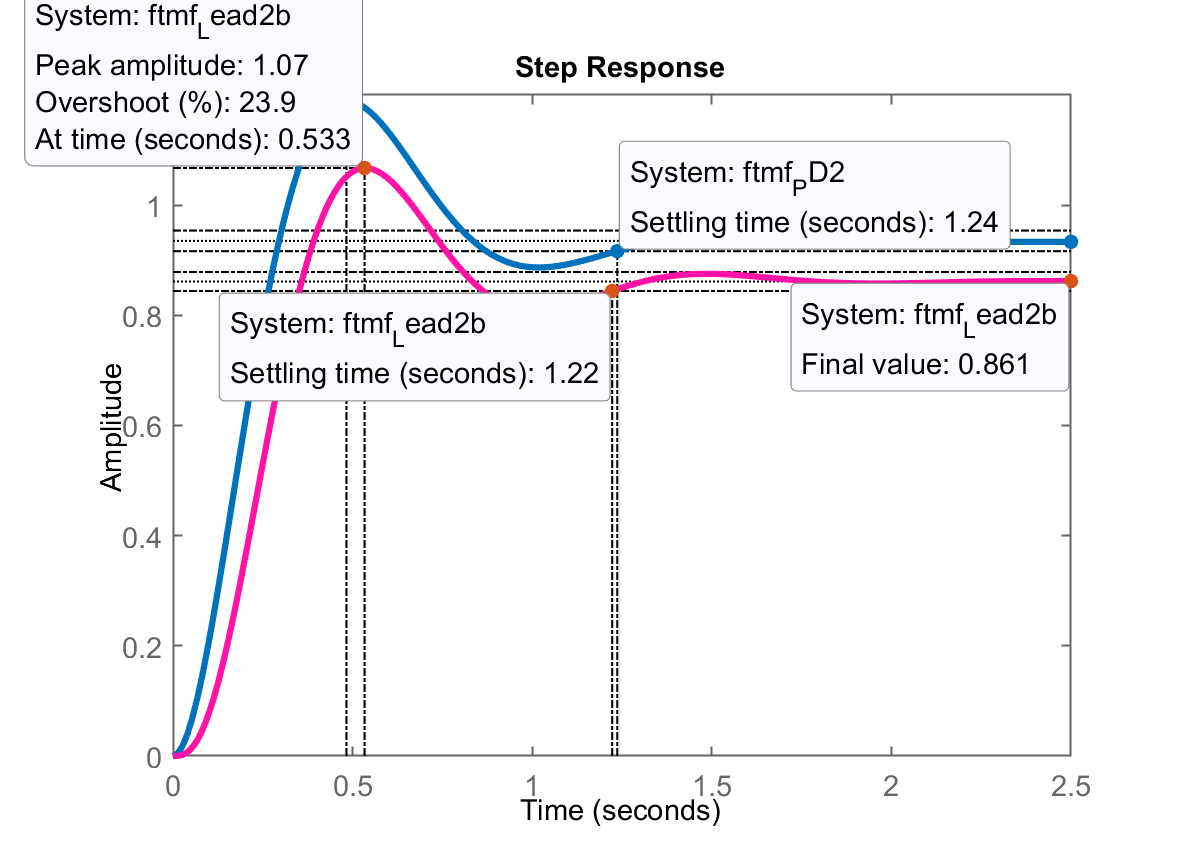
Percebe-se que o $t_s$ até diminuiu, mas o erro não baixou tanto quanto o desejado. E o $\%OS\vert_{Lead2b}=7\%$ , o que significa que ainda pode-se aumentar mais o ganho do Lead2b a fim de reduzir o $e(\infty)$ . Outros valores de ganhos poderiam ser testados, mas a ideia é não perder mais tempo com este projeto.

Projeto do Lead3

E se o zero do Lead ao invés de cancelar o segundo polo mais lento da planta (em $s=-2$ ), cancelasse o polo mais lento da planta em $s=-1$ ?

>> Lead3=tf(poly(-1),poly(-12))
Lead3 =

  s + 1
  ------
  s + 12

>> ftma_Lead3=Lead3*G;
>> subplot(121); rlocus(ftma_Lead2)
>> hold on; sgrid(zeta,0);
>> plot(polos_MFd, 'md')
>> axis([-15 2 -10 10])
>> subplot(122); rlocus(ftma_Lead3)
>> hold on; sgrid(zeta,0);
>> plot(polos_MFd, 'md')
>> axis([-15 2 -10 10])

Comparando RL do Lead2 com o Lead3:

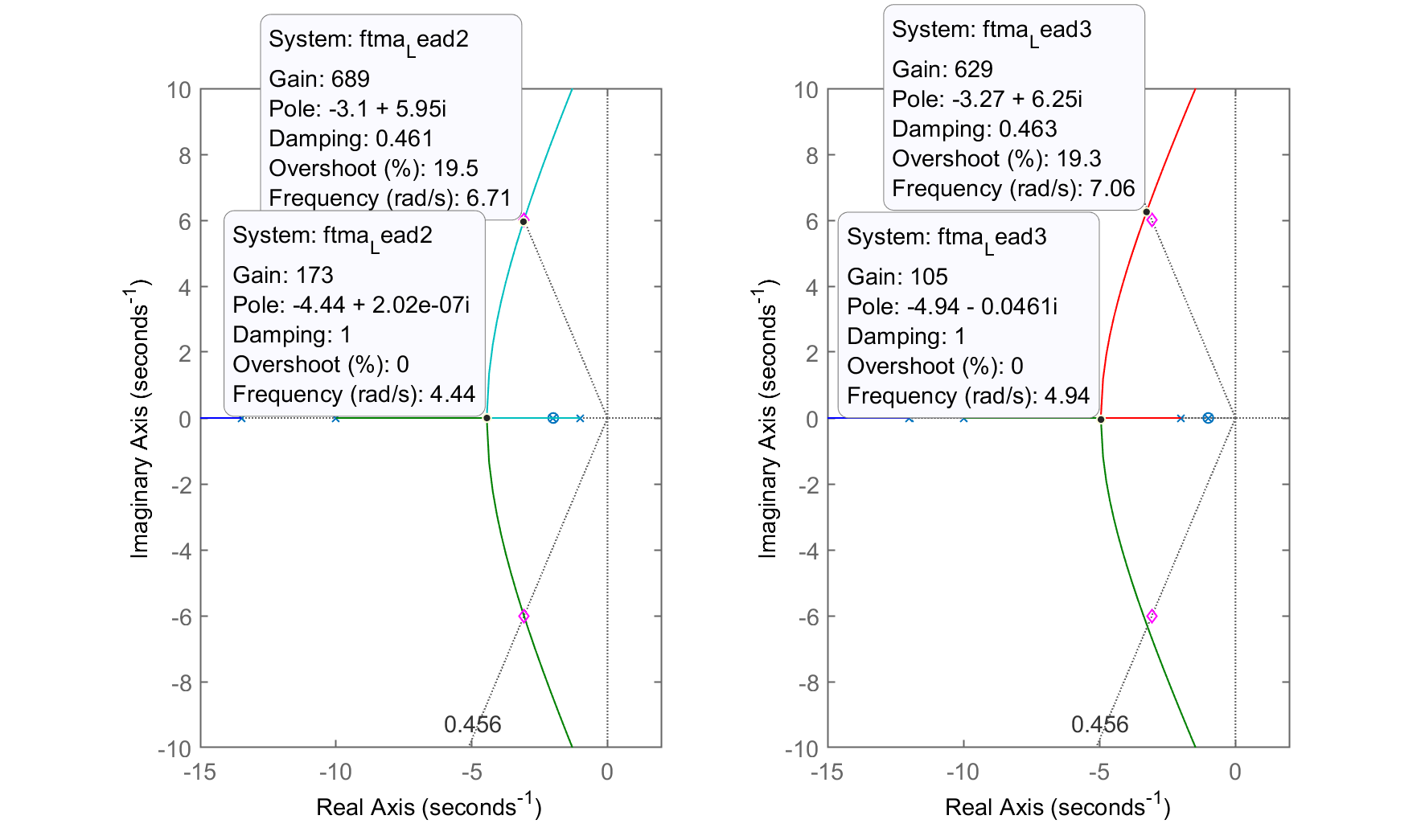
Percebe-se pouca diferença. As partes reais dos pontos destacados nos 2 RLs mostram que no caso do Lead3 (RL da direita), estes polos estão mais afastados do eixo $j \omega$ , mas não tanto assim.

Fechando a malha…

>> K_Lead3=630; % por inspeção do datatip no gráfico do RL
>> ftmf_Lead3=feedback(K_Lead3*ftma_Lead3, 1);
>> figure;
>> step(ftmf_Lead2b, ftmf_Lead3)
>> legend('Lead_{2(b)}', 'Lead_3')

Comparando resposta a entrada degrau entre Lead3 e Lead2, obtemos:

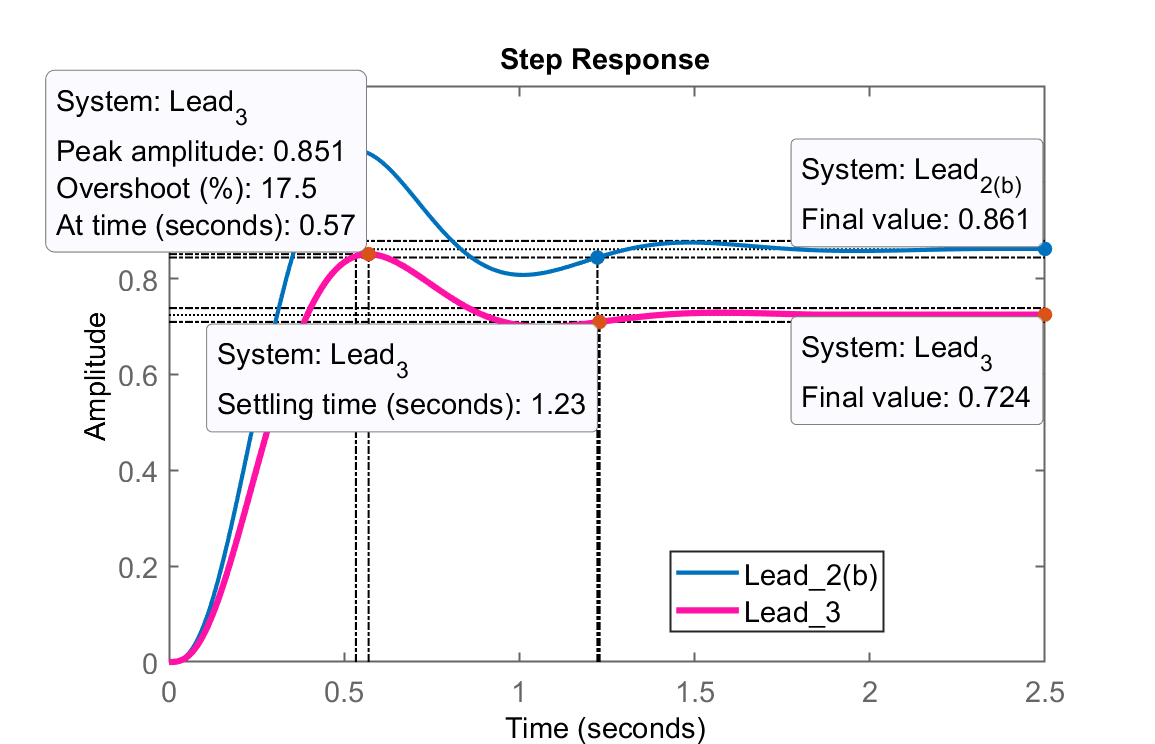
Obs.: Notamos pela resposta do Lead3, que ainda é possível aumentar seu ganho de forma a reduzir o $e(\infty)$ . No mais, os 2 Lead’s respondem quase da mesma forma.

Mas com o que deveriámos nos preocupar no caso de projetos de controladores com ação derivativa (PD e Lead) ?

Amplitudes das Ações de Controle

O que ainda não foi monitorado em aulas passadas, foram as amplitudes geradas pelos controladores, ou seja, as amplitudes das ações de controle, $u(t)$ , para cada controlador.

Vamos perceber que controladores com ação derivativa geram amplitudes bastante elevadas, na prática saturando drivers de potência que atuam sobre um processo.

Comparando ações de controle do:

Controlador Proporcional;
PI;
PD.

Calculando $u(t)$ …

Não necessitamos repassar nossos controladores para um ambiente gráfico de simulação como o Simulink. Podemos “enganar” a função step() do Matlab para obter o gráfico de $u(t)$ a partir da janela de comandos do Matlab. Ver “Como obter gráficos de u(t) e e(t) na linha de comandos do Matlab”. No caso, realizamos algo como:

Plot(u (t)) = step ⎛ ⎝ ⎜ ⎜ ⎜ C ( s ) 1 + C ( s ) G ( s )                aux ⎞ ⎠ ⎟ ⎟ ⎟

$\text{Plot(}u(t)\text{)} = \text{step}\left( \underbrace{ \dfrac{C(s)}{1+C(s)G(s)}}_{\text{aux}} \right)$

>> aux_Kp = 100/(1+100*G)
aux_Kp =

  100 s^3 + 1300 s^2 + 3200 s + 2000
  ----------------------------------
      s^3 + 13 s^2 + 32 s + 120

>> zpk(C_PI1)
ans =

  (s+0.8)
  -------
     s

>> aux_PI1 = (K_PI1*C_PI1)/(1+K_PI1*C_PI1*G)
aux_PI1 =

       35.036 s (s+10) (s+2) (s+1) (s+0.8)
  ---------------------------------------------
  s (s+10.41) (s+0.7348) (s^2 + 1.856s + 3.665)

>> aux_PD2 = (K_PD2*PD2)/(1+K_PD2*PD2*G);
>> step(aux_Kp)   % sem erro, Ok
>> step(aux_PI1)  % sem erro, Ok
>> step(aux_PD2)
Error using 'DynamicSystem/step',
Cannot simulate the time response of improper (non-causal)
models.
>> % Verificando o problema...
>> zpk(aux_PD2)
ans =

  55.062 (s+10) (s+5.241) (s+2) (s+1)
  -----------------------------------
   (s+6.866) (s^2 + 6.134s + 44.95)

>> zpk(PD2)
ans =

  (s+5.241)

Problema para calcular $u(t)$ !?

O problema (no caso de aux_PD2) é que foi gerada (corretamente) uma transfer function onde o grau do numerador é maior que o grau do denominador. Se algebricamente realizarmos a transformada inversa de Laplace de uma função transferência deste tipo, vamos descobrir que necessitamos de amostras futuras do próprio sinal de saída da planta para resolver esta transformada, o que obviamente é impossível. Não temos como “prever” a amplitude futura de nenhum sinal. Então o Matlab, pela forma como internamente foi implementada a função step() não está tão incorreto assim.

O problema é: — há alguma forma de contornar este problema?

A solução consiste em acrescentar um pólo da equação do PD que está gerando o problema. Mas acrescentar este polo muito distante do pólo mais rápido da $FTMA(s)$ original do sistema. Na prática, um valor $10\times$ maior já resolve o problema. Neste caso, vamos colocar este polo extra em $s=-1000$ (muito distante do polo mais rápido da planta; isto implica que este polo praticamente não influencia na resposta do sistema, mas evita que a aplicaçao da função step() sobre aux_PD2 resulte em erro):

>> PD2b=tf(poly(-5.241),poly(-1000))
PD2b =

  s + 5.241
  ---------
  s + 1000

>> aux_PD2 = (K_PD2*PD2b)/(1+K_PD2*PD2b*G);
>> zpk(aux_PD2)
ans =

  55.062 (s+1000) (s+10) (s+5.241) (s+2) (s+1)
  --------------------------------------------
    (s+1000)^2 (s+9.996) (s+1.977) (s+1.027)

>> % Note que agora o grau do numerador = grau do denominador 
>> % Finalmente...
>> step(aux_Kp, aux_PI1, aux_PD2) 
>> legend('Kp (K=100)', 'PI_1', 'PD_2')
>> title('Ações de Controle, u(t)')

E agora podemos finalmente comparar as amplitudes das ações de controle geradas por 3 controladores diferentes:

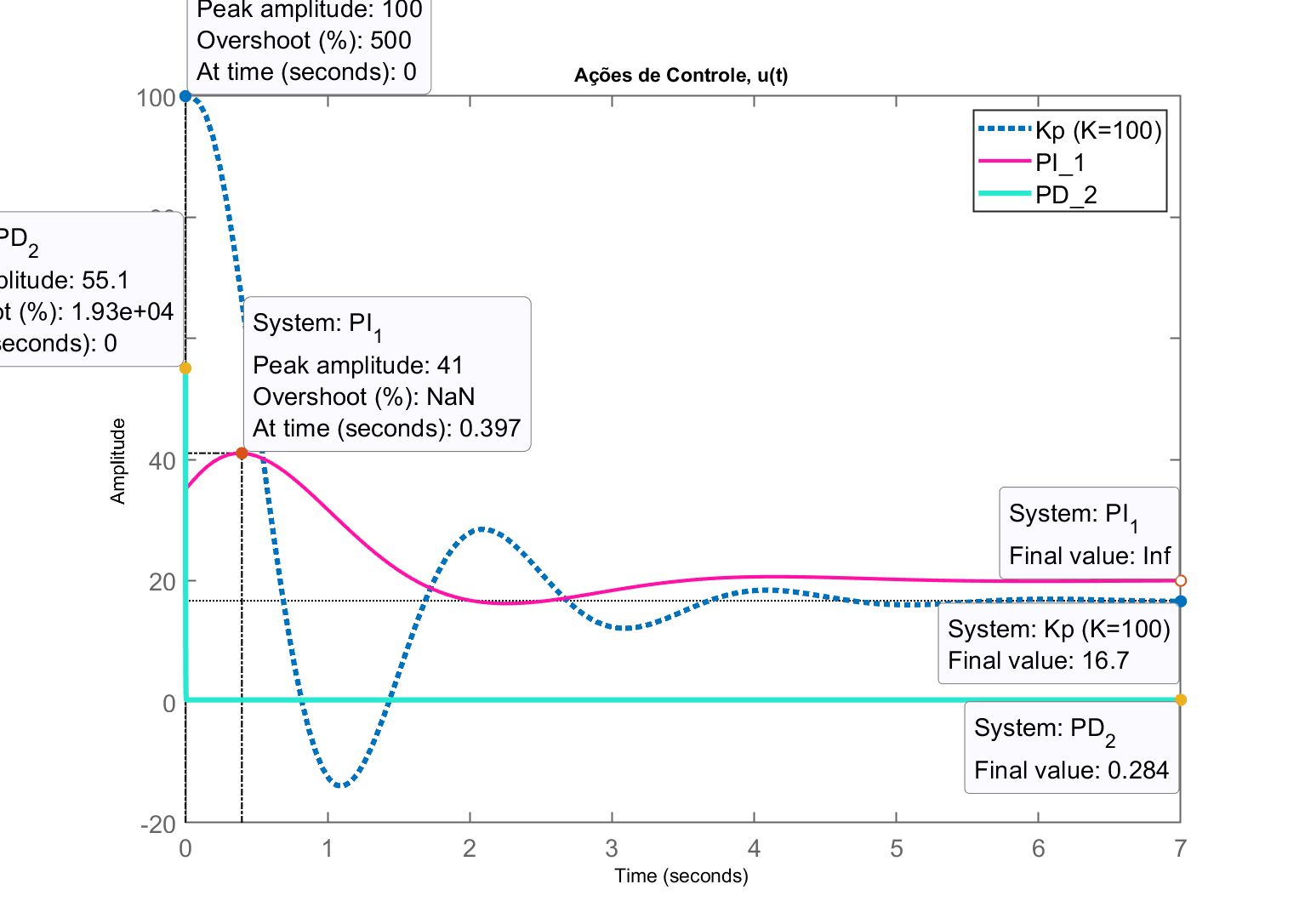
Ressaltando ação de controle do PD

>> aux_Lead2b = (K_lead2b*Lead2)/(1+K_lead2b*Lead2*G);
>> figure;
>> step(aux_PD2, aux_Lead2b)
>> legend('PD_2', 'Lead_{2(b)}')
>> title('Ações de Controle, u(t)')

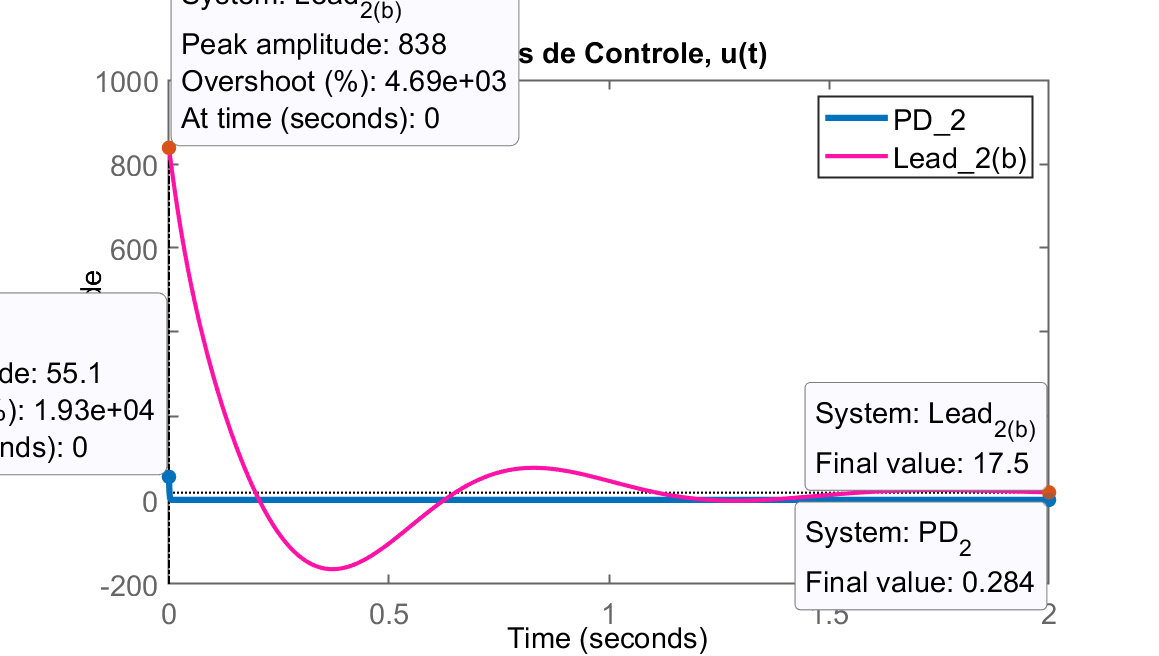
Obs.: Repare no valor inicial de $u(t)$ dos controladores, com o valor adotado para o ganho genérico ( $K$ ) dos mesmos:

>> K_lead2b
K_lead2b =
       838.44
>> zpk(PD2b)
ans =

  (s+5.241)
  ---------
  (s+1000)

>> K_PD2
K_PD2 =
       55.062

Fim, para esta tarde é tudo. Próxima aula está previsto o projeto de controlador PID e do controlador por Avanço-Atraso de Fase. Note que nesta “nova etapa”, estes 2 controladores elevam um pouco mais a ordem do sistema. Estes 2 controladores são de 2a-ordem, em comparação com os controladores anteriores estudados que são apenas de 1a-ordem. Isto implica mais incógnitas para resolver no projeto destes últimos 2 controladores…

Não esquecer de salvar dados para a próxima aula…

>> save dados
>> diary off

Prof. Fernando Passold, em 21/11/2022.