Gráficos de e
O objetivo neste documento é apresentar uma forma de obter gráficos da ação de controle e do sinal de erro num sistema em malha-fechada, usando o Matlab, sem a necessidade de usar o Simulink.
Deduzindo
Observando o sistema realimentado unitário abaixo:

Notamos que:
então:
ou organizando melhor, notamos que:
note que: .
Perceba que quando usamos o comando step(FTMF) no Malab, o mesmo está realizando:
A função step multiplica a transfer function passada como argumento de entrada pela transformada de Laplace da função Degrau, realiza a transformada inversa de Laplace, calcula as primeiras amostras (valores) do resultado desta inversa e "plota" o resultado destes cálculos na forma de um gráfico.
Normalmente quando fechamos uma malha tradicional de controle, como o mostrado na primeira figura acima, realizamos algo como:
e para obter o gráfico da resposta do sistema em malha-fechada, realizamos no Matlab:
>> step(FTMF)este comando termina por realizar:
Então, podemos adapatar a forma como trabalha a função step para gerar o gráfico de ou .
Anteriormente deduzimos:
Então note que a parte da expressão transformamos em argumento de entrada para a função step() e conseguimos obter o gráfico de :
e assim, para obter o gráfico de quando o sistema em malha fechada é submetido à uma entrada degrau, fazendo no Matlab, algo como:
>> aux=Kp/(1+Kp*G7);>> % gráfico de u(t)>> figure; step(aux)Exemplo: suponha o sesguinte sistema:
No Matlab:
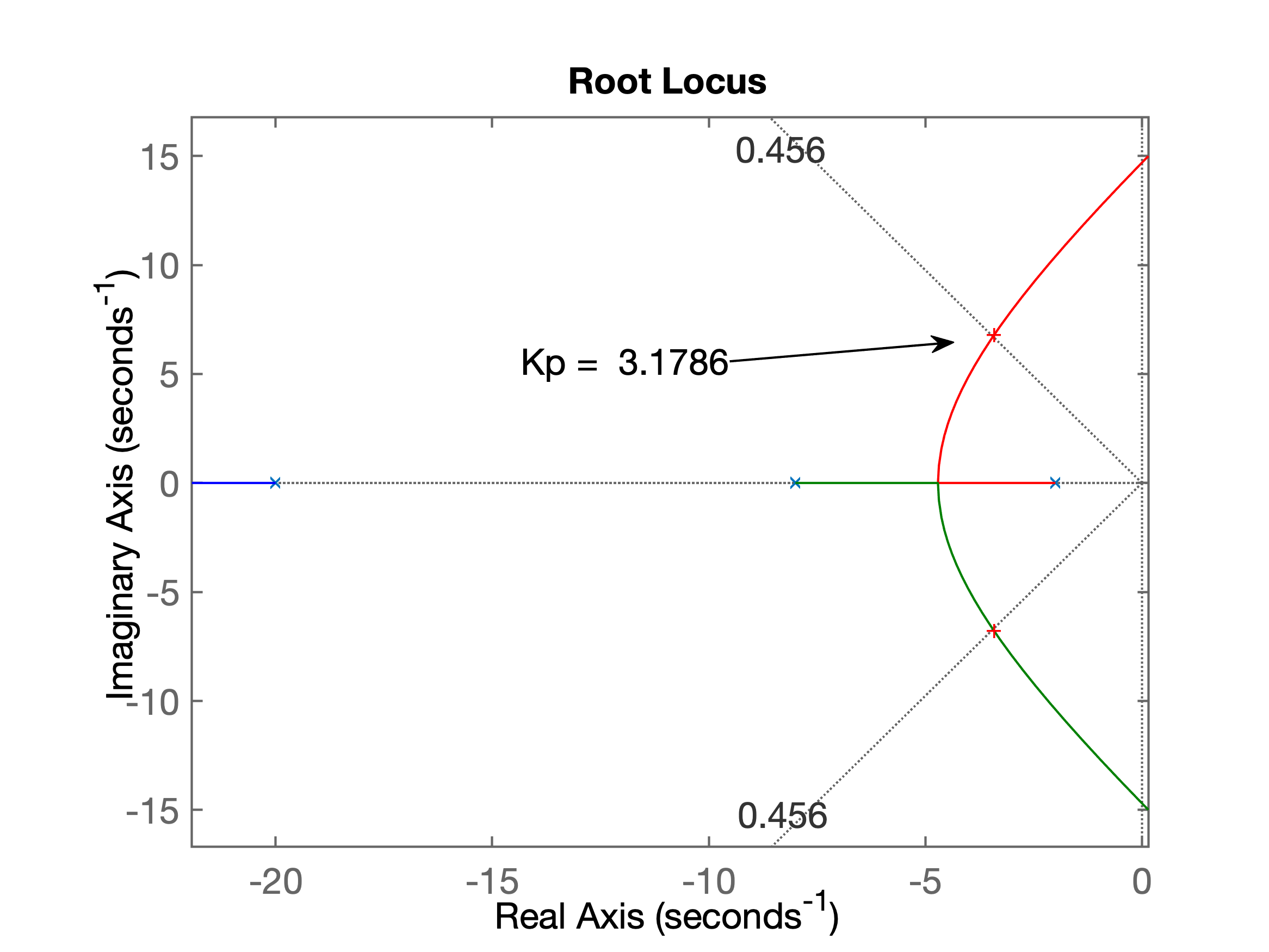
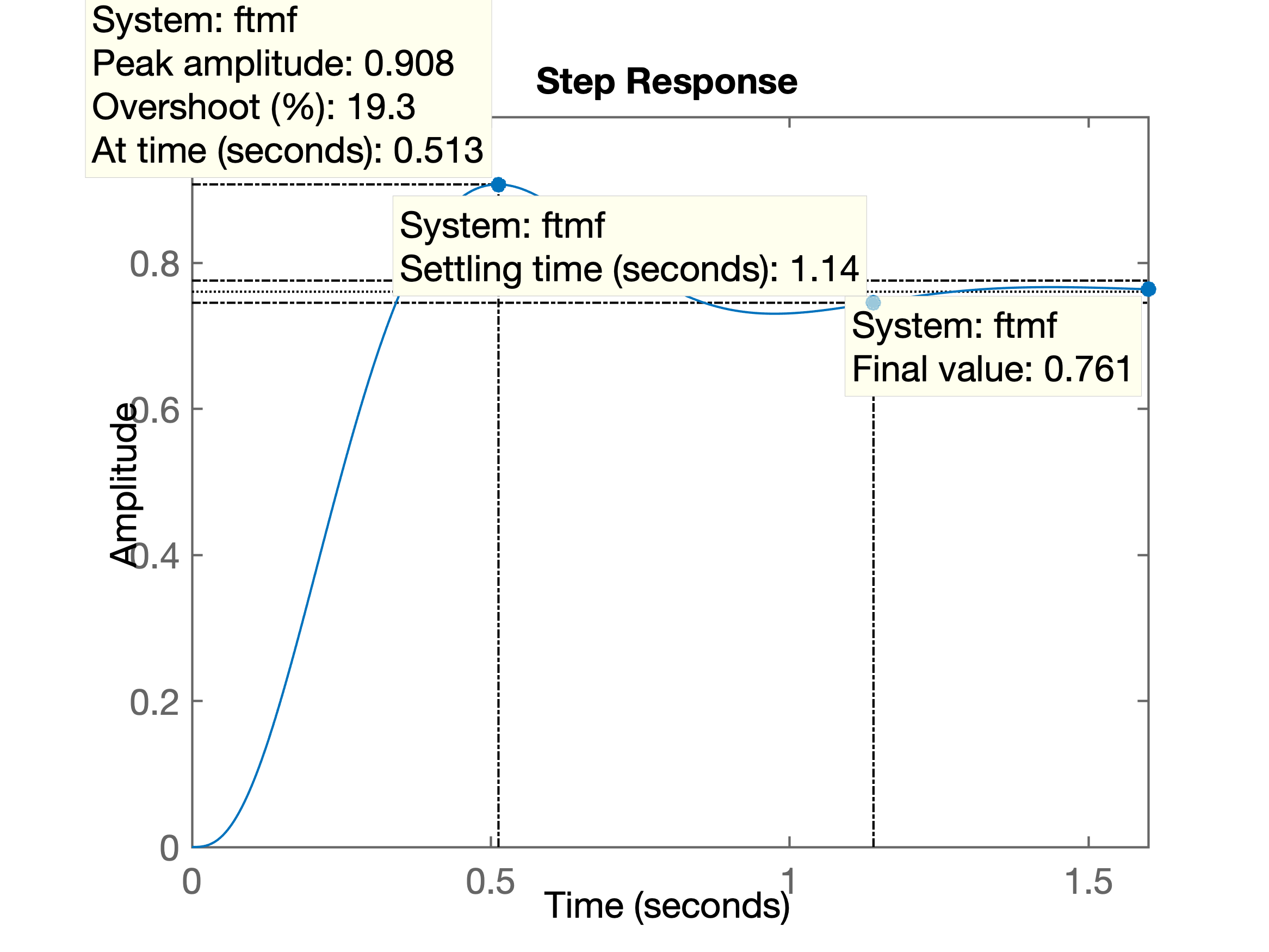
>> % ingressando a planta:>> G7=tf(320,poly([-20 -8 -2]));>> % fechando a malha com granho proporcional e %OS=20%>> rlocus(G7)>> OS=20;>> zeta=(-log(OS/100))./(sqrt(pi^2+(log(OS/100)^2)))zeta = 0.4559>> [Kp,polosMF]=rlocfind(G7)Select a point in the graphics windowselected_point = -3.4410 + 6.7943iKp = 3.1786polosMF = -23.1680 + 0.0000i -3.4160 + 6.7857i -3.4160 - 6.7857i>> ftmf=feedback(Kp*G7, 1);>> figure; step(ftmf)Que gerou o seguinte RL e resposta ao degrau:
 |  |
|---|---|
| (a) RL para | (b) Resposta ao degrau, |
Para se obter também o gráfico de fazemos então:
Calculamos:
x>> aux=Kp/(1+Kp*G7);>> zpk(aux)ans = 3.1786 (s+20) (s+8) (s+2) -------------------------------- (s+23.17) (s^2 + 6.832s + 57.72) Continuous-time zero/pole/gain model.>> figure; step(aux)O que nos permite vizualizar as amplitudes desenvolvidas pela ação de controle :
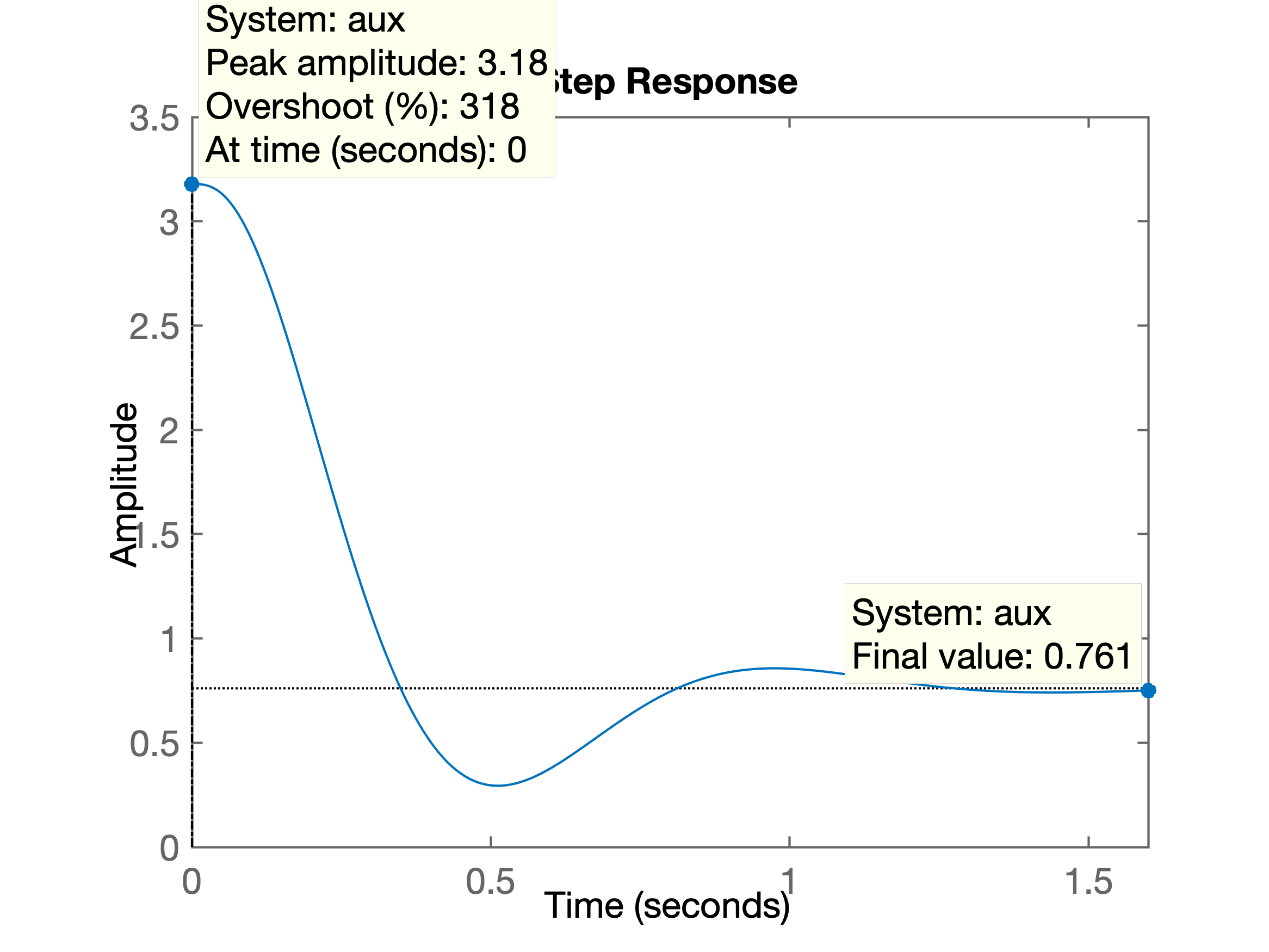
Porém a função step só trabalha com polinômios de entrada causais.
Por exemplo, observe o que acontece se projetamos um PD e queremos observar as amplitudes desenvolvidas por este controlador:
Exemplo: observando ação de controle desenvolvida por um PD.
Neste exemplo, vamos incorporar um PD à planta já adotada anteriormente
Obs.: Não estará sendo mostrado aqui, como o PD foi obtido.
A equação do PD é:
Tentado obter o gráfico de gerado pelo PD:
>> C_PD=tf([1 14.28], 1)C_PD = s + 14.28 Continuous-time transfer function.>> K_PD=0.690759;>> aux=K_PD*C_PD/(1+K_PD*C_PD*G7);>> zpk(aux)ans = 0.69076 (s+20) (s+14.28) (s+8) (s+2) ------------------------------------ (s+16.27) (s^2 + 13.73s + 213.7) Continuous-time zero/pole/gain model.>> figure; step(aux)Error using DynamicSystem/step (line 95)Cannot simulate the time response of improper(non-causal) models. Neste caso, o Matlab não finalizou a funçã step() por considerar a função transferência passada como argumento de de entrada, como um sistema não causal.
De fato, analizando a equação de aux notamos que o grau do numerador é superior ao grau do denominador:
Como contornar este problema?
Neste caso, lembrando que queremos:
Falta multiplicar a expressão anterior aux pela transformada de Laplace do Degrau:
Calculando a nova expressão, teremos:
Se à expressão aux2 aplicarmos uma entrada impulso, realizarmos a transformada inversa de Laplace da mesma e plotamos os resultado para o período inicial de tempo, teremos obtido nosso objetivo que é o gráfico de :
Notamos que a função impulse() do Matlab fornece justamente a resposta temporal ao impulso da função transferência passada como argumento de entrada para a mesma.
Então para ober o gráfico de para o nosso PD, terminamos de fazer agora:
>> degrau=tf(1,[1 0])degrau = 1 - s Continuous-time zero/pole/gain model.>> aux2=degrau*aux;>> zpk(aux2)ans = 0.69076 (s+20) (s+14.28) (s+8) (s+2) ------------------------------------ s (s+16.27) (s^2 + 13.73s + 213.7) Continuous-time zero/pole/gain model.>> figure; impulse(aux2)Note que desta vez a função aux2 é causal.
O gráfico de para o PD fica então:
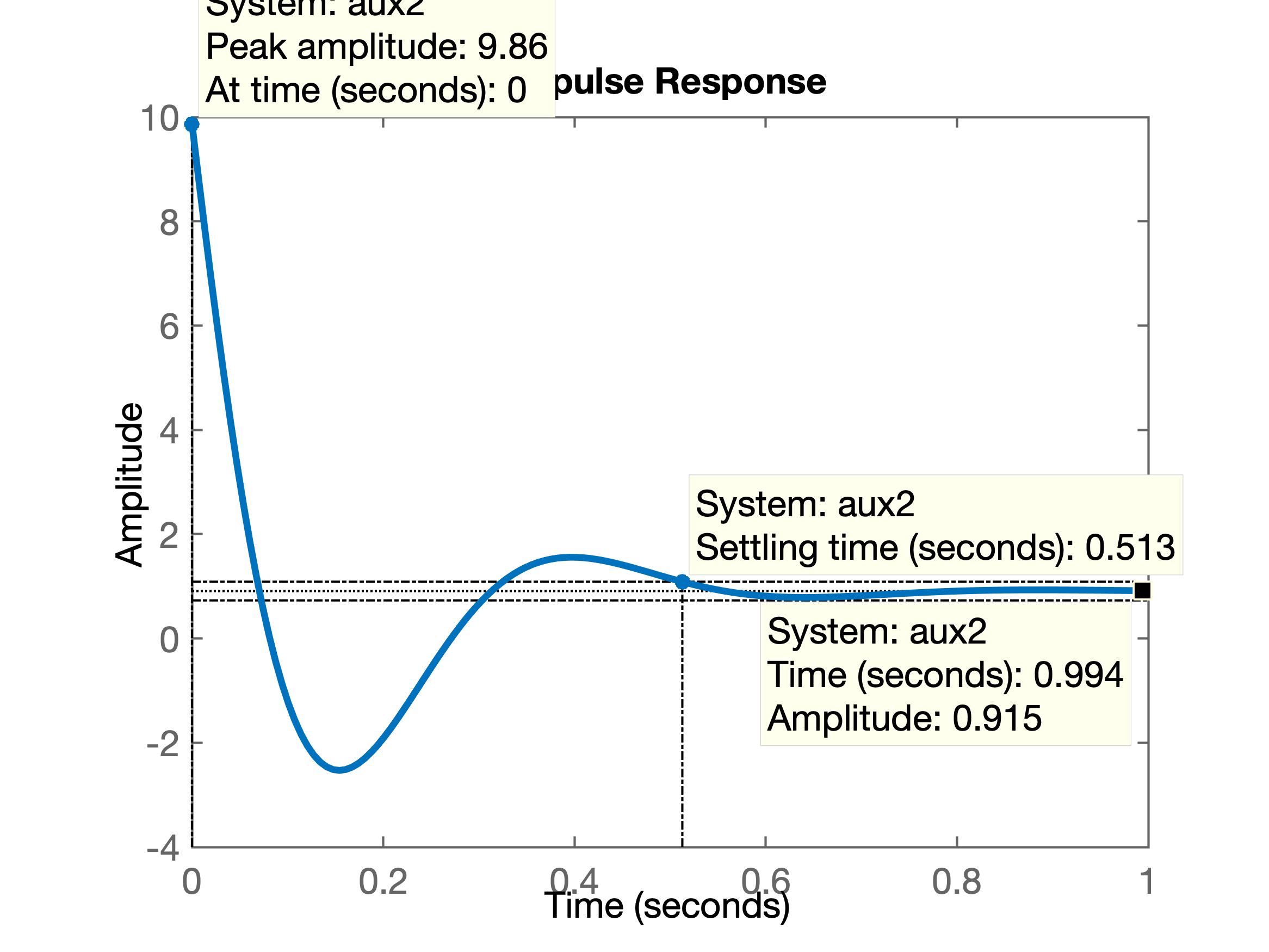
Podemos opcionalmente, mesclar num mesmo gráfico, a resposta temporal do sistema, com o gráfico de anterior, usando a função plotyy do Matlab.
Mas para usar esta função temos que criar os vetores usados como dados de entrada para a função plotyy():
>> % fechando malha do PD (não feito anteriormente)>> ftmf_PD=feedback(K_PD*C_PD*G7, 1); >> [u, t]=impulse(aux2); % gera vetores t x u(t)>> [y, t2]=step(ftmf_PD); % gera vetoree t2 x y(t)>> figure; plotyy(t2,y, t,u)>> legend('y(t)','u(t)')O que gera o gráfico:
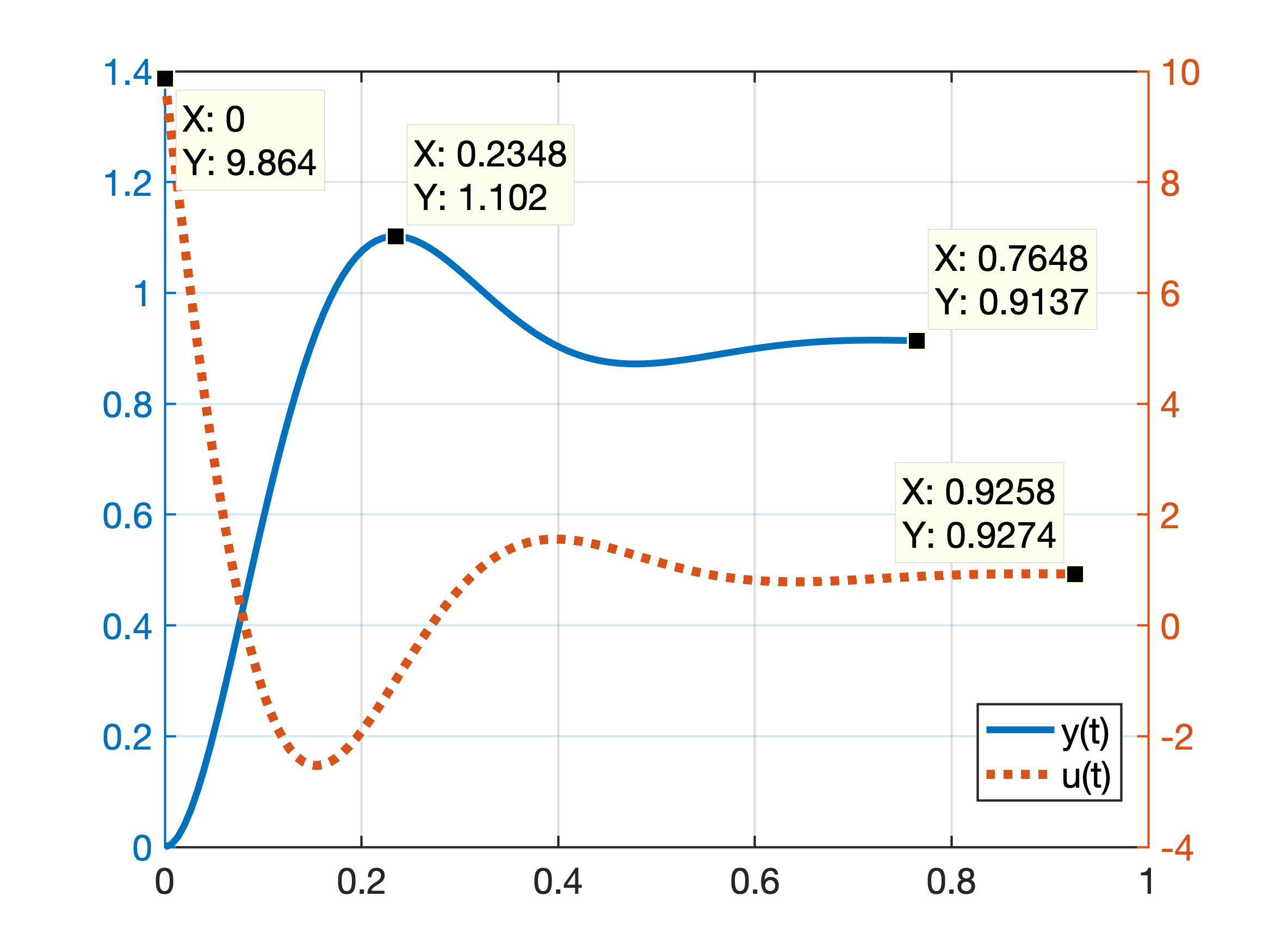
Mas talvez, mostrar os gráficos de e de maneira isolada seja melhor para mostrar pontos importantes em cada um deles:
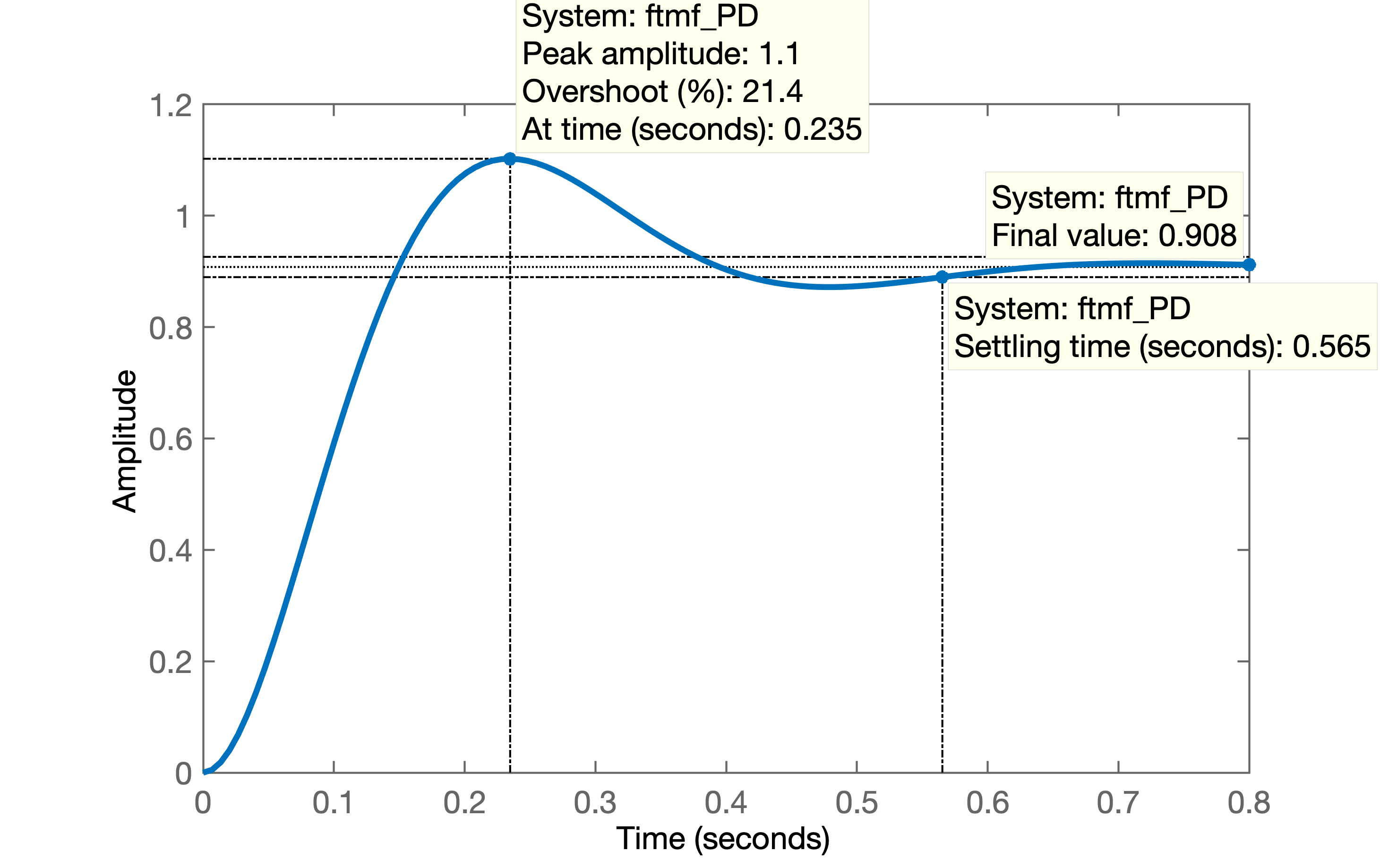 |  |
|---|---|
| (a) Resposta ao degrau, | (b) Resposta ao degrau, |
Gráfico de
O gráfico de pode ser obtido usando uma estratégia semelhante à adotada para plotar o gráfico de .
Neste caso, analisando o diagrama em blocos abaixo e extraíndo equações, teremos:

e no Matlab, realizamos então:
testando:
>> aux3=1/(1+K_PD*C_PD*G7);>> zpk(aux3)ans = (s+20) (s+8) (s+2) -------------------------------- (s+16.27) (s^2 + 13.73s + 213.7) Continuous-time zero/pole/gain model.>> figure; step(aux3)>> title('Erro para PD sobre planta G_7(s)')O que gera o gráfico:
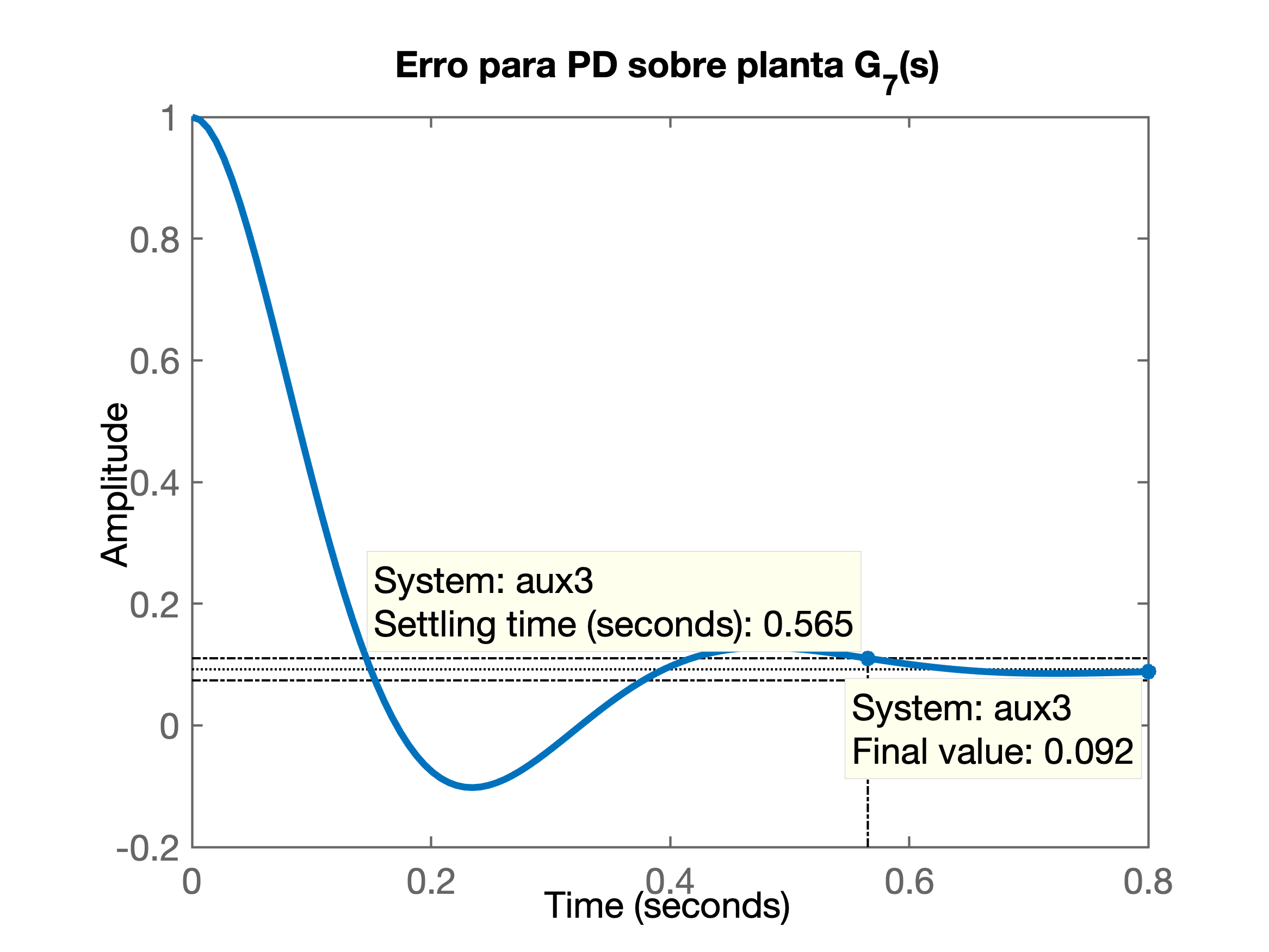
Fim
Fernando Passold, em 11/06/2020