Introdução

A idéia é criar um documento digital retratando os comandos usados no Matlab, acrescendo referências aos gráficos, equações e comentários, de forma fácil, num arquivo texto compatível com Markdown. Mais sobre Markdown e metodologia sugerida ver: Uso do MATLAB nas aulas de Controle + documentação Markdown → https://fpassold.github.io/Controle_2/sugestao_uso_matlab_em_controle.html

Então, logo depois de iniciar o Matlab, na sua janela de comandos (CLI) vamos dar o seguinte comando:

xxxxxxxxxx
>> diary aula09092024.txt

Isto fará com o que Matlab repasse para o arquivo acima, todos os comandos ingressados na sua CLI.

Projeto de Controladores

Ingressando a Planta

A idéia é trabalhar com uma mesma planta, explorando diferentes tipos de controladores. Percebendo quando certo tipo de ação de controle é mais desejada que outra, percebendo se requisitos de controle podem ser atendidos e percebendo que certas plantas se "casam" melhor com certos tipos de controladores. Então ao invés de mudar de planta cada vez que se muda a ação de controle, vamos projetar vários controladores diferentes para o mesmo tipo de planta, colocando o foco no raciocínio à ser adotado na definição de cada controlador.

Iniciando em: Projeto de Controladores Proporcional e com Ação Integral → https://fpassold.github.io/Controle_2/PI_parte1.html

A planta sugerida é do tipo 0 de 3a-ordem, sem zeros. Algo como:

$G(s)=\dfrac{K}{(s+p_1)(s+p_2)(s+p_3)}$

Onde os pólos $p_1$ e $p_2$ estariam mais próximos do eixo $j \omega$, ou seja, acabam dominando a resposta em relação ao terceiro pólo (que estaria mais afastado dos 2 primeiros).

Suponha então que a planta seja:

$G(s)=\dfrac{1}{(s+1)(s+4)(s+10)}$

Usando Matlab:

xxxxxxxxxx
>> G=tf ( 1, poly( [ -1 -4 -10 ] ) )    % ingressando a tf
​
G =
​
             1
------------------------
  s^3 + 15 s^2 + 54 s + 40
​
Continuous-time transfer function.
​
>> zpk(G) % conferindo entrada de dados
​
ans =
​
          1
------------------
  (s+10) (s+4) (s+1)
​
Continuous-time zero/pole/gain model.
​
>> step(G) % verificando resposta em MA para degrau unitário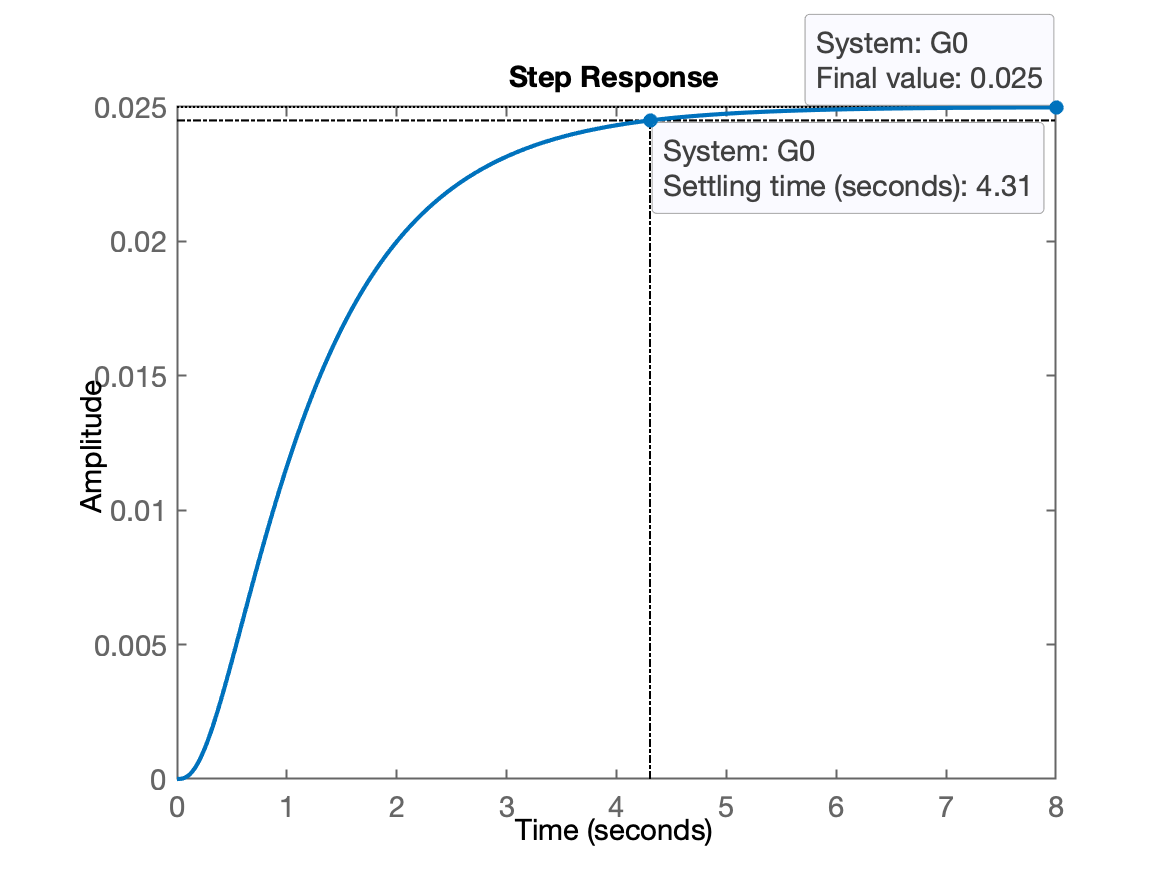

O gráfico nos permite perceber a "velocidade" ou tempo de resposta da planta. E percebemos também o "ganho DC" da planta (valor final, em regime permanente alcançado pela planta) -- apenas 0,025. Ou seja, se a planta recebe um degrau unitário na sua entrada, evolui até seu valor final de 0,025 -- um ganho DC bastante baixo.

Lembrado do Teorema do Valor Final associado com Transformada de Laplace, temos que:

$y(t)\vert_{t \to \infty} = y(\infty) = \displaystyle \lim_{s \to 0} \; s \cdot Y(s)$

Neste caso, $Y(s)=R(s) \cdot G(s)$, onde $R(s)=$ transformada de Laplace do sinal de entrada usado para excitar a planta, no caso, uma entrada degrau unitário, então $R(s)=1/s$. Assim temos:

$y(\infty)=\displaystyle \lim_{s \to 0} \cancel{s} \cdot \left( \underbrace{\dfrac{1}{\cancel{s}}}_{\text{Degrau}} \right) \cdot \left( \underbrace{\dfrac{1}{(s+1)(s+4)(s+10)}}_{G(s)} \right)$

O que resulta:

$y(\infty)=\dfrac{1}{(1)(4)(10)}=\dfrac{1}{40}$

O que numericamente resulta:

xxxxxxxxxx
>> 1/40
ans =
        0.025

Note que este valor coincide com o valor final atingido pela planta no gráfico anterior.

Como este ganho é muito baixo, vamos acrescentar artificialmente um ganho na nossa planta para modificar este valor. Suponha que queremos que o ganho DC seja de 0,5, então:

$0,5=\dfrac{K}{(1)(4)(10)} \quad \therefore \quad K=20$

Verificando com ajuda do Matlab:

xxxxxxxxxx
>> G=tf ( 20, poly( [ -1 -4 -10 ] ) )
​
G =
​
             20
------------------------
  s^3 + 15 s^2 + 54 s + 40
​
Continuous-time transfer function.
​
>> dcgain(G)    % Matlab aplica teorema do valor final usando entrada degrau na tf repassada
ans =
          0.5
>> figure; step(G)  % confirmando valor final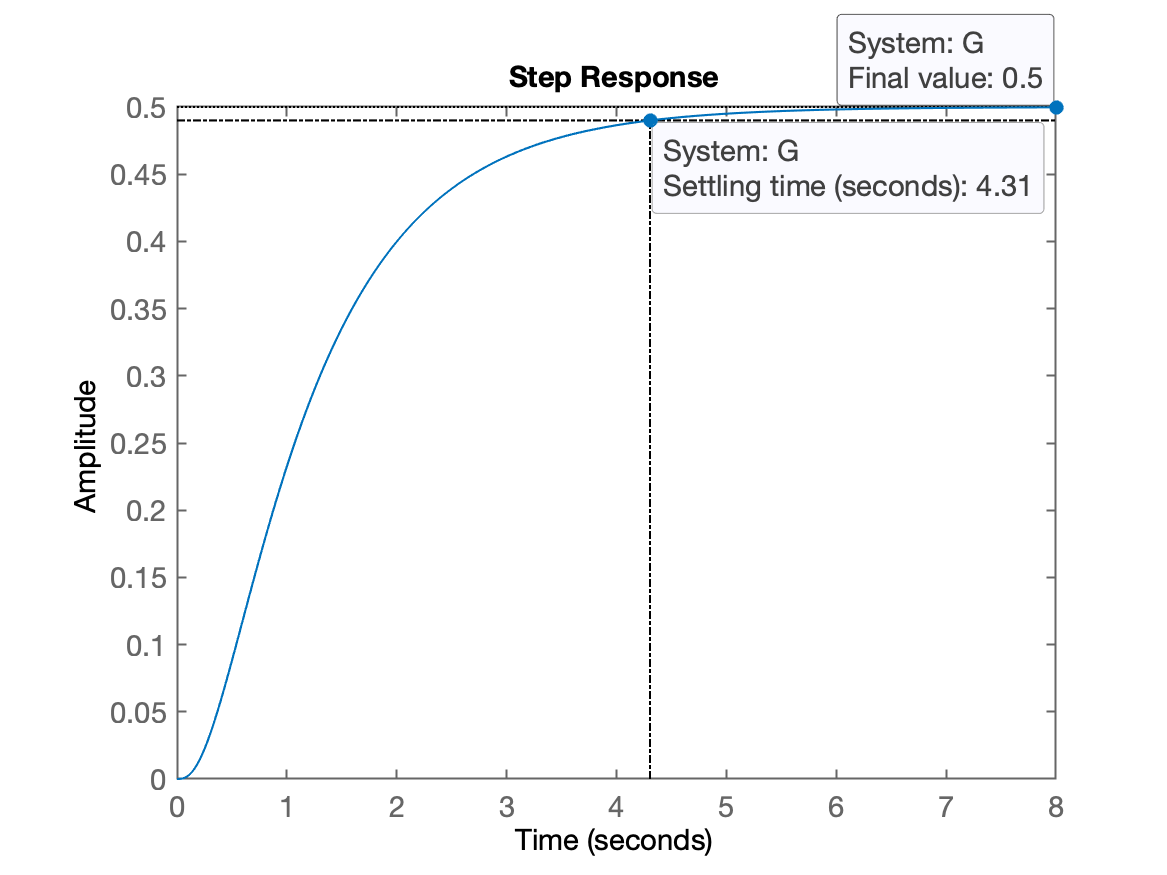

Resta agora iniciar o projeto de algum controlador, iniciando pelo mais simples, que seria simplesmente um controlador proporcional.

Controlador Proporcional

Este tipo de controlador fecha uma malha de realimentação unitária, simplesmente aplicando um ganho ao sinal de erro no canal de realimentação:

$C(s)=K$

o que implica que a planta vai receber o seguinte tipo de sinal, $u(t)=$ sinal de controle para a mesma:

$u(t)=K \cdot e(t)$

onde $e(t)=$ erro, calculado da seguinte forma:

$e(t)=r(t)-y(t)$

onde $r(t)=$ referência usada; $y(t)=$ resposta planta.

Este controlador simplemente faz:

$u(t)=K \left( r(t)-y(t) \right)$

Mas nenhum projeto de controle pode ser considerado um projeto sem requisitos de controle. Vamos supor neste caso, que queremos:

• Reduzir tempo de resposta da planta (em MA) em 3x;
• Manter erro em MF abaixo de 10%;
• Tolerável resposta com overshoot máximo de 10%;

Iniciando o projeto, levantando o root-locus deste sistema:

xxxxxxxxxx
>> figure; rlocus(G)
>> % vamos sobrepor a linha guia para valores constantes de \zeta com base no %OS desejado
>> OS=10; % overshoot
>> zeta=(-log(OS/100))/(sqrt(pi^2+(log(OS/100)^2)))
zeta =
      0.59116
>> hold on  % Obs.: realizar foco sobre figura do RL (não do Step)
>> sgrid(zeta, 0)
>> % realizando zoom na região de interesse:
>> axis([-13 1 -9 9])   % "padronizando" o zoom para todos os estudantes

Temos então o seguinte RL:

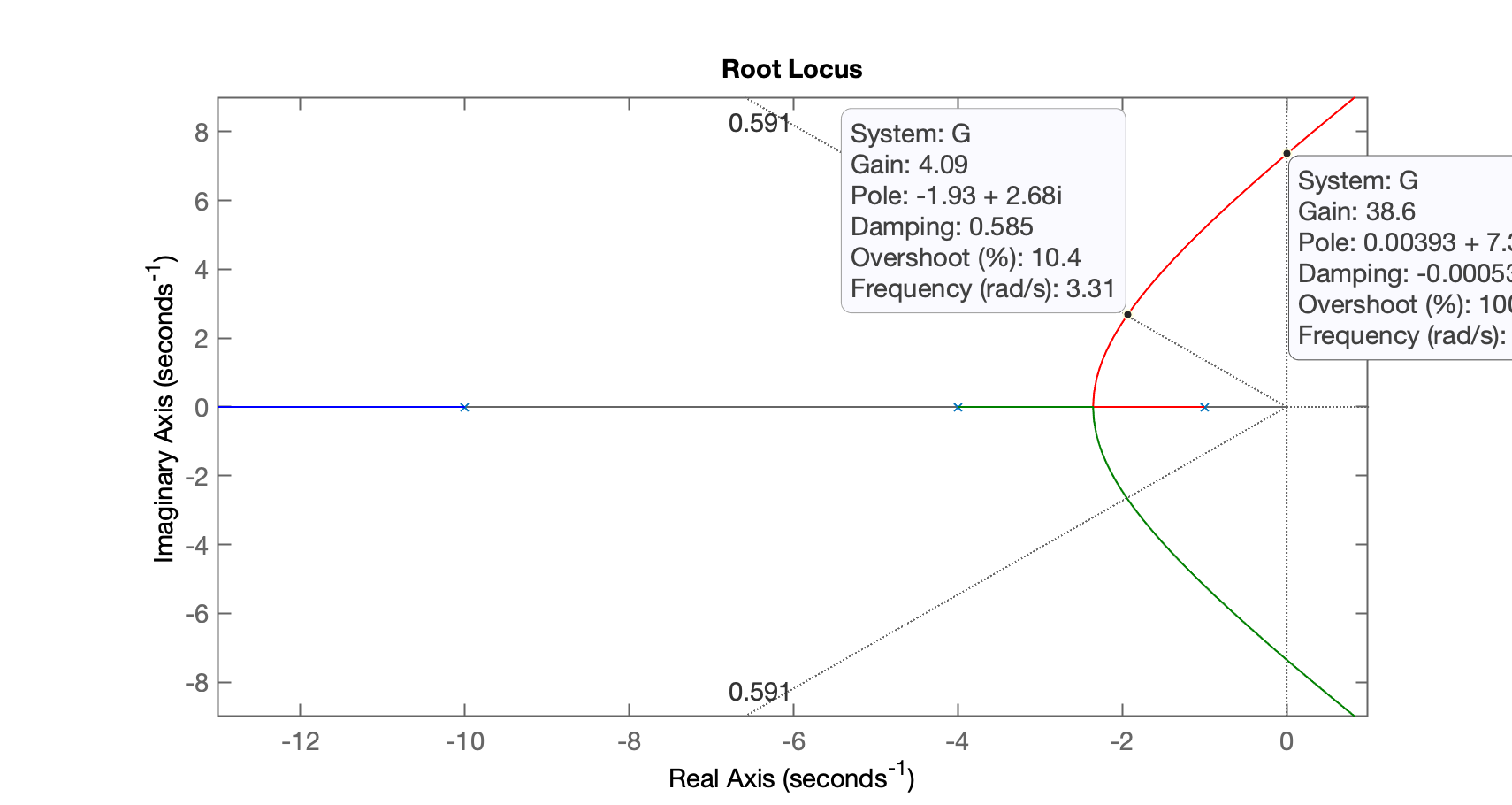
Notamos que:

• Ganho máximo em torno de $K=38,6$;
• Ganho para $\%OS=10\%$ quando $K \cong 4$.

Fechando a malha om ganho $K=4$:

xxxxxxxxxx
>> K=4;
>> ftmf = feedback(K*G, 1);
>> pole(ftmf)
ans =
      -11.112 +          0i
      -1.9438 +     2.6496i
      -1.9438 -     2.6496i
>> figure; step(1*ftmf)     % resposta ao degrau unitário (1) em MF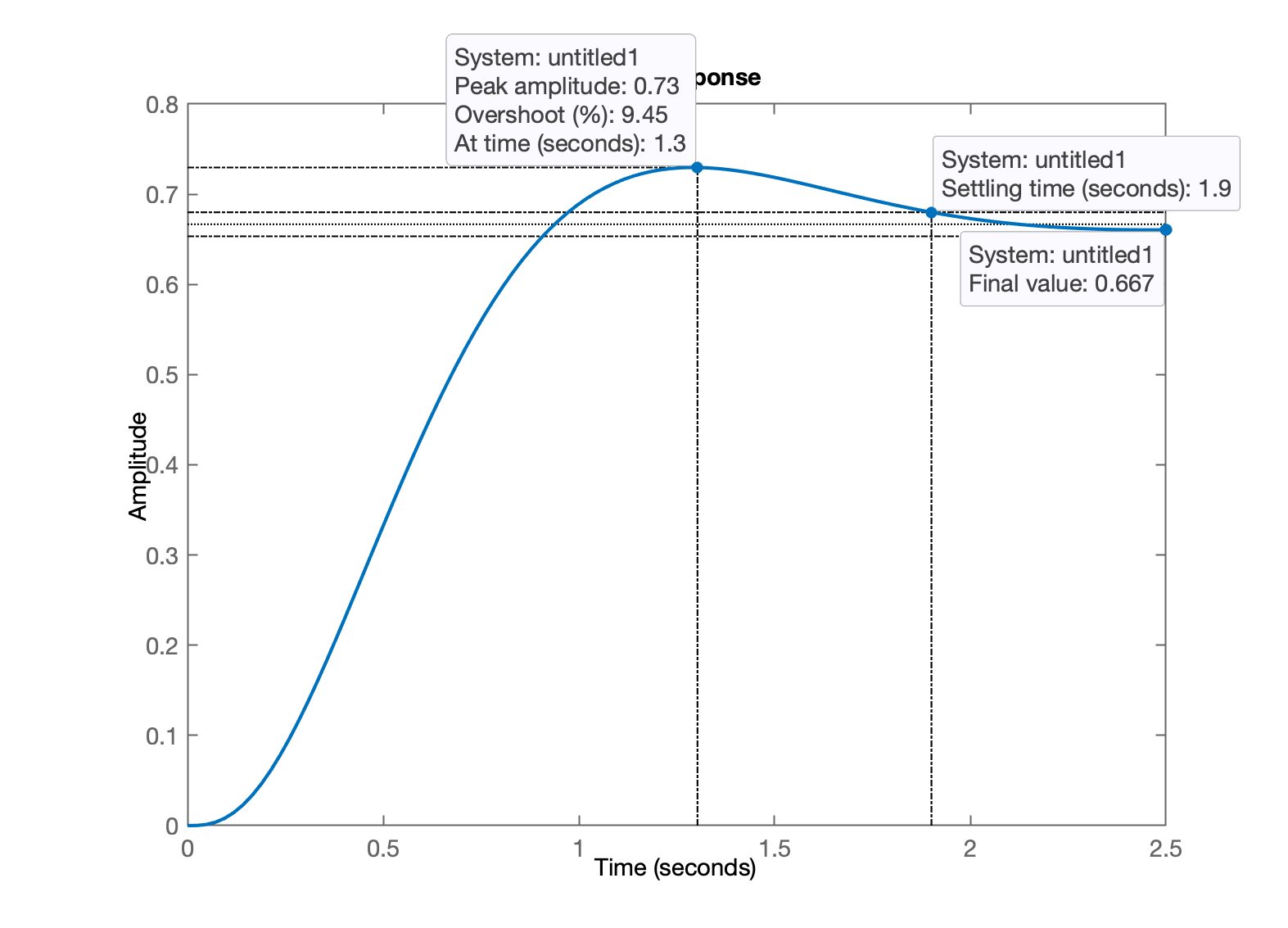

Nota-se:

• $\%OS < 10\%$, ✔️;
• $t_s=1,9$ segundos. Comparando com resposta em MA: $t_s=4,31$ segundos, ou, aceleramos a planta $2,27 \times$(em comparação com resposta em MA):

xxxxxxxxxx
4.31/1.9
ans =
       2.2684

Falta perceber o erro em regime permanente.

Se $y(\infty)=0,667$, então temos um erro de:

xxxxxxxxxx
>> dcgain(ftmf)
ans =
      0.66667
>> erro= ((1-dcgain(ftmf))/1)*100  % computando o erro em %
erro =
       33.333

Obviamente percebemos que com este valor de ganho, mantivemos o $\%OS$ abaixo do desejado, mas o erro é muito maior que os 10% desejados. Como esta planta é um sistema do tipo 0, a teoria dos erro no informa que sempre haverá erro de regime permanente enquanto não acrescentarmos alguma ação integral. Mas podemos aumentar o valor do ganho para reduzir o valor deste erro. Partindo então um novo projeto de controlador Proporcional.

Controlador Proporcional 2

O objetivo agora é usando teoria do erro calcular valor do ganho para manter erro abaixo do patamar desejado e então verificar o que acontece...

Teoria do erro → https://fpassold.github.io/Controle_2/3_erros/erros.pdf

A planta é um sistema tipo 0, o que significa que o controlador proporcional não é capaz de eliminar erro em regime permanente, já que falta ação integral. Mas podemos deduzir que valor de ganho deveria ser adotado para manter erro abaixo do valor desejado:

$e(\infty)=\dfrac{1}{1+K_p}$

$K_p=\lim_{s \to 0} FTMA(s)$

$e(\infty)=0,1$ (10% para entrada degrau unitário)

$e(\infty)=0,1=\dfrac{1}{1+K_p}$

$K_p=\dfrac{1-0,1}{0,1}$

Obtendo os valores numéricos com auxílio do Matlab:

xxxxxxxxxx
>> Kp=(1-0.1)/0.1
Kp =
     9

$K_p=\displaystyle\lim_{s \to 0} FTMA(s) = \displaystyle\lim_{s \to 0} K \cdot G(s) = 9$

O cálculo do $\displaystyle\lim_{s \to 0} G(s)=$ pode ser obtido usando a função dcgain(G):

xxxxxxxxxx
>> limite=dcgain(G)
limite =
          0.5

Então:

$K \cdot 0,5 = 9$

Ou, usando Matlab:

xxxxxxxxxx
>> K2=Kp/limite
K2 =
    18

Fechando a malha e comprovando teoria do erro:

xxxxxxxxxx
>> ftmf2=feedback(K2*G,1);
>> figure; step(ftmf2)

Obtemos o gráfico:

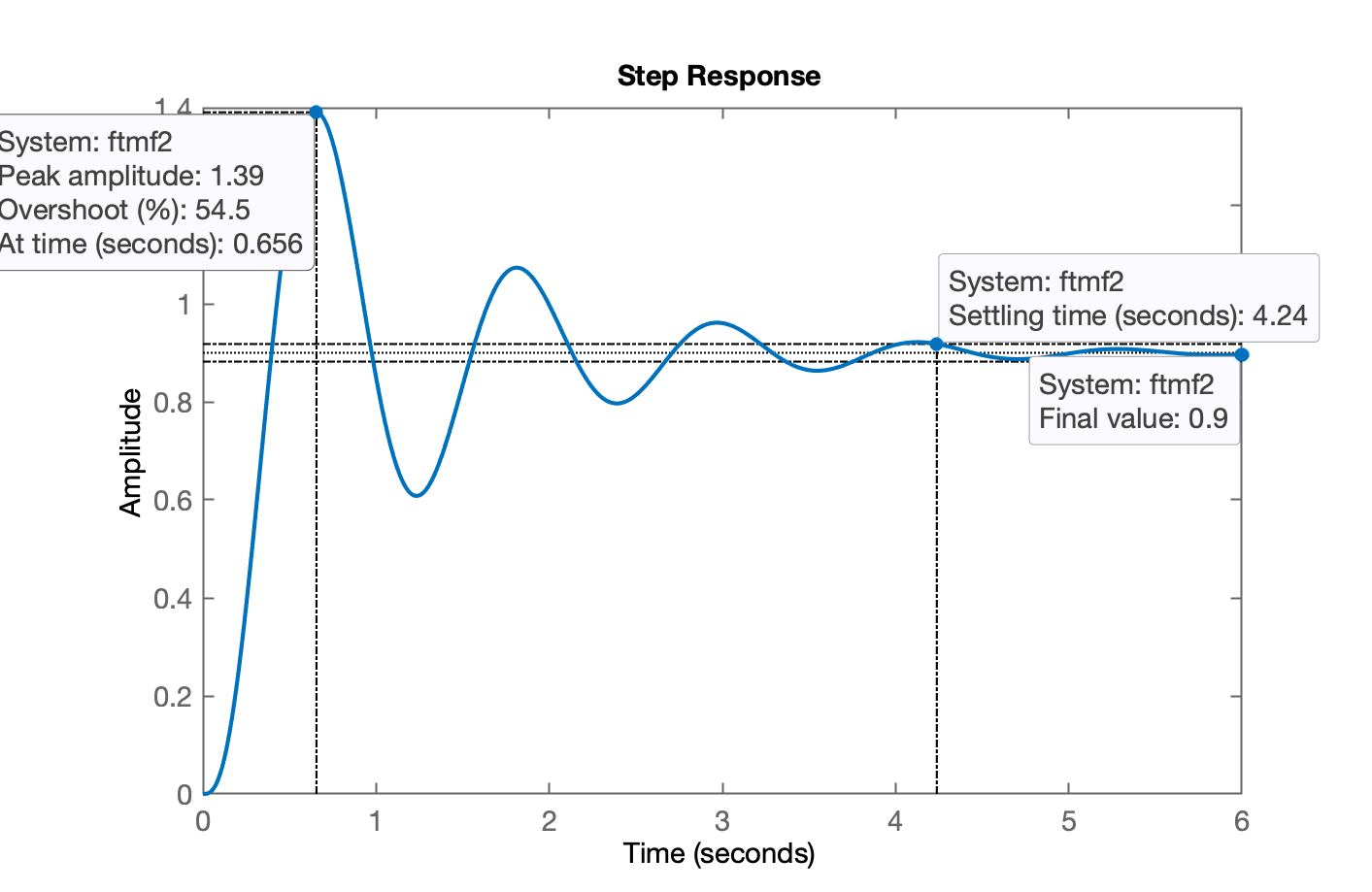
Comentários:

• o erro ficou no máximo requirido (10%), mas...
• $t_s$ aumentou consideravelmente, $t_s=4,42$ segundos. E era desejado:

xxxxxxxxxx
>> 4.31/3   % reduzir 3 vezes o ts de MA
ans =
       1.4367

• o $\%OS$ aumentou muito, 39% em relação à entrada degrau.

Conclusão final: o erro foi mantido no limite do desejado, mas o o tempo de resposta aumentou consideravelmente devido à resposta oscilatória do sistema (acima do desejado).

Então não há muito mais a fazer para "melhorar" um controlador proporcional. Poderíamos pensar em zerar o erro em regime permanente, acrescentando ação integral, mas então passamos para um novo tipo de controlador.

Controlador com Ação Integral Pura

O objetivo agora é eliminar o erro de regime permanente mas tentando manter os outros requisitos de controle:

xxxxxxxxxx
>> C_I=tf(1,[1 0]) % ingressando a tf deste controlador C(s)
​
C_I =
 
  1
  -
  s
 
Continuous-time transfer function.
​
>> ftma_I = C_I*G;  % obtendo a equação de malha-direta ou FTMA com este controlador
>> zpk(ftma_I)      % confirmando resultado obtido
​
ans =
 
           20
  --------------------
  s (s+10) (s+4) (s+1)
 
Continuous-time zero/pole/gain model.
​
>> % continuando o projeto, levantando o RL da planta com este controlador:
>> figure; rlocus(ftma_I)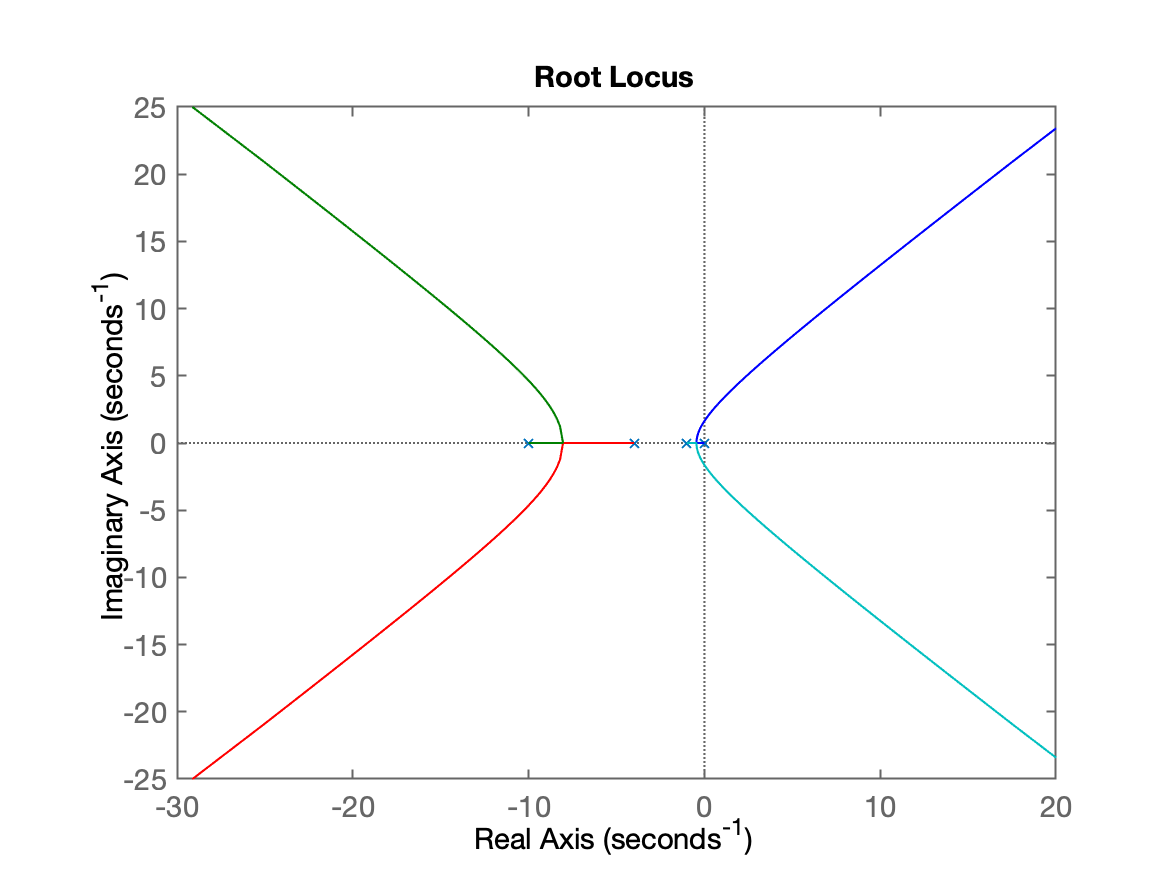

Realizando zoom na região de interesse (dos pólos dominantes) e definindo ganho do controlador:

xxxxxxxxxx
>> axis([-1.75 1 -3 3])
>> hold; sgrid(zeta, 0)
Current plot held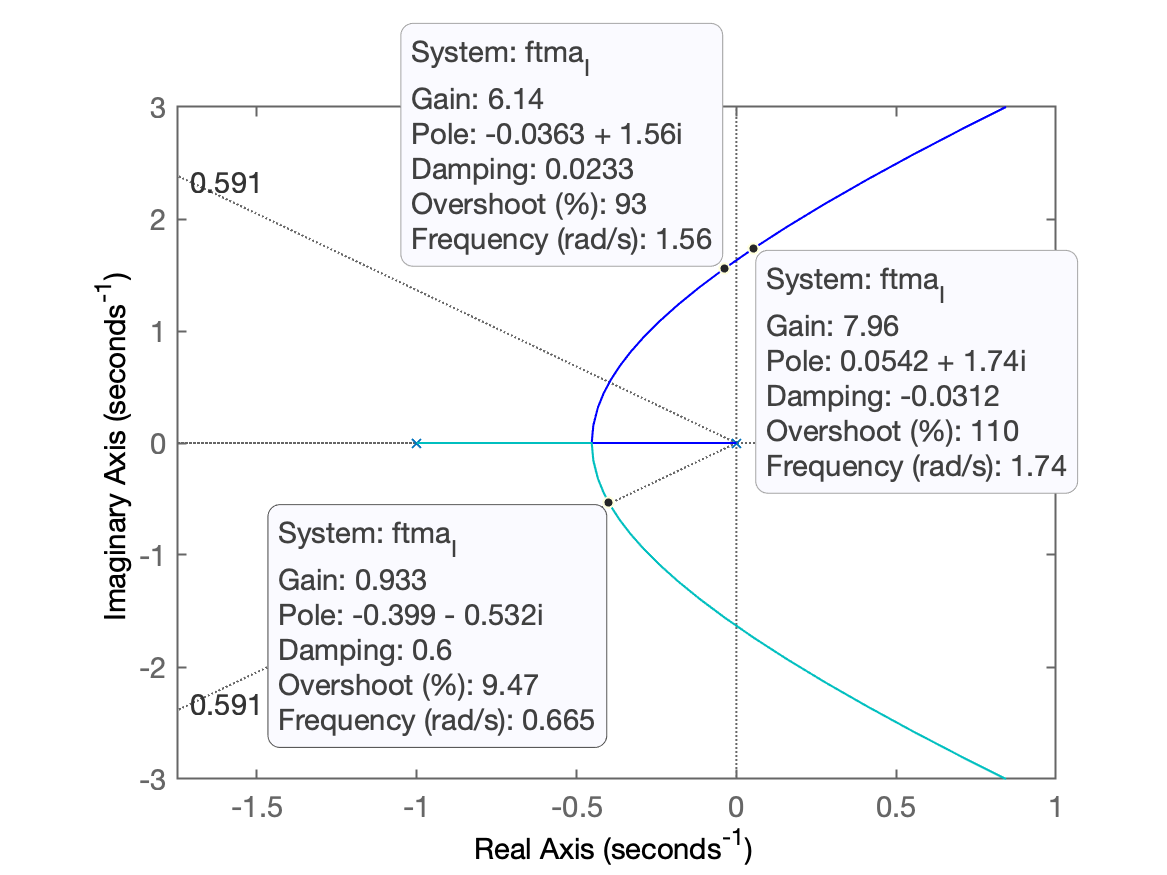

Algumas considerações:

• Ganho máximo, $6,14 < K_i < 7,96$. Obviamente não usaremos ganho tão elevado.

Notamos que as curvas do RL cruzam a linha guia do $\zeta$ correspondendo à $\%OS=10\%$ quando o ganho se encontra na faixa de ganho igual à 0,93:

xxxxxxxxxx
>> K_I=0.93;
>> ftmf_I=feedback(K_I*ftma_I, 1);
>> figure; step(ftmf_I)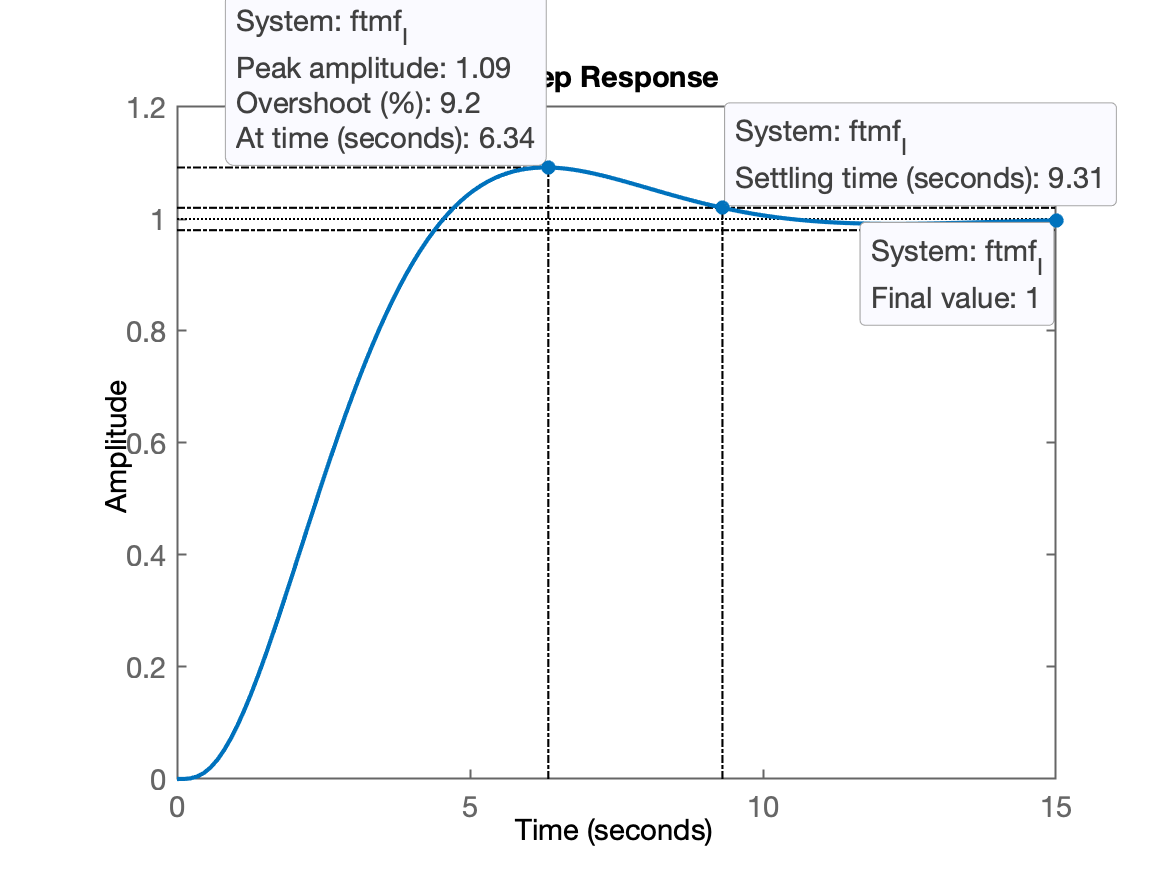

Comentários:

• Realmente o erro de regime permanente foi eliminado ($y(\infty)=1,0$, igual à amplitude da entrada degrau unitário adorada como referência para o sistema);

• mas....

  • $t_s=9,31$ segundos ficou muito maior que o desejado;
  • $\%OS=9,2\%$ que corresponde ao desejado.

Se por acaso fosse usado ganho unitário para a ação integral obteríamos a seguinte resposta:

xxxxxxxxxx
>> ftmf_I2=feedback(1*ftma_I, 1);
>> figure; step(ftmf_I2)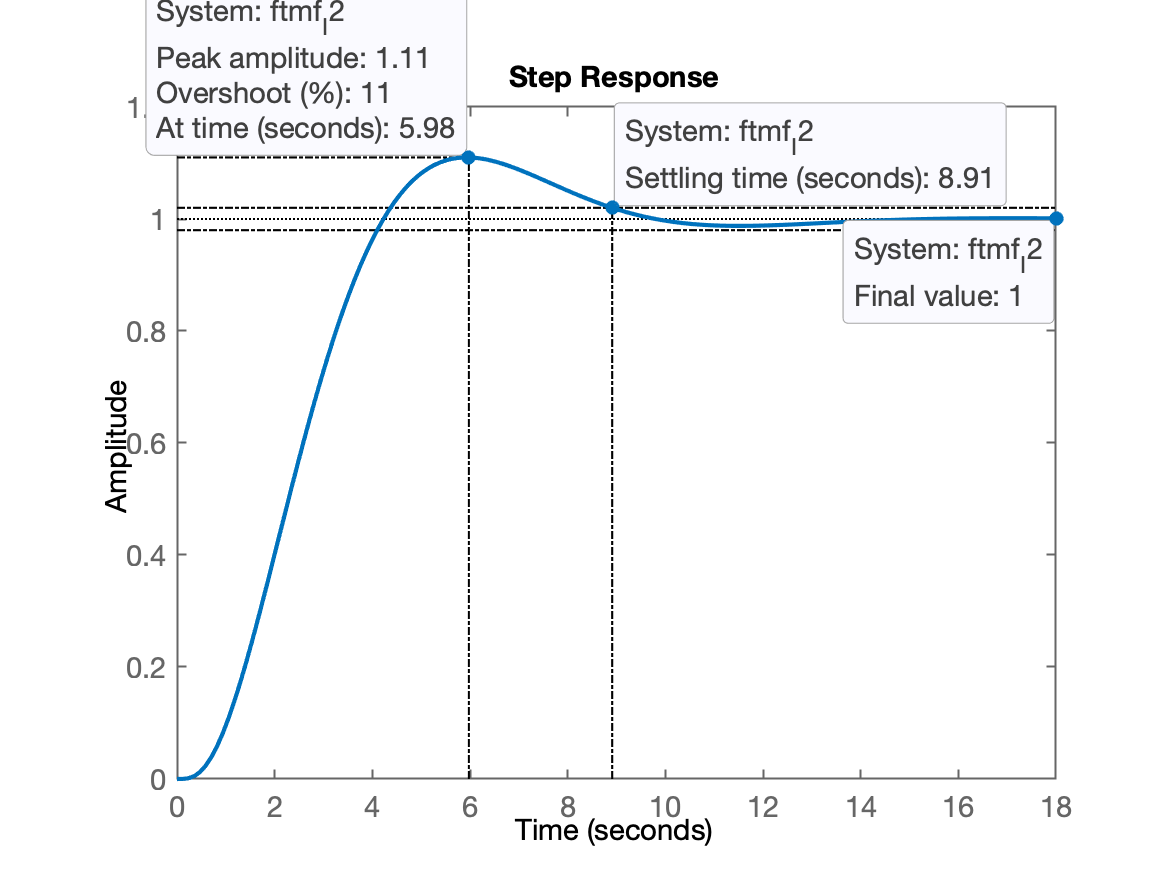

Comentário: ganho unitário para ação integral já faz $\%OS$ ficar acima do desejado. Porém, como o ganho aumentou, o sistema respondeu um pouco mais rápido: $t_s=8,91$ segundos.

Note que acrescentar um pólo na origem (a ação integral) normalmente faz um sistema em MF responder de forma mais lenta (apesar de zerar o erro). Uma forma de "consertar" este problema é fazer a ação Integral trabalhar em paralelo com a ação Proporcional, e assim, estaríamos partindo para um controlador PI.

Controlador PI

Equação geral do PI:

$C_{PI}(s)=K_p+\dfrac{K_i}{s}$

$C_{PI}(s)=\dfrac{K_p \left( s + \dfrac{K_i}{K_p} \right)}{s}$

Referências:

• Projeto de Controladores com Ação Integral (Aula #2: 2022/2) (aula de 17/10/2022) → https://fpassold.github.io/Controle_2/control2inf_2020_2/17102022.html
• Projeto de PI (por contribuição angular) + Lag; (Aula de 30/10/2020) → https://fpassold.github.io/Controle_2/PI_angular_Lag.html

Encerrando atividades no Matlab

Vamos continuar o projeto deste controlador na próxima aula. Mas antes de "abandonar" o Matlab vamos gravar os dados já levantados (para facilitar a continuação na próxima aula) e vamos fechar o arquivo "diary" recém criado:

>> save planta  % cria arquivo planta.mat com variáveis já calculadas nesta seção de trabalho
>> diary off
>> quit

Fernando Passold, em 9/09/2024