Exemplo uso inicial Matlab
Aula de 26/10/2023
Tópicos abordados:
- Exemplo uso inicial Matlab
Introdução
Comando diary
Recomenda-se ao entrar no Matlab, criar um "diário" dos comandos usados nesta seção de trabalho. Algo como:
>> diary aula_26oct2023.txt
Isto faz com o que o Matlab crie um arquivo texto usando o nome que foi indicado (no caso: aula_26oct2023.txt). Este arquivo é criado em segundo plano, refletindo todos os comandos, resultados (e erros) cometidos durante sua utilização, até que o usuário dê um diary off.
⚠️ O comando diary off encera a geração deste aquivo e fecha este arquivo (importante para usuários Windows caso contrário o arquivo não é "fechado" e acaba sendo perdido)
Outros comandos iniciais básicos
>> pwd % este comando confirma o diretório atual de trabalho no Matlab
ans =
'/Users/fernandopassold/Documents/MATLAB'
>> ver % descobrir versão do Matlab e toolboxes instalados
-----------------------------------------------------------------------------------------------------
MATLAB Version: 9.7.0.1190202 (R2019b)
MATLAB License Number: 968398
Operating System: macOS Version: 13.6 Build: 22G120
Java Version: Java 1.8.0_202-b08 with Oracle Corporation Java HotSpot(TM) 64-Bit Server VM mixed mode
-----------------------------------------------------------------------------------------------------
MATLAB Version 9.7 (R2019b)
Simulink Version 10.0 (R2019b)
Audio Toolbox Version 2.1 (R2019b)
Communications Toolbox Version 7.2 (R2019b)
Computer Vision Toolbox Version 9.1 (R2019b)
Control System Toolbox Version 10.7 (R2019b)
Curve Fitting Toolbox Version 3.5.10 (R2019b)
DSP System Toolbox Version 9.9 (R2019b)
Deep Learning Toolbox Version 13.0 (R2019b)
Fixed-Point Designer Version 6.4 (R2019b)
Fuzzy Logic Toolbox Version 2.6 (R2019b)
Global Optimization Toolbox Version 4.2 (R2019b)
Image Acquisition Toolbox Version 6.1 (R2019b)
Image Processing Toolbox Version 11.0 (R2019b)
MATLAB Parallel Server Version 7.1 (R2019b)
MATLAB Report Generator Version 5.7 (R2019b)
Optimization Toolbox Version 8.4 (R2019b)
Parallel Computing Toolbox Version 7.1 (R2019b)
Partial Differential Equation Toolbox Version 3.3 (R2019b)
ROS Toolbox Version 1.0 (R2019b)
Reinforcement Learning Toolbox Version 1.1 (R2019b)
Robotics System Toolbox Version 3.0 (R2019b)
Sensor Fusion and Tracking Toolbox Version 1.2 (R2019b)
Signal Processing Toolbox Version 8.3 (R2019b)
SimEvents Version 5.7 (R2019b)
Simscape Version 4.7 (R2019b)
Simscape Driveline Version 3.0 (R2019b)
Simscape Electrical Version 7.2 (R2019b)
Simscape Fluids Version 2.7 (R2019b)
Simscape Multibody Version 7.0 (R2019b)
Simulink 3D Animation Version 8.3 (R2019b)
Simulink Control Design Version 5.4 (R2019b)
Simulink Report Generator Version 5.7 (R2019b)
Stateflow Version 10.1 (R2019b)
Statistics and Machine Learning Toolbox Version 11.6 (R2019b)
Symbolic Math Toolbox Version 8.4 (R2019b)
System Identification Toolbox Version 9.11 (R2019b)
mem
>> memory % Descobrir como o Matlab usa se sistema (só Windows)
Function MEMORY is not available on this platform.}
Operações matemáticas simples
Seguem exemplos de operações matemáticas simples:
>> 5+7
ans =
12
>> cos(pi/4) % Lembrar que argumento de entrada sempre será radianos
ans =
0.70711
O comando format
O Matlab permite expressar resultados numéricos de diferentes formas:
>> format shorteng
i=15/10E3
i =
1.5000e-003
>> format shortg
2/4
ans =
0.5
4/4
ans =
1
>> help format
<strong>format</strong> Set output format.
<strong>format</strong> with no inputs sets the output format to the default appropriate
for the class of the variable. For float variables, the default is
<strong>format</strong> SHORT.
<strong>format</strong> does not affect how MATLAB computations are done. Computations
on float variables, namely single or double, are done in appropriate
floating point precision, no matter how those variables are displayed.
Computations on integer variables are done natively in integer. Integer
variables are always displayed to the appropriate number of digits for
the class, for example, 3 digits to display the INT8 range -128:127.
<strong>format</strong> SHORT and LONG do not affect the display of integer variables.
<strong>format</strong> may be used to switch between different output display formats
of all float variables as follows:
<strong>format</strong> SHORT Scaled fixed point format with 5 digits.
<strong>format</strong> LONG Scaled fixed point format with 15 digits for double
and 7 digits for single.
<strong>format</strong> SHORTE Floating point format with 5 digits.
<strong>format</strong> LONGE Floating point format with 15 digits for double and
7 digits for single.
<strong>format</strong> SHORTG Best of fixed or floating point format with 5
digits.
<strong>format</strong> LONGG Best of fixed or floating point format with 15
digits for double and 7 digits for single.
<strong>format</strong> SHORTENG Engineering format that has at least 5 digits
and a power that is a multiple of three
<strong>format</strong> LONGENG Engineering format that has exactly 16 significant
digits and a power that is a multiple of three.
<strong>format</strong> may be used to switch between different output display formats
of all numeric variables as follows:
<strong>format</strong> HEX Hexadecimal format.
<strong>format</strong> + The symbols +, - and blank are printed
for positive, negative and zero elements.
Imaginary parts are ignored.
<strong>format</strong> BANK Fixed format for dollars and cents.
<strong>format</strong> RAT Approximation by ratio of small integers. Numbers
with a large numerator or large denominator are
replaced by *.
<strong>format</strong> may be used to affect the spacing in the display of all
variables as follows:
<strong>format</strong> COMPACT Suppresses extra line-feeds.
<strong>format</strong> LOOSE Puts the extra line-feeds back in.
Example:
format short, pi, single(pi)
displays both double and single pi with 5 digits as 3.1416 while
format long, pi, single(pi)
displays pi as 3.141592653589793 and single(pi) as 3.1415927.
format, intmax('uint64'), realmax
shows these values as 18446744073709551615 and 1.7977e+308 while
format hex, intmax('uint64'), realmax
shows them as ffffffffffffffff and 7fefffffffffffff respectively.
The HEX display corresponds to the internal representation of the value
and is not the same as the hexadecimal notation in the C programming
language.
See also <a href="matlab:help disp">disp</a>, <a href="matlab:help display">display</a>, <a href="matlab:help isnumeric">isnumeric</a>, <a href="matlab:help isfloat">isfloat</a>, <a href="matlab:help isinteger">isinteger</a>.
<a href="matlab:doc format">Documentation for format</a>
Exemplificando o comando format:
>> a=2/4
a =
0.5
>> format rat
>> a
a =
1/2
>> format shortg % formato mais recomendado
>> b=4;
>> c=a*b
c =
2
>> size(c) % descobrir as dimensões da variável
ans =
1 1
Números complexos
>> a=[1+2*i 1-2*i] % tentando ingressar números complexos
a =
1.003 0.997
>> a=[1+i*2 1-i*2] % tentando ingressar números complexos
a =
1.003 0.997
>> a=[1+j*2 1-j*2] % tentando ingressar números complexos
a =
1 + 2i 1 - 2i
>> % Obs.: Antes não "funcinou" porque variável i já havia sido criada e usada
>> size(a)
ans =
1 2
>> b=5*j*7 % operação com números complexos
b =
0 + 35i
>> c=sqrt(-4) % raiz quadrada resultando em número imaginário
c =
0 + 2i
>> size(c)
ans =
1 1
Descobrindo variáveis já criadas
>> who % apenas lista variáveis existentes
Your variables are:
a ans b c i
>> whos % lista variáveis e passa informações sobre tipo e dimensões das mesmas
Name Size Bytes Class Attributes
a 1x2 32 double complex
ans 1x2 16 double
b 1x1 16 double complex
c 1x1 16 double complex
i 1x1 8 double
format shortg & format long
>> a=5/7
a =
0.71429
>> format long % mostrando todas as casas decimais
>> a
a =
0.714285714285714
>> format shortg % mostrando até 4 ou 5 casas decimais se necessário
>> a
a =
0.71429
Criando vetores e matrizes
>> a = ones(100,100); % cria matriz de 100 x 100 repleta de 1's
>> size(a) % confirmando tamanho da matriz criada
ans =
100 100
>> whos
Name Size Bytes Class Attributes
a 100x100 80000 double
ans 1x2 16 double
b 1x1 16 double complex
c 1x1 16 double complex
i 1x1 8 double
Limpando variáveis da memório (comando clear)
>> clear a % apaga variável a
>> whos
Name Size Bytes Class Attributes
ans 1x2 16 double
b 1x1 16 double complex
c 1x1 16 double complex
i 1x1 8 double
>> clear all % apaga todas as variáveis
>> whos % confirmando que não há mais variáveis
>>
Mais operações com números complexos
>> a = 2+2*i
a =
2 + 2i
>> b = sqrt(a)
b =
1.5538 + 0.64359i
>> a_real = abs(a) % calculando o módulo de um número complexo
a_real =
2.8284
>> sqrt(2^2+2^2) % confirmando resultado anterior
ans =
2.8284
>> a_angle = angle(a) % extraíndo angulo de um número complexo
a_angle =
0.7854
>> a_degrees = a_angle*180/pi % convertendo resutado de rad para graus
a_degrees =
45
>> b = 4*2
b =
8
>> b = 4*a
b =
8 + 8i
>> c = a^2
c =
0 + 8i
Operações com matrizes
>> a = [1 2; 3 4];
a
a =
1 2
3 4
>> size(a)
ans =
2 2
>> b = ones(2,2)
b =
1 1
1 1
>> c = a*b % multiplicação de matrizes
c =
3 3
7 7
>> d = [1,-1]
d =
1 -1
>> e = a*d % tentando multiplicar estas raízes
Error using
Incorrect dimensions for matrix multiplication. Check that the number of
columns in the first matrix matches the number of rows in the second matrix.
To perform elementwise multiplication, use '.*'.
>> e = a.*d % multiplicação elemento-à-elemento
e =
1 -2
3 -4
>> f = d*a % esta multiplicação (de matrizes), funciona
f =
-2 -2
>> who % confirmando tipos de variáveis
Your variables are:
a a_degrees ans c e
a_angle a_real b d f
>> A = 100 % Matlab diferencia maiúsculas de minúsculas
A =
100
>> a
a =
1 2
3 4
>> pi % constante pi (pré-definida)
ans =
3.1416
>> A=[1 2; 3 4]; b=[5; 6]; y=[7; 8]; % multiplas declarações na mesma linha
>> b
b =
5
6
>> x = (y-b)/A
Error using
Matrix dimensions must agree.
>> aux=y-b
aux =
2
2
>> aux = aux' % realizando transposta de uma matriz
aux =
2 2
>> x=aux/A
x =
-1 1
>> x=(y-b)\A
x =
1 1.5
x=(y-b)\A
x =
1 '' 1.5
Criando gráficos
Comando ezplot()
help ezplot
<strong>ezplot</strong> (NOT RECOMMENDED) Easy to use function plotter
==========================================================
<strong>ezplot</strong> is not recommended. Use FPLOT or FIMPLICIT instead.
==========================================================
<strong>ezplot</strong>(FUN) plots the function FUN(X) over the default domain
-2*PI < X < 2*PI, where FUN(X) is an explicitly defined function of X.
<strong>ezplot</strong>(FUN2) plots the implicitly defined function FUN2(X,Y) = 0 over
the default domain -2*PI < X < 2*PI and -2*PI < Y < 2*PI.
<strong>ezplot</strong>(FUN,[A,B]) plots FUN(X) over A < X < B.
<strong>ezplot</strong>(FUN2,[A,B]) plots FUN2(X,Y) = 0 over A < X < B and A < Y < B.
<strong>ezplot</strong>(FUN2,[XMIN,XMAX,YMIN,YMAX]) plots FUN2(X,Y) = 0 over
XMIN < X < XMAX and YMIN < Y < YMAX.
<strong>ezplot</strong>(FUNX,FUNY) plots the parametrically defined planar curve FUNX(T)
and FUNY(T) over the default domain 0 < T < 2*PI.
<strong>ezplot</strong>(FUNX,FUNY,[TMIN,TMAX]) plots FUNX(T) and FUNY(T) over
TMIN < T < TMAX.
<strong>ezplot</strong>(FUN,[A,B],FIG), <strong>ezplot</strong>(FUN2,[XMIN,XMAX,YMIN,YMAX],FIG), or
<strong>ezplot</strong>(FUNX,FUNY,[TMIN,TMAX],FIG) plots the function over the
specified domain in the figure window FIG.
<strong>ezplot</strong>(AX,...) plots into AX instead of GCA or FIG.
H = <strong>ezplot</strong>(...) returns handles to the plotted objects in H.
Examples:
The easiest way to express a function is via a string:
ezplot('x^2 - 2*x + 1')
One programming technique is to vectorize the string expression using
the array operators .* (TIMES), ./ (RDIVIDE), .\ (LDIVIDE), .^ (POWER).
This makes the algorithm more efficient since it can perform multiple
function evaluations at once.
ezplot('x.*y + x.^2 - y.^2 - 1')
You may also use a function handle to an existing function. Function
handles are more powerful and efficient than string expressions.
ezplot(@humps)
ezplot(@cos,@sin)
<strong>ezplot</strong> plots the variables in string expressions alphabetically.
subplot(1,2,1), ezplot('1./z - log(z) + log(-1+z) + t - 1')
To avoid this ambiguity, specify the order with an anonymous function:
subplot(1,2,2), ezplot(@(z,t)1./z - log(z) + log(-1+z) + t - 1)
If your function has additional parameters, for example k in myfun:
%-----------------------%
function z = myfun(x,y,k)
z = x.^k - y.^k - 1;
%-----------------------%
then you may use an anonymous function to specify that parameter:
ezplot(@(x,y)myfun(x,y,2))
See also <a href="matlab:help ezcontour">ezcontour</a>, <a href="matlab:help ezcontourf">ezcontourf</a>, <a href="matlab:help ezmesh">ezmesh</a>, <a href="matlab:help ezmeshc">ezmeshc</a>, <a href="matlab:help ezplot3">ezplot3</a>, <a href="matlab:help ezpolar">ezpolar</a>,
<a href="matlab:help ezsurf">ezsurf</a>, <a href="matlab:help ezsurfc">ezsurfc</a>, <a href="matlab:help plot">plot</a>, <a href="matlab:help vectorize">vectorize</a>, <a href="matlab:help function_handle">function_handle</a>.
<a href="matlab:doc ezplot">Documentation for ezplot</a>
<a href="matlab:matlab.internal.language.introspective.overloads.displayOverloads('ezplot')">Other functions named ezplot</a>
>> ezplot('sin(2*pi*t)+(1/3)*sin(2*pi*3*t)+(1/5)*sin(2*pi*5*t)', [0 1.5])
>> xlabel('tempo (s)')
>> ylabel('y(t)')
>> grid
>> title('Onda Quadrada até 5a-harmônica')
Resultado:
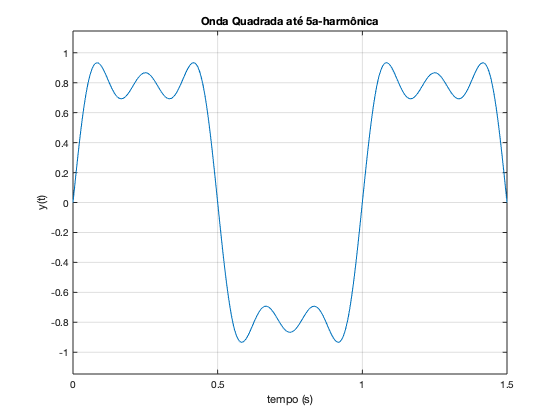
O gráfico anterior segue resolução "default" do Matlab para a tela do computador (algo como 96 dpi) e fontes de tamanho reduzido, bom para visualizações na tela, mas ruim para incorporação, redimensionamento ou impressão de documentos usando estes gráficos.
Se aconselha então, na janela do gráfico, modificar algums propriedaddes, ativando a opção "Export Setup" e modificar alguns parâmetros:
- Resolução: 150 dpi
- Tamanho de fonte mínima: 14 pts
- Espessura das linhas para mínimo de 1 pts
Obs.: Não será necessário repetir todos estes ajustes para cada figura, basta, uma vez completado estes ajustes, ativar "Save Template", escolher um nome e nas próximas janelas gráficas, fazer: "Load Template" e clicar no botão "Apply".
Seguindo estas orientações, um gráfico de melhor qualidade pode ser obtido:
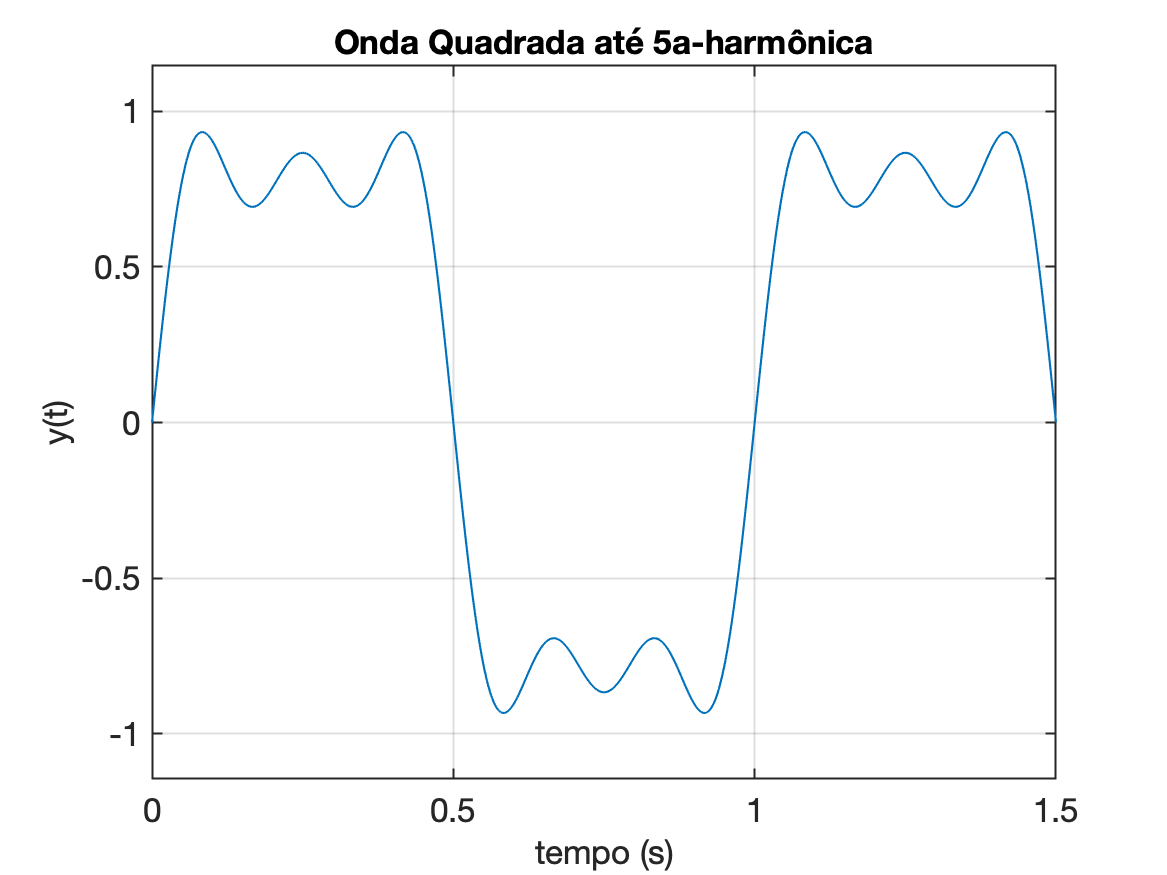
Plotando vetores (comando plot)
>> t=[0:0.01:1.5]; % criando vetor inicio:incremento:fim
>> size(t)
ans =
1 151
>> t=[1,1:10] % criando matriz de 1 linha x n-colunas (vetor)
t =
1 1 2 3 4 5 6 7 8 9 10
>> t=[1,1:10]' % fazendo transposta do vetor criado
t =
1
1
2
3
4
5
6
7
8
9
10
>> t=[0:0.01:1.5]; % recriando vetor 0<t<1.5; incremento de 10 ms
>> t(1,1:10) % mostrando conteúdo de seus 10 primeiros elementos
ans =
Columns 1 through 5
0 0.01 0.02 0.03 0.04
Columns 6 through 10
0.05 0.06 0.07 0.08 0.09
>> t(1,1:10)'
ans =
0
0.01
0.02
0.03
0.04
0.05
0.06
0.07
0.08
0.09
>> % Sintetizando até 5a-harmônica de uma onda quadrada de 1 Hz
>> y=sin(2*pi*t)+(1/3)*sin(2*pi*3*t)+(1/5)*sin(2*pi*5*t);
>> [t(1,1:10)' y(1,1:10)'] % mostrando como uma matriz 10x2, conteúdo t x y(t)
ans =
0 0
0.01 0.18705
0.02 0.3656
0.03 0.52779
0.04 0.66708
0.05 0.77869
0.06 0.85994
0.07 0.91044
0.08 0.93199
0.09 0.92834
>> size(ans)
ans =
10 2
>> figure; plot(t,y)
Melhorando a onda quadrada anterior...
>> % acrescentando mais componentes às harmônicas da onda quadrada
>> y2=sin(2*pi*t)+(1/3)*sin(2*pi*3*t)+(1/5)*sin(2*pi*5*t)+(1/7)*sin(2*pi*7*t)+(1/9)*sin(2*pi*9*t);
whos
Name Size Bytes Class Attributes
A 2x2 32 double
a 2x2 32 double
a_angle 1x1 8 double
a_degrees 1x1 8 double
a_real 1x1 8 double
ans 1x2 16 double
aux 1x2 16 double
b 2x1 16 double
c 2x2 32 double
d 1x2 16 double
e 2x2 32 double
f 1x2 16 double
t 1x151 1208 double
x 1x2 16 double
y 1x151 1208 double
y2 1x151 1208 double
>> figure; plot(t,y,'b--', t,y2,'m-') % Note já estamos mostrando 2 curvas com marcadores diferentes, cores diferentes e estilos de linha diferentes
Outra janela gráfica deve ter sido aberta mostrando 2 curvas.
Opções do comando plot()
help plot
<strong>plot</strong> Linear plot.
<strong>plot</strong>(X,Y) plots vector Y versus vector X. If X or Y is a matrix,
then the vector is plotted versus the rows or columns of the matrix,
whichever line up. If X is a scalar and Y is a vector, disconnected
line objects are created and plotted as discrete points vertically at
X.
<strong>plot</strong>(Y) plots the columns of Y versus their index.
If Y is complex, <strong>plot</strong>(Y) is equivalent to <strong>plot</strong>(real(Y),imag(Y)).
In all other uses of <strong>plot</strong>, the imaginary part is ignored.
Various line types, plot symbols and colors may be obtained with
<strong>plot</strong>(X,Y,S) where S is a character string made from one element
from any or all the following 3 columns:
b blue . point - solid
g green o circle : dotted
r red x x-mark -. dashdot
c cyan + plus -- dashed
m magenta * star (none) no line
y yellow s square
k black d diamond
w white v triangle (down)
^ triangle (up)
< triangle (left)
> triangle (right)
p pentagram
h hexagram
For example, <strong>plot</strong>(X,Y,'c+:') plots a cyan dotted line with a plus
at each data point; <strong>plot</strong>(X,Y,'bd') plots blue diamond at each data
point but does not draw any line.
<strong>plot</strong>(X1,Y1,S1,X2,Y2,S2,X3,Y3,S3,...) combines the plots defined by
the (X,Y,S) triples, where the X's and Y's are vectors or matrices
and the S's are strings.
For example, <strong>plot</strong>(X,Y,'y-',X,Y,'go') plots the data twice, with a
solid yellow line interpolating green circles at the data points.
The <strong>plot</strong> command, if no color is specified, makes automatic use of
the colors specified by the axes ColorOrder property. By default,
<strong>plot</strong> cycles through the colors in the ColorOrder property. For
monochrome systems, <strong>plot</strong> cycles over the axes LineStyleOrder property.
Note that RGB colors in the ColorOrder property may differ from
similarly-named colors in the (X,Y,S) triples. For example, the
second axes ColorOrder property is medium green with RGB [0 .5 0],
while <strong>plot</strong>(X,Y,'g') plots a green line with RGB [0 1 0].
If you do not specify a marker type, <strong>plot</strong> uses no marker.
If you do not specify a line style, <strong>plot</strong> uses a solid line.
<strong>plot</strong>(AX,...) plots into the axes with handle AX.
<strong>plot</strong> returns a column vector of handles to lineseries objects, one
handle per plotted line.
The X,Y pairs, or X,Y,S triples, can be followed by
parameter/value pairs to specify additional properties
of the lines. For example, <strong>plot</strong>(X,Y,'LineWidth',2,'Color',[.6 0 0])
will create a plot with a dark red line width of 2 points.
Example
x = -pi:pi/10:pi;
y = tan(sin(x)) - sin(tan(x));
plot(x,y,'--rs','LineWidth',2,...
'MarkerEdgeColor','k',...
'MarkerFaceColor','g',...
'MarkerSize',10)
See also <a href="matlab:help plottools">plottools</a>, <a href="matlab:help semilogx">semilogx</a>, <a href="matlab:help semilogy">semilogy</a>, <a href="matlab:help loglog">loglog</a>, <a href="matlab:help plotyy">plotyy</a>, <a href="matlab:help plot3">plot3</a>, <a href="matlab:help grid">grid</a>,
<a href="matlab:help title">title</a>, <a href="matlab:help xlabel">xlabel</a>, <a href="matlab:help ylabel">ylabel</a>, <a href="matlab:help axis">axis</a>, <a href="matlab:help axes">axes</a>, <a href="matlab:help hold">hold</a>, <a href="matlab:help legend">legend</a>, <a href="matlab:help subplot">subplot</a>, <a href="matlab:help scatter">scatter</a>.
<a href="matlab:doc plot">Documentation for plot</a>
<a href="matlab:matlab.internal.language.introspective.overloads.displayOverloads('plot')">Other functions named plot</a>
Modificando o gráfico anterior:
figure; plot(t,y,'bo--', t,y2,'ms-')
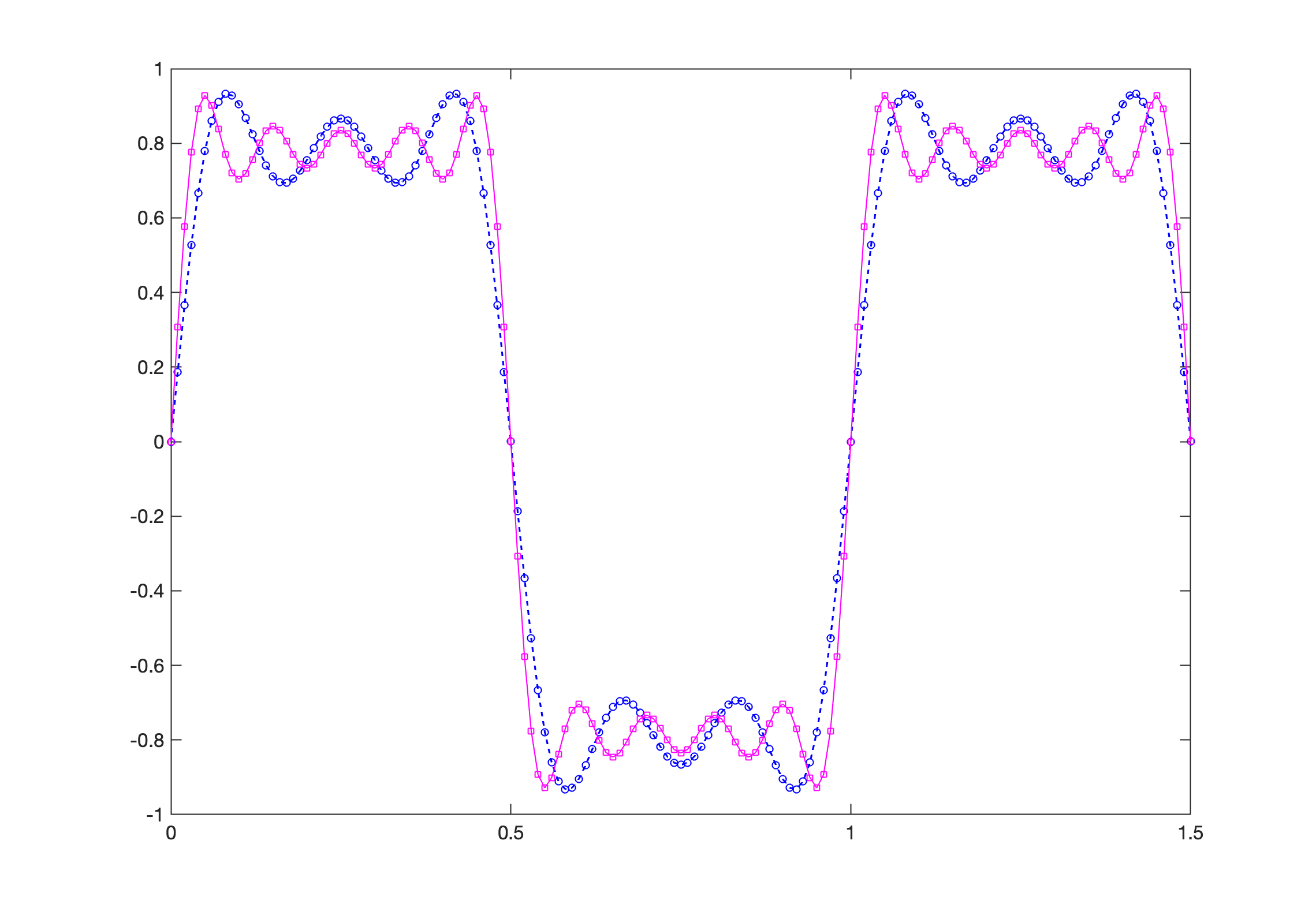
Salvando figuras para formato Markdown
Já que o Matlab está criando um arquivo texto em segundo plano, podemos aproveitar e incluir comandos que, para o Matlab não fazem sentido (são comentários), mas que podem fazer sentido para algum editor de arquivos compatível com Markdown.
Neste caso:
% comentário
% A linha abaixo gera uma figura em editores compatíveis markdown
% 
Num editor compatível Markdown, o comando anterior, faria aparecer a figura em questão:

Aprofundando conhecimentos em Markdown
Para os eventuais interessados em Markdown, recomenda-se:
-
Para aprender a programar equações usando LaTeX:
-
Introdução à Markdown: https://www.markdownguide.org
-
Editor free Markdown, sugestão: http://pad.haroopress.com
-
Outros editores compatÌveis com Markdown mas com mais/outras funções:
- Mapa mental: https://obsidian.md
- Notas: https://www.notion.so
Fim.
Fernando Passold, em 26/10/2023