Série de Fourier

A Série de Fourier é uma ferramenta matemática usada para decompor funções periódicas em uma soma de funções senoidais (seno e cosseno). Isso é especialmente útil em análise de sinais, processamento de imagem e outras áreas da engenharia e física. Essencialmente, qualquer função periódica pode ser expressa como uma soma infinita de senos e cossenos com frequências múltiplas da frequência fundamental da função.

Equações da Série de Fourier

A Série de Fourier para uma função periódica $f(t)$ com período $T$ é dada por:

$f(t) = a_0 + \displaystyle\sum_{n=1}^{\infty}\left[ a_n \cos\left( \dfrac{2\pi n t}{T} \right) + b_n \sin\left( \dfrac{2\pi n t}{T} \right) \right]$

Onde:

• $a_0$ é o coeficiente do valor médio (ou "nível DC");
• $a_n$ e $b_n$ são os coeficientes dos termos cossenoidais e senoidais, respectivamente.

Os coeficientes $a_n$ e $b_n$são calculados como:

$a_0=\dfrac{2}{T} \displaystyle\int_{0}^{T} f(t)dt$

$a_n=\dfrac{2}{T} \displaystyle\int_{0}^{T} f(t) \cos \left( \dfrac{2\pi n t}{T} \right)dt$

$b_n=\dfrac{2}{T} \displaystyle\int_{0}^{T} f(t) \sin \left( \dfrac{2\pi n t}{T} \right)dt$

A página da Wikipédia (em Português ou Inglês (mais completa)) traz como exemplo, os termos da Série para diferentes tipos de onda.

Mais informações também disponíveis em Controle 1/Sinais & Sistemas (Prof. Fernando Passold): Série de Fourier.

Exemplo: Onda Quadrada

Você também pode consultar a páginda da Wolfrgam MathWorld ou a página Wiki sobre Square wave ou a página da Swarthmore College (Dpto. de Engenharia).

Uma onda quadrada com ciclo de trabalho de 50% (ou seja, metade do tempo está em um nível alto e metade do tempo em um nível baixo) pode ser representada matematicamente como:

$\begin{cases}1 & \text{se } 0 < t < \frac{T}{2} \\-1 & \text{se } \frac{T}{2} < t < T\end{cases}$

Vamos calcular os coeficientes da Série de Fourier para essa função:

Coeficiente $a_0$:

$a_0=\dfrac{2}{T} \displaystyle\int_{0}^{T} f(t)dt = \dfrac{2}{T} \left( \int_{0}^{\frac{T}{2}} 1\, dt + \int_{\frac{T}{2}}^{T} -1 \, dt\right) = \dfrac{2}{T} \left( \dfrac{T}{2} - \dfrac{T}{2} \right) = 0$

Coeficientes $a_n$:

$a_n=\dfrac{2}{T} \displaystyle\int_{0}^{T} f(t) \cos \left( \dfrac{2\pi n t}{T} \right)dt$

Dividimos o intervalo em duas partes:

$a_n=\dfrac{2}{T}\left[ \displaystyle\int_{0}^{ \frac{T}{2} } \cos \left( \dfrac{2\pi n t}{T} \right)dt + \int_{\frac{T}{2}}^{T} - \cos \left( \dfrac{2\pi n t}{T} \right)dt \right]$

Devido à simetria da função cosseno:

$a_n=\dfrac{2}{T} \left( \left[ \dfrac{T}{2} \cdot \dfrac{ \sin \left( \dfrac{2\pi n t}{T} \right) }{ \dfrac{2\pi n}{T} } \right]_{0}^{ \frac{T}{2} } - \left[ \dfrac{T}{2} \cdot \dfrac{ \sin \left( \dfrac{2\pi n t}{T} \right) }{ \dfrac{2\pi n}{T} } \right]_{ \frac{T}{2} }^{T} \right) = 0$

Coeficientes $b_n$:

$b_n=\dfrac{2}{T} \displaystyle\int_{0}^{T} f(t) \sin \left( \dfrac{2\pi n t}{T} \right)dt$

Dividimos o intervalo em duas partes:

$b_n=\dfrac{2}{T}\left[ \displaystyle\int_{0}^{\frac{T}{2}} \sin \left( \dfrac{2\pi n t}{T} \right)dt + \int_{\frac{T}{2}}^{T} - \sin \left( \dfrac{2\pi n t}{T} \right)dt \right]$

Para a primeita integral temos:

$\displaystyle\int_{0}^{\frac{T}{2}} \sin \left( \dfrac{2\pi n t}{T} \right)dt = \left[ -\dfrac{T}{2\pi n} \cdot \cos \left( \dfrac{2\pi n t}{T} \right) \right]_{0}^{\frac{T}{2}} = -\dfrac{T}{2\pi n} \Big[ \cos (\pi n) - 1 \Big]$

Para a segunda integral teremos:

$\displaystyle\int_{0}^{\frac{T}{2}} \sin \left( \dfrac{2\pi n t}{T} \right)dt = \left[ -\dfrac{T}{2\pi n} \cdot \cos \left( \dfrac{2\pi n t}{T} \right) \right]_{\frac{T}{2}}^{T} = -\dfrac{T}{2\pi n} \Big[ \cos (2\pi n) - \cos(\pi n) \Big]$

Como $\cos(2\pi n)=1$ e $\cos(\pi n)=(-1)^n$, ficamos então com:

$b_n=\dfrac{2}{T}\left[ -\dfrac{T}{2\pi n}\Big( (-1)^n-1 \Big) + \dfrac{T}{2\pi n}\Big( 1 - (-1)^n \Big) \right]$

Para valores ímpares de $n$: o termo: $(-1)^n=-1$ e assim

o termo $b_n$ deixa de ser nulo apenas para valores ímpares de $n$:

$b_n=\dfrac{2}{T} \left[ -\dfrac{T}{2\pi n}(-2) + \dfrac{T}{2\pi n}(2) \right] = \dfrac{2}{T} \cdot \dfrac{2T}{2\pi n} = \dfrac{4}{\pi n}$

O termo $b_n$ deixa de ser nulo apenas para valores ímpares de $n$:

$b_n=\dfrac{4}{n\pi}$

Conclusão:

Portanto, a Série de Fourier de uma onda quadrada com ciclo de trabalho de 50% (que alterna entre $1$ e $-1$ com metade do período para cada nível) é:

$f(t)=\dfrac{4}{\pi} \sin\left( \dfrac{2\pi t}{T} \right) + \dfrac{4}{3\pi} \sin\left( \dfrac{6\pi t}{T} \right) + \dfrac{4}{5\pi} \sin\left( \dfrac{10\pi t}{T} \right) + \ldots$

Isso representa a decomposição da onda quadrada em uma soma infinita de senos com frequências ímpares múltiplas da frequência fundamental, ponderadas pelos coeficientes: $\dfrac{4}{n\pi}$.

Exemplo numérico

Seja uma onda quadrada, com duty-cycle = 50%, com amplitude $A$ e nível DC (offset) $=a_0$. Isto é, onda fica 50% do tempo na amplitude $y(t)=a_0+A$ e a outra metade do tempo na amplitude $y(t)=a_o-A$.

A Série de Fourier para esta onda quadrada, fica:

$y(t)=a_0+\displaystyle\sum_{n=1}^{\infty} a_n \cdot \sin(n\cdot 2\pi \cdot f \cdot t)$

Onde: $a_0=$ valor médio (nível DC) do sinal (vulgo "*offset"); $a_n=$ amplitude da harmônica $n$; $f=$ frequência original (fundamental) da onda (em Hz); $t=$ variável tempo (em segundos). $n=(i \cdot 2) + 1$, com $0<i<\infty$, onde $n=$ número da harmônica (resulta apenas valores ímpares); $i \subset \mathcal{Z}$.

A onda quadrada só possui compoenentes do seno e harmônicas Ímpares, com amplitudes:

$a_n=\dfrac{A}{n}$

Onde: $A=$ Amplitude de pico da onda quadrada;

Podemos ilustrar a síntese de uma onda quadrada usando Série de Fourier através de um código.

Código no Matlab:

% Onda quadrada usando série de Fourier
% Fernando Passold, em 28/05/2024
​
fprintf('\nOnda quadrada usando série de Fourier\n\n');
f = input("Freq. da onda em Hz: ? ");
T = 1/f;
ciclos = 2;
fs = 100*f;     % 100 pts por ciclo da onda original
t_fim = ciclos*T;
t = 0:1/fs:t_fim;   % cria vetor tempo t[k]. incremento T=1/fs (valores em segundos)
amostras = length(t);
​
A = input('Amplitude: ? ');
a0 = input('Nível DC: ? ');
​
h = input("Até que harmônica: ? ");
​
y = zeros(amostras,1);  % inicializa vetor y[k]
handler=figure;
Freq=0:f:f*h;     % Freq de cada harmônica (em Hz)
Mag=zeros(1,length(Freq));  % Mag de cada harmômica (em Volts)
Freq(1)=0;
Mag(1)=a0;
y = a0*ones(1,amostras);     % inicializa y[k]=nível DC;
fprintf('Pausado na harmônica:\n');
fprintf('n=  0');
for n=1:h     % incremento 2: onda quadrada só harmônicas ímpares
    % Deterctando se harmônica n atual é ìmpar:
    Mag(n+1)=0;
    maior=max(Mag);
    if mod(n,2)>0
        Mag(n+1)=A/n;
        y=y+(A/n)*sin(n*2*pi*f.*t);
        figure(handler)
        subplot(2,1,1)
        plot([0 t_fim], [a0 a0], 'c--', t,y, 'b-', 'LineWidth', 2)
        xlabel('Tempo (segundos)');
        ylabel('Amplitude (Volts)');
        title('Série Fourier Onda Quadrada');
        xlim([0 t_fim])
        subplot(2,1,2)
        stem(Freq, Mag, 'LineWidth', 2, 'MarkerSize', 8);
        xlabel('Frequência (Hz)');
        ylabel('Amplitude (Volts)');
        title('Componentes do Espectro');
        texto=['Harmônicas = ' num2str(n)];
        text(0.7*h*f, maior*0.75, texto, 'FontSize', 14)
        %        12123
        fprintf('\b\b\b\b\b');  % retrocede apagando 5 espaços.
        fprintf('n=%3i', n);
        pause
    end
end
fprintf('\n\t\tFreq\t\tMag\t\tMag(dB)\n');
disp([Freq' Mag' 20*log10(Mag)'])
fprintf('Fim\n');
    

Exemplo de execução:

>> onda_quadrada
​
Onda quadrada usando série de Fourier
​
Freq. da onda em Hz: ? 1000
Amplitude: ? 2.5
Nível DC: ? 2.5
Até que harmônica: ? 25
Pausado na harmônica:
n= 25
        Freq        Mag     Mag(dB)
            0          2.5       7.9588
         1000          2.5       7.9588
         2000            0         -Inf
         3000      0.83333      -1.5836
         4000            0         -Inf
         5000          0.5      -6.0206
         6000            0         -Inf
         7000      0.35714      -8.9432
         8000            0         -Inf
         9000      0.27778      -11.126
        10000            0         -Inf
        11000      0.22727      -12.869
        12000            0         -Inf
        13000      0.19231       -14.32
        14000            0         -Inf
        15000      0.16667      -15.563
        16000            0         -Inf
        17000      0.14706       -16.65
        18000            0         -Inf
        19000      0.13158      -17.616
        20000            0         -Inf
        21000      0.11905      -18.486
        22000            0         -Inf
        23000       0.1087      -19.276
        24000            0         -Inf
        25000          0.1          -20
Fim
>> 

Gráfico animado:

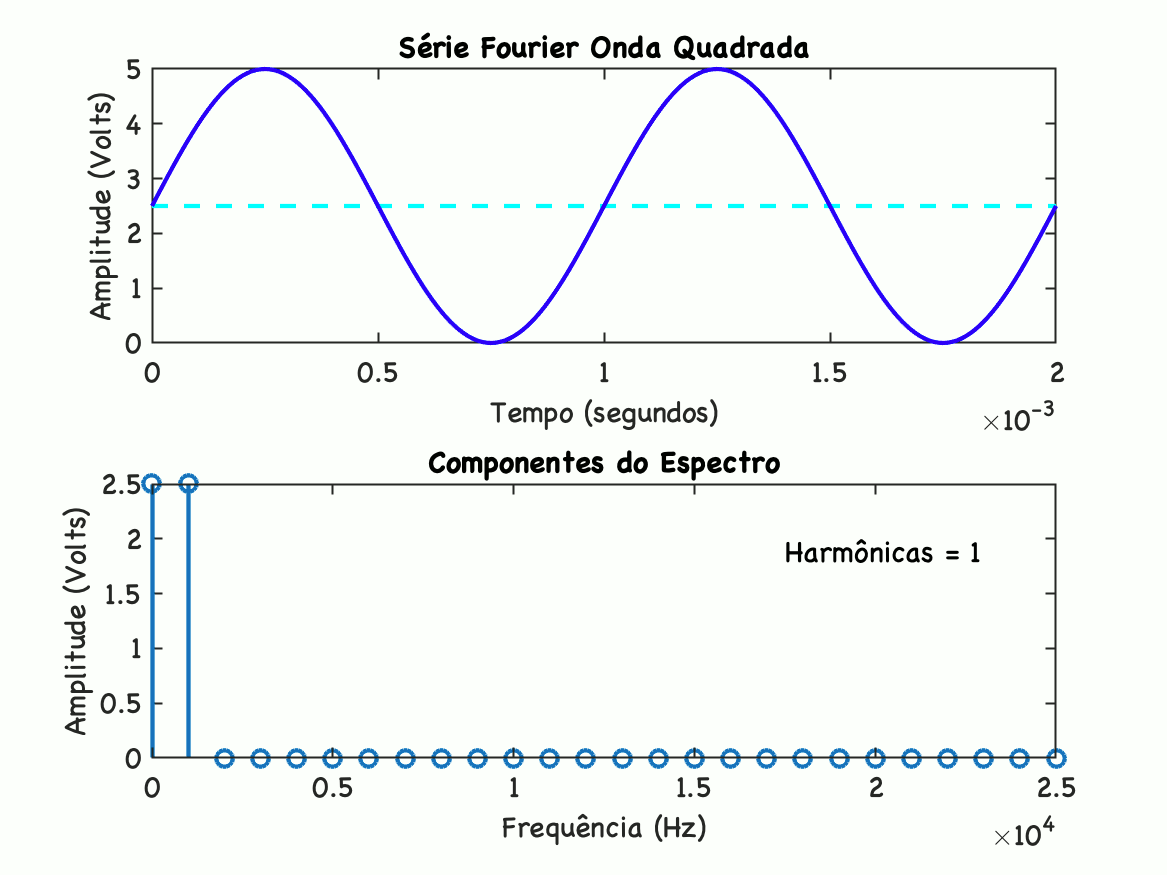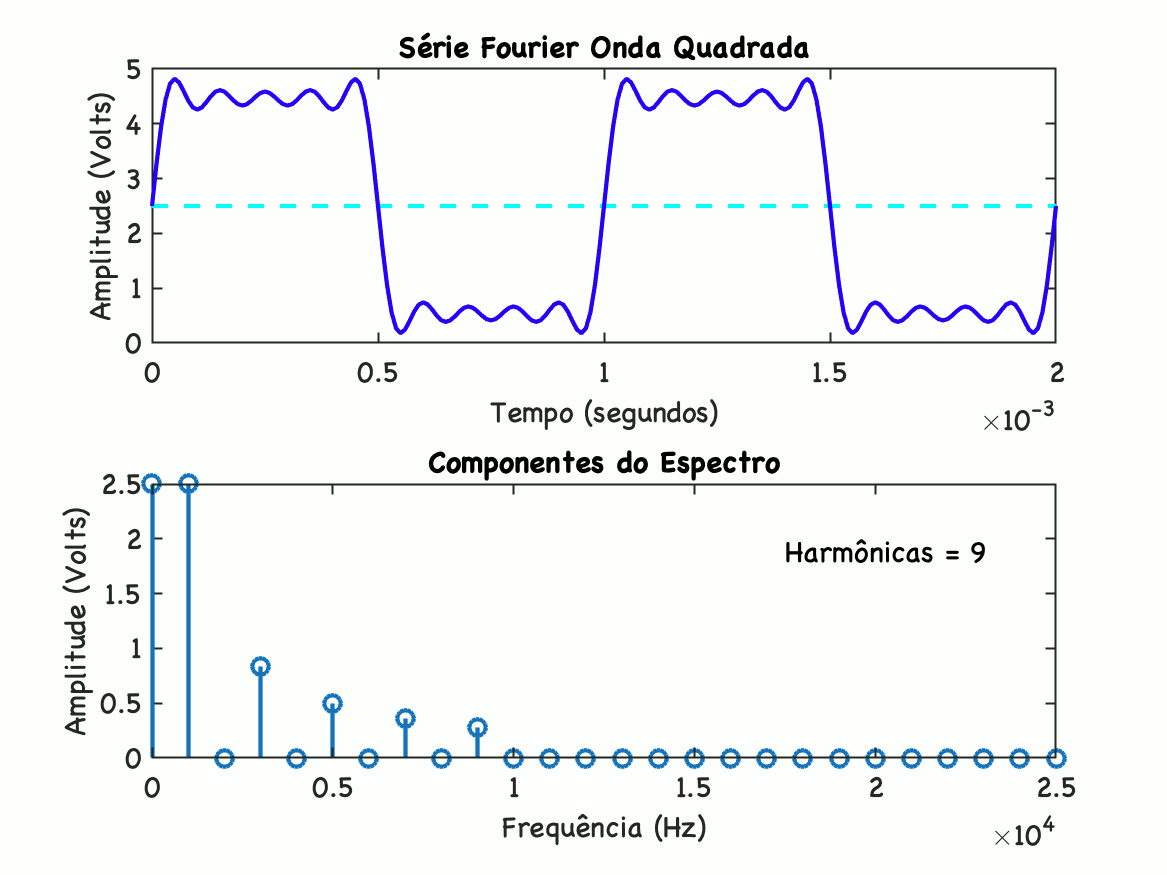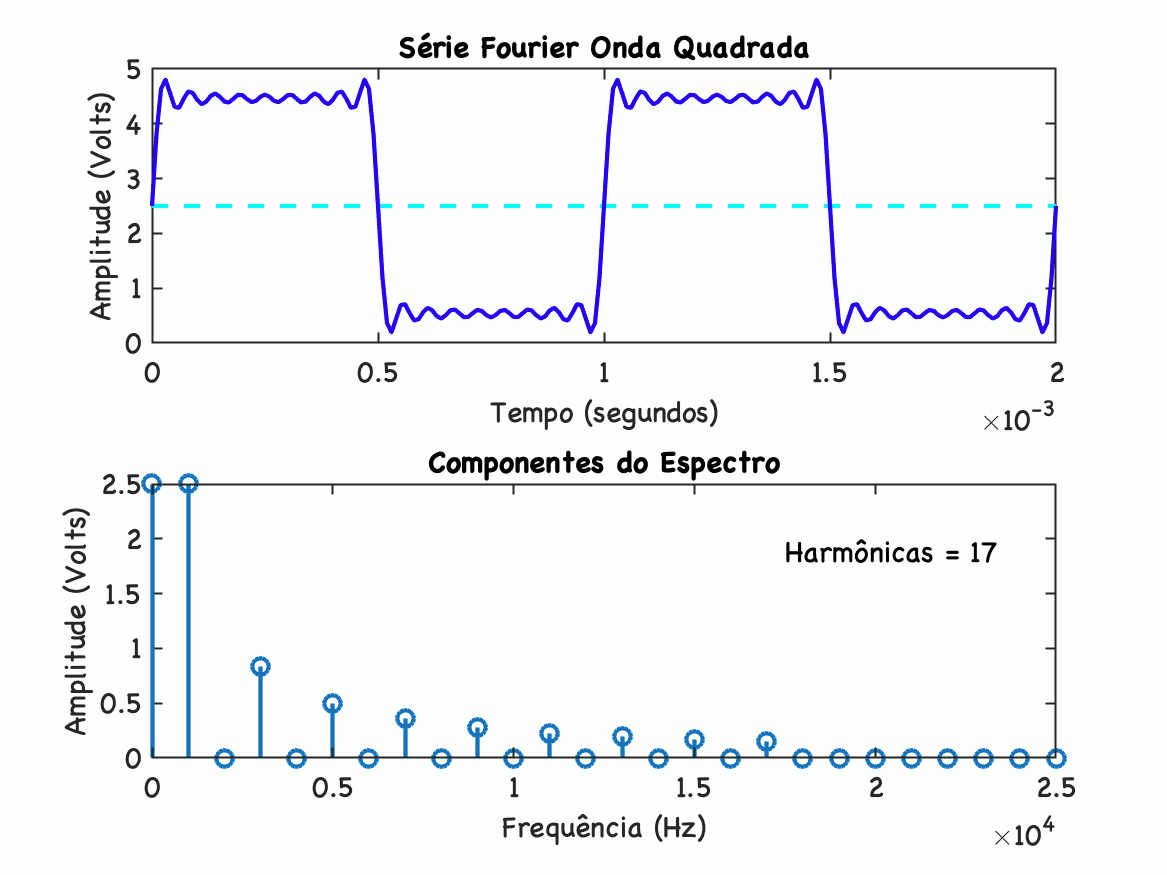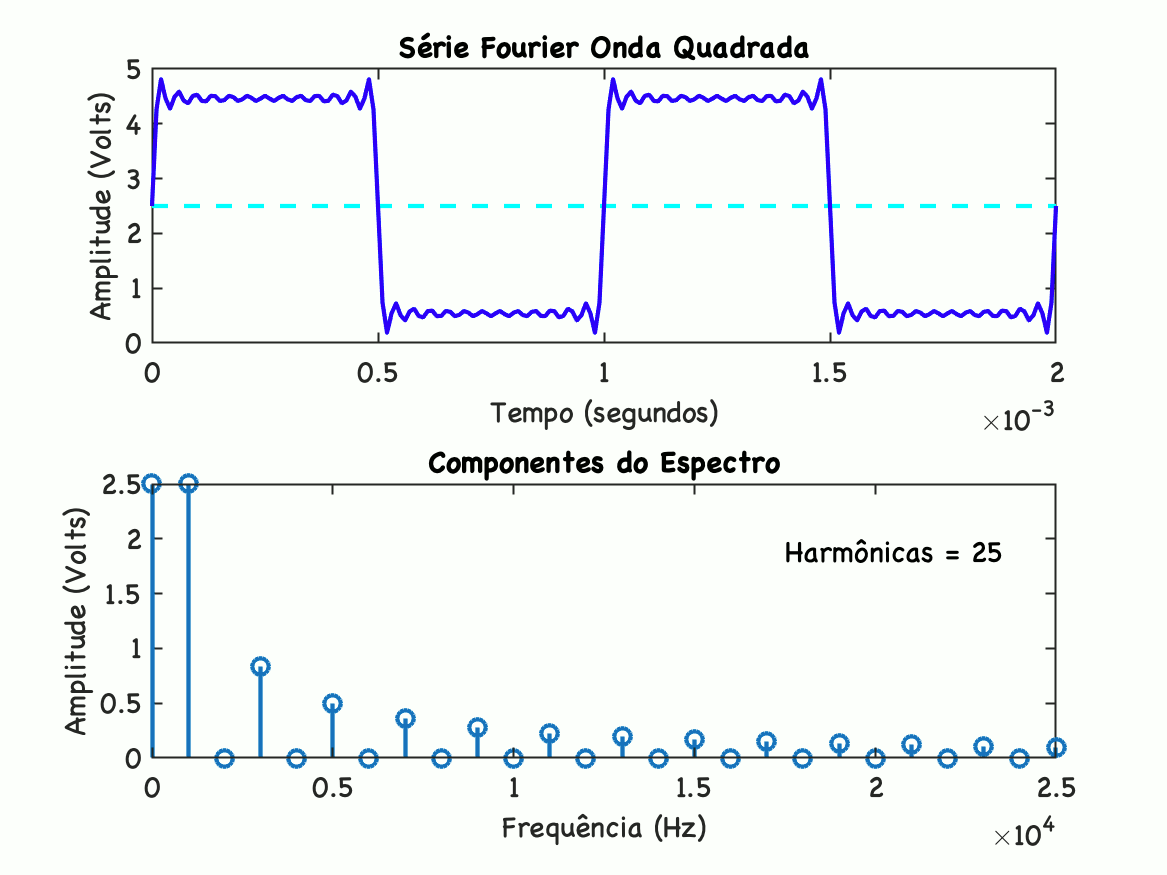
Note que o gráfico acima é dividido em 2 seções. A superior mostra a síntese da onda somando os varios componentes sentidas. A seção inferior, mostra o espectro de frequência da onda. A medida que mais senóides (mais harmônicas) são acrescentas à onda, cada onda seguindo determinada amplitude, mais a onda sintetizada se aproximada da onda desejada original. Note que o amplitude na frequência 0 (zero) (seção inferior), corresponde ao nível DC do sinal.