Uso do Octave

• Uso do Octave
  • Instalação do Octave
  • Primeiro Teste
  • Instalando pacotes (comandos extras)
  • Para listar pacotes já instalados
    • Pacotes Interessantes para nosso caso de uso
  • Para instalar pacotes
    • Pacotes mínimos para área de Controle
  • Novidades no pacote Control
  • Atualizando pacotes já instalados
  • Executando o pacote "control"
  • Exemplo de Uso: Projeto de um Controlador Proporcional
    • Outras funções do Octave

---

Instalação do Octave

O Octave pode ser obtido à partir de: https://octave.org/download.html.

No Windows, o arquivo de instalação ocupa 364 MB na versão 7.2.0. Porém, depois de instalado (descompactado), e acrescentado os pacotes que necessitaremos para trabalhar na área de controle, o Octave passa a ocupar aproximadamente 2,17 GBytes.

No Linux/Ubuntu, a versão snap do Octave 7.2.0 uma vez instalado (sem nenhum pacote extra) ocupa aproximadamente 345 Mbytes. Mas, diferente da versão para Windows, no Linux/Ubuntu, cada pacote (comandos/funções) extras deve se instalado à mão conforme se mostra à seguir e então, o espaço ocupado em disco aumenta.

Segue um janela de comandos comum do Octave:

Primeiro Teste

Vamos tentar imprimir um simples gráfico:

>> t=0:0.01:2;                  % cria vetor tempo
>> pi                           % constante pi
ans = 3.1416
>> y=2*sin(2*pi*1*t);           % cria onda senoidal 1 Hz
>> % suponha um FPB com fc = 1 Hz, queda de 3 dB em 1 Hz:
>> G=10^(-3/20)                 % calculando "ganho" do FPB
G = 0.7079
>> y2=G*2*sin(2*pi*1*t-pi/4);   % senóide de saída, defasagem de 45 graus
>> plot(t,y, t,y2)              % plotando 2 curvas
>> legend('Input', 'Output')    % legenda

Se não houve erros de digitação, uma janela gráfica como a mostrada abaixo deve ter sido gerada:

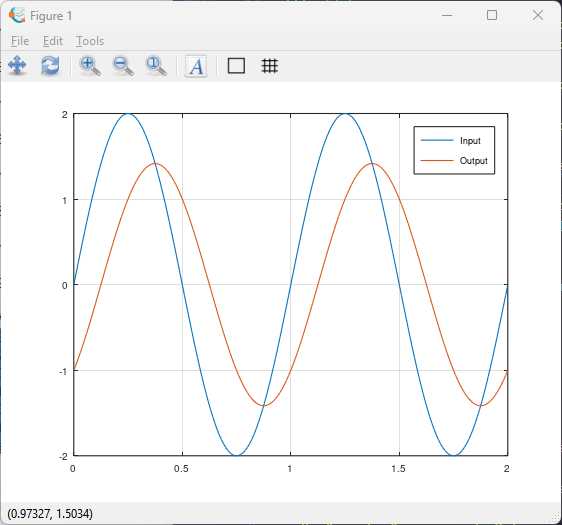
Instalando pacotes (comandos extras)

De forma a ampliar as possibilidades de uso do Octave com a área de Controle Automático, se sugere a instalação de algumas ferramentas extras, chamadas de "pacotes".

Os "pacotes" no caso do Octave, são equivalentes aos "toolboxes" no caso do Matlab.

Para listar pacotes já instalados

Para listar pacotes já instalados no Octave, fazer:

>> pkg list
Package Name         | Version | Installation directory
---------------------+---------+-----------------------
              audio  |   2.0.5 | C:\Program Files\GNU Octave\Octave-7.2.0\mingw64\share\octave\packages\audio-2.0.5
             biosig  |   2.4.2 | C:\Program Files\GNU Octave\Octave-7.2.0\mingw64\share\octave\packages\biosig-2.4.2
     communications  |   1.2.4 | C:\Program Files\GNU Octave\Octave-7.2.0\mingw64\share\octave\packages\communications-1.2.4
            control  |   3.4.0 | C:\Users\fpassold\AppData\Roaming\octave\api-v57\packages\control-3.4.0
     data-smoothing  |   1.3.0 | C:\Program Files\GNU Octave\Octave-7.2.0\mingw64\share\octave\packages\data-smoothing-1.3.0
           database  |   2.4.4 | C:\Program Files\GNU Octave\Octave-7.2.0\mingw64\share\octave\packages\database-2.4.4
...

Repare que eventualmente alguns pacote já estão instalados (caso do Windows). Entre eles o "control" A lista acima é maior, mas apenas uma parte foi mostrada.

Pacotes Interessantes para nosso caso de uso

No nosso caso estamos interessados nos pacotes:

• control
• data-smoothing
• fits
• generate_html
• geometry
• miscellaneous
• symbolic
• signal

Para instalar pacotes

Para descobrir que pacotes estão disponíveis (e versão dos mesmos):

>> pkg list -forge
Octave Forge provides these packages:
  arduino 0.10.0
  audio 2.0.5
  bim 1.1.5
  bsltl 1.3.1
  cgi 0.1.2
  communications 1.2.4
  control 3.4.0
  data-smoothing 1.3.0
  database 2.4.4
  dataframe 1.2.0
  dicom 0.5.1
  divand 1.1.2
  doctest 0.7.0
  econometrics 1.1.2
  fem-fenics 0.0.5
  financial 0.5.3
  fits 1.0.7
  fpl 1.3.5
  fuzzy-logic-toolkit 0.4.6
  ga 0.10.3
  general 2.1.2
  generate_html 0.3.3
  geometry 4.0.0
  gsl 2.1.1
  image 2.14.0
  image-acquisition 0.2.2
  instrument-control 0.8.0
  interval 3.2.1
  io 2.6.4
  level-set 0.3.0
  linear-algebra 2.2.3
  lssa 0.1.4
  ltfat 2.3.1
  mapping 1.4.2
  matgeom 1.2.3
  miscellaneous 1.3.0
  msh 1.0.10
  mvn 1.1.0
  nan 3.7.0
  ncarray 1.0.5
  netcdf 1.0.16
  nurbs 1.4.3
  ocl 1.2.0
  ocs 0.1.5
  octclip 2.0.1
  octproj 2.0.1
  optics 0.1.4
  optim 1.6.2
  optiminterp 0.3.7
  parallel 4.0.1
  quaternion 2.4.0
  queueing 1.2.7
  secs1d 0.0.9
  secs2d unknown
  secs3d 0.0.1
  signal 1.4.3
  sockets 1.4.0
  sparsersb 1.0.9
  splines 1.3.4
  statistics 1.4.3
  stk 2.7.0
  strings 1.3.0
  struct 1.0.18
  symbolic 3.0.1
  tisean 0.2.3
  tsa 4.6.3
  vibes 0.2.0
  video 2.0.2
  vrml 1.0.13
  windows 1.6.3
  zeromq 1.5.5
>>

Obs.: a listagem acima é resultado do Octave sendo executado no Windows.

Se for necessário instalar pacotes (caso do Linux), use o comando:

>> pkg install -forge <package_name>

A opção -forge carrega diretamente do repositório internet da Octave (obviamente exige conexão à internet).

Por exemplo:

>> pkg install -forge symbolic
For information about changes from previous versions of the symbolic package, run 'news symbolic'.
>>

Se você deseja instalar pacotes e acompanhar o processo de download e instalação, use a opção -verbose, mas isto pode gerar longas mensagens:

Por exemplo:

>> pkg install -forge -verbose control
mkdir (/tmp/oct-T38v9D)
untar (/tmp/control-3.4.0-RNDqAP.tar.gz, /tmp/oct-T38v9D)
checking for mkoctfile... /app/bin/mkoctfile-7.2.0 --verbose
checking for octave-config... /app/bin/octave-config-7.2.0
checking whether the C++ compiler works... yes
checking for C++ compiler default output file name... a.out
checking for suffix of executables...
checking whether we are cross compiling... no
checking for suffix of object files... o
checking whether we are using the GNU C++ compiler... yes
checking whether g++ accepts -g... yes
checking   is_real_type or isreal... isreal
checking   is_cell or iscell... iscell
checking   is_object or isobject... isobject
checking   is_complex_type or iscomplex... iscomplex
checking   is_numeric_type or isnumeric... isnumeric
checking for g77... no
checking for xlf... no
checking for f77... no
checking for frt... no
checking for pgf77... no
checking for cf77... no
checking for fort77... no

checking for pghpf... no
checking for epcf90... no
checking for gfortran... gfortran
checking whether we are using the GNU Fortran 77 compiler... yes
checking whether gfortran accepts -g... yes
checking for library containing dgges... no
configure: creating ./config.status
config.status: creating Makefile.conf
config.status: creating config.h
make: Entrando no diretório '/tmp/oct-T38v9D/control-3.4.0/src'

tar -xzf slicot.tar.gz
/app/bin/mkoctfile-7.2.0 --verbose -Wall -Wno-deprecated-declarations  __control_helper_functions__.cc
g++ -c -I/app/include -fPIC -I/app/include/octave-7.2.0/octave/.. -I/app/include/octave-7.2.0/octave -I/app/include  -pthread -fopenmp -O2 -g -pipe -Wp,-D_FORTIFY_SOURCE=2 -fexceptions -fstack-protector-strong -grecord-gcc-switches  -Wall -Wno-deprecated-declarations   __control_helper_functions__.cc -o /tmp/oct-PTj2gZ.o
mkdir sltmp
mv slicot/src/*.f ./sltmp
mv slicot/src_aux/*.f ./sltmp
if [ "0" = "1" ]; then \
        echo "copy routines using DGGES"; \
        cp SB04OD.fortran ./sltmp/SB04OD.f; \
        cp SG03AD.fortran ./sltmp/SG03AD.f; \
        cp SG03BD.fortran ./sltmp/SG03BD.f; \
fi;
cp AB08NX.fortran ./sltmp/AB08NX.f
cp AG08BY.fortran ./sltmp/AG08BY.f
cp SB01BY.fortran ./sltmp/SB01BY.f
cp SB01FY.fortran ./sltmp/SB01FY.f

gfortran -c -fPIC -g -O2 -std=legacy     UD01MZ.f -o UD01MZ.o
gfortran -c -fPIC -g -O2 -std=legacy     UD01ND.f -o UD01ND.o
gfortran -c -fPIC -g -O2 -std=legacy     UE01MD.f -o UE01MD.o
ar -rc slicotlibrary.a ./sltmp/*.o
rm -rf sltmp slicot
LDFLAGS="-L/app/lib  -lopenblas  -L/app/lib -L/usr/lib/gcc/x86_64-unknown-linux-gnu/11.3.0 -L/usr/lib/gcc/x86_64-unknown-linux-gnu/11.3.0/../../../x86_64-linux-gnu -L/usr/lib/gcc/x86_64-unknown-linux-gnu/11.3.0/../../../../lib64 -L/lib/x86_64-linux-gnu -L/lib/../lib64 -L/usr/lib/x86_64-linux-gnu -L/usr/lib/../lib64 -L/usr/lib/gcc/x86_64-unknown-linux-gnu/11.3.0/../../../../x86_64-unknown-linux-gnu/lib -L/usr/lib/gcc/x86_64-unknown-linux-gnu/11.3.0/../../.. -lgfortran -lm -lquadmath" \
    /app/bin/mkoctfile-7.2.0 --verbose -Wall -Wno-deprecated-declarations  __control_slicot_functions__.cc common.cc slicotlibrary.a
g++ -c -I/app/include -fPIC -I/app/include/octave-7.2.0/octave/.. -I/app/include/octave-7.2.0/octave -I/app/include  -pthread -fopenmp -O2 -g -pipe -Wp,-D_FORTIFY_SOURCE=2 -fexceptions -fstack-protector-strong -grecord-gcc-switches  -Wall -Wno-deprecated-declarations   __control_slicot_functions__.cc -o /tmp/oct-2fVEiL.o
g++ -c -I/app/include -fPIC -I/app/include/octave-7.2.0/octave/.. -I/app/include/octave-7.2.0/octave -I/app/include  -pthread -fopenmp -O2 -g -pipe -Wp,-D_FORTIFY_SOURCE=2 -fexceptions -fstack-protector-strong -grecord-gcc-switches  -Wall -Wno-deprecated-declarations   common.cc -o /tmp/oct-x9Eujr.o
g++ -I/app/include/octave-7.2.0/octave/.. -I/app/include/octave-7.2.0/octave -I/app/include  -pthread -fopenmp -O2 -g -pipe -Wp,-D_FORTIFY_SOURCE=2 -fexceptions -fstack-protector-strong -grecord-gcc-switches  -Wall -Wno-deprecated-declarations -o __control_slicot_functions__.oct  /tmp/oct-2fVEiL.o /tmp/oct-x9Eujr.o  slicotlibrary.a  -shared -Wl,-Bsymbolic -L/app/lib  -lopenblas  -L/app/lib -L/usr/lib/gcc/x86_64-unknown-linux-gnu/11.3.0 -L/usr/lib/gcc/x86_64-unknown-linux-gnu/11.3.0/../../../x86_64-linux-gnu -L/usr/lib/gcc/x86_64-unknown-linux-gnu/11.3.0/../../../../lib64 -L/lib/x86_64-linux-gnu -L/lib/../lib64 -L/usr/lib/x86_64-linux-gnu -L/usr/lib/../lib64 -L/usr/lib/gcc/x86_64-unknown-linux-gnu/11.3.0/../../../../x86_64-unknown-linux-gnu/lib -L/usr/lib/gcc/x86_64-unknown-linux-gnu/11.3.0/../../.. -lgfortran -lm -lquadmath  -L/app/lib -shared -Wl,-Bsymbolic  -L/app/lib -Wl,-z,relro,-z,now -Wl,--as-needed
make: Saindo do diretório '/tmp/oct-T38v9D/control-3.4.0/src'

copyfile /tmp/oct-T38v9D/control-3.4.0/src/__control_helper_functions__.oct /tmp/oct-T38v9D/control-3.4.0/src/__control_slicot_functions__.oct /tmp/oct-T38v9D/control-3.4.0/inst/x86_64-pc-linux-gnu-api-v57
For information about changes from previous versions of the control package, run 'newscontrol'.
>>

Pacotes mínimos para área de Controle

Os pacotes mínimos necessários para a área de Controle Automático Clássico aparecem listados abaixo:

>> ver
----------------------------------------------------------------------
GNU Octave Version: 7.2.0 (hg id: 6c1e310b2230)
GNU Octave License: GNU General Public License
Operating System: Linux 5.15.0-56-generic #62-Ubuntu SMP Tue Nov 22 19:54:14 UTC 2022 x86_64
----------------------------------------------------------------------
Package Name  | Version | Installation directory
--------------+---------+-----------------------
     control *|   3.4.0 | .../.var/app/org.octave.Octave/data/octave/api-v57/packages/control-3.4.0
      signal *|   1.4.3 | .../.var/app/org.octave.Octave/data/octave/api-v57/packages/signal-1.4.3
    symbolic *|   3.0.1 | .../.var/app/org.octave.Octave/data/octave/api-v57/packages/symbolic-3.0.1
>>

Novidades no pacote Control

>> news control

Alguns destaques:

• Declare tf([1],[1]) as static gain
• Returned num and den of tfdate have same length (bug #43947)
• Fixes for Octave 7.1.0: removed deprecated .+ operator and unsupported plot style
• Fixed time response for first order systems
• new function rlocusx providing gain, damping and frequency for selected poles together with the possibility to generate open loop bode plots and simulations of the closed loop for selected closed loop poles.
• Fixed several issues in bode, c2d, lsim and step (control-3.3.0, Release Date: 2021-06-19).
• Fixed issues in legends of time and frequency responses when requested for multiple systems.
• Added discretization method foh to c2d.
• Fixed transposing a tfploy.
• new function sgrid (control-3.2.0, Release Date: 2019-04-01)
• new function: ss2ss.
• added demos to rlocus, pzmap, bode, nichols, nyquist, impulse, lsim, ramp and step.
• improved pzmap to plot with only zeros.
• New function: damp (control-3.1.0, Release Date: 2018-03-11).
• The new function imp_invar.m converts a Laplace tranfer function to a discrete tranfer function.
• Function lsim now plots inputs as well.

Atualizando pacotes já instalados

De vez em quando pode ser interessante atualizar os pacotes já instalados. Para tanto, simplesmente execute:

>> pkg update

>> pkg update
For information about changes from previous versions of the netcdf package, run 'news netcdf'.
For information about changes from previous versions of the symbolic package, run 'news symbolic'.
For information about changes from previous versions of the windows package, run 'news windows'.
>>

Obs.: usar a opção "global" apenas se deseja aplicar alterações à todos os usuários e se tiver permissão (estiver executando o Octave como) de administrador para acessar/alterar arquivos de instalação, senão ocorrerão erros!

Executando o pacote "control"

Informações adicionais sobre este pacote podem ser encontradas em:

• https://octave.sourceforge.io/control/#:~:text=Octave Forge is a collection of packages providing,Design. Latest package release. Version. 3.2.0. Date. 2019-04-01. (Sept/2022).

• ou https://octave.sourceforge.io/control/index.html;

• ou https://octave.sourceforge.io/control/overview.html.

Segue lista das funções mais utilizadas:

Obs.: ANTES de chamar qualquer função associado a este pacote, você deve "carregar" este pacote executando comandos como:

>> pkg load control
>> pkg load symbolic
>>

Segue exemplo de ingresso de uma "transfer function" (função transferência):

objeto tf, exemplo de uso:

>> s = tf('s');
>> G = 1/(s+1)
>> z = tf('z', tsam);
>> z = tf('z', 0.2);
>> Gd = 0.095/(z-0.9)
>> sys = tf (num,den);
>> G = tf([1, 5, 7], [1, 8, 6])
>> sys = tf (num,den,tsam);

Exemplo$_2$:

>> num=poly([0, -2])
num =
   1   2   0

>> den=poly([-1, -4, -8]);
>> G=tf(num,den)
Transfer function 'G' from input 'u1' to output ...

             s^2 + 2 s
 y1:  ------------------------
      s^3 + 13 s^2 + 44 s + 32

Continuous-time model.
>> zpk(G)
Transfer function 'ans' from input 'u1' to output ...

             s^2 + 2 s
 y1:  ------------------------
      s^3 + 13 s^2 + 44 s + 32

Continuous-time model.
>> % conferindo detalhes da função transferência:
>> pole(G)
ans =
  -8
  -4
  -1

>> zero(G)
ans =
  -2
   0
>> % de outra forma:
>> [z,p,k]=tf2zp(G)
z = [](0x1)
p =

  -10
   -4
   -1

k = 40
>>

Note: a função tf2zp() (disponível no pacote signal) permite obter um resultado simular ao que seria obtido usando a função zpk() do MATLAB

---

Exemplo de Uso: Projeto de um Controlador Proporcional

Seja uma planta como:

$$G(s)=\dfrac{40}{(s+1)(s+4)(s+10)}$$

O projeto de um controlador Proporcional com sobressinal máximo de 10% poderia ser desenvolvido como:

>> % Nâo esquecer de carregar certos pacotes:
>> pkg load control
>> pkg load symbolic
>> 
>> G=tf(40,poly([-1 -4 -10]))   % ingressando a planta

Transfer function 'G' from input 'u1' to output ...

                 40
 y1:  ------------------------
      s^3 + 15 s^2 + 54 s + 40

Continuous-time model.
>> pole(G)  % confirmando polos da planta
ans =

  -10
   -4
   -1

>> zero(G)  % confirmando zeros da planta
ans = [](0x1)
>> dcgain(G)    % confirmando ganho DC da planta
ans = 1
>> % Isto significa que um degrau de amplitude u(t)=1 na entrada da planta 
>> % faz saída convergir para y(∞)=1
>> % confirmando aplicando degrau unitário na planta:
>> step(G)

O que deve ter gerado o seguinte gráfico:

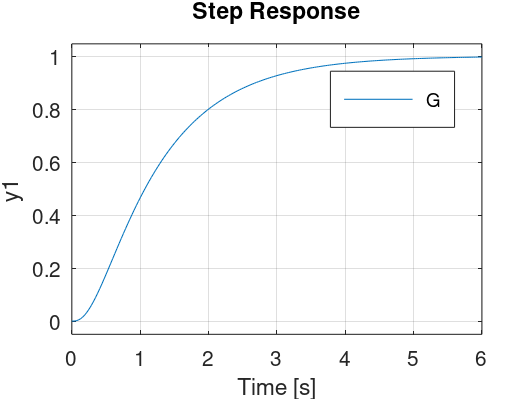
Temos que fechar a malha definindo um ganho para o controlador, evitando o sobressinal máximo desejado, então:

>> OS=10;   % valor do sobressinal em porcentagem
>> zeta=(-log(OS/100))/(sqrt(pi^2+(log(OS/100)^2)))
zeta = 0.5912
>> rlocus(G)
>> hold on;
>> sgrid(zeta,0)
error: sgrid: W argument (1) must have positive values larger than 0
error: called from
    sgrid at line 147 column 7
>> % sgrid obriga 2 parâmetros de entrada no mínimo

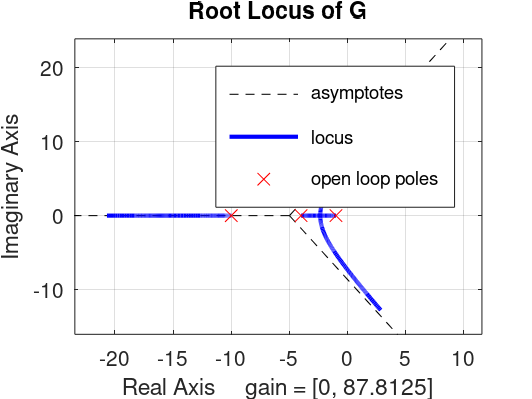
Mas podemos traçar uma reta axial que parte da origem do plano-s. Conhecendo-se o valor do $\zeta$ podemos determinar o ângulo $\alpha$, ver figura a seguir:

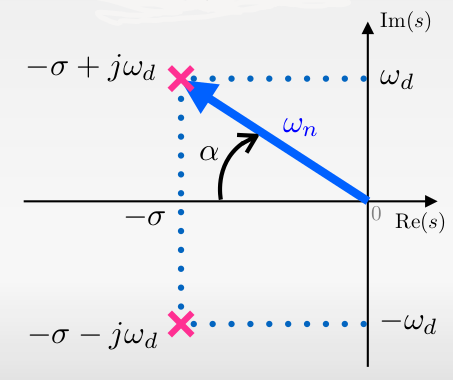
A figura anterior mostra polos de um sistema de 2a-ordem, do tipo:

$$\dfrac{Y(s)}{R(s)}=\dfrac{K}{(s+p_1)(s+p_2)}=K \left( \dfrac{\omega_n^2}{s^2+2\zeta\omega s + \omega_n^2} \right)$$

com polos em: $s=\sigma \pm j \omega_d$, onde:

$\sigma=\omega_n \zeta=\omega_n \cos(\alpha)$;
$\omega_d = \omega_n \sqrt{1-\zeta^2}=\omega_n \sin(\alpha)$;
$\zeta=\cos(\alpha)$;
$\sin(\alpha)=\sqrt{1-\zeta^2}$.

então: $\alpha=\arccos(\zeta)$

>> alpha=acos(zeta)
alpha = 0.9383
>> % convertendo para graus:
>> alpha_deg=alpha*180/pi
alpha_deg = 53.761

Podemos "automatizar" este cálculo e incluir os comandos para imprimir a reta correspondente a valores constantes de $\zeta$, criando uma nova função, neste caso, chamada de sgrid2(), cujo código aparece em seguinda:

function sgrid2 (zeta)
  % função para plotar linha guia do zeta na última janela gráfica ativa
  % a partir do valor de zetam calcula o angulo alpha e traça a reta
  % que corresponde a linha guia
  % Fernando Passold, em 29/12/2022
  alpha=acos(zeta); % angulo correspondente ao zeta
  % fig=gcf(); % descobre numero da última janela ativa atual - dá no mesmo que fazer:
  fig = get (0, "currentfigure"); % recupera número da última figura ativa
  % Capturando limite da figura atual
  xlim=get(gca(),"xlim");
  ylim=get(gca(),"ylim");
  min_x=min(xlim);
  x=[0 min_x]; % vetor pontos da reta
  y2=abs(min_x)*tan(alpha);
  y=[0 y2];
  hold on;
  plot(x,y,"color","cyan"); % ,"linestyle","--");
  % sobre propriedades de plot ver:
  % https://docs.octave.org/v6.3.0/Line-Properties.html
  y=[0 -y2];
  plot(x,y,"color","cyan");
  shg % show the graph window
  % Note: shg is equivalent to figure (gcf) assuming that a current figure exists.
end

O resultado da aplicação da mesma na figura anterior gera:

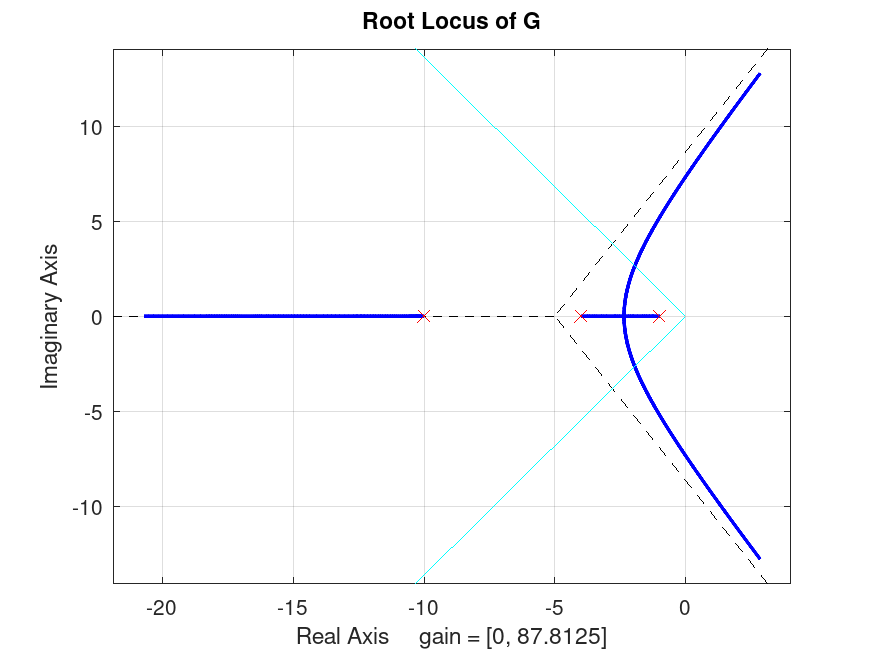
Podemos usar o comando >> legend off para sumir com o quadro que aparece junto a figura.

O Ocatve não possui uma função chamada rlocfind() como no caso do MATLAB, mas possui uma função similar: rlocusx().

No caso deste exemplo, resultaria em algo como:

>> figure; rlocusx(G)

O que acaba gerando uma figura como a mostrada à seguir:

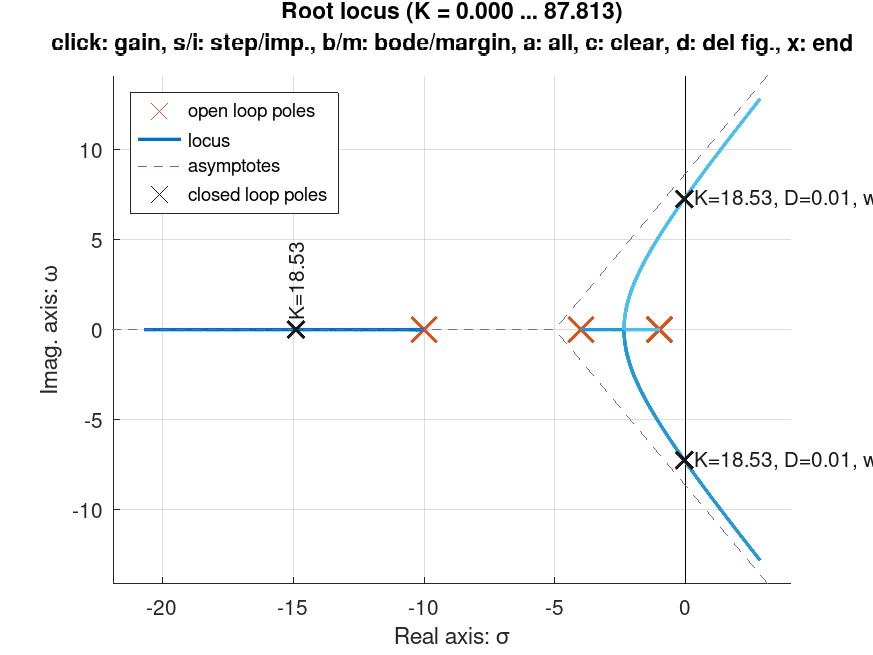
Mas note no exemplo anterior, que não foi possível imprimir uma linha guia para valores constantes de $\zeta$.

Note que rlocuxx() entretanto traz outras opções. Uma vez ingressado este comando, a janela gráfica entra em modo interativo aceitando os seguintes comandos (https://octave.sourceforge.io/control/function/rlocusx.html):

Tecla	Resultado
clique-esquerdo	mostra valor do ganho, polos de MF, $\zeta$ e $\omega_n$
s	"step" = Resposta ao degrau unitário para ganho no ponto escolhido
b	"bode" = Diagrama de Bode
m	"margin" = Diagrama de Bode com margens de estabilidade (ganho e fase)
a	"all" = Plota os 4 gŕaficos anteriores
c	"clear" = limpa todas as anotações já feitas
d	"delete" = apaga todas as figuras abertas
x	"eXit" = sair do modo interativo

Por exemplo, apontando mais de uma posição no RL, podemos obter uma figura como:

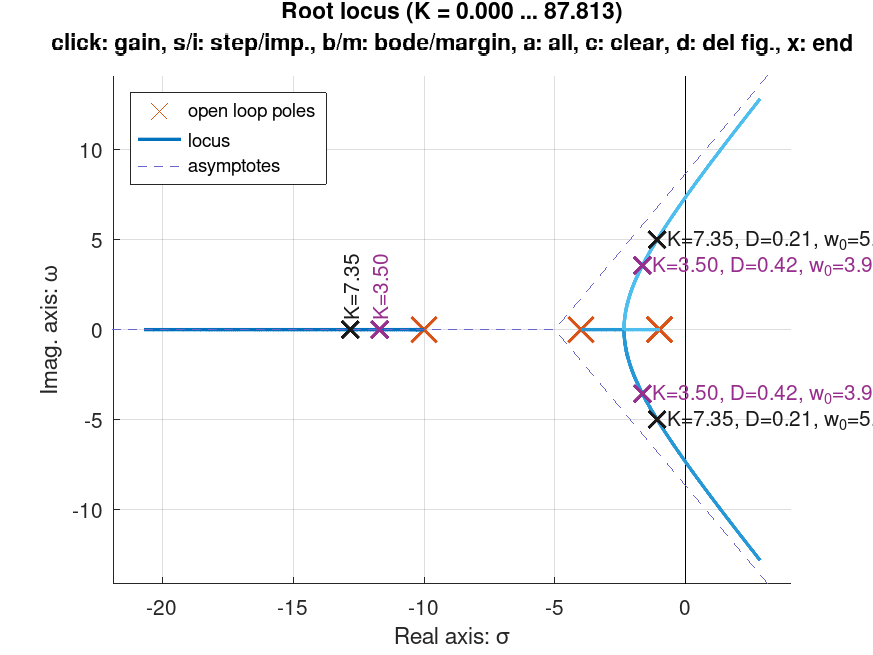
O diagrama de bode com as margens de ganho e de fase são mostradas na próxima figura:

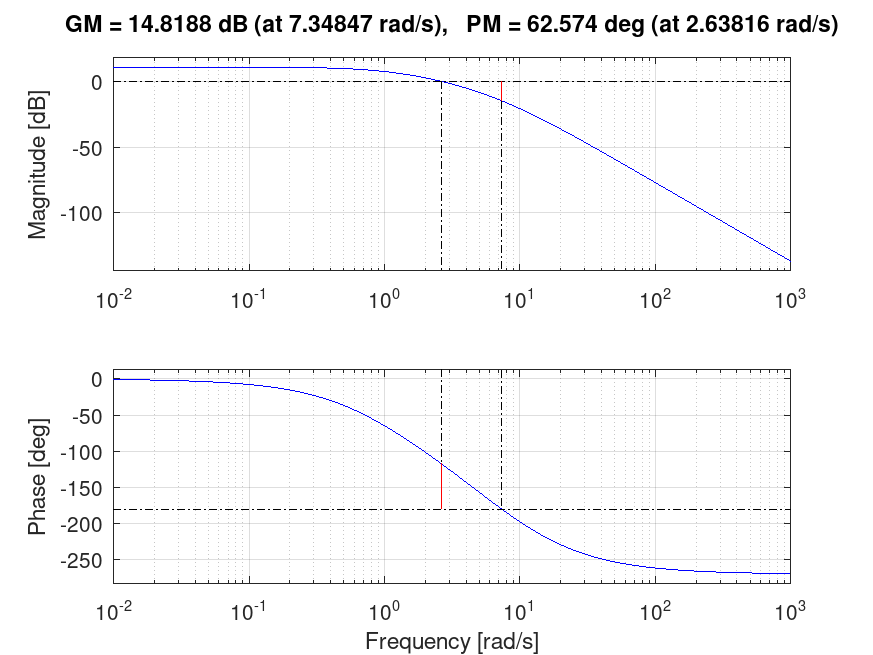
E a resposta à entrada degrau unitário para o ponto escolhido ($K=3,5$) fica:

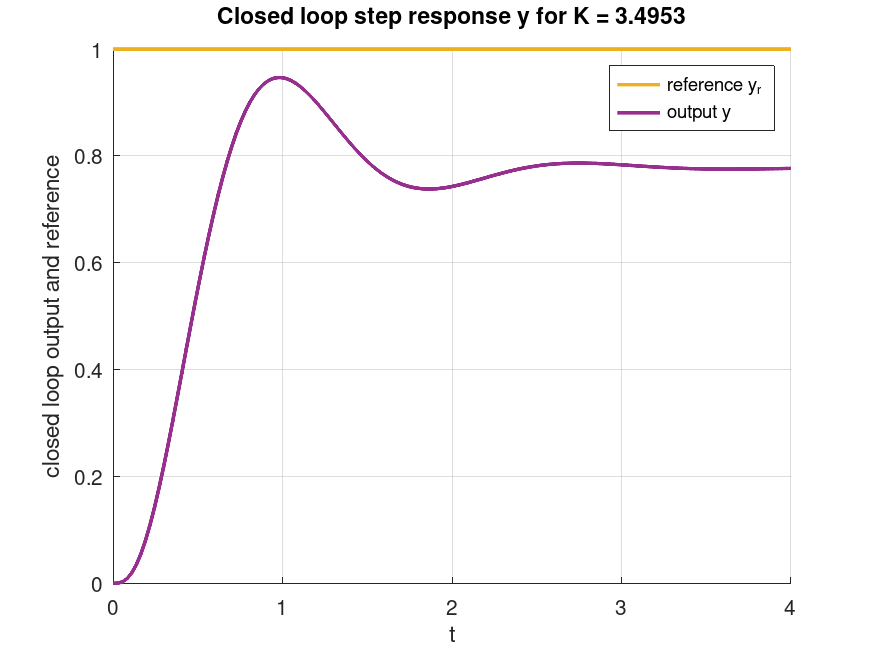
E clicamos "x" para sair do modo interativo e voltar para a janela de comandos do Octave.

A única limitação é que no RL mostrado, não aparece nenhuma linha guia referente a valores constantes de $\zeta$, o que dificulta um pouco a sintonia do controlador. Faltaria "combinar" a função rlocusx() com sgrid2()...

Mas podemos tentar descobrir o ponto no RL com $\zeta=0.5912$:

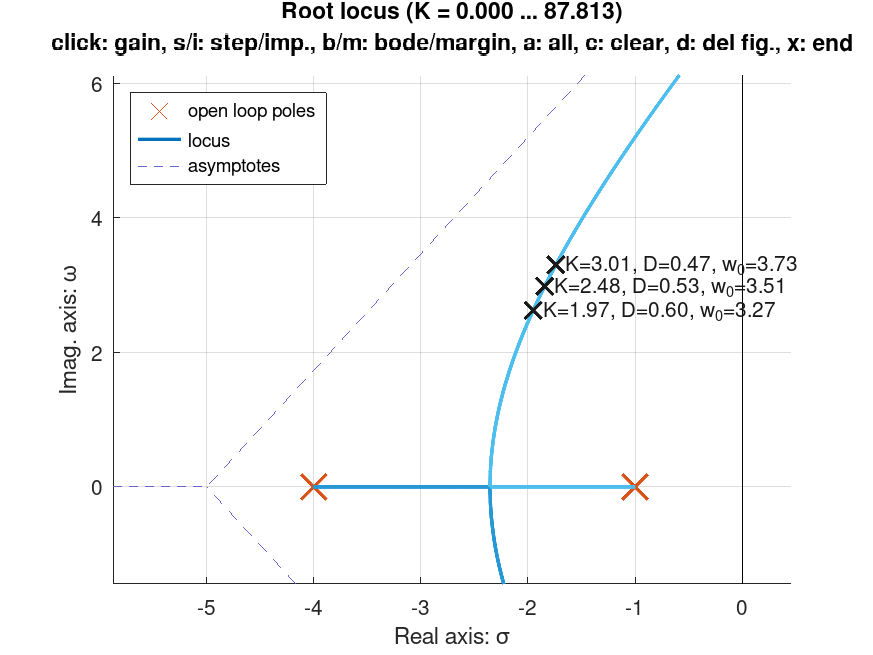
Encontramos um ganho aproximado de $K=1,97$ ($\zeta=0,6$).

Fechando a malha com $K=1,95$ vamos obter:

>> ftma=K*G

Transfer function 'ftma' from input 'u1' to output ...

                 78
 y1:  ------------------------
      s^3 + 15 s^2 + 54 s + 40

>> H=tf(1,1)

Transfer function 'H' from input 'u1' to output ...

 y1:  1

Static gain.
>> ftmf=feedback(ftma, H, -1)

Transfer function 'ftmf' from input 'u1' to output ...

                 78
 y1:  -------------------------
      s^3 + 15 s^2 + 54 s + 118

Continuous-time model.
>> % gráfico da resposta ao degrau:
>> figure; step(ftmf)
>>

E a seguinte figura é gerada:

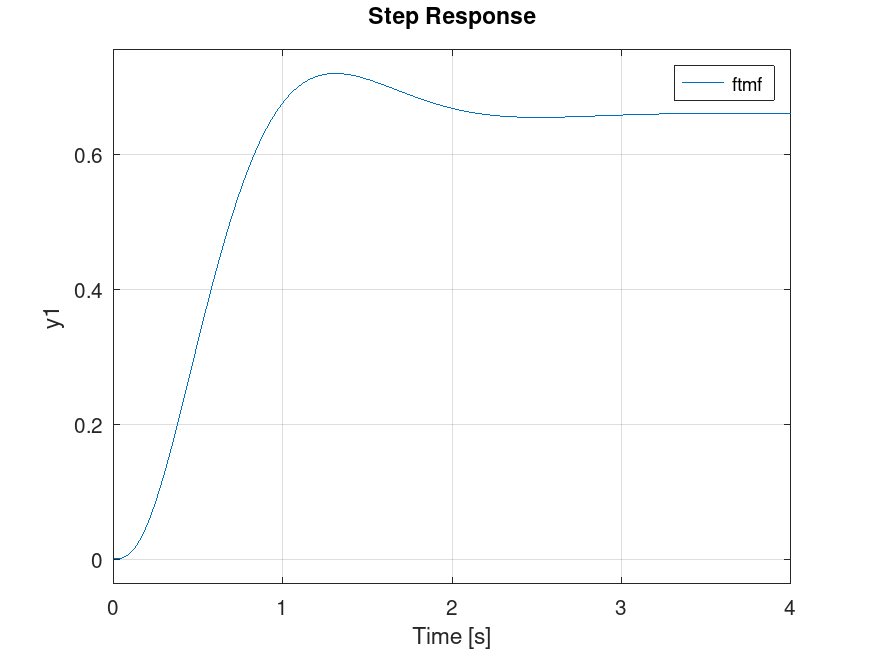
Percebemos um grande erro de regime permanente, $e(\infty)=33,9$:

>> dcgain(ftmf)
ans = 0.6610
>> erro=(1-dcgain(ftmf))/1*100
erro = 33.898
>>

Por curiosidade, usando este controlador e limitando o erro à 10%, teríamos que usar outro valor de ganho:

Lembrando da Teoria do Erro:

$$e_{\text{Step}}(\infty)=\lim_{s \to 0} s \, E(s) = \dfrac{1}{1+\lim_{s \to 0} FTMA(s)}=\dfrac{1}{1+K_p}$$

onde $K_p=$constante do erro estático de posição.

Neste caso, $e(\infty)=10\%=0,1$, então $K_p$ deveria assumir o valor:

$$\begin{array}{rcl} 0,1 &=& \dfrac{1}{1+K_p}\\ K_p &=& \dfrac{1-0,1}{0,1}=9 \end{array}$$

Calculando a constante $K_p$ para esta planta:

$$\begin{array}{rcl} \lim_{s \to 0} FTMA(s) &=& \lim_{s \to 0} \dfrac{K \cdot 40}{(s+1)(s+4)(s+10)}\\ &=& \dfrac{40 K}{(1)(4)(10)}\\ &=& K \end{array}$$

Então $K=K_p=9$. Testando:

>> ftma2=9*G

Transfer function 'ftma2' from input 'u1' to output ...

                360
 y1:  ------------------------
      s^3 + 15 s^2 + 54 s + 40

Continuous-time model.

>> % Conferindo detalhes da FTMA2(s):
>> [z,p,k]=tf2zp(ftma2)
z = [](0x1)
p =

  -10
   -4
   -1

k = 360
>>
>> ftmf2=feedback(ftma2, H, -1);
>> figure; step(ftmf2)
>>

E obtemos a resposta:

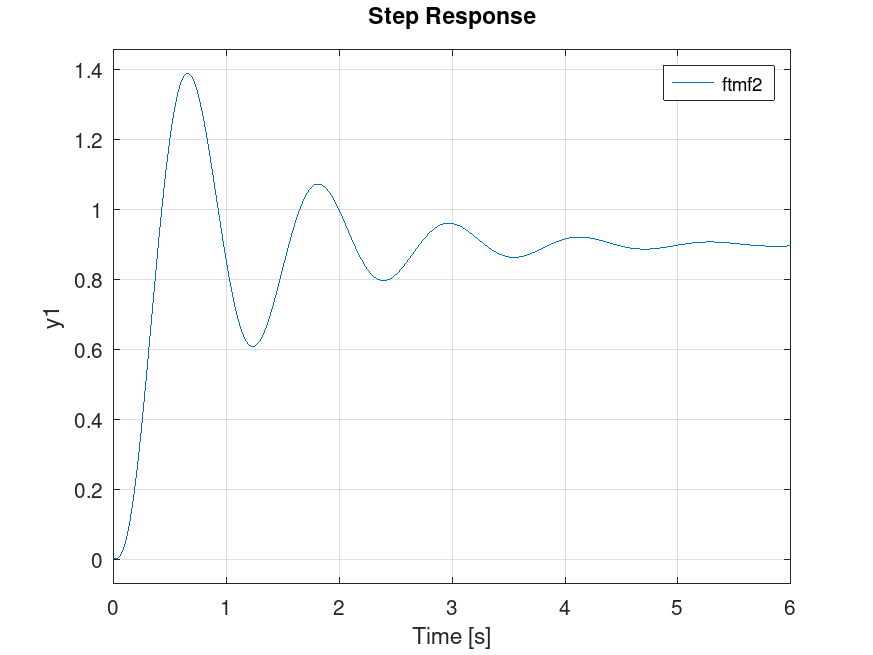
Faltaria obter informações sobre as características de resposta do sitema (função stepinfo() no MATLAB).

Outras funções do Octave

• Blocos em série: $G(s)=G_1(s) \cdot G_2(s)$ >> G = series(G1, G2)

• Blocos em paralelo: $G(s)=G_1(s)+G_2(s)$ >> G = parallel(G1, G2)

• Realimentação: $G(s)=\dfrac{G_1(s)}{1+G_1(s)G_2(s)}$ >> G = feedback(G1, G2, -1)

• Resíduos de uma função transferência: >> [r,p,k]=residue (num,den)

Exemplo: Seja a seguinte função transferência:

$$G(s)=\dfrac{4s+6}{2s^3+10s^2+16s+8}\qquad \text{eq. (1)}$$

supondo que esta função foi gerada à partir da eq. diferencial:

$$\dfrac{2\,d^3 y}{dt^3}+\dfrac{10\,d^2 y}{dt^2} + \dfrac{16\,dy}{dt} + 8y = \dfrac{4\,du}{dt}+6u$$

A expansão em frações parciais de (1), rende:

>> num=[4 6];
>> den=[2 10 16 8];
>> [r,p,k]=residue(num,den)
r =

  -1
   1
   1

p =

  -2
  -2
  -1

k = [](0x0)
>>

Resultado da expanção:

$$\begin{array}{rcl} G(s) &=& \dfrac{4s+6}{2s^3+10s^2+16s+8}\\ &=& - \dfrac{1}{(s+2)} + \dfrac{1}{(s+2)} - \dfrac{1}{(s+1)}\\ \end{array}$$

Lembrando da tabela de transformadas de Laplace:

$f(t)$	$F(s))$
$e^{at}$	$\dfrac{1}{s-a}$

vamos obter:

$$g(t)=-e^{-2t}+e^{-2t}+1e^{-t}$$

---

Fim