Média x Mediana

A diferença entre o valor médio (ou média) e a mediana está no modo como eles resumem um conjunto de dados:

• Valor médio (média aritmética): É a soma de todos os valores dividida pelo número total de valores. Ele é influenciado por valores extremos (outliers).

  $\text{Media} = \dfrac{\sum_{i=1}^{n} x_i}{n}$

• Mediana: É o valor central de um conjunto de dados ordenado. Se o número de dados for ímpar, a mediana é o valor do meio. Se for par, é a média dos dois valores centrais. A mediana é menos sensível a valores extremos.

Código Exemplo

Segue um exemplo de programa em C que gera números aleatórios, calcula a média e a mediana de um conjunto de dados:

​x
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
​
// Função de comparação para usar com qsort
int compare(const void *a, const void *b) {
    return (*(int*)a - *(int*)b);
}
​
// Função para calcular a média
double calcular_media(int arr[], int tamanho) {
    int soma = 0;
    for (int i = 0; i < tamanho; i++) {
        soma += arr[i];
    }
    return (double)soma / tamanho;
}
​
// Função para calcular a mediana
double calcular_mediana(int arr[], int tamanho) {
    // Ordenar o array
    qsort(arr, tamanho, sizeof(int), compare);
​
    if (tamanho % 2 == 0) {
        // Se o número de elementos for par, a mediana é a média dos dois valores centrais
        return (arr[tamanho / 2 - 1] + arr[tamanho / 2]) / 2.0;
    } else {
        // Se o número de elementos for ímpar, a mediana é o valor central
        return arr[tamanho / 2];
    }
}
​
int main() {
    int tamanho = 10;
    int valores[tamanho];
​
    // Inicializa a semente do gerador de números aleatórios
    srand(time(0));
​
    // Gera números aleatórios entre 0 e 100
    printf("Valores gerados: ");
    for (int i = 0; i < tamanho; i++) {
        valores[i] = rand() % 101;
        printf("%d ", valores[i]);
    }
    printf("\n");
​
    // Calcula e exibe a média
    double media = calcular_media(valores, tamanho);
    printf("Média: %.2f\n", media);
​
    // Calcula e exibe a mediana
    double mediana = calcular_mediana(valores, tamanho);
    printf("Mediana: %.2f\n", mediana);
​
    return 0;
}

Detalhes do código

1. Geração de valores aleatórios: O programa usa a função rand() para gerar números entre 0 e 100.
2. Média: A função calcular_media() soma todos os elementos e divide pelo número total de valores.
3. Mediana: A função calcular_mediana() ordena os valores com qsort() e, dependendo se o tamanho do array é ímpar ou par, calcula o valor central.
4. Saída: O programa imprime os valores gerados, a média e a mediana.

Diferença entre os cálculos

• A média considera todos os valores igualmente e pode ser influenciada por valores muito altos ou baixos.
• A mediana se concentra no valor central e é menos afetada por valores extremos. Se houver um número muito grande ou muito pequeno, ele terá um impacto mínimo na mediana, enquanto afetará diretamente a média. Detalhe: exige ordenar os dados⚠️

Métodos de Ordenação

Função qsort

A função qsort ("Quick Sort") já faz parte da biblioteca padrão do C (stdlib.h), então não é necessário implementar o código de ordenação manualmente. A função qsort() pode ser usada diretamente para ordenar arrays de maneira eficiente.

qsort:

• A função qsort tem a seguinte sintaxe:

xxxxxxxxxx
void qsort(void *base, size_t num, size_t size, int (*compar)(const void *, const void *));

• Parâmetros:

  • base: ponteiro para o primeiro elemento do array.
  • num: número de elementos no array.
  • size: tamanho em bytes de cada elemento.
  • compar: função de comparação que define a ordem dos elementos.

No código anterior, foir importada a biblioteca stdlib.h, que contém a função qsort(). A função de comparação compare() já está escrita e fornecida no código. Essa função compara dois inteiros para que qsort() saiba como ordenar os elementos.

Outros métodos de ordenação podem ser usados como Método da Bolha ("Buble Sort") ou Método da Inserção.

Bubble Sort no Arduino

Se você está programando em C para Arduino, onde a função qsort() da biblioteca padrão não está disponível, será necessário implementar sua própria função de ordenação. A seguir, é apresentado um código que implementa as funções calcular_media e calcular_mediana, além de uma simples função de ordenação (bubble sort) necessário para calcular a mediana.

Aqui está o código modificado para Arduino:

xxxxxxxxxx
// Função para calcular a média
double calcular_media(int arr[], int tamanho) {
    int soma = 0;
    for (int i = 0; i < tamanho; i++) {
        soma += arr[i];
    }
    return (double)soma / tamanho;
}
​
// Função para calcular a mediana
double calcular_mediana(int arr[], int tamanho) {
    // Ordenar o array usando bubble sort
    for (int i = 0; i < tamanho - 1; i++) {
        for (int j = 0; j < tamanho - i - 1; j++) {
            if (arr[j] > arr[j + 1]) {
                // Troca os elementos
                int temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
            }
        }
    }
​
    // Verifica se o tamanho é par ou ímpar para calcular a mediana
    if (tamanho % 2 == 0) {
        // Se for par, retorna a média dos dois valores centrais
        return (arr[tamanho / 2 - 1] + arr[tamanho / 2]) / 2.0;
    } else {
        // Se for ímpar, retorna o valor central
        return arr[tamanho / 2];
    }
}
​
void setup() {
    Serial.begin(9600);
    
    int tamanho = 10;
    int valores[tamanho];
​
    // Gera números aleatórios entre 0 e 100
    randomSeed(analogRead(0)); // Usa o ruído do pino analógico para inicializar a semente do gerador de números aleatórios
    Serial.println("Valores gerados: ");
    for (int i = 0; i < tamanho; i++) {
        valores[i] = random(0, 101);
        Serial.print(valores[i]);
        Serial.print(" ");
    }
    Serial.println();
​
    // Calcula e exibe a média
    double media = calcular_media(valores, tamanho);
    Serial.print("Média: ");
    Serial.println(media);
​
    // Calcula e exibe a mediana
    double mediana = calcular_mediana(valores, tamanho);
    Serial.print("Mediana: ");
    Serial.println(mediana);
}
​
void loop() {
    // Não há nada a ser feito no loop
}

Detalhes do código:

1. Função calcular_media: Soma todos os valores do array e divide pelo número de elementos, retornando a média.

2. Função calcular_mediana:

   • Usa o algoritmo bubble sort para ordenar os elementos do array. Este algoritmo é simples e fácil de implementar, embora não seja o mais eficiente.

   • Após a ordenação, verifica se o tamanho do array é par ou ímpar:

     • Se for par, calcula a média dos dois elementos centrais.
     • Se for ímpar, retorna o valor central.

3. Geração de números aleatórios: A função randomSeed(analogRead(0)) usa a leitura de um pino analógico para inicializar a semente do gerador de números aleatórios. Os valores são gerados com random(0, 101) e variam de 0 a 100.

4. Saída: O programa imprime os valores gerados, a média e a mediana no monitor serial.

Esse código pode ser carregado diretamente no Arduino usando a IDE. No loop principal (loop()), não há necessidade de ação contínua, pois todo o trabalho é feito no setup().

Sobrecarga Computacional

Calcular a mediana geralmente envolve uma sobrecarga computacional maior que calcular a média, principalmente porque a mediana exige que os dados sejam ordenados, enquanto a média pode ser calculada diretamente com uma única passagem pelos dados.

Análise de complexidade

1. Calcular a média:

   • Para calcular a média, você percorre o array uma única vez, somando os elementos.
   • Complexidade: $O(n)$, onde $n$ é o número de elementos. Ou seja, a operação é linear no tamanho do array.

2. Calcular a mediana:

   • O cálculo da mediana requer que os dados sejam ordenados. No caso do bubble sort que implementamos, a ordenação tem complexidade $O(n^2)$.
   • Após ordenar, a mediana é obtida diretamente no valor central, o que é uma operação $O(1)$.
   • Complexidade total: $O(n^2)$ com o algoritmo de ordenação escolhido (bubble sort).

Acompanhe no gráfico abaixo:

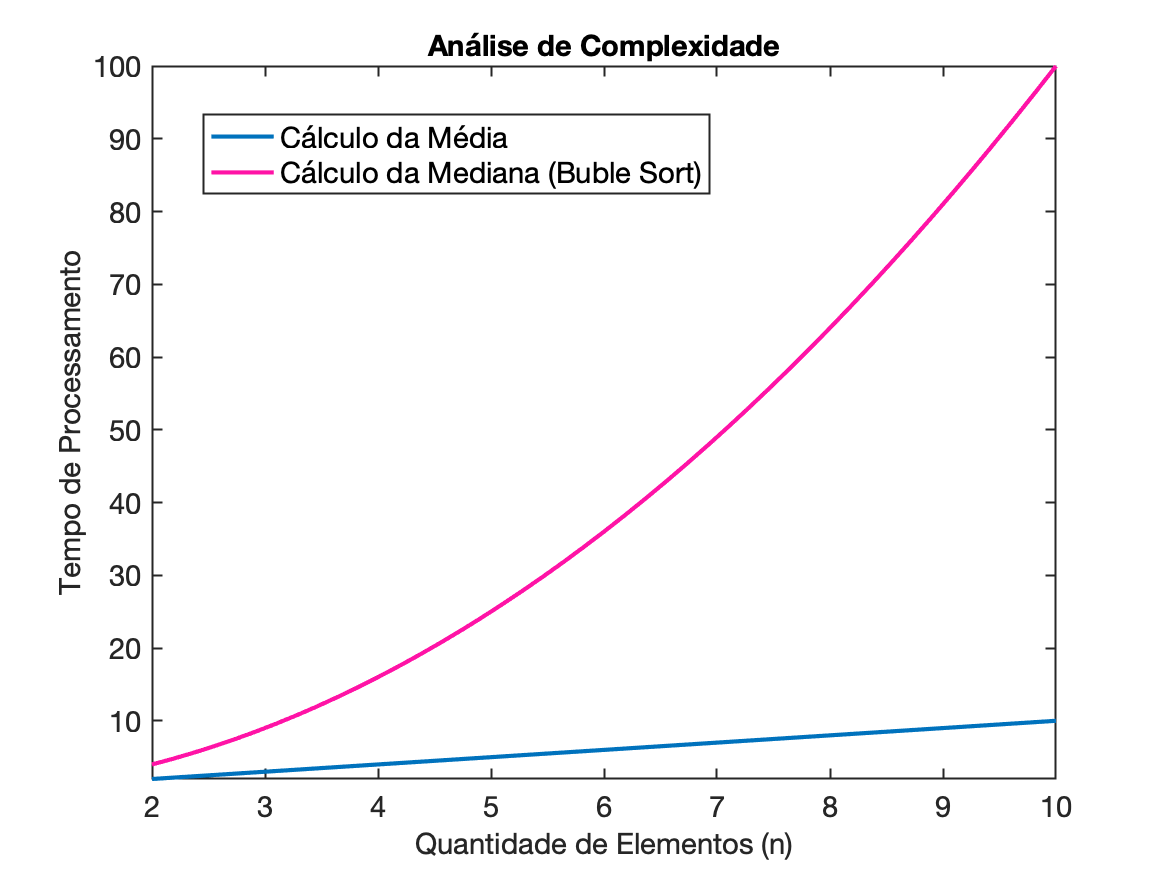
Comparação

• Média: $O(n)$.
• Mediana: $O(n^2)$ com bubble sort (existem algoritmos mais eficientes, como o quicksort ou heapsort, com complexidade O$(n \log n),$ mas mesmo assim a ordenação será mais lenta que calcular a média).

Estimativa da maior diferença

Para estimar a maior diferença possível, consideremos o tempo de execução em função do número de elementos $(n)$.

• Média: Com complexidade $O(n)$, o tempo cresce linearmente com $n$.
• Mediana: Com complexidade $O(n^2)$, o tempo cresce quadraticamente com $n$.

Se usarmos uma proporção entre as duas complexidades, podemos dizer que para grandes valores de $n$, o tempo necessário para calcular a mediana será aproximadamente proporcional ao quadrado do tempo para calcular a média.

Exemplo prático

• Se calcular a média para $n = 1000$ leva $T$ unidades de tempo, então calcular a mediana, com bubble sort, pode levar até $1000$ vezes mais tempo (ou seja, $T \times 1000).$

Em termos de fator de diferença:

$\dfrac{O(n^2)}{O(n)} = n$

Portanto, a maior diferença possível entre o tempo de cálculo da mediana e da média será proporcional ao número de elementos (n). Isso significa que se você tem 1000 elementos, o cálculo da mediana pode ser até 1000 vezes mais lento do que o cálculo da média, dependendo do algoritmo de ordenação usado.

Otimização

Caso a sobrecarga computacional para o cálculo da mediana seja uma preocupação, você pode usar algoritmos de ordenação mais eficientes, como o quicksort ou o heapsort, que têm complexidade $O(n \log n)$, reduzindo o fator de diferença para algo entre O$(\log n)$ e $n$. Isso ainda será mais lento que a média, mas muito mais eficiente que o bubble sort.

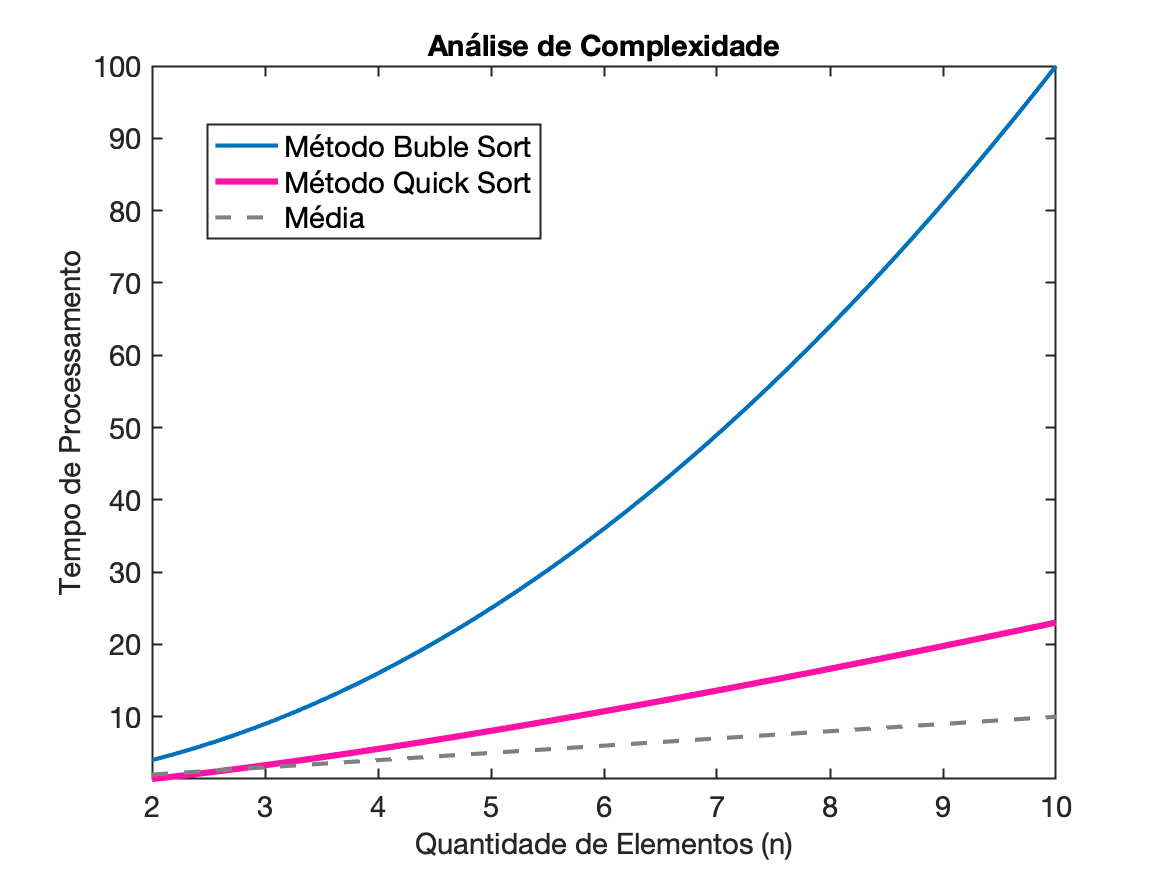
Implementado Quicksort

O método quicksort é um algoritmo de ordenação eficiente que usa a técnica de divisão para conquistar ("divide to conquer"). Aqui está um exemplo de implementação do quicksort em C, que pode ser utilizado para ordenar um array de inteiros:

xxxxxxxxxx
#include <stdio.h>
​
// Função para trocar dois elementos
void troca(int *a, int *b) {
    int temp = *a;
    *a = *b;
    *b = temp;
}
​
// Particiona o array e retorna o índice do pivô
int particionar(int arr[], int baixo, int alto) {
    int pivo = arr[alto]; // Escolhe o último elemento como pivô
    int i = (baixo - 1); // Índice do menor elemento
​
    for (int j = baixo; j < alto; j++) {
        // Se o elemento atual é menor ou igual ao pivô
        if (arr[j] <= pivo) {
            i++; // Incrementa o índice do menor elemento
            troca(&arr[i], &arr[j]); // Troca os elementos
        }
    }
    troca(&arr[i + 1], &arr[alto]); // Coloca o pivô na posição correta
    return (i + 1); // Retorna o índice do pivô
}
​
// Função recursiva para implementar o quicksort
void quicksort(int arr[], int baixo, int alto) {
    if (baixo < alto) {
        // Particiona o array e obtém o índice do pivô
        int pivoIndex = particionar(arr, baixo, alto);
        
        // Chama recursivamente para as duas metades
        quicksort(arr, baixo, pivoIndex - 1);
        quicksort(arr, pivoIndex + 1, alto);
    }
}
​
// Função para imprimir o array
void imprimirArray(int arr[], int tamanho) {
    for (int i = 0; i < tamanho; i++) {
        printf("%d ", arr[i]);
    }
    printf("\n");
}
​
int main() {
    int valores[] = {34, 7, 23, 32, 5, 62};
    int tamanho = sizeof(valores) / sizeof(valores[0]);
​
    printf("Array original: ");
    imprimirArray(valores, tamanho);
​
    quicksort(valores, 0, tamanho - 1);
​
    printf("Array ordenado: ");
    imprimirArray(valores, tamanho);
​
    return 0;
}

Detalhes do código:

1. Função troca: Troca dois elementos usando ponteiros.

2. Função particionar:

   • Escolhe o último elemento do array como pivô.
   • Percorre o array, movendo elementos menores ou iguais ao pivô para a esquerda.
   • Coloca o pivô em sua posição correta e retorna seu índice.

3. Função quicksort:

   • Chama recursivamente o quicksort nas duas metades do array, separadas pelo índice do pivô.

4. Função imprimirArray: Imprime os elementos do array.

5. Função main:

   • Define um array de inteiros, calcula seu tamanho e imprime o array original.
   • Chama a função quicksort para ordenar o array.
   • Imprime o array ordenado.

Usos

Você pode compilar e executar esse código em qualquer ambiente C. O quicksort é geralmente mais eficiente do que o bubble sort e tem um desempenho médio de $O(n \log n)$, tornando-o uma escolha adequada para ordenar dados de maneira eficiente. Se precisar de mais alguma informação ou ajuda, é só avisar!

🌊 Fernando Passold 📬 ,