Unsplash, Yilan County, Taiwan.

Aula #2) Sintonia de PID

Tentando sintonizar um PID usando diferentes métodos.

Método 1) Resposta em MA para entrada degrau

Observando como a planta reage para uma entrada degrau unitário:

>> G=tf(20,poly([-1 -2])) % sismples sistema de 2a-ordem

G =

       20
  -------------
  s^2 + 3 s + 2

Continuous-time transfer function.

>> % Verificando:
>> zpk(G)

      20
  -----------
  (s+2) (s+1)

Continuous-time zero/pole/gain model.

>> % Verificando valor final da planta para entrada degrau, regime permanente:
>> dcgain(G)
ans =
    10
>> % Planta vai atingir o valor 10 em regime permanente: $y(\infty)=10$.
>> % Observando como esta planta reage para entrada degrau unitário (em MA)
>> step(G)
%

Gráfico da resposta ao degrau (em MA):

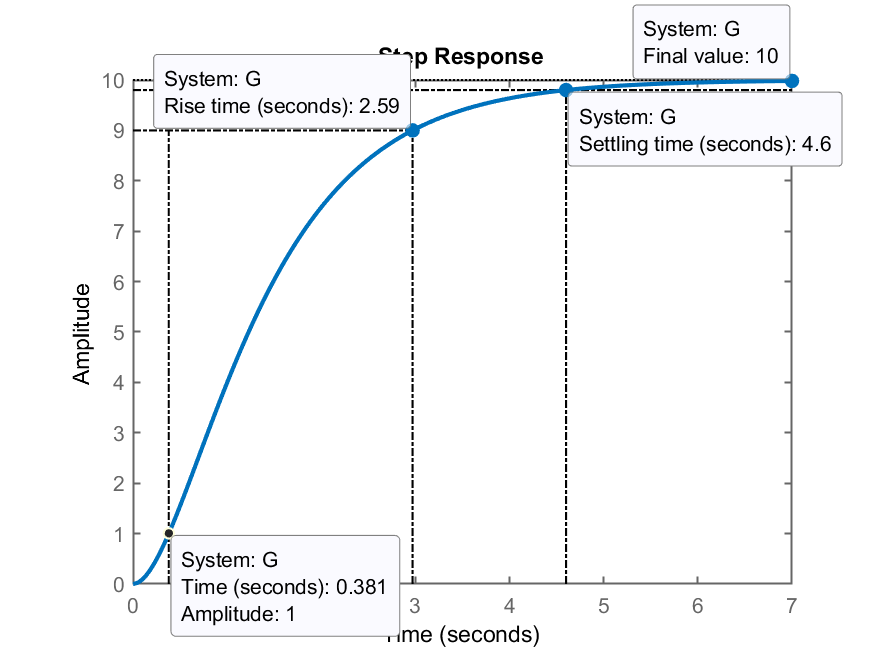
Usando o método 1 temos que obter os parâmetros $L$ e $T$ .

Usando-se a ferramenta de “Basic Fitting“ do Matlab:

Na janela do gráfico, na barra de menu, selecionar: Tools >> Basic Fitting:

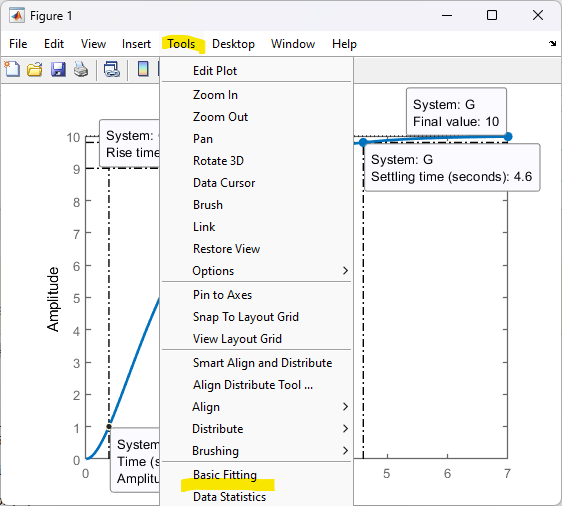
Deve-se abrir a janela deste app, onde algums ajustes devem ser feitos, entre eles:

No quadro “Plot fits”, selecionar: “[x] 8th degree polynomial”:

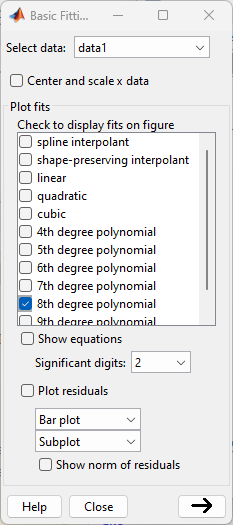
Clicar então no botão inferior -->. A janela anterior aumenta para:

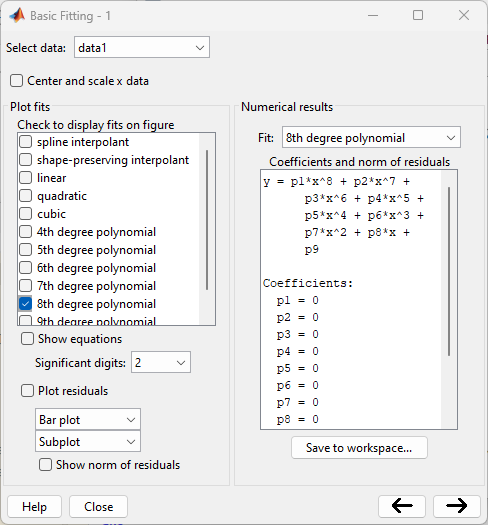
Você vai clicar agora em Save to workspace e deve surgir outra janela:

Clicar agora em Ok. Esta última janela se fecha e na janela de comandos do Matlab deve surgir a mensagem:

Variables have been created in the base workspace.

Supõe-se então que dados foram salvos no workspace. No caso, as variáveis fit, normresid e resids. Nos interessa apenas a variável fit. Explorando esta variável:

>> fit
fit = 
     type: 'polynomial degree 8'
    coeff: [0 0 0 0 0 0 0 0 0]
>> % Tentando extrair o polinômio criado no "fitting":
>> p=fit.coeff % extraindo apenas o polinômio da curva levantada
p =
     0     0     0     0     0     0     0     0     0

Notamos o polinômio vazio.

Deveríamos ter percebdo que o Matlab no momento em que tentamos aproximar a curva de um polinômio de 8a-ordem nos advertiu de que mais de uma solução havia sido encontrada, que o grau do polinômio era maior ou igual ao número de amostras usadas para levantá-lo:

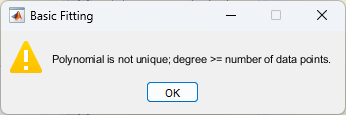
Se faz necessário “forçar” o Matlab a criar o mesmo gráfico da resposta ao degrau da planta, mas usando mais pontos. Uma solução é especificar a variável $t$ usada para gerar $y(t)$ no comando step():

>> t=0:0.01:5; % cria vetor t entre 0 à 5 segundos com incremento de 0,01 segundos
>> [y, t]=step(G,t); % gera vetor y com resposta ao degrau

O comando anterior, da forma que foi usado, não gera gráfico na tela. Então:

>> figure; plot(t,y)
>> grid;

Temos então um novo gráfico e a ferramenta “Basic fitting” deve ser ativada novamente:

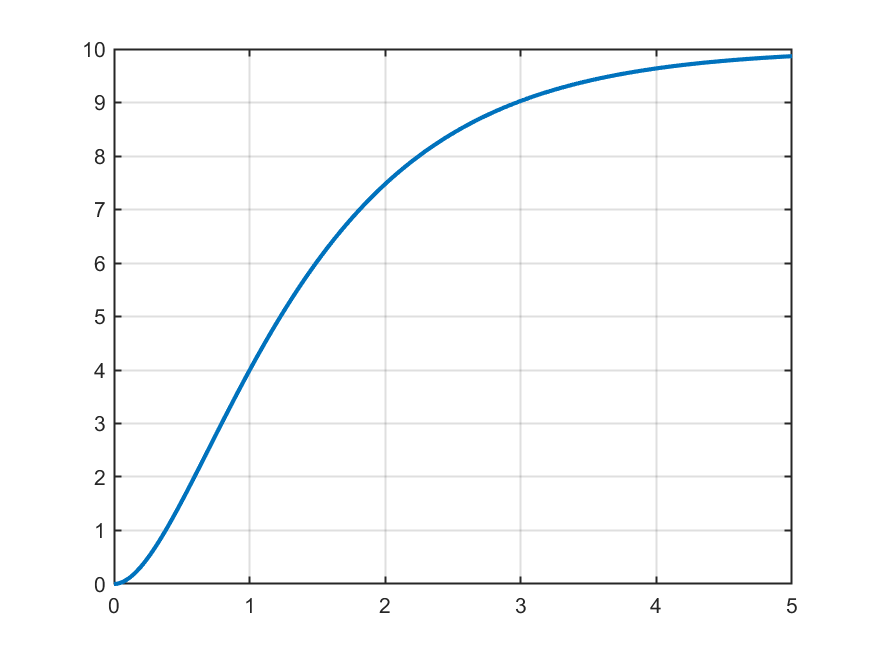
Ativando “Basic fitting” e agora reparamos que agora temos como prosseguir:

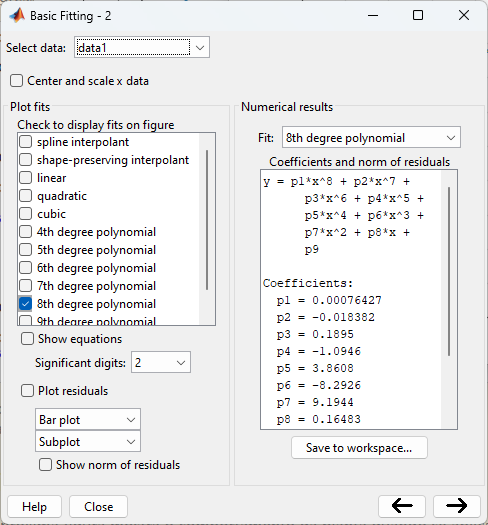
Note que na janela do gráfico surgiram 2 curvas: “data1” (dados originais; curva em azul) e “8th degree” (curva levantada, na cor amarela que mau se destaca):

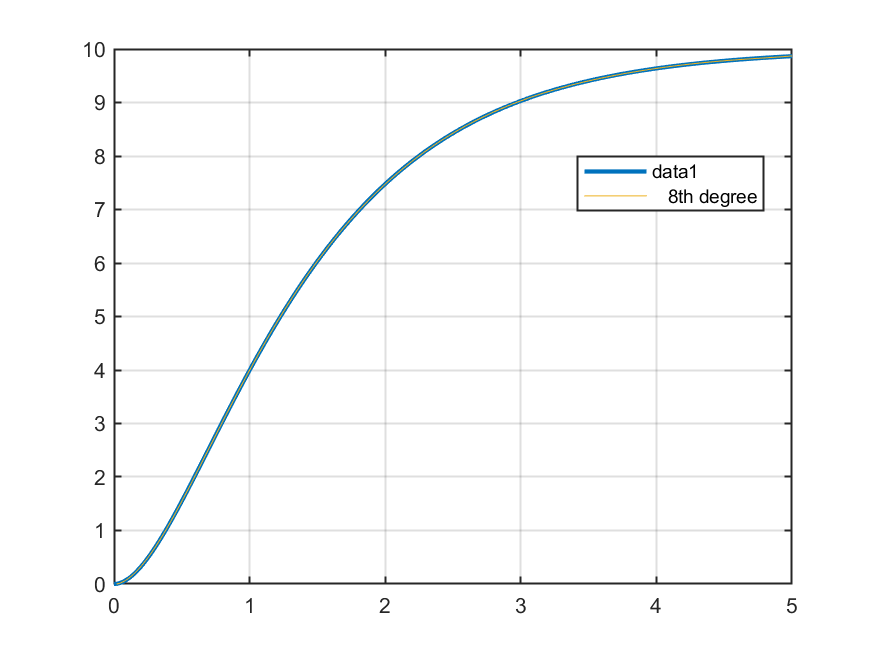
Agora podemos salvar os dados da curva aproximada de 8a-ordem, clicando em “Save to workspace”. Na janela de comandos do Matlab deve aparecer:

Variables have been created in the base workspace.

Nesta caso, os dados foram regravados (sobrescreveram) as mesmas variáveis anteriores, entre elas,fit.

Analisando a variável fit temos agora:

>> fit
fit = 
     type: 'polynomial degree 8'
    coeff: [1×9 double]
>> p = fit.coeff % extraindo os coeficientes do polinômio
p =
  Columns 1 through 5
   0.00076427    -0.018382       0.1895      -1.0946       3.8608
  Columns 6 through 9
      -8.2926       9.1944      0.16483    -0.008144
>> % Descobrindo pontos min/máx de inflexão da curva, realizando deriavada primeira:
>> d_p = polyder(p)
d_p =
  Columns 1 through 5
    0.0061142     -0.12867        1.137       -5.473       15.443
  Columns 6 through 8
      -24.878       18.389      0.16483
>> % Realizando a derivada 2a para descobrir valores máximos e mínimos
>> dd_p = polyder(d_p)
dd_p =
  Columns 1 through 5
     0.042799     -0.77203        5.685      -21.892       46.329
  Columns 6 through 7
      -49.755       18.389
>> % Calculando-se as raízes de dd_p para descobrir os pontos de inflexão
>> % da curva aproximada (polinônimo de 8a-orde)
>> roots(dd_p)
ans =
       4.7795 +          0i
       4.0438 +    0.74241i
       4.0438 -    0.74241i
        2.236 +     1.6142i
        2.236 -     1.6142i
      0.69928 +          0i
>> % Pelo gráfico anterior, nota-se que o ponto de inflexão ocorre em:
x = ans(6) % 6o-valor da resposta anterior, isolado na variável x
x =
      0.69928
>> % Este seria o ponto de partida da reta que queremos sobrepor 
>> % à curva de resposta da planta

Levantando os dados que faltam para determinar a reta tangente à curva de resposta da planta e que passe pelo ponto de inflexão, lembramos da equaçao da reta:

y = a \cdot t + b

$y = a \cdot t + b$

O valor de $a$ corresponde ao valor da derivada primeira da curva aproximada (variável d_p) no ponto de inflexão (ponto $x$ ):

>> a = polyval(d_p, x) % usa eq. dp/dt para calcular y' no ponto x
a =
       5.0064
>> % Descobrindo o valor de y(t) qunado t=x
>> y_aux = polyval(p,x)
y_aux =
       2.5284
>> % Lembrando da eq. da reta, temos como determinar 'b'
>> b = y_aux - a*x
b =
     -0.97246
>> % Eq. (polinomio) da reta tangente:
>> reta=[a b];
>> % Verificando...
>> % Criando-se gráfico da reta que se sobrepõe à curva anterior:
>> y_reta = a.*t + b;
>> figure;
>> plot(t,y,'k-', t,y_reta,'b--')
>> grid
>> legend('curva original', 'reta tangente')
>> axis([0 5 -3 12]) % realizando um "zoom" na área de interesse

Deve ter sido gerado um gráfico semelhante à:

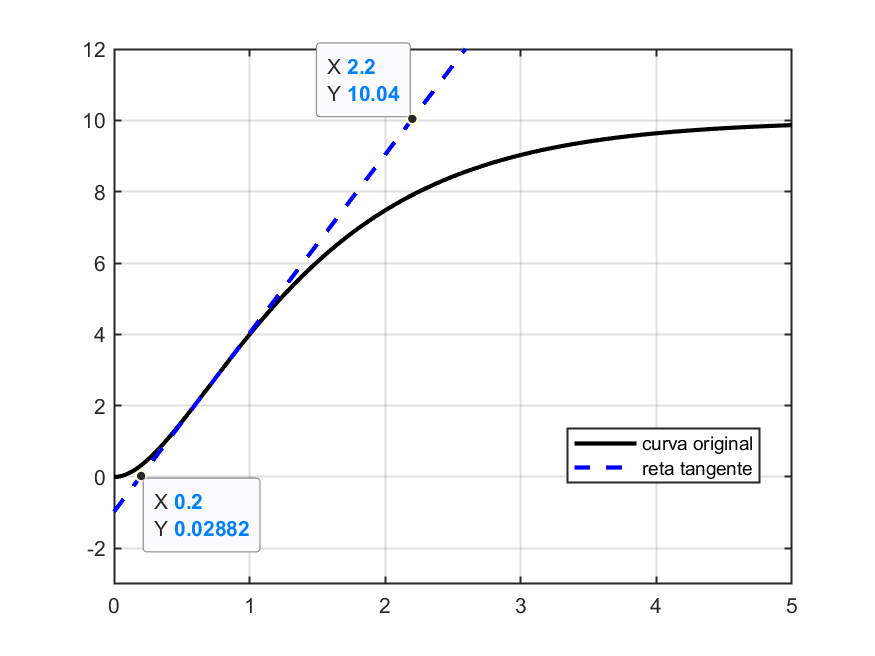
Extraindo-se agora, desta última figura, os parâmetros $L$ e $T$ , teremos:

$L$ corresponde ao ponto no qual a reta cruza o eixo quando $y=0$ , então:

y 0 ∴ t = = = a \cdot t + b a \cdot t + b - b a

$\begin{array}{rcl} y &=& a \cdot t + b\\ 0 &=& a \cdot t + b\\ \therefore &&\\ t &=& - \dfrac{b}{a} \end{array}$

No Matlab:

>> axis([0 5 -3 12]) % realizando um "zoom" na área de interesse
>> L=-b/a
L =
      0.19424

E o parâmetro $T$ pode ser determinando, descobrindo-se $t_1$ , onde $t_1=L+T$ . Aplicando-se estes dados na equação da reta, teremos algo como:

y 10 ∴ t 1 = = = a \cdot t + b a \cdot t 1 + b ( 10 - b ) a

$\begin{array}{rcl} y &=& a \cdot t + b\\ 10 &=& a \cdot t_1 + b\\ \therefore & & \\ t_1 &=& \dfrac{(10-b)}{a} \end{array}$

No Matlab:

>> t1 = (10-b)/a
t1 =
       2.1917
>> % e então:
>> T=t1-L
T =
       1.9975

Aplicando-se os parâmetros $L$ e $T$ na equação do PID teremos:

C (s) = 0 , 6 T ( s + 1 L ) 2 s

$C(s)= \dfrac{0,6 \; T \; \left( s + \frac{1}{L} \right)^2}{s}$

No Matlab:

>> s=tf('s');
>> C_PI1=0.6*T*(s+1/L)^2/s

C_PI1 =

  1.198 s^2 + 12.34 s + 31.76
  ---------------------------
               s

Continuous-time transfer function.

>> zpk(C_PI1)

ans =

  1.1985 (s+5.148)^2
  ------------------
          s

Continuous-time zero/pole/gain model.

Fechando a malha com este controlador:

>> ftma_PI1=C_PI1*G;
>> % verificando:
>> zpk(ftma_PI1)

  23.97 (s+5.148)^2
  -----------------
    s (s+2) (s+1)

Continuous-time zero/pole/gain model.

>> % fechando a malha
>> ftmf_PI1=feedback(ftma_PI1,1);
>> % Verificando onde ficaram os pólos de MF deste sistema:
>> pole(ftmf_PI1)
ans =
      -11.437 +     4.9308i
      -11.437 -     4.9308i
      -4.0954 +          0i
>> % Verificando os zeros deste sistema (destino dos polos)
>> zero(ftmf_PI1)
ans =
      -5.1482
      -5.1482
>> figure; step(ftmf_PI1)
>> stepinfo(ftmf_PI1)

        RiseTime: 0.057703
    SettlingTime: 0.37717
     SettlingMin: 0.91776
     SettlingMax: 1.1569
       Overshoot: 15.687
      Undershoot: 0
            Peak: 1.1569
        PeakTime: 0.15703

A resposta ao degrua unitário usando-se este controlador, fica:

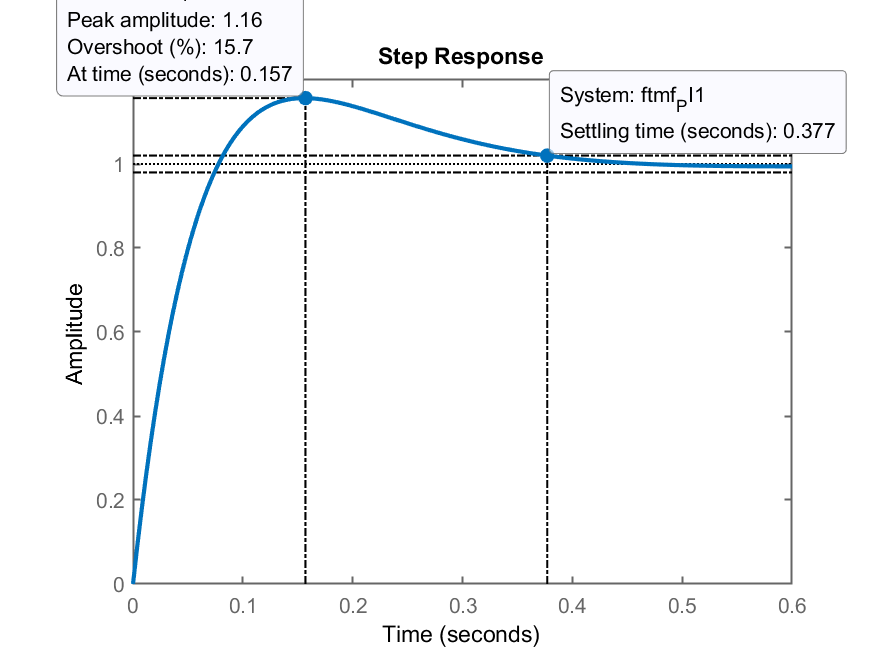
Salvando os dados para uso posterior

>> save dados

[Fim]

Fernando Passold, em 20/10/2022