Trabalho Final Lab de Controle II

Trabalho Final Lab de Controle II

Título do trabalho

Título do trabalho: Controladores PID com Anti-Windup

Este trabalho está previsto para ser realizado em duplas de alunos.

Data de entrega: 08/12/2022, arquivo PDF, enviado por email para fpassold@upf.br

Objetivo do trabalho

A objetivo deste trabalho é que o estudante entenda o que é o problema da "saturação na ação integral" (ou efeito "windup") ocorrendo com um controlador típico PID; que tome conhecimento de diferentes técnicas para minimizar este problema e que em especial acabe usando (simulando e comparando) a técnica "back-calculation" com certa planta/exemplo.

Conteúdo do Trabalho

Sugere-se dividir o trabalho nos seguintes tópicos:

1. O problema da Saturação Integral

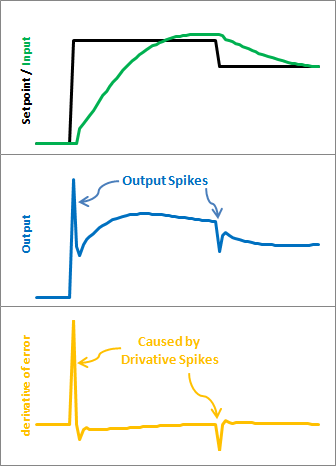
Uma dos problemas mais comuns com o controlador PID é como fazê-lo lidar com o efeito de "windup" ou de Saturação Integral. O "windup" ou problema da "saturação integral" é o resultado causado pelo acúmulo de uma soma de erro muito grande quando a variável de processo está se aproximando do Setpoint de maneira lenta. Isso resulta em uma quantidade significativa de sobressinal e controle ineficiente.

Note que o componente Integral é a única parte de um controlador PID com memória de longo prazo. Enquanto os componentes Proporcional e Derivativo ajudam a reagir a erros de forma instantânea, a ação Integral é o único fator que melhorar a qualidade da malha de controle ao longo do tempo.

Exemplo 3.1 de Sobrecarga da Ação Integral

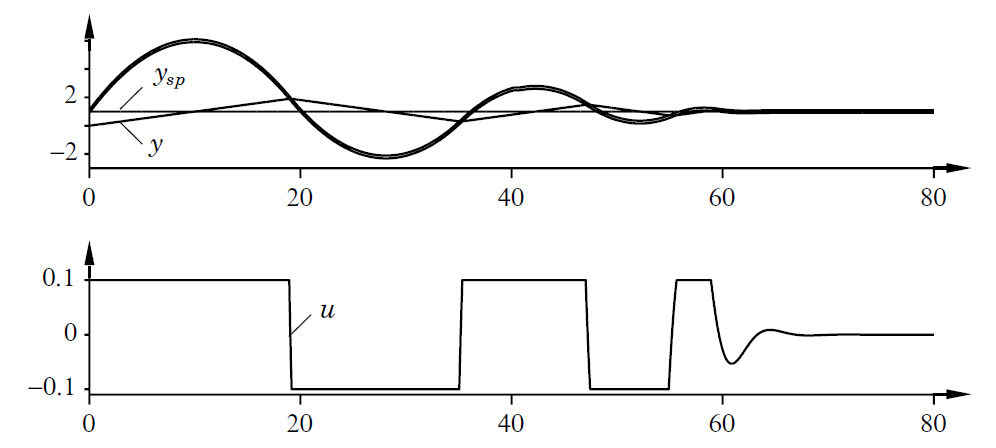
A próxima figura (Fig 3.18 originalmente em [1]) demonstra o fenômeno do "windup". Ela mostra o controle de um processo tipo 1 (integratico) atuando com um controlador Integral. A figura mostra a saída do processo $y(t)$ , a referência (setpoint), ou $y_{sp}(t)$ , o sinal de controle $u(t)$ e a ação integral $I(t)$ .

A mudança inicial da referência (setpoint, variável $y_{sp}(t)$ ) é tão grande que o atuador satura num valor máximo ( $=0.1$ ).

Note que o termo integral aumenta inicialmente porque o erro é positivo; ele atinge seu maior valor no tempo $t = 10$ quando o erro passa por zero.

A saída permanece saturada neste ponto por causa do grande valor do termo integral. Ele não abandona o limite de saturação até que o erro tenha sido negativo por um tempo suficientemente longo para deixar a parte integral descer a um nível pequeno.

O sistema não sai do limite de saturação até que o erro tenha se tornado negativo por um tempo suficientemente longo para deixar a parte integral descer a um nível pequeno.

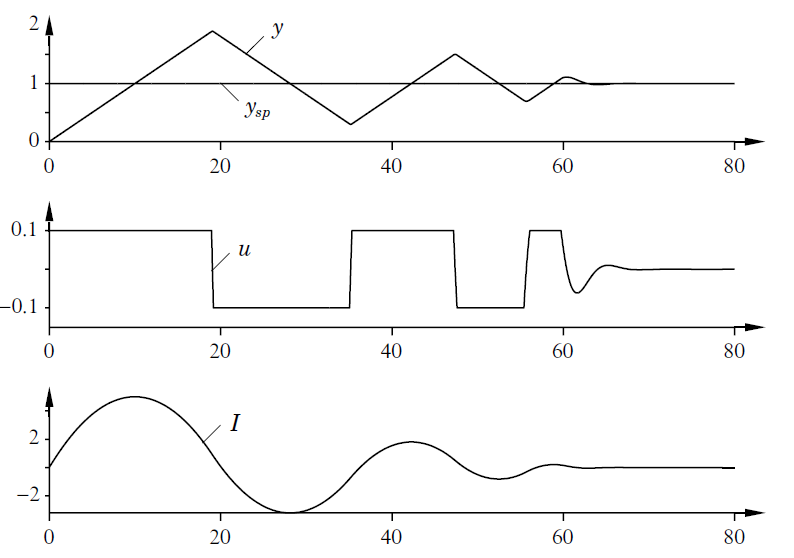
Observe que o sinal de controle comuta entre seus limites máximo ( $=0,1$ ) e mínimo ( $=-0,1$ ) várias vezes. O efeito final é uma grande sobrecarga (pela ação integral) e uma oscilação amortecida onde o sinal de controle oscila de um extremo ao outro como no caso de um relé (ou controlador on/off). Mas a saída finalmente se aproxima bastante do ponto de ajuste ( $y(t) \cong y_{sp}(t)$ ), motivo pelo qual o atuador não satura. O sistema então se comporta linearmente e estabiliza.

A próxima figura mostra o que ocorre quando um controlador com anti-windup é aplicado ao sistema simulado na Figura 3.18. Observe que a saída do integrador é rapidamente redefinida para um valor tal que a saída do controlador está no limite de saturação e a integral tem um valor negativo durante a fase inicial, quando o atuador está saturado.

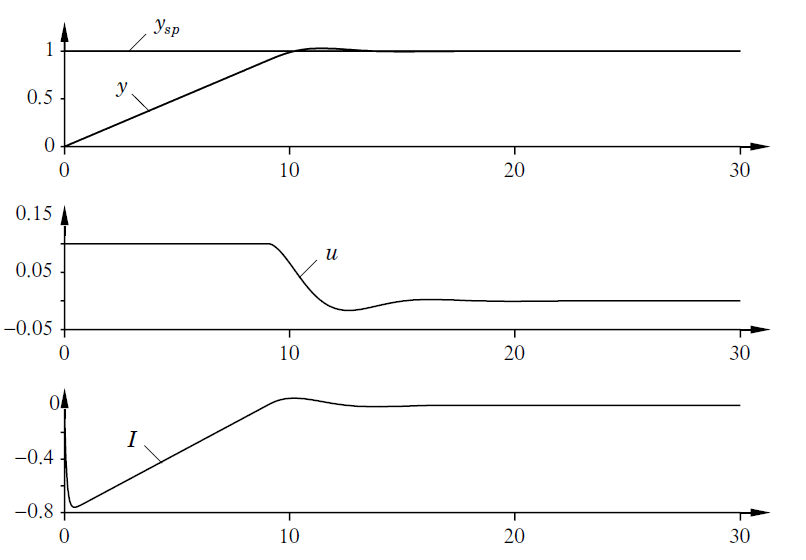
A figura anterior corresponde a fig 3.20 de [1] e mostra o impacto causado pela aplicação de um Controlador Integral com anti-windup ao sistema apresentado no início deste exemplo (figura 3.18). Os diagramas mostram a saída do processo $y(t)$ , setpoint (referência) -- que Astrom chama de $y_{sp}(t)$ , o sinal de controle $u(t)$ e a ação integral $I(t)$ .

Esse comportamento é drasticamente diferente da figura do (Figura 3.18), onde a integral tem um valor positivo durante o transiente inicial. Observe também a melhoria drástica no desempenho em comparação com o controlador PI comum usado na Figura 3.18.

O exemplo de PID com Anti-windup da MathWorks

Para tentar demonstrar o problema da "saturação integral", os estudantes devem mostrar um PID simples (sem anti-windup) tentando controlar um sistema do tipo:

G(s)=\dfrac{1}{10s+1}e^{-2s}

Trata-se de um sistema de 1a-ordem com atraso de transporte (atraso na resposta). Note que esta planta só aceita valores de entrada na faixa de $-10 \ldots +10$ Volts. Isto é, seu driver de potência satura se recebe valores superiores aos que foram indicados. Esta é a planta usada como exemplo no "tutorial" sobre Controle PID com Anti-Windup disponibilizado pela MathWorks (fabricante do software Matlab), disponível à partir de: "Anti-Windup Control Using PID Controller Block" (https://www.mathworks.com/help/simulink/slref/anti-windup-control-using-a-pid-controller.html).

Esta planta/processo, com as características indicadas anteriormente pode/deve ser simulada usando o Matlab/Simulink para demonstrar os problemas que surgem e mostrar a efetividade (ou não) de soluções que podem ser empregadas para tentar minimizar o problema. Para efeitos de simulação, siga o mesmo procedimento adotado no material da Mathwork: suponha que a referência seja uma entrada degrau de amplitude 5, já incorpore o bloco de atraso no tempo ("Dead Time") e o bloco de Saturação ("Plant Actuator"), já nas primeiras simulações com um PID sem Anti-Windup -- veja figura à seguir.

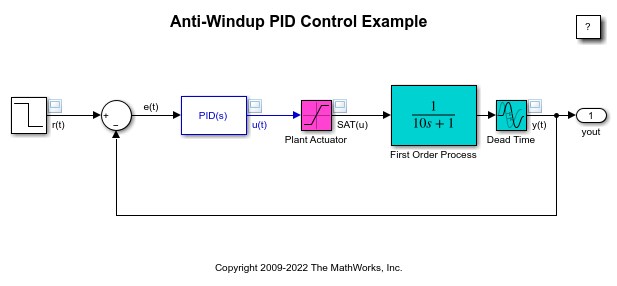
A ideia é que os estudantes, iniciem o trabalho simulando como um PID sem Anti-Windup aplicado nesta planta, faz o sistema se comportar em malha-fechada e assim primeiramente entender o problema da "saturação integral", comum na prática. Os estudantes devem mostrar e comentar o resultado desta simulação.

Detalhes: sintonizar um PID para um processo lento com atraso de transporte pode ser complicado e demandar tempo. Sugere-se que para a planta citada anteriormente, os estudantes adotem os seguintes parâmetros para o PID fornecido "de fábrica" no Matlab/Simulink:

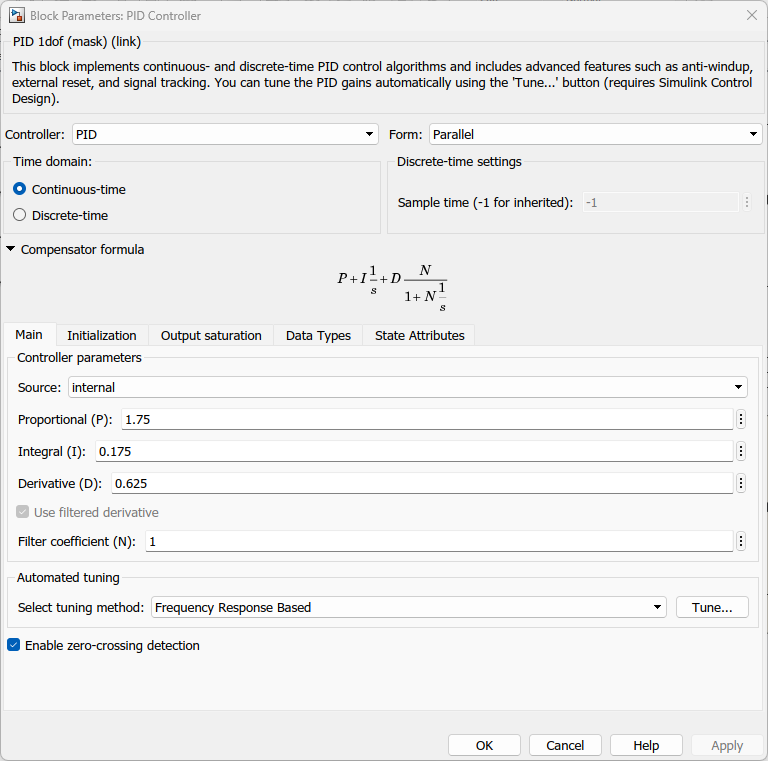
2. Abordagens para Anti-Windup

A seguir os estudantes devem apresentar uma teoria mínima associada com a abordagem que será adotada para minimizar os efeitos da saturação.

O PID fornecido de "fábrica" pela Marhworks no Simulink disponibiliza 2 técnicas para minimiar o efeito "windup":

"Back-Calculation", ou método do Cálculo Retroativo, e;
"Integrator Clamping", ou método da "Integração Condicional".

Em especial neste trabalho (e para fins de simplificação), espera-se que os estudantes explorem apenas a técnica back-calculation.

2.1 Método do cálculo retroativo ou "backup-calculating"

Este método descrito brevemente na página WEB da MathWorks à respeito de controlador PID com Anti_Windup ("Anti-Windup Control Using PID Controller Block": https://www.mathworks.com/help/simulink/slref/anti-windup-control-using-a-pid-controller.html#responsive_offcanvas ) foi proposto originalmente por Åström e Hägglund em 1995 [1].

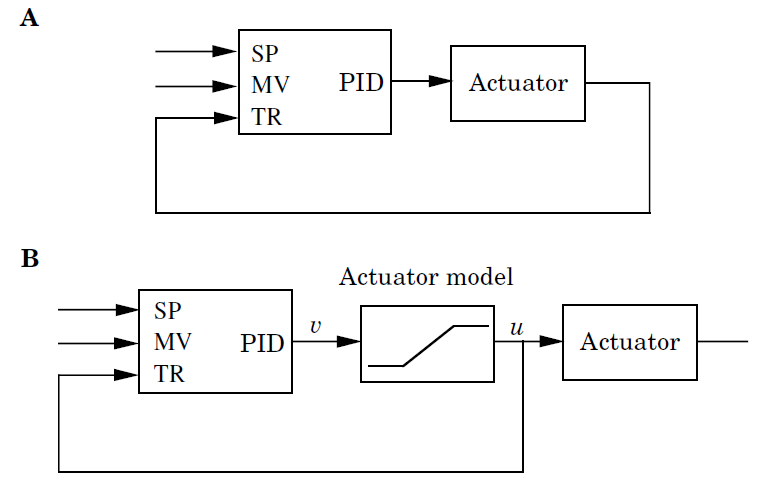
A próxima figura ilustra na forma de um diagrama em blocos, esta proposta de PID com anti-windup:

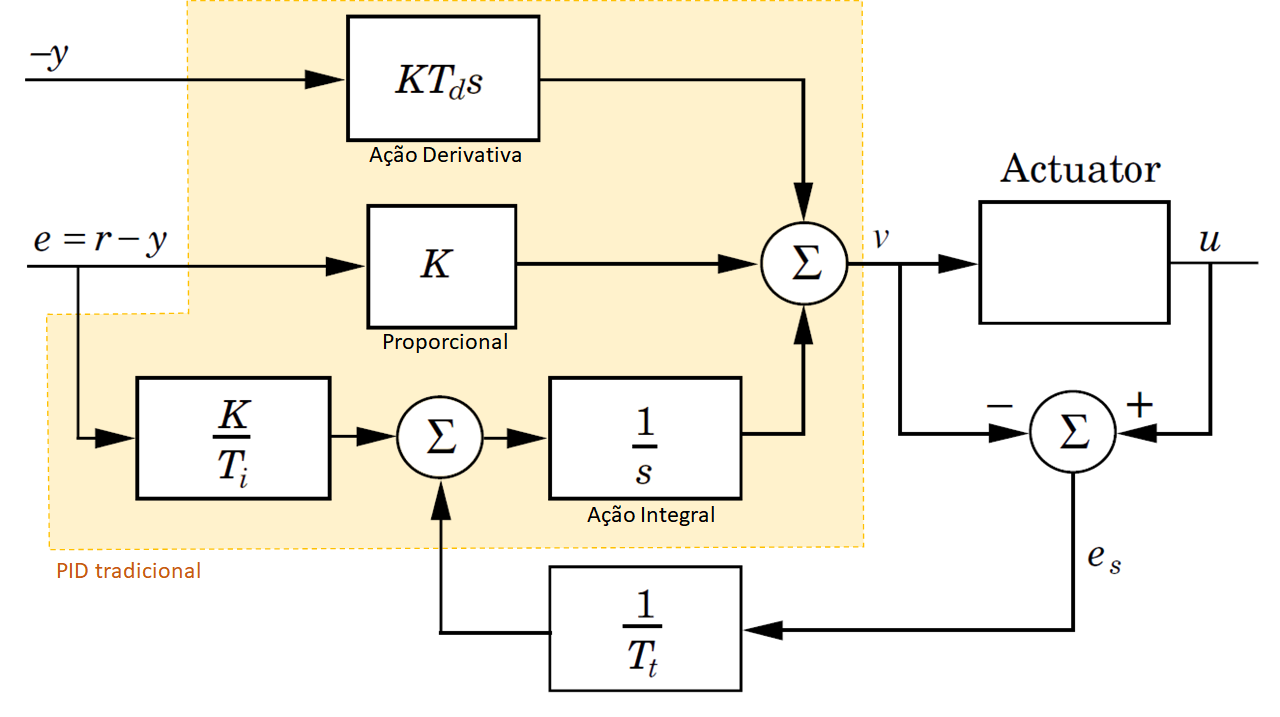
Trata-se da figura 3.19(a), adaptada de [1] e mostra um diagrama de blocos de um controlador PID com anti-windup baseado em cálculo retroativo ("back-calculation").

Note que esta figura já mostra a Ação Derivativa atuando não sobre o sinal do erro, $e(t)$ , mas sobre a saída da planta: $-y(t)$ . Isto é feito para evitar o que se chama de "derivative quicks", ou "derivative spikes": "saltos" na ação derivativa enm função de mudanças bruscas no sinal de referência, $r(t)$ (Ver [2]). A ideia é evitar amplitudes elevadas ocasionadas pela aplicação da derivada sobre um sinal de erro que varia muito rápido (aos saltos), em função de mudanças bruscas no sinal de referência (saltos/degrau mudando de amplitude). Como a planta normalmente reage mais lentamente e possui sua própria dinâmica ("inércia"), realizar $dy(t)/dt$ ao invés de $de(t)/dt$ visa gerar sinais menos oscilatórios e de menor amplitudes. A próxima figura (adaptada de [2]) mostra os "famosos" derivative spikes:

Voltando a figura do diagrama de blocos, o bloco "Atuador" pode incluir um modelo matemático completo do driver de potência (uma espécie de filtro passa-baixas), incluindo um bloco de saturação que contempla os limites físicos/reais do sinal de entrada usado pelo driver de potência.

O bloco atuador no caso da planta usada como exemplo pela MathWorks, seria simplesmente o bloco "Saturation" do Simulink com os parâmetros:

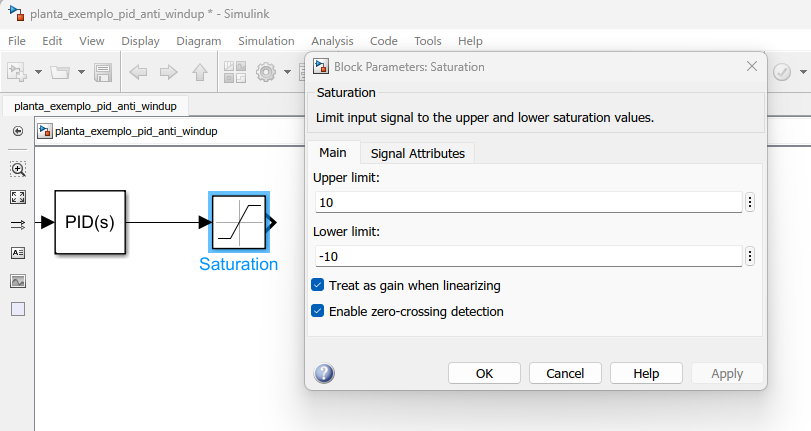
O sistema proposto conta com um laço extra de feedback gerado pela medição da saída atual do atuador, $u(t)$ , formando um sinal de erro, $e_s(t)$ , como sendo a diferença entre a saída gerada pelo controlador (PID ou outro), $v(t)$ e a saída do atuador, $u(t)$ . O sinal $e_s(t)$ é repassado então para o bloco integrador através do ganho $1/T_t$ . O sinal $e_s(t)$ é nulo (zerado) quando não há saturação. Neste caso, esta abordagem não afeta a operação normal do atuador enquanto ele não satura. Quando o atuador satura, o sinal $e_s(t)$ é diferente de zero. O laço de realimentação tradicional é "quebrado" porque o sinal $u(t)$ fornecido à planta se torna constante (saturado). Neste caso, atua o laço extra de realimentação que usa/passa por um integrador (bloco $1/s$ ). Este bloco trabalha com um sinal do tipo:

a(t)=\dfrac{1}{T_t}\,e_s(t)+\dfrac{K}{T_i}\,e(t)

onde $e(t)=$ sinal de erro do processo ( $e(t)=r(t)-y(t)$ ).

A ideia neste caso é que a saída deste integrador tenda à zero. Em regime permanente, a equação anterior fica:

e_s(t)= - \dfrac{K\,T_t}{T_i}\,e(t)

Como $e_s(t)=u(t)-v(t)$ , teremos então que:

v(t)=u_{lim}+\dfrac{K\,T_t}{T_i}\,e(t)

onde $u_{lim}=$ valor máximo de saturação do atuador (da variável de controle).

Uma vez que os sinais $e(t)$ e $u_{lim}$ possuem o mesmo sinal, resulta que $v(t)$ sempre será maior que $u_{lim}$ , em magnitude. Isto evita o integrador de saturar.

A taxa/razão, na qual a saída do controlador é "resetada" é ditada pelo ganho do laço de realimentação: $1/T_t$ , onde $T_t$ pode ser interpretado como uma constante de temp que determina que tão rápido a integral é resetada. Åström denomina $T_t$ de constante de tempo de seguimento ou tracking time constant [1].

Inicialmente pode parecer vantajoso escolher sempre um valor muito pequeno para a constante de tempo $T_t$ , porque o integrador é "resetado" rapidamente. No entanto, alguns cuidados devem ser tomados ao introduzir o anti-windup em sistemas com ação derivada. Se a constante de tempo $T_t$ for muito pequena, erros espúrios podem causar saturação da saída, o que acidentalmente reseta o integrador. Åström e Hägglund [1] recomendam que a constante de tempo de rastreamento $T_t$ deve ser maior que $T_d$ (tempo derivativo) e menor que $T_i$ (tempo integrativo). A "regra de ouro" sugerida é adotar: $T_t = \sqrt{T_i\,T_d}$ .

Observação: Caso o estudante apresente este método, sugere-se que o mesmo simule ao menos, 5 diferentes valores de $T_t$ para mostrar e compreender sua influência na redução do enfeito de windup. Sugere-se valores como: $T_f=[0,5 \; 1 \; 2 \; 5 \; 10 \; 20 \; 40]$ segundos..

Sugere-se que os estudantes comparem a atuação do PID "tradicional" com o PID com anti-windup baseado neste método, como é mostrado na próxima figura:

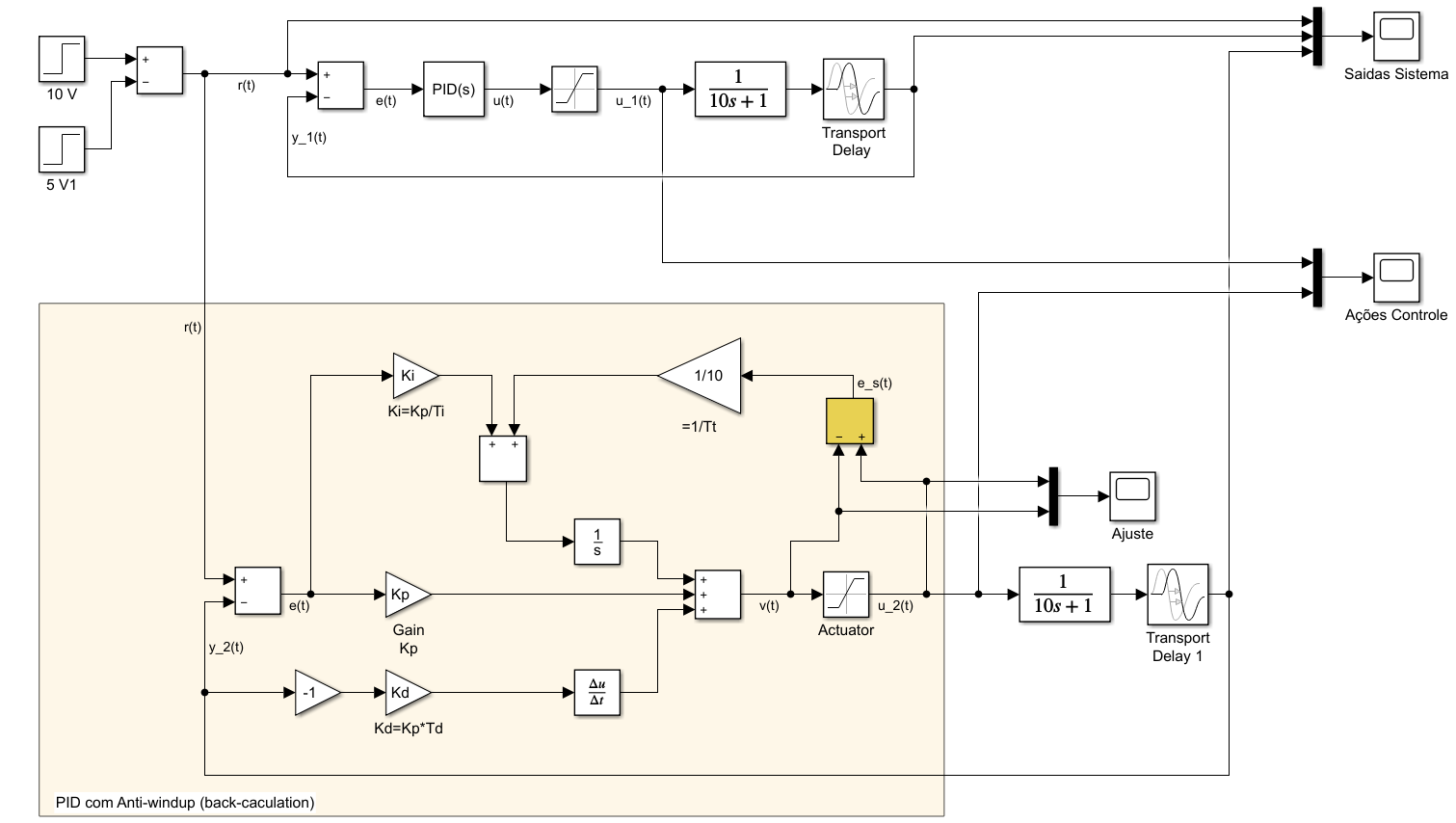
O resultado da simulação do bloco mostrado na figura anterior, gerou as seguintes respostas do sistema:

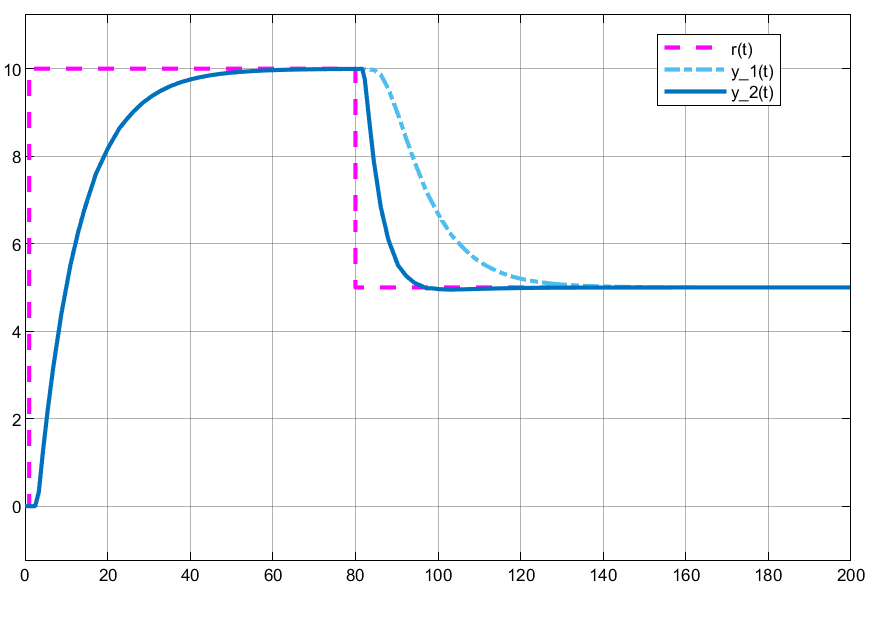
As ações de controle geradas aparecem na próxima figura:

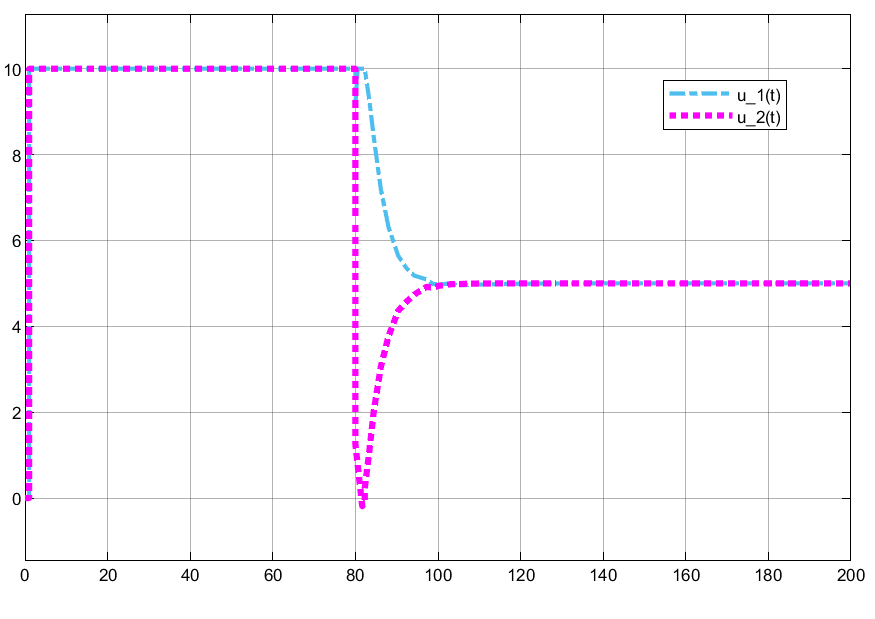
E os ajustes realizados para ação anti-windup aparecem na próxima figura:

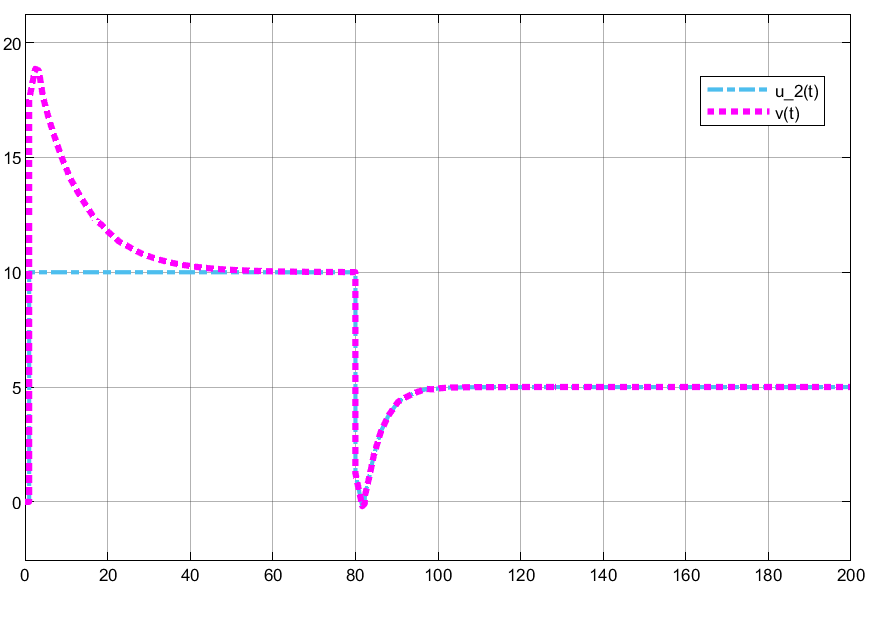
Na simulação anterior foi adotado $T_f=10$ segundos.

2.2 Controlador no modo "Integrator Clamping"

O método da "Integração Condicional" ou Integrator Clamping, aparece no tópico "Conditional Integration" (ou "Integração condicional"), pág. 85 de [1]. É uma alternativa ao método back-calculation.

Neste método, a integração é "desligada" quando o sinal de controle está distante do estado estacionário (valor de referência desejado). A ação integral é, portanto, usada apenas quando certas condições são cumpridas, caso contrário, o termo integral é mantido constante (ou num estado de "saturação"). Por isto este método também é conhecido como integrator clamping (ou tamponamento do integrador).

As condições em que a integração é inibida podem ser expressas de muitas maneiras diferentes. A figura à seguir (figura 3.26 de [1]), mostra uma simulação desta técnica aplicada no Exemplo 3.1 (de [1], mostrado no início deste documento), com a integração condicional ocorrendo de tal forma que o termo integral é mantido constante durante a saturação.

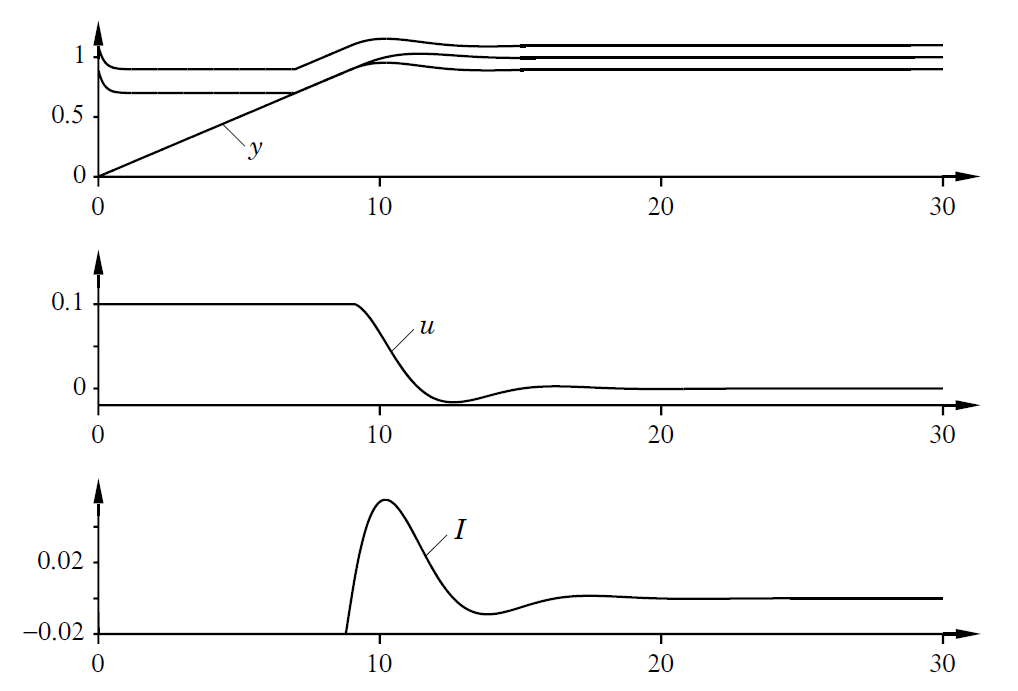
A figura anterior mostra o resultado de uma simulação do sistema do Exemplo 3.1 com integração condicional. São mostrados os seguintes sinais: a banda proporcional, a saída do processo $y(t)$ , o sinal de controle $u(t)$ e a ação integral $I(t)$ .

Algumas condições de comutação diferentes são agora consideradas. Uma abordagem simples é desativar a integração quando o erro de controle é grande. Outra abordagem é desligar a integração durante a saturação. Ambos os métodos têm a desvantagem de que o controlador pode ficar travado num erro de controle diferente de zero se o termo integral tiver um valor grande no momento do desligamento da ação integral.

Para tentar contornar o problema anterior, a integração pode ser desligada quando o controlador está saturado e a atualização da ação integral é realizada de tal forma que faz com que o sinal de controle fique na saturação.

Suponha, por exemplo, que o controlador fique saturado no limite superior. A integração é então desativada se o erro de controle for positivo, mas não se for negativo.

Alguns métodos de integração condicional destinam-se principalmente à inicialização de processos em lote, quando pode haver grandes alterações no setpoint.

Uma versão em particular, usada em controle de temperatura, define uma banda proporcional fora do setpoint quando há grandes desvios de controle. O deslocamento pode ser usado para ajustar a resposta transitória obtida durante o arranque do processo. Os parâmetros utilizados são denominados cut-back ou preload -- ver próxima figura:

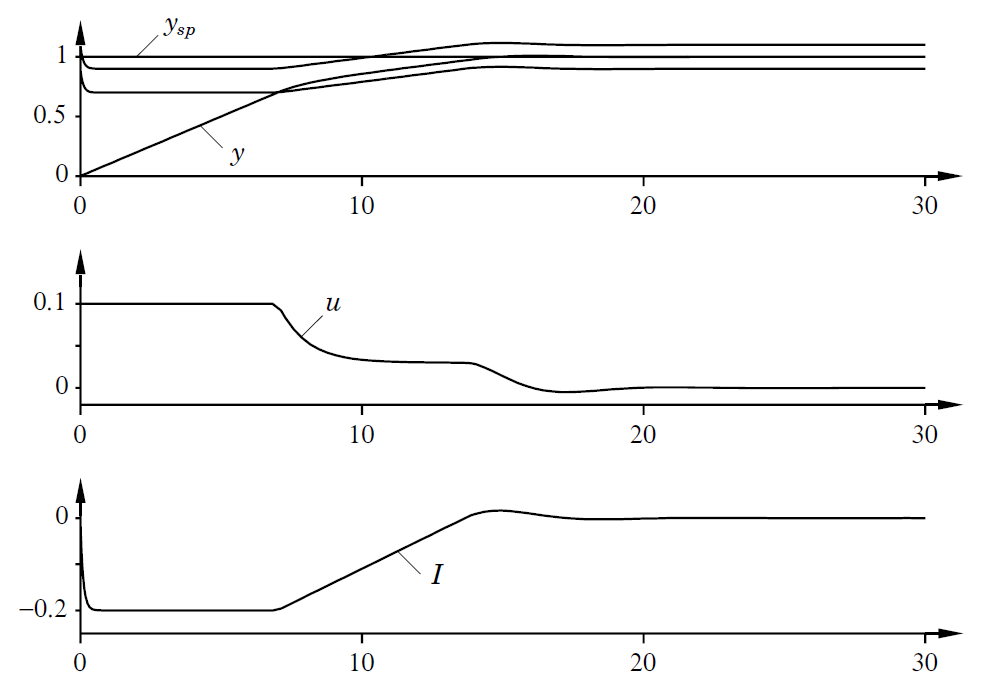
A figura anterior (originalmente figura 3.27 de [1]), mpostra um ajuste da banda proporcional usando parâmetros de corte (cut-back). Os diagramas mostram a banda proporcional, o ponto de ajuste $y_{sp}(t)$ , a saída do processo $y(t)$ , o sinal de controle $u(t)$ e a ação integral $I(t)$ .

Neste sistema, a banda proporcional é posicionada com uma extremidade no ponto de ajuste (sinal de referência, $r(t)$ ou $y_{sp}(t)$ ) e a outra extremidade na direção do valor medido ( $y(t)$ ) quando há grandes variações. Estes métodos podem ajudar a eliminar o problema do windup principalmente nos casos de sistemas que sofrem perturbações.

A Banda Proporcional:

A noção de banda proporcional é útil para compreender o efeito de windup e explicar os esquemas de anti-windup. A banda proporcional corresponde ao intervalo do sinal de controle no qual o atuador não satura se o valor instantâneo da saída do processo ou seu valor previsto (referência) estiver dentro desta faixa. Para o controlador PID sem limitação na sua ação derivativa, o sinal de controle é resultado de:

$u=K(b\,y_{sp}-y)+I-K\,T_d\,\frac{dy}{dt} \qquad$ (3.24)

Podemos tentar prever a saída do processo, $y_p$ como:

$y_p=y+T_d \, \frac{dy}{dt}$

Pode-se definir a banda proporcional $[y_l, y_h]$ como:

$y_l = b \, y_{sp} + \dfrac{I-u_{max}}{K}\qquad$ (3.25(a))

$y_h = b \, y_{sp} + \dfrac{I-u_{min}}{K}\qquad$ (3.25(b))

onde: $u_{min}$ e $u_{max}$ são os valores para o sinal de controle para os quais o atuador satura.

O controlador opera de modo linear (sem saturação), se o sinal previsto apra saída do processo, $y_p$ , estiver dentro da banda proporcional. O sinal de controle satura quando $y_p$ estiver fora da banca proporcional.

Note que a banda proporcional pode ser deslocada mudando-se o termo integral nas equações (3.25).

Para ilustrar a utilidade do conceito da "banda proporcional", a proxima figura mostra a banda proporcional (fig 3.24 de [1]). Esta figura pode ser comparada com uma figura inicial já mostrada neste documento (fig 3.18 de [1]) para o caso do Exemplo 3.1.

A figura anterior mostra a banda proporcional para o caso do Exemplo 3.1. O diagrama superior mostra a saída do processo $y(t)$ e a banda proporcional. O diagrama inferior mostra o sinal de controle $u(t)$ .

Note que a banda proporcional começa a se mover para cima porque o termo integral aumenta. Isso implica que a saída não atinge a banda proporcional até que esta seja muito maior do que o *setpoint$.

Quando a banda proporcional é atingida, o sinal de controle diminui rapidamente. Entretanto, a banda proporcional muda tão rapidamente, que a saída se move muito rapidamente através da banda, e esse processo se repete vários vezes.

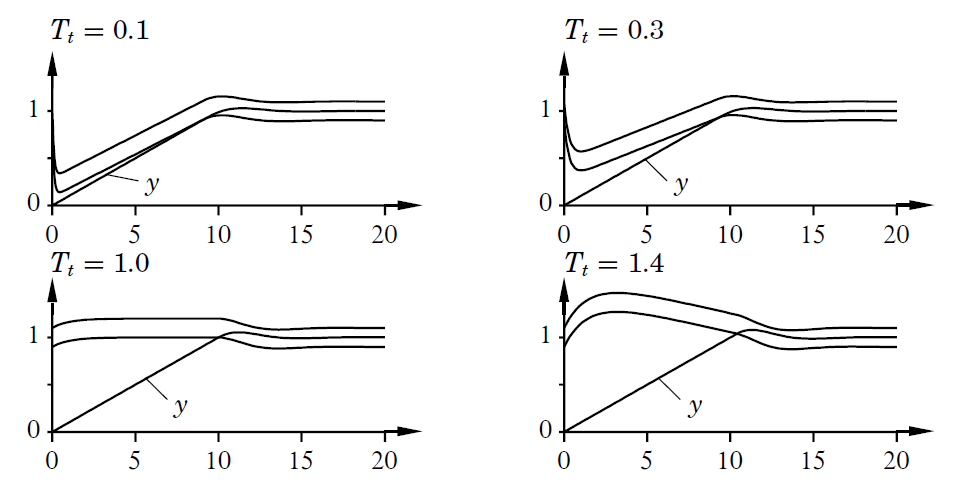
A próxima figura (fig 3.25 de [1]) mostra a banda proporcional para um sistema de controlador com anti-windup por back-calculation com diferentes valores para a constante de tempo de seguimento $T_t$ (tracking time constant).

A figura anterior mostra que a constante de tempo de rastreamento tem um influência significativa na banda proporcional. Devido ao rastreamento, a banda proporcional é movida para mais perto da saída do processo.

Que tão rápido esta aproximação é realizada depende da constante de tempo de rastreamento $T_t$ . Entretanto, note que pode haver uma desvantagem em movê-lo muito rapidamente, uma vez que a saída prevista pode então se mover para a banda proporcional por causa do ruído e fazer com que o sinal de controle diminua desnecessariamente.

Outros métodos

Outros métodos/abordagens podem ser adotados. De fato, o Simulink traz na sua biblioteca de PID´s, um PID com a opção de "Rastreamento", incorporando uma modificação na técnica back-calculation, chamada de tracking mode por [1].

A próxima figura apenas ilustra um PID com anti-windup por back-calculation que trabalha no modo tracking:

Na figura anterior, $SP$ se refere à "Set Point" (sinal de referência), $MV$ se refere à Manipulated Value (ou "Variável Manipulada") que corresponde a saída monitorada (sensoriada) do processo, ou sinal $y(t)$ , e $TR$ se refere ao sinal de TRacking. O novo sinal de entrada $TR$ neste PID, chamado de tracking signal é o que a saída do controlador tentará seguir.

A próxima figura, traz um diagrama em blocos que permite entender um pouco melhor esta nova estrutura de PID:

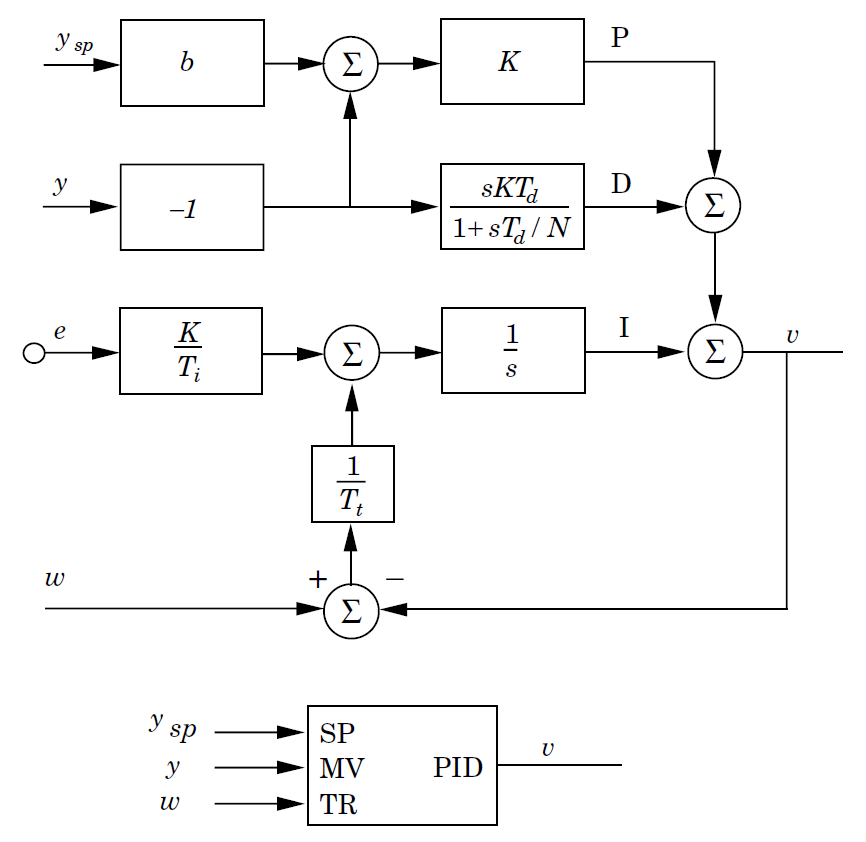
A figura anterior também é adaptada de [1] (Fig 3.22). Ela mostra que nesta abordagem o controlador possui três entradas: o setpoint (neste caso, $y_{sp}(t)$ ), a saída medida do processo ( $y(t)$ ), e um sinal de rastreamento ( $w(t)$ ). A nova entrada "TR" (ou $w(t)$ ) é chamada de sinal de rastreamento porque a saída do controlador seguirá esse sinal. Observe que o rastreamento é inibido quando $w = v$ .

Note este PID presente na biblioteca de blocos disponíveis no Matlab/Simulink:

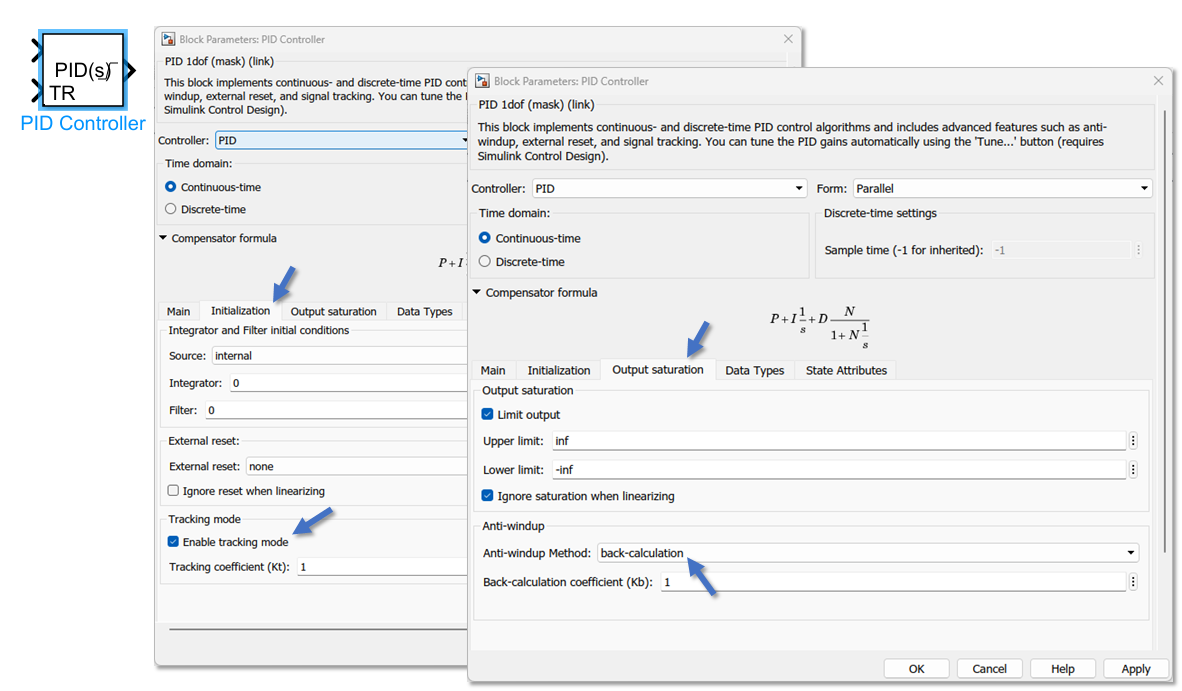
Mas atenção, esta técnica (este PID), não está previsto para ser explorado neste trabalho.

Referências

[1] Åström, KJ & Hägglund, T 1995, PID Controllers: Theory, Design, and Tuning. 1a-ed., ISA - The Instrumentation, Systems and Automation Society, Research Triangle Park, North Carolina. -- Disponível em 29/11/2022.

[2] Improving the Beginner’s PID – Derivative Kick, Blog, URL: http://brettbeauregard.com/blog/2011/04/improving-the-beginner’s-pid-derivative-kick/ (acessado em 01/12/2022).

[3] Anderson, Mondi; How to Tune a PID Controller, Realpars, Postado em 11/01/2021, URL: https://realpars.com/pid-tuning/ (acessado em 01/11/2022).

[4] Zhuge, Scott; PID Control Theory, Crystal Instruments, Postado em 24/08/2020, URL: https://www.crystalinstruments.com/blog/2020/8/23/pid-control-theory (acessado em 01/11/2022).

Fernando Passold, em 30/11/2022 ~ 02/12/2022.