Photo by Johannes Plenio on Unsplash

Lab 1) PID (alógico) e sintonização

Objetivo: a ideia desta aula é recapitular detalhes importantes sobre o controlador PID analógico, adotar algum método de sintonia e simular o método e o PID sobre uma planta hipotética.

O PID Analógico

Controladores PID (Proporcional + Integral + Derivativo) são amplamente adotados na indústria. Sua função de transferência no formatpo bastante didático é:

u (t) = K p e (t) + K i \int t 0 e (τ) d τ + K d d e ( t ) d t

$\mathrm {u} (t)=K_{p}{e(t)}+K_{i}\int _{0}^{t}{e(\tau )}\,{d\tau }+K_{d}{\frac {de(t)}{dt}}$

Sua transformada de Laplace leva à:

C (s) = K p + K i s + K d \cdot s = K c (1 + 1 T i \cdot s + T d \cdot s)

$C(s)=K_p + \dfrac{K_i}{s} + K_d \cdot s = K_c \left( 1 + \dfrac{1}{T_i \cdot s} + T_d \cdot s \right)$

ou ainda:

C (s) = K c (T d T i s 2 + T i s + 1 T i s) = K d s 2 + K p s + K i s

$C(s)=K_c \left( \dfrac{T_d\,T_i\,s^2 + T_i\,s + 1}{T_i \,s} \right) = \dfrac{K_d\,s^2 + K_p\,s + K_i}{s}$

onde: $K_p=$ ganho proporcional; $K_i=$ ganho integral; $K_d=$ ganho derivativo; $K_c=$ ganho geral do PID; $T_i=$ constante de tempo integral; $T_d=$ constante de tempo derivativo.

Métodos de Sintonia baseados em Ziegler-Nichols

O procedimento de seleção dos parâmetros do controlador PID de modo a serem atendidas as especificações de desempenho é conhecido como “sintonia do controlador”. Nichols e Ziegler (em 1942) propuseram regras práticas para sintonia de controladores PID, baseados na resposta experimental da planta à ser controlada.

Referência:

Ziegler, J.G & Nichols, N. B. (1942). “Optimum settings for automatic controllers” (PDF.pdf). Transactions of the ASME. 64: 759–768. Archived from the original (PDF.pdf) on 2017-09-18.
Ziegler–Nichols Tuning Rules for PID, Microstar Laboratories (disponível em 13/10/2022).

Método 1 (Resposta ao Degrau da Planta em MA)

Este método é aplicado quando a planta não envolve integradores nem polos complexos conjugados dominantes, ou seja, sua resposta é do tipo super-amortecida ou criticamente amortecida. Nestes casos, o sistema responde de forma similar a um simples sistema de 1a-ordem com exceção da curvatura existente no início da resposta. Algo como:

lab_controle_2_lab_1_fig_1.drawio

Neste tipo de resposta, alguns parâmetros importantes nos interessam:

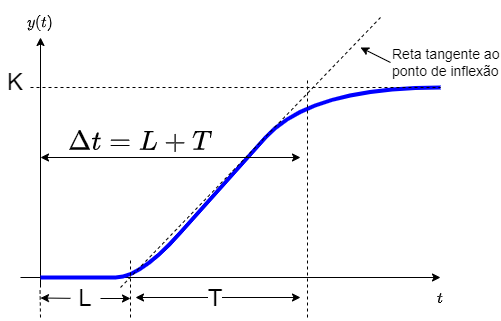
lab_controle_2_resposta_metodo_1_ZH.drawio

Nos interessam: o tempo de atraso, $L$ e a constante de tempo $T$ .

Baseado nestes valores, Ziegler e Nichols sugerem a seguinte tabela para sintonia de um PID:

	$K_c$	$T_i$	$T_d$
P	$T/L$	$\infty$	0
PI	$0,9 \cdot T/L$	$L/0,3$	0
PID	$1,2 \cdot T/L$	$2 \cdot L$	$0,5 \cdot L$

Desta forma, o PID fica:

C (s) = = = K c (1 + 1 T i s + T d s) 1, 2 T L (1 + 1 2 L s + 1 2 L s) 0, 6 T ( s + 1 L ) 2 s

$\begin{array}{rcl} C(s) &=& K_c \left( 1 + \dfrac{1}{T_i\,s} + T_d\,s \right)\\ &=& 1,2 \, \dfrac{T}{L} \left( 1 + \dfrac{1}{2L \, s} + \dfrac{1}{2}L\,s \right)\\ &=& 0,6 T \dfrac{\left( s + \dfrac{1}{L} \right)^2}{s} \end{array}$

Método 2: Busca por $K_u$

Neste segundo método, fecha-se a malha com um simples ganho proporcional (mesmo se já houver um PID no sistema, basta “reseter” as ações de contorle integral e derivativas) e neste caso, se varia o ganho do controlador até que o sistema propositalmente entre em oscilação. Neste caso, a idéiua é posicionar os pólos complexos dominantes de malha-fechada, propostitalmente sobre o eixo $j\omega$ do plano-s. A transformada inversa de Laplace para um sistema que em malha-fechada apresenta pólos complexos, com parte real nula, inmplica numa onda sinosoidal com certa defasagem, ou seja, uma “oscilação sustentada”.

No caso de um PID, se ajusta seus valores para: $T_i=\infty$ e $T_d=0$ , acabando-se por usar apenas ação de controle proporcional. Aumenta-se então o valor de $K_p$ de 0 até $K_u$ (Ultimate gain, ou ganho crítico). Quando $K_p=K_u$ a saída da planta deve assumir e manter oscilações com amplitudes constantes, como mostrado na próxima figura.

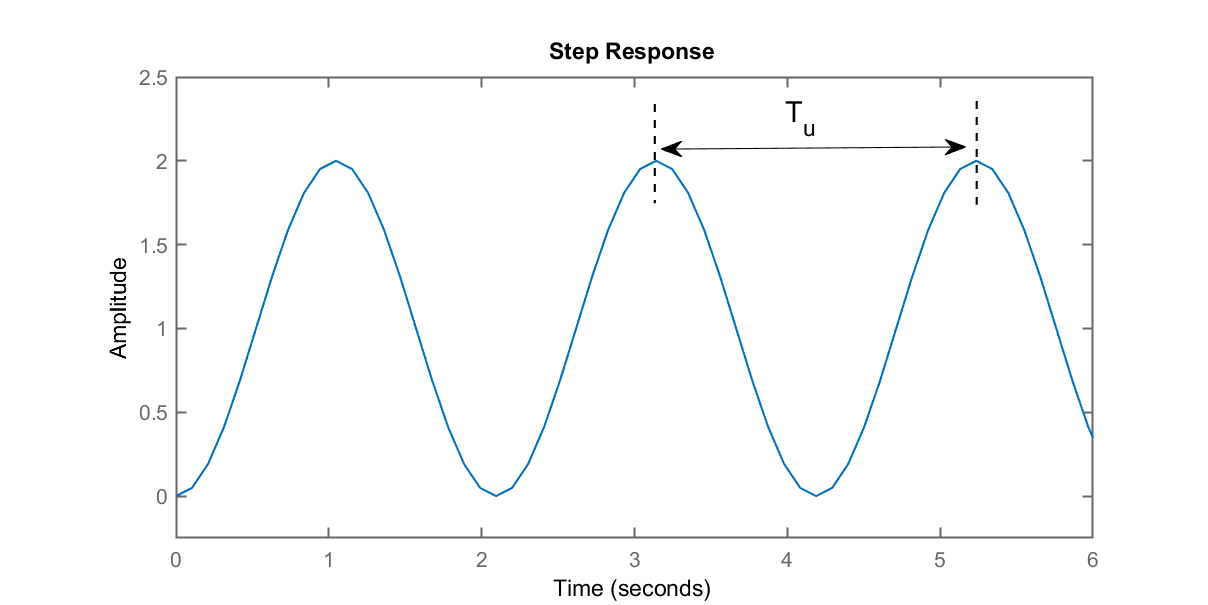
Onde $T_u=$ período da oscilação.

Neste caso, Ziegler-Nichols sugerem outra combinação de valores para sintonia de um PID:

Controlador	$K_c$	$T_i$	$T_d$
P	$0,50 \cdot K_u$	$\infty$	0
PI	$0,45 \cdot K_u$	$0,83 \cdot T_u$	0
PID	$0,60 \cdot K_u$	$0,5 \cdot K_u$	$0,125 \cdot T_u$

ou:

Controlador	$K_c$	$T_i$	$T_d$
P	$0,5 \cdot K_u$	0	0
PI	$0,45 \cdot K_u$	$1,2\cdot(K_p/T_u)$	0
PID	$0,60 \cdot K_u$	$2 \cdot (K_p/T_u)$	$(K_pT_u)/8$

Obs.: outras tabelas para ajuste dos parâmetros do PID baseados no método de Ziegler-Nichols podem ser facilmente encontradas. Por exemplo, a página Wiki em português (menos completa) ou página Wiki em inglês (mais completa). O detalhe é que é comum que os valores sugeridos por Zieglher-Nichols levem à overshoots iniciais da ordem de 50%. Motivo pelo qual, outros autores, sugerem diferentes valores para ajuste inicial dos parâmetros do PID:

Controlador	$K_{p}$	$T_{i}$	$T_{d}$	$K_{i}$	$K_{d}$
P	$0.50K_{u}$	–	–	–	–
PI	$0.45\,K_{u}$	$0.8{\dot{3}}\,T_{u}$	–	$0.54\,(K_u/T_u)$
PD	$0.80\,K_{u}$	–	$0.125\,T_{u}$	–	$0.100\,K_{u}\,T_{u}$
PID clássico	$0.60\,K_{u}$	$0.50\,T_{u}$	$0.125\,T_{u}$	$1.2\,(K_{u}/T_{u})$	$0.075\,K_{u}\,T_{u}$
Regra Integrador de Pessen	$0.70\,K_{u}$	$0.40\,T_{u}$	$0.150\,T_{u}$	$1.75\,(K_{u}/T_{u})$	$0.105\,K_{u}\,T_{u}$
Algum overshoot	$0.3\dot{3}\,K_{u}$	$0.50\,T_{u}$	$0.33\dot{3}\,T_{u}$	$0.{6}\dot{6}\,(K_{u}/T_{u})$	$0.11\dot{1}\,K_{u}\,T_{u}$
Sem overshoot	$0.20\,K_{u}$	$0.50\, T_{u}$	$0.33\dot{3}\,T_{u}$	$0.40\,(K_{u}/T_{u})$	$0.06\dot{6}\,K_{u}\,T_{u}$

Tabela originalmente diponível em: https://en.wikipedia.org/wiki/Ziegler%E2%80%93Nichols_method (em 13/10/2022).

Método 3: Método do relé

Neste caso, se fecha a malha do sistema com um simples controlador proporcional e se programa seu chaveamento entre 2 valores (o que seria on “on”/“off”) conforme o erro seja positivo ou negativo. Este tipo de controlador também é conhecido como controlador “bang-bang“.

De forma mais simples, sua lei de controle fica como:

u (t) = {U 1 U 2 se: e (t) > 0 se: e (t) \leq 0

$u(t) = \begin{cases} U_1 & \text{se: } e(t)>0\\ U_2 & \text{se: } e(t)\le 0 \end{cases}$

ou seja, o sinal de controle $u(t)$ aplicado à planta, varia entre 2 valores fixos: $U_1=$ maior valor e $U_2=$ menor valor; $e(t)=$ sinal de erro. Não necessariamente o valor de $U_1=\text{"on"}=100\%$ e $U_2=\text{"off"}=0\%$ .

Aplicar este tipo de sinal de controle à um sistema, o levará uma oscilação. A ideia aqui é justamente se capturar o período desta oscilação, que coincide justamente com $T_u$ . Com base em outros dados associados com este método (ver figura anterior) se pode inferir o ultimate gain, ou $K_u$ :

K u = 4 b π a

$K_u = \dfrac{4\,b}{\pi \, a}$

onde: $a=$ amplitude da oscilação (faixa da oscilação) dos valores aplicados na entrada da planta (“process variable“); e $b=$ amplitude de oscilação (faixa de oscilação) do sinal de saída da planta.

De posse de $K_u$ e $T_u$ busca-se pelos valores sugeridos para os parâmetros do PID baseados no método de Ziegler-Nichols.

Melhorias no PID tradicional

Mas… na prática o PID pode não ser usado exatamente deste forma. Ocorrem 2 problemas na utilização do PID neste formato (simples):

Saturação da ação integral: resultado do efeito acumulado de integração no integrador principalmente evidenciado quando o sistema à ser controlado possui algum elemento de saturação. Este efeito é conhecido como efeito “wind-up”.
Sensibilidade à ruídos: a parte derivativa pode deixar este controlador substancialmente sensível para sinais sensoriados ruidosos (caso de taco geradores por exemplo).

PID com Filtro Derivativo

O problema da susceptibilidade do PID para com informações ruidosas provenientes de uma planta pode ser solucionado com o uso proposital de um filtro derivativo.

Se analisamos o diagrama de Bode da ação Derivativa pura de um PID percebemos o seguinte diagrama:

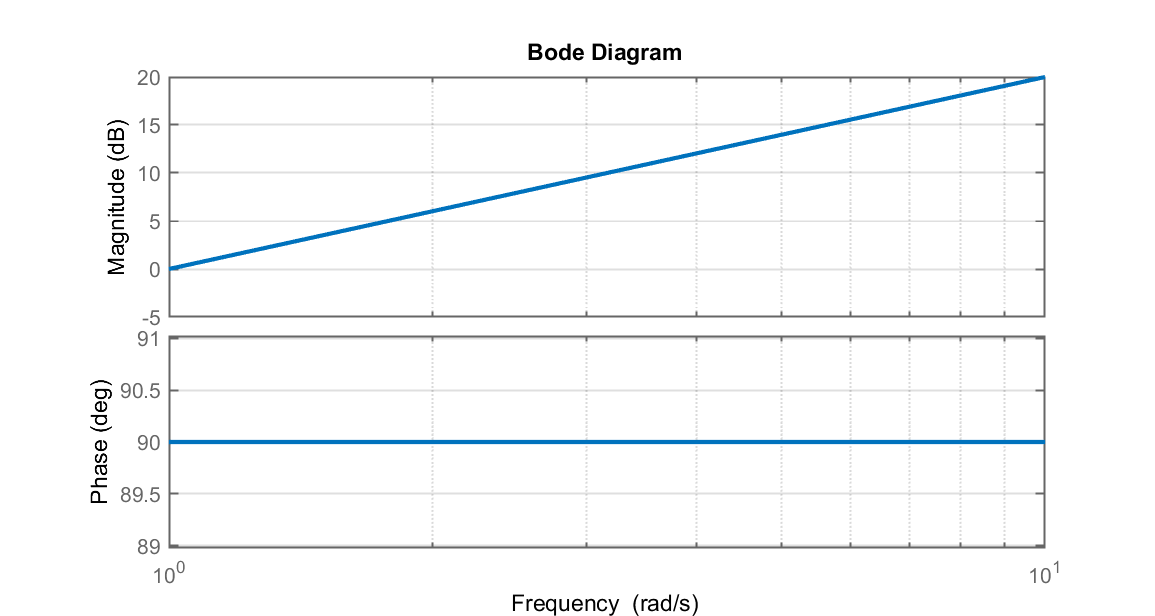
Analisando-se melhor a figura acima, percebemos, pelo diagrama de magnitude, que o ganho de uma ação derivativa pura só aumenta à taxa de 20 db/década, sem limite e conforme a frequência aumenta, o que na prática significa que componentes (sinal de erro) de alta frequência, serão amplificados. O que pode deixar o sinal de atuação (saída) do PID muito oscilatório (ruidoso).

Uma forma simples de atenuar este comportamento é limitar o ganho para frequências elevadas. A equação do PID passa à ser:

C (s) = K p + K i 1 s + K d ⎛ ⎝ ⎜ ⎜ N 1 + N s ⎞ ⎠ ⎟ ⎟

$C(s)=K_p + K_i \, \dfrac{1}{s} + K_d \left( \dfrac{N}{1+\dfrac{N}{s} } \right)$

Note pela expressão anterior, que a ação derivativa incorpora agora um filtro, ou seja:

D (s) = K d ⎛ ⎝ ⎜ ⎜ N 1 + N s ⎞ ⎠ ⎟ ⎟ = K d [N \cdot s ( s + N )]

$D(s)=K_d \, \left( \dfrac{N}{1+\dfrac{N}{s}} \right) = K_d \, \left[ \dfrac{N \cdot s}{(s+N)} \right]$

onde $N=$ coeficiente do filtro.

Suponha que $N=100$ e observe o que ocorre com a expressão anterior:

D (s) = 100 \cdot s ( s + 100 )

$D(s)=\dfrac{100 \cdot s}{(s+100)}$

ou seja, um sistema com:

zero na origem (a ação derivativa pura);
polo em $s=-100$ ;
ganho (quando $\omega \to \infty$ ) igual à $20 \log_{10}(100)=40$ dB.

O diagrama de bode desta última expressão rende:

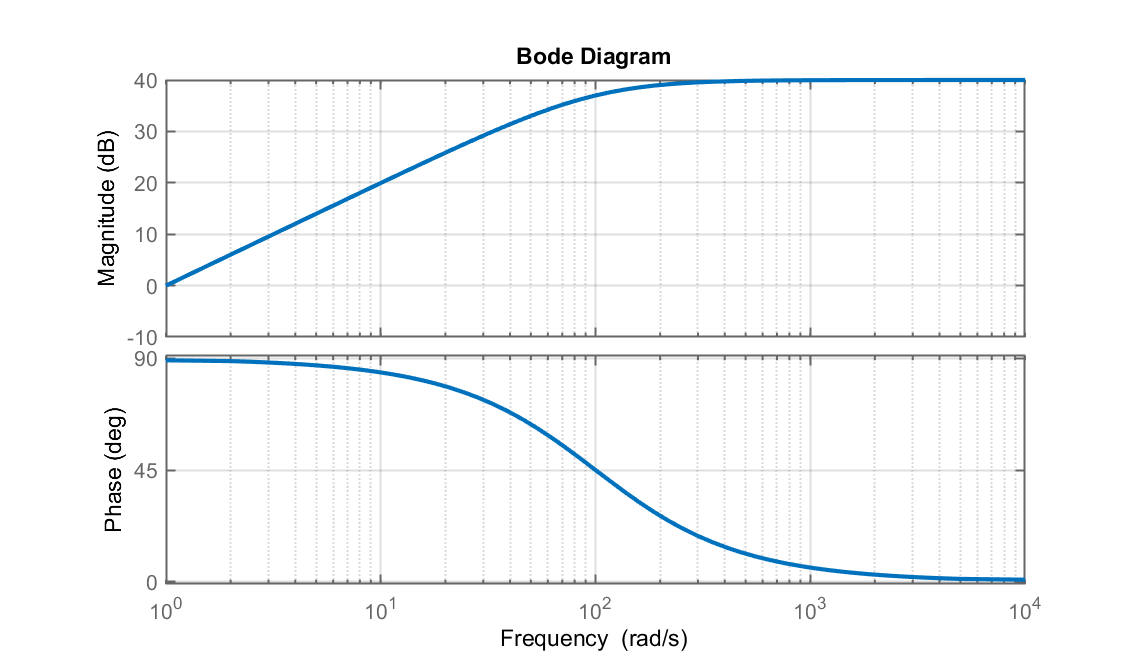
Ou seja, analisando-se o diagrama de magnitude, ser percebe que agora o ganho é limitado em altas frequências ao valor de $N$ (ou seja de 100; $20\cdot \log_{10}(100)=40$ dB) e esta limitação ocorre à partir da frequência de $\omega_c=N$ (100 rad/s). Para frequências abaixo de $\omega_c$ esta expressão atua como uma ação derivativa pura. Esta estratégia acaba então limitando em algo o resultado de ações derivativas sobre sinais (de erro) ruidosos.

Comparando o Diagrama de Bode de um PID com ação derivativa pura e outro com ação derivativa filtrada, teremos algo como:

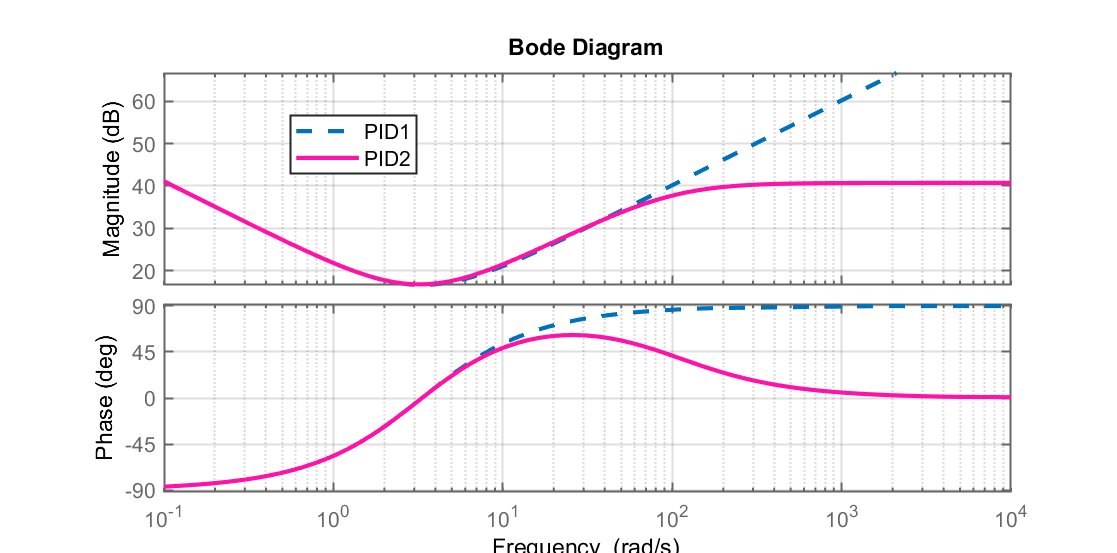
Note que o bloco “PID” disponibilizado pelo Matlab/Simulink já incorpora a ação derivativa com filtragem:

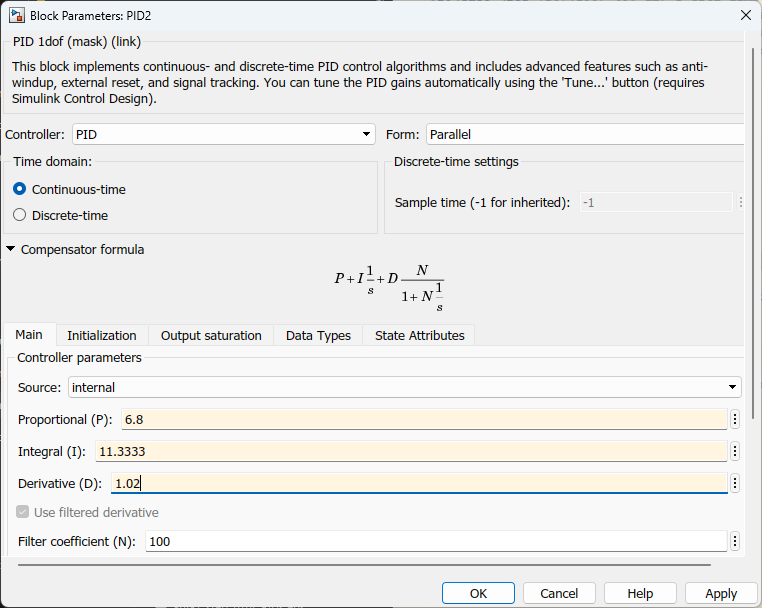
A idéia agora é testar estas abordagens e sintonizar um PID para certa planta.

Planta adotada para simulações com PID

A seguinte planta será adotada para testar o PID:

G (s) = 20 ( s + 1 ) ( s + 2 )

$G(s)=\dfrac{20}{(s+1)(s+2)}$

Ingressando com a mesma no Matlab:

>> G=tf( 20, poly([-1 -2]) )

G =

          10
  -------------------
  0.5 s^2 + 1.5 s + 1

Continuous-time transfer function.

>> zpk(G) % conferindo...

ans =

      20
  -----------
  (s+2) (s+1)

Continuous-time zero/pole/gain model.

>> dcgain(G) % ganho DC da planta
ans =
    10

Note que esta planta apresenta um ganho DC não nulo, isto é, ser for injetado um degrau unitário na sua entrada, sua saída vai tender para $y(\infty)=10$ .

Sintonia de PID usando Método 1

A próxima figura mostra o comportamento da planta quando se aplica um degrau unitário entrada da planta (em malha-aberta):

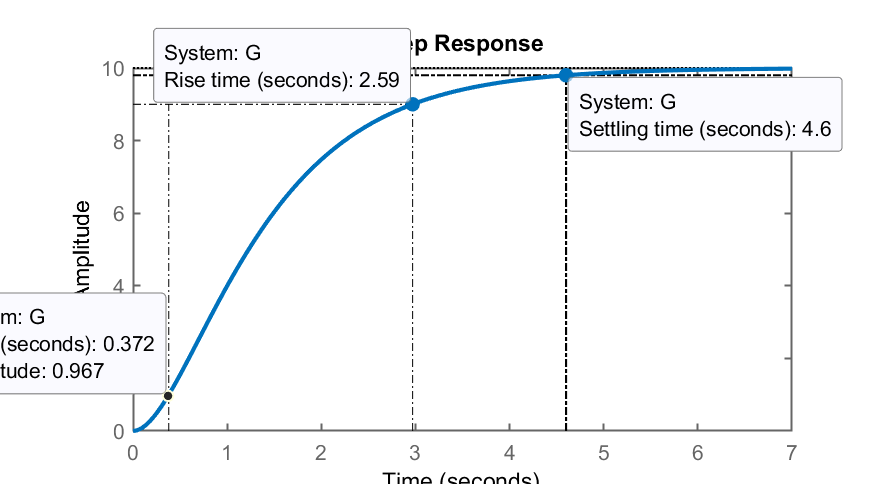
Pode-se capturar os seguintes valores desta resposta:

$L=0,3$ ;
$T=1,7$ .

Procedendo com a simulação do PID para este caso:

>> % Extraíndo dados do gráfico
>> L=0.3; T=1.7;
>> Kc=1.2*T/L; Ti=2*L; Td=0.5*L;
>> Ki=Kc/Ti; Kd=Kc*Td;
>> % Listando [Kc Ki Kd]:
>> [Kc Ki Kd]
ans =
          6.8       11.333         1.02
>>

A equação final do PID com filtro derivativo, considerando $N=100$ fica:

C (s) = 6, 8 + 11 , 333 s + 1, 02 (100 1 + 100 s)

$C(s)=6,8 + \dfrac{11,333}{s} + 1,02 \left( \dfrac{100}{1+\frac{100}{s} } \right)$

Ingressando no Matlab:

>> s=tf('s');
>> PID2=6.8+11.3333/s+1.02*(100/(1+(100/s)))

PID2 =

  108.8 s^2 + 691.3 s + 1133
  --------------------------
         s^2 + 100 s

Continuous-time transfer function.

>> zpk(PID2)

ans =

  108.8 (s^2 + 6.354s + 10.42)
  ----------------------------
           s (s+100)

Continuous-time zero/pole/gain model.

>> zero(PID2)
ans =
      -3.1771 +    0.56814i
      -3.1771 -    0.56814i
>> pole(PID2)
ans =
     0
  -100
>>

Note o segundo polo corresponde a frequência de corte do filtro derivativo.

Um PID com ação derivativa pura fica:

>> PID1=6.8+11.3333/s+1.02*s

PID1 =

  1.02 s^2 + 6.8 s + 11.33
  ------------------------
             s

Continuous-time transfer function.

>> zpk(PID1)

ans =

  1.02 (s+3.339) (s+3.328)
  ------------------------
             s

Continuous-time zero/pole/gain model.

>> zero(PID1)
ans =
       -3.339
      -3.3276
>> pole(PID1)
ans =
     0
>>

Neste caso, notamos apenas um polo na origem que corresponde à ação integrativa pura.

Podemos levantar um diagrama de Bode comparando o impacto destes PIDs no sistema:

>> % Cálculos para primeiro PID (ação derivativa pura)
>> ftma_PID1=PID1*G;
>> zpk(ftma_PID1)

ans =

  20.4 (s+3.339) (s+3.328)
  ------------------------
       s (s+2) (s+1)
>>
>> % Cálculos para segundo PID (ação derivativa filtrada)
>> ftma_PID2=PID2*G;
>> zpk(ftma_PID2)

ans =

  2176 (s^2 + 6.354s + 10.42)
  ---------------------------
     s (s+100) (s+2) (s+1)

Continuous-time zero/pole/gain model.

>> figure; bode (G, PID1, PID2, ftma_PID)

O último comando vai render a seguinte figura:

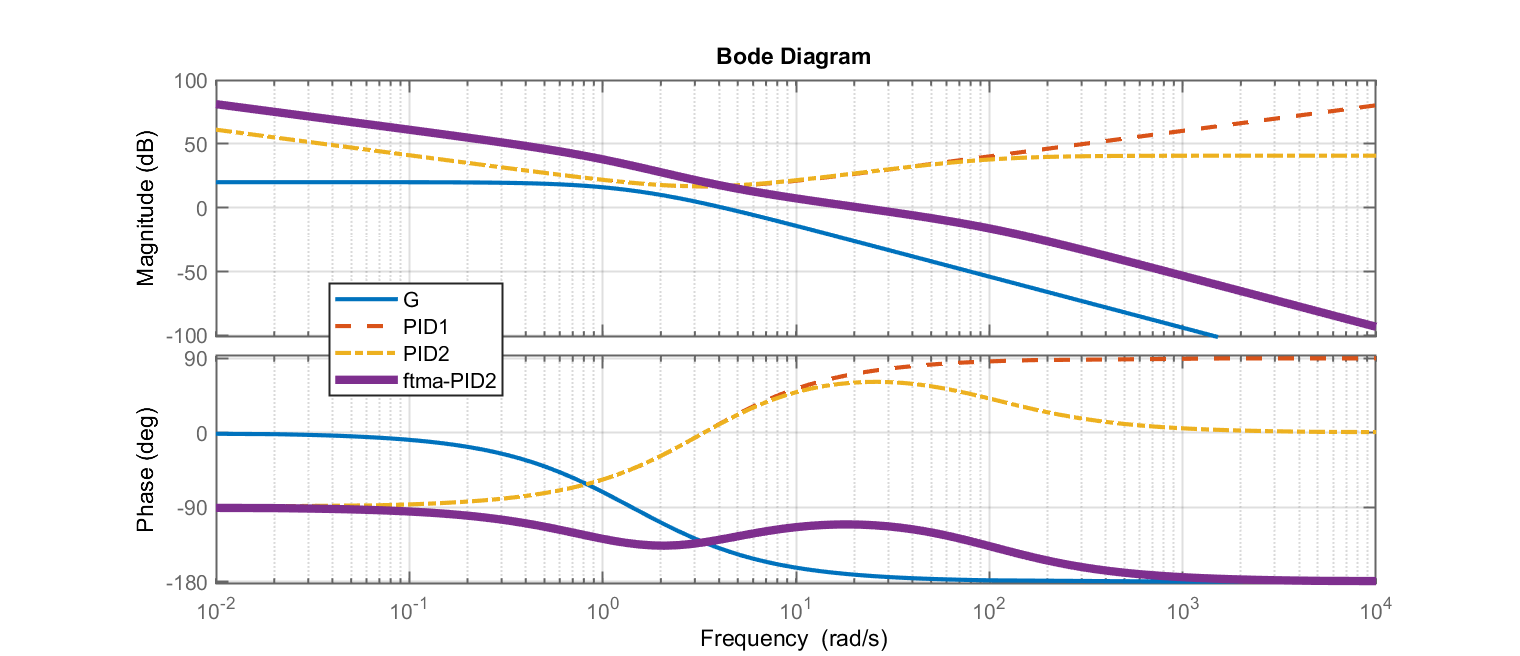
Podemos agora fechar a malha para os PIDs:

>> ftmf_PID1=feedback(ftma_PID1,1);
>> ftmf_PID2=feedback(ftma_PID2,1);
>> figure; step(ftmf_PID1, ftmf_PID2)

Obtemos a seguinte resposta para a planta com os PIDs:

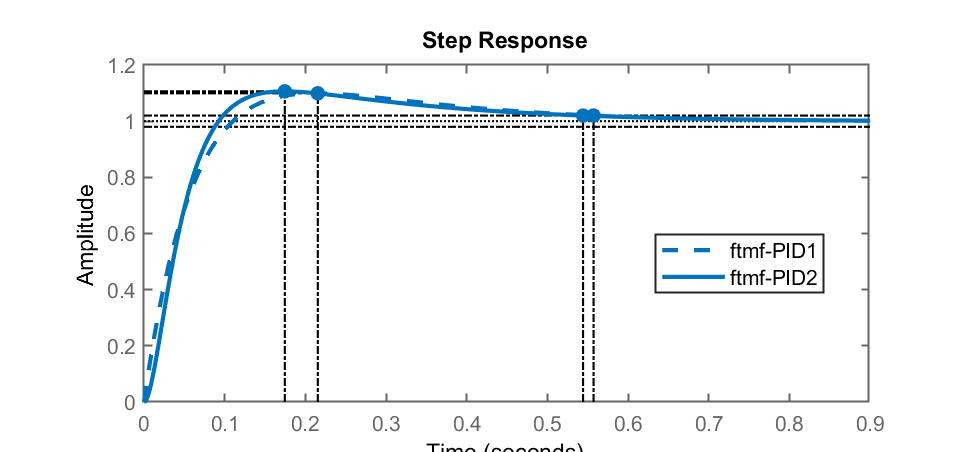
Esta planta também poderia ser simulada usando-se o Simulink:

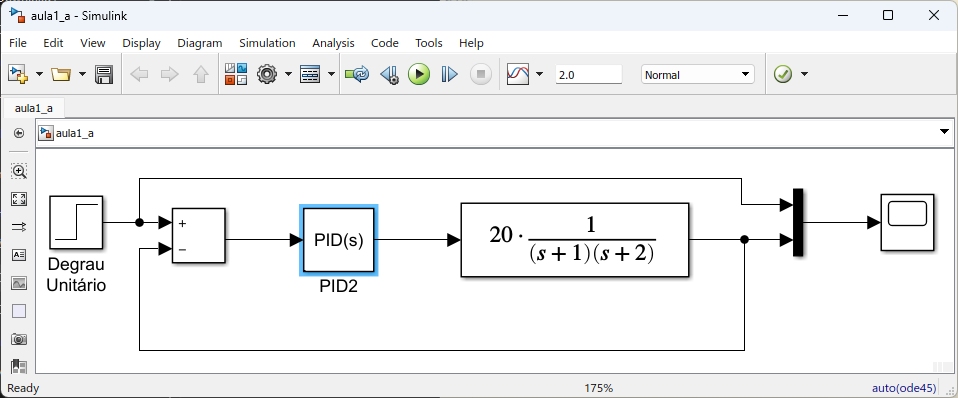
aula1_a.slx.png

Onde a planta foi ingressada na forma de: Biblioteca do Simulink>>Continuos>>Zero-Pole:

Tarefas

Simule a planta $G(s)$ com o PID usando o Matlab/Simulink para a mesma entrada degrau unitário e observe os resultados.
Sugere-se ainda variar os ganhos do PID para comprovar se sucede o que sugere a próxima tabela:

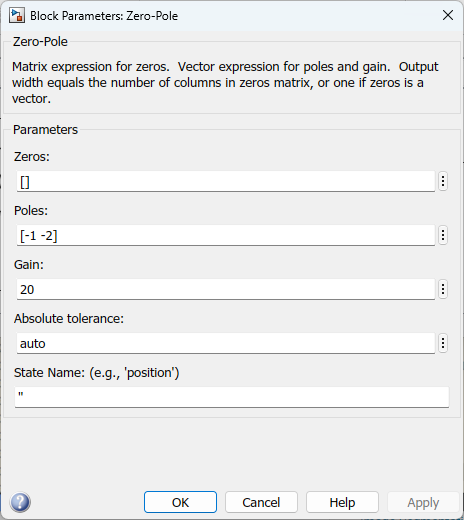
Parâmetro	Tempo de subida	Overshoot	Tempo de assentamento	Erro regime permanente	Estabilidade
$K_{p} \; \uparrow$	Diminui	Aumenta	Pequena mudança	Diminui	Degrada
$K_{i} \; \uparrow$	Diminui	Aumenta	Aumenta	Eliminado	Degrada
$K_{d} \; \uparrow$	Pequena alteração	Diminui	Diminui	Sem efeito	Melhora se $K_d$ é pequeno

Existe uma simulação de comportamento de sistema conforme se variam os parâmetros de um PID que pode ser vista na página [Wikipedia: PID controller] (em inglês):

Mais questões **:

Simule a planta $G(s)$ com o PID usando o Matlab/Simulink mas desta vez com uma entrada senoidal que deve variar sua amplitude entre 0 e 2 com período de oscilação de 1,5 segundas e observe os resultados.
Idem ao item (2) anterior, mas agora acrescente (some) um sinal ruidoso à saída da planta, simulando um sensor ruidoso e observe os resultados obtidos para um PID sem filtro derivativo e com filtro derivativo. Considere que o ruído possua amplitude de apenas 0,1 (valor do pico) e que oscila numa frequência de $10000/(2\pi)$ Hz. Mostre num gráficos os sinais de saída dos 2 controladores (do PID com ação derivativa pura e do PID com ação derivativa filtrada).
Repita o procedimento de sintonia do PID considerando agora a planta: $G_2(s)=\dfrac{20}{s^2 + 4s + 8}$ . Mostre o procedimento de sintonia adotado acompanhado de suas figuras e mostre o resultado final obtido com o PID sintonizado.

Obs.: para realizar o item (3) sugere-se o seguinte diagrama de blocos no Simulink:

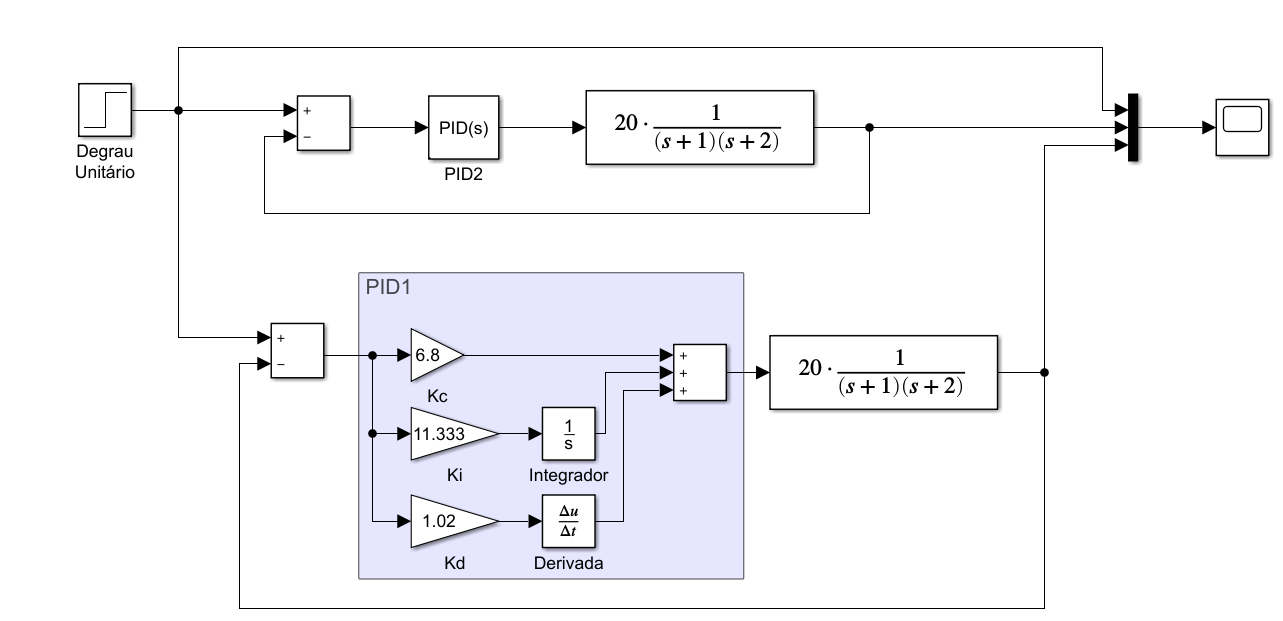
aula1_PIDs.slx.png

[Fim].

Observações

Você pode tentar usar o seguinte comando para gerar figuras .png à partir dos diagramas de blocos gerados via Simulink:

>> % gerar imagem PNG à partir de "aula1_a.slx"
>> print('-saula1_a', '-dpng', '-r200', 'aula1_a.slx.png')
>> print('-saula1_a', '-djpeg', '-r150', 'aula1_a.slx.jpg')

Prof. Fernando Passold, em 13/10/2022