Projeto Contador Síncrono 2021/2

Projeto deste semestre:

Como resolver?

1) Quantos FF's?

Solução:

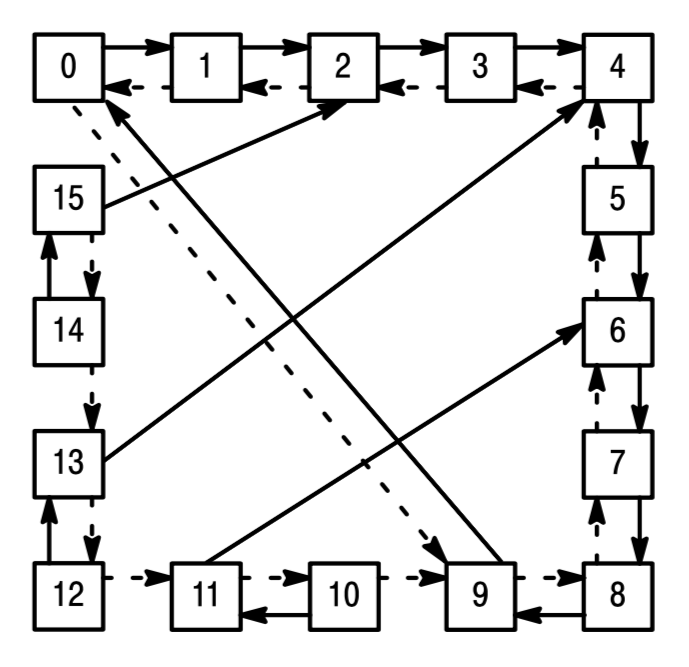
Considerações iniciais: o contador proposto possui 6 estados. 6 estados => 3 FF's. 3 FF's. permitem $2^3=8$$2^3=8$ estados diferentes, isto significa que 2 estados (ou combinações de contagem) não fazem parte da sequencia prevista para contagem. Estes estados/combinações podem ser usados como condições "don't care" durante a realização do projeto.

As combinações binárias ou estados que não são atingidas pelo circuto usando os 3 FF's, são os estados: 0 e 5.

2) Como continuar?

Solução: Levantar tabela de transição.

A tabela de transição relaciona como o contador parte de certo estado atual, $q(t)$$q(t)$ e evolui para o próximo estado, $Q(t+1)$$Q(t+1)$, à cada novo pulso ativo de clock e dependendo do nível lógico da variável $M$$M$. Para simplificar o projeto é mais prático considerar a variável $M$$M$ que controla forma como esta contador funciona, como sendo a MSB (mais significativa), assim, a tabela que relaciona $q(t)⟶Q(t+1)$$q(t) \longrightarrow Q(t+1)$ é mais fácil de se construída, além do que, fica dividida entre a forma como o contador deve se comportar quando $M=0$$M=0$ e quando $M=1$$M=1$. Outro detalhe no momento da confecção desta tabela (de transição): os estados atuais do circuito são relacionados seguindo a sequencia numérica crescente tradicional, não a forma como o contador se comporta. Isto exige alguma atenção no momento de completar as colunas $Q(t+1)$$Q(t+1)$ (você deve considerar o nível lógico da entrada $M$$M$ e as condições atuais de contagem, $q(t)$$q(t)$). Note que este circuito vai fazer uso de 3 FF's, assim, esta tabela relaciona: $M{q}_2(t)q_1(t)q_0(t)⟶Q_2(t+1)Q_1(t+1)Q_0(t+1)$$M\,q_2(t)\,q_1(t)\,q_0(t) \longrightarrow Q_2(t+1)\,Q_1(t+1)\,Q_0(t+1)$; a fim de simplificar esta representação, vamos simplesmente escrever na tabela as colunas $|M{q}_2{q}_1{q}_0|⟶|Q_2{Q}_1{Q}_0|$$|M\,q_2\,q_1\,q_0| \longrightarrow |Q_2\,Q_1\,Q_0|$.

Em resumo esta tabela (de transição) é necessária para que possamos estabelecer a forma como devem ser ajustadas as entradas de cada FF adotado (no caso, FF's D) para que o circuito realize cada uma das transições (de estado) desejadas: $q_i(t)⟶Q_i(t+1)|D_i(t)$$q_i(t) \longrightarrow Q_i(t+1) \, | \, D_i(t)$.

Num primeiro momento, a tabela de transição fica igual com a representada abaixo:

Terminando/completando a tabela:

$q(t)⟶Q(t+1)$$q(t) \longrightarrow Q(t+1)$

Considerando a tabela de transição do FF adotado teremos:

$\begin{array}{cccc}q(t)& ⟶& Q(t+1)& D(t)\\ 0& & 0& 0\\ 0& & 1& 1\\ 1& & 0& 0\\ 1& & 1& 1\end{array}$$\begin{array}{ccc|c} q(t) & \longrightarrow & Q(t+1) & D(t) \\ \hline 0 && 0 & 0\\ 0 && 1 & 1\\ 1 && 0 & 0\\ 1 && 1 & 1\\ \end{array}$

Nota-se que para "programar" o FF-D, basta simplesmente "copiar" na entrada $D$$D$, o próximo estado que o mesmo deve assumir, $Q(t+1)$$Q(t+1)$. No caso do FF-JK seria diferente, mas optamos pelo FF-D para não quer levantar uma tabela de transição que relaciona 6 colunas de saída: $3\times F{F}^{\prime }s\times 2$$3 \times FF's \times 2$ entradas ($J$$J$ e $K$$K$).

Completando então a Tabela de transição do circuito:

Lembrando que qualquer linha incorreta relacionada acima, vai levar a um comportamento incorredo do circuito.

Continuando...

3) Levantando as equações para as entradas de controle dos FFs adotados:

Através de Mapas de Karnaugh para cada um dos FF's:

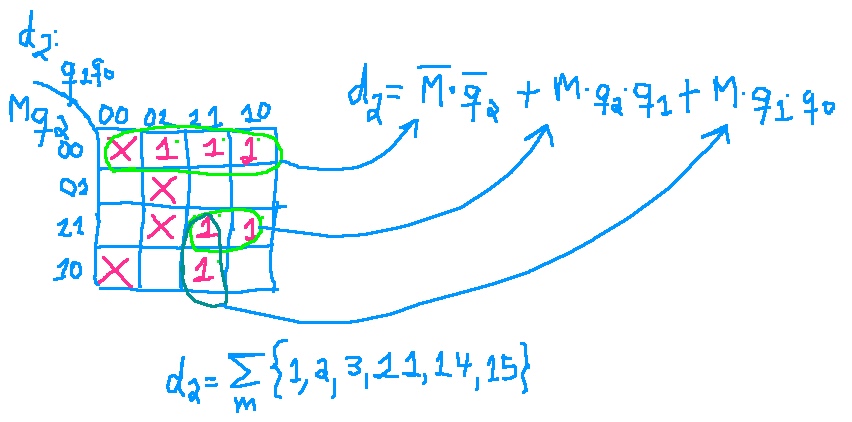
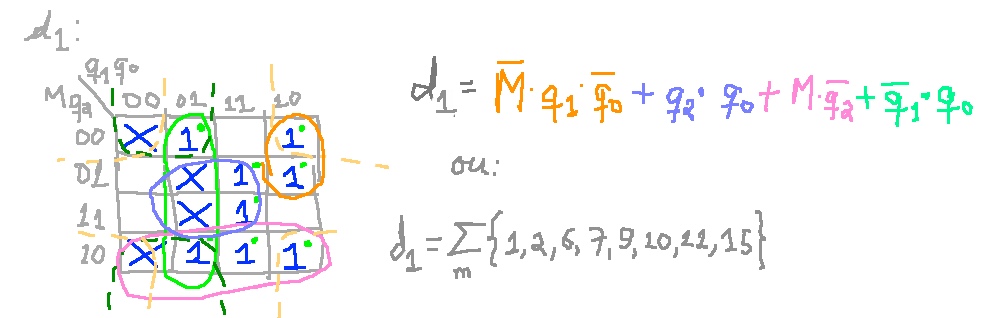
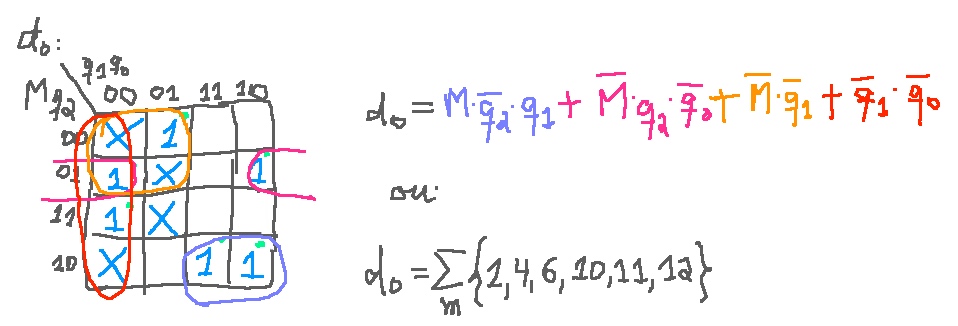
Esta solução, baseada em Mapas de Karnaugh, pressupõe que serão usadas portas lógicas básicas. Isto leva a um total de:

• portas AND(3) x 5 $⟶$$\longrightarrow$ 2 x CI's;
• portas AND(2) x 6 $⟶$$\longrightarrow$ 2 x CI's;
• portas OR(3) x 1 $⟶$$\longrightarrow$ 1 x CI;
• portas OR(4) x 2 $⟶$$\longrightarrow$ 1 x CI;

Total somente para a parte de comando dos FF's: 6 x CI's + CI para os 3 x FF's D (com saída $\bar{Q}$$\overline{Q}$).

Lembrando que queremos usar o CI 74LS175 (Quad FF type D), à exemplo do que já foi usado em semestre anterior, para outro contador síncrono "diferente", ver: https://fpassold.github.io/Digitais_2/2020_1/projeto_contador_sincrono_2020_1.html:

Segue o Datasheet da Motorola para 74LS175:

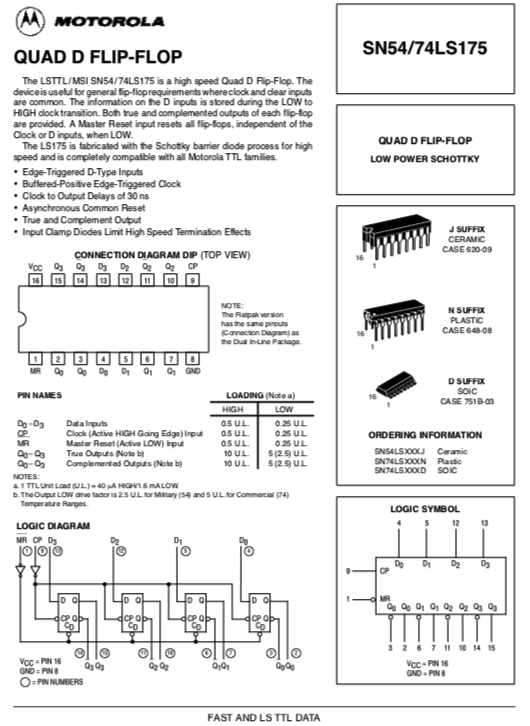
Revela:

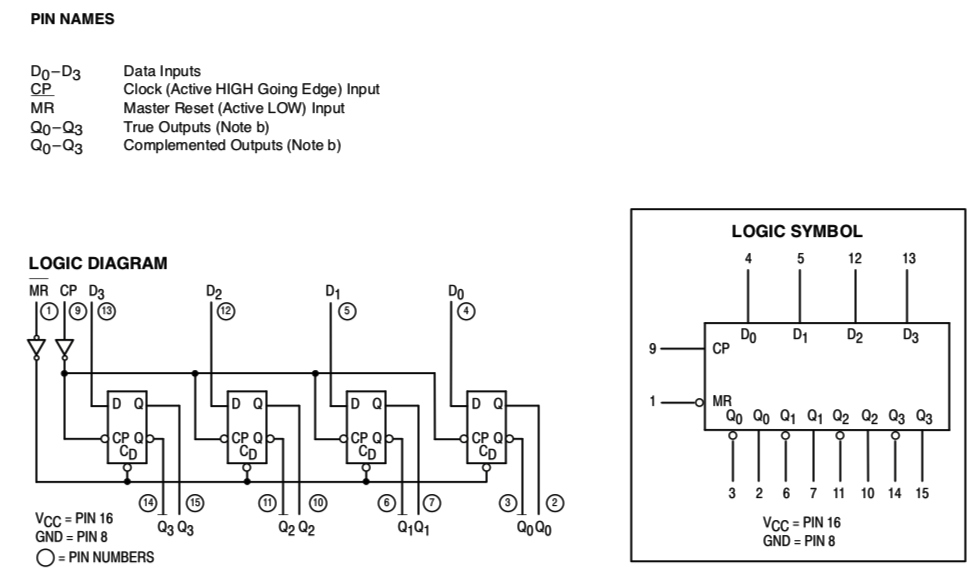
4) Mais considerações para o projeto...

Podemos usar a pastilha 74LS175, mas... existe um porém, se esta pastilha for usada, só conseguimos inicializar o circuito no estado: $q_2{q}_1{q}_0={000}_{(2)}=0_{10}$$q_2q_1q_0=000_{(2)}=0_{10}$ e percebe-se que justamente este estado não está previsto neste projeto.

Supondo que ativamos o "Master Reset" do 74LS175 quando o circuto é recém alimentado fazendo uso de um circuito RC, somos obrigados à analizar os Mapas de Karnaugh anteriores para prever como o circuito se comportará quando colocado no estado inicial "0".

A questão é:

• O circuito depois de inicializado em "0", converge para algum estado previsto para sua sequência normal de operação (e isto ainda depende do nível lógico da variável $M$$M$)? Notar que eventualmente o circuito inicializado em "0" pode não prosseguir para nenhum outro estado e neste caso, fica "paralisado" neste estado, resultado num circuito aparentemente inoperante, mas que na verdade, possui um erro (descuido) de projeto.

Então somos obrigados à prever como o circuito se comporta quando for inicializado no estado "0".

As situações à serem verificadas são as seguintes:

• $Q(t+1)=?$$Q(t+1)=?$ quando $M=0$$M=0$ e $q(t)=0$$q(t)=0$;
• $Q(t+1)=?$$Q(t+1)=?$ quando $M=1$$M=1$ e $q(t)=0$$q(t)=0$;

Então, analizando os Mapas de Karnaugh e agrupamentos realizados para cada entrada dos FF's, temos:

• Quando $M=0$$M=0$ e $q(t)=0$$q(t)=0$, temos: $\begin{array}{c}M|q_2{q}_1{q}_0=0|{000}_{(2)}⟶\{\begin{array}{rcl}{d}_2& =& 1\\ d_1& =& 0\\ d_0& =& 1\end{array}\to Q_2{Q}_1{Q}_0={101}_{(2)}=5_{(10)}\end{array}$$M\,|\,q_2\,q_1\,q_0=0\,|000_{(2)} \longrightarrow \left\{ \begin{array}{rcl}d_2 &=&1\\ d_1 &=& 0\\ d_0 &=&1 \end{array} \right. \quad \rightarrow \quad Q_2\,Q_1\,Q_0=101_{(2)}=5_{(10)}$;

  Note que no Mapa K para $D_2$$D_2$, a célula correspodente ao estado atual $=0|{000}_{(2)}$$=0|000_{(2)}$, foi incluída num agrupamento, portando, o próximo estado assumido por este FF será 1, ou $Q_2(t+1)=1$$Q_2(t+1)=1$. Ou você pode considerar a equação levantada para $D_2$$D_2$: $D_2=\bar{M}\cdot \overline{q_2}+M\cdot q_2\cdot q_1+M\cdot q_1\cdot q_0$$D_2=\overline{M}\cdot\overline{q_2}+M\cdot q_2\cdot q_1+M\cdot q_1 \cdot q_0$ e teremos neste caso: $D_2=\bar{0}\cdot \bar{0}+M\cdot 0\cdot 0+0\cdot 0\cdot 0$$D_2=\overline{0}\cdot\overline{0}+M\cdot 0\cdot 0+0\cdot 0 \cdot 0$ $D_2=1$$D_2=1$ ou seja: $Q_2(t+1)=1$$Q_2(t+1)=1$. Note que no Mapa K para $D_1$$D_1$, a célula correspodente ao estado atual $=0|{000}_{(2)}$$=0|000_{(2)}$, não foi incluída num agrupamento, portando, o próximo estado assumido por este FF será 0, ou $Q_1(t+1)=0$$Q_1(t+1)=0$. Por fim, note que no Mapa K para $D_0$$D_0$, a célula correspodente ao estado atual $=0|{000}_{(2)}$$=0|000_{(2)}$, foi incluída num agrupamento, portando, o próximo estado assumido por este FF será 1, ou $Q_0(t+1)=1$$Q_0(t+1)=1$.

• Quando $M=1$$M=1$ e $q(t)=0$$q(t)=0$, temos: $\begin{array}{c}M|q_2{q}_1{q}_0=1|{000}_{(2)}⟶\{\begin{array}{rcl}{d}_2& =& 0\\ d_1& =& 1\\ d_0& =& 1\end{array}\to Q_2{Q}_1{Q}_0={011}_{(2)}=3_{(10)}\end{array}$$M\,|\,q_2\,q_1\,q_0=1\,|000_{(2)} \longrightarrow \left\{ \begin{array}{rcl}d_2 &=&0\\ d_1 &=& 1\\ d_0 &=&1 \end{array} \right. \quad \rightarrow \quad Q_2\,Q_1\,Q_0=011_{(2)}=3_{(10)}$;

• Notamos que o "5" também não faz parte da sequencia prevista para a contagem, então nossa análise deve prosseguir:

  • Quando $M=0$$M=0$ e $q(t)=$$q(t)=$5, temos: $\begin{array}{c}M|q_2{q}_1{q}_0=0|{101}_{(2)}⟶\{\begin{array}{rcl}{d}_2& =& 0\\ d_1& =& 1\\ d_0& =& 1\end{array}\to Q_2{Q}_1{Q}_0={011}_{(2)}=3_{(10)}\end{array}$$M\,|\,q_2\,q_1\,q_0=0\,|101_{(2)} \longrightarrow \left\{ \begin{array}{rcl}d_2 &=&0\\ d_1 &=&1\\ d_0 &=&1 \end{array} \right. \quad \rightarrow \quad Q_2\,Q_1\,Q_0=011_{(2)}=3_{(10)}$;
  • Quando $M=1$$M=1$ e $q(t)=$$q(t)=$5, temos: $\begin{array}{c}M|q_2{q}_1{q}_0=1|{101}_{(2)}⟶\{\begin{array}{rcl}{d}_2& =& 0\\ d_1& =& 1\\ d_0& =& 0\end{array}\to Q_2{Q}_1{Q}_0={010}_{(2)}=2_{(10)}\end{array}$$M\,|\,q_2\,q_1\,q_0=1\,|101_{(2)} \longrightarrow \left\{ \begin{array}{rcl}d_2 &=&0\\ d_1 &=& 1\\ d_0 &=&0 \end{array} \right. \quad \rightarrow \quad Q_2\,Q_1\,Q_0=010_{(2)}=2_{(10)}$;

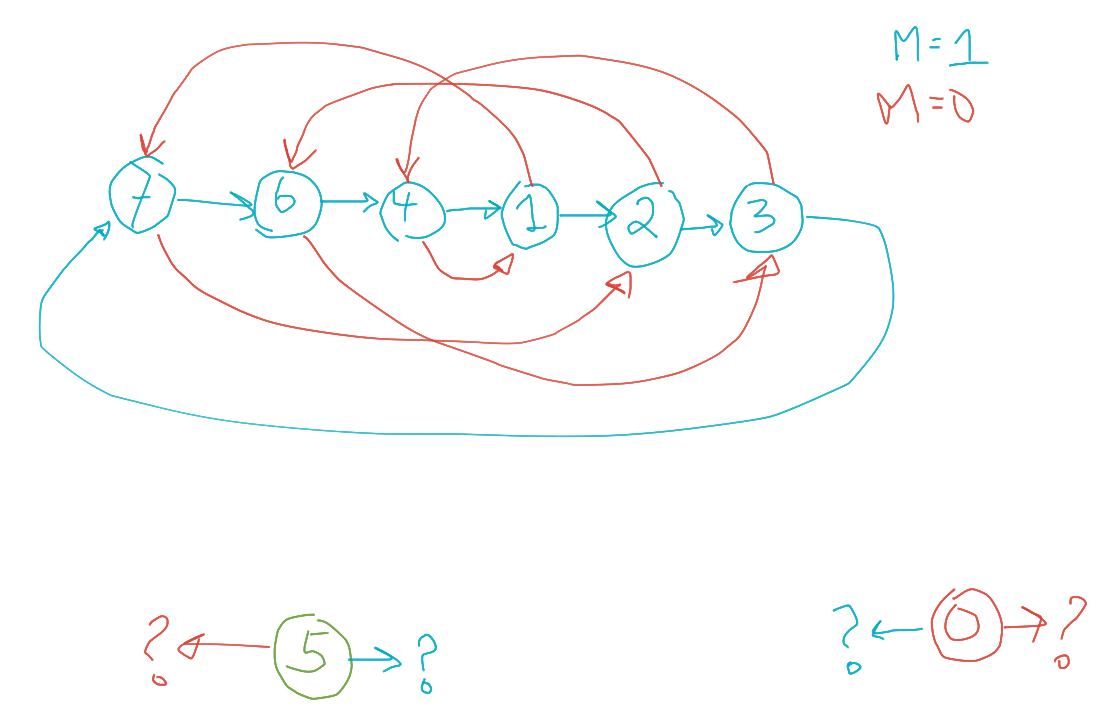
Podemos resumir todo este comportamento num diagrama de estados final:

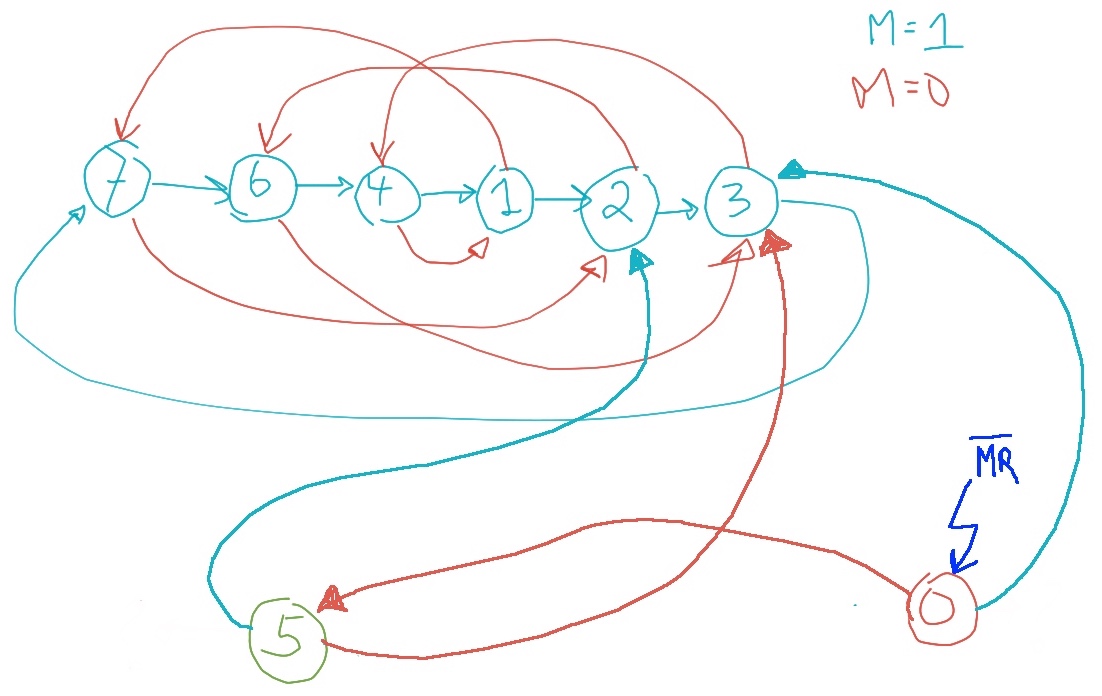
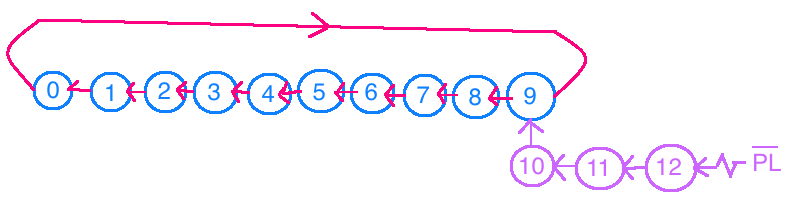
Note que esta sequencia incomum caso o circuito seja inicializado em "0" também ocorre com a pastilha comercial 74LS190 quando a mesma é inicializada (usado PL = "Parallel Load") com o estado "12" por exemplo:

No caso desta pastilha se foi realizado o "PL" com $q(t)={12}_{(10)}$$q(t)=12_{(10)}$, e o mesmo estiver ajustado para contar de maneira crescente, a seguinte sequencia de estados será assumida: E se estiver no modo descrente, esta pastilha vai realizar:

Então o fato de eventualmente o circuito apresentar um comportamento inicial estranho não desabona o projeto. O importante é garantir que se os FF's internos da pastilha 74LS175 forem inicializados com uma borda ascendente de "Master Reset", que o circuito evolua para a sequência de estados esperada.

5) Últimas considerações...

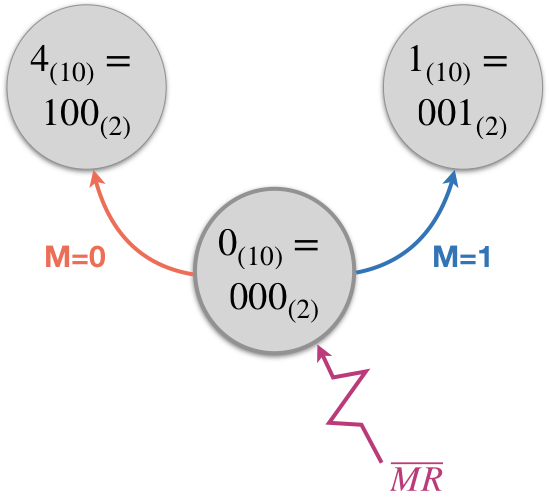
Porém... Uma opção que temos para evitar esta inicialização algo confusa e considerando que só podemos iniciar os FF's do nosso circuito no estado "0" (uso do pino de Master Reset da pastilha 74LS175), uma opção mais interessante e possível já que estamos realizando o projeto, é definir explicitamente quais os próximos estados desejados para o nosso circuito depois que os FF's iniciam todos resetados.

Ou seja, ao invés de deixar a "própia sorte", poderíamos "forçar" as transições iniciais e realizar algo como:

• $\overline{MR}$$\overline{MR}$ e $M=0\Rightarrow M|q_2{q}_1{q}_0=0|{000}_{(2)}=0_{(10)}⟶Q_2{Q}_1{Q}_0=4_{(10)}={100}_{(2)}$$M=0 \quad \Rightarrow \quad M\,|\,q_2\,q_1\,q_0=0|000_{(2)}=0_{(10)} \quad \longrightarrow \quad Q_2\,Q_1\,Q_0=4_{(10)}=100_{(2)}$;
• $\overline{MR}$$\overline{MR}$ e $M=1\Rightarrow M|q_2{q}_1{q}_0=1|{000}_{(2)}=8_{(10)}⟶Q_2{Q}_1{Q}_0=1_{(10)}={001}_{(2)}$$M=1 \quad \Rightarrow \quad M\,|\,q_2\,q_1\,q_0=1|000_{(2)}=8_{(10)} \quad \longrightarrow \quad Q_2\,Q_1\,Q_0=1_{(10)}=001_{(2)}$.

Ou seja, significa que queremos agora fazer (diagrama de estados final):

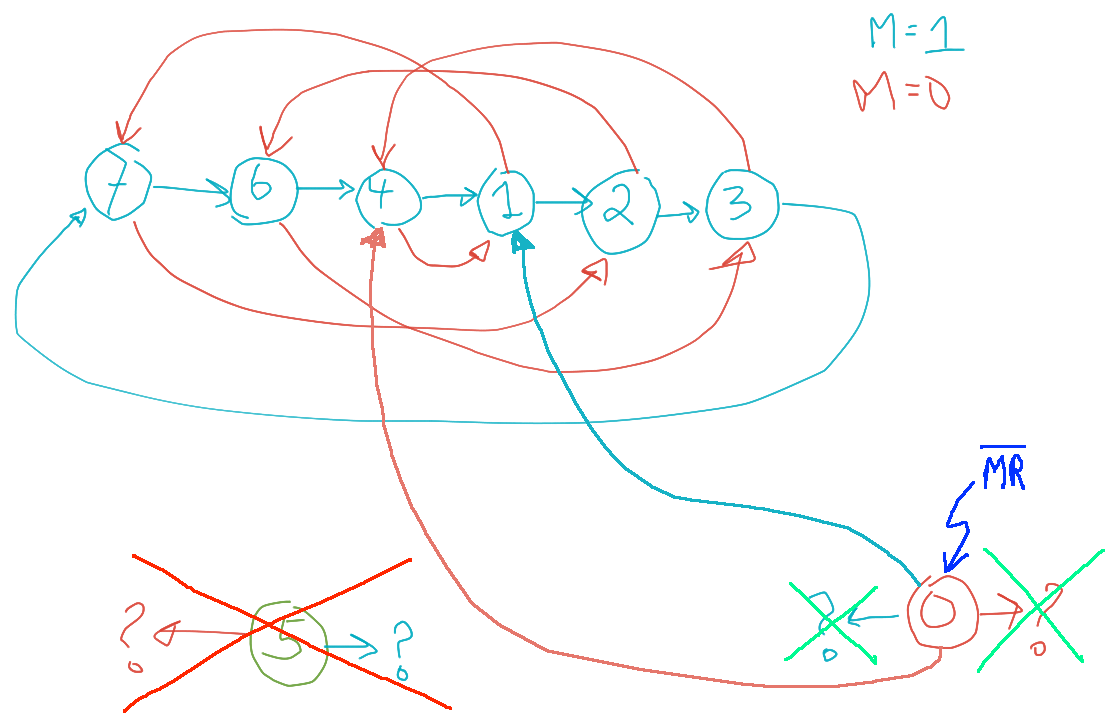
Isto significa que temos que alterar algumas linhas na nossa tabela de transição do circuito para "forçar" estas transições iniciais...

Até aqui em 08/10/2021.

Continuando o projeto em 15/10/2021.

Considerando como podemos implementar o circuito de comando dos FF's...

Ao invés de gastar 6 CI's apenas com portas lógicas básicas necessárias para propiciar o comando desejado aos FF's-D, poderíamos implementar as equações necessárias para $D_2$$D_2$, $D_1$$D_1$ e $D_0$$D_0$ usando DEC ou MUX. Neste caso, "programamos" as tabelas verdade necessárias para as entradas $D$$D$ da forma que queremos (incluindo as transições iniciais para o estado inicial "0").

A solução usando DEC, implica, usar $1\times$$1 \times$ CI DEC de 4 para 16 linhas (uma pastilha de 24 pinos) mais:

• Para $D_2$$D_2$ será necessário uma porta AND (ou NAND) de 6 entradas: $D_2=\sum _m\{1,2,3,11,14,15\}⟵6$$D_2=\sum_{m} \left\{ 1, 2, 3, 11, 14, 15\right\} \quad \longleftarrow \quad 6$ combinações que levam à $D_2=1$$D_2=1$.
• Para $D_1$$D_1$ será necessário uma porta AND (ou NAND) de 8 entradas: $D_1=\sum _m\{1,2,6,7,9,10,11,15\}⟵8$$D_1=\sum_{m} \left\{ 1, 2, 6, 7, 9, 10, 11, 15 \right\} \quad \longleftarrow \quad 8$ combinações que levam à $D_1=1$$D_1=1$.
• Para $D_0$$D_0$ será necessária uma porta AND (ou NAND) de 6 entradas: $D_0=\sum _m\{1,4,6,10,11,12\}⟵6$$D_0=\sum_{m} \left\{ 1, 4, 6, 10, 11, 12 \right\} \quad \longleftarrow \quad 6$ combinações que levam à $D_0=1$$D_0=1$.

Resumindo, além do DEC serão necessárias + 3 pastilhas (AND/NAND) de 8 entradas (existente comercialmente), totalizando uma solução que empregaria: $1\times$$1 \times$ 74LS175 ($4\times$$4 \times$ FF's) + 1 CI DEC 4/16 + 3 CI's AND/NAND(8) = 5 pastilhas).

A solução usando MUX exigiria um MUX de 16 canais de saída para cada FF, também uma pastilha "grande" (de 24 pinos). Mas a "programação" destes MUXes também pode ser realizada usando MUXes de 8 canais de saída (pastilhas "tradicionais" de 14 ou 16 pinos). Neste caso, estariámos empregado: $1\times$$1 \times$ 74LS175 ($4\times$$4 \times$ FF's) + 3 CIs MUX 3/8 + 1 CI portas NOT = 5 pastilhas no total.

Optando pela solução usando MUXes:

• Opção 1) Usar MUXes de 4 canais de entrada (pastilha de 24 pinos);
• Opção 2) Usar MUXes de 3 canais de entrada (pastilha de 14/16 pinos):

Optando pela opção 2: Usando MUXES de 8 canais de saída.

Programando os MUXes:

Lembrando a "programação" especial desejado para o circuito quando o mesmo inicia com os FF's resetados (circuito inicia com borda ascendente da entrada Master Reset do CI 74LS175):

$0\stackrel{M=0}{\to }4\therefore D_2{D}_1{D}_0={100}_{(2)}=4_{(10)}$$0 \xrightarrow[]{M=0} 4 \quad \therefore \quad D_2\,D_1\,D_0=100_{(2)}=4_{(10)}$.

$0\stackrel{M=1}{\to }1\therefore D_2{D}_1{D}_0={001}_{(2)}=1_{(10)}$$0 \xrightarrow[]{M=1} 1 \quad \therefore \quad D_2\,D_1\,D_0=001_{(2)}=1_{(10)}$.

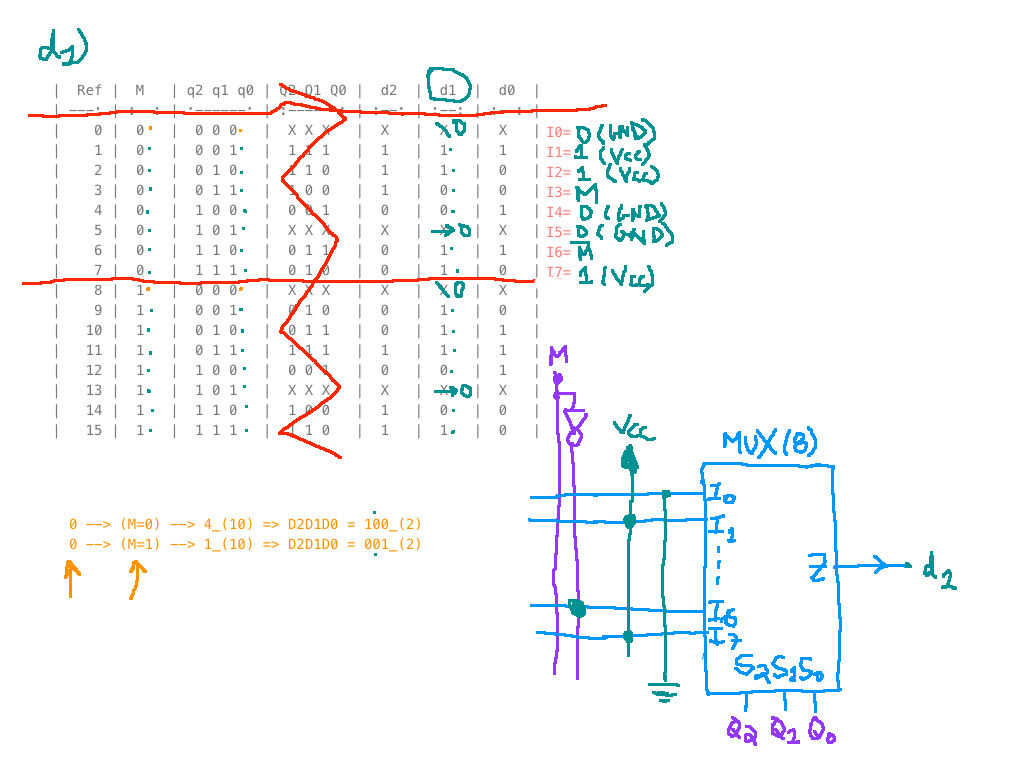
Programação do MUX(8) para $D_2$$D_2$:

xxxxxxxxxx
                S2 S1 S0
|  Ref |  M   | q2 q1 q0 |   d2   | Entradas (programação) do MUX
|    0 |  0   |  0 0 0   |   1(*) | I0=/M --> 0 --> (M=0) --> D2=1
|    1 |  0   |  0 0 1   |   1    | I1=/M 
|    2 |  0   |  0 1 0   |   1    | I2=/M
|    3 |  0   |  0 1 1   |   1    | I3=1 (Vcc)
|    4 |  0   |  1 0 0   |   0    | I4=0 (GND)
|    5 |  0   |  1 0 1   |   X    | I5=0 (GND) --> Implica em 5 --> 0 (M=X)
|    6 |  0   |  1 1 0   |   0    | I6=M
|    7 |  0   |  1 1 1   |   0    | I7=M
----------------------------------
|  8/0 |  1   |  0 0 0   |   0(*) | --> 0 --> (M=1) --> D2=0
|  9/1 |  1   |  0 0 1   |   0    |
| 10/2 |  1   |  0 1 0   |   0    |
| 11/3 |  1   |  0 1 1   |   1    |
| 12/4 |  1   |  1 0 0   |   0    |
| 13/5 |  1   |  1 0 1   |   X    |
| 14/6 |  1   |  1 1 0   |   1    |
| 15/7 |  1   |  1 1 1   |   1    |

Programação do MUX(8) para $D_1$$D_1$:

Programação do MUX(8) para $D_0$$D_0$:

xxxxxxxxxx
|  Ref |  M   | q2 q1 q0 | Q2 Q1 Q0 |  d0  | Programção do MUX
-------------------------------------------------
|    0 |  0   |  0 0 0   |  X X X   |  0(*)| I0=  M  % 0 --> (M=0) --> d0=0
|    1 |  0   |  0 0 1   |  1 1 1   |  1   | I1= /M
|    2 |  0   |  0 1 0   |  1 1 0   |  0   | I2=  M
|    3 |  0   |  0 1 1   |  1 0 0   |  0   | I3=  M
|    4 |  0   |  1 0 0   |  0 0 1   |  1   | I4=  1 (Vcc)
|    5 |  0   |  1 0 1   |  X X X   |  X   | I5=  0  % 5 --> (M=X) --> d0=0
|    6 |  0   |  1 1 0   |  0 1 1   |  1   | I6= /M
|    7 |  0   |  1 1 1   |  0 1 0   |  0   | I7=  0 (Vcc)
------------------------------------------------
|  8/0 |  1   |  0 0 0   |  X X X   |  1(*)| % 0 --> (M=1) ---> d0=1
|  9/1 |  1   |  0 0 1   |  0 1 0   |  0   |
| 10/2 |  1   |  0 1 0   |  0 1 1   |  1   |
| 11/3 |  1   |  0 1 1   |  1 1 1   |  1   |
| 12/4 |  1   |  1 0 0   |  0 0 1   |  1   |
| 13/5 |  1   |  1 0 1   |  X X X   |  X   |
| 14/6 |  1   |  1 1 0   |  1 0 0   |  0   |
| 15/7 |  1   |  1 1 1   |  1 1 0   |  0   |

5) Circuito elétrico/lógico final

Parte da pastilha com FF's-D:

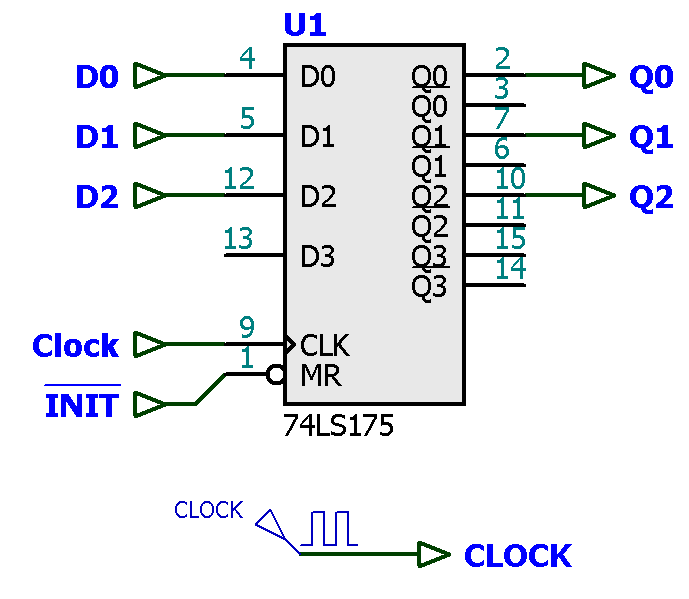
Parte da entrada $M$$M$ e visualização do estado atual:

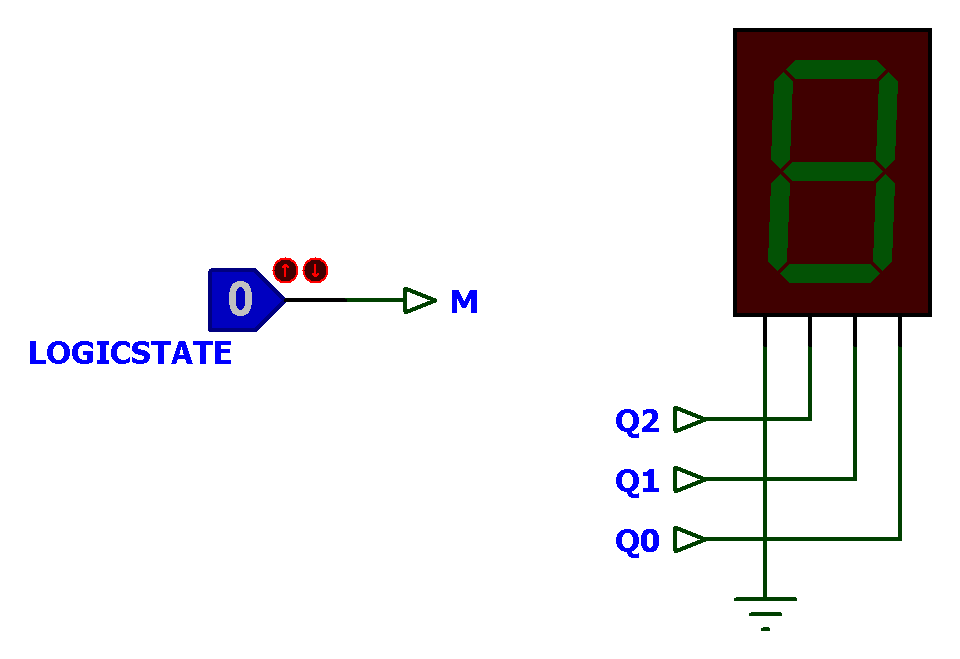
Parte dos MUXes (programação dos comandos dos FF's):

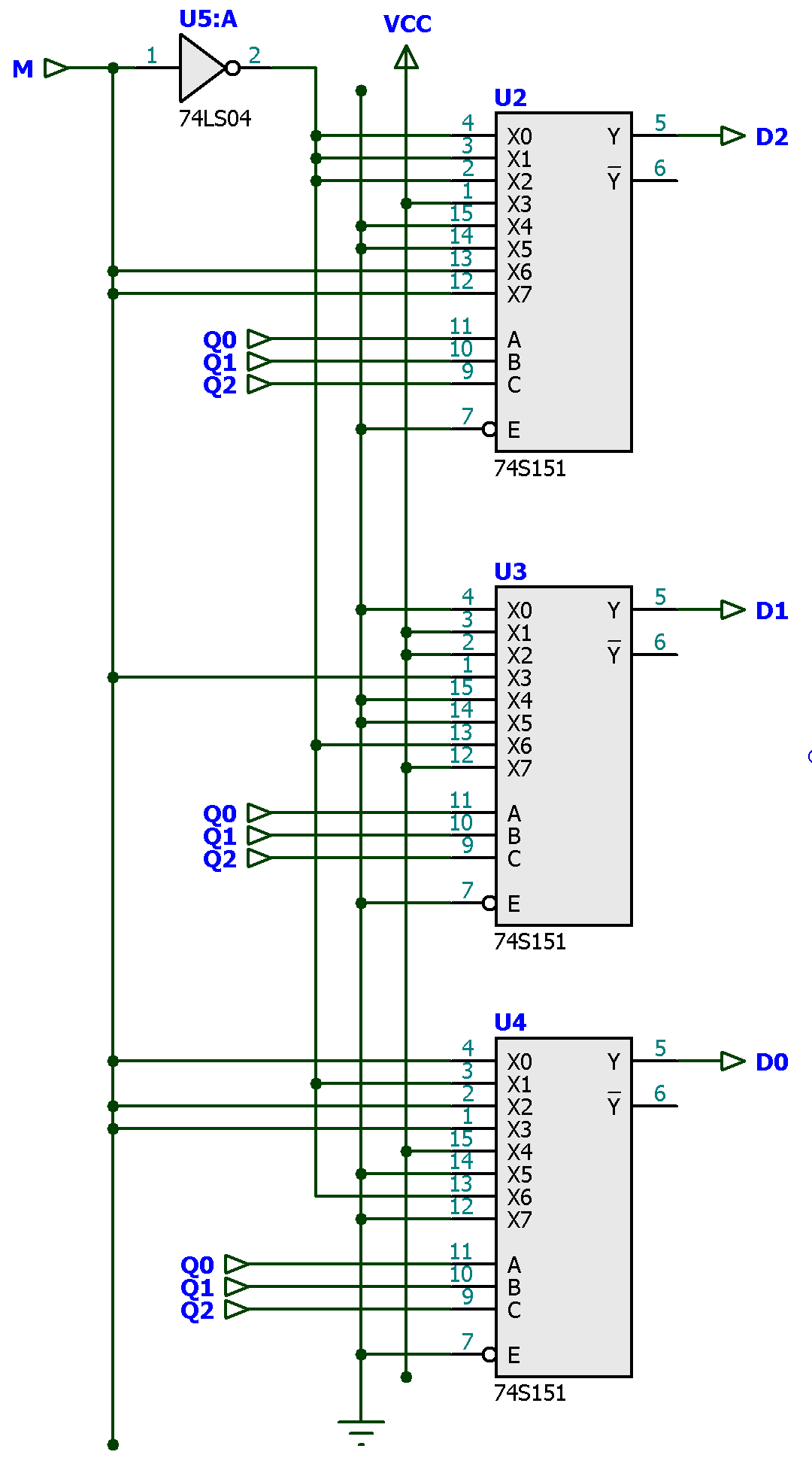
Parte extra (opcional) que organiza um "painel mímico" que visa imitar o digrama de estados proposto para este contador:

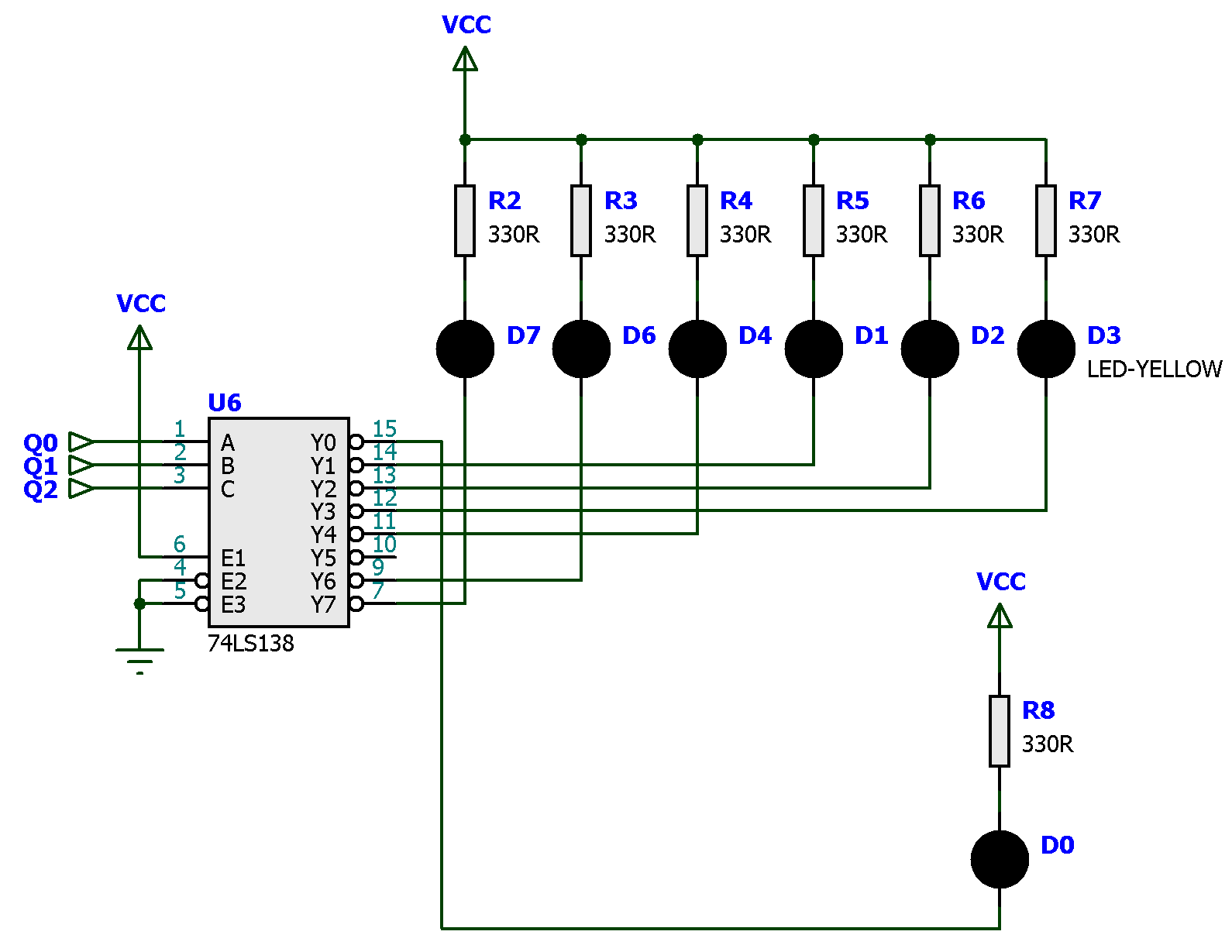
Alimentação dos CIs:

6) Simulações

As figuras à seguir mostram o diagrama de estados desejado o resultado simulado do circuito:

Simulação iniciando circuito com $M=1$$\textcolor{blue}{M=1}$ :

Simulação	Diagrama Estados

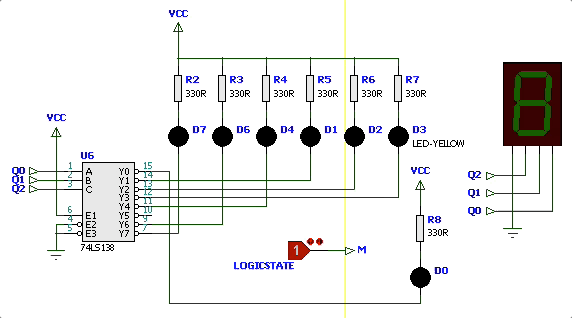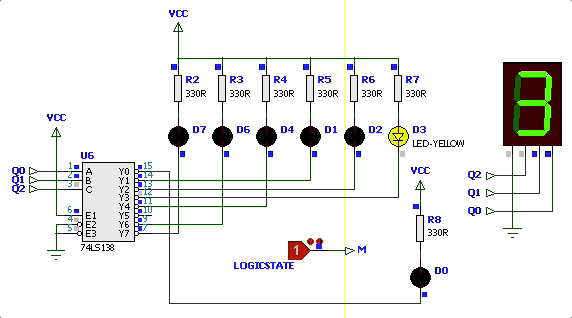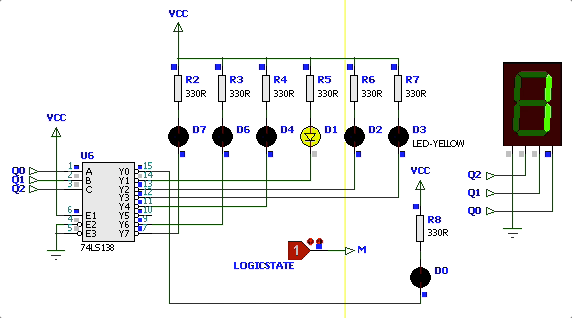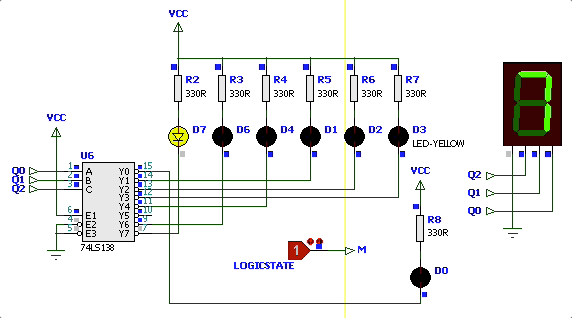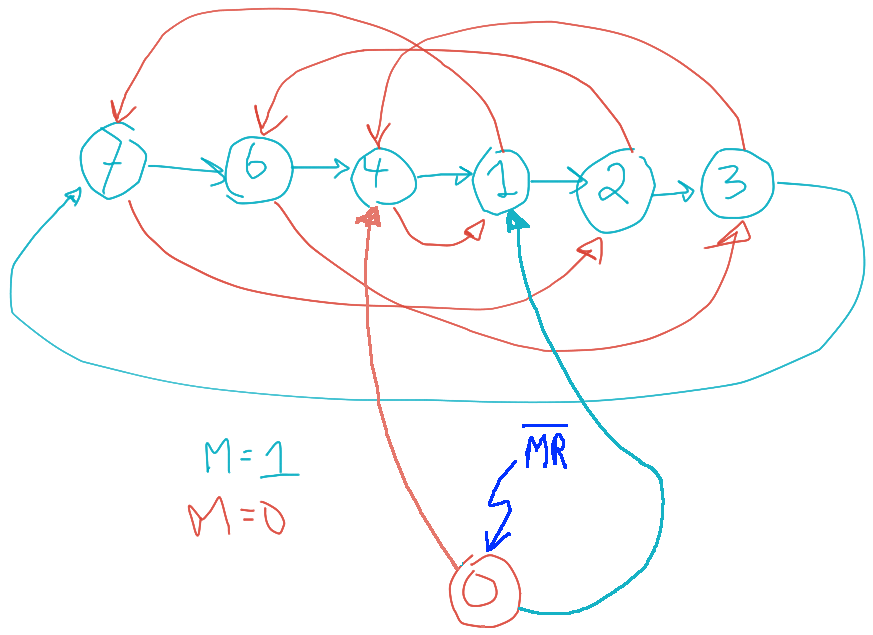Simulação iniciando circuito com $M=0$$\textcolor{red}{M=0}$:

Simulação	Diagrama Estados

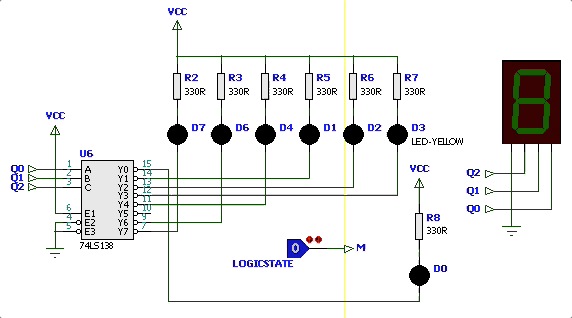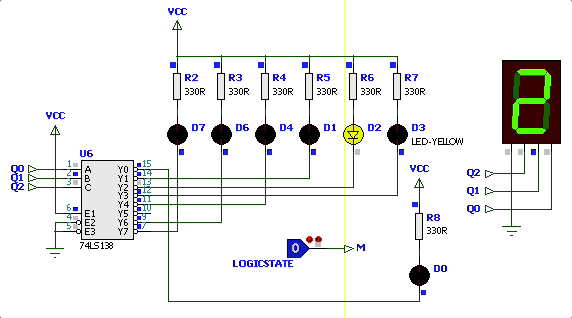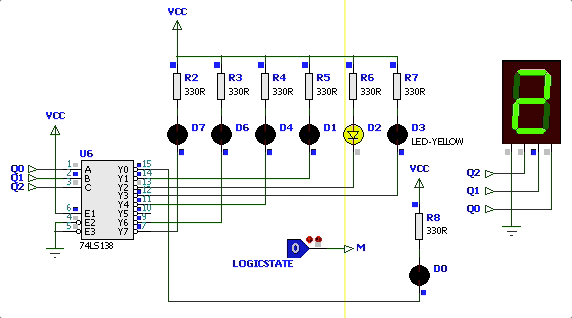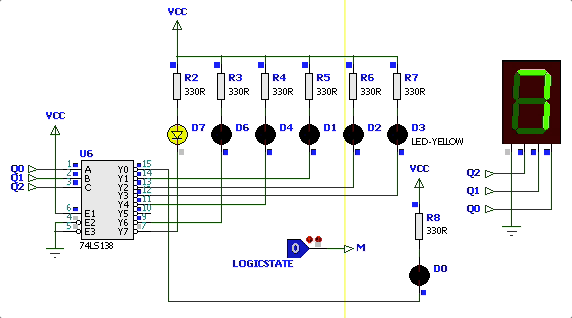Simulação variando $M$$M$ com circuito em execução:

Simulação	Diagrama de Estados

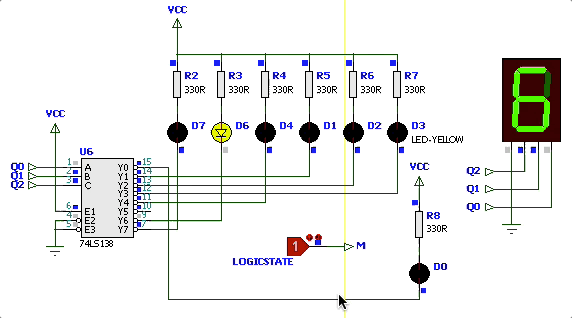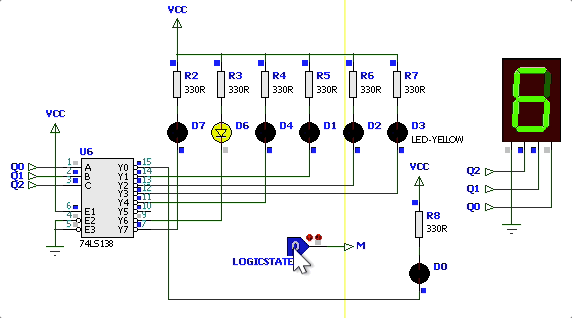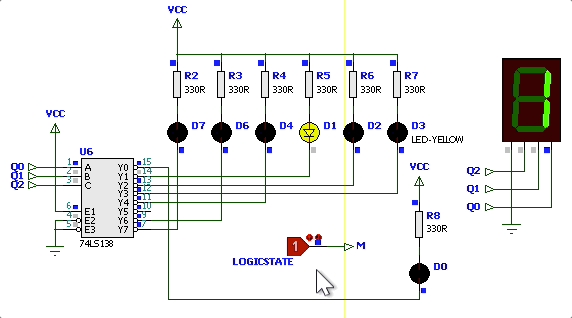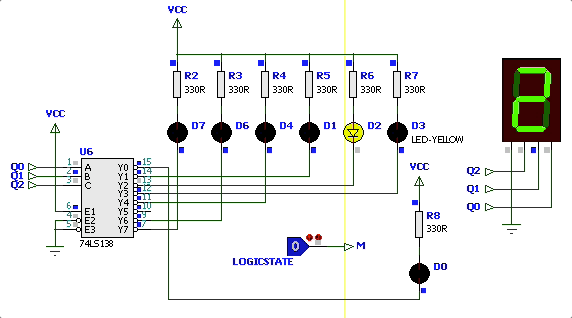Lista de Material:

• U1: 1 x CI 74LS175 (Quad FF D, $\uparrow$$\uparrow$ com $\overline{MR}$$\overline{MR}$);
• U2, U3, U4: 3 x CIs 74LS151 (MUX-8);
• U5: 1 x 74LS04 (6 x NOT);
• U6: 1 x 74LS138 (DEC 3/8);
• D0, D1, D2, D3, D4, D6, D7: 7x Leds mini-vermelhos alto-contraste;
• R2, R3, R4, R5, R6, R6, R8: 7 x Resistores de 330$\mathrm{\Omega }$$\ohm$;
• 1 módulo-display 7-segmentos;
• Fonte de alimentação;
• Gerador de sinais.

Prof. Fernando Passold, em 15.10.2021.