
Projeto de PID por Emulação
Seja a planta (Exemplo 9.5 de Nise1):
para o qual se deseja:
- tempo de pico, , menor que 2/3 que sistema com Controlador Proporcional;
- overshoot máximo tolerado = 20%;
Controlador Proporcional
A sintonia de um controlador proporcional para este sistema leva à :
xxxxxxxxxx>> G=tf(poly(-8),poly([-3 -6 -10]));>> zpk(G) (s+8) ------------------ (s+10) (s+6) (s+3) Continuous-time zero/pole/gain model.>> OS=20;>> zeta=(-log(OS/100))/(sqrt(pi^2+(log(OS/100)^2)))zeta = 0.45595>> rlocus(G)>> hold on; sgrid(zeta,0)>> [K,polosMF]=rlocfind(G)Select a point in the graphics windowselected_point = -5.4147 + 10.526iK = 120.61polosMF = -5.4149 + 10.526i -5.4149 - 10.526i -8.1702 + 0i>> K=120;>> ftmf=feedback(K*G,1);>> figure; step(ftmf)>> stepinfo(ftmf) RiseTime: 0.13053 SettlingTime: 0.70447 SettlingMin: 0.78987 SettlingMax: 1.0148 Overshoot: 20.509 Undershoot: 0 Peak: 1.0148 <--- valor do pico PeakTime: 0.29769 <--- tempo do picoTendo sido obtidos os seguintes resultados:
| RL com Controlador Proporcional | Resposta ao Degrau |
|---|---|
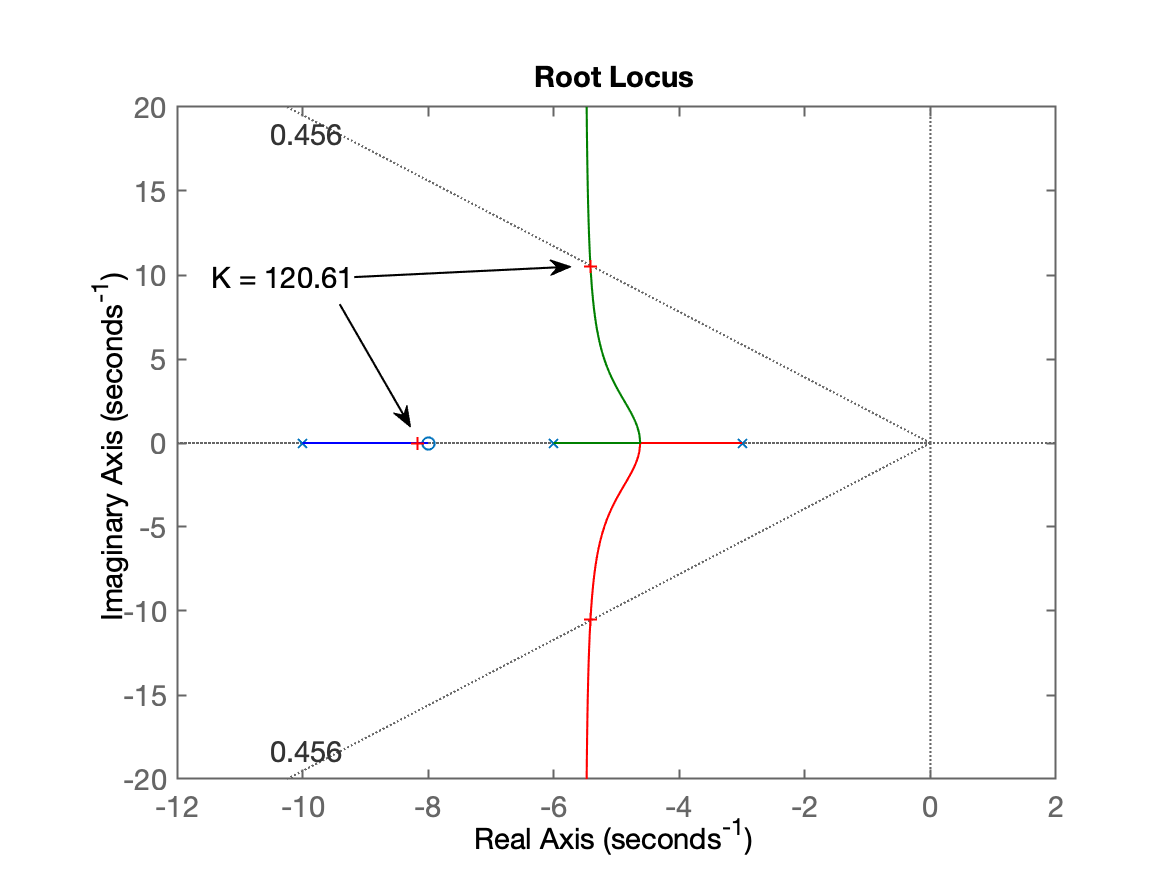 | 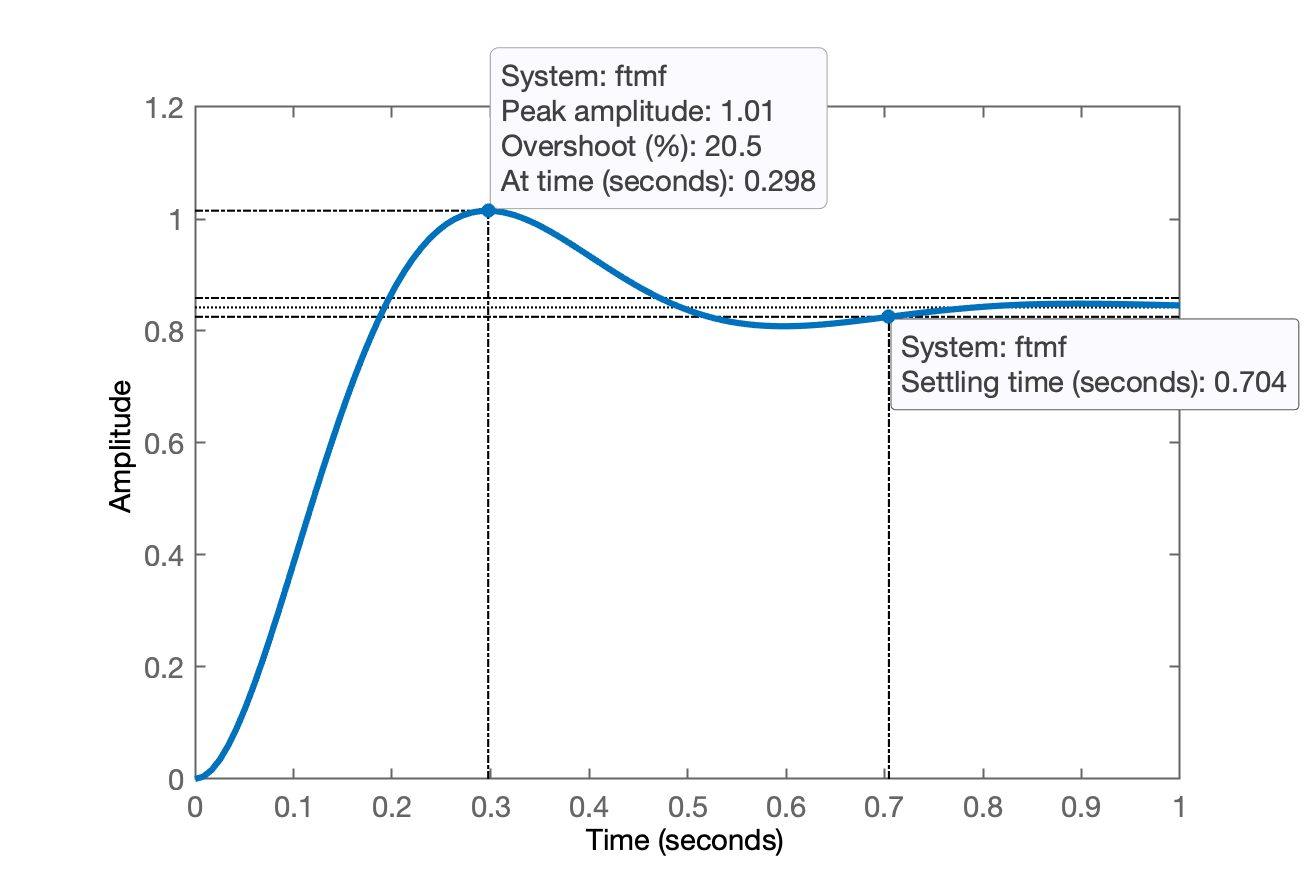 |
Isto significa que para o PID é esperado ou segundos. Note que o controlador Proporcional não garante erro nulo para este tipo de sistema. De fato, o erro neste caso se manteve em: .
Controlador PID tradicional (analógico)
Um PID analógico segue a equação:
ou mais simplesmente:
ou seja, um sistema com 2 zeros e 1 pólo na origem que corresponde ao integrador.
Para esta planta, foi definido um PID com a seguinte equação (para rever todo o projeto: clique em: Exemplo de Projeto de PID (Disciplina de Controle Automático II)):
Este PID leva aos seguintes resultados:
xxxxxxxxxx>> PID=tf(poly([-2.5 -40.02]),[1 0]); % usando valores já definidos>> zpk(PID) (s+40.02) (s+2.5) ----------------- s Continuous-time zero/pole/gain model.>> ftma_PID=PID*G;>> zpk(ftma_PID) (s+40.02) (s+8) (s+2.5) ----------------------- s (s+10) (s+6) (s+3) Continuous-time zero/pole/gain model.>> figure; rlocus(ftma_PID)>> hold on; sgrid(zeta,0)>> K_PID=7.8645; % usando valores já definidos>> ftmf_PID=feedback(K_PID*ftma_PID, 1);>> polosMF=pole(ftmf_PID)polosMF = -8.134 + 15.705i -8.134 - 15.705i -8.1175 + 0i -2.479 + 0i>> plot(real(polosMF),imag(polosMF), 'r+') % mostra os pólos de MF no RL>> figure; step(ftmf_PID)>> stepinfo(ftmf_PID) RiseTime: 0.076558 SettlingTime: 0.45247 SettlingMin: 0.92232 SettlingMax: 1.2211 Overshoot: 22.112 Undershoot: 0 Peak: 1.2211 PeakTime: 0.16985 <--- desejado tp <= 0,19846Resultados obtidos:
| RL com PID | Zoom sobre o RL |
|---|---|
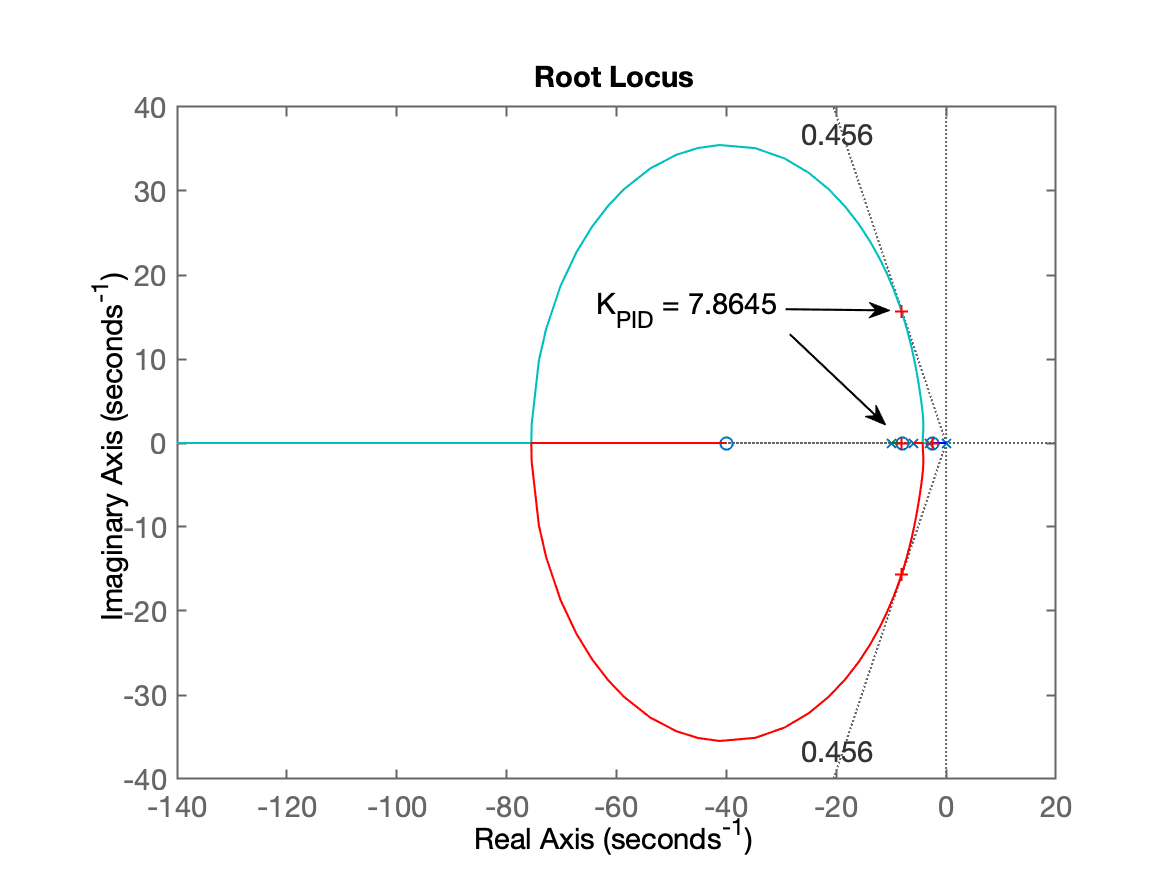 | 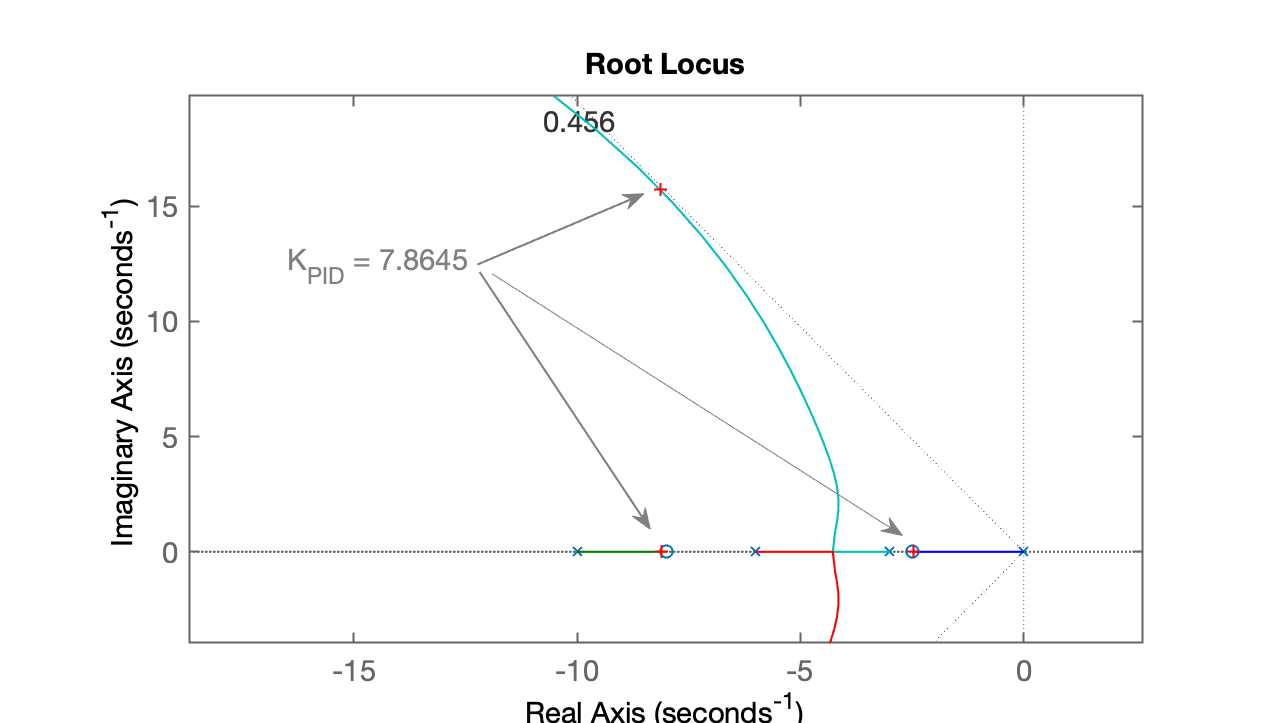 |
| Resposta ao Degrau | |
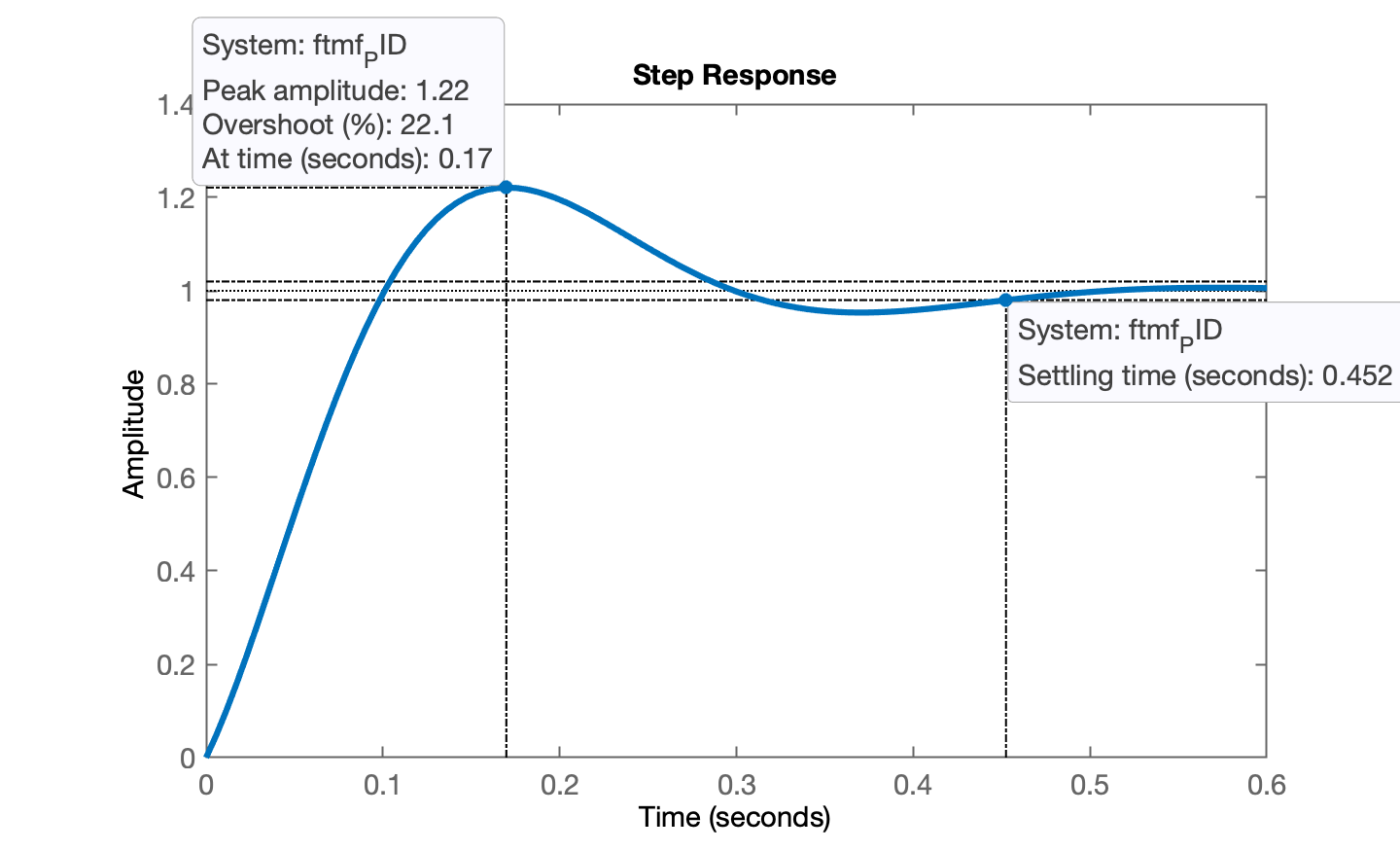 |
A idéia é "transformar" este PID analógico num digital usando transformação bilinear, no caso, o método de Tustin.
PID Digital
O aproximação bilinear de Tustin (ou regra do Trapézio) permite "passar" do plano-s para o plano-z e vice-versa, fazendo:
ou
Obs.: Este método só funciona quando o sistema contínuo no tempo é estável.
O primeiro detalhe é definir um valor adequado para o período de amostragem, . Na prática é melhor que a frequência de amostragem fique entre 20 à 10 vezes a maior frequência da planta ("banda passante").
No caso da nossa planta:
O pólo mais rápido está localizado em rad/s. Convertendo para frequência em Hz, obtemos:
xxxxxxxxxx>> f=10/(2*pi) % em Hz (pólo + rápido da planta)f = 1.5915>> f=6/(2*pi) % em Hz (2o-pólo + rápido da planta)f = 0.95493>> fs=(20*10)/(2*pi)fs = 31.831>> fs=(10*10)/(2*pi)fs = 15.915>> fs=20 % "meio termo">> T=1/fs % período de amostragem adotadoT = 0.051a-versão (usando Tustin)
A eq. analógica do PID:
então sua versão digital usando Tustin fica:
Mas... uma inspeção na equação acima mostra que este processo de discretização gerou um controlador com polos sobre o círculo unitário (), o que implica num controlador marginalmente estável, que pode causar problemas. Repare que não importa o ganho geral adotado para este PID, um dos traçados do RL correspondente aos pontos de partida dos pólos em , pode levar a um traçado que sai imediatamente para fora do círculo unitário assim que .
Podemos até continuar o projeto apenas para confirmar que esta aproximação resultará num sistema instável em MF...
O MATLAB facilita usar a aproximação bilinear de Tustin, usando a função c2d( . , . , 'tustin'):
xxxxxxxxxx>> help c2d c2d Converts continuous-time dynamic system to discrete time. SYSD = c2d(SYSC,TS,METHOD) computes a discrete-time model SYSD with sample time TS that approximates the continuous-time model SYSC. The string METHOD selects the discretization method among the following: 'zoh' Zero-order hold on the inputs 'foh' Linear interpolation of inputs 'impulse' Impulse-invariant discretization 'tustin' Bilinear (Tustin) approximation. 'matched' Matched pole-zero method (for SISO systems only). 'least-squares' Least-squares minimization of the error between frequency responses of the continuous and discrete systems (for SISO systems only). The default is 'zoh' when METHOD is omitted. The sample time TS should be specified in the time units of SYSC (see "TimeUnit" property).No caso do PID analógico para esta planta ficaria então:
xxxxxxxxxx>> Kp = 334.4315;>> Ki = 786.9258;>> Kd = 7.8645;>> PIDa = tf([Kd Kp Ki],[1 0])PIDa = 7.864 s^2 + 334.4 s + 786.9 --------------------------- s Continuous-time transfer function.>> zpk(PIDa) 7.8645 (s+40.02) (s+2.5) ------------------------ s Continuous-time zero/pole/gain model.>> % Convertendo para PID digital usando Tustin>> PIDd=c2d(PIDa, T, 'tustin')PIDd = 668.7 z^2 - 589.8 z - 0.1784 ---------------------------- z^2 - 1 Sample time: 0.05 secondsDiscrete-time transfer function.>> zpk(PIDd) 668.68 (z-0.8824) (z+0.0003023) ------------------------------- (z+1) (z-1) Sample time: 0.05 secondsDiscrete-time zero/pole/gain model.Repare nos pólos em no plano-z para este sistema e como isto resulta ruim para os traçados do RL:
xxxxxxxxxx>> zerosPIDd = zero(PIDd) % extrair zeros do PID digitalzerosPIDd = 0.88235 -0.00030229>> PIDd2 = tf(poly(zerosPIDd),poly([-1 1]),T); % eq. do PID sem o ganho genérico>> zpk(PIDd2) (z-0.8824) (z+0.0003023) ------------------------ (z+1) (z-1) Sample time: 0.05 secondsDiscrete-time zero/pole/gain model.>> BoG = c2d(G, T); % "digitalizando" planta incorpotando ZOH>> ftma_PIDd = PIDd2*BoG; % FTMA(z) deste sistema>> zpk(ftma_PIDd) 0.0010449 (z+0.8326) (z-0.8824) (z-0.6703) (z+0.0003023) -------------------------------------------------------- (z+1) (z-1) (z-0.8607) (z-0.7408) (z-0.6065) Sample time: 0.05 secondsDiscrete-time zero/pole/gain model.>> figure; rlocus(ftma_PIDd)>> hold on; zgrid(zeta,0) % linha guia correspondente ao %OS=20%>> K_PIDd = 668.68;>> ftmf_PIDd = feedback(K_PIDd*ftma_PIDd, 1);>> polosMF_PIDd=pole(ftmf_PIDd)polosMF_PIDd = -1.0445 + 0i 0.50173 + 0.61388i 0.50173 - 0.61388i 0.88322 + 0i 0.66713 + 0i>> hold on;>> plot(real(polosMF_PIDd),imag(polosMF_PIDd), 'r+', 'MarkerSize', 10, 'LineWidth', 2)>> figure; step(ftmf_PIDd)RL deste sistema:
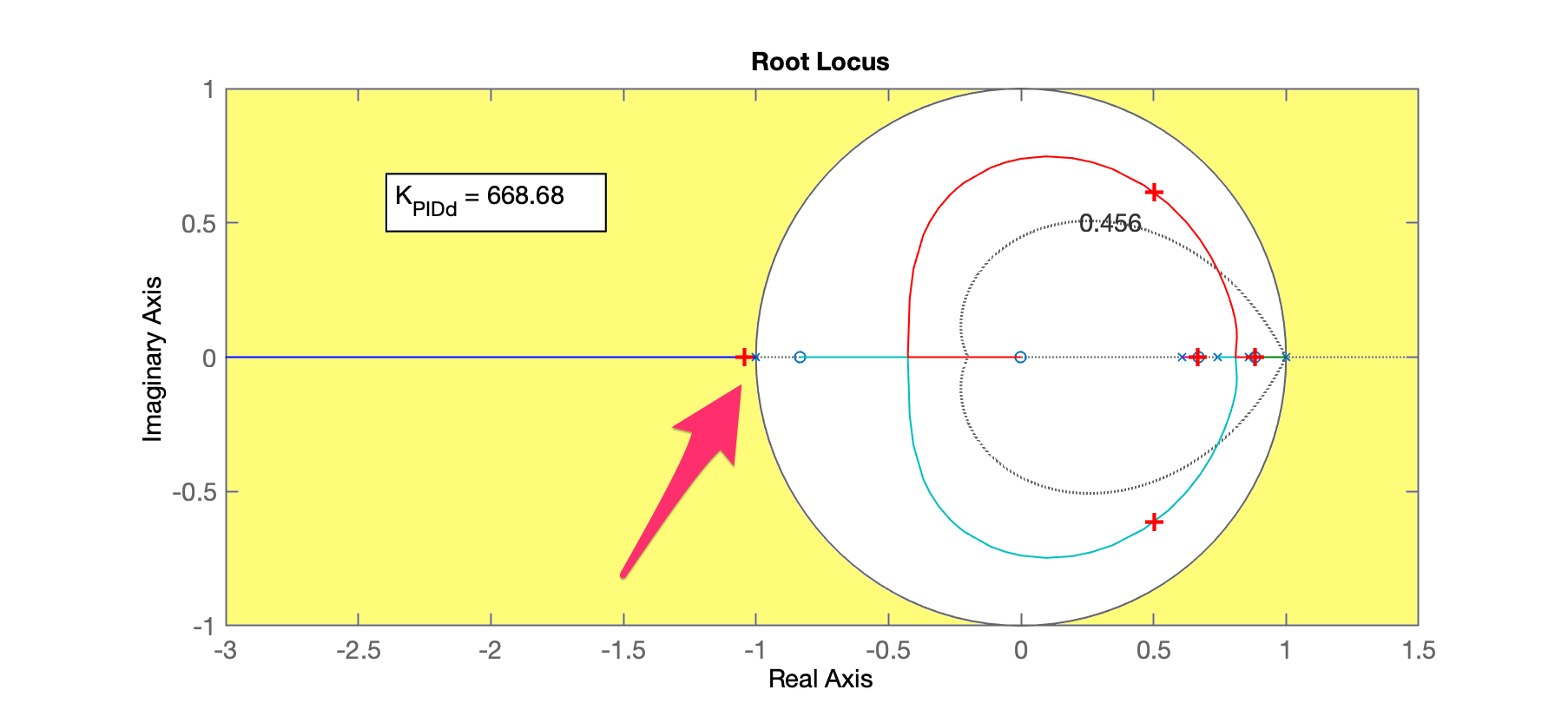
Note: qualquer ganho já faria o traçado do RL correspondente ao pólo do PIDd em , "caminhar" para fora do círculo unitário, na direção de . levando o sistema à instabilidade.
Resposta ao degrau unitário:
| Resposta ao degrau | Parte inicial da resposta ao degrau |
|---|---|
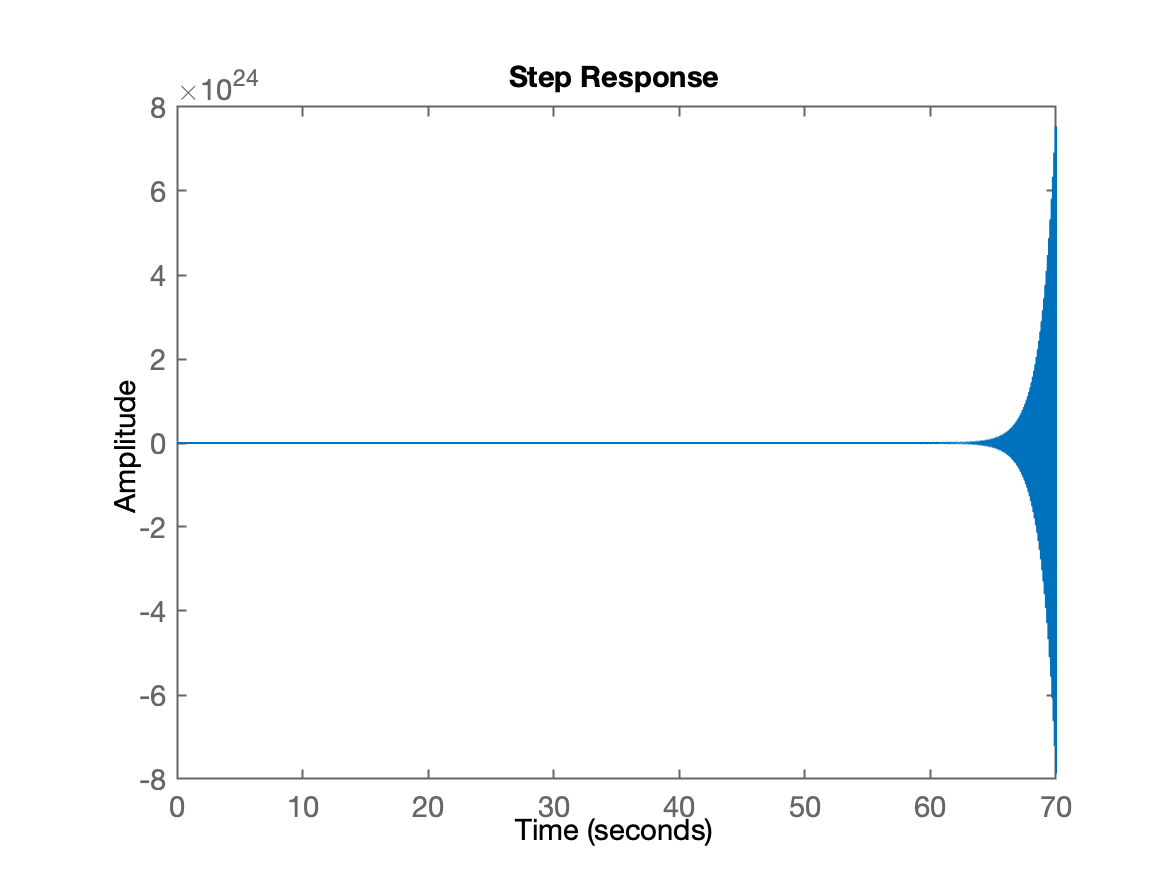 | 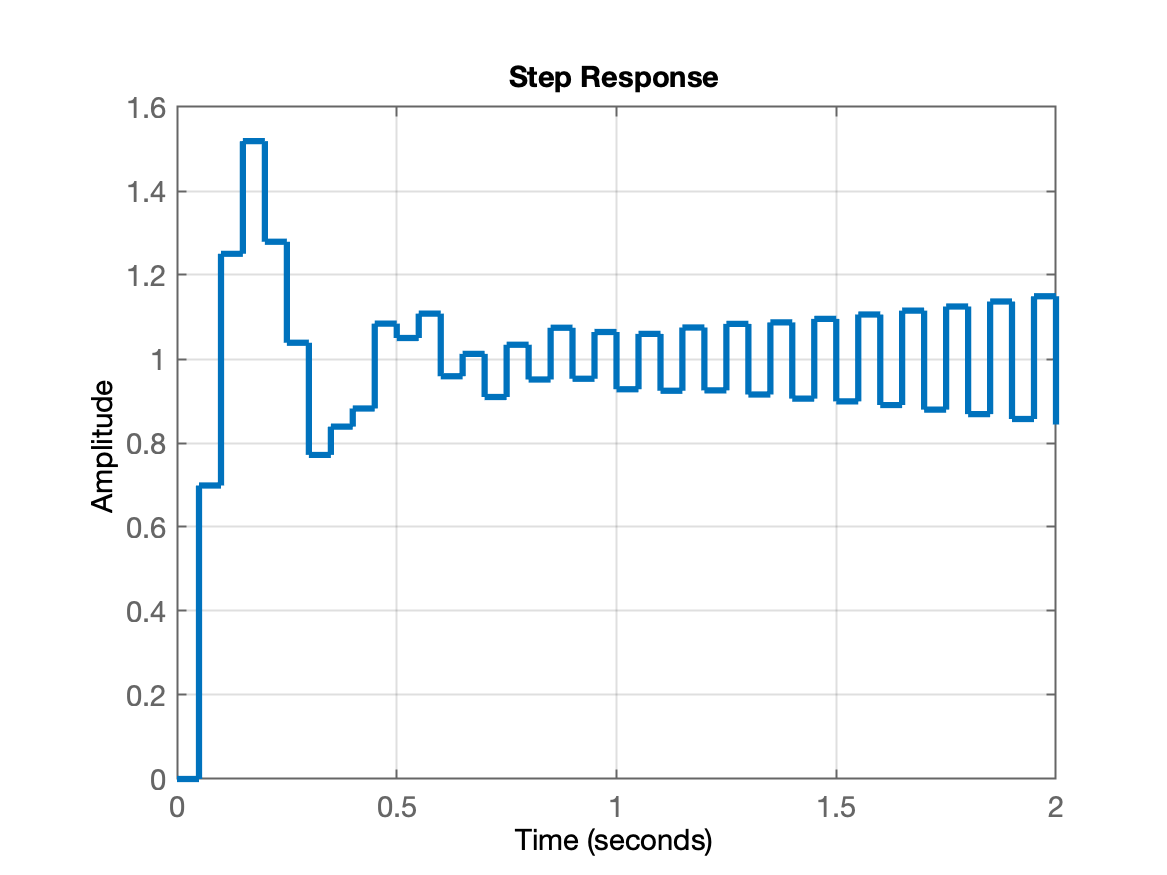 >> xlim([0 2]) |
Soluções?
Se quisermos insistir em aproximação por transformação bilinear podemos optar por outros métodos:
- BackwardEuler, ou;
- ForwardEuler.
O MATLAB permite adotar uma destas ouras aproximações, mas não com a função c2d e sim usando opções na função pid:
xxxxxxxxxx>> help pid pid Create a pid controller in parallel form. Construction: SYS = pid(Kp,Ki,Kd,Tf) creates a continuous-time pid controller in parallel form with a first-order derivative filter: Ki Kd*s Kp + ---- + -------- s Tf*s+1 The scalars Kp, Ki, Kd, and Tf specify the proportional gain, integral gain, derivative gain, and filter time constant. The Tf value must be nonnegative for stability. The default values are Kp=1, Ki=0, Kd=0, and Tf=0. If a parameter is omitted, its default value is used. For example, pid(Kp,Ki,Kd) creates a pid controller with pure derivative term. The resulting SYS is of type pid if Kp,Ki,Kd,Tf are all real, and of type GENSS if one of the gains is tunable (see REALP and GENMAT). SYS = pid(Kp,Ki,Kd,Tf,Ts) creates a discrete-time pid controller with sample time Ts>0. The discrete-time pid formula is Kd Kp + Ki * IF(z) + -------------- Tf + DF(z) where IF(z) and DF(z) are the discrete integrator formulas for the integral and derivative terms. Use the "IFormula" and "DFormula" properties to specify these formulas. Available formulas include: 'ForwardEuler' Ts/(z-1) 'BackwardEuler' Ts*z/(z-1) 'Trapezoidal' (Ts/2)*(z+1)/(z-1) The default formula is ForwardEuler. The 'IFormula' and 'DFormula' settings are ignored for continuous-time PIDs. The following settings are disallowed because they generate unstable PIDs: (1) (Kd > 0, Tf = 0) and DFormula='Trapezoidal' (2) (Kd > 0, Tf > 0) and DFormula='ForwardEuler' and Ts>=2*Tf You can set additional properties by using name/value pairs. For example, sys = pid(1,2,3,0.5,0.1,'IFormula','T','TimeUnit','min') also specifies the integral-term formula and the time units. Type "properties(pid)" for a complete list of pid properties, and type help pid.<PropertyName> for help on a particular property.Com a função pid, a metodologia empregada para discretizar o termo integral e o termo derivado pode ser especificada de forma independentemente. Especificar um método de integração Trapezoidal corresponde à transformação bilinear de Tustin. Alternativamente, um método de integração BackwardEuler ou ForwardEuler pode ser especificado (ForwardEuler é o padrão). Observe que a função pid não permitirá que você empregue um método de integração trapezoidal para o termo derivado (a menos que o filtro de derivada de primeira ordem esteja incluído) devido aos problemas de estabilidade mencionados acima.
Segue um exemplo de comando para definir um controlador digital usando a função pid:
xxxxxxxxxxC = pid(Kp,Ki,Kd,'Ts',Ts,'IFormula','Trapezoidal','DFormula','ForwardEuler')Obs.: a função pip só está presente dentro do Control Systems Toolbox (a partir do MATLAB versão 7.14 (2013)).
2a-versão (usando Euler e Tustin, sem filtro derivativo)
Usando a função pid.
xxxxxxxxxx>> PIDd_2a = pid(Kp, Ki, Kd, 'Ts', T, 'IFormula','Trapezoidal','DFormula','ForwardEuler')PIDd_2a = Ts*(z+1) z-1 Kp + Ki * -------- + Kd * ------ 2*(z-1) Ts with Kp = 334, Ki = 787, Kd = 7.86, Ts = 0.05 Sample time: 0.05 secondsDiscrete-time PID controller in parallel form.>> zpk(PIDd_2a) 157.29 (z+1.134) (z-0.8828) --------------------------- (z-1) Sample time: 0.05 secondsDiscrete-time zero/pole/gain model.Podemos verificar como ficou o RL desta versão do PID:
xxxxxxxxxx>> zeros_PIDd_2a = zero(PIDd_2a) % separando os zeros deste PIDzeros_PIDd_2a = -1.1341 0.88278>> PIDd_2aux = tf(poly(zeros_PIDd_2a), poly(1), T); % PID sem o ganho geral>> zpk(PIDd_2aux) (z+1.134) (z-0.8828) -------------------- (z-1) Sample time: 0.05 secondsDiscrete-time zero/pole/gain model.>> ftma_PIDd_2a = PIDd_2aux*BoG;>> figure; rlocus(ftma_PIDd_2a)>> hold on; zgrid(zeta,0)>> plot(real(polosMF_PIDd),imag(polosMF_PIDd), 'r+', 'MarkerSize', 10, 'LineWidth', 2)>> ftmf_PIDd_2a = feedback(157.29*ftma_PIDd_2a, 1);>> polosMF_PID_2a = pole(ftmf_PIDd_2a)polosMF_PID_2a = 0.57293 + 0.60728i 0.57293 - 0.60728i 0.88365 + 0i 0.66732 + 0i>> plot(real(polosMF_PID_2a),imag(polosMF_PID_2a), 'r+', 'MarkerSize', 10, 'LineWidth', 2)>> axis([-1.5 1.5 -1.5 1.5])>> axis equal>> figure; step(ftmf_PID, ftmf_PIDd_2a)>> legend('PID analógico', 'PID digital (2a-versão)')RL com esta versão do PID:
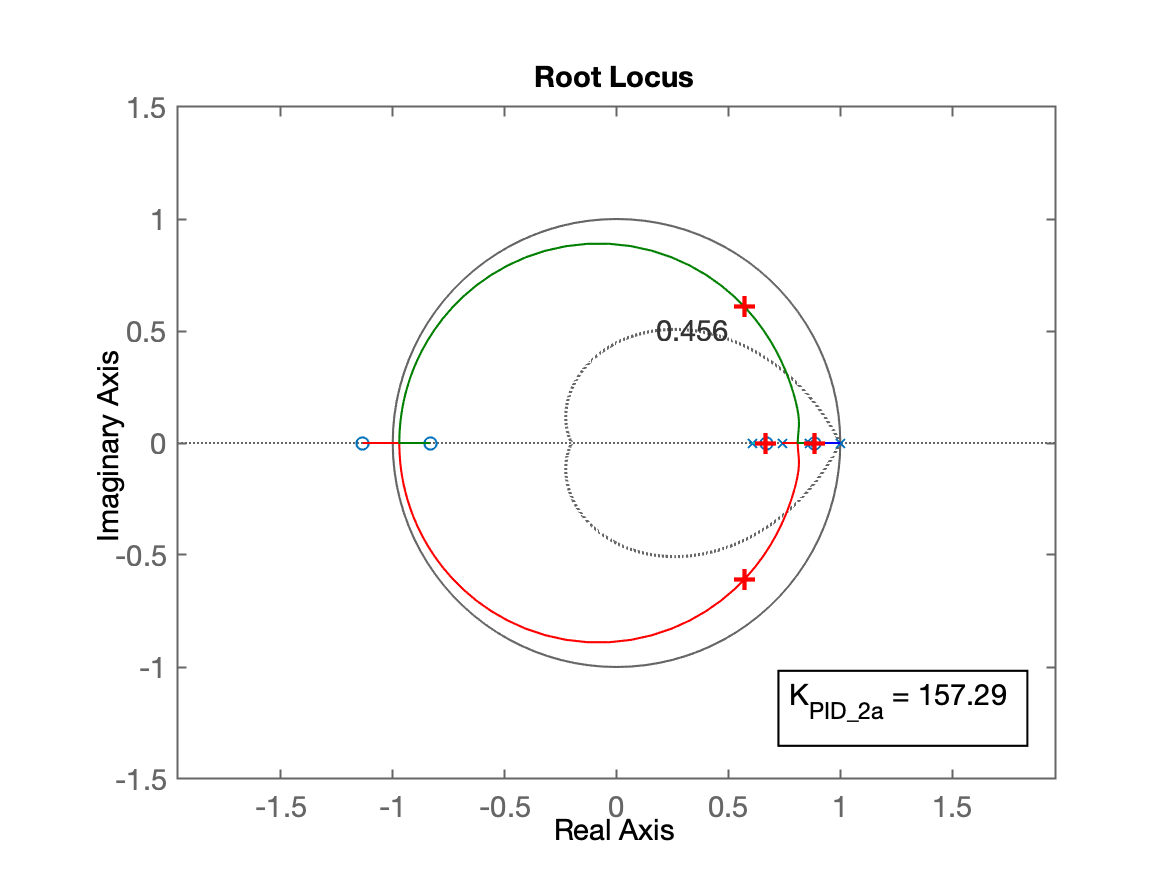
Resposta ao degrau:
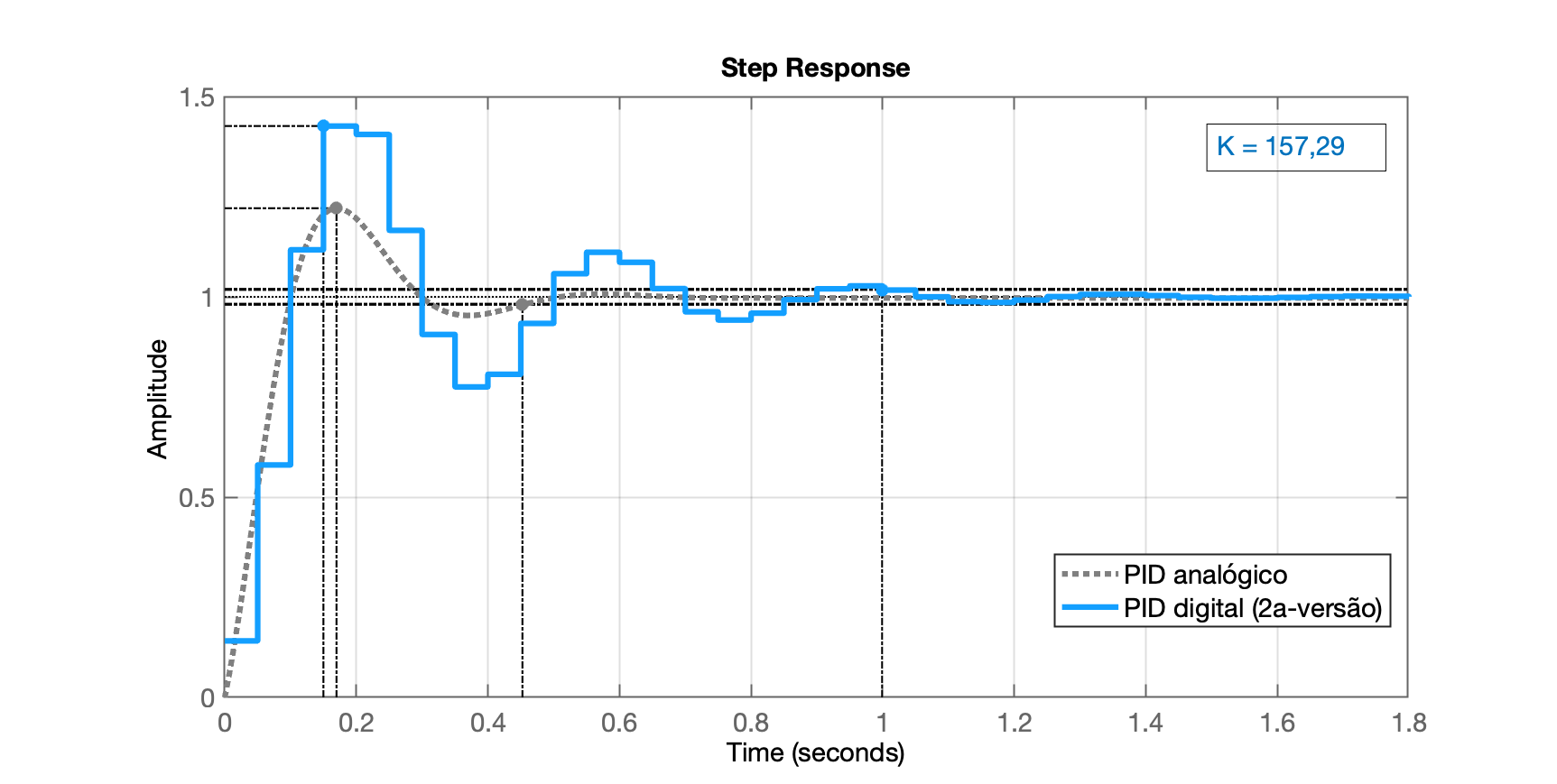
Note que o tempo do pico é praticamente o mesmo entre os 2 PIDs. Notamos que o overshoot ficou algo elevado, mas isto já era previsível observando o RL anterior. Se o ganho (geral) for reduzido para: , obtemos:
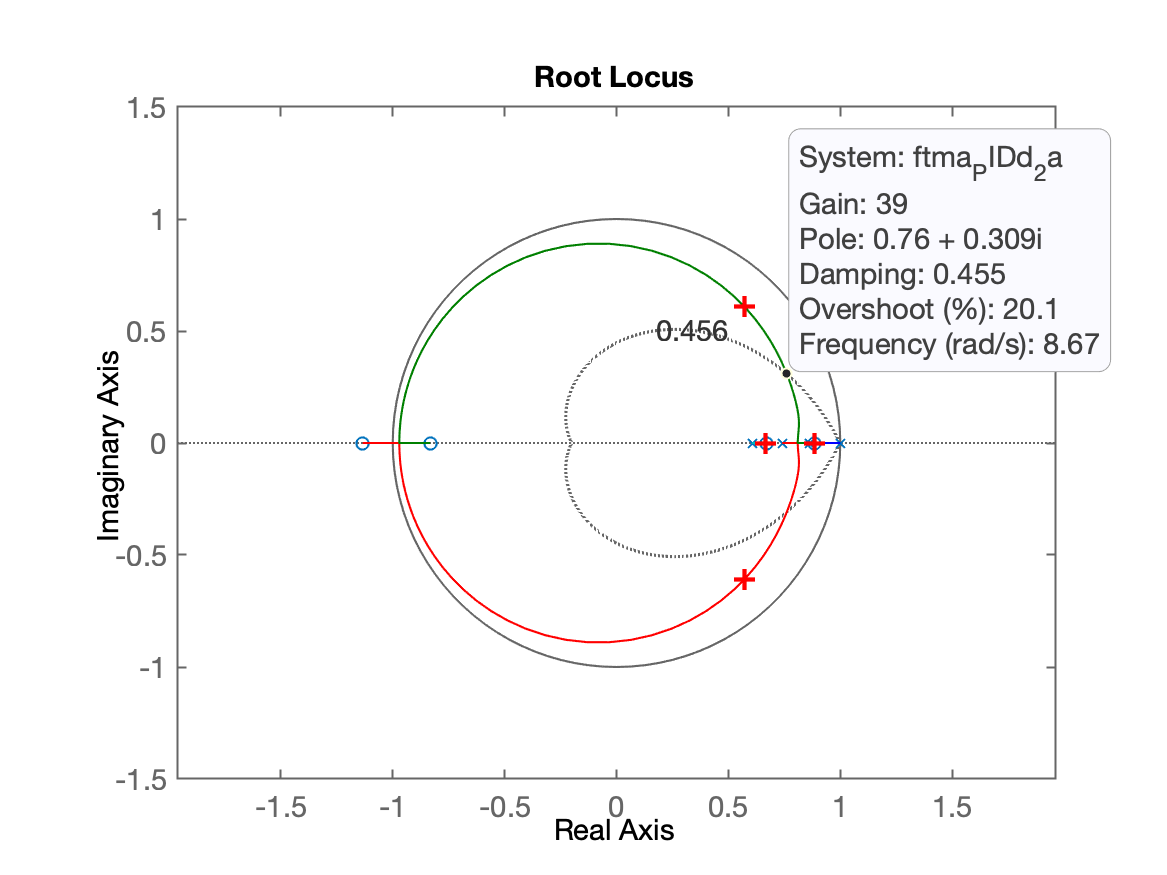
e:
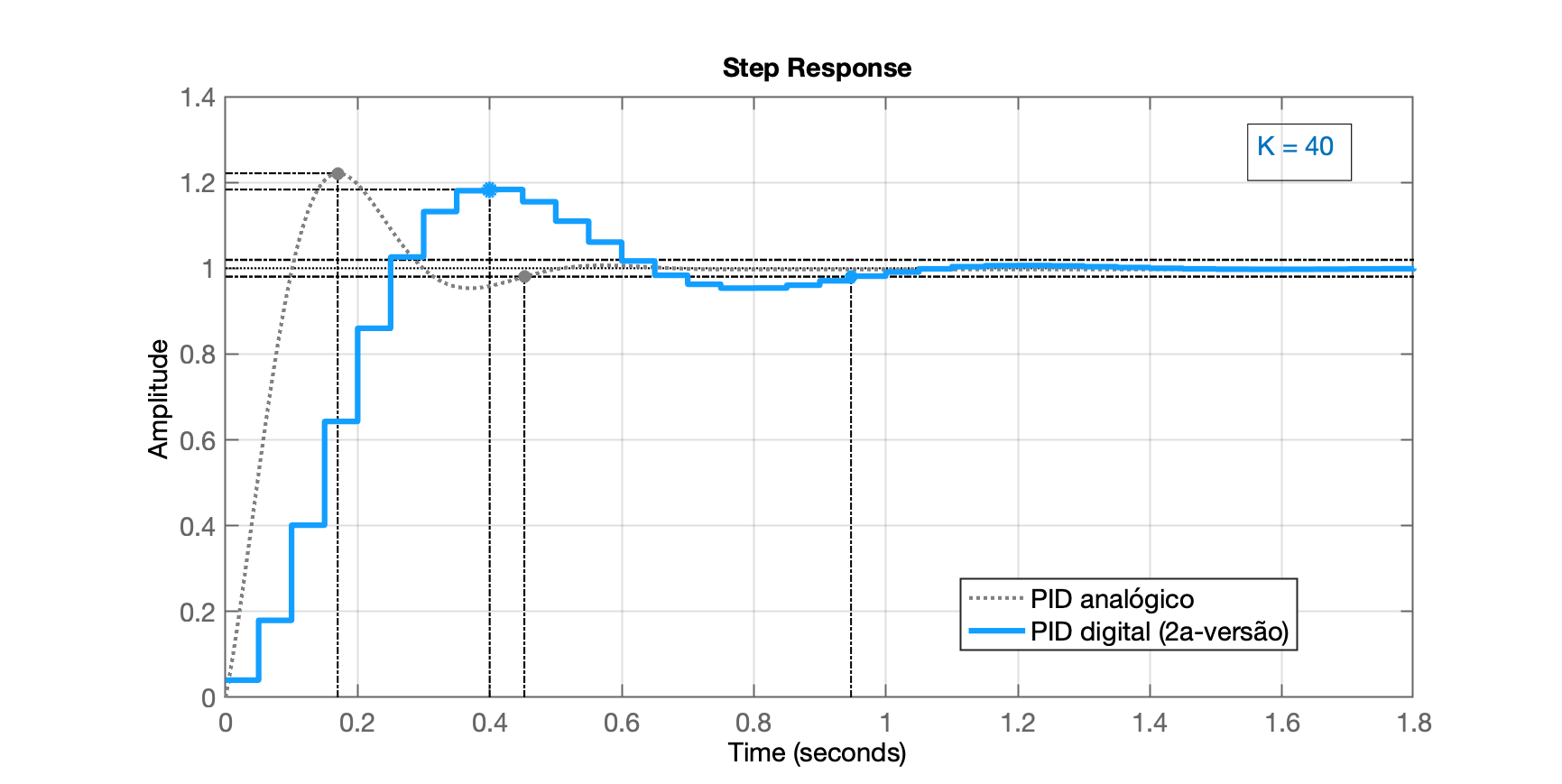
Neste caso, o tempo do pico foi deslocado (aumentou), mas o tempo de assentamento foi ligeiramente reduzido porque diminuiram as oscilações do sistema com este ganho (geral) menor.
Note que um "ajuste fino" ainda se faz necessário para esta versão digital do PID para obter melhores resultados.
Fernando Passold, em 03/06/2025