Projeto de Controlador LEAD (PD+FPB)

Aula de 11/11/2020

Projeto usando contribuição angular e script "" e "" (ambos devem estar na mesma pasta):

Note que para usar este script, algumas variáveis devem estar prontas de antemão, isto é, já devem existir no workspace do Matlab. Seriam as variaveis G (referente ao $G(s)$) e variável T (referente ao período de amostragem adotado). Você pode preparar estas variáveis antes de executar o script ou pode editar o script e incorporar estas variaveis. Neste último caso, editar o trecho entre as linhas 10 à 16 (para informar $G(s)$) e entre as linhas 19 à 21 (para informar $T$ adotado):

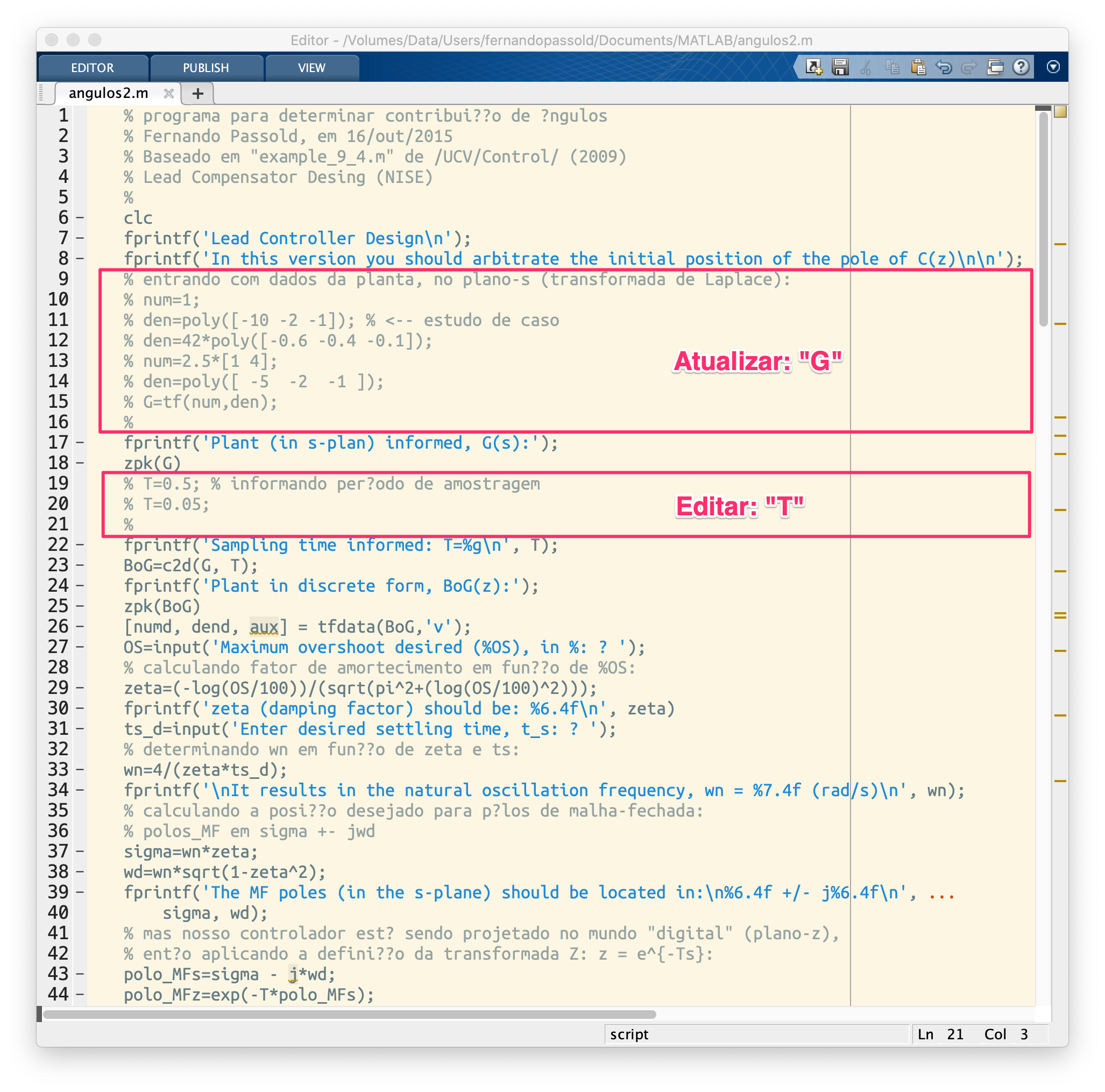
Neste caso em particular, vamos entrar com $G(s)$ e $T$ à mão:

xxxxxxxxxx
>> G=tf(1, poly ( [ -1 -2 -10 ] ) );
>> zpk(G)
 
          1
  ------------------
  (s+10) (s+2) (s+1)
 
Continuous-time zero/pole/gain model.
​
>> T=0.1;

Neste projeto, vamos alocar o pólo do Compensador Lead em $z=0,1$, manter $\%OS=10\%$ e tentar realizar o projeto para $t_s \le 1,5$ (segundos):

xxxxxxxxxx
>> angulos2
Lead Controller Design
In this version you should arbitrate the initial position of the pole of C(z)
​
Plant (in s-plan) informed, G(s):
ans =
​
          1
------------------
  (s+10) (s+2) (s+1)
​
Continuous-time zero/pole/gain model.
​
Sampling time informed: T=0.1
Plant in discrete form, BoG(z):
ans =
​
  0.00012224 (z+2.747) (z+0.1903)
  --------------------------------
  (z-0.9048) (z-0.8187) (z-0.3679)
​
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.
​
Maximum overshoot desired (%OS), in %: ? 10
zeta (damping factor) should be: 0.5912
Enter desired settling time, t_s: ? 1.5
​
It results in the natural oscillation frequency, wn =  4.5109 (rad/s)
The MF poles (in the s-plane) should be located in:
2.6667 +/- j3.6383
Localization of MF poles in the z-plane should be:
z = 0.7158 +/- j0.2726
​
Enter the position of the controller pole (z-plane): ? 0.1
Working with the temporary FTMA(z)...
Open poles = 0.904837
Open poles = 0.818731
Open poles = 0.367879
Open poles = 0.1
Open zeros = -2.74711
Open zeros = -0.190308
Angular contribution of each pole in the z-plane:
 p1 = 0.9048 --> 124.74^o
 p2 = 0.8187 --> 110.69^o
 p3 = 0.3679 --> 38.08^o
 p4 = 0.1000 --> 23.88^o
Sum of angular contribution of poles: 297.39^o
Check the figure window -> Paused (enter to continue)...
​
Angular contribution of each zero in the z-plane:
 z1 = -2.7471 --> 4.50^o
 z2 = -0.1903 --> 16.74^o
Sum of angular contribution of zeros: 21.24^o
Final angle for the zero of C(z): 96.1444^o
​
Ok, determining the position for zero of C (z)...
Final position for the Lead zero: z_c=0.7451
Updating final RL graph...
The Lead controller final result is (variable C):
ans =
​
  (z-0.7451)
  ----------
   (z-0.1)
​
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.
​
>>

Até aqui, temos as seguintes figuras geradas:

Contribuições angulares	RL final
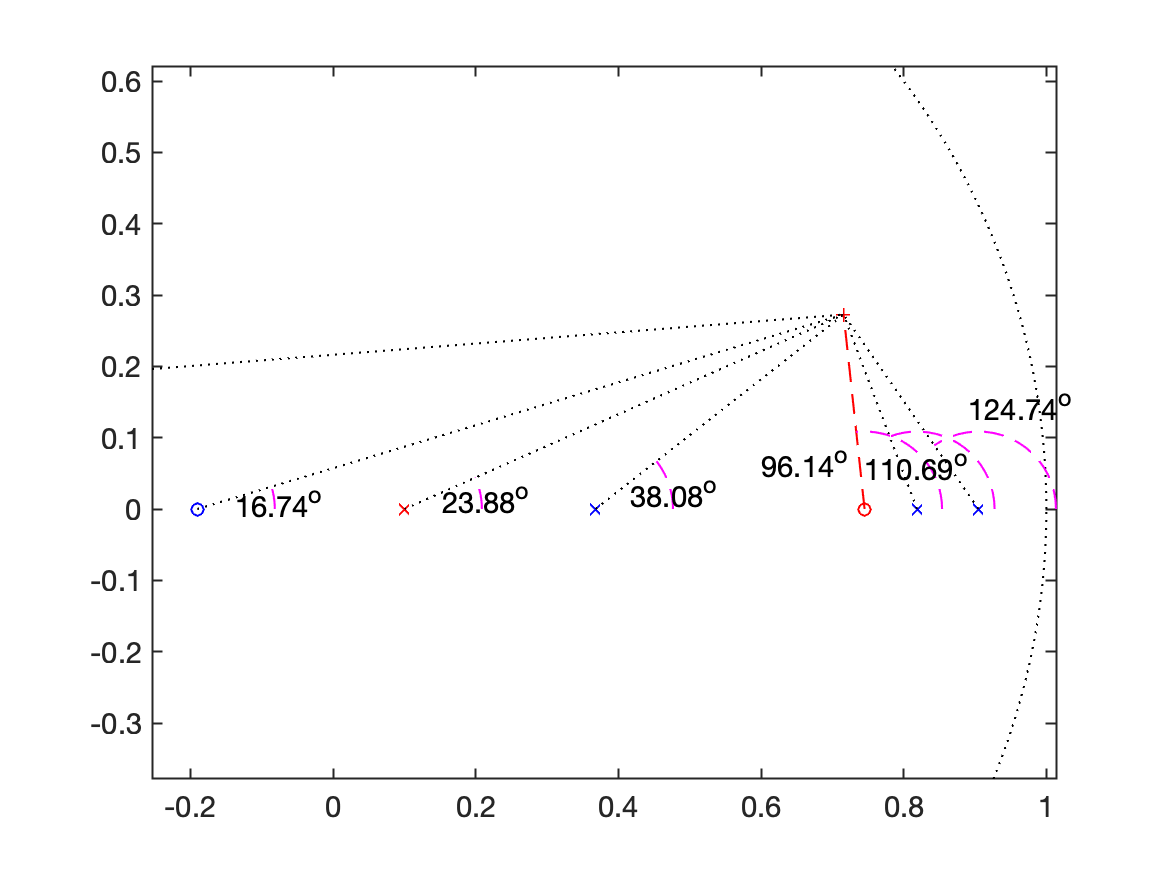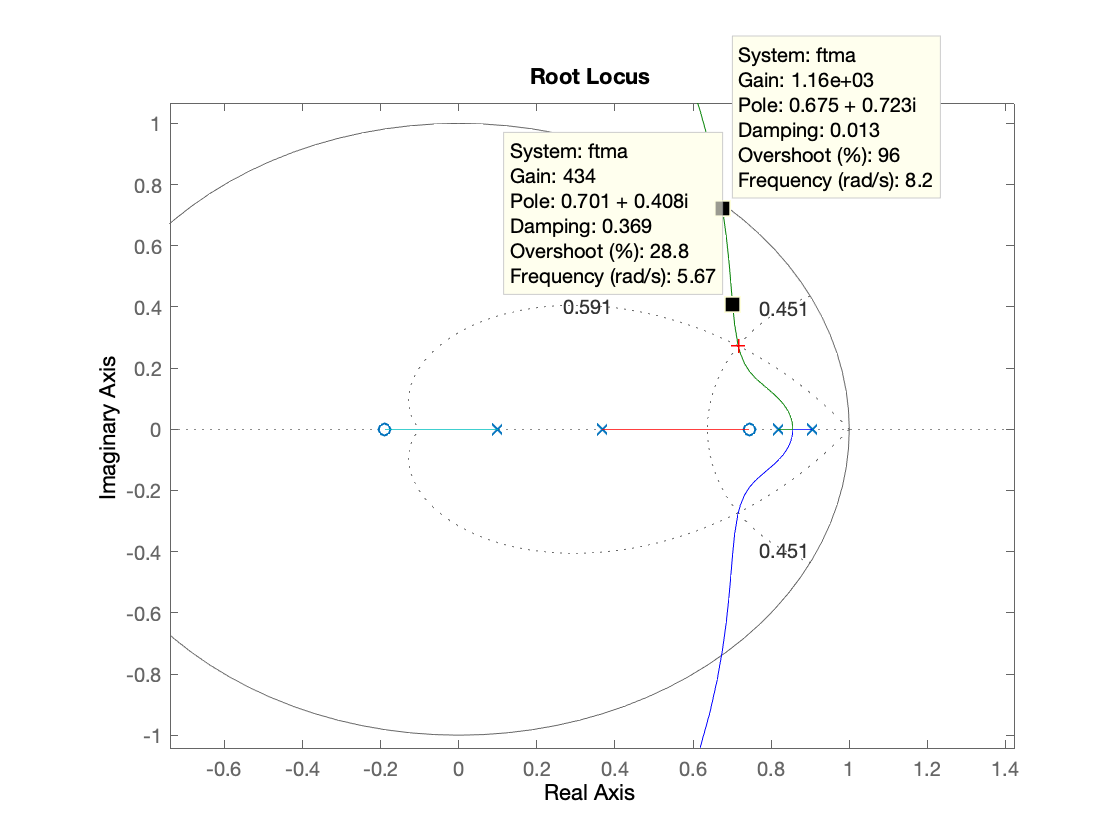Note a linha pontilha vermelha indica a posição (e ângulo) onde deveria ser localizado o pólo deste controlador.	Note que são ressaltandos 2 pontos de ganho diferentes no RL. O ganho crítico (ou máximo, $K_u \cong 1160$) e outro ponto de ganho: $K=434$ (prevendo $\%OS=28,8\%$).

O script anterior não determina o ganho que deve ser usado, apenas automatiza a determinação do local do pólo do controlador. Então, continuando o projeto:

xxxxxxxxxx
>> zpk(BoG)
​
ans =
​
  0.00012224 (z+2.747) (z+0.1903)
  --------------------------------
  (z-0.9048) (z-0.8187) (z-0.3679)
​
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.
​
>> zpk(C)
​
ans =
​
  (z-0.7451)
  ----------
   (z-0.1)
​
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.
​
>> C_Lead=C; % apenas copiando tf de uma variável para outra
>> FTMA_Lead=C_Lead*BoG;
>> figure; rlocus(FTMA_Lead)
>> hold on;
>> zgrid(zeta,0);
>> plot(real(polo_MFz), imag(polo_MFz),'r+');
>> [K_Lead, polosMF]=rlocfind(FTMA_Lead)
>> Select a point in the graphics window
selected_point =
   0.7199 + 0.2752i
​
K_Lead =
  262.9846
​
polosMF =
   0.7155 + 0.2744i
   0.7155 - 0.2744i
   0.6921 + 0.0000i
   0.0362 + 0.0000i
​
>> format compact % evitar que Matlab pule tantas linhas em branco

Gráfico do RL mostrando o ganho adotado:

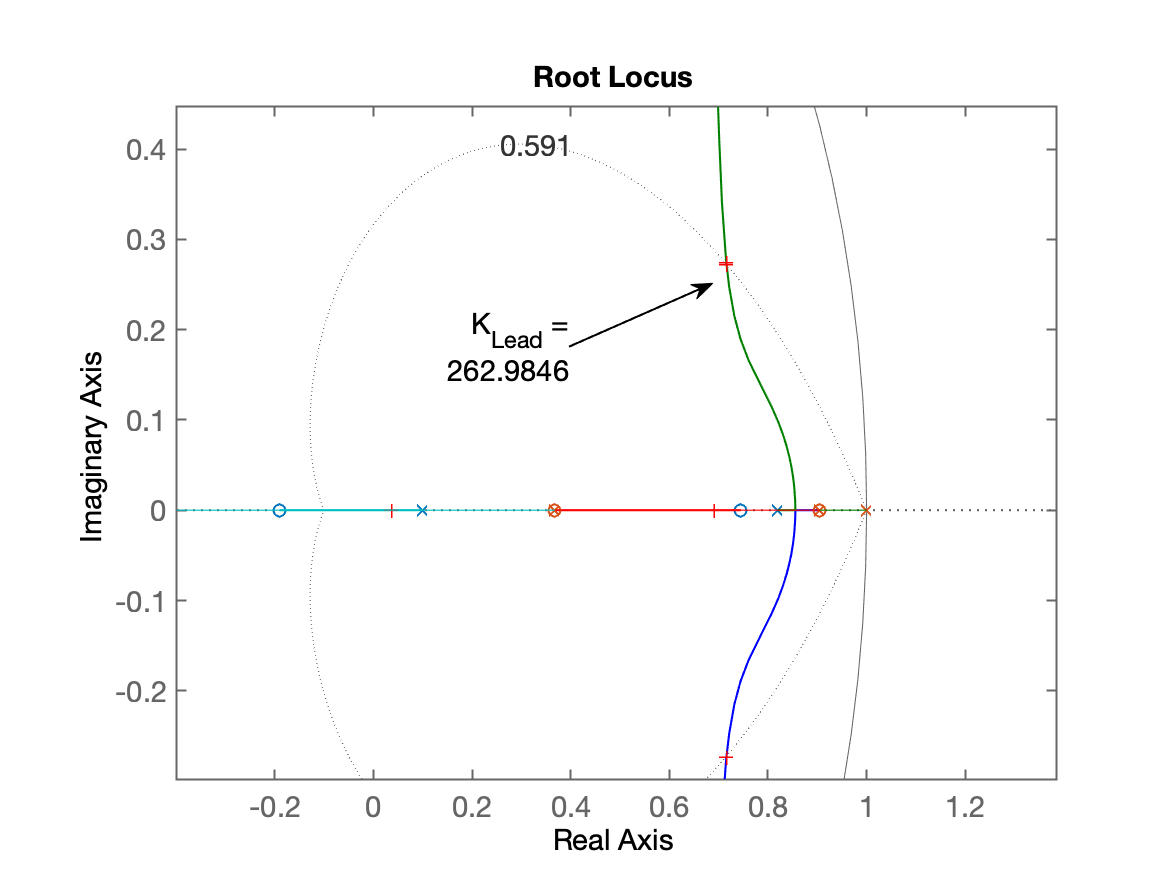
Fechando a malha com ganho obtido anteriormente:

xxxxxxxxxx
>> ftmf_Lead=feedback(K_Lead*FTMA_Lead, 1);
>> figure; step(ftmf_Lead)

Resposta ao degrau obtida para este primeiro projeto do Lead:

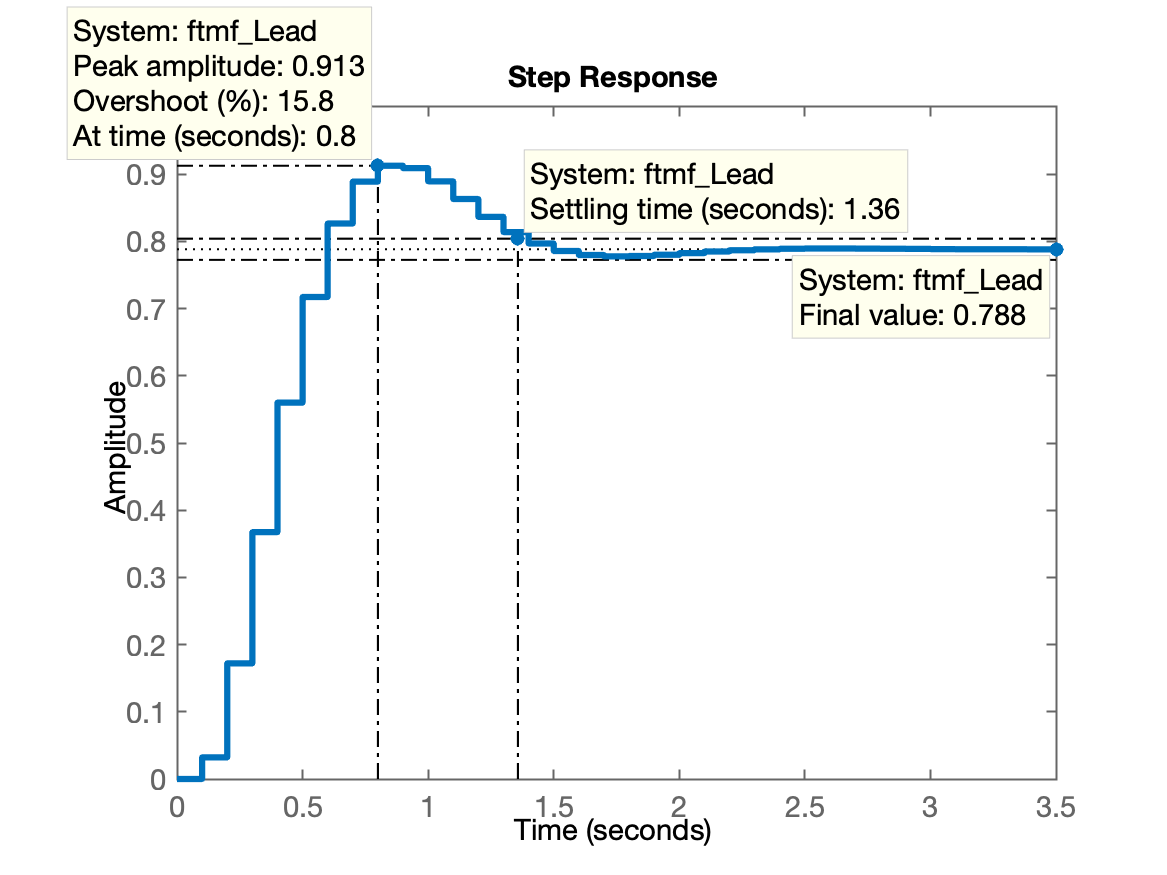
Notamos no gráfico que até foi possível atingir um $t_s < 1,5$ segundos. Mas (como esperado), o erro é de quase 25% e o overshoot em relação à referência adotada (entrada degrau unitário) poderia ser aumentado até $y[kT]\big|_{max}=1,10$ e o valor máximo (de pico) atingido, foi de 0,913. Isto significa que temos "espaço" para aumentar o ganho deste Lead.

Aumentando ganho de forma a reduzir erro em regime permanente do Lead (apesar do RL para este controlador, indicar que provavelmente o $t_s$ sofrerá um aumento):

xxxxxxxxxx
>> K_Lead2=360; % esperando baixar o erro, eventualmente aumenta ts
>> ftmf_Lead2=feedback(K_Lead2*FTMA_Lead, 1);
>> figure; step(ftmf_Lead, ftmf_Lead2)

E então as seguintes figuras são obtidas:

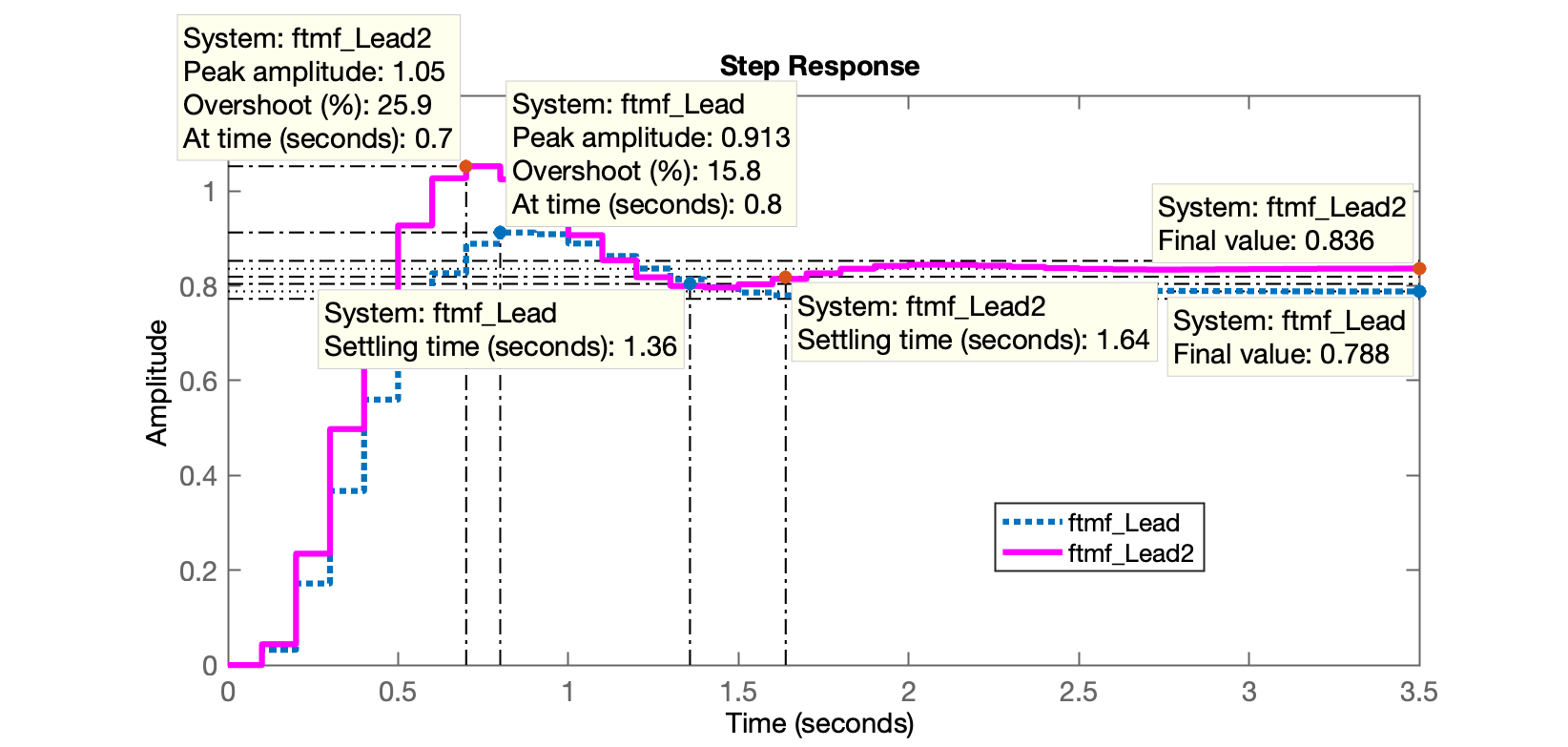
Como esperado, o overshoot aumentou (mas ainda estamos abaixo de $y[kT]<1,10$ ou $<10\%$), o erro foi um pouco reduzido (eventualmente menos que o esperado), e o tempo de assentamento, $t_s$ aumentou ligeiramente para 1,64 segundos (contra 1,36 que ocorreu antes).

Obs.: um ajuste final deste Lead poderia ser obtido usando-se o APP Control System Designer do Matlab.

Fim