Projeto de Controlador Deadbeat

Aplicando este controlador na planta adotada no "estudo de caso".

Lembrando dados da planta:

>> load planta    % carregando dados de projetos anteriores
>> zpk(G)         % eq. da planta no mundo contínuo
​
          1
------------------
  (s+10) (s+2) (s+1)
​
Continuous-time zero/pole/gain model.
​
>> T           % lembrando do período de amostragem adotado
T =
    0.1000
>> zpk(BoG)    % lembrando da "versão digital" da planta
​
  0.00012224 (z+2.747) (z+0.1903)
  --------------------------------
  (z-0.9048) (z-0.8187) (z-0.3679)
​
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.
​
>> % capturando informações dos pólos e zeros de BoG(z)
>> [numd, dend] = tfdata(BoG, 'v')
numd =
   1.0e-03 *
         0    0.1222    0.3591    0.0639
dend =
    1.0000   -2.0914    1.3749   -0.2725
>> zeros_BoG = roots(numd)
zeros_BoG =
   -2.7471
   -0.1903
>> polos_BoG = roots(dend)
polos_BoG =
    0.9048
    0.8187
    0.3679
>> % ou outra forma maios simples de obter estas mesmas informações:
>> polos_BoG=pole(BoG)
polos_BoG =
    0.9048
    0.8187
    0.3679
>> zeros_BoG=zero(BoG)
zeros_BoG =
   -2.7471
   -0.1903
>> % Especificando controlador Deadbeat que é praticamente
>> % a função inversa de BoG(z) com excessão de pólos/zeros instáveis:
>> % Iniciando a "montagem" do controlador DeadBeat:
>> C_dead=tf( poly(polos_BoG) , poly(zeros_BoG(2)), T);
zpk(C_dead)
​
  (z-0.9048) (z-0.8187) (z-0.3679)
  --------------------------------
             (z+0.1903)
​
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.
​
>> % comparando a eq. obtida notamos que:
>> % a) o grau no denominador < grau do numerador ==> sist. não causal
>> % b) os cancelamentos possíveis foram realizados:
>> zpk(BoG)    % Comparando com eq. da planta:
​
  0.00012224 (z+2.747) (z+0.1903)
  --------------------------------
  (z-0.9048) (z-0.8187) (z-0.3679)
​
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.
​
>> % Acrescentando 2 pólos que faltam ao DeadBeat
>> % Numa primeira versão (tentativa): integradores duplos:
>> % pólos duplos em z=1
>> C_dead=tf( poly(polos_BoG) , poly( [zeros_BoG(2)  1  1 ] ), T);
>> zpk(C_dead)
​
  (z-0.9048) (z-0.8187) (z-0.3679)
  --------------------------------
         (z-1)^2 (z+0.1903)
​
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.
​
>> % Infelizmente neste caso, esta versão não serve:
>> ftma_dead=C_dead*BoG;
>> zpk(ftma_dead)
​
  0.00012224 (z+2.747) (z-0.9048) (z-0.8187) (z-0.3679) (z+0.1903)
  ----------------------------------------------------------------
        (z+0.1903) (z-0.3679) (z-0.8187) (z-0.9048) (z-1)^2
​
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.
​
>> rlocus(ftma_dead)

O RL obtido para esta primeira versão do Deadbeat é mostrado à seguir:

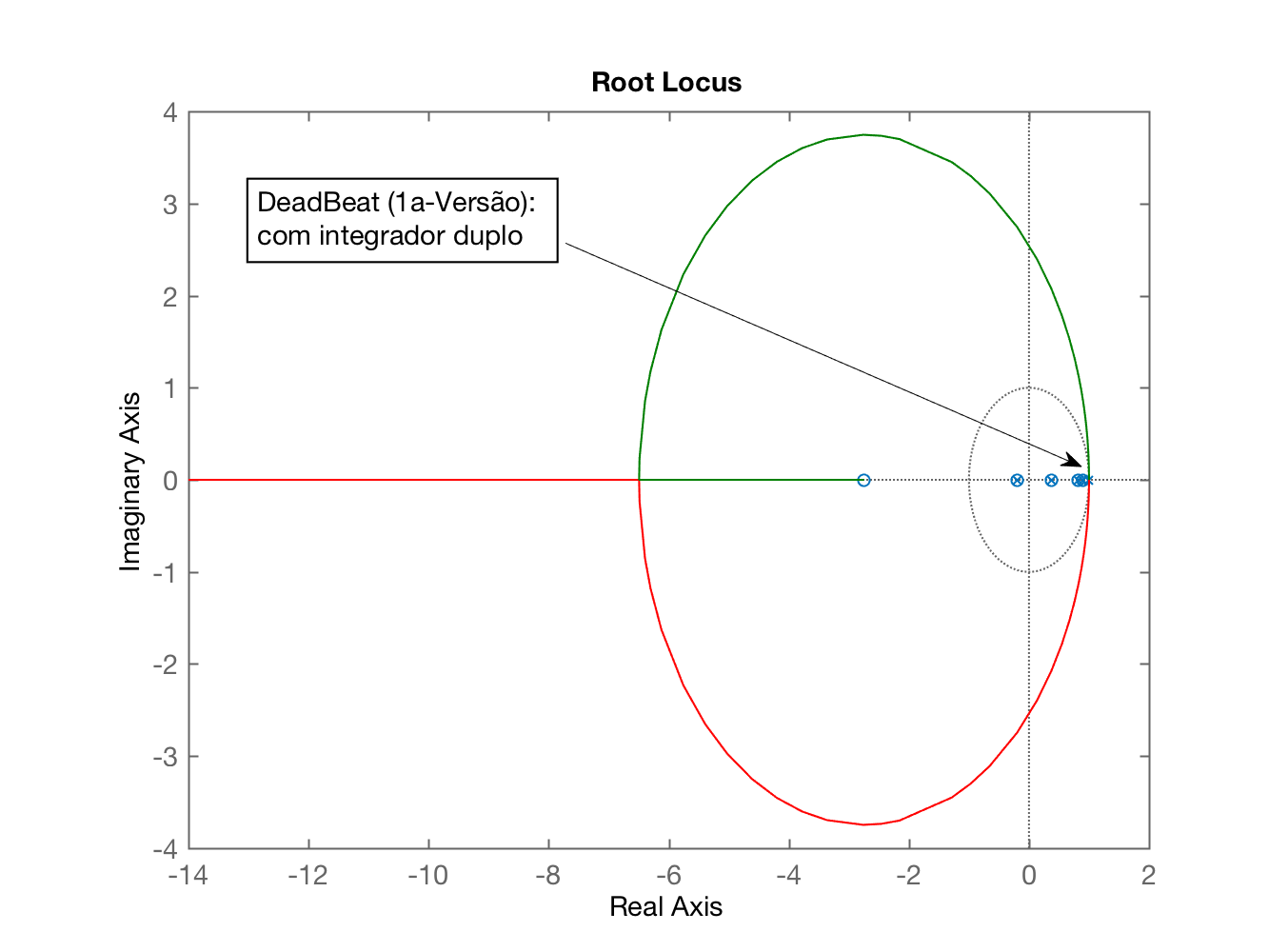
Note que muitos cancelamentos foram realizados, mas infelizmente, os 2 pólos duplos em $z=1$, criaram 2 traçados de RL que já partem da borda do círculo unitário (em $z=1$) para fora do circulo unitário para qualquer valor de ganho $K>0$. Então, esta opção é inviável, já deixa nosso sistema instável de partida.

Temos que definir uma nova posição para os 2 pólos que faltam. Pela teoria já estudada, percebemos que é útil manter um dos integradores (um dos pólos em $z=1$) para garantir erro nulo para entrada degrau, mas o outro pólo que falta definir não pode se localizar neste mesmo lugar. Este pólo deve ser estável, portanto, deve estar dentro do círculo unitário: em $z = -1 < \text{pólo extra} < 1$. Supondo que o ponto de partida (break out) para sugir no RL na metade do caminho entre estes 2 pólos, o ideal seria que este ponto de partida coincidesse com a origem do plano-$z$ para garantir o menor tempo de resposta possível (teríamos 2 pólos de malha fechada reais em $z=0$). Apostando então nesta proposta, colocamos este pólo extra, exatamente do outro lado do círculo unitário em $z=-1$.

>> % 2a-versão para o Deadbeat:
>> C_dead=tf( poly(polos_BoG) , poly( [zeros_BoG(2)  1  -1 ] ), T);
>> ftma_dead=C_dead*BoG;
>> figure; rlocus(ftma_dead)

Desta vez é gerado o seguinte RL:

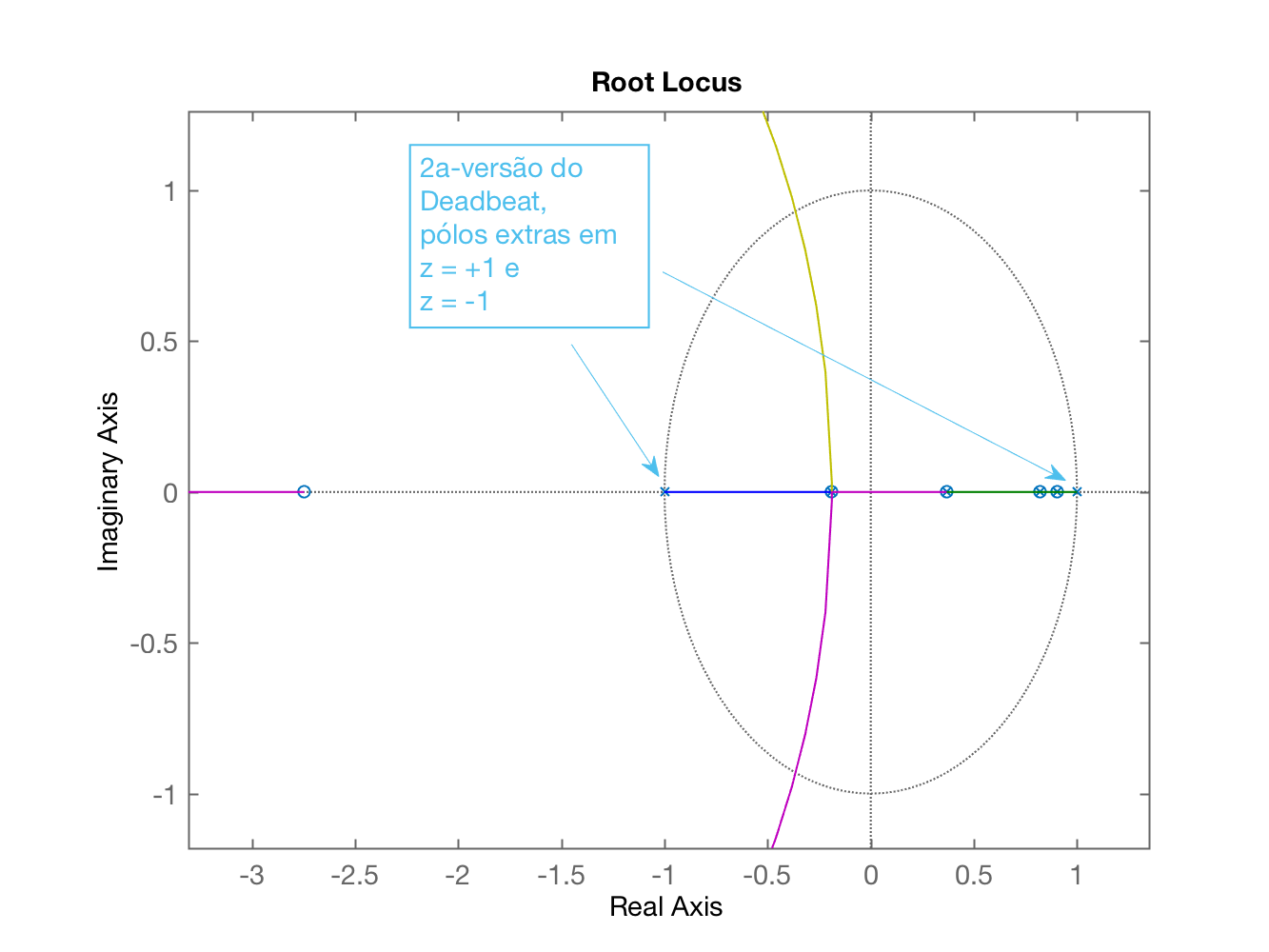
Percebemos que esta opção é bem melhor que primeira, mas que poderia ser melhorada. O que ocorre é que nesta 2a-versão termos pólos complexos dentro do circulo unitário (estáveis), mas na parte negativa real do plano-$z$, o que implica que teremos uma resposta sub-amortecida, mas mais oscilatória que o desejado, porque pólos de MF na parte real negativa do plano-$z$ implicam em alternânciad e sinal nos componentes da transformada inversa $Z$ entre cada instante de amostragem, ou seja, uma oscilação muito maior que a desejada, o que, se for possível, devemos evitar.

Surge então uma 3a-proposta: ao invés de colocar o pólo extra em $z=-1$, aproximamos um pouco mais este pólo de $z=0$. Na verdade, colocaremos este pólo exatra em $z=-0.5$. A idéia aqui é deslocar o ponto de partida do novo RL que será gerado, para a parte positiva real do plano-$z$, ou até, se tivemos "sorte", fazê-lo recair justo sobre a origem no plano-$z$. Testando:

>> % Melhorando um pouco mais o C_dead
>> C_dead=tf( poly(polos_BoG) , poly( [zeros_BoG(2)  1  -0.5 ] ), T);
>> ftma_dead=C_dead*BoG;
>> figure; rlocus(ftma_dead)

Segue o RL obtido para esta 3a-versão:

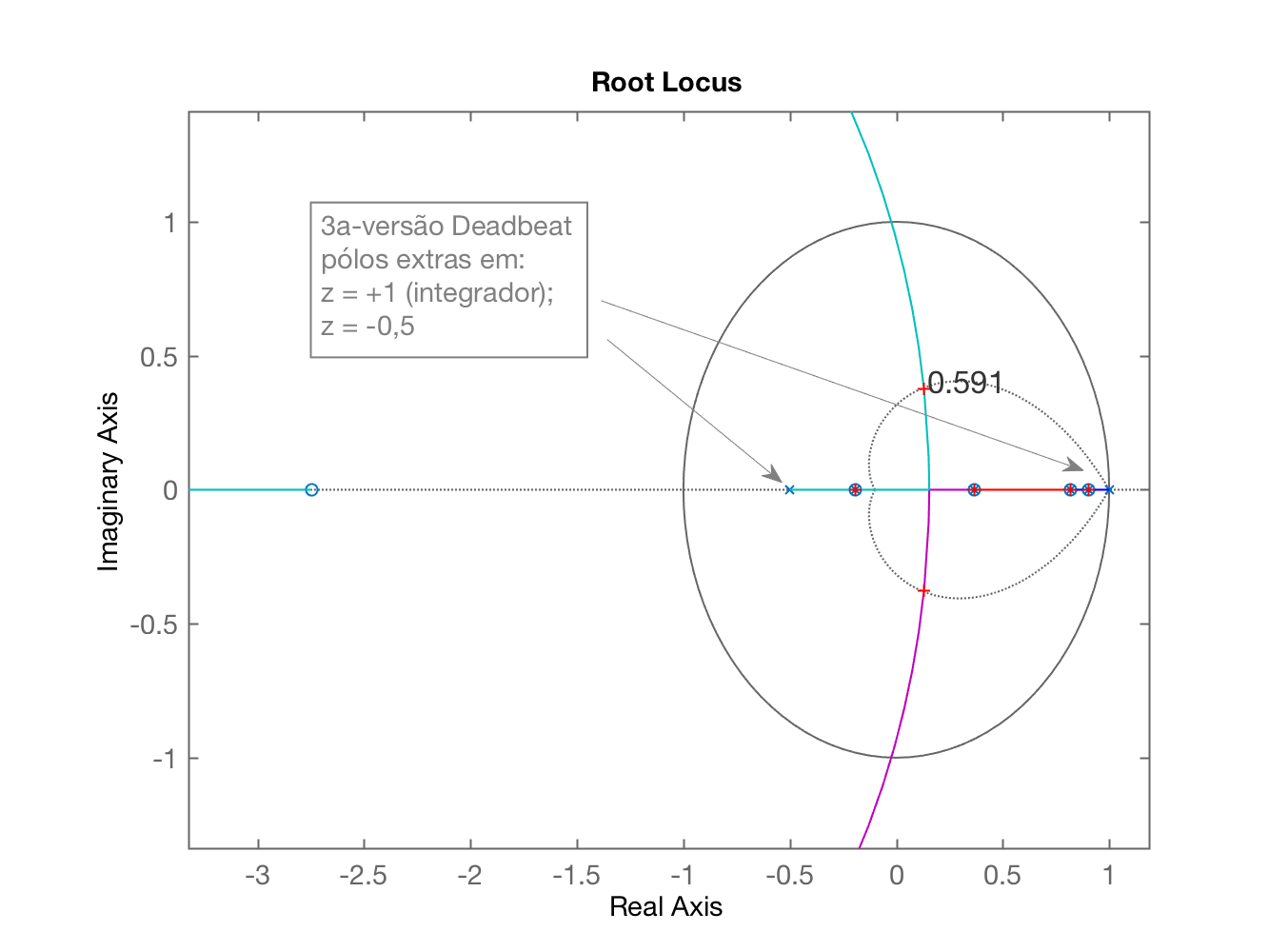
Pelo gráfico se percebe que esta solução é melhor que a 2a-versão, até sugere que talvez posicionar o pólo extra em $z=-0,7$ talvez faça com o ponto de partida coincida com a origem do plano-$z$. Mas a fim de não alongar ainda mais o tempo já consumido na proposta deste tipo de controlador, vamos ficar com esta versão, da forma como está.

>> % Então nosso controlador Deadbeat assumira os
>> % seguintes pólos e zeros:
>> zpk(C_dead)
​
  (z-0.9048) (z-0.8187) (z-0.3679)
  --------------------------------
      (z-1) (z+0.5) (z+0.1903)
​
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.
​
>> OS    % lembrando o sinalsinal que estava sendo adotado
OS =
    10
>> % sobrepondo a linha guia do \zeta para estes %OS no RL:
>> hold on; zgrid(zeta,0)
>> % Encontrando o ganho para o controlador
>> [K_dead, polosMF] = rlocfind(ftma_dead)
Select a point in the graphics window
selected_point =
   0.1385 - 0.3778i
K_dead =
   1.9619e+03
polosMF =
   0.9048 + 0.0000i
   0.8187 + 0.0000i
   0.1301 + 0.3767i
   0.1301 - 0.3767i
  -0.1903 + 0.0000i
   0.3679 + 0.0000i
>> % Fechando a malha com este ganho
>> ftmf_dead = feedback(K_dead*ftma_dead, 1);
>> figure; step(ftmf_dead)

O que gera a seguinte curva de resposta em MF para entrada degrau unitário:

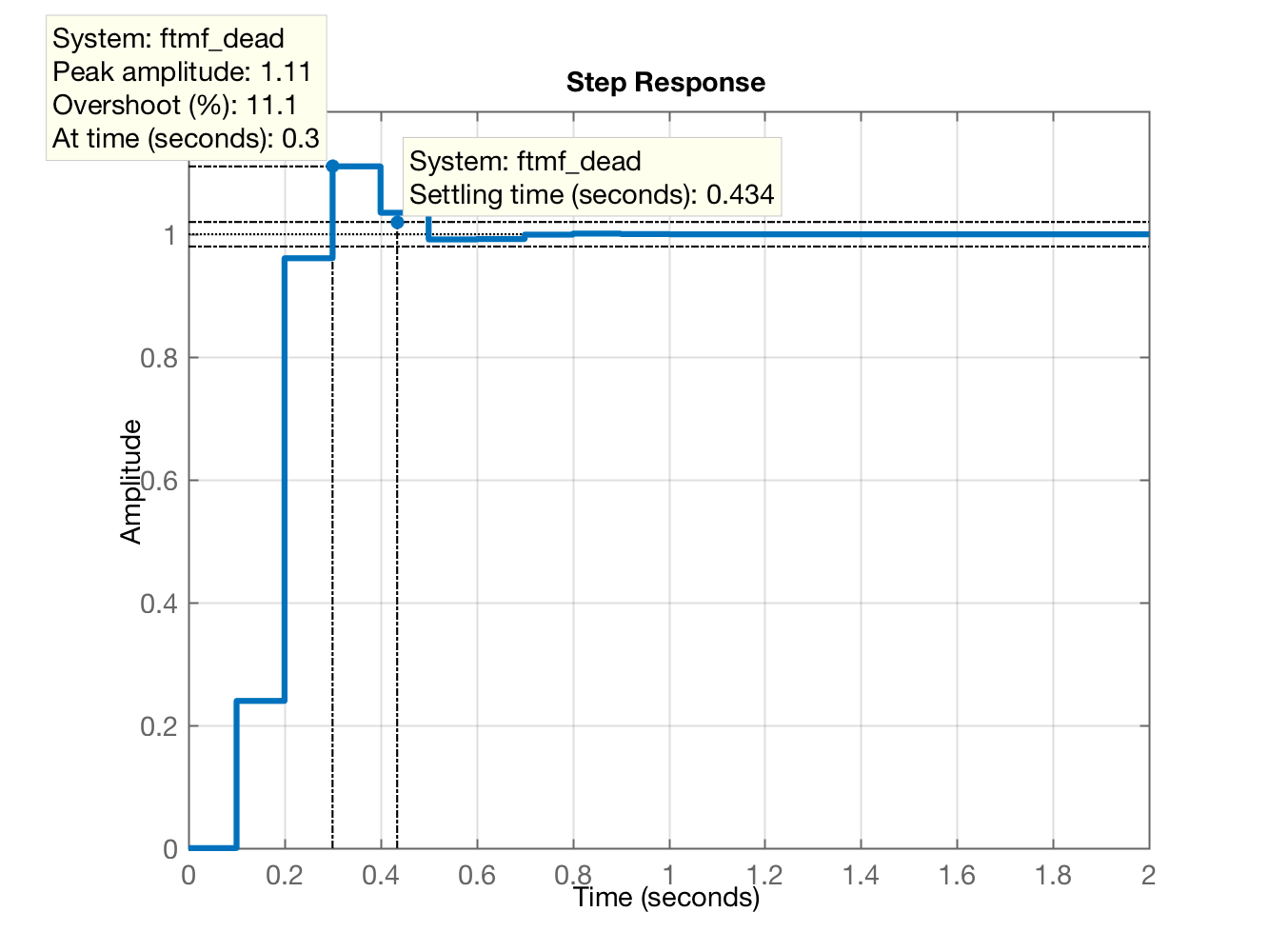
Notamos que excedemos um pouco o $\%OS$ especificado: $\%OS \le 10\%$. Um pequeno ajuste no ganho (redução do mesmo), deve corrigir este detalhe:

>> OS        % consultando %PS desejado
OS =
    10
>> K_dead    % consultado ganho originalmente adotado
K_dead =
   1.9619e+03
>> % simulando outra versão com ganho ligeiramente menor
>> ftmf_dead2 = feedback(1800*ftma_dead, 1);
>> figure; step(ftmf_dead, ftmf_dead2)
>> legend('Lead (K=1961,9)', 'Lead (K=1800)')

E obtemos então como resposta:

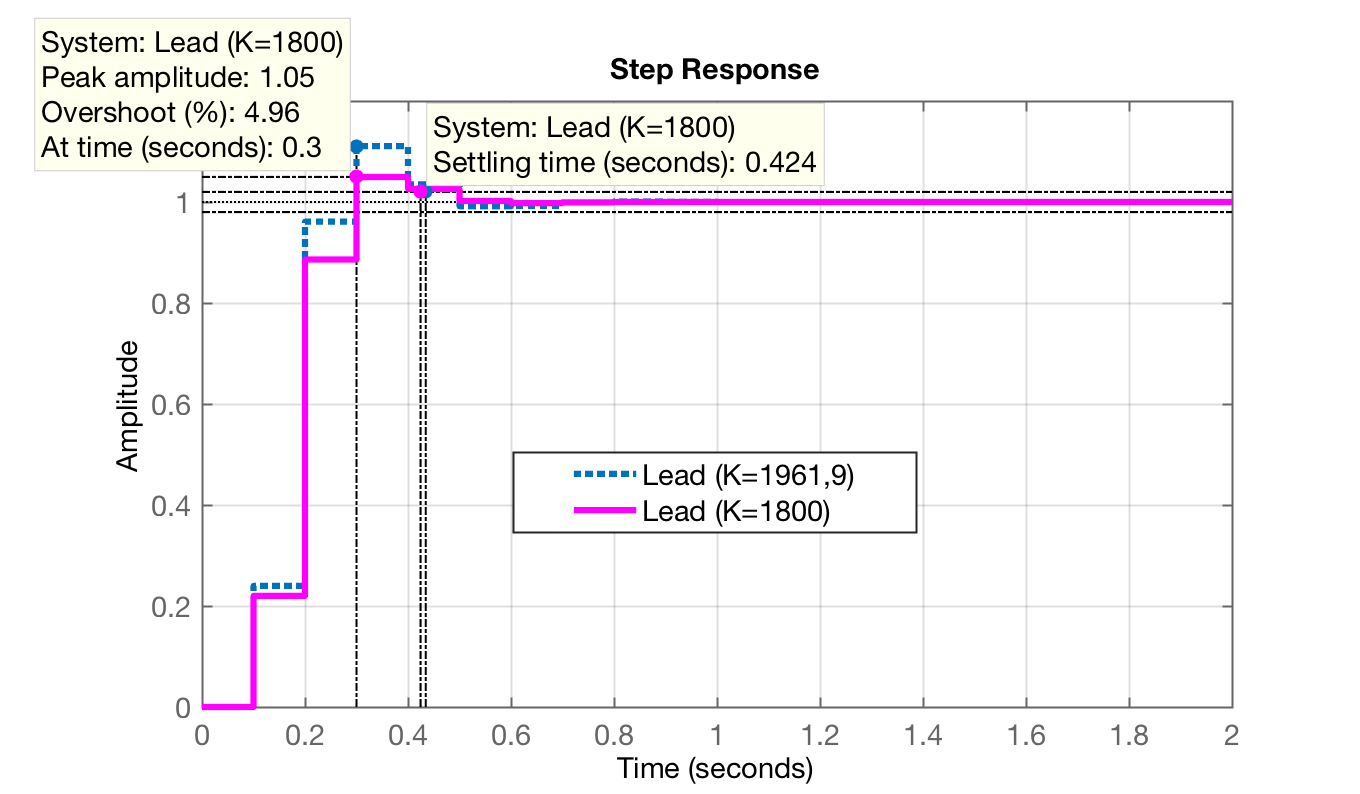
Efetivamente notamos que foi fácil restringir $\%OS \le 10\%$.

Por fim, a título de curiosidade, podemos comparar o desempenho deste controlador com outro rápido como o PD (ou Lead) já realizado anteriormente. Então:

>> figure; step(ftmf_PD, ftmf_dead)
>> legend('PD', 'DeadBeat')

E teremos o gráfico:

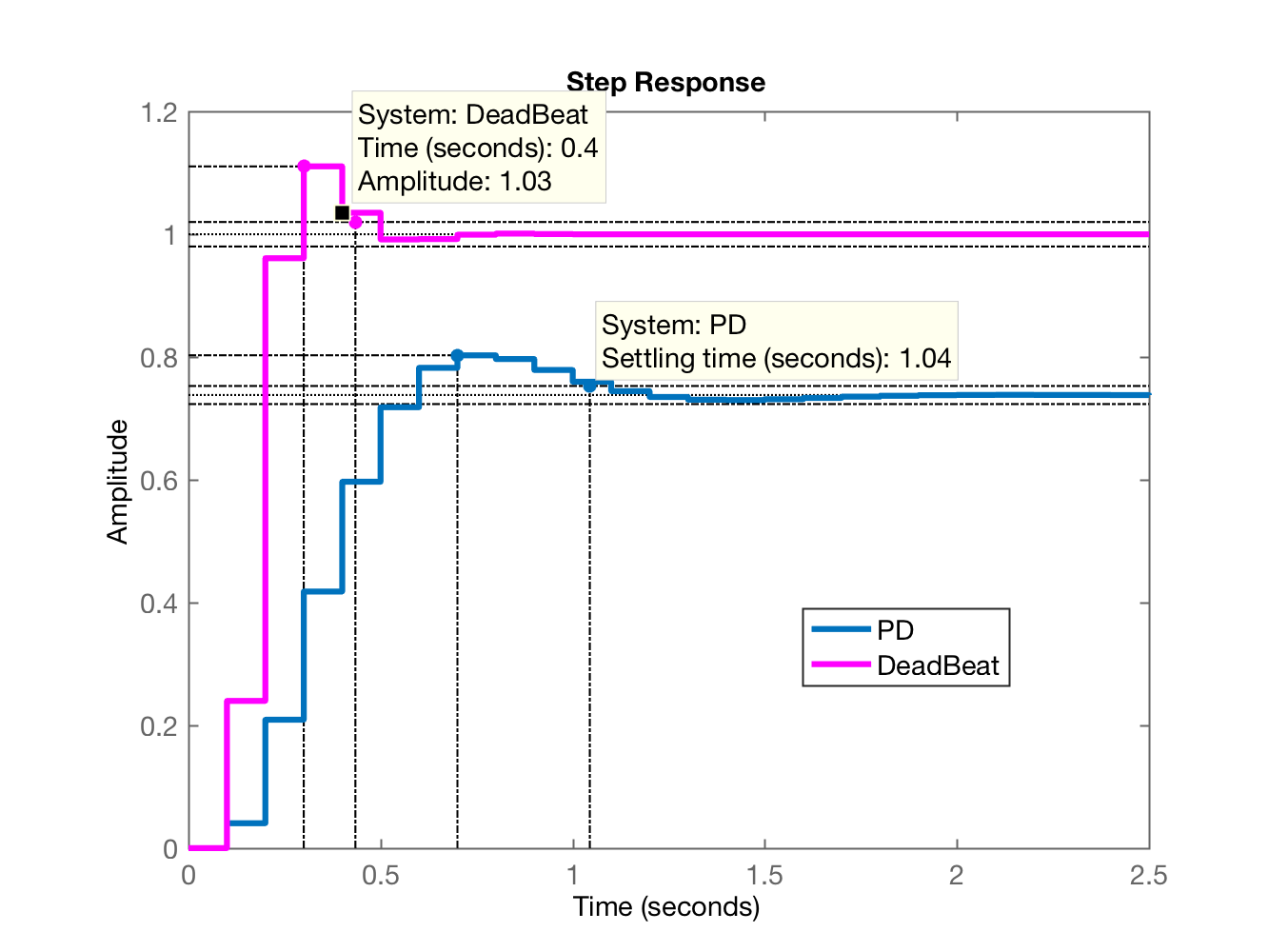
Onde podemos perceber que o controlador Deadbeat é mais rápido que o PD além de garantir erro nulo para entrada degrau (em função da presença do integrador), mesmo num caso como este, no qual não foi poss'viel cancelar todos os pólos e zeros da planta. Mas é bom é bom lembrar que este resultado não é "gratuito": isto se deve à fortes atuações (fortes amplitudes) geradas pela ação de controle, $u[kT]$ para estes tipos de controladores. Notar que o ganho do Deadbeat ficou em 1800 e o ganho do PD está em $K_{PD} = 331.6362$, isto nos dá uma ideia dos valores inicias das ações de controle de cada um destes controlares, o que significa que na vida real é altamente provavel que estes controladores "saturem" o driver de potência instalado entre o controlador e a planta.

Salvando a seção de trabalho atual para a próxim aula:

>> save planta2
>> diary off
>> quit

Arquivo planta2.mat disponivel.

Fernando Passold, em 09.06.2021