Controlador Dead-Beat

Exemplo_1

Seja uma planta definida como:

$G(s)=\dfrac{10}{(s+1)(s+10)}$

que é amostrada à $T=0,1$ segundos.

O projeto de um controlador do tipo dead-beat para esta planta fica:

xxxxxxxxxx
>> G=tf(10, poly([-1 -10]));
>> zpk(G)
​
       10
  ------------
  (s+10) (s+1)
  
>> % Amostrando a planta:
>> T=0.1;
>> BoG=c2d(G,T);
>> zpk(BoG) % verificando
​
   0.035501 (z+0.6945)
  ---------------------
  (z-0.9048) (z-0.3679)
​
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.
​
>> polos_BoG=pole(BoG) % isolando os pólos de BoG(z)
polos_BoG =
    0.9048
    0.3679
>> zeros_BoG=zero(BoG) % isolando os zeros de BoG(z)
zeros_BoG =
    -0.6945
>> % Montando a equação do Deadbeat para esta planta:
>> C_deadbeat=tf( poly(polos_BoG), poly(zeros_BoG) ,T);
>> zpk(C_deadbeat) % verificando
​
  (z-0.9048) (z-0.3679)
  ---------------------
       (z+0.6945)
​
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.
​
>> % Propositalmente até este ponto apenas cancelamos pólos e zeros
>> % mas grau do numerador > grau denominador ==> sitema irealizável
>> % Necessitamos aumentar grau do denominador ==> incluindo integrador
>> C_deadbeat=tf( poly(polos_BoG), poly([zeros_BoG 1]) ,T);
>> zpk(C_deadbeat)
​
  (z-0.9048) (z-0.3679)
  ---------------------
    (z-1) (z+0.6945)
​
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.
​
>> % Calculando FTMA(z)
>> ftma_deadbeat=C_deadbeat*BoG;
>> zpk(ftma_deadbeat)
​
  0.035501 (z+0.6945) (z-0.9048) (z-0.3679)
  -----------------------------------------
   (z+0.6945) (z-0.9048) (z-1) (z-0.3679)
​
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.
​
>> % Usando função "minreal()" do MATLAB para forçar
>> % cancelamento de pólos e zeros
>> ftma_deadbeat2=minreal(ftma_deadbeat, 1E-4);
>> zpk(ftma_deadbeat2)
​
  0.035501
  --------
   (z-1)
​
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.
​
>> % Confirmando o RL final com o controlador
>> figure; rlocus(ftma_deadbeat)

RL para o Controlador Deadbeat:

RL do Controlador Deadbeat	RL desejado (implicações)
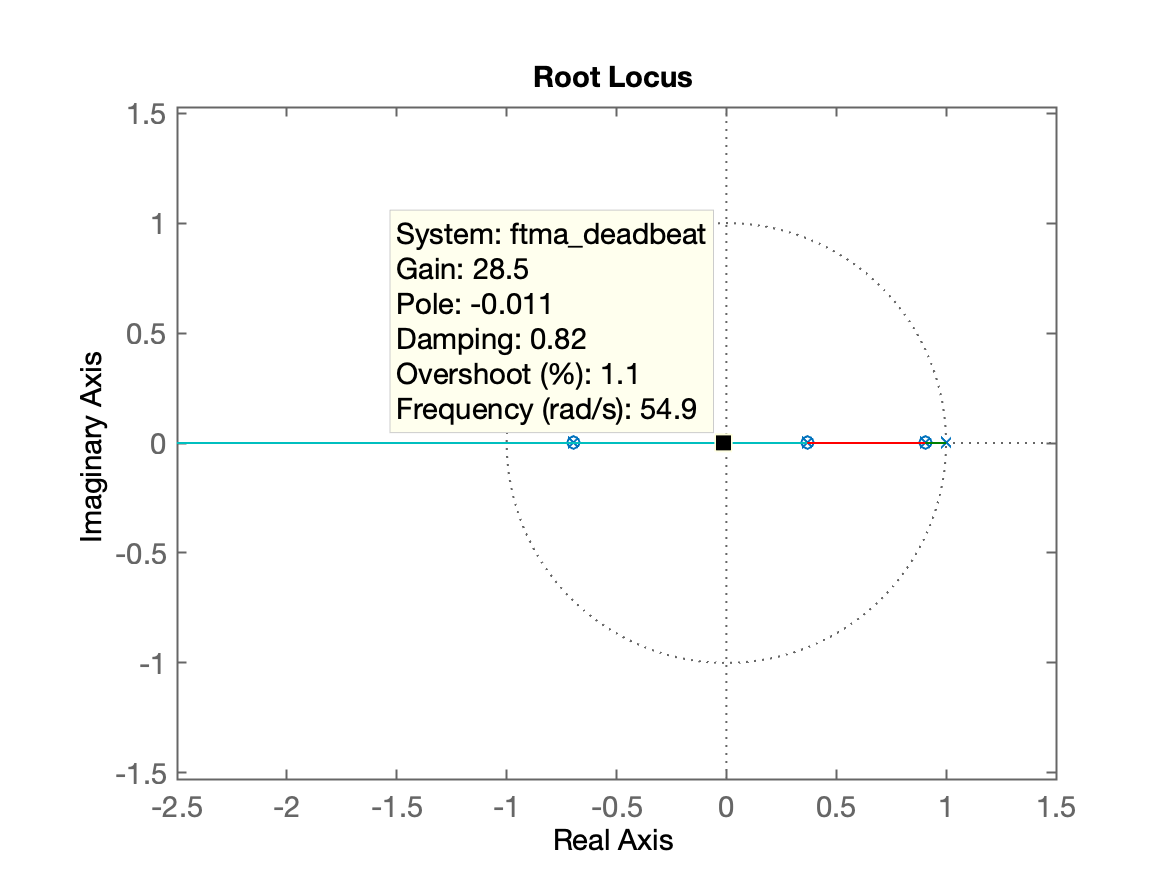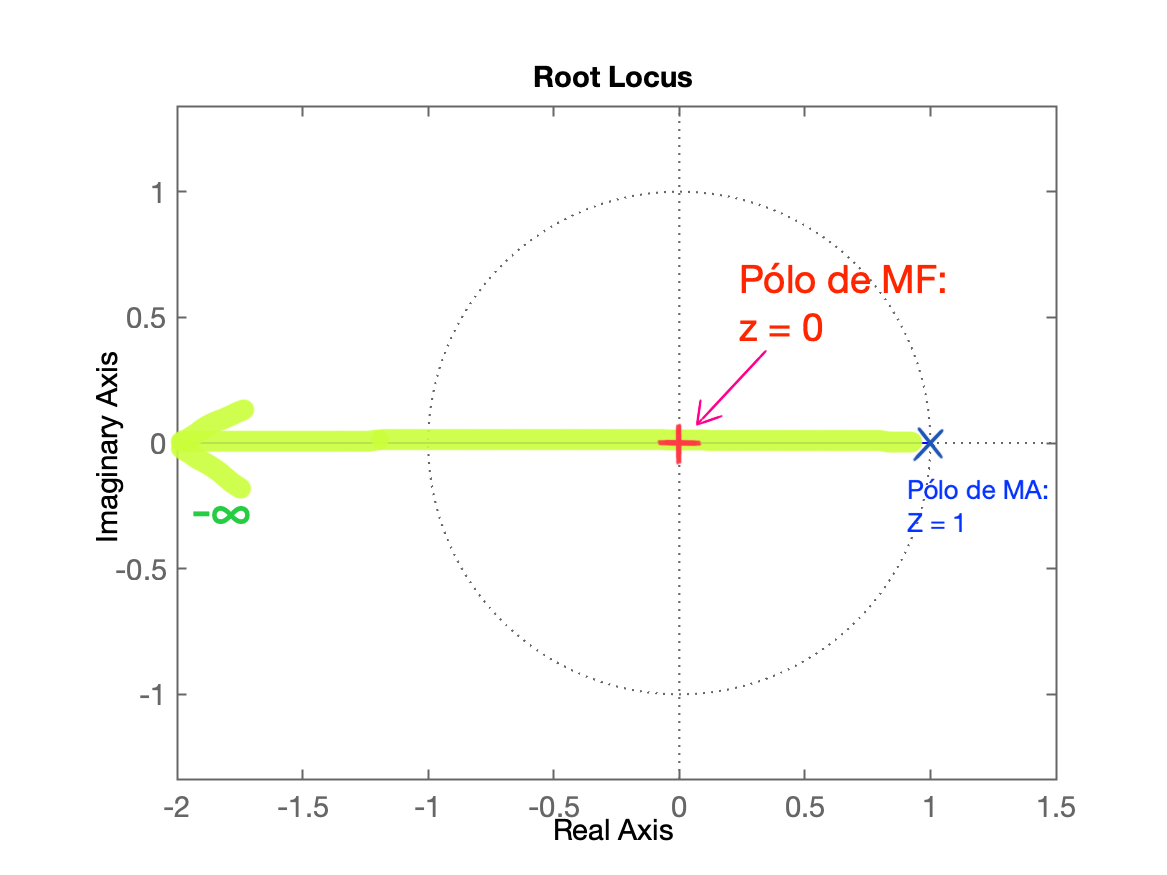Obs.: Note os cancelamentos pólos/zeros ocorridos.	Posição do ganho.

Pela teoria vista, é desejado que:

$FTMA(z)=\dfrac{1}{(z-1)}$

Então definimos o ganho do controlador para garantir isto:

xxxxxxxxxx
>> % Definindo ganho do controlador
>> K_deadbeat=1/0.035501
K_deadbeat =
    28.1682
>> % fechando a malha e confirmando resposta rápida
>> ftmf_deadbeat=feedback(K_deadbeat*ftma_deadbeat, 1);
>> figure; step(ftmf_deadbeat)

Resposta ao degrau obtida para controlador deadbeat:

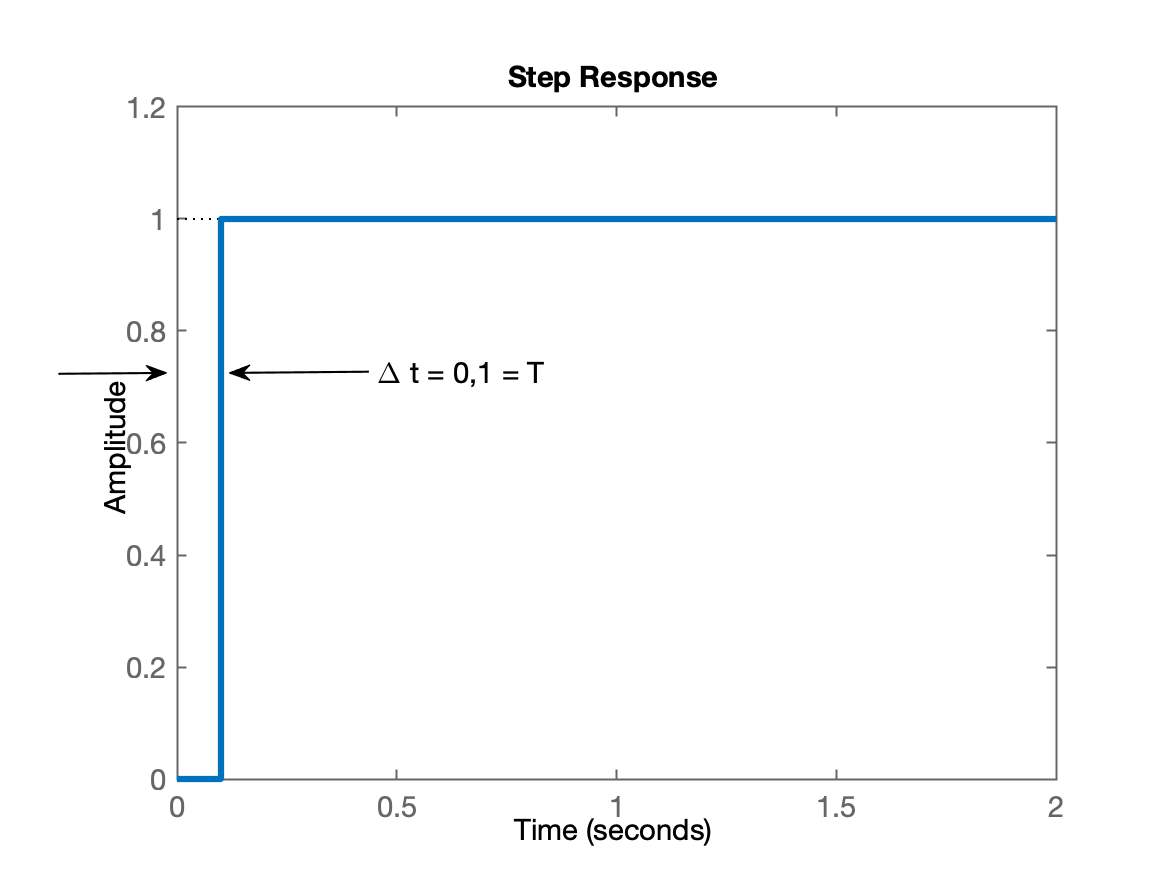
Ou seja, a planta à partir de $k=1$ (segunda amostra) já estava em regime permamente.

xxxxxxxxxx
>> % Note como ficou a FTMF(z) com este controlador
>> zpk(ftmf_deadbeat)
​
        (z+0.6945) (z-0.9048) (z-0.3679)
---------------------------------------------
  (z+0.6945) (z-0.9048) (z-0.3679) (z-1.17e-05)
​
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.
​
>> % ou usando a função "minreal()" do Matlab para enfatizar
>> % os cancelamentos pólos/zeros que ocorreram
>> ftmf_deadbeat2=minreal(ftmf_deadbeat,1E-4);
>> zpk(ftmf_deadbeat2)
​
    0.99999
------------
  (z-1.17e-05)
​
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.
​
>>

Note que praticamente obtivemos o tipo de equação desejada:

$FTMF(z)=\dfrac{1}{z}$

Apesar da planta entrar em regime permanete (e sem erro) à partir da segunda amostra ($k=1$), não observamos ainda as amplitudes geradas para esta ação de controle.

Verificando as amplitudades geradas por esta ação de controle:

xxxxxxxxxx
>> aux_deadbeat=K_deadbeat*C_deadbeat/(1+K_deadbeat*ftma_deadbeat);
>> figure; step(aux_deadbeat)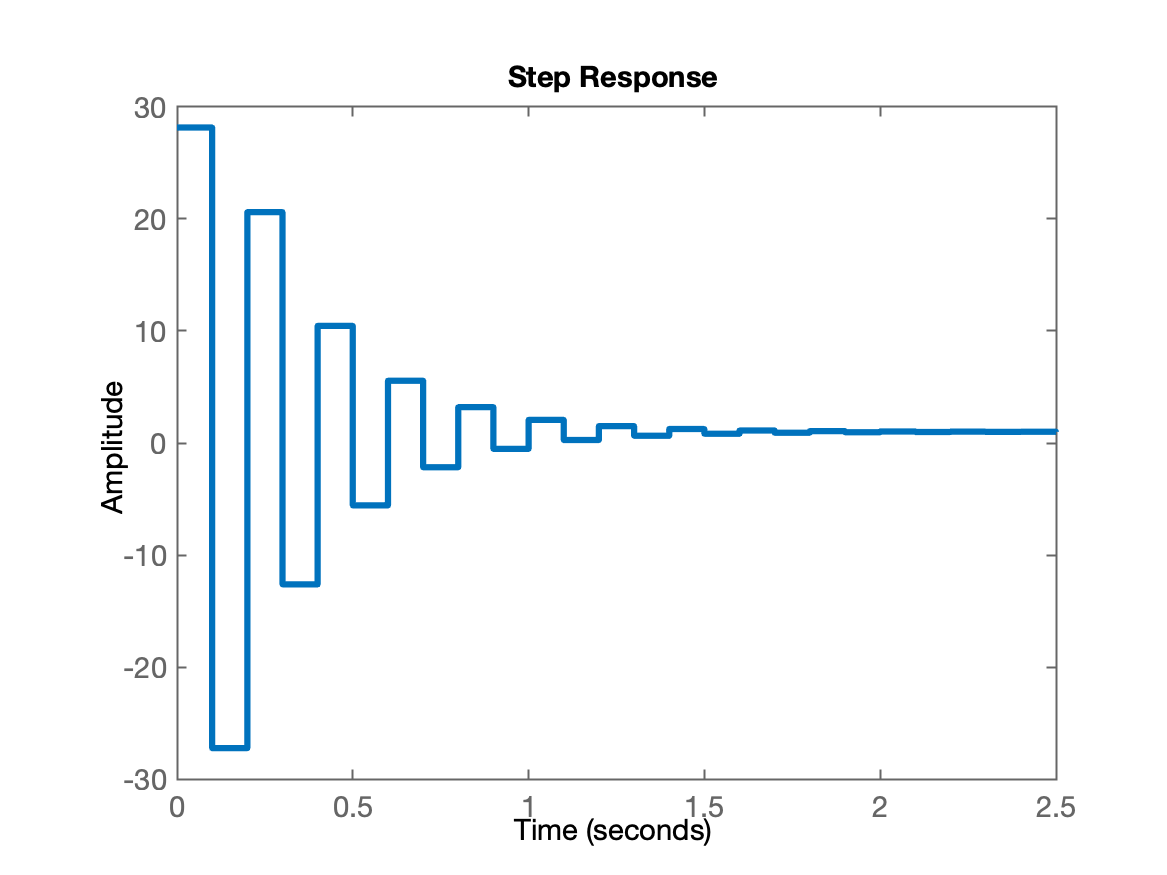

Comparando com Controlador Proporcional

Não temos como comparar estas amplitudes com as que seriam geradas por um controlador proporcional. Então segue rápido projeto de Controlador Proporcional para esta planta:

xxxxxxxxxx
>> OS=20; % supondo overshoot máximo de 20%
>> zeta = (-log(OS/100))/(sqrt(pi^2 + (log(OS/100)^2)));
>> hold on
>> zgrid(zeta,0)
>> [Kp, polosMF]=rlocfind(BoG)
Select a point in the graphics window
selected_point =
   0.5361 + 0.4558i
Kp =
    6.1144
polosMF =
   0.5278 + 0.4528i
   0.5278 - 0.4528i
>> ftmf_Kp=feedback(Kp*BoG, 1);
>> figure; step(ftmf_Kp)

RL p/Controlador Proporcional	Resposta ao Degrau Controlador Proporcioanl

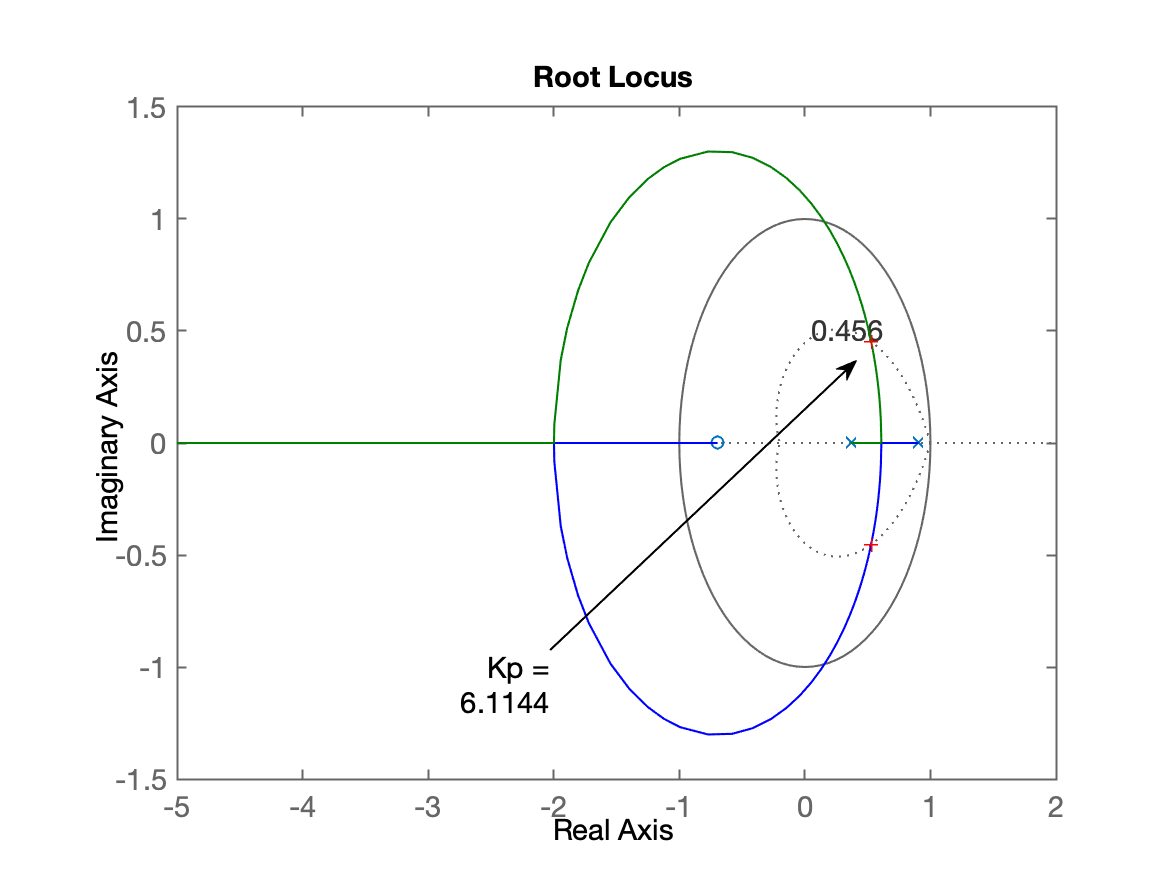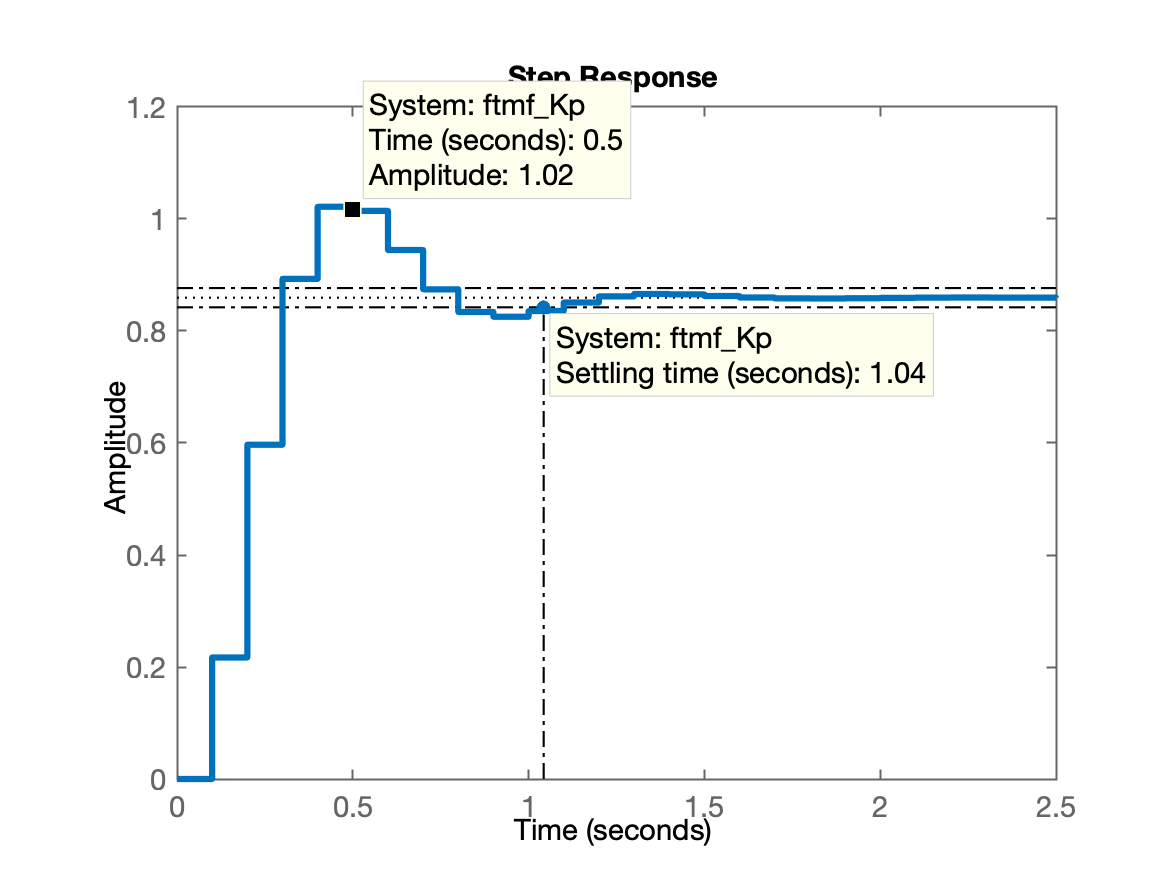Voltando à comparação das amplitudes de ações de controle geradas por diferentes controladores...

xxxxxxxxxx
>> % Calculando amplitude ação do Controlar Proporcional
>> aux_Kp=Kp/(1+Kp*BoG);
>> % Comparando as amplitudades das ações de controle
>> figure; step(aux_Kp, aux_deadbeat)

Gráfico das amplitudes das ações controle para Controlador Proporcional e Deabeat:

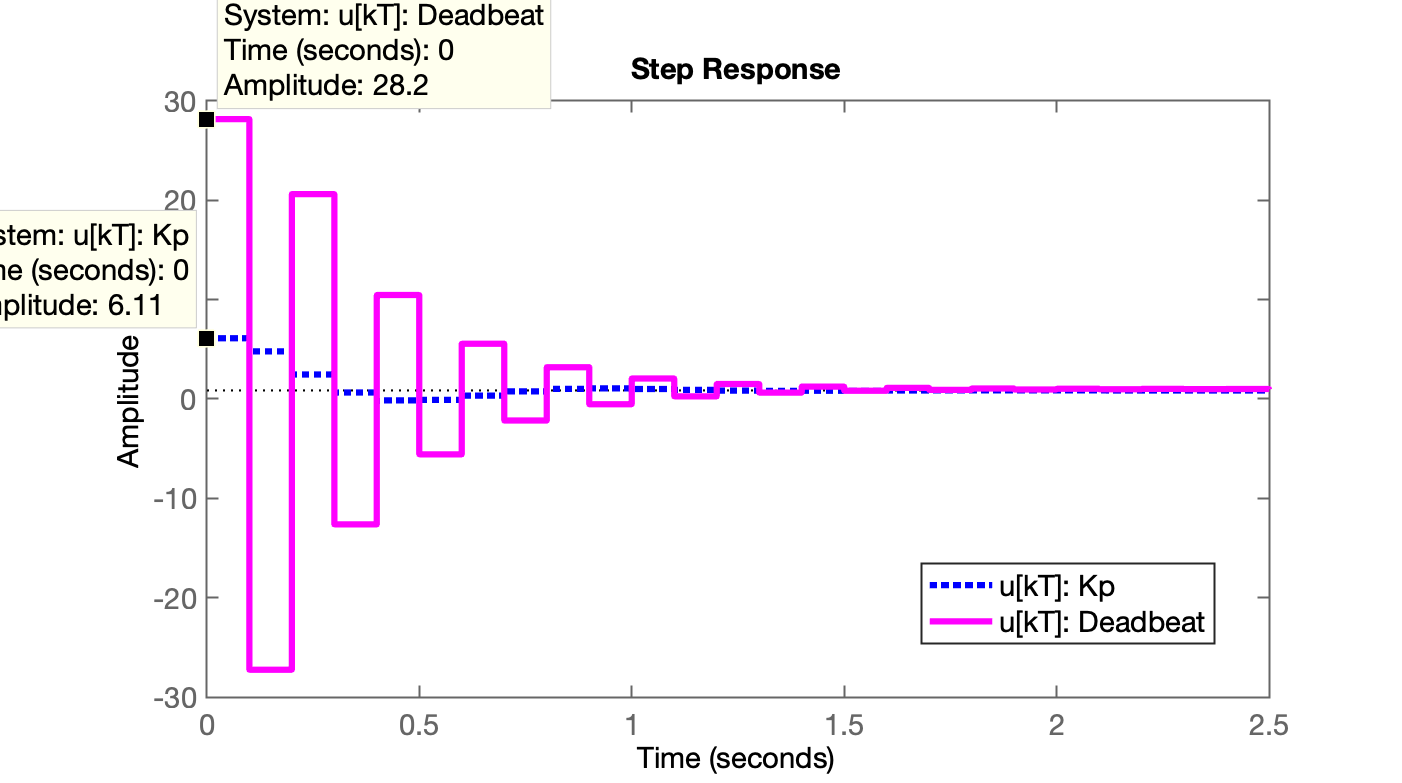
Repare que o controlador deadbeat gera expressivas ações de controle, quase $5 \times$ superiores às de um controlador proporcional:

xxxxxxxxxx
>> 28.2/6.11
ans =
    4.6154
>>

Fim